Evidence of sp2-like Hybridization of Silicon Valence Orbitals in Thin and Thick Si Grown on α-Phase Si(111)√3 × √3R30°-Bi
Abstract
:1. Introduction
2. Materials and Methods
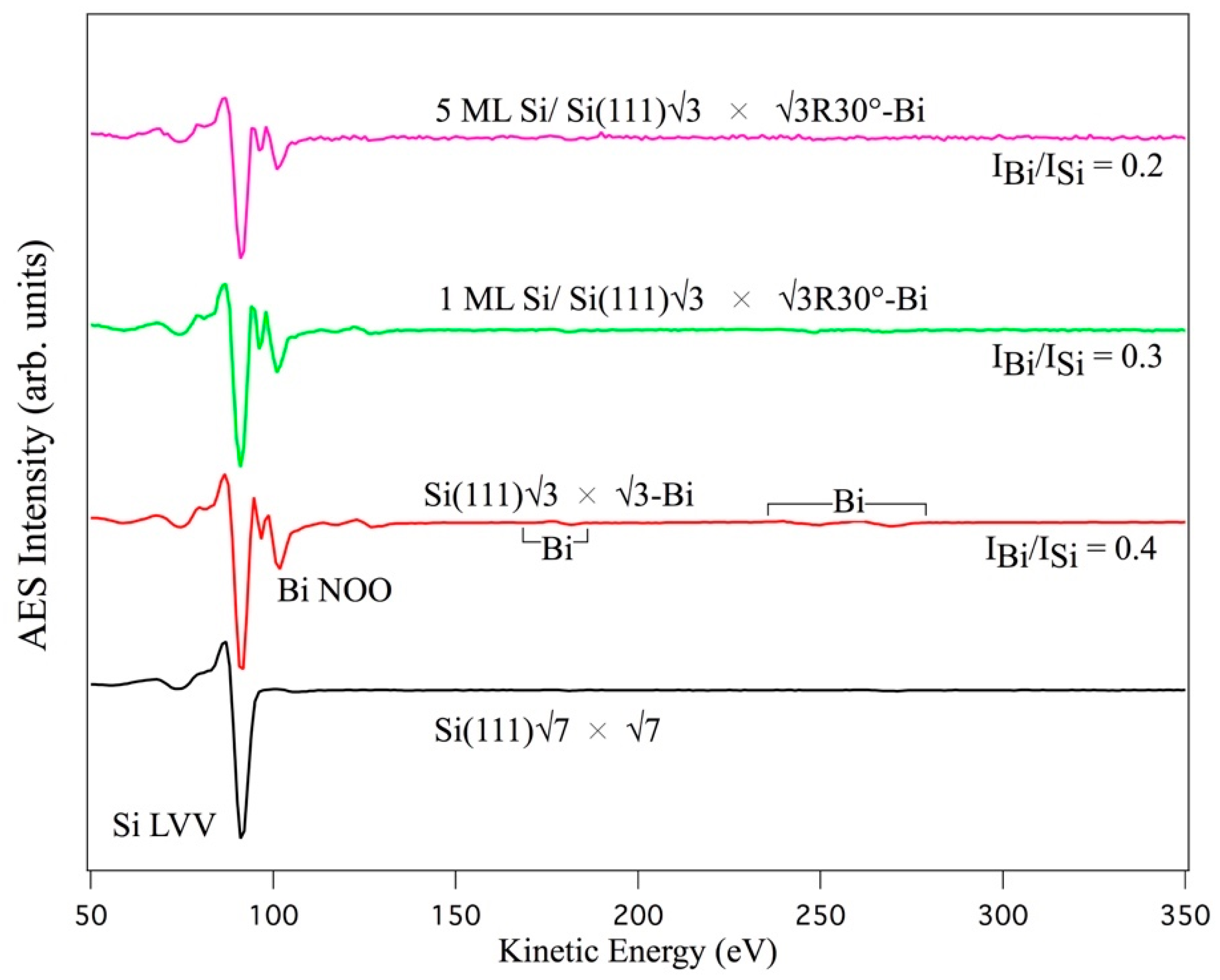
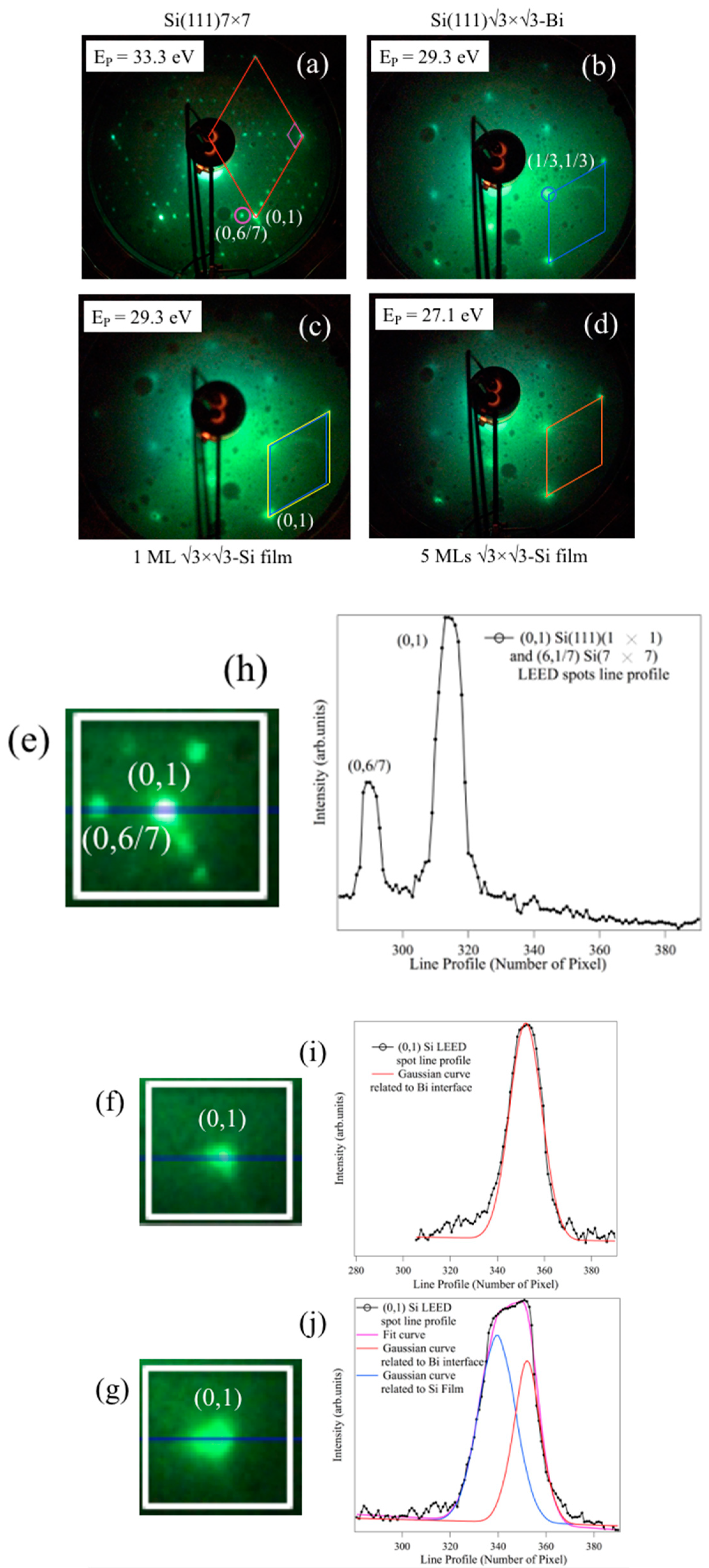
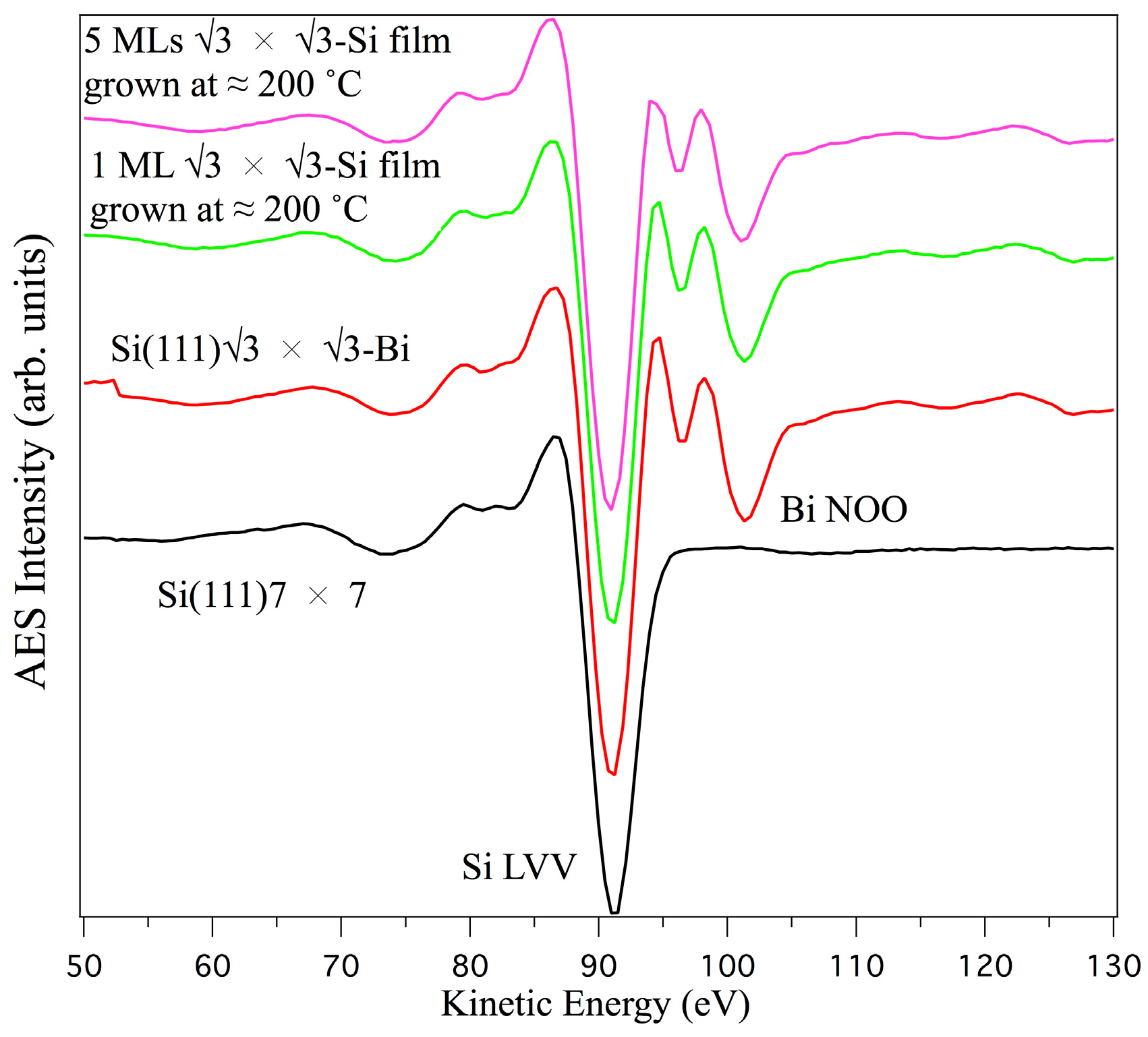
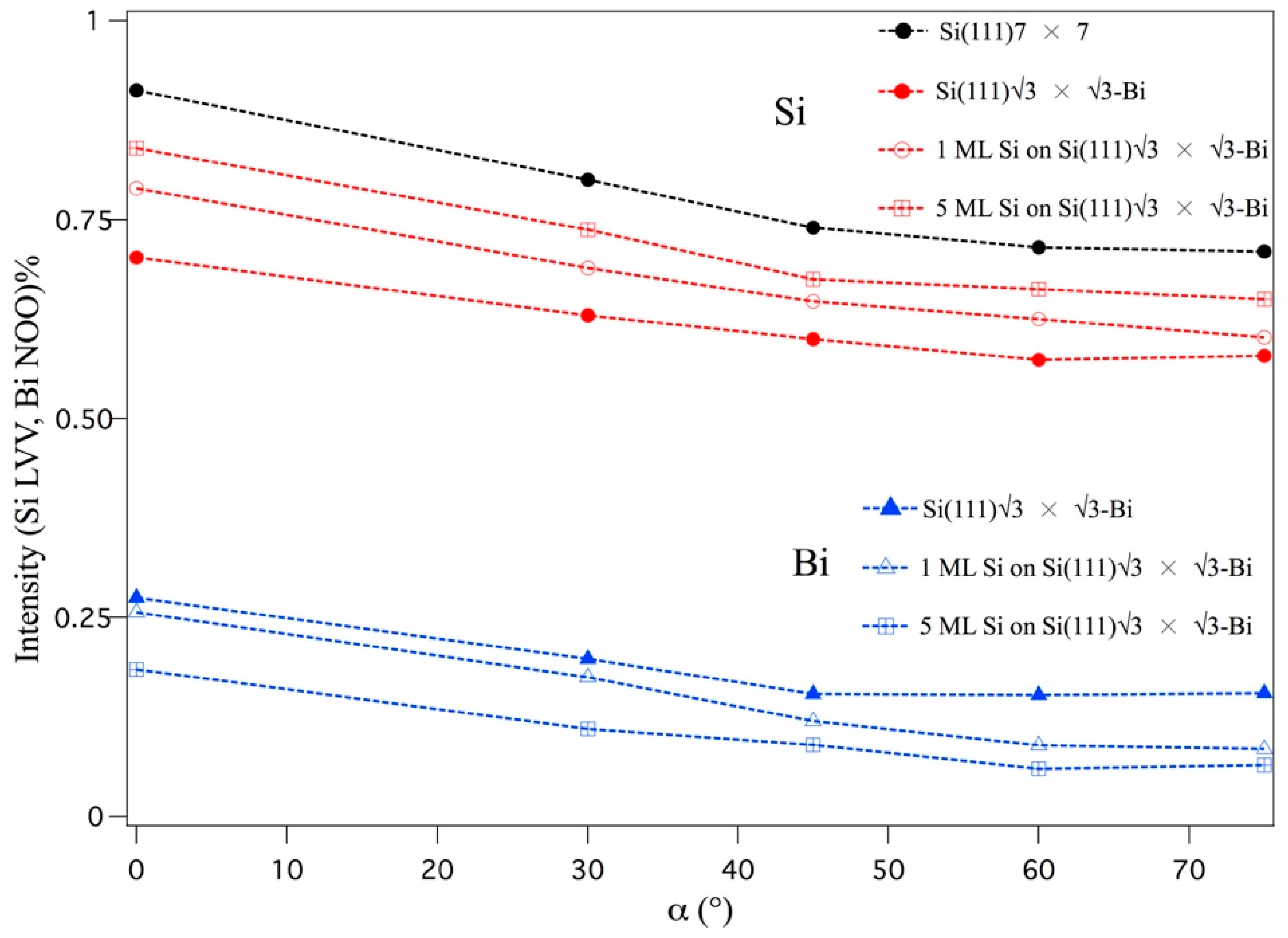
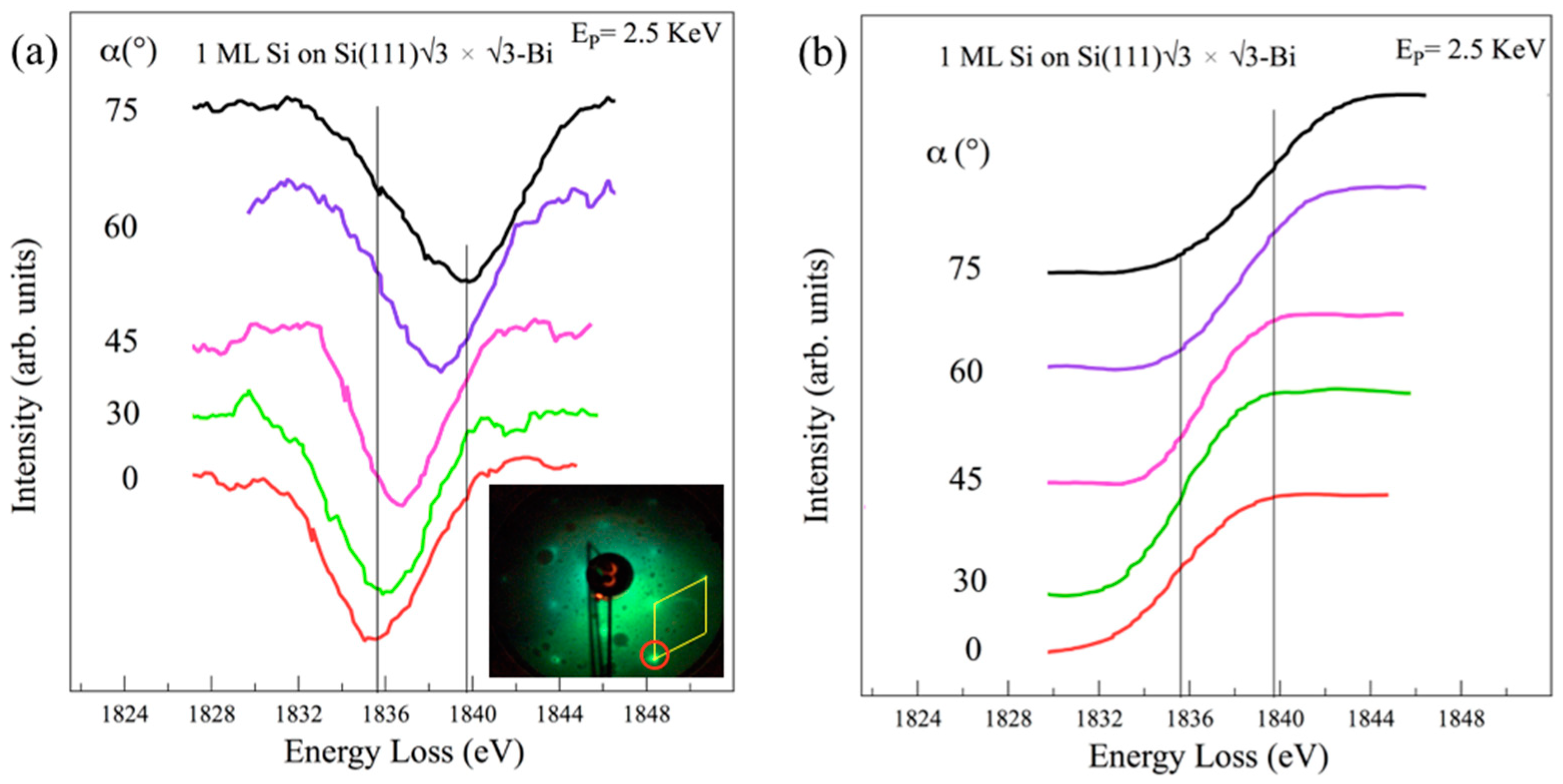
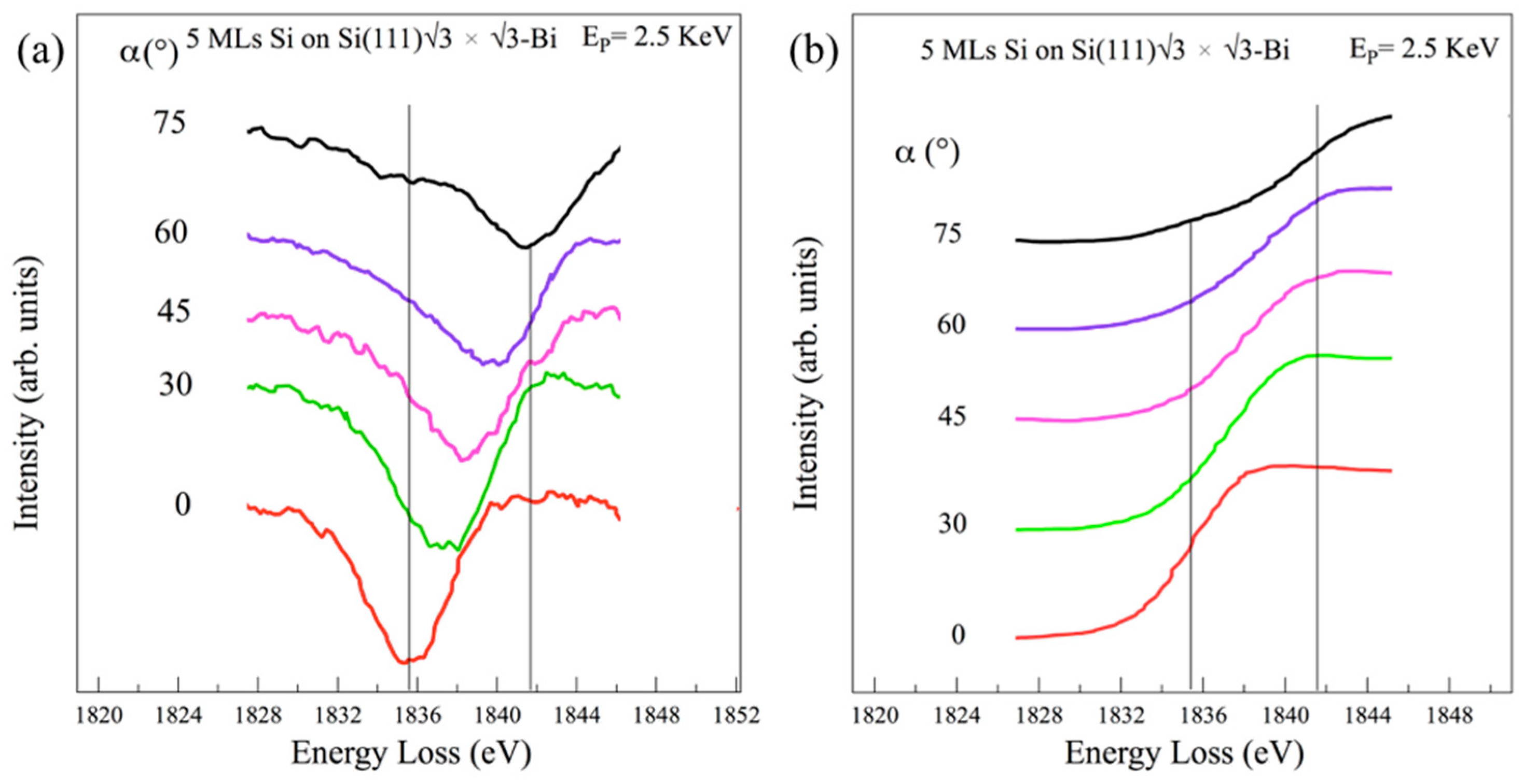
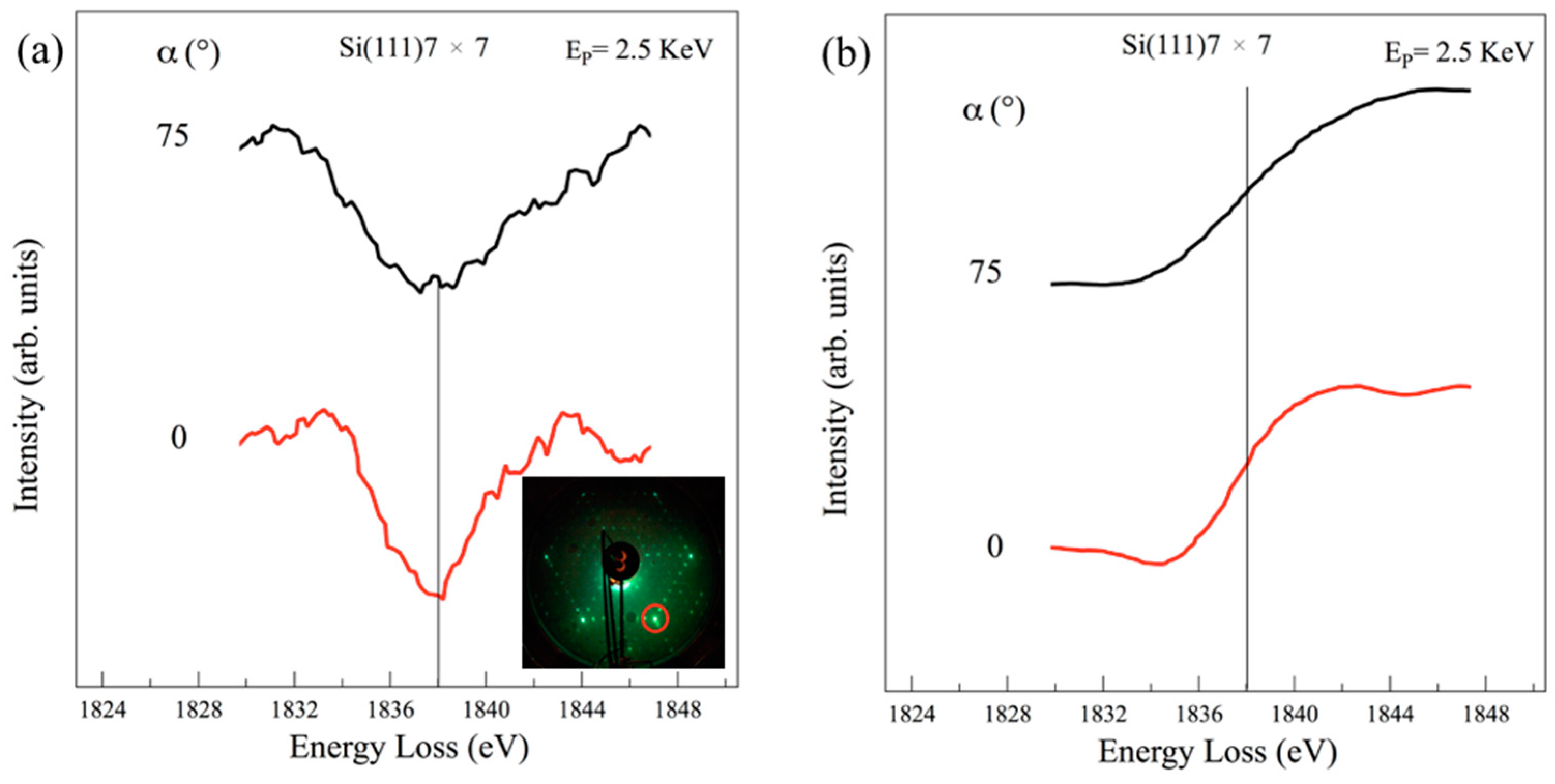
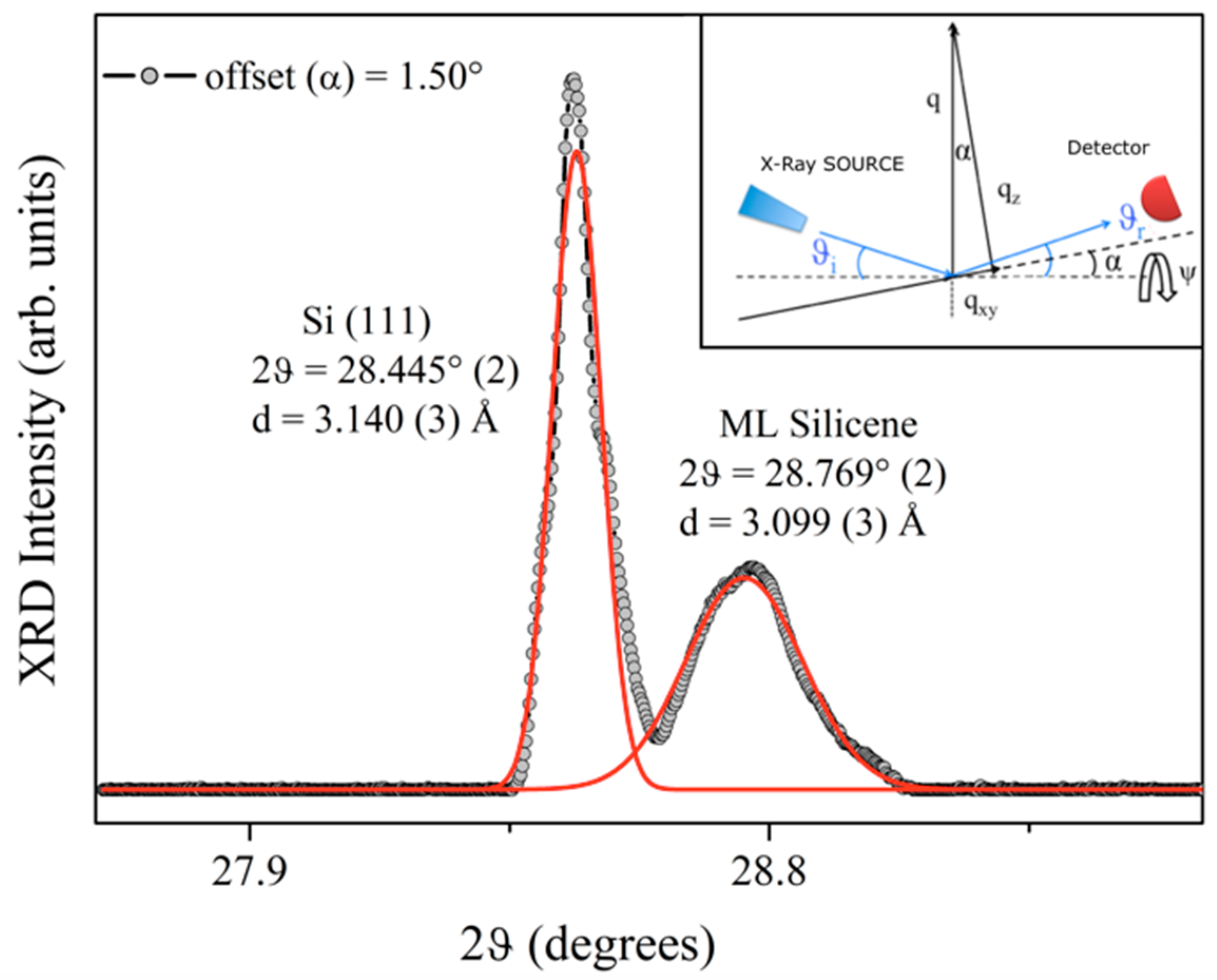
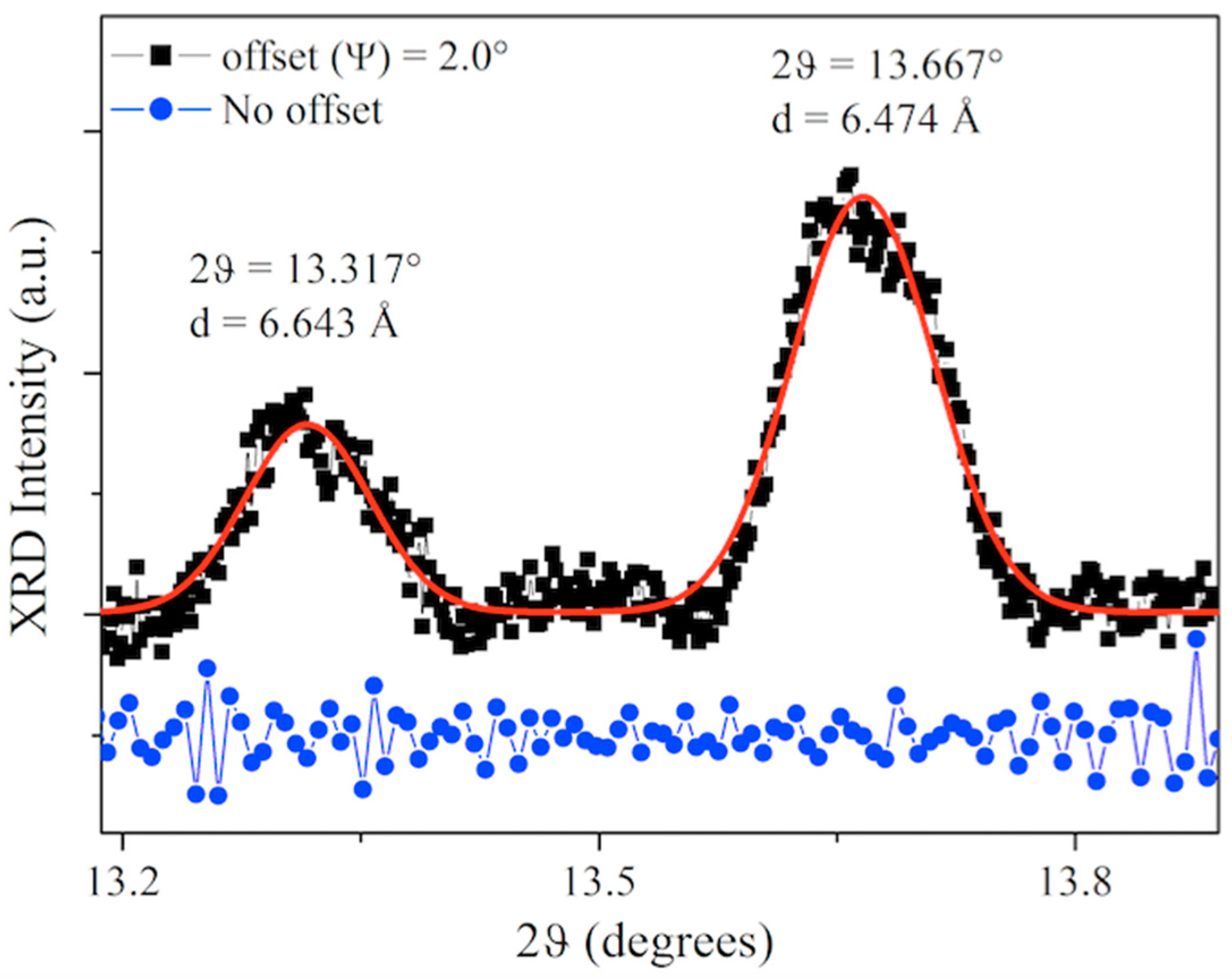
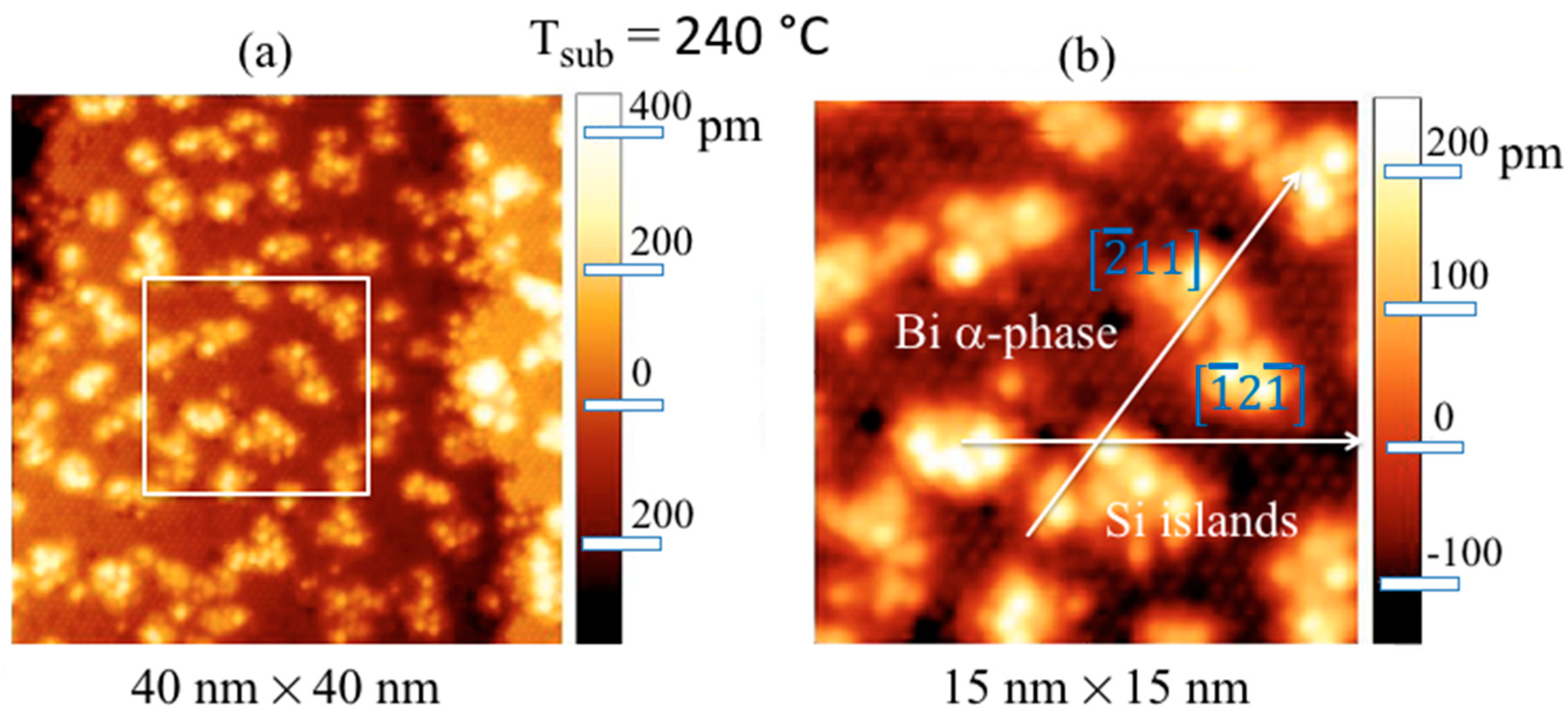
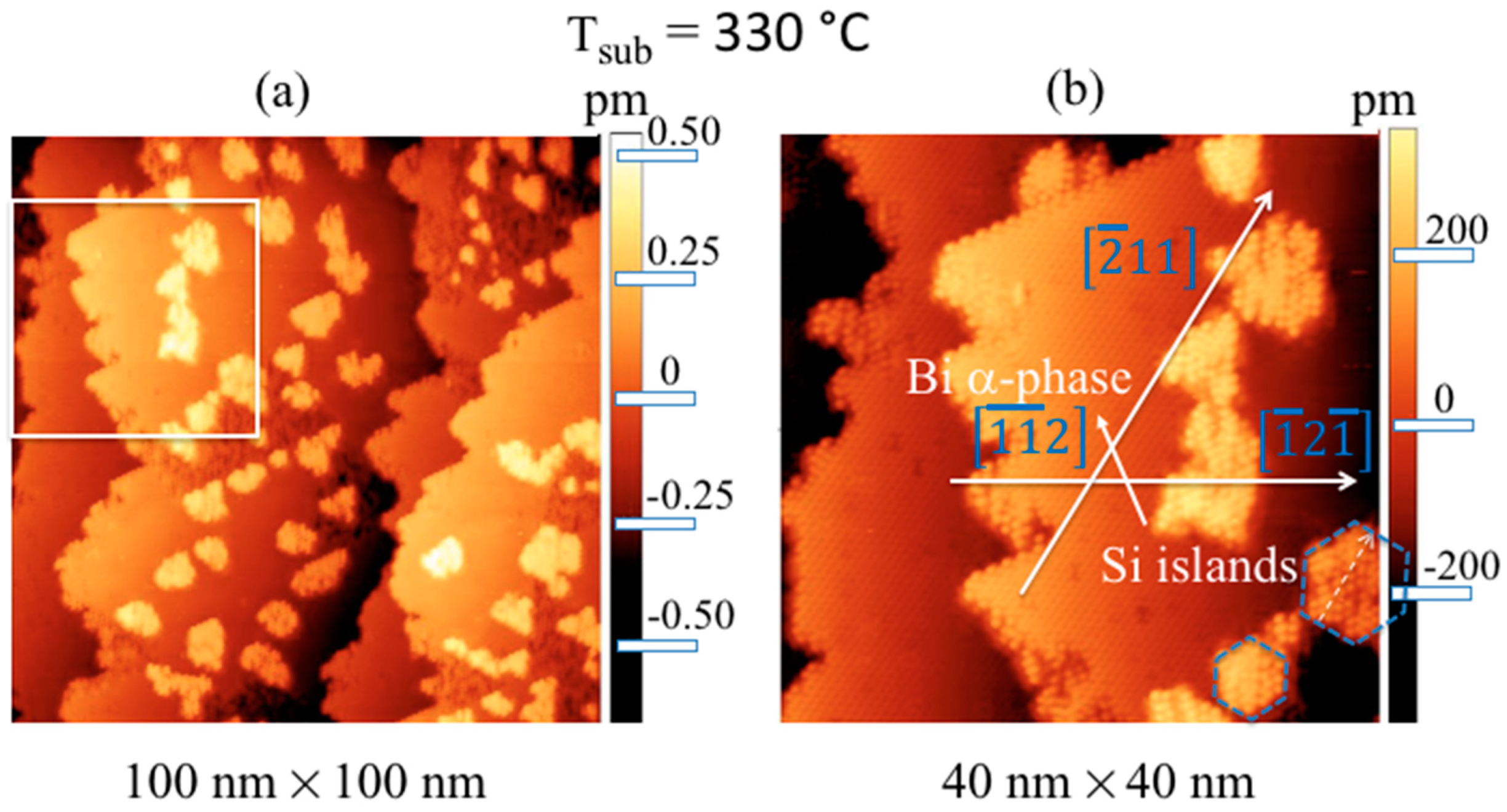
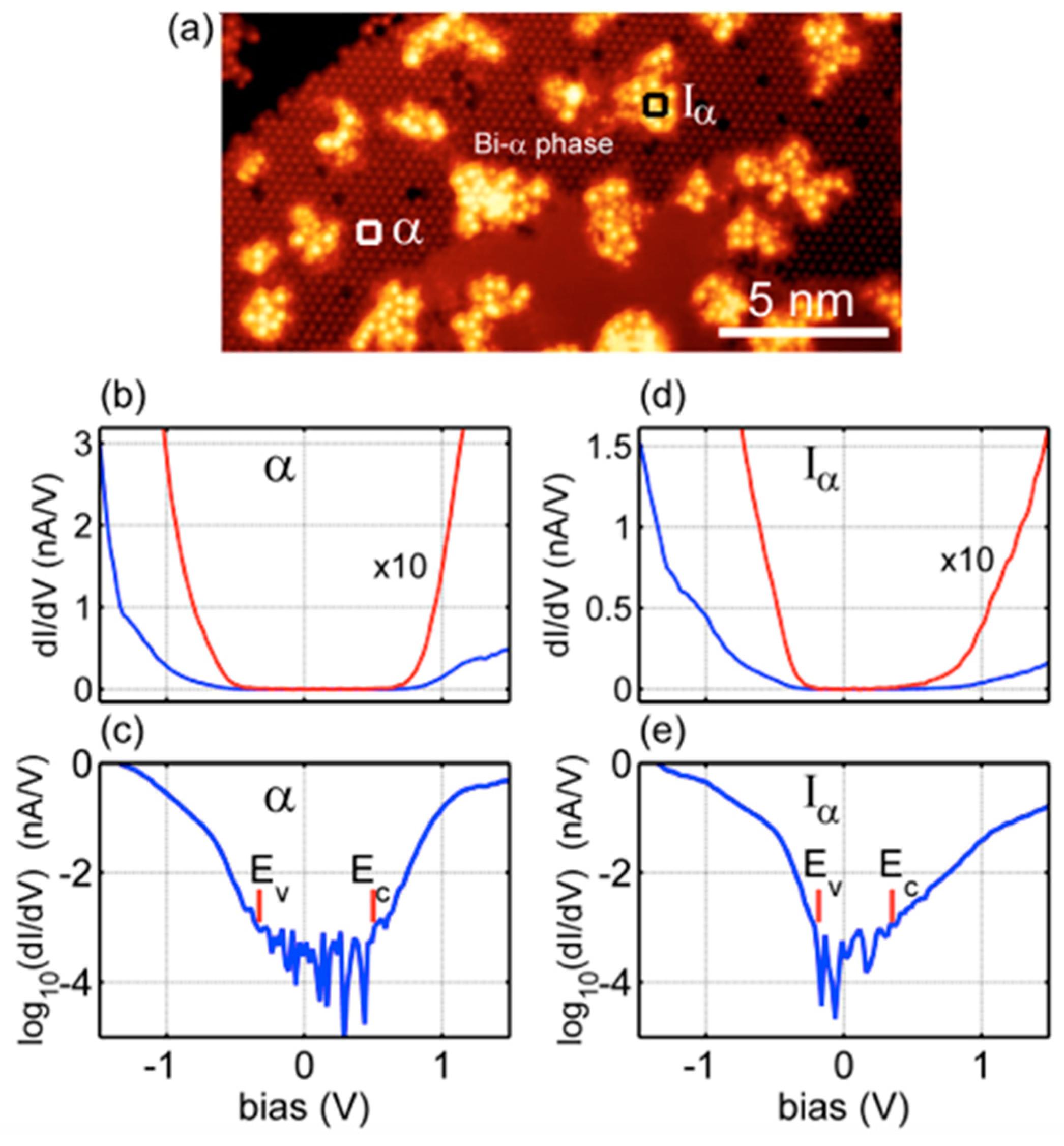
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Available online: https://www.nobelprize.org/prizes/physics/2010/ (accessed on 19 January 2022).
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef] [PubMed]
- Vogt, P.; De Padova, P.; Quaresima, C.; Avila, J.; Frantzeskakis, E.; Asensio, M.C.; Resta, A.; Ealet, B.; Le Lay, G. Compelling experimental evidence for graphenelike two-dimensional silicon. Phys. Rev. Lett. 2012, 108, 155501–155505. [Google Scholar] [CrossRef]
- Mannix, A.J.; Zhou, X.-F.; Kiraly, B.; Wood, J.D.; Alducin, D.; Myers, B.D.; Liu, X.; Fisher, B.L.; Santiago, U.; Guest, J.R.; et al. Synthesis of borophenes: Anisotropic, two-dimensional boron polymorphs. Science 2015, 350, 1513–1516. [Google Scholar] [CrossRef] [Green Version]
- Tao, M.-L.; Tu, Y.-B.; Sun, K.; Wang, Y.-L.; Xie, Z.-B.; Liu, L.; Shi, M.-X.; Wang, J.-Z. Gallenene epitaxially grown on Si(111). 2D Mater. 2018, 5, 035009. [Google Scholar] [CrossRef]
- Dávila, M.E.; Xian, L.; Cahangirov, S.; Rubio, A.; Le Lay, G. Germanene: A novel two-dimensional germanium allotrope akin to graphene and silicene. New J. Phys. 2014, 16, 095002. [Google Scholar] [CrossRef]
- Zhu, F.-F.; Chen, W.-J.; Xu, Y.; Gao, C.-L.; Guan, D.-D.; Li, C.-H.; Qian, D.; Zhang, S.-C.; Jia, J.-F. Epitaxial growth of two-dimensional stanene. Nat. Mat. 2015, 14, 1020–1025. [Google Scholar] [CrossRef]
- Yuhara, J.; He, B.; Matsunami, N.; Nakatake, M.; Le Lay, G. Graphene’s latest cousin: Plumbene epitaxial growth on a “nano water cube”. Adv. Mater. 2019, 31, 1901017. [Google Scholar] [CrossRef]
- Li, L.; Yu, Y.; Ye, G.J.; Ge, Q.; Ou, X.; Wu, H.; Feng, D.; Chen, X.H.; Zhang, Y. Black phosphorus field-effect transistors. Nat. Nanotechnol. 2014, 9, 372–377. [Google Scholar] [CrossRef] [Green Version]
- Shah, J.; Wang, W.; Sohail, H.M.; Uhrberg, R.I.G. Experimental evidence of monolayer arsenene: An exotic 2D semiconducting material. 2D Mater. 2020, 7, 025013. [Google Scholar] [CrossRef]
- Lei, T.; Liu, C.; Zhao, J.-L.; Li, J.-M.; Li, Y.-P.; Wang, J.-O.; Wu, R.; Qian, H.-J.; Wang, H.-Q.; Ibrahim, K. Electronic structure of antimonene grown on Sb2Te3 (111) and Bi2Te3 substrates. J. Appl. Phys. 2016, 119, 015302. [Google Scholar] [CrossRef]
- Reis, F.; Li, G.; Dudy, L.; Bauernfeind, M.; Glass, S.; Hanke, W.; Thomale, R.; Schäfer, J.; Claessen, R. Bismuthene on a SiC substrate: A candidate for a high-temperature quantum spin Hall material. Science 2017, 357, 287–290. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, J.; Dai, Y.; Ma, Y.; Dai, X.; Ho, W.; Xie, M. Ultrathin β-tellurium layers grown on highly oriented pyrolytic graphite by molecular-beam epitaxy. Nanoscale 2017, 9, 15945–15948. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qin, J.; Qiu, G.; Jian, J.; Zhou, H.; Yang, L.; Charnas, A.; Zemlyanov, D.Y.; Xu, X.; Xu, C.-Y.; Wu, W.; et al. Controlled growth of a large-size 2D selenium nanosheet and its electronic and optoelectronic applications. ACS Nano 2017, 11, 10222–10229. [Google Scholar] [CrossRef] [PubMed]
- De Padova, P.; Avila, J.; Resta, A.; Razado-Colambo, I.; Quaresima, C.; Ottaviani, C.; Olivieri, B.; Bruhn, T.; Vogt, P.; Asensio, M.C.; et al. The quasiparticle band dispersion in epitaxial multilayer silicene. J. Phys. Condens. Matter. 2013, 25, 382202. [Google Scholar] [CrossRef] [PubMed]
- De Padova, P.; Vogt, P.; Resta, A.; Avila, J.; Razado-Colambo, I.; Quaresima, C.; Ottaviani, C.; Olivieri, B.; Bruhn, T.; Hirahara, T.; et al. Evidence of Dirac fermions in multilayer silicene. Appl. Phys. Lett. 2013, 102, 163106. [Google Scholar] [CrossRef] [Green Version]
- Vogt, P.; Capiod, P.; Berthe, M.; Resta, A.; De Padova, P.; Bruhn, T.; Le Lay, G.; Grandidier, B. Synthesis and electrical conductivity of multilayer silicene. Appl. Phys. Lett. 2014, 104, 021602. [Google Scholar] [CrossRef]
- Grazianetti, C.; Cinquanta, E.; Tao, L.; De Padova, P.; Quaresima, C.; Ottaviani, C.; Akinwande, D.; Molle, A. Silicon nanosheets: Crossover between multilayer silicene and diamond-like growth regime. ACS Nano 2017, 11, 3376–3382. [Google Scholar] [CrossRef]
- Tao, L.; Cinquanta, E.; Chiappe, D.; Grazianetti, C.; Fanciulli, M.; Dubey, M.; Molle, A.; Akinwande, D. Silicene field-effect transistors operating at room temperature. Nat. Nanotech. 2015, 10, 227–231. [Google Scholar] [CrossRef]
- De Padova, P.; Ottaviani, C.; Quaresima, C.; Olivieri, B.; Imperatori, P.; Salomon, E.; Angot, T.; Quagliano, L.; Romano, C.; Vona, A.; et al. 24h stability of thick multilayer silicene in air. 2D Mater. 2014, 1, 021003. [Google Scholar] [CrossRef]
- De Padova, P.; Generosi, A.; Paci, B.; Ottaviani, C.; Quaresima, C.; Olivieri, B.; Salomon, E.; Angot, T.; Le Lay, G. Multilayer silicene: Clear evidence. 2D Mater. 2016, 3, 031011. [Google Scholar] [CrossRef] [Green Version]
- Meng, L.; Wng, Y.; Zhang, L.; Du, S.; Wu, R.; Li, L.; Yi, Z.; Li, G.; Zhou, H.; Hofer, W.A. Buckled silicene formation on Ir(111). Nano Lett. 2013, 13, 685–690. [Google Scholar] [CrossRef] [PubMed]
- Fleurence, A.; Friedlein, R.; Ozaki, T.; Kawai, H.; Wang, Y.; Yamada-Takamura, Y. Experimental evidence for epitaxial silicene on diboride thin films. Phys. Rev. Lett. 2012, 108, 245501. [Google Scholar] [CrossRef]
- De Padova, P.; Feng, H.; Zhuang, J.; Li, Z.; Generosi, A.; Paci, B.; Ottaviani, C.; Quaresima, C.; Olivieri, B.; Krawiec, M.; et al. Synthesis of multilayer silicene on Si(111)√3×√3-Ag. J. Phys. Chem. C 2017, 121, 27182–27190. [Google Scholar] [CrossRef]
- De Padova, P.; Generosi, A.; Paci, B.; Ottaviani, C.; Quaresima, C.; Olivieri, B.; Kopciuszynski, M.; Zurawek, L.; Zdyb, R.; Krawiec, M. New findings on multilayer silicene on Si(111)√3×√3R30°-Ag. Materials 2019, 12, 2258. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mrezguia, H.; Giovanelli, L.; Ksari, Y.; Akremi, A.; Themlin, J.-M. Unoccupied electronic states of 2D Si onAg-√3-Si(111). J. Phys. Condens. Matter. 2021, 33, 225002. [Google Scholar] [CrossRef]
- Xu, Y.X.; Cao, X.R.; Xu, L.H.; Zheng, F.; Wu, S.Q.; Zhu, Z.Z. Silicene adsorption on the bismuth-passivated Si(111)√3×√3 surface: A first-principles study. Mater. Chem. Phys. 2018, 216, 8–13. [Google Scholar] [CrossRef]
- Takahashi, T.; Izumi, K.; Ishikawa, T.; Kikuta, S. Evidence for a trimer in the √3×√3-Bi structure on the Si(111) surface by x-ray diffraction under the nearly normal incidence condition. Surf. Sci. Lett. 1987, 183, L302–L312. [Google Scholar] [CrossRef]
- Takahashi, T.; Nakatani, S.; Ishikawa, T.; Kikuta, S. Surface structure analysis of Si(111)√3×√3-Bi by x-ray diffraction-approach to the solution of the phase problem. Surf. Sci. Lett. 1987, 191, L825–L834. [Google Scholar]
- Park, Y.C.; Abukawa, T.; Higashiyama, K. Analysis of the atomic structure of the Si(111)√3×√3-Bi surface by x-ray photoelectron diffraction. Jpn. J. Appl. Phys. 1987, 26, L1335–L1337. [Google Scholar] [CrossRef]
- Shioda, R.; Kawazu, A.; Baski, A.A.; Quate, C.F.; Nogami, J. Bi on Si(111): Two phases of the √3x√3 surface reconstruction. Phys. Rev. B 1993, 48, 4895–4898. [Google Scholar] [CrossRef] [PubMed]
- Park, C.; Bakhtizin, R.Z.; Hashizume, T.; Sakurai, T. Scanning tunneling microscopy of √3×√3-Bi reconstruction on the Si(111) surface. Jpn. J. Appl. Phys. 1993, 32, L290–L293. [Google Scholar] [CrossRef]
- Park, C.; Bakhtizin, R.Z.; Hashizume, T.; Sakurai, T. Structure of the Bi/Si(111) surface by field-ion scanning tunneling microscopy. Jpn. J. Appl. Phys. 1993, 32, 1416–1418. [Google Scholar] [CrossRef]
- Bakhtizin, R.Z.; Park, C.; Hashizume, T.; Sakurai, T. Atomic structure of Bi on the Si(111) surface. J. Vac. Sci. Technol. B 1994, 12, 2052–2054. [Google Scholar] [CrossRef]
- Roesler, J.M.; Sieger, M.T.; Miller, T.; Chiang, T.-C. New experimental technique of photoelectron holography applied ti Bi trimers on Si(111). Surf. Sci. Lett. 1997, 380, L485–L490. [Google Scholar] [CrossRef]
- Cheng, C.; Kunc, K. Structure and stability of Bi layers on Si(111) and Ge(111) surfaces. Phys. Rev. B 1997, 56, 10283–10288. [Google Scholar] [CrossRef]
- Roesler, J.M.; Miller, T.; Chiang, T.-C. Photoelectron holography studies of Bi on Si(111). Surf. Sci. 1998, 417, L1143–L1147. [Google Scholar] [CrossRef]
- Nakatani, S.; Takahashi, T.; Kuruwahara, Y.; Aono, M. Use of x-ray reflectivity for determining the Si(111)√3×√3-Bi surface structures. Phys. Rev. B 1995, 52, R8711–R8714. [Google Scholar] [CrossRef]
- Miwa, R.H.; Schmidt, T.M.; Srivastava, G.P. Bi covered Si(111) surface revisited. J. Phys. Condens. Matter. 2003, 15, 2441–2447. [Google Scholar] [CrossRef]
- Yaginuma, S.; Nagao, T.; Sadowski, J.T.; Saito, M.; Nagaoka, K.; Fujikawa, Y.; Sakurai, T.; Nakayama, T. Origin of flat morphology and high crystallinity of ultrathin bismuth films. Surf. Sci. 2007, 601, 3593–3600. [Google Scholar] [CrossRef]
- Wan, K.J.; Guo, T.; Ford, W.K.; Hermanson, J.C. Initial growth of Bi films on a Si(111) substrate: Two phases of √3×√3 low-energy-electron-diffraction pattern and their geometric structures. Phys. Rev. B 1991, 44, 3471–3474. [Google Scholar] [CrossRef] [PubMed]
- Woicik, J.C.; Franklin, G.E.; Liu, C.; Martinez, R.E.; Hwong, I.-S.; Bedzyk, M.J.; Patel, J.R.; Golovchenko, J.A. Structural determination of the Si(111) √3×√3-Bi surface by x-ray standing waves and scanning tunneling microscopy. Phys. Rev. B 1994, 50, 12246–12249. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kuzumaki, T.; Shirasawa, T.; Mizuno, S.; Ueno, N.; Tochihara, H.; Sakamoto, K. Re-investigation of the Bi-induced Si(111)√3x√3 surfaces by low-energy electron diffraction. Surf. Sci. 2010, 604, 1044–1048. [Google Scholar] [CrossRef]
- Berntsen, M.H.; Götberg, O.; Tjernberg, O. Reinvestigation of the giant Rashba- split states on Bi-covered Si(111). Phys. Rev. B 2018, 97, 125148. [Google Scholar] [CrossRef] [Green Version]
- Chi, L.; Nogami, J.; Singh, C.V. Bias dependence and defect analysis of Bi on Si(111) 3 × 3 β-phase. Phys. Rev. B 2021, 103, 075405. [Google Scholar] [CrossRef]
- Cheung, T.T.P. Orientation dependence of the carbon K edge in graphite measured by reflection electron energy-losss-pectroscopy. Phys. Rev. B. 1985, 31, 4792–4797. [Google Scholar] [CrossRef]
- De Padova, P.; Quaresima, C.; Olivieri, B.; Perfetti, P.; Le Lay, G. sp2-like hybridization of silicon valence orbitals in silicene nanoribbons. Appl. Phys. Lett. 2011, 98, 081909. [Google Scholar] [CrossRef]
- Gunnella, R.; Davoli, I.; Bernardini, R.; De Crescenzi, M. Inelastic processes versus diffraction effects: Polar-angle energy-loss spectra of the graphite E edge. Phys. Rev. B 1995, 52, 17091–17098. [Google Scholar] [CrossRef]
- Hamon, A.L.; Verbeeck, J.; Schryvers, D.; Benedik, J.; Sanden, R. ELNES study of carbon K-edge spectra of plasma deposited carbon films. J. Mater. Chem. 2004, 14, 2030–2035. [Google Scholar] [CrossRef]
- Cupolillo, A.; Ligato, N.; Osman, S.; Caputi, L.S. Carbon K-edge electron-energy-loss near-edge structure in the reflection mode on graphene/Ni(111). Appl. Phys. Lett. 2006, 109, 161603. [Google Scholar] [CrossRef]
- Leapman, R.D.; Silcox, J. Orientation dependence of core edges in electron-energy-loss spectrafrom anisotropic materials. Phys. Rev. Lett. 1979, 42, 1361–1364. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garagnani, D.; De Padova, P.; Ottaviani, C.; Quaresima, C.; Generosi, A.; Paci, B.; Olivieri, B.; Jałochowski, M.; Krawiec, M. Evidence of sp2-like Hybridization of Silicon Valence Orbitals in Thin and Thick Si Grown on α-Phase Si(111)√3 × √3R30°-Bi. Materials 2022, 15, 1730. https://doi.org/10.3390/ma15051730
Garagnani D, De Padova P, Ottaviani C, Quaresima C, Generosi A, Paci B, Olivieri B, Jałochowski M, Krawiec M. Evidence of sp2-like Hybridization of Silicon Valence Orbitals in Thin and Thick Si Grown on α-Phase Si(111)√3 × √3R30°-Bi. Materials. 2022; 15(5):1730. https://doi.org/10.3390/ma15051730
Chicago/Turabian StyleGaragnani, David, Paola De Padova, Carlo Ottaviani, Claudio Quaresima, Amanda Generosi, Barbara Paci, Bruno Olivieri, Mieczysław Jałochowski, and Mariusz Krawiec. 2022. "Evidence of sp2-like Hybridization of Silicon Valence Orbitals in Thin and Thick Si Grown on α-Phase Si(111)√3 × √3R30°-Bi" Materials 15, no. 5: 1730. https://doi.org/10.3390/ma15051730
APA StyleGaragnani, D., De Padova, P., Ottaviani, C., Quaresima, C., Generosi, A., Paci, B., Olivieri, B., Jałochowski, M., & Krawiec, M. (2022). Evidence of sp2-like Hybridization of Silicon Valence Orbitals in Thin and Thick Si Grown on α-Phase Si(111)√3 × √3R30°-Bi. Materials, 15(5), 1730. https://doi.org/10.3390/ma15051730






