High Temperature In Situ Optical Observation and Structural Optimization Numerical Simulation of High Nitrogen Steel (Cr18Mn18N)
Abstract
:1. Introduction
1.1. Theory
1.1.1. Governing Equations
1.1.2. Fluid-Solid Heat Transfer Equations
1.1.3. Species Transport Equations
1.1.4. Stress-Strain Relationship
2. Experimental
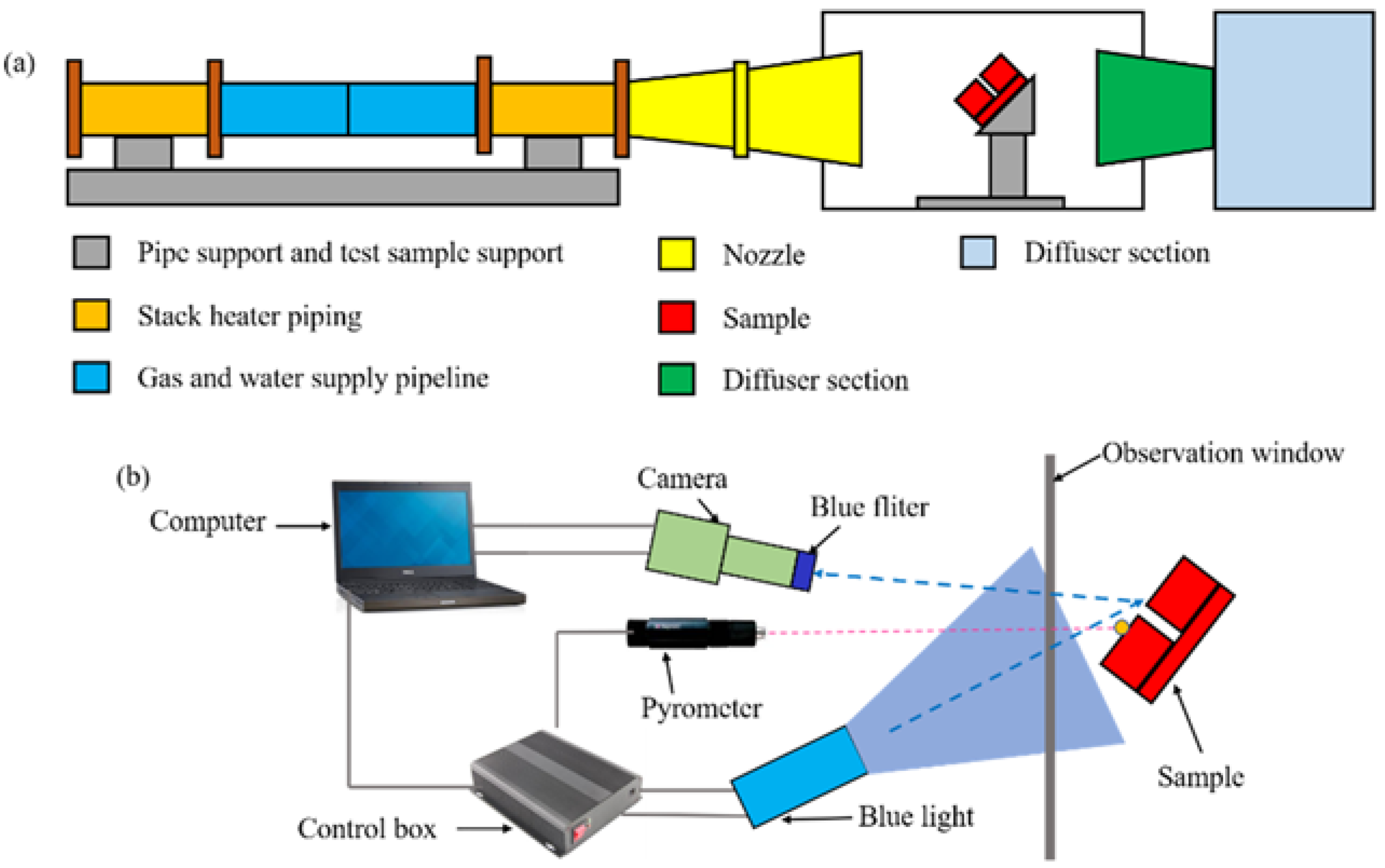
2.1. Experimental Setup
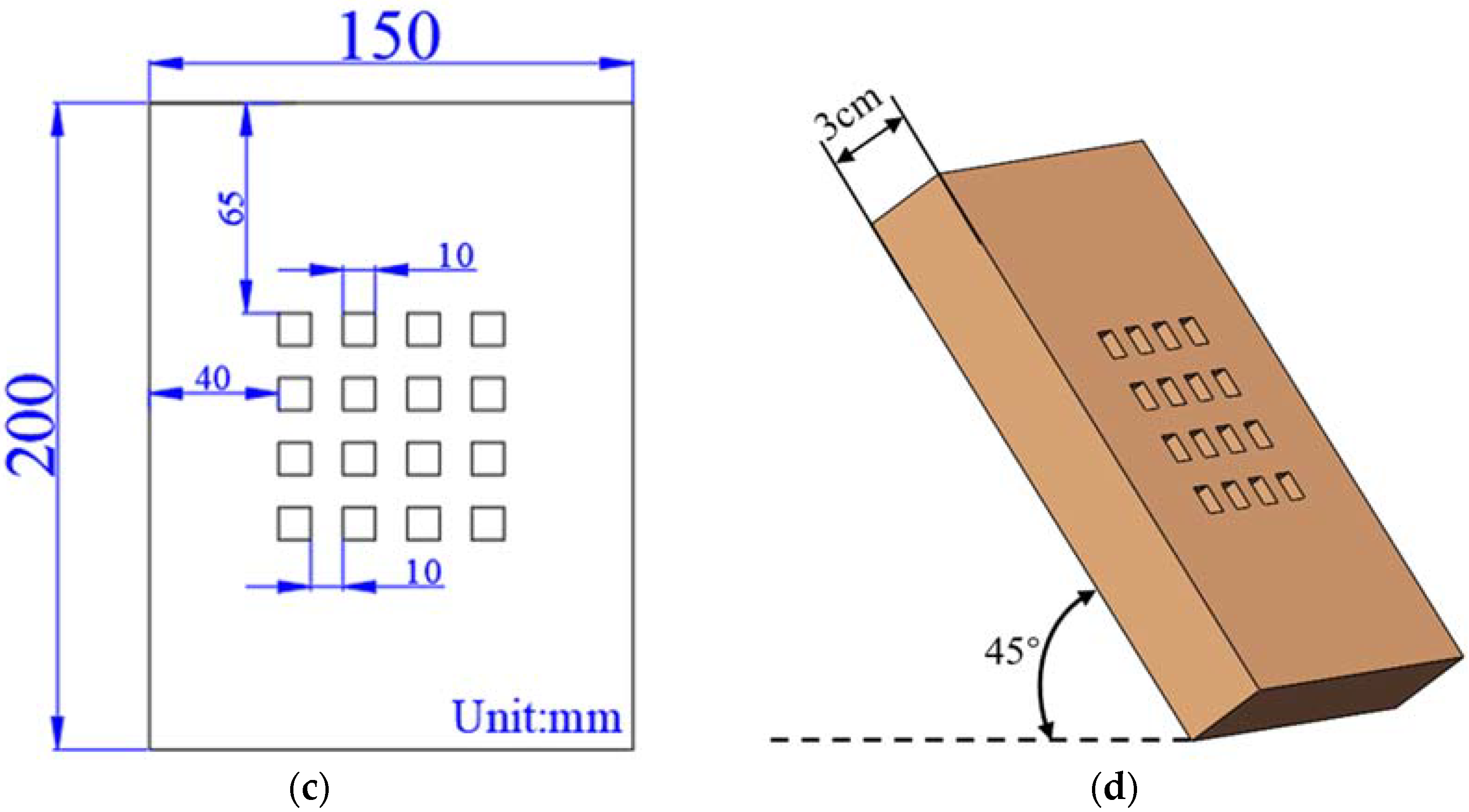
2.2. Material Selection and Preparation
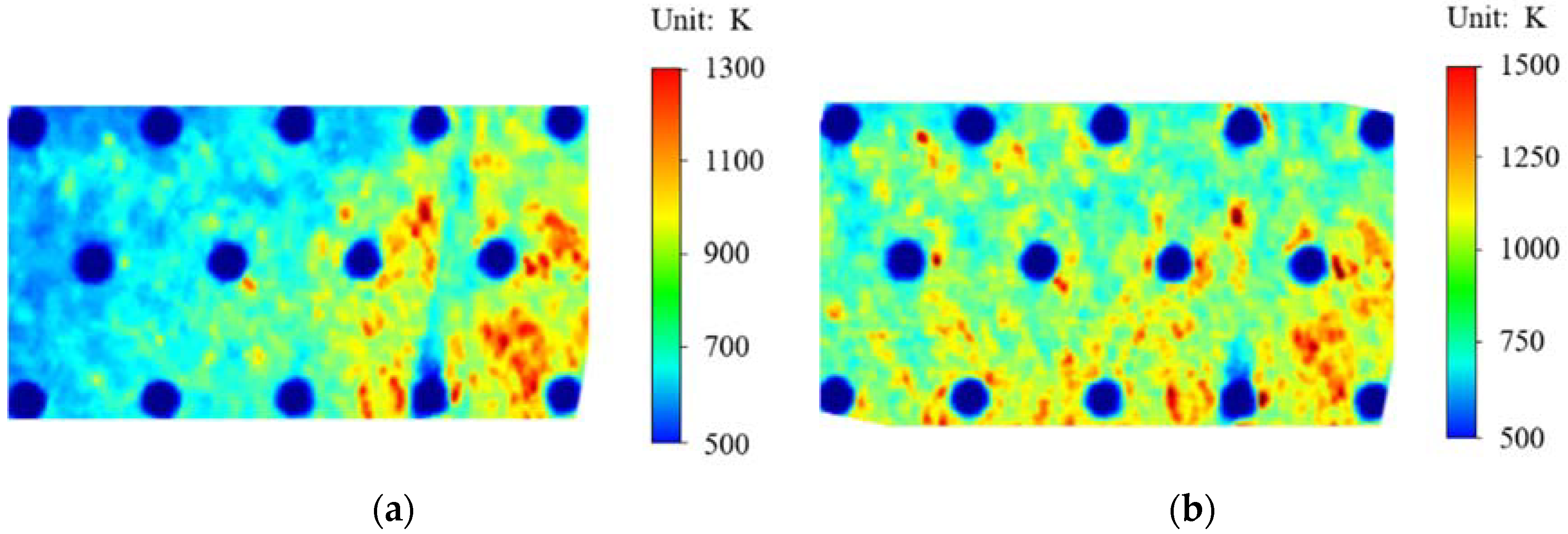
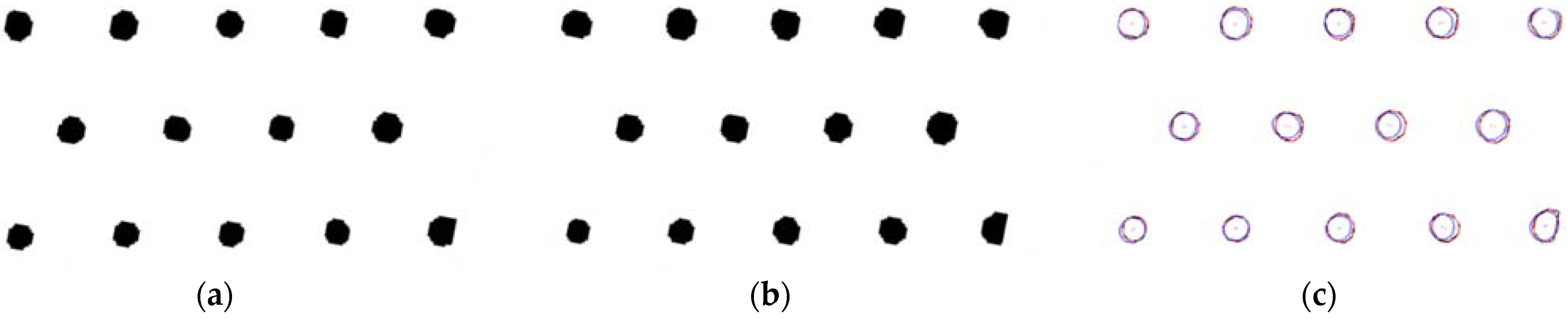
2.3. Experimental Results
3. Numerical Model and Result
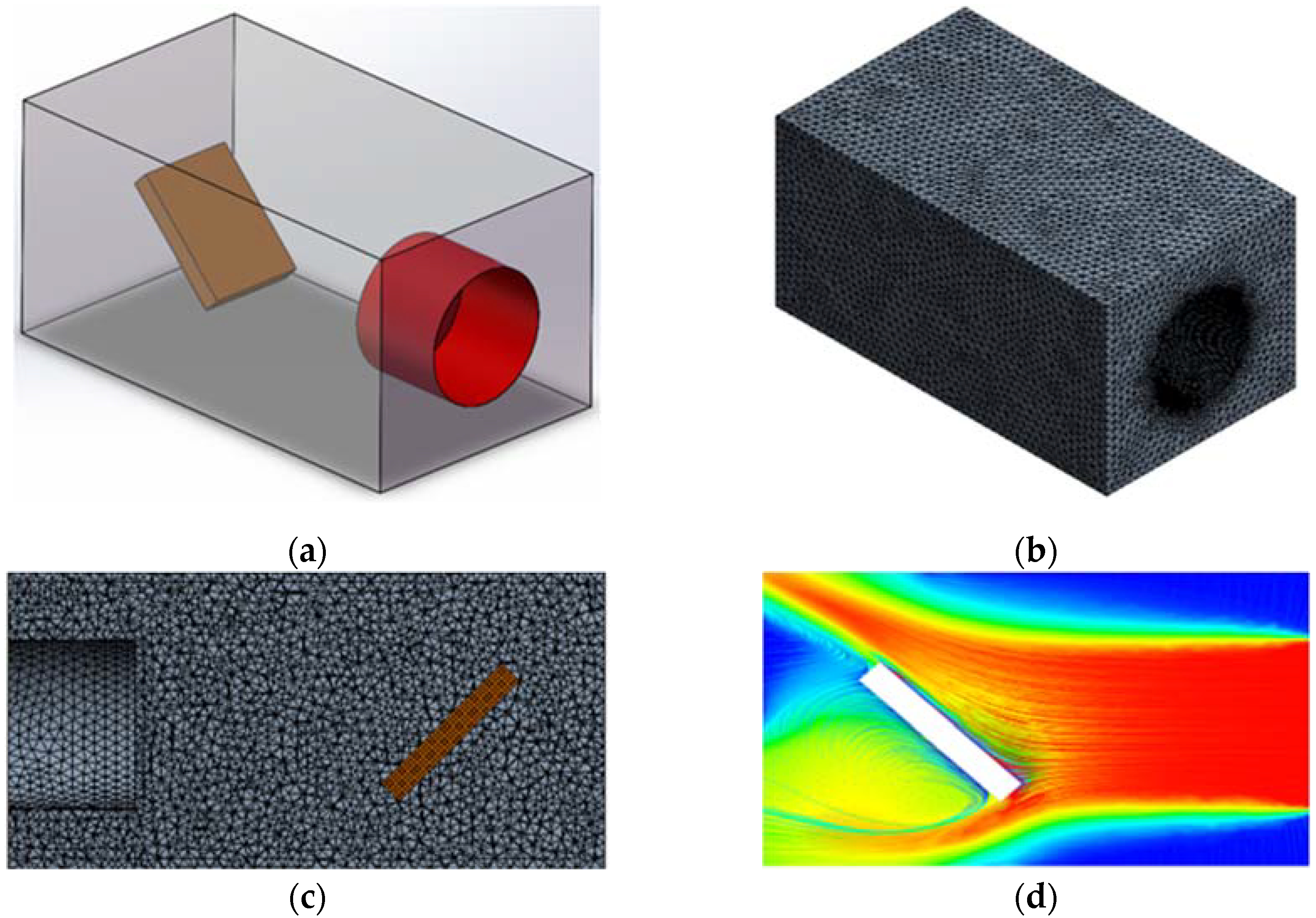
3.1. Numerical Model
3.2. Results
4. Conclusions
- (1)
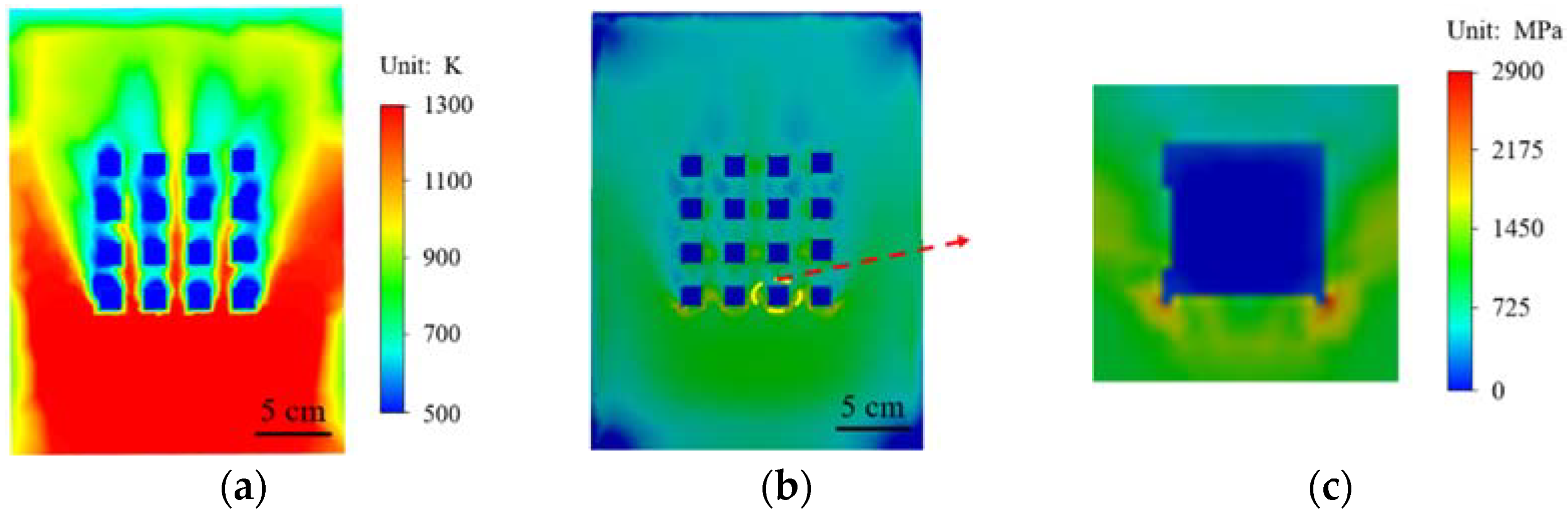
- Through the temperature synchronous deformation measurement equipment, the image of the high nitrogen steel material with prefabricated pores under the high temperature arc wind tunnel is collected. The prefabricated structure and materials are well preserved under the high temperature arc wind tunnel, and the temperature is up to 1500 K, indicating that the prefabricated pore structure has a good thermal protection effect on the high nitrogen steel material.
- (2)
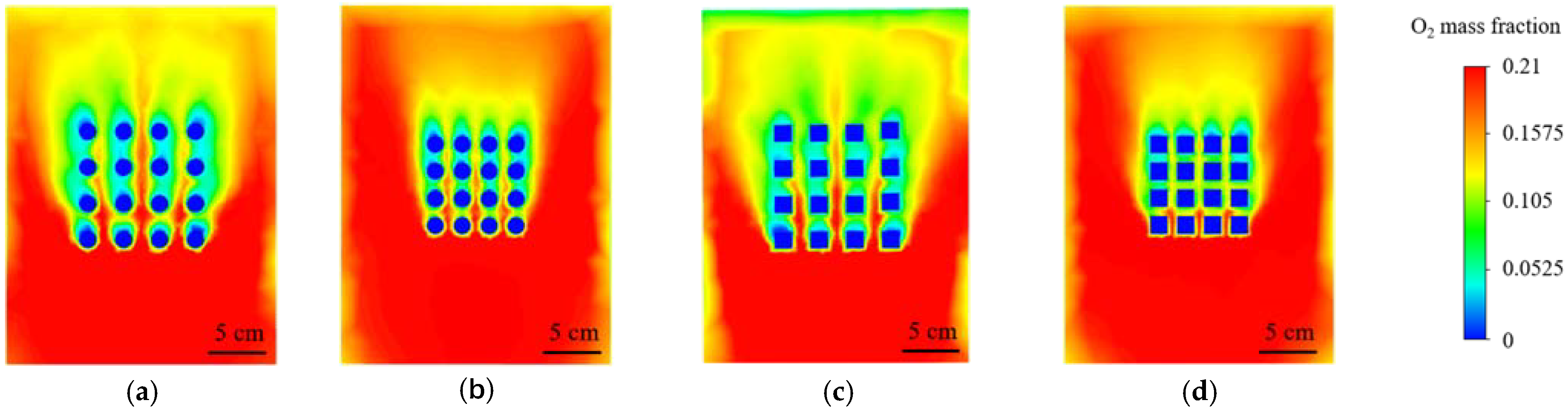
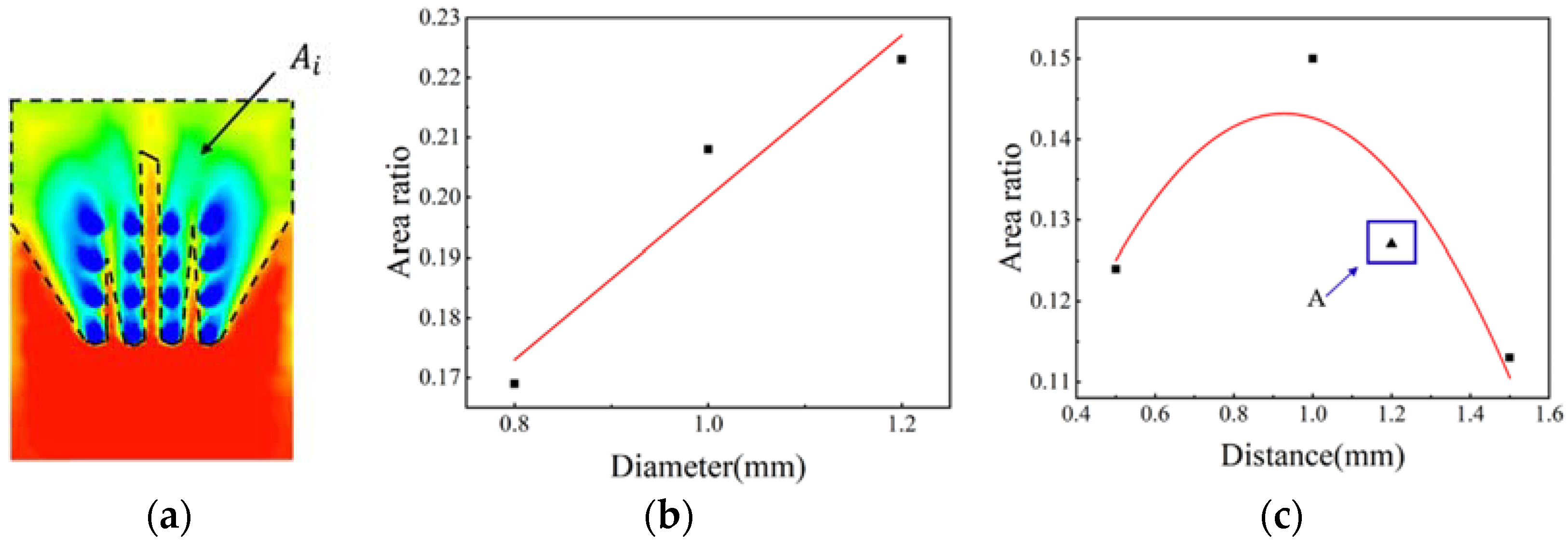
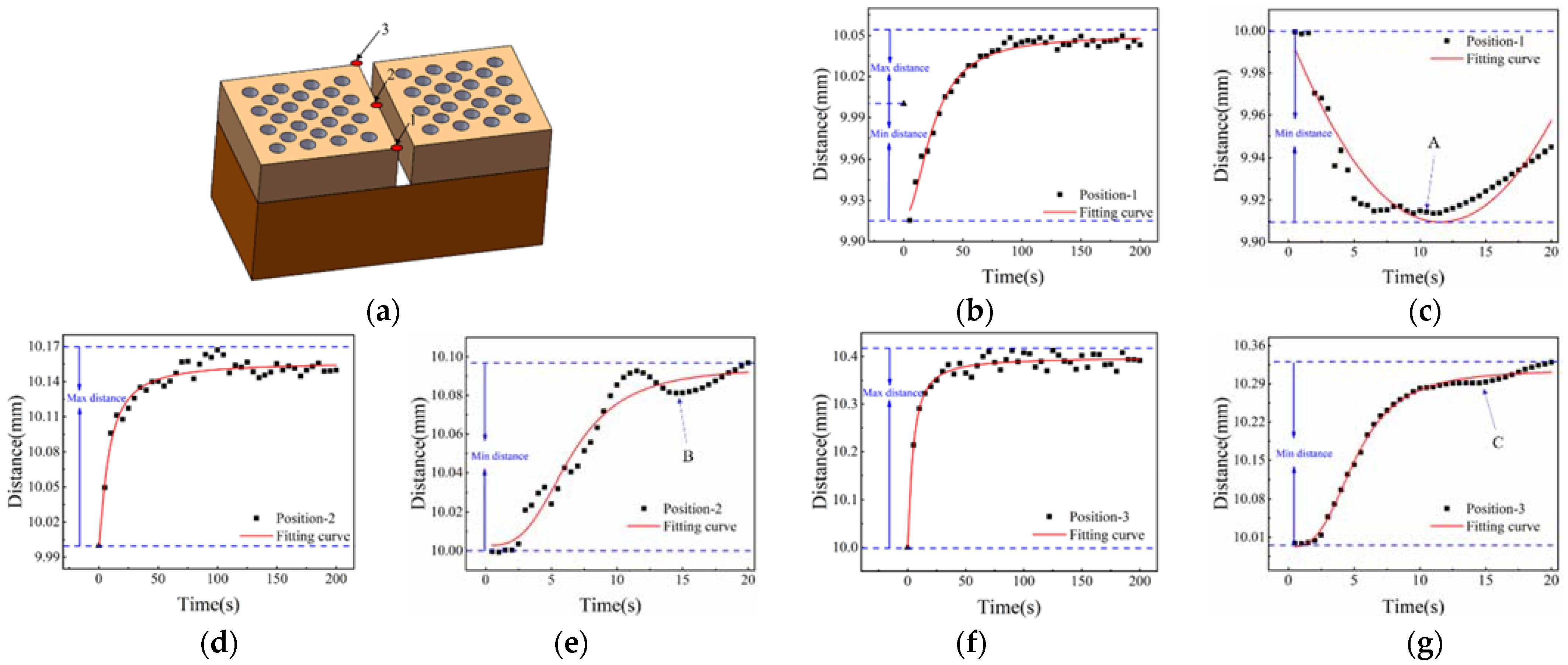
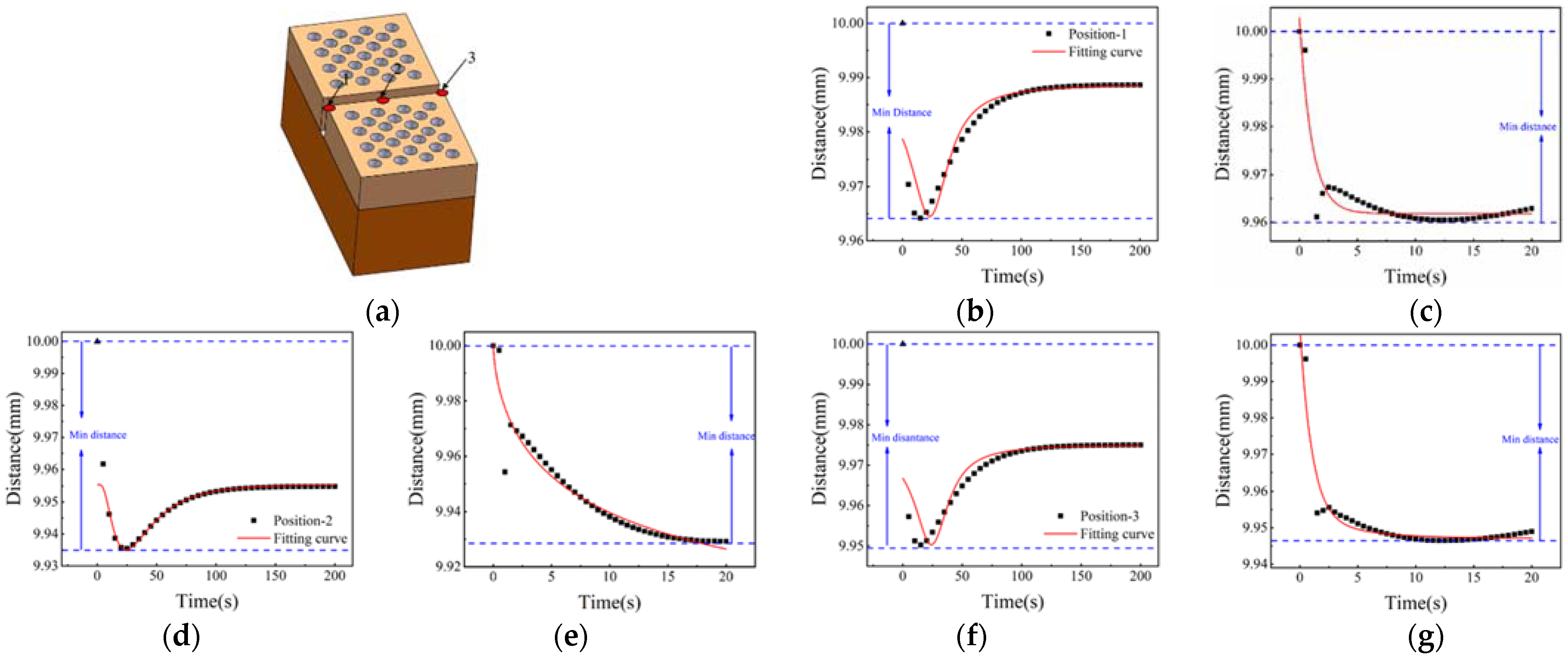
- In the numerical simulation, different array structures are compared. The simulation results show that the porous circular array structure has a better thermal protection effect than other structures, and the stress concentration is smaller than other array structures, indicating that the porous array structure has a better thermal protection effect in high temperature environments.
- (3)
- Finally, in the numerical simulation, the spliced components are established by using the porous array structure, the heating simulation is carried out in different directions of the spliced components, the temperature and stress nephogram of the spliced components are given, and the variation law of the gap of the spliced components is obtained, which provides theoretical and experimental support for the further application of material.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tang, S.; Deng, J.; Wang, S.; Liu, W.; Yang, K. Ablation behaviors of ultra-high temperature ceramic composites. Mater. Sci. Eng. A 2007, 465, 1–7. [Google Scholar] [CrossRef]
- Tang, Y.; Yue, M.; Fang, X.; Feng, X. Evolution of surface droplets and flow patterns on C/SiC during thermal ablation. J. Eur. Ceram. Soc. 2019, 39, 3566–3574. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, J.; Yue, M.; Yue, W.; Qu, Z.; Wang, X.; Jiang, J.; Tang, Y.; Feng, X. High-temperature thermal expansion behaviour of C/SiC studied using an in-situ optical visualisation method and numerical simulations in a quartz lamp array heating environment. Ceram. Int. 2021, 47, 12547–12556. [Google Scholar] [CrossRef]
- Masuyama, F.; Hiromatsu, K.; Hasegawa, Y. High temperature oxidation behavior of high nitrogen ferritic steels. ISIJ Int. 1996, 36, 825–833. [Google Scholar] [CrossRef]
- Berns, H.; Escher, C.; Streich, W. Martensitic high nitrogen steel for applications at elevated temperature. In High Nitrogen Steels’98, Proceedings of the 5th International Conference on High Nitrogen Steels, Espoo, Finland, 24–26 May 1998; Stockholm, Sweden, 27–28 May 1998; Hanninen, H., Hertzman, S., Romu, J., Eds.; Trans Tech Publications Ltd.: Zurich, Switzerland, 1999; pp. 443–448. [Google Scholar]
- Wang, W.; Zhang, Y.; Xu, L.; Li, X. Mechanical properties of high-strength Q960 steel at elevated temperature. Fire Saf. J. 2020, 114, 9. [Google Scholar] [CrossRef]
- Chen, J.; Young, B.; Uy, B. Behavior of high strength structural steel at elevated temperatures. J. Struct. Eng. 2006, 132, 1948–1954. [Google Scholar] [CrossRef] [Green Version]
- Matsubara, S.; Yamaguchi, T.; Masuyama, F. High Temperature Oxidation Behavior of High Nitrogen 9%Cr Steels. ISIJ Int. 2018, 58, 2095–2101. [Google Scholar] [CrossRef] [Green Version]
- Zhang, R.; Wu, B. Effect of Temperature and Pressure on the Nitrogen Content of High Nitrogen Steel. In Advanced Research on Material Science, Enviroment Science and Computer Science III; Zhang, H., Jin, D., Zhao, X.J., Eds.; Trans Tech Publications Ltd.: Zurich, Switzerland, 2014; p. 24. [Google Scholar]
- Ran, Q.; Liu, Q.; Xu, Y.; Xu, W.; Li, J.; Xiao, X.; Hu, J.; Jiang, L. Nitrogen-induced selective high-temperature internal oxidation behavior in duplex stainless steels 19Cr-10Mn-0.3Ni-Xn. Corros. Sci. 2015, 98, 737–747. [Google Scholar] [CrossRef]
- Camanho, P.; Davila, C.; de Moura, M.F. Numerical Simulation of Mixed-Mode Progressive Delamination in Composite Materials. J. Compos. Mater. 2016, 37, 1415–1438. [Google Scholar] [CrossRef]
- Kasat, G.; Khopkar, A.; Ranade, V.; Pandit, A. CFD simulation of liquid-phase mixing in solid–liquid stirred reactor. Chem. Eng. Sci. 2008, 63, 3877–3885. [Google Scholar] [CrossRef]
- Ma, B.; Wan, M.; Liu, Z.; Li, X.; Wu, X.; Diao, K. Experimental and Numerical Determination of Hot Forming Limit Curve of Advanced High-Strength Steel. J. Mater. Eng. Perform. 2017, 26, 3299–3306. [Google Scholar] [CrossRef]
- Sui, D.; Chen, F.; Zhang, P.; Cui, Z. Numerical Simulation of Microstructure Evolution for SA508-3 Steel during Inhomogeneous Hot Deformation Process. Iron Steel Res. Int. 2014, 21, 1022–1029. [Google Scholar] [CrossRef]
- Yu, Y.; Ming, P.; Zhou, S. Numerical Study on Transient Heat Transfer of a Quartz Lamp Heating System. Math. Probl. Eng. 2014. [Google Scholar] [CrossRef]
- Gan, Z.; Yu, G.; He, X.; Li, S. Numerical simulation of thermal behavior and multicomponent mass transfer in direct laser deposition of Co-base alloy on steel. Int. J. Heat Mass Transf. 2017, 104, 28–38. [Google Scholar] [CrossRef] [Green Version]
- Meng, F.; Dong, S.; Jiang, H.; Wang, J. A fast algorithm for long-term fluid-solid conjugate heat transfer process. J. B. Univ. Technol. 2017, 43, 1224–1230. [Google Scholar]
- Rui, Z.; Li, Y.; Lin, Y.S. Analysis of oxygen permeation through dense ceramic membranes with chemical reactions of finite rate. Chem. Eng. Sci. 2009, 64, 172–179. [Google Scholar] [CrossRef]
- Lei, D.; Fu, X.; Ren, Y.; Yao, F.; Wang, Z. Temperature and thermal stress analysis of parabolic trough receivers. Renew. Energ. 2019, 136, 403–413. [Google Scholar] [CrossRef]
- Ou, D.; Chen, L.; Dong, Y.; Lin, X.; Li, F.; Yu, X. Measurements of gas temperature and atomic oxygen density in the arc-heated wind tunnel based on TDLAS. J. Exp. Fluid Mech. 2015, 29, 62–67. [Google Scholar]
- Momozawa, A.; Yokote, N.; Terutsuki, D.; Komurasaki, K. Dynamic oxidation of SiC with arc-heated plasma wind tunnel and laser heating. Vacuum 2021, 185, 109899. [Google Scholar] [CrossRef]
- Fang, X.; Yu, H.; Zhang, G.; Su, H.; Tang, H.; Feng, X. In situ observation and measurement of composites subjected to extremely high temperature. Rev. Sci. Instrum. 2014, 85, 035104. [Google Scholar] [CrossRef] [Green Version]
- Fang, X.; Qu, Z.; Zhang, C.; Feng, X. In-situ testing of surface evolution of SiC during thermal ablation: Mechanisms of formation, flowing and growth of liquid silica beads. Ceram. Int. 2017, 43, 7040–7047. [Google Scholar] [CrossRef]
- Valeri, G.; Koohbor, B.; Kidane, A.; Sutton, M.A. Determining the tensile response of materials at high temperature using DIC and the Virtual Fields Method. Opt. Lasers Eng. 2017, 91, 53–61. [Google Scholar] [CrossRef]
- Thai, T.; Smith, A.J.; Rowley, R.; Gradl, P.; Berke, R. Change of exposure time mid-test in high temperature DIC measurement. Meas. Sci. Technol. 2020, 31, 11. [Google Scholar] [CrossRef] [Green Version]
- Tang, Y.; Yue, M.; Fang, X.; Feng, X. Synchronous full-field measurement of temperature and deformation based on separated radiation and reflected light. Opt. Lasers Eng. 2019, 116, 94–102. [Google Scholar] [CrossRef]
- Su, H.; Fang, X.; Qu, Z.; Zhang, C.; Yan, B.; Feng, X. Synchronous Full-Field Measurement of Temperature and Deformation of C/SiC Composite Subjected to Flame Heating at High Temperature. Exp. Mech. 2016, 56, 659–671. [Google Scholar] [CrossRef]







| Type | Density (kg/m3) | Specific Heat (J/(kg·K)) | Thermal Conductivity (W/(m·K)) | Coefficient of Thermal Expansion (K−1) |
|---|---|---|---|---|
| Cr18Mn18N | 7540 | 460 | 30 | 0.6 × 10−5 |
| Air | - | 1006.43 | 0.0242 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, S.; Kong, Y.; Yue, W.; Tang, Y. High Temperature In Situ Optical Observation and Structural Optimization Numerical Simulation of High Nitrogen Steel (Cr18Mn18N). Materials 2022, 15, 1805. https://doi.org/10.3390/ma15051805
Zhu S, Kong Y, Yue W, Tang Y. High Temperature In Situ Optical Observation and Structural Optimization Numerical Simulation of High Nitrogen Steel (Cr18Mn18N). Materials. 2022; 15(5):1805. https://doi.org/10.3390/ma15051805
Chicago/Turabian StyleZhu, Shilong, Yi Kong, Wen Yue, and Yunlong Tang. 2022. "High Temperature In Situ Optical Observation and Structural Optimization Numerical Simulation of High Nitrogen Steel (Cr18Mn18N)" Materials 15, no. 5: 1805. https://doi.org/10.3390/ma15051805





