Unified Stress–Strain Model of FRP-Confined Square and Circle Rubber Concrete Columns
Abstract
:1. Introduction
2. Database
3. Analytical Modeling
3.1. Peak Stress and Peak Strain
3.2. Axial–Lateral Strain Relationship
3.3. Stress–Strain Relationship
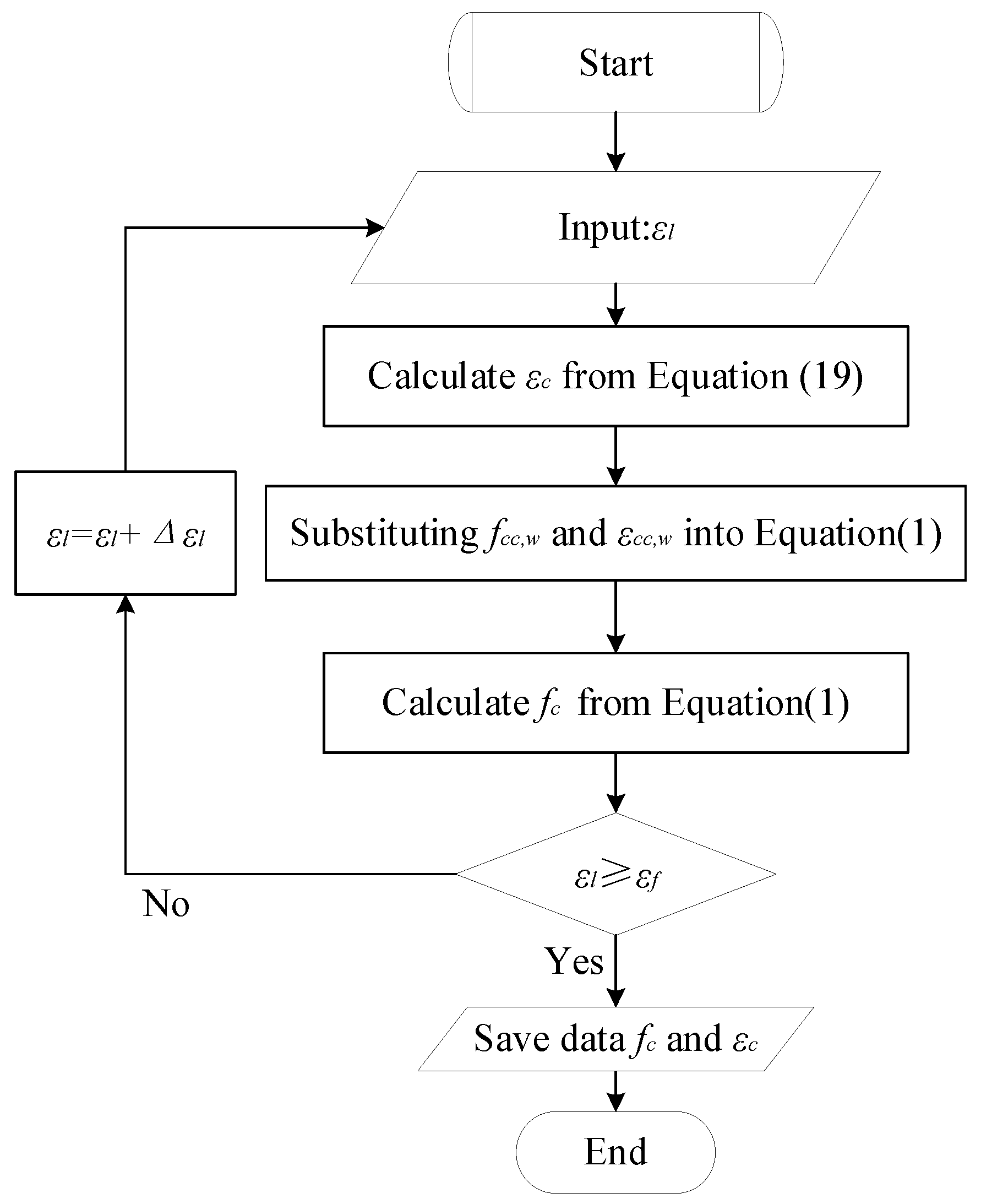
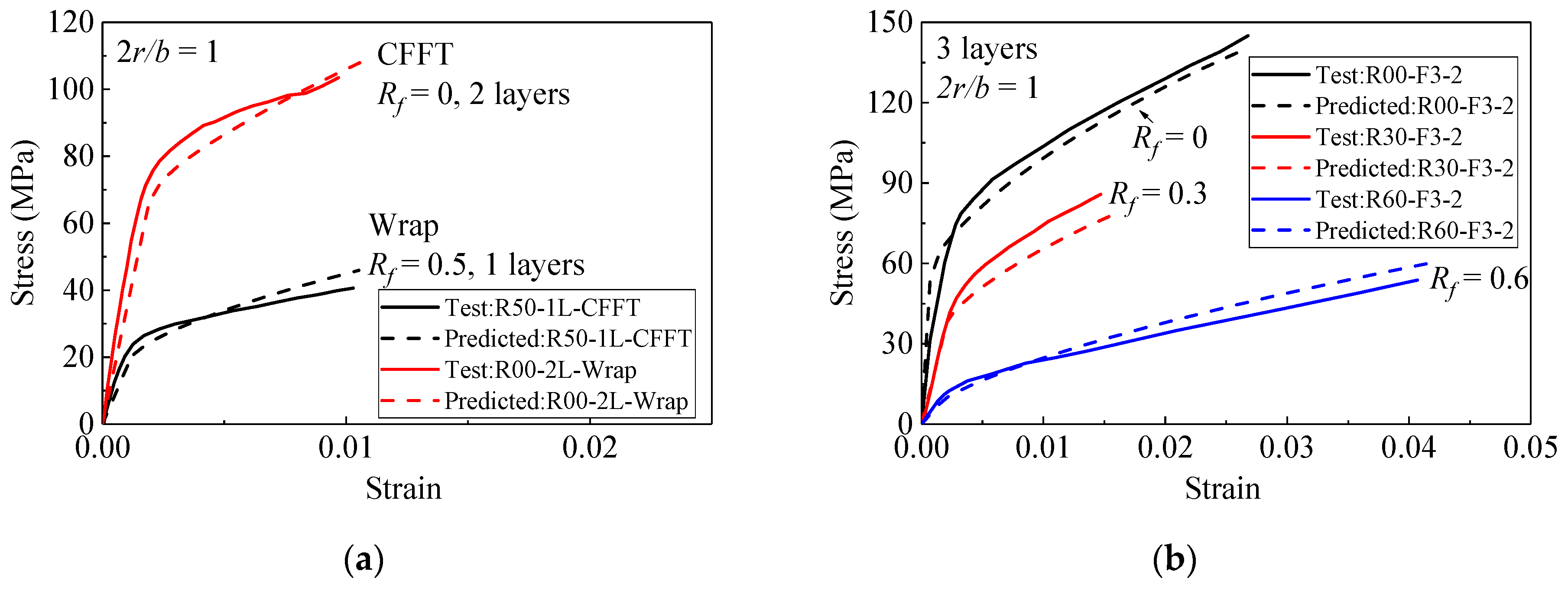
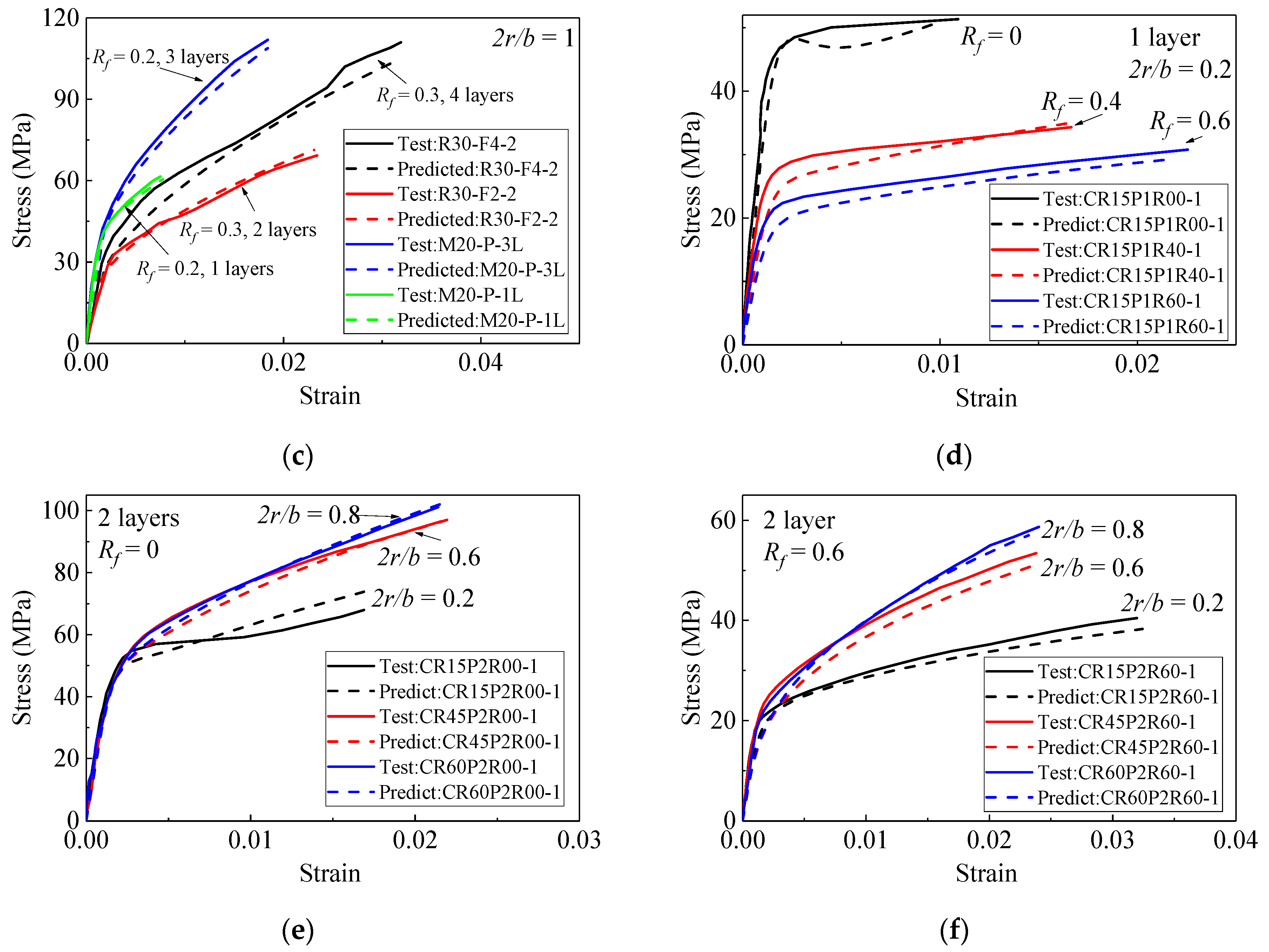
4. Model Prediction
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jiang, C.; Wu, Y.-F. Axial Strength of Eccentrically Loaded FRP-Confined Short Concrete Columns. Polymers 2020, 12, 1261. [Google Scholar] [CrossRef]
- Jiang, C.; Yuan, F.; Wu, Y.-F.; Zhao, X.-M. Effect of Interfacial Bond on Plastic Hinge Length of FRP-Confined RC Columns. J. Compos. Constr. 2019, 23. [Google Scholar] [CrossRef]
- Cao, Y.; Wu, Y.-F.; Jiang, C. Stress–strain relationship of FRP-confined concrete columns under combined axial load and bending moment. Compos. B. Eng. 2018, 134, 207–217. [Google Scholar] [CrossRef]
- Tijani, I.A.; Jiang, C.; Lim, C.W.; Wu, Y.F. Effect of Load Eccentricity on the Mechanical Response of FRP-Confined Predamaged Concrete under Compression. J. Compos. Constr. 2020, 24. [Google Scholar] [CrossRef]
- Jiang, C.; Wu, Y.F.; Wu, G. Plastic Hinge Length of FRP-Confined Square RC Columns. J. Compos. Constr. 2014, 18. [Google Scholar] [CrossRef]
- Tijani, I.A.; Jiang, C.; Lim, C.W.; Wu, Y.F. Eccentrically Loaded Concrete under Nonuniform Passive Confinement. J. Struct. Eng. 2022, 148. [Google Scholar] [CrossRef]
- Youssf, O.; ElGawady, M.A.; Mills, J.E. Static cyclic behaviour of FRP-confined crumb rubber concrete columns. Eng. Struct. 2016, 113, 371–387. [Google Scholar] [CrossRef]
- Moustafa, A.; ElGawady, M.A. Strain Rate Effect on Properties of Rubberized Concrete Confined with Glass Fiber–Reinforced Polymers. J. Compos. Constr. 2016, 20, 04016014. [Google Scholar] [CrossRef]
- Gholampour, A.; Ozbakkaloglu, T.; Hassanli, R. Behavior of rubberized concrete under active confinement. Constr. Build. Mater. 2017, 138, 372–382. [Google Scholar] [CrossRef]
- Chan, C.W.; Yu, T.; Zhang, S.S.; Xuc, Q.F. Compressive behaviour of FRP-confined rubber concrete. Constr. Build. Mater. 2019, 211, 416–426. [Google Scholar] [CrossRef]
- Bompa, D.V.; Elghazouli, A.Y. Stress–strain response and practical design expressions for FRP-confined recycled tyre rubber concrete. Constr. Build. Mater. 2020, 237, 117633. [Google Scholar] [CrossRef]
- Cao, Y.-G.; Hou, C.; Liu, M.-Y.; Jiang, C. Effects of predamage and load cyclic on compression behavior of fiber reinforced polymer-confined concrete. Struct. Concr. 2021, 22, 1784–1799. [Google Scholar] [CrossRef]
- Wang, Z.; Hajirasouliha, I.; Guadagnini, M.; Pilakoutas, K. Axial behaviour of FRP-confined rubberised concrete: An experimental investigation. Constr. Build. Mater. 2021, 267, 121023. [Google Scholar] [CrossRef]
- Can, H. Study on the Stress–Strain Model of CFRP-Confined Rubber Concrete under Different Loading Path; Wuhan University of Technology: Wuhan, China, 2020. (In Chinese) [Google Scholar]
- Yang, Z. Axial Compressive Properties and Application of CFRP-Confined Rubber Square Concrete Columns; Wuhan University of Technology: Wuhan, China, 2020. (In Chinese) [Google Scholar]
- Oprişan, G.; Enţuc, I.-S.; Mihai, P.; Toma, I.-O.; Ţăranu, N.; Budescu, M.; Munteanu, V. Behaviour of Rubberized Concrete Short Columns Confined by Aramid Fibre Reinforced Polymer Jackets Subjected to Compression. Adv. Civ. Eng. 2019, 2019, 1–11. [Google Scholar] [CrossRef]
- Hassanli, R.; Youssf, O.; Vincent, T.; Mills, J.E.; Manalo, A.; Gravina, R. Experimental Study on Compressive Behavior of FRP-Confined Expansive Rubberized Concrete. J. Compos. Constr. 2020, 24, 04020034. [Google Scholar] [CrossRef]
- Youssf, O.; Hassanli, R.; Mills, J.E. Mechanical performance of FRP-confined and unconfined crumb rubber concrete containing high rubber content. J. Build. Eng. 2017, 11, 115–126. [Google Scholar] [CrossRef]
- Youssf, O.; ElGawady, M.A.; Mills, J.E.; Ma, X. An experimental investigation of crumb rubber concrete confined by fibre reinforced polymer tubes. Constr. Build. Mater. 2014, 53, 522–532. [Google Scholar] [CrossRef]
- Tufail, R.F.; Feng, X.; Farooq, D.; Abdelmelek, N.; Lublóy, É. Behavior and Strength Predictions for CFRP-confined Rubberized Concrete under Axial Compression. Period. Polytech. Civ. Eng. 2021, 66, 1–19. [Google Scholar] [CrossRef]
- Raffoul, S.; Escolano-Margarit, D.; Garcia, R.; Guadagnini, M.; Pilakoutas, K. Constitutive Model for Rubberized Concrete Passively Confined with FRP Laminates. J. Compos. Constr. 2019, 23, 04019044. [Google Scholar] [CrossRef]
- Yang, J.-Q.; Feng, P. Analysis-oriented models for FRP-confined concrete: 3D interpretation and general methodology. Eng. Struct. 2020, 216, 110749. [Google Scholar] [CrossRef]
- Teng, J.G.; Lin, G.; Yu, T. Analysis-Oriented Stress–strain Model for Concrete under Combined FRP-Steel Confinement. J. Compos. Constr. 2015, 19, 04014084. [Google Scholar] [CrossRef]
- Pan, Y.; Wan, L.; Wu, X. Analysis-oriented stress–strain model of CFRP-confined concrete with preload. J. Southwest Jiaotong Uni. 2015, 50, 461–465. [Google Scholar]
- Jiang, T.; Teng, J.G. Analysis-oriented stress–strain models for FRP–confined concrete. Eng. Struct. 2007, 29, 2968–2986. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Ye, L.P.; Lam, L.; Teng, J.G. A Unified Analysis-oriented Model for Confined Concrete and Its Applications. In Proceedings of the International Symposium on Confined Concrete, Changsha, China, 12–14 June 2004. [Google Scholar]
- Richart, F.E.; Brandtzæg, A.; Brown, R.L. A Study of the Failure of Concrete under Combined Compressive Stresses; University of Illinois at Urbana Champaign, College of Engineering: Champaign, IL, USA, 1928. [Google Scholar]
- Popovics, S. A numerical approach to the complete stress–strain curve of concrete. Cem. Concr. Res. 1973, 3, 583–599. [Google Scholar] [CrossRef]
- Bompa, D.V.; Elghazouli, A.Y.; Xu, B.; Stafford, P.J.; Ruiz-Teran, A.M. Experimental assessment and constitutive modelling of rubberised concrete materials. Constr. Build. Mater. 2017, 137, 246–260. [Google Scholar] [CrossRef] [Green Version]
- Ozbakkaloglu, T.; Lim, J.C.; Vincent, T. FRP-confined concrete in circular sections: Review and assessment of stress–strain models. Eng. Struct. 2013, 49, 1068–1088. [Google Scholar] [CrossRef]
- Teng, J.G.; Huang, Y.L.; Lam, L.; Ye, L.P. Theoretical model for fiber-reinforced polymer-confined concrete. J. Compos. Constr. 2007, 11, 201–210. [Google Scholar] [CrossRef]
- Cao, Y.G.; Jiang, C.; Wu, Y.F. Cross-Sectional Unification on the Stress–strain Model of Concrete Subjected to High Passive Confinement by Fiber-Reinforced Polymer. Polymers 2016, 8, 186. [Google Scholar] [CrossRef] [Green Version]
- Abbasnia, R.; Hosseinpour, F.; Rostamian, M.; Ziaadiny, H. Cyclic and monotonic behavior of FRP-confined concrete rectangular prisms with different aspect ratios. Constr. Build. Mater. 2013, 40, 118–125. [Google Scholar] [CrossRef]
- Abbasnia, R.; Ahmadi, R.; Ziaadiny, H. Effect of confinement level, aspect ratio and concrete strength on the cyclic stress–strain behavior of FRP-confined concrete prisms. Compos. B. Eng. 2012, 43, 825–831. [Google Scholar] [CrossRef]
- Nisticò, N. R.C. square sections confined by FRP: A numerical procedure for predicting stress–strain relationships. Compos. B. Eng. 2014, 59, 238–247. [Google Scholar] [CrossRef]
- Wei, Y.-Y.; Wu, Y.-F. Unified stress–strain model of concrete for FRP-confined columns. Constr. Build. Mater. 2012, 26, 381–392. [Google Scholar] [CrossRef]
- Teng, J.G.; Zhao, J.L.; Yu, T.; Li, L.-J.; Guo, Y.C. Behavior of FRP-confined compound concrete containing recycled concrete lumps. J. Compos. Constr. 2016, 20, 04015038. [Google Scholar] [CrossRef]
- Xie, T.; Ozbakkaloglu, T. Behavior of recycled aggregate concrete-filled basalt and carbon FRP tubes. Constr. Build. Mater. 2016, 105, 132–143. [Google Scholar] [CrossRef]
- Cao, Y.-G.; Zhang, Y.; Liu, M.-Y.; Lu, Z.-F.; Jiang, C. Analysis-oriented stress–strain model for FRP-confined predamaged concrete. J. Build. Eng. 2021, 36, 10–1016. [Google Scholar] [CrossRef]
- Dai, J.-G.; Bai, Y.-L.; Teng, J.G. Behavior and Modeling of Concrete Confined with FRP Composites of Large Deformability. J. Compos. Constr. 2011, 15, 963–973. [Google Scholar] [CrossRef]
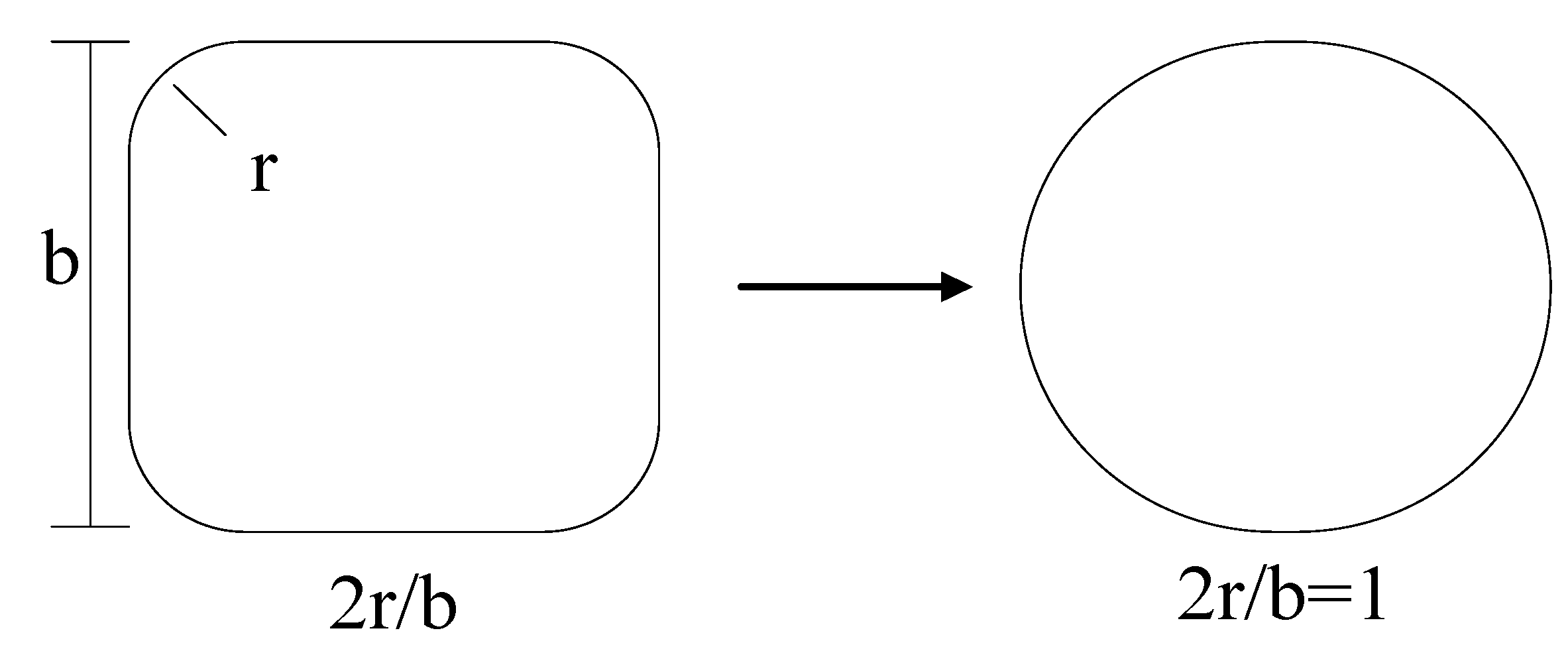

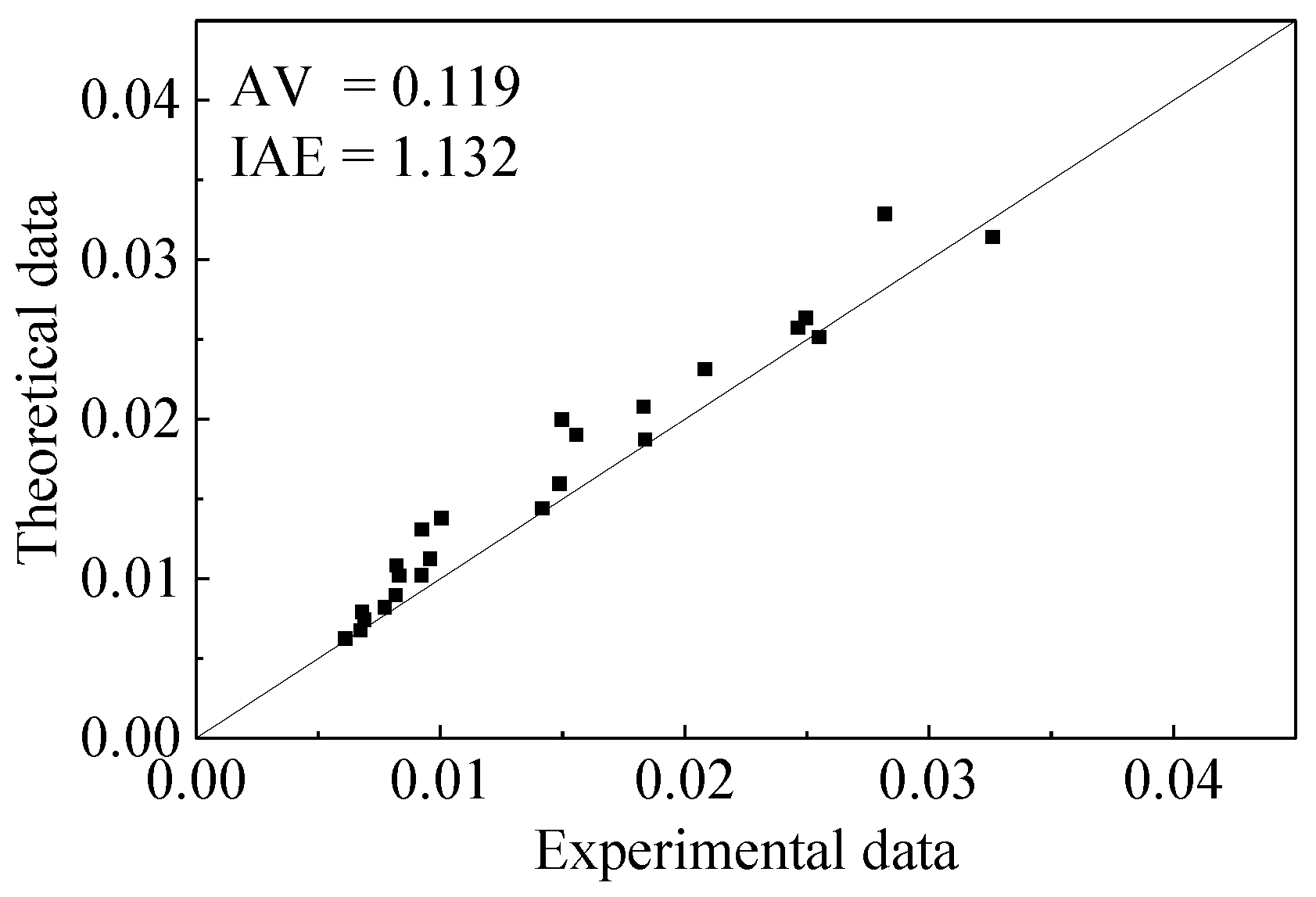
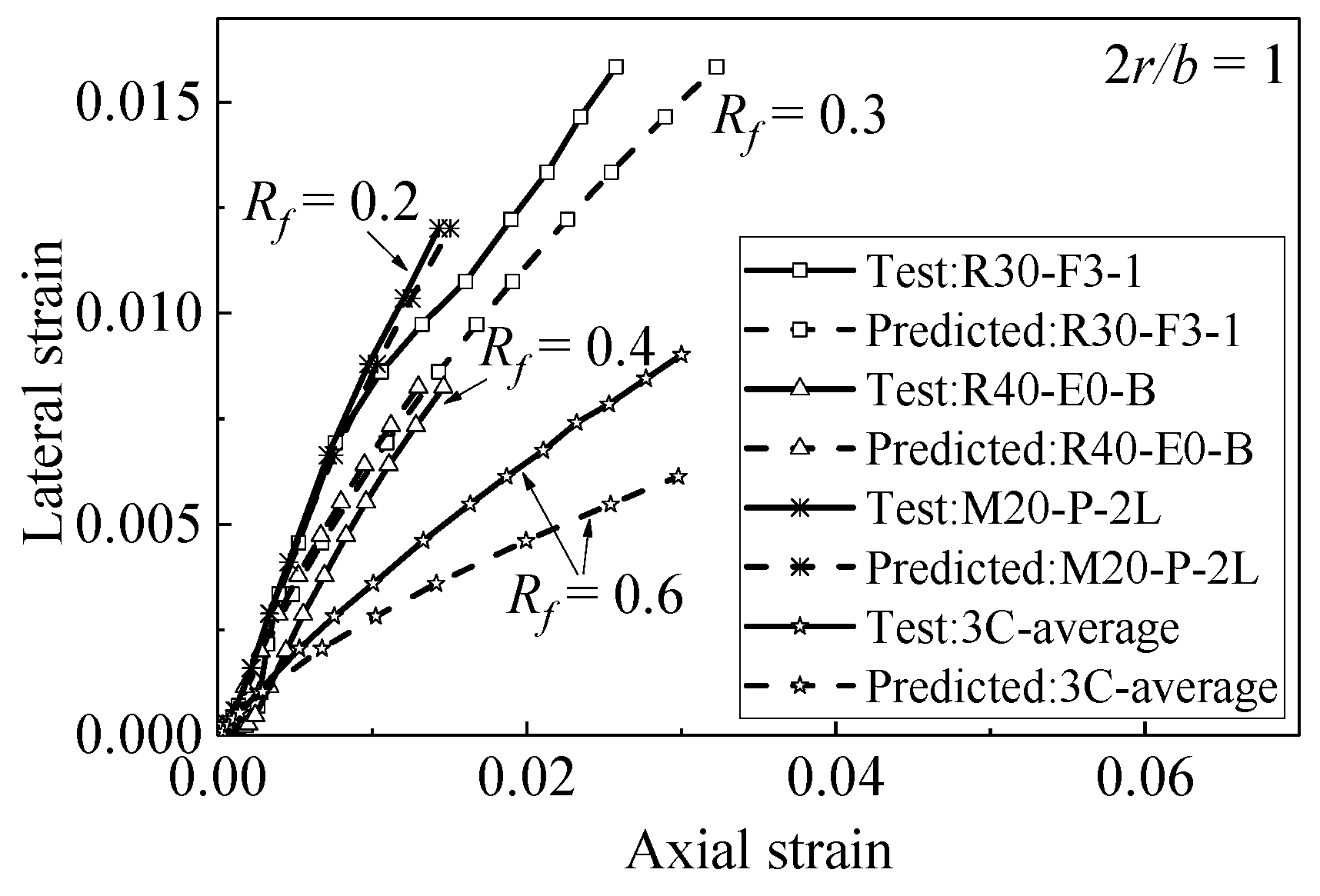
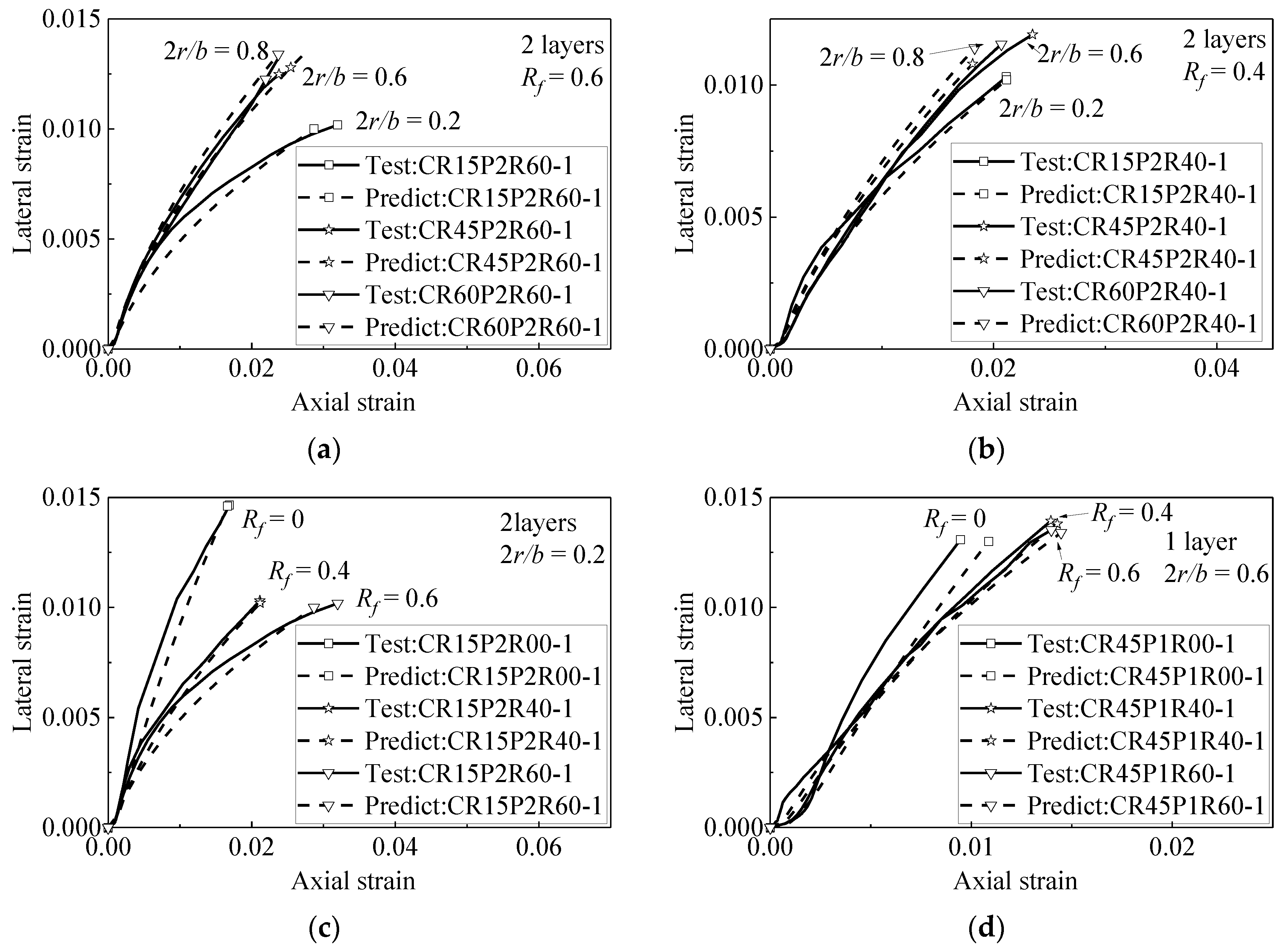
| Reference | Number of Specimens | FRP Type | Rf | εco (×10−3) | fco (MPa) | b × h (mm) | Retrofit Method | 2r/b |
|---|---|---|---|---|---|---|---|---|
| Hou [14] | 64 | CFRP | 0–0.6 | 1.6–2 | 16–45 | 150 × 300 | Wrap | 1 |
| Zhang [15] | 72 | CFRP | 0–0.6 | 1.1–2.2 | 10.3–37.2 | 150 × 300 | Wrap | 0.2–0.8 |
| Chan et al. [10] | 8 | GFRP | 0–0.75 | 2.2–2.7 | 13.9–53 | 150 × 300 | Wrap | 1 |
| Cao et al [12] | 12 | CFRP | 0–0.3 | 2.1–2.6 | 18.3–25.4 | 150 × 300 | Wrap | 1 |
| Bompa [11] | 22 | AFRP | 0–0.6 | 1.37–2.61 | 7.1–69.5 | 150 × 300 | Wrap | 1 |
| Oprisan et al [16] | 3 | AFRP | 0.4 | 0.69 | 10.97 | 100 × 200 | Wrap | 0.12 |
| Hassanli et al. [17] | 9 | CFRP | 0–0.4 | 1.7–1.95 | 20.7–32.0 | 100 × 200 | Wrap | 1 |
| Youssf et al. [18] | 12 | CFRP | 0–0.5 | 1.71–1.95 | 21.6–64.4 | 150 × 300 | Wrap | 1 |
| Youssf et al. [19] | 14 | CFRP | 0–0.2 | 1.67–2.43 | 39.2–62.5 | 100 × 200 | CFFT | 1 |
| Tufail et al. [20] | 9 | CFRP | 0.5 | 1.75 | 8–19 | 150 × 300 | CFFT & Wrap | 1 |
| Raffoul et al. [21] | 10 | CFRP & AFRP | 0.6 | 1.35 | 6.8–8.2 | 100 × 200 & 150 × 300 | Wrap | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Y.; Zhao, G.; Zhang, Y.; Hou, C.; Mao, L. Unified Stress–Strain Model of FRP-Confined Square and Circle Rubber Concrete Columns. Materials 2022, 15, 1832. https://doi.org/10.3390/ma15051832
Cao Y, Zhao G, Zhang Y, Hou C, Mao L. Unified Stress–Strain Model of FRP-Confined Square and Circle Rubber Concrete Columns. Materials. 2022; 15(5):1832. https://doi.org/10.3390/ma15051832
Chicago/Turabian StyleCao, Yugui, Guoxu Zhao, Yang Zhang, Can Hou, and Ling Mao. 2022. "Unified Stress–Strain Model of FRP-Confined Square and Circle Rubber Concrete Columns" Materials 15, no. 5: 1832. https://doi.org/10.3390/ma15051832
APA StyleCao, Y., Zhao, G., Zhang, Y., Hou, C., & Mao, L. (2022). Unified Stress–Strain Model of FRP-Confined Square and Circle Rubber Concrete Columns. Materials, 15(5), 1832. https://doi.org/10.3390/ma15051832





