Thermoelectric Properties of Cu2Te Nanoparticle Incorporated N-Type Bi2Te2.7Se0.3
Abstract
:1. Introduction
2. Materials and Methods
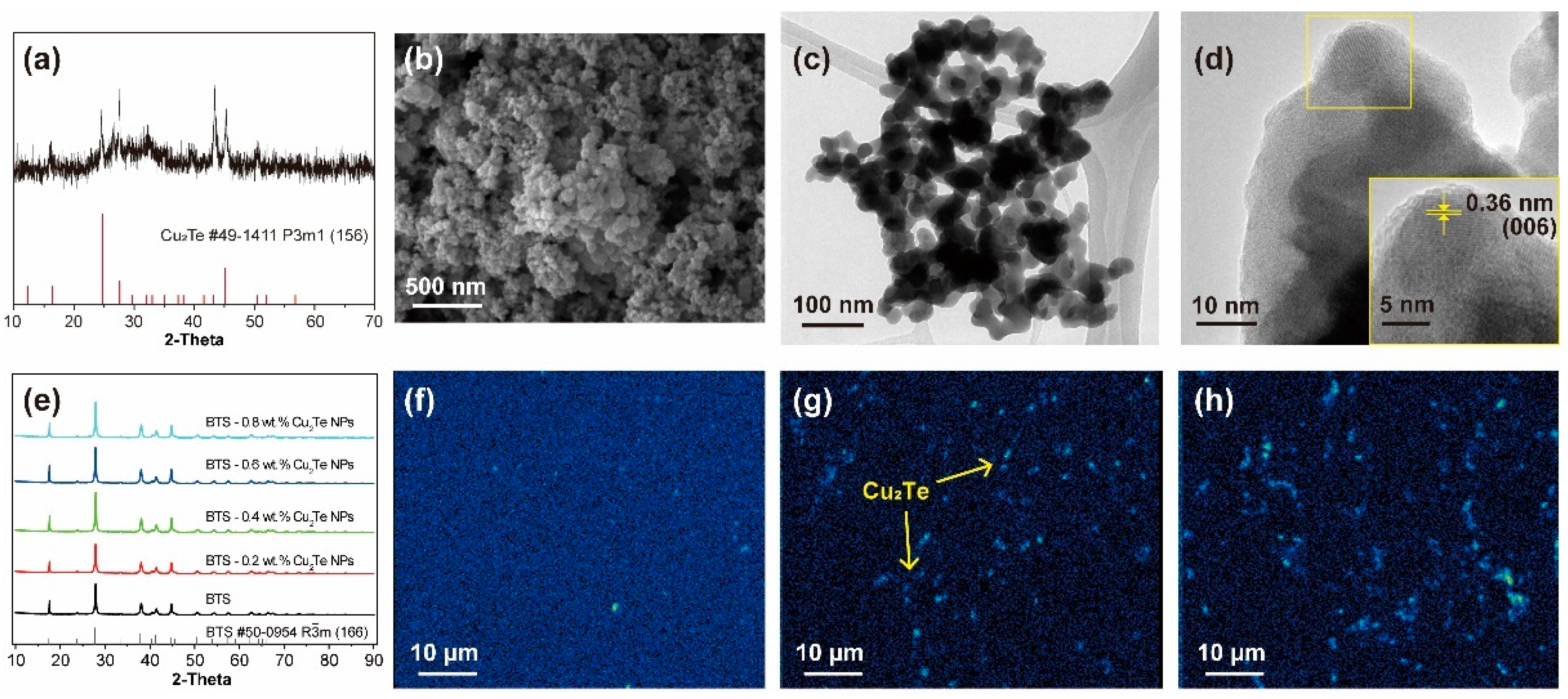
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Snyder, G.J.; Toberer, E.S. Complex thermoelectric materials. Nat. Mater. 2008, 7, 105–114. [Google Scholar] [CrossRef] [PubMed]
- Shi, X.-L.; Zou, J.; Chen, Z.-G. Advanced thermoelectric design: From materials and structures to devices. Chem. Rev. 2020, 120, 7399–7515. [Google Scholar] [CrossRef] [PubMed]
- Funahashi, R.; Barbier, T.; Combe, E. Thermoelectric materials for middle and high temperature ranges. J. Mater. Res. 2015, 30, 2544–2557. [Google Scholar] [CrossRef]
- Shi, X.; Yang, J.; Wu, L.; Salvador, J.R.; Zhang, C.; Villaire, W.L.; Haddad, D.; Yang, J.; Zhu, Y.; Li, Q. Band structure engineering and thermoelectric properties of charge-compensated filled skutterudites. Sci. Rep. 2015, 5, 14641. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pei, Y.; Tan, G.; Feng, D.; Zheng, L.; Tan, Q.; Xie, X.; Gong, S.; Chen, Y.; Li, J.F.; He, J. Integrating band structure engineering with all-scale hierarchical structuring for high thermoelectric performance in PbTe system. Adv. Energy Mater. 2017, 7, 1601450. [Google Scholar] [CrossRef]
- Yoon, J.S.; Song, J.M.; Rahman, J.U.; Lee, S.; Seo, W.S.; Lee, K.H.; Kim, S.; Kim, H.-S.; Kim, S.-I.; Shin, W.H. High thermoelectric performance of melt-spun CuxBi0.5Sb1.5Te3 by synergetic effect of carrier tuning and phonon engineering. Acta Mater. 2018, 158, 289–296. [Google Scholar] [CrossRef]
- Jood, P.; Male, J.P.; Anand, S.; Matsushita, Y.; Takagiwa, Y.; Kanatzidis, M.G.; Snyder, G.J.; Ohta, M. Na doping in PbTe: Solubility, band convergence, phase boundary mapping, and thermoelectric properties. J. Am. Chem. Soc. 2020, 142, 15464–15475. [Google Scholar] [CrossRef] [PubMed]
- Poudel, B.; Hao, Q.; Ma, Y.; Lan, Y.; Minnich, A.; Yu, B.; Yan, X.; Wang, D.; Muto, A.; Vashaee, D. High-thermoelectric performance of nanostructured bismuth antimony telluride bulk alloys. Science 2008, 320, 634–638. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cai, X.; Rong, Z.; Yang, F.; Gan, Z.; Li, G. Improved thermoelectric properties of Bi2Te3−xSex alloys by melt spinning and resistance pressing sintering. J. Phys. D Appl. Phys. 2014, 47, 115101. [Google Scholar] [CrossRef]
- Ahn, K.; Biswas, K.; He, J.; Chung, I.; Dravid, V.; Kanatzidis, M.G. Enhanced thermoelectric properties of p-type nanostructured PbTe–MTe (M = Cd, Hg) materials. Energy Environ. Sci. 2013, 6, 1529–1537. [Google Scholar] [CrossRef]
- Shin, W.H.; Roh, J.W.; Ryu, B.; Chang, H.J.; Kim, H.S.; Lee, S.; Seo, W.S.; Ahn, K. Enhancing thermoelectric performances of bismuth antimony telluride via synergistic combination of multiscale structuring and band alignment by FeTe2 incorporation. ACS Appl. Mater. Interfaces 2018, 10, 3689–3698. [Google Scholar] [CrossRef]
- Kim, S.I.; Lee, K.H.; Mun, H.A.; Kim, H.S.; Hwang, S.W.; Roh, J.W.; Yang, D.J.; Shin, W.H.; Li, X.S.; Lee, Y.H. Dense dislocation arrays embedded in grain boundaries for high-performance bulk thermoelectrics. Science 2015, 348, 109–114. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Koh, Y.K.; Vineis, C.; Calawa, S.; Walsh, M.; Cahill, D.G. Lattice thermal conductivity of nanostructured thermoelectric materials based on PbTe. Appl. Phys. Lett. 2009, 94, 153101. [Google Scholar] [CrossRef]
- Wu, H.; Carrete, J.; Zhang, Z.; Qu, Y.; Shen, X.; Wang, Z.; Zhao, L.-D.; He, J. Strong enhancement of phonon scattering through nanoscale grains in lead sulfide thermoelectrics. NPG Asia Mater. 2014, 6, e108. [Google Scholar] [CrossRef]
- Faleev, S.V.; Léonard, F. Theory of enhancement of thermoelectric properties of materials with nanoinclusions. Phys. Rev. B 2008, 77, 214304. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Qin, X.; Li, D.; Zhang, J.; Li, C.; Liu, Y.; Song, C.; Xin, H.; Guo, H. Enhanced thermoelectric performance of Cu2Se/Bi0.4Sb1.6Te3 nanocomposites at elevated temperatures. Appl. Phys. Lett. 2016, 108, 062104. [Google Scholar] [CrossRef]
- Cho, H.; Back, S.Y.; Yun, J.H.; Byeon, S.; Jin, H.; Rhyee, J.-S. Thermoelectric properties and low-energy carrier filtering by Mo microparticle dispersion in an n-type (CuI)0.003Bi2(Te, Se)3 bulk matrix. ACS Appl. Mater. Interfaces 2020, 12, 38076–38084. [Google Scholar] [CrossRef]
- Tan, G.; Shi, F.; Hao, S.; Zhao, L.-D.; Chi, H.; Zhang, X.; Uher, C.; Wolverton, C.; Dravid, V.P.; Kanatzidis, M.G. Non-equilibrium processing leads to record high thermoelectric figure of merit in PbTe–SrTe. Nat. Commun. 2016, 7, 12167. [Google Scholar] [CrossRef]
- Kim, S.I.; Hwang, S.; Roh, J.W.; Ahn, K.; Yeon, D.-H.; Lee, K.H.; Kim, S.W. Experimental evidence of enhancement of thermoelectric properties in tellurium nanoparticle-embedded bismuth antimony telluride. J. Mater. Res. 2012, 27, 2449–2456. [Google Scholar] [CrossRef]
- Li, S.; Liu, X.; Liu, Y.; Liu, F.; Luo, J.; Pan, F. Optimized hetero-interfaces by tuning 2D SnS2 thickness in Bi2Te2.7Se0.3/SnS2 nanocomposites to enhance thermoelectric performance. Nano Energy 2017, 39, 297–305. [Google Scholar] [CrossRef]
- Wu, H.-J.; Yen, W.-T. High thermoelectric performance in Cu-doped Bi2Te3 with carrier-type transition. Acta Mater. 2018, 157, 33–41. [Google Scholar] [CrossRef]
- Lognoné, Q.; Gascoin, F. Reactivity, stability and thermoelectric properties of n-Bi2Te3 doped with different copper amounts. J. Alloys Compd. 2014, 610, 1–5. [Google Scholar] [CrossRef]
- Han, M.-K.; Jin, Y.; Lee, D.-H.; Kim, S.-J. Thermoelectric properties of Bi2Te3: CuI and the effect of its doping with Pb atoms. Materials 2017, 10, 1235. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, W.S.; Zhang, Q.; Lan, Y.; Chen, S.; Yan, X.; Zhang, Q.; Wang, H.; Wang, D.; Chen, G.; Ren, Z. Thermoelectric property studies on Cu-doped n-type CuxBi2Te2.7Se0.3 nanocomposites. Adv. Energy Mater. 2011, 1, 577–587. [Google Scholar] [CrossRef]
- Ioffe, A.F. Physics of Semiconductors; Academic Press: Cambridge, MA, USA, 1960. [Google Scholar]
- Rahman, M.W.; Rahman, S.I.; Ahmed, S.N.; Hoque, M.A. Numerical Analysis of CdS: O/CdTe Thin Film Solar Cell using Cu2Te BSF Layer. In Proceedings of the 9th International Conference on Electrical and Computer Engineering (ICECE), Dhaka, Bangladesh, 20–22 December 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 279–282. [Google Scholar]
- Li, F.; Zhai, R.; Wu, Y.; Xu, Z.; Zhao, X.; Zhu, T. Enhanced thermoelectric performance of n-type bismuth-telluride-based alloys via In alloying and hot deformation for mid-temperature power generation. J. Mater. 2018, 4, 208–214. [Google Scholar] [CrossRef]
- Sun, T.; Samani, M.K.; Khosravian, N.; Ang, K.M.; Yan, Q.; Tay, B.K.; Hng, H.H. Enhanced thermoelectric properties of n-type Bi2Te2.7Se0.3 thin films through the introduction of Pt nanoinclusions by pulsed laser deposition. Nano Energy 2014, 8, 223–230. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y.; Xi, L.; Qiu, R.; Shi, X.; Zhang, P.; Zhang, W. Electronic structure of antifluorite Cu2X (X = S, Se, Te) within the modified Becke-Johnson potential plus an on-site Coulomb U. J. Chem. Phys. 2014, 140, 074702. [Google Scholar] [CrossRef] [PubMed]
- Kittel, C. Introduction to Solid State Physics, 6th ed.; John Wiley & Sons. Inc.: New York, NY, USA, 2005. [Google Scholar]
- Kim, M.; Kim, S.I.; Kim, S.W.; Kim, H.S.; Lee, K.H. Weighted Mobility Ratio Engineering for High-Performance Bi-Te-Based Thermoelectric Materials via Suppression of Minority Carrier Transport. Adv. Mater. 2021, 33, 2005931. [Google Scholar] [CrossRef] [PubMed]
- Witting, I.T.; Chasapis, T.C.; Ricci, F.; Peters, M.; Heinz, N.A.; Hautier, G.; Snyder, G.J. The thermoelectric properties of bismuth telluride. Adv. Electron. Mater. 2019, 5, 1800904. [Google Scholar] [CrossRef]
- Lee, K.H.; Kim, Y.-M.; Park, C.O.; Shin, W.H.; Kim, S.W.; Kim, H.-S.; Kim, S.-I. Cumulative Defect Structures for Experimentally-Attainable Low Thermal Conductivity in Thermoelectric (Bi, Sb)2Te3 Alloys. Mater. Today Energy 2021, 21, 100795. [Google Scholar] [CrossRef]
- Parasuraman, R.; Wu, Y.; Ordonez-Miranda, J.; Volz, S.; Umarji, A.M. Particle size effect on the thermal conductivity reduction of silicon based thermoelectric composites. Sustain. Energy Fuels 2018, 2, 1764–1771. [Google Scholar] [CrossRef]


| Lattice Constant for a (Å) | Lattice Constant for c (Å) | |
|---|---|---|
| BTS | 4.3619 | 30.3632 |
| BTS-0.2 wt.% Cu2Te NPs | 4.3614 | 30.3604 |
| BTS-0.4 wt.% Cu2Te NPs | 4.3615 | 30.3641 |
| BTS-0.6 wt.% Cu2Te NPs | 4.3610 | 30.3606 |
| BTS-0.8 wt.% Cu2Te NPs | 4.3614 | 30.3650 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, Y.-J.; Kim, H.-S.; Won, J.H.; Kim, M.; Kang, M.; Jang, E.Y.; Binh, N.V.; Kim, S.-i.; Moon, K.-S.; Roh, J.W.; et al. Thermoelectric Properties of Cu2Te Nanoparticle Incorporated N-Type Bi2Te2.7Se0.3. Materials 2022, 15, 2284. https://doi.org/10.3390/ma15062284
Jung Y-J, Kim H-S, Won JH, Kim M, Kang M, Jang EY, Binh NV, Kim S-i, Moon K-S, Roh JW, et al. Thermoelectric Properties of Cu2Te Nanoparticle Incorporated N-Type Bi2Te2.7Se0.3. Materials. 2022; 15(6):2284. https://doi.org/10.3390/ma15062284
Chicago/Turabian StyleJung, Yong-Jae, Hyun-Sik Kim, Jong Ho Won, Minkyung Kim, Minji Kang, Eun Young Jang, Nguyen Vu Binh, Sang-il Kim, Kyoung-Seok Moon, Jong Wook Roh, and et al. 2022. "Thermoelectric Properties of Cu2Te Nanoparticle Incorporated N-Type Bi2Te2.7Se0.3" Materials 15, no. 6: 2284. https://doi.org/10.3390/ma15062284
APA StyleJung, Y.-J., Kim, H.-S., Won, J. H., Kim, M., Kang, M., Jang, E. Y., Binh, N. V., Kim, S.-i., Moon, K.-S., Roh, J. W., Nam, W. H., Koo, S.-M., Oh, J.-M., Cho, J. Y., & Shin, W. H. (2022). Thermoelectric Properties of Cu2Te Nanoparticle Incorporated N-Type Bi2Te2.7Se0.3. Materials, 15(6), 2284. https://doi.org/10.3390/ma15062284










