Electric and Dielectric Properties in Low-Frequency Fields of Composites Consisting of Silicone Rubber and Al Particles for Flexible Electronic Devices
Abstract
:1. Introduction
2. Materials and Methods
- -
- for sample A: and (10 g of each component, A and B);
- -
- for sample B: and (9.9 g of each component, A and B);
- -
- for sample C: and (9.8 g of each component, A and B);
- -
- for sample D: and (9.5 g of each component, A and B);
- -
- for sample E: and (9 g of each component, A and B).
3. Results and Discussion
3.1. SEM–EDX Results
3.2. Complex Impedance and Electrical Modulus
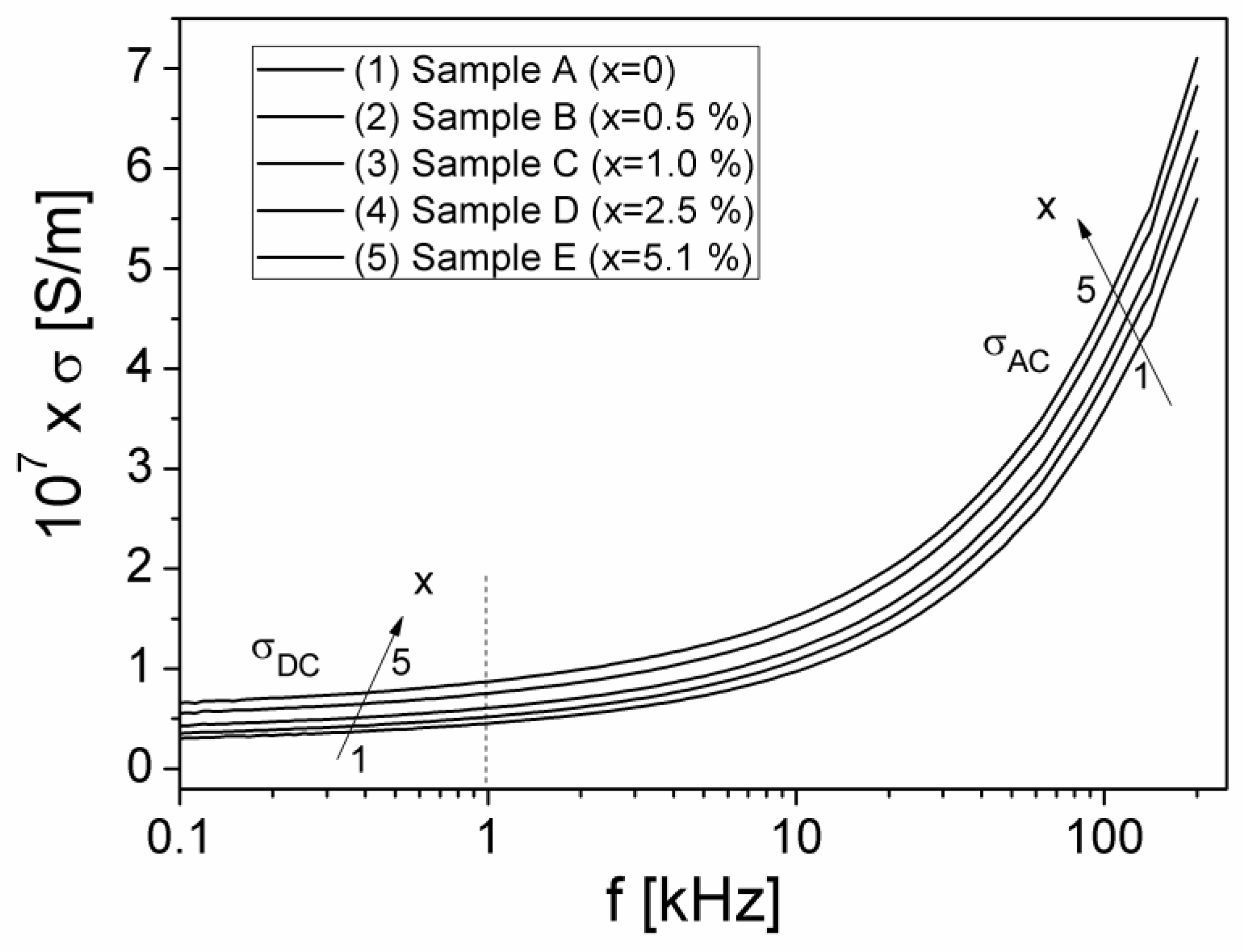
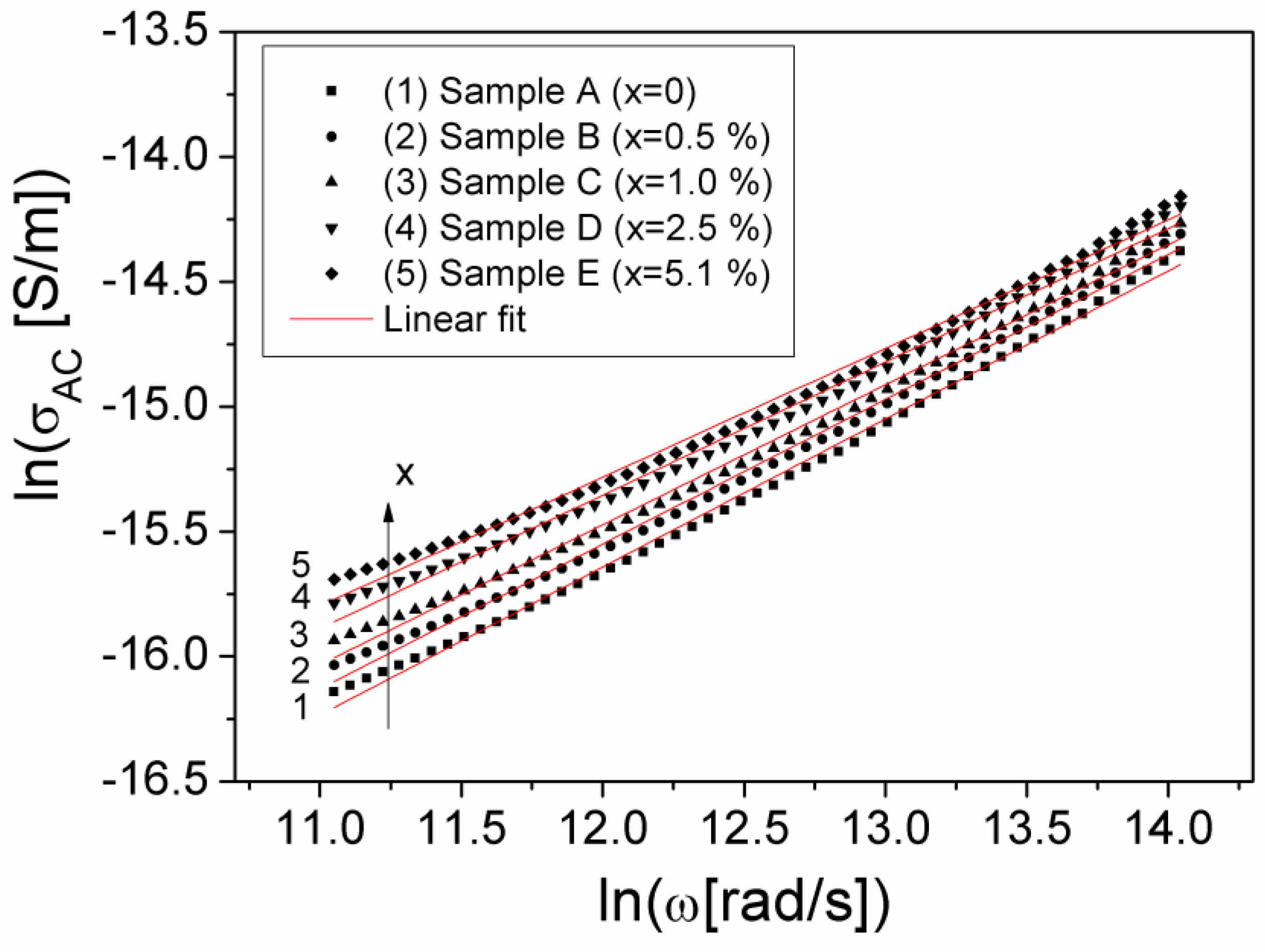
3.3. The Electrical Conductivity
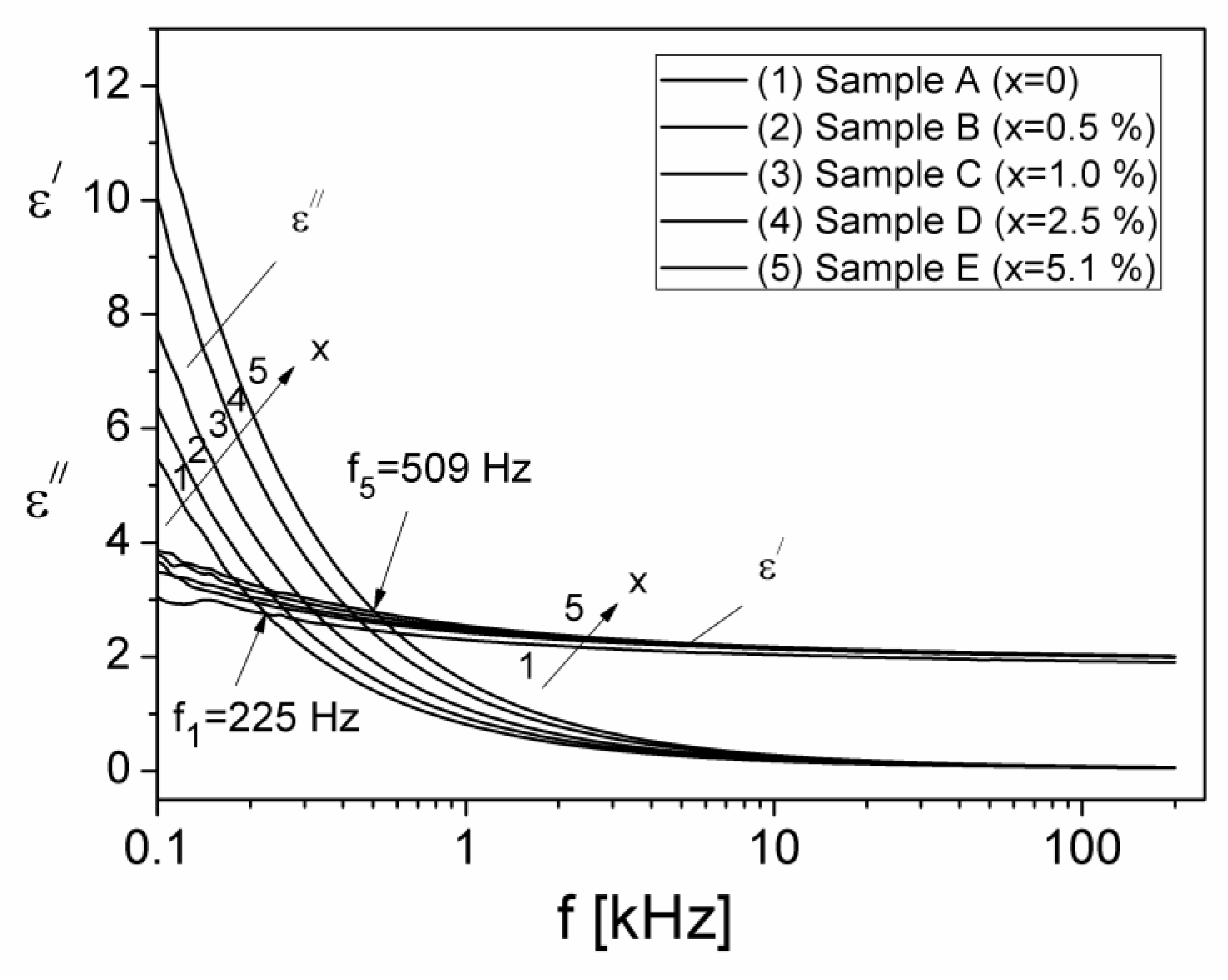
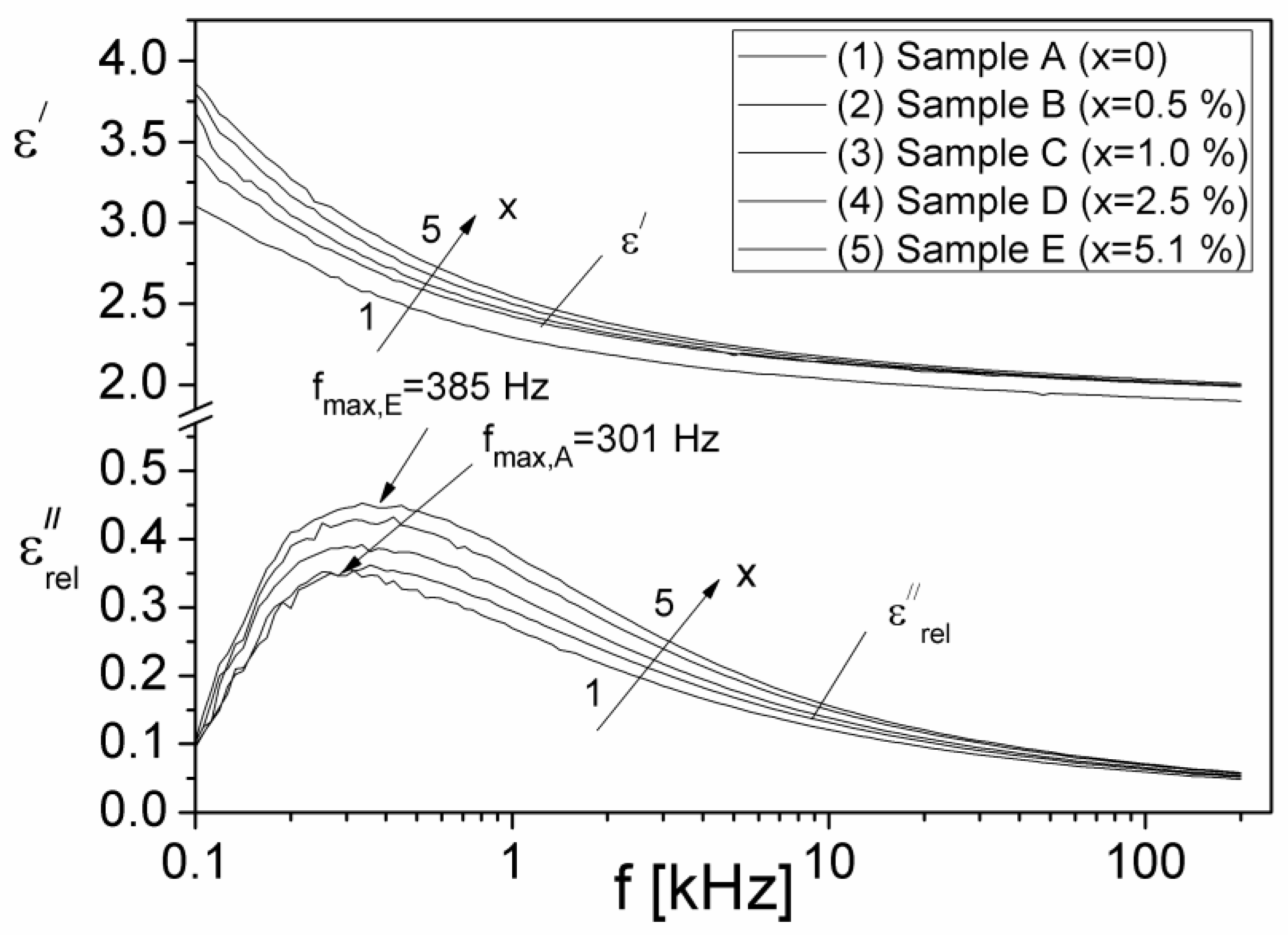
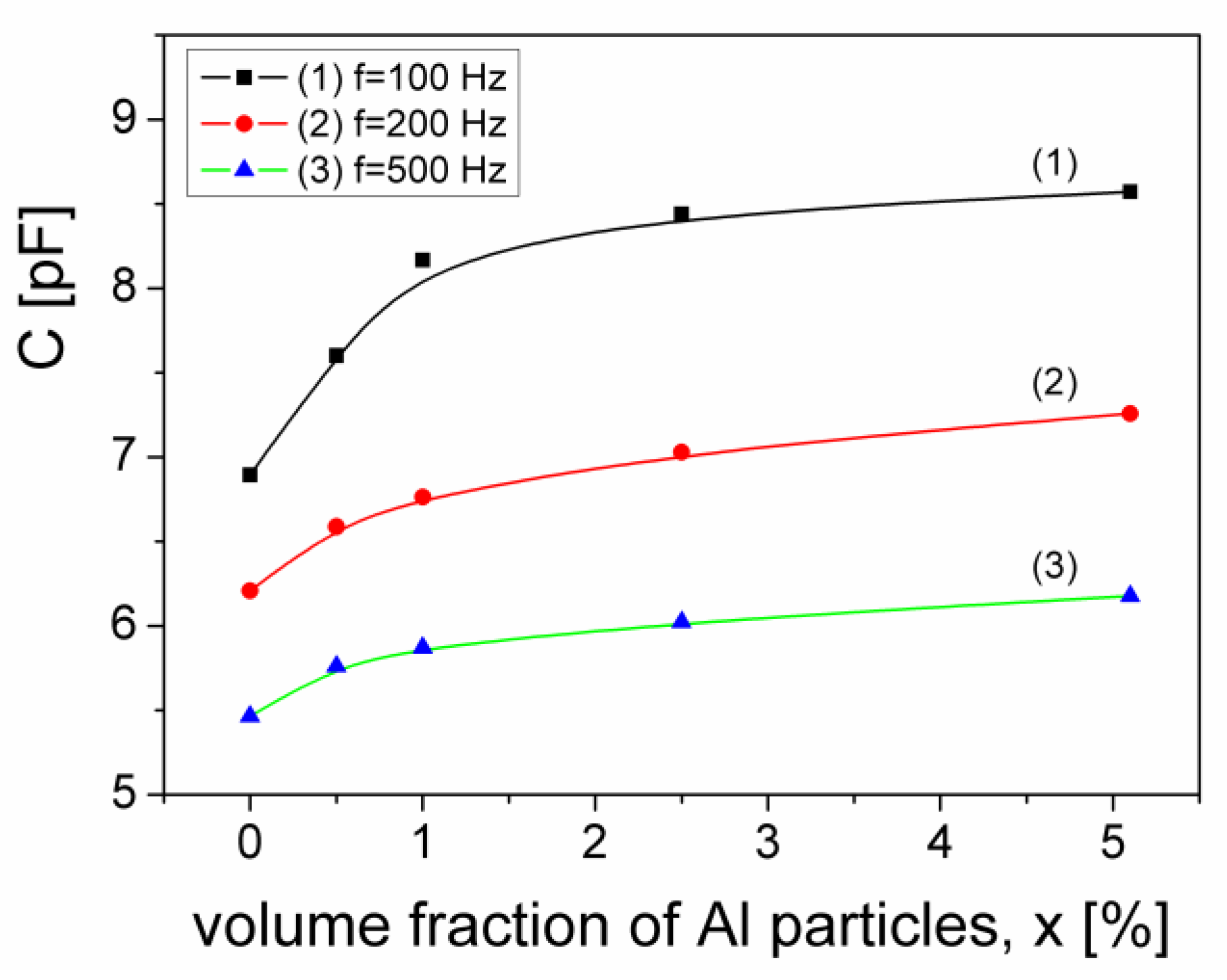
3.4. The Dielectric Permittivity
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Parameswaranpillai, J.; Hameed, N.; Kurian, T.; Yu, Y. (Eds.) Introduction to Nanomaterials and Nanocomposites. In Nanocomposite Materials, Synthesis, Properties and Applications; Chapter 1; CRC Press Taylor & Francis Group: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Bica, I.; Anitas, E.M.; Averis, L.M.E.; Bunoiu, M. Magnetodielectric effects in composite materials based on paraffin, carbonyl iron and grapheme. J. Ind. Eng. Chem. 2015, 21, 1323–1327. [Google Scholar] [CrossRef]
- Fornes, T.; Yoon, P.; Keskkula, H.; Paul, D. Nylon 6 nanocomposites: The effect of matrix molecular weight. Polymer 2001, 42, 09929–09940. [Google Scholar] [CrossRef]
- Marin, C.N.; Malaescu, I.; Sfirloaga, P.; Teusdea, A. Electric and magnetic properties of a composite consisting of silicone rubber and ferrofluid. J. Ind. Eng. Chem. 2021, 101, 405–413. [Google Scholar] [CrossRef]
- Ramakrishna, S.; Mayer, J.; Wintermantel, E.; Leong, K.V. Biomedical applicatons of polymer-composite materials: A review. Compos. Sci. Technol. 2001, 61, 1189–1224. [Google Scholar] [CrossRef]
- Hammami, H.; Arous, M.; Lagache, M.; Kallel, A. Study of the interfacial MWS relaxation by dielectric spectroscopy in unidirectional PZT fibres/epoxy resin composites. J. Alloys Compd. 2007, 430, 1–8. [Google Scholar] [CrossRef]
- Yakovenko, O.S.; Matzui, L.Y.; Vovchenko, L.L.; Lozitsky, O.V.; Prokopov, O.I.; Lazarenko, O.A.; Zhuravkov, A.V.; Oliynyk, V.V.; Launets, V.L.; Trukhanov, S.V.; et al. Electrophysical properties of epoxy-based composites with graphite nanoplatelets and magnetically aligned magnetite. Mol. Cryst. Liq. Cryst. 2018, 661, 68–80. [Google Scholar] [CrossRef]
- Gonzalez-Benito, J.; Martínez-Tarifa, J.; Sepúlveda-García, M.E.; Portillo, R.A.; Gonzalez-Gaitano, G. Composites based on HDPE filled with BaTiO3 submicrometric particles. Morphology, structure and dielectric properties. Polym. Test. 2013, 32, 1342–1349. [Google Scholar] [CrossRef]
- Zhang, Z.F.; Bai, X.F.; Zha, J.W.; Li, W.K.; Dang, Z.M. Preparation and dielectric of BaTiO3/epoxy nanocomposites for embedded capacitor application. Compos. Sci. Technol. 2014, 97, 100–105. [Google Scholar] [CrossRef]
- Baji, A.; Mai, Y.W.; Li, Q.; Liu, Y. Nanoscale investigation of ferroelectric properties in electrospun barium titanate/polyvinylidene fluoride composite fibers using piezoresponse force microscopy. Compos. Sci. Technol. 2011, 71, 1435–1440. [Google Scholar] [CrossRef]
- Jamal, E.M.A.; Joy, P.A.; Kurian, P.; Anantharaman, M.R. Synthesis of nickel-rubber nanocomposites and evaluation of their dielectric properties. Mater. Sci. Eng. B 2009, 156, 24–31. [Google Scholar] [CrossRef] [Green Version]
- Al-Ghamdi, A.A.; Al-Hartomy, O.A.; Al-Salamy, F.; El-Mossalamy, E.H.; Daiem, A.M.A.; El-Tantawy, F. Novel electromagnetic interference shielding effectiveness in the microwave band of magnetic nitrile butadiene rubber/magnetite nanocomposites. J. Appl. Polym. Sci. 2012, 125, 2604–2613. [Google Scholar] [CrossRef]
- Namitha, L.K.; Chameswary, J.; Ananthakumar, S.; Sebastian, M.T. Effect of micro- and nano-fillers on the properties of silicone rubber-alumina flexible microwave substrate. Ceram. Int. 2013, 39, 7077–7087. [Google Scholar] [CrossRef]
- Pantazi, A.; Palade, S.; Berbecaru, C.; Veca, M.; Dinescu, A.; Şchiopu, V.; Oprea, O.; Dragoman, D. Dielectric properties of composites containing silicone rubber and multiwall carbon nanotubes decorated with gold. Rom. Rep. Phys. 2016, 68, 648–657. [Google Scholar]
- Stiubianu, G.; Bele, A.; Cazacu, M.; Racles, C.; Vlad, S.; Ignat, M. Dielectric silicone elastomers with mixed ceramic nanoparticles. Mater. Res. Bull. 2015, 71, 67–74. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.; Zhang, Q.M. Fully functionalized high dielectric constant nanophase polymers with high electromechanical response. Adv. Mater. 2005, 17, 1153–1158. [Google Scholar] [CrossRef]
- Sui, X.; Zhou, W.; Dong, L.; Wang, Z.; Liu, X.; Zhou, A.; Cai, J.; Chen, Q. A novel fiber-reinforced silicone rubber composite with Al particles for enhanced dielectric and thermal properties. Adv. Polym. Technol. 2018, 37, 1507–1516. [Google Scholar] [CrossRef]
- Zhou, W.Y.; Cai, J.T.; Zhou, A.N. Thermal properties of the aluminum particle reinforced silicone rubber composites. Adv. Mater. Res. 2011, 194–196, 1680–1684. [Google Scholar] [CrossRef]
- Gao, B.Z.; Xu, J.Z.; Peng, J.J.; Kang, F.Y.; Du, H.D.; Li, J.; Chiang, S.W.; Xu, C.J.; Hu, N.; Ning, X.S. Experimental and theoretical studies of effective thermal conductivity of composites made of silicone rubber and Al2O3 particles. Thermochim. Acta 2015, 614, 1–8. [Google Scholar] [CrossRef]
- Madidi, F.; Momen, G.; Farzaneh, M. Dielectric properties of TiO2/silicone rubber micro and nanocomposites. Adv. Mater. Sci. Eng. 2018, 2018, 4682076. [Google Scholar] [CrossRef] [Green Version]
- Available online: https://www.prochima.com/ENG/ (accessed on 29 January 2022).
- Available online: https://www.sigmaaldrich.com/RO/en/product/aldrich/11009?context=product (accessed on 3 February 2022).
- Lungu, A.; Malaescu, I.; Marin, C.N.; Vlazan, P.; Sfirloaga, P. The electrical properties of manganese ferrite powders prepared by two different methods. Phys. B Condens. Matter 2015, 462, 80–85. [Google Scholar] [CrossRef]
- ASTM D150-98; Standard Test Methods for AC Loss Characteristics and Permittivity (Dielectric Constant) of Solid Electrical Insulation. ASTM International: West Conshohocken, PA, USA, 2004. [CrossRef]
- Goswami, A.; Goswami, A.P. Dielectric and optical properties of ZnS films. Thin Solid Film 1973, 16, 175–185. [Google Scholar] [CrossRef]
- Debye, P. Polar Molecules; Chemical Catalog Company, Inc.: New York, NY, USA, 1929. [Google Scholar]
- Barsoukov, E.; Macdonald, J.R. Impedance Spectroscopy: Theory, Experiments and Applications; Wiley: New York, NY, USA, 2005. [Google Scholar]
- Stoia, M.; Pacurariu, C.; Mihali, C.; Malaescu, I.; Marin, C.N.; Capraru, A. Manganese ferrite-polyaniline hybrid materials: Electrical and magnetic properties. Ceram. Int. 2019, 45, 2725–2735. [Google Scholar] [CrossRef]
- Rajnak, M.; Kurimsky, J.; Dolnik, B.; Kopcansky, P.; Tomasovicova, N.; Taculescu-Moaca, E.A.; Timko, M. Dielectric-spectroscopy approach to ferrofluid nanoparticle clustering induced by an external electric field. Phys. Rev. E 2014, 90, 032310. [Google Scholar] [CrossRef] [PubMed]
- Horn, T.; Deutschlander, S.; Lowen, H.; Maret, G.; Keim, P. Fluctuations of ori-entational order and clustering in a two-dimensional colloidal system under quenched disorder. Phys. Rev. E 2013, 88, 062305. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Harun, M.H.; Saion, E.; Kassim, A.; Mahmud, E.; Hussain, M.Y.; Mustafa, I.S. Dielectric properties of poly (vinyl alcohol)/polypyrrole composite polymer films. J. Adv. Sci. Arts 2009, 1, 9–16. [Google Scholar]
- Wubbenhorst, M.; van Turnhout, J. Analysis of complex dielectric spectra. I. One-dimensional derivative techniques and three-dimensional modeling. J. Non-Cryst. Solids. 2002, 305, 40–49. [Google Scholar] [CrossRef]
- Malaescu, I.; Lungu, A.; Marin, C.N.; Sfirloaga, P.; Vlazan, P.; Brindusoiu, S.; Poienar, M. Temperature dependence of the dynamic electrical properties of Cu1+xMn1-xO2 (x = 0 and 0.06) crednerite materials. Ceram. Int. 2018, 44, 11610–11616. [Google Scholar] [CrossRef]
- Asandulesa, M.; Kostromin, S.; Tameev, A.; Aleksandrov, A.; Bronnikov, S. Molecular dynamics and conductivity of a PTB7: PC71BM photovoltaic polymer blend: A dielectric spectroscopy study. ACS Appl. Polym. Mater. 2021, 3, 4869–4878. [Google Scholar] [CrossRef]
- Jonscher, A.K. Universal Relaxation Law, 1st ed.; Chelsea Dielectrics Press: London, UK, 1996. [Google Scholar]
- Jankowska, I.A.; Pogorzelec-Glaser, K.; Lawniczak, P.; Matczak, M.; Pankiewicz, R. New liquid-free proton conductive nanocomposite based on imidazole-functionalized cellulose nanofibers. Cellulose 2021, 28, 843–854. [Google Scholar] [CrossRef]
- Funke, K. Jump relaxation in solid electrolytes. Prog. Solid State Chem. 1993, 22, 111–195. [Google Scholar] [CrossRef]
- Lalanne, M.; Demont, P.; Barnabé, A. Ac conductivity and dielectric properties of CuFe1-xCrxO2: Mg delafossite. J. Phys. D Appl. Phys. 2011, 44, 185401. [Google Scholar] [CrossRef] [Green Version]
- Hill, R.M. Hopping conduction in amorphous solids. Philos. Mag. 1971, 24, 1307. [Google Scholar] [CrossRef]
- Mott, N.F.; Davis, E.A. Electronic Processes in Non-Crystalline Materials; Clarendon: Oxford, UK, 1979. [Google Scholar]
- Lalanne, M.; Barnabé, A.; Mathieu, F.; Tailhades, P. Synthesis and thermostructural studies of a CuFe(1-x)Cr(x)O(2) delafossite solid solution with. Inorg. Chem. 2009, 48, 6065–6071. [Google Scholar] [CrossRef] [PubMed]
- Mollah, S.; Som, K.K.; Bose, K.; Chaudhuri, B.K. AC conductivity in Bi4Sr3Ca3CuyOx (y = 0–5) and Bi4Sr3Ca3-zLizCu4Ox, (z = 0.1–1.0) semiconducting oxide glasses. J. Appl. Phys. 1993, 74, 931–937. [Google Scholar] [CrossRef]
- Scaife, B.K.P. Principles of Dielectrics; Clarendon Press: Oxford, UK, 1998. [Google Scholar]




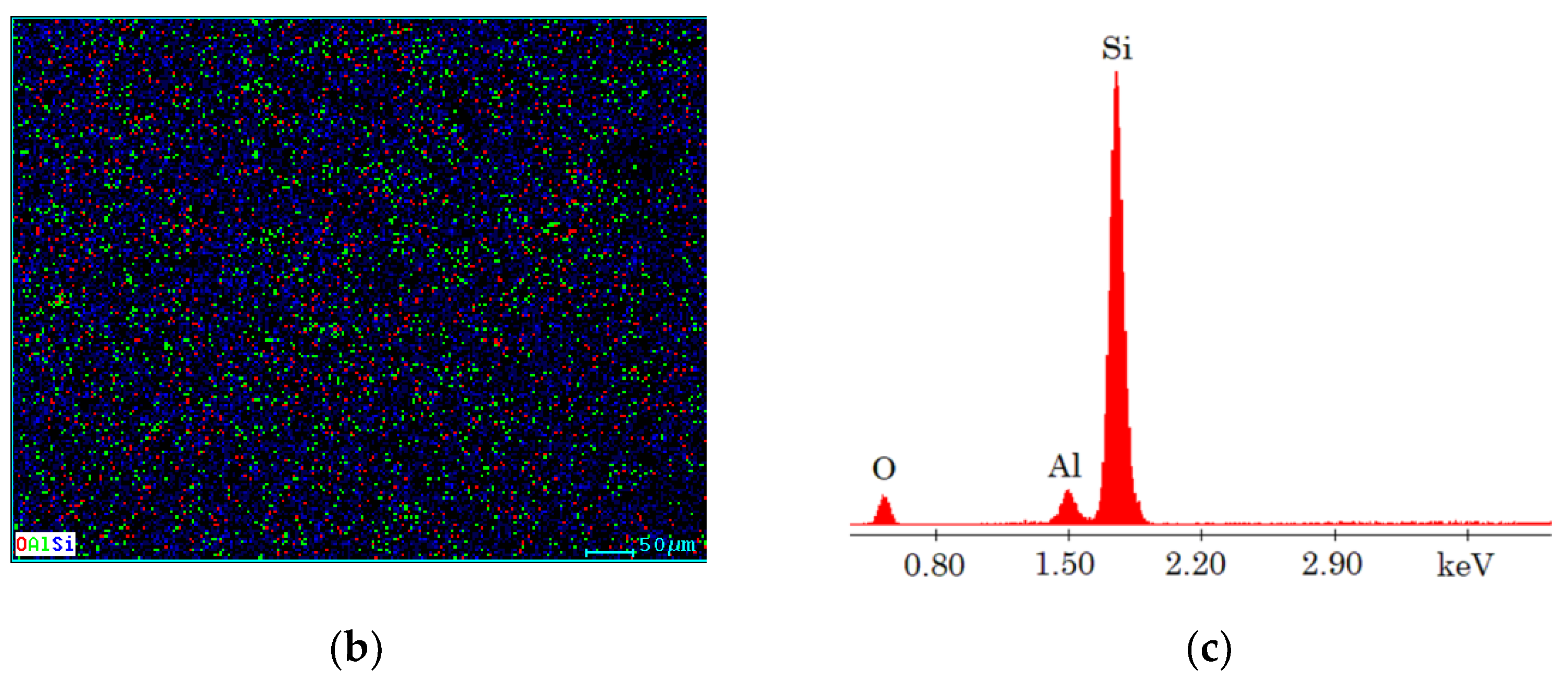
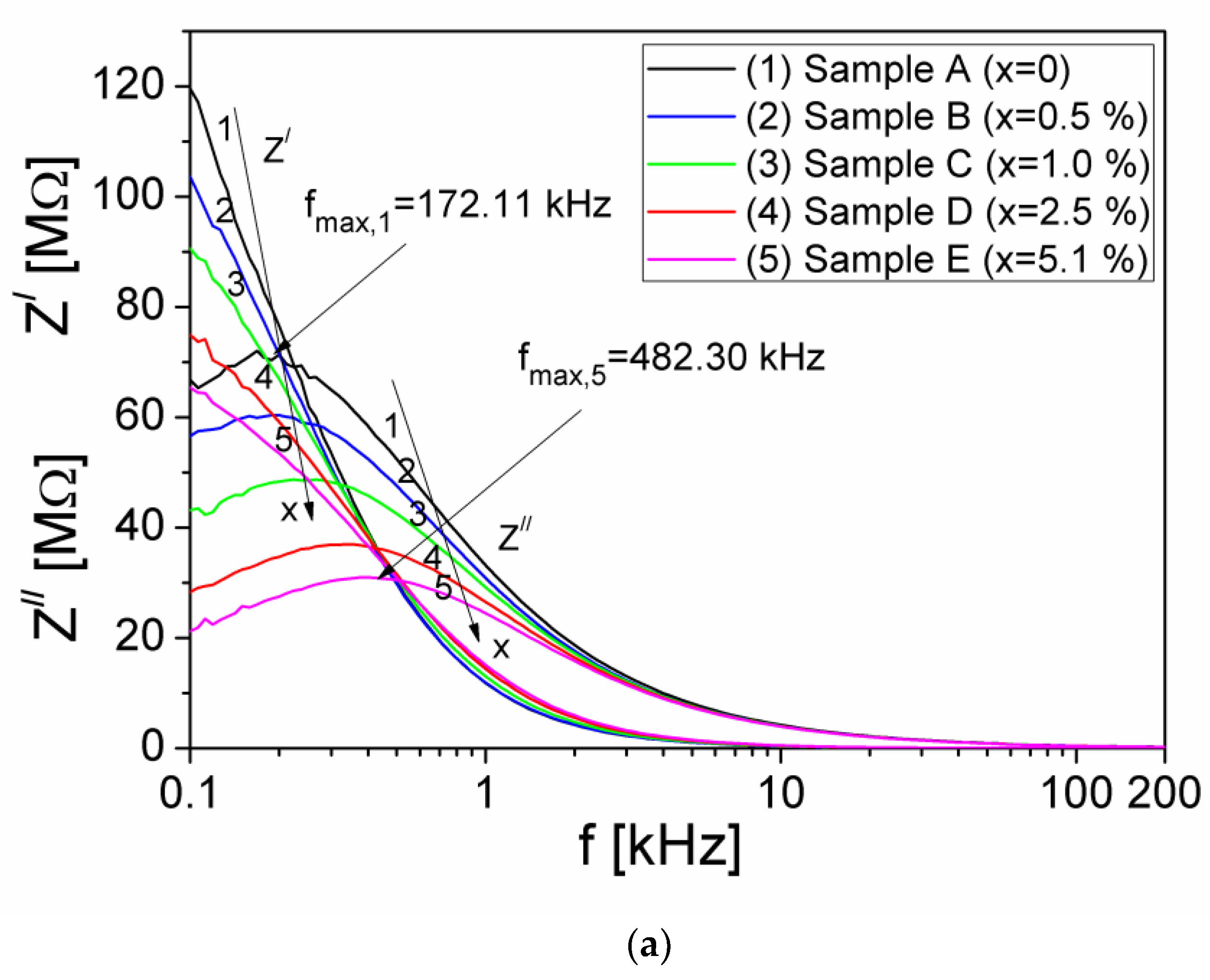
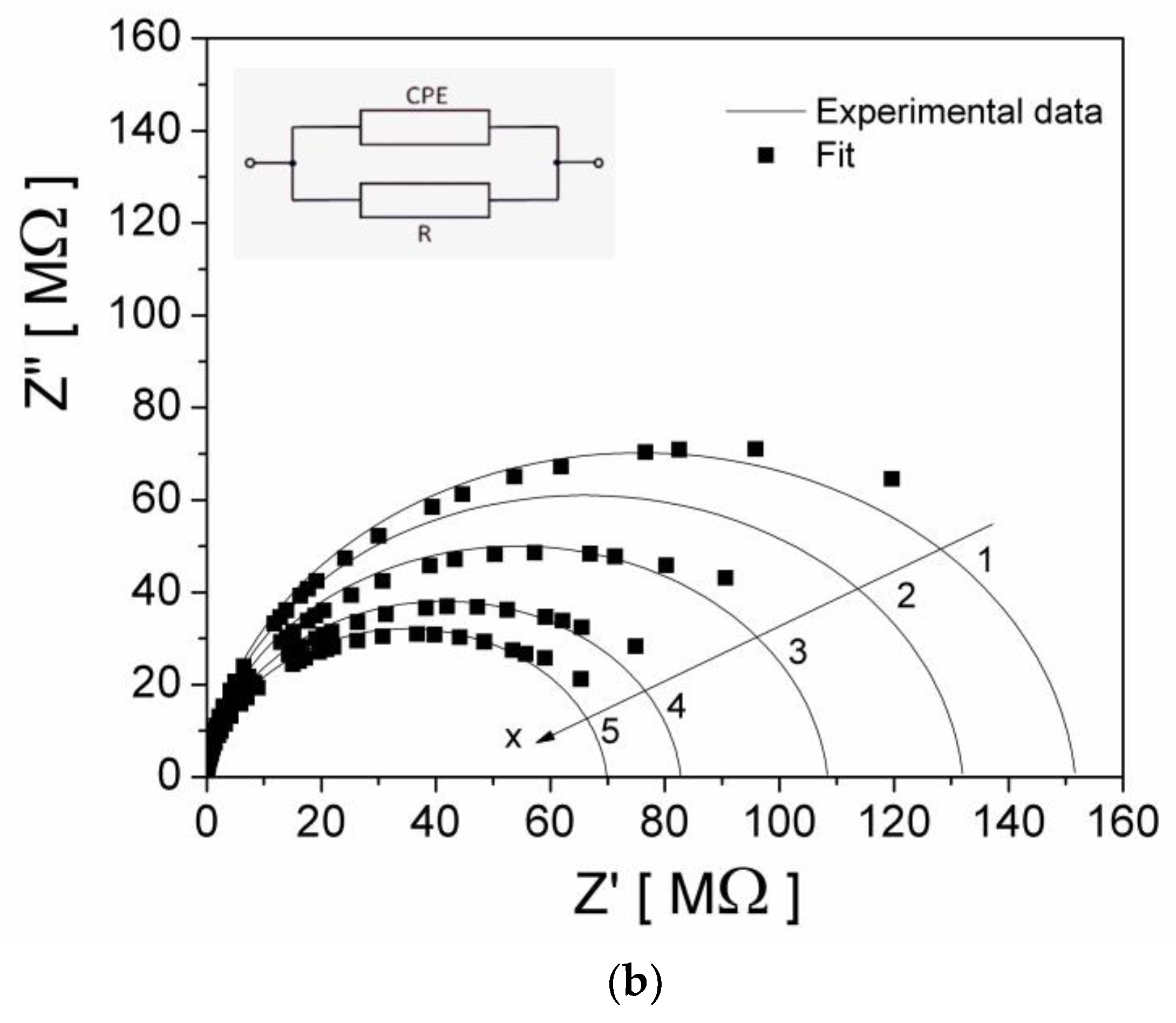
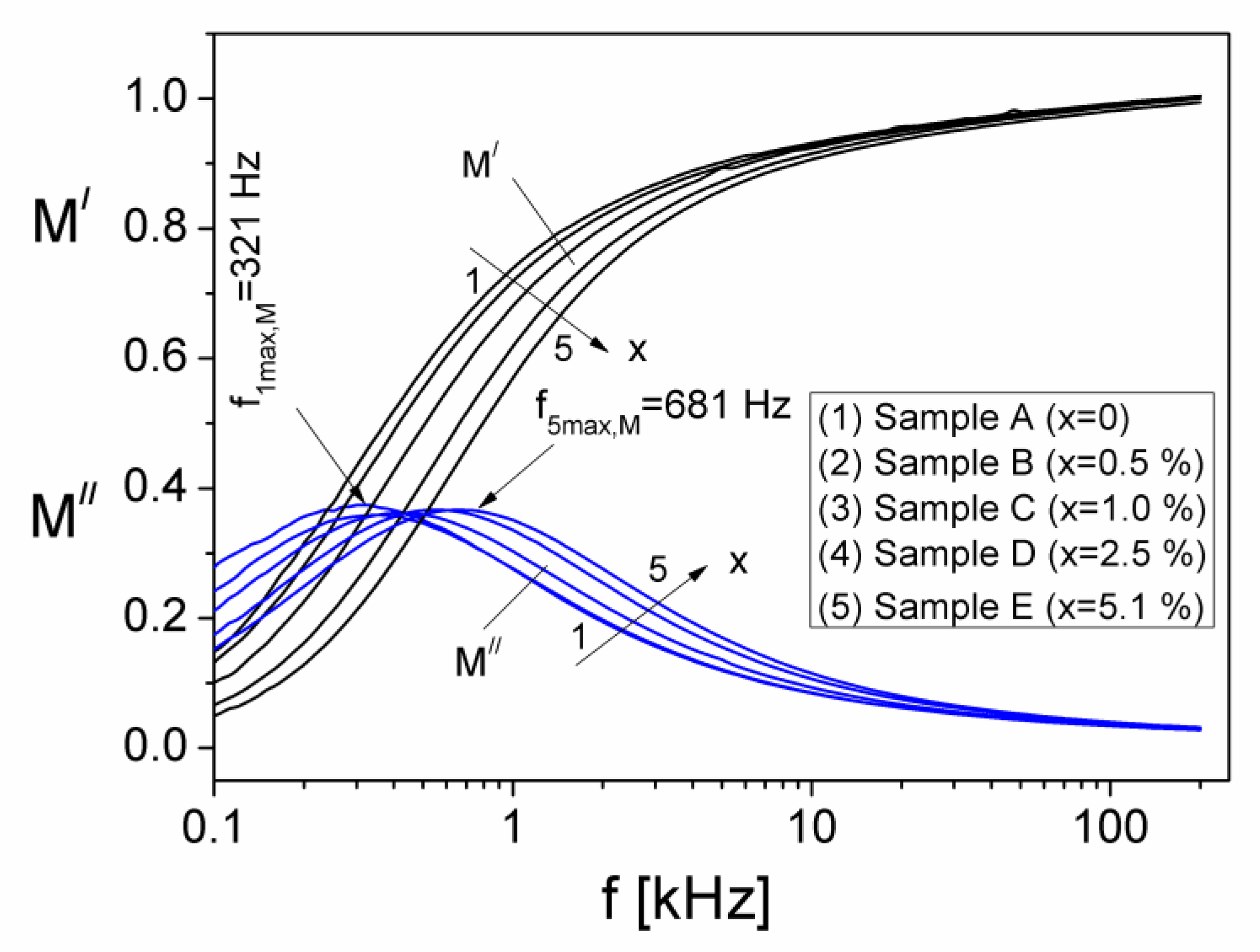

| Samples | A (x = 0) | B (x = 0.5%) | C (x = 1%) | D (x = 2.5%) | E (x = 5.1%) |
|---|---|---|---|---|---|
| 0.925 | 0.763 | 0.558 | 0.413 | 0.330 | |
| R[Ω] | 1.5166∙108 | 1.3203∙108 | 1.0841∙108 | 8.2876∙107 | 6.987∙107 |
| P[sk/Ω] | 6.7444∙10−12 | 7.1842∙10−12 | 7.3427·10−12 | 7.5766∙10−12 | 7.6777∙10−12 |
| k | 0.95118 | 0.94992 | 0.94841 | 0.94638 | 0.94593 |
| 0.496 | 0.447 | 0.370 | 0.292 | 0.237 | |
| 0.529 | 0.476 | 0.456 | 0.446 | 0.413 | |
| 2.637·10−8 | 3.029·10−8 | 3.689·10−8 | 4.826·10−8 | 5.725·10−8 | |
| n | 0.593 | 0.579 | 0.561 | 0.534 | 0.515 |
| A0 [S/msn] | 1.315·10−10 | 1.687·10−10 | 2.282·10−10 | 3.566·10−10 | 4.772·10−10 |
| 7.625·103 | 7.820·103 | 8.647·103 | 9.803·103 | 10.890·103 | |
| 7.30 | 6.89 | 6.57 | 6.11 | 5.92 |
| f [Hz] | |
|---|---|
| 100 | 24.3 |
| 200 | 16.9 |
| 500 | 13.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teusdea, A.; Malaescu, I.; Sfirloaga, P.; Marin, C.N. Electric and Dielectric Properties in Low-Frequency Fields of Composites Consisting of Silicone Rubber and Al Particles for Flexible Electronic Devices. Materials 2022, 15, 2309. https://doi.org/10.3390/ma15062309
Teusdea A, Malaescu I, Sfirloaga P, Marin CN. Electric and Dielectric Properties in Low-Frequency Fields of Composites Consisting of Silicone Rubber and Al Particles for Flexible Electronic Devices. Materials. 2022; 15(6):2309. https://doi.org/10.3390/ma15062309
Chicago/Turabian StyleTeusdea, Alexandrina, Iosif Malaescu, Paula Sfirloaga, and Catalin Nicolae Marin. 2022. "Electric and Dielectric Properties in Low-Frequency Fields of Composites Consisting of Silicone Rubber and Al Particles for Flexible Electronic Devices" Materials 15, no. 6: 2309. https://doi.org/10.3390/ma15062309
APA StyleTeusdea, A., Malaescu, I., Sfirloaga, P., & Marin, C. N. (2022). Electric and Dielectric Properties in Low-Frequency Fields of Composites Consisting of Silicone Rubber and Al Particles for Flexible Electronic Devices. Materials, 15(6), 2309. https://doi.org/10.3390/ma15062309







