Combinatorial Study of Phase Composition, Microstructure and Mechanical Behavior of Co-Cr-Fe-Ni Nanocrystalline Film Processed by Multiple-Beam-Sputtering Physical Vapor Deposition
Abstract
:1. Introduction
2. Materials and Methods
2.1. Processing of the Combinatorial Film and Selection of the Studied Locations
2.2. Study of the Chemical Composition
2.3. Investigation of the Microstructure and the Crystallographic Texture
2.4. Nanoindentation
3. Results
3.1. Chemical and Phase Composition in the Studied Locations of the Film
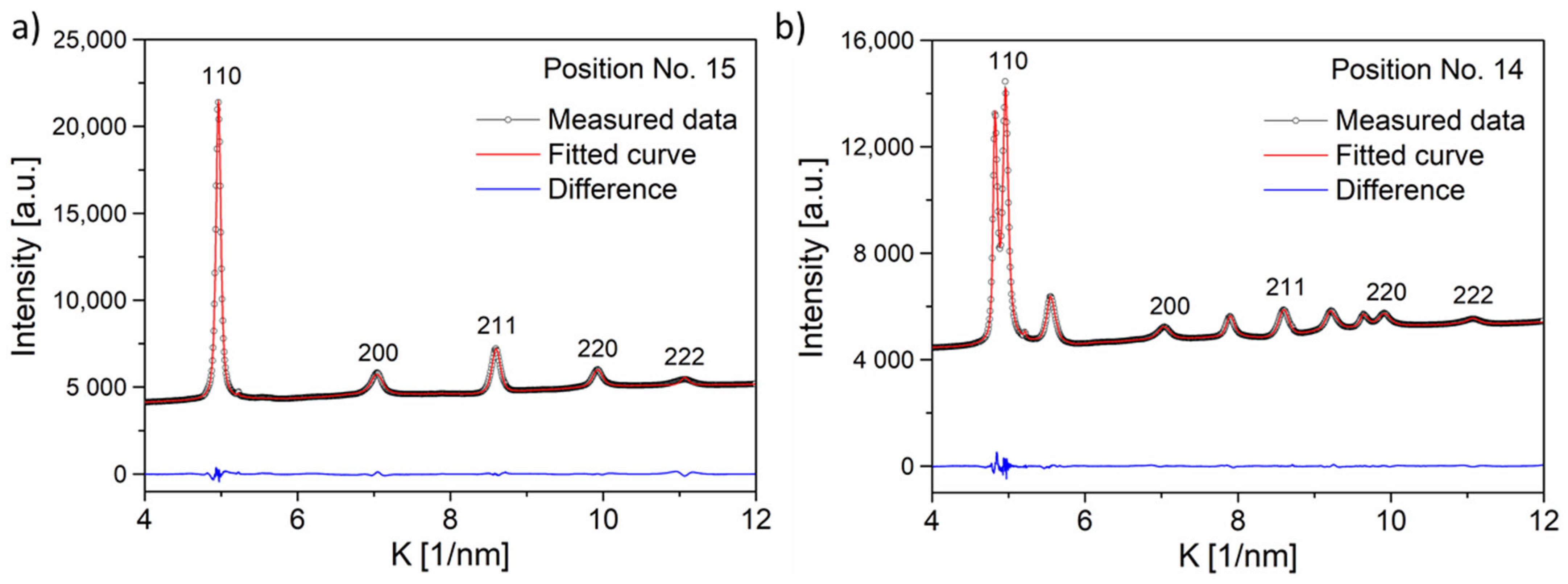
3.2. Characterization of the Microstructure by XLPA and TEM
3.3. Hardness and Elastic Modulus as Determined by Nanoindentation
4. Discussion
4.1. Comparison between the Experimentally Determined Phase Composition and the Equilibrium Phase Diagrams
4.2. Variation of the Microstructure and the Mechanical Performance as a Function of the Position on the Combinatorial Film Surface
5. Conclusions
- For most of the thin film, a single-phase fcc structure was formed. Close to the periphery of the disk sample between Fe-Co and Co-Cr sources, the main phases were bcc and hcp, respectively. Comparison between the experimentally determined phases and the equilibrium phase diagrams revealed that the phase composition was not in thermodynamic equilibrium for the majority of the combinatorial sample. Equilibrium single-phase fcc region was developed in the middle of the disk where the four constituents have nearly equal fractions.
- The thin film consists of columns growing perpendicular to the layer surface. These columns are fragmented into spherical nanograins with the size of about 10–20 nm, irrespective of the chemical composition. These grains correspond to the crystallites whose size was determined by XLPA. Very high dislocation density (60–280 × 1014 m−2) and twin fault probability (0.9–4.6%) were also observed by XLPA for all studied locations. Correlation between the chemical composition and the lattice defect density was not revealed.
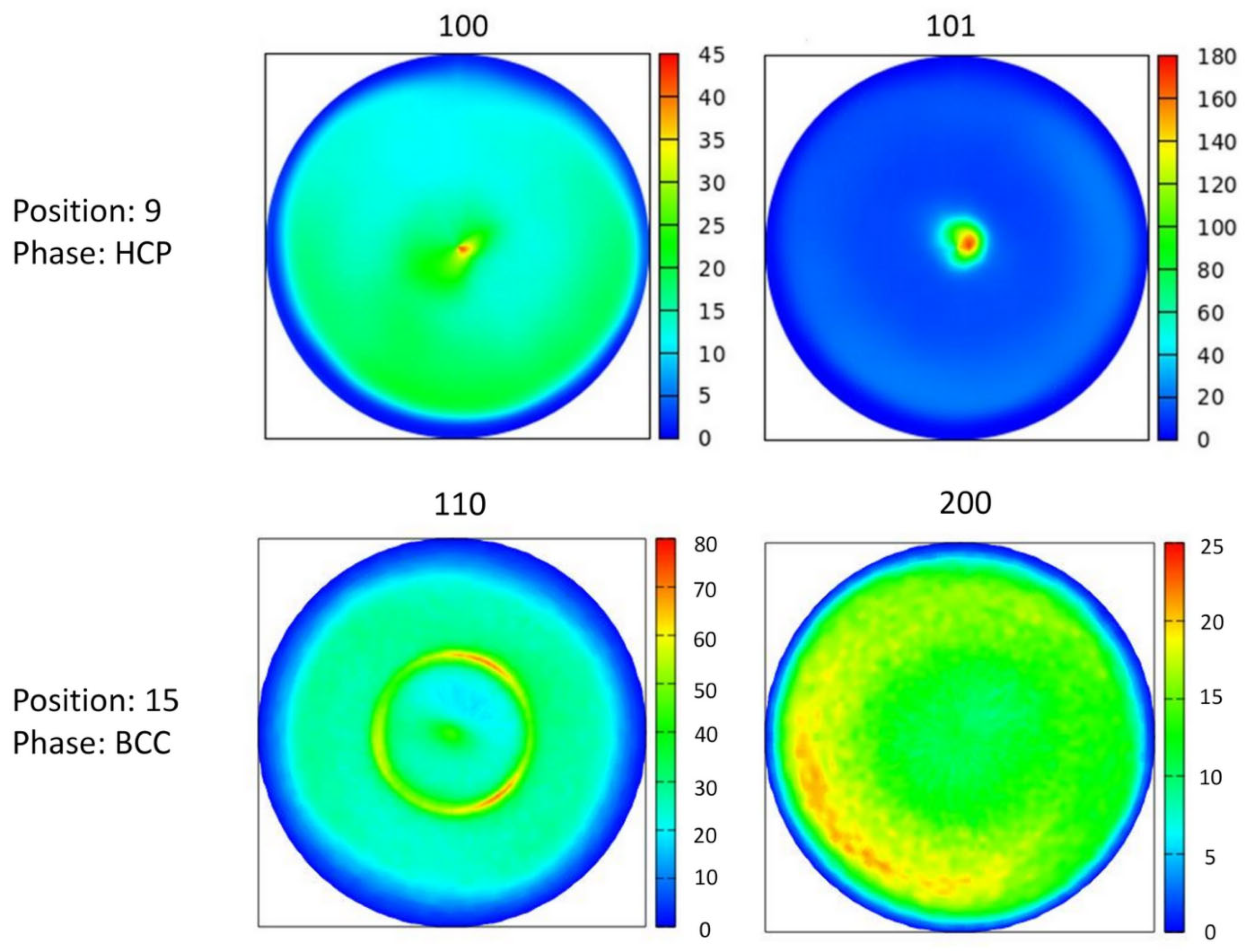
- In all fcc points, a strong 111 fiber texture was observed. For the hcp phase, both 100 and 101 texture components co-exist. Between Fe and Co PVD sources, where a single-phase bcc structure was identified, the texture was characterized by a stronger 111 and a weaker 110 components.
- Although, strict correlation between the mechanical performance and the composition could not be determined, it was revealed that the highest hardness (~11.8 GPa) was achieved for the composition 42% Co–45% Cr–5% Fe–8% Ni (at.%). In this point, the major phase was hcp which has a lower number of easy-slip systems compared to fcc or bcc structures, resulting in a higher hardness.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cantor, B.; Chang, I.T.H.; Knight, P.; Vincent, A.J.B. Microstructural development in equiatomic multicomponent alloys. Mater. Sci. Eng. A 2004, 375, 213–218. [Google Scholar] [CrossRef]
- Yeh, J.W.; Chen, S.K.; Lin, S.J.; Gan, J.Y.; Chin, T.S.; Shun, T.T.; Tsau, C.H.; Chang, S.Y. Nanostructured high-entropy alloys with multiple principal elements: Novel alloy design concepts and outcomes. Adv. Eng. Mater. 2004, 6, 299–303. [Google Scholar] [CrossRef]
- Yeh, J.W. Alloy design strategies and future trends in high-entropy alloys. JOM 2013, 65, 1759–1771. [Google Scholar] [CrossRef]
- Li, W.; Liu, P.; Liaw, P.K. Microstructures and properties of high-entropy alloy films and coatings: A review. Mater. Res. Lett. 2018, 6, 199–229. [Google Scholar] [CrossRef] [Green Version]
- Hung, P.T.; Kawasaki, M.; Han, J.K.; Lábár, J.L.; Gubicza, J. Microstructure evolution in a nanocrystalline CoCrFeNi multi-principal element alloy during annealing. Mater. Charact. 2021, 171, 110807. [Google Scholar] [CrossRef]
- Laplanche, G.; Kostka, A.; Reinhart, C.; Hunfeld, J.; Eggeler, G.; George, E.P. Reasons for the superior mechanical properties of medium-entropy CrCoNi compared to high-entropy CrMnFeCoNi. Acta Mater. 2017, 128, 292–303. [Google Scholar] [CrossRef]
- Wang, W.R.; Wang, W.L.; Wang, S.C.; Tsai, Y.C.; Lai, C.H.; Yeh, J.W. Effects of Al addition on the microstructure and mechanical property of AlxCoCrFeNi high-entropy alloys. Intermetallics 2012, 26, 44–51. [Google Scholar] [CrossRef]
- Wang, C.; Ji, W.; Fu, Z. Mechanical alloying and spark plasma sintering of CoCrFeNiMnAl high-entropy alloy. Adv. Powder Technol. 2014, 25, 1334–1338. [Google Scholar] [CrossRef]
- Tsau, C.H.; Yang, Y.C.; Lee, C.C.; Wu, L.Y.; Huang, H.J. The Low Electrical Resistivity of the High-entropy Alloy Oxide Thin Films. Procedia Eng. 2012, 36, 246–252. [Google Scholar] [CrossRef] [Green Version]
- Qiu, Y.; Thomas, S.; Fabijanic, D.; Barlow, A.J.; Fraser, H.L.; Birbilis, N. Microstructural evolution, electrochemical and corrosion properties of Al x CoCrFeNiTi y high entropy alloys. Mater. Des. 2019, 170, 107698. [Google Scholar] [CrossRef]
- Huo, W.; Liu, X.; Tan, S.; Fang, F.; Xie, Z.; Shang, J.; Jiang, J. Ultrahigh hardness and high electrical resistivity in nano-twinned, nanocrystalline high-entropy alloy films. Appl. Surf. Sci. 2018, 439, 222–225. [Google Scholar] [CrossRef]
- Qiu, Y.; Thomas, S.; Gibson, M.A.; Fraser, H.L.; Pohl, K.; Birbilis, N. Microstructure and corrosion properties of the low-density single-phase compositionally complex alloy AlTiVCr. Corros. Sci. 2018, 133, 386–396. [Google Scholar] [CrossRef]
- Senkov, O.N.; Scott, J.M.; Senkova, S.V.; Meisenkothen, F.; Miracle, D.B.; Woodward, C.F. Microstructure and elevated temperature properties of a refractory TaNbHfZrTi alloy. J. Mater. Sci. 2012, 47, 4062–4074. [Google Scholar] [CrossRef]
- Kim, Y.S.; Park, H.J.; Mun, S.C.; Jumaev, E.; Hong, S.H.; Song, G.; Kim, J.T.; Park, Y.K.; Kim, K.S.; Jeong, S., II; et al. Investigation of structure and mechanical properties of TiZrHfNiCuCo high entropy alloy thin films synthesized by magnetron sputtering. J. Alloys Compd. 2019, 797, 834–841. [Google Scholar] [CrossRef]
- Haciismailoglu, M.C.; Sarlar, K.; Tekgül, A.; Kucuk, I. Thermally evaporated FeMGaMnSi (M[dbnd]Co, Ni) high entropy alloy thin films: Magnetic and magnetoresistance properties. J. Non. Cryst. Solids 2020, 539, 120063. [Google Scholar] [CrossRef]
- Khan, N.A.; Akhavan, B.; Zhou, C.; Zhou, H.; Chang, L.; Wang, Y.; Liu, Y.; Fu, L.; Bilek, M.M.; Liu, Z. RF magnetron sputtered AlCoCrCu0.5FeNi high entropy alloy (HEA) thin films with tuned microstructure and chemical composition. J. Alloys Compd. 2020, 836, 155348. [Google Scholar] [CrossRef]
- Nagy, P.; Rohbeck, N.; Roussely, G.; Sortais, P.; Lábár, J.L.; Gubicza, J.; Michler, J.; Pethö, L. Processing and characterization of a multibeam sputtered nanocrystalline CoCrFeNi high-entropy alloy film. Surf. Coatings Technol. 2020, 386, 125465. [Google Scholar] [CrossRef]
- Dolique, V.; Thomann, A.L.; Brault, P.; Tessier, Y.; Gillon, P. Thermal stability of AlCoCrCuFeNi high entropy alloy thin films studied by in-situ XRD analysis. Surf. Coatings Technol. 2010, 204, 1989–1992. [Google Scholar] [CrossRef] [Green Version]
- Marshal, A.; Pradeep, K.G.; Music, D.; Wang, L.; Petracic, O.; Schneider, J.M. Combinatorial evaluation of phase formation and magnetic properties of FeMnCoCrAl high entropy alloy thin film library. Sci. Rep. 2019, 9, 7864. [Google Scholar] [CrossRef] [Green Version]
- Kauffmann, A.; Stüber, M.; Leiste, H.; Ulrich, S.; Schlabach, S.; Szabó, D.V.; Seils, S.; Gorr, B.; Chen, H.; Seifert, H.J.; et al. Combinatorial exploration of the High Entropy Alloy System Co-Cr-Fe-Mn-Ni. Surf. Coatings Technol. 2017, 325, 174–180. [Google Scholar] [CrossRef] [Green Version]
- Nagy, P.; Rohbeck, N.; Hegedűs, Z.; Michler, J.; Pethö, L.; Lábár, J.L.; Gubicza, J. Microstructure, Hardness, and Elastic Modulus of a Multibeam-Sputtered Nanocrystalline Co-Cr-Fe-Ni Compositional Complex Alloy Film. Materials 2021, 14, 3357. [Google Scholar] [CrossRef]
- Shi, Y.; Yang, B.; Rack, P.D.; Guo, S.; Liaw, P.K.; Zhao, Y. High-throughput synthesis and corrosion behavior of sputter-deposited nanocrystalline Alx(CoCrFeNi)100-x combinatorial high-entropy alloys. Mater. Des. 2020, 195, 109018. [Google Scholar] [CrossRef]
- Xiao, B.; Wang, X.; Savan, A.; Ludwig, A. Phase constitution of the noble metal thin-film complex solid solution system Ag-Ir-Pd-Pt-Ru in dependence of elemental compositions and annealing temperatures. Nano Res. 2021, 1–10. [Google Scholar] [CrossRef]
- Krysiak, O.A.; Schumacher, S.; Savan, A.; Schuhmann, W.; Ludwig, A.; Andronescu, C. Searching novel complex solid solution electrocatalysts in unconventional element combinations. Nano Res. 2021, 1–5. [Google Scholar] [CrossRef]
- Barad, H.N.; Alarcón-Correa, M.; Salinas, G.; Oren, E.; Peter, F.; Kuhn, A.; Fischer, P. Combinatorial growth of multinary nanostructured thin functional films. Mater. Today 2021, 50, 89–99. [Google Scholar] [CrossRef]
- Gao, L.; Liao, W.; Zhang, H.; Utama Surjadi, J.; Sun, D.; Lu, Y. Microstructure, Mechanical and Corrosion Behaviors of CoCrFeNiAl 0.3 High Entropy Alloy (HEA) Films. Coatings 2017, 7, 156. [Google Scholar] [CrossRef]
- Nelson, J.B.; Riley, D.P. An experimental investigation of extrapolation methods in the derivation of accurate unit-cell dimensions of crystals. Proc. Phys. Soc. 1945, 57, 160–177. [Google Scholar] [CrossRef]
- Gubicza, J. X-ray Line Profile Analysis in Materials Science; IGI Global: Hershey, PA, USA, 2014; ISBN 9781466658523. [Google Scholar]
- Ribárik, G.; Gubicza, J.; Ungár, T. Correlation between strength and microstructure of ball-milled Al-Mg alloys determined by X-ray diffraction. Mater. Sci. Eng. A 2004, 387–389, 343–347. [Google Scholar] [CrossRef]
- Lábár, J.L. DiffMap: A new free computer program to process scanned electron diffraction patterns. Resolut. Discov. 2022. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- He, F.; Wang, Z.; Wu, Q.; Niu, S.; Li, J.; Wang, J.; Liu, C.T. Solid solution island of the Co-Cr-Fe-Ni high entropy alloy system. Scr. Mater. 2017, 131, 42–46. [Google Scholar] [CrossRef]
- Gorsse, S.; Senkov, O.N. About the reliability of CALPHAD predictions in multicomponent systems. Entropy 2018, 20, 899. [Google Scholar] [CrossRef] [Green Version]
- Osaka, T.; Takai, M.; Hayashi, K.; Ohashi, K.; Saito, M.; Yamada, K. A soft magnetic CoNiFe film with high saturation magnetic flux density and low coercivity. Nature 1998, 392, 796–798. [Google Scholar] [CrossRef]
- Yoo, Y.K.; Xue, Q.; Chu, Y.S.; Xu, S.; Hangen, U.; Lee, H.C.; Stein, W.; Xiang, X.D. Identification of amorphous phases in the Fe-Ni-Co ternary alloy system using continuous phase diagram material chips. Intermetallics 2006, 14, 241–247. [Google Scholar] [CrossRef]
- Wróbel, J.S.; Nguyen-Manh, D.; Lavrentiev, M.Y.; Muzyk, M.; Dudarev, S.L. Phase stability of ternary fcc and bcc Fe-Cr-Ni alloys. Phys. Rev. B Condens. Matter Mater. Phys. 2015, 91, 91. [Google Scholar] [CrossRef] [Green Version]
- Omori, T.; Sato, J.; Shinagawa, K.; Ohnuma, I.; Oikawa, K.; Kainuma, R.; Ishida, K. Experimental determination of phase equilibria in the Co-Cr-Ni system. J. Phase Equilibria Diffus. 2014, 35, 178–185. [Google Scholar] [CrossRef]
- Zhao, N.; Liu, W.; Wang, J.J.; Lu, X.G.; Zhang, L. Thermodynamic assessment of the Ni–Co–Cr system and Diffusion Study of its fcc phase. Calphad Comput. Coupling Phase Diagrams Thermochem. 2020, 71, 101996. [Google Scholar] [CrossRef]
- Wang, P.; Hu, B.; Huang, X.; Zheng, C. Thermodynamic assessment of the Co–Cr–Ni, Co–Cr–W and Co–Ni–W. Calphad Comput. Coupling Phase Diagrams Thermochem. 2021, 73, 102252. [Google Scholar] [CrossRef]
- Jacob, A.; Povoden-Karadeniz, E.; Kozeschnik, E. Revised thermodynamic description of the Fe-Cr system based on an improved sublattice model of the σ phase. Calphad Comput. Coupling Phase Diagrams Thermochem. 2018, 60, 16–28. [Google Scholar] [CrossRef]
- Köster, W. Das System Eisen-Kobalt-Chrom. Arch. Für Das Eisenhüttenwes. 1932, 6, 113–116. [Google Scholar] [CrossRef]
- Péter, L.; Fekete, É.; Kapoor, G.; Gubicza, J. Influence of the preparation conditions on the microstructure of electrodeposited nanocrystalline Ni–Mo alloys. Electrochim. Acta 2021, 382, 138352. [Google Scholar] [CrossRef]
- Kolonits, T.; Czigány, Z.; Péter, L.; Bakonyi, I.; Gubicza, J. Influence of bath additives on the thermal stability of the nanostructure and hardness of Ni films processed by electrodeposition. Coatings 2019, 9, 644. [Google Scholar] [CrossRef] [Green Version]
- Kolonits, T.; Czigány, Z.; Péter, L.; Bakonyi, I.; Gubicza, J. Improved hardness and thermal stability of nanocrystalline nickel electrodeposited with the addition of cysteine. Nanomaterials 2020, 10, 2254. [Google Scholar] [CrossRef]
- Gubicza, J.; Hung, P.T.; Kawasaki, M.; Han, J.K.; Zhao, Y.; Xue, Y.; Lábár, J.L. Influence of severe plastic deformation on the microstructure and hardness of a CoCrFeNi high-entropy alloy: A comparison with CoCrFeNiMn. Mater. Charact. 2019, 154, 304–314. [Google Scholar] [CrossRef]
- Gubicza, J. Defect Structure and Properties of Nanomaterials, 2nd and Extended ed.; Woodhead Publishing: Duxford, UK, 2017. [Google Scholar]
- Kapoor, G.; Péter, L.; Fekete, É.; Lábár, J.L.; Gubicza, J. The influence of Mo addition on the microstructure and its thermal stability for electrodeposited Ni films. Mater. Charact. 2018, 145, 563–572. [Google Scholar] [CrossRef]
- Zhang, A.; Han, J.; Su, B.; Li, P.; Meng, J. Microstructure, mechanical properties and tribological performance of CoCrFeNi high entropy alloy matrix self-lubricating composite. Mater. Des. 2017, 114, 253–263. [Google Scholar] [CrossRef]
- Yan, X.; Zhang, X.; Wang, F.; Stockdale, T.; Dzenis, Y.; Nastasi, M.; Cui, B. Fabrication of ODS Austenitic Steels and CoCrFeNi High-Entropy Alloys by Spark Plasma Sintering for Nuclear Energy Applications. JOM 2019, 71, 2856–2867. [Google Scholar] [CrossRef]
- Wang, J.; Guo, T.; Li, J.; Jia, W.; Kou, H. Microstructure and mechanical properties of non-equilibrium solidified CoCrFeNi high entropy alloy. Mater. Chem. Phys. 2018, 210, 192–196. [Google Scholar] [CrossRef]
- Huo, W.; Zhou, H.; Fang, F.; Hu, X.; Xie, Z.; Jiang, J. Strain-rate effect upon the tensile behavior of CoCrFeNi high-entropy alloys. Mater. Sci. Eng. A 2017, 689, 366–369. [Google Scholar] [CrossRef]
- Lin, Y.; Yang, T.; Lang, L.; Shan, C.; Deng, H.; Hu, W.; Gao, F. Enhanced radiation tolerance of the Ni-Co-Cr-Fe high-entropy alloy as revealed from primary damage. Acta Mater. 2020, 196, 133–143. [Google Scholar] [CrossRef]


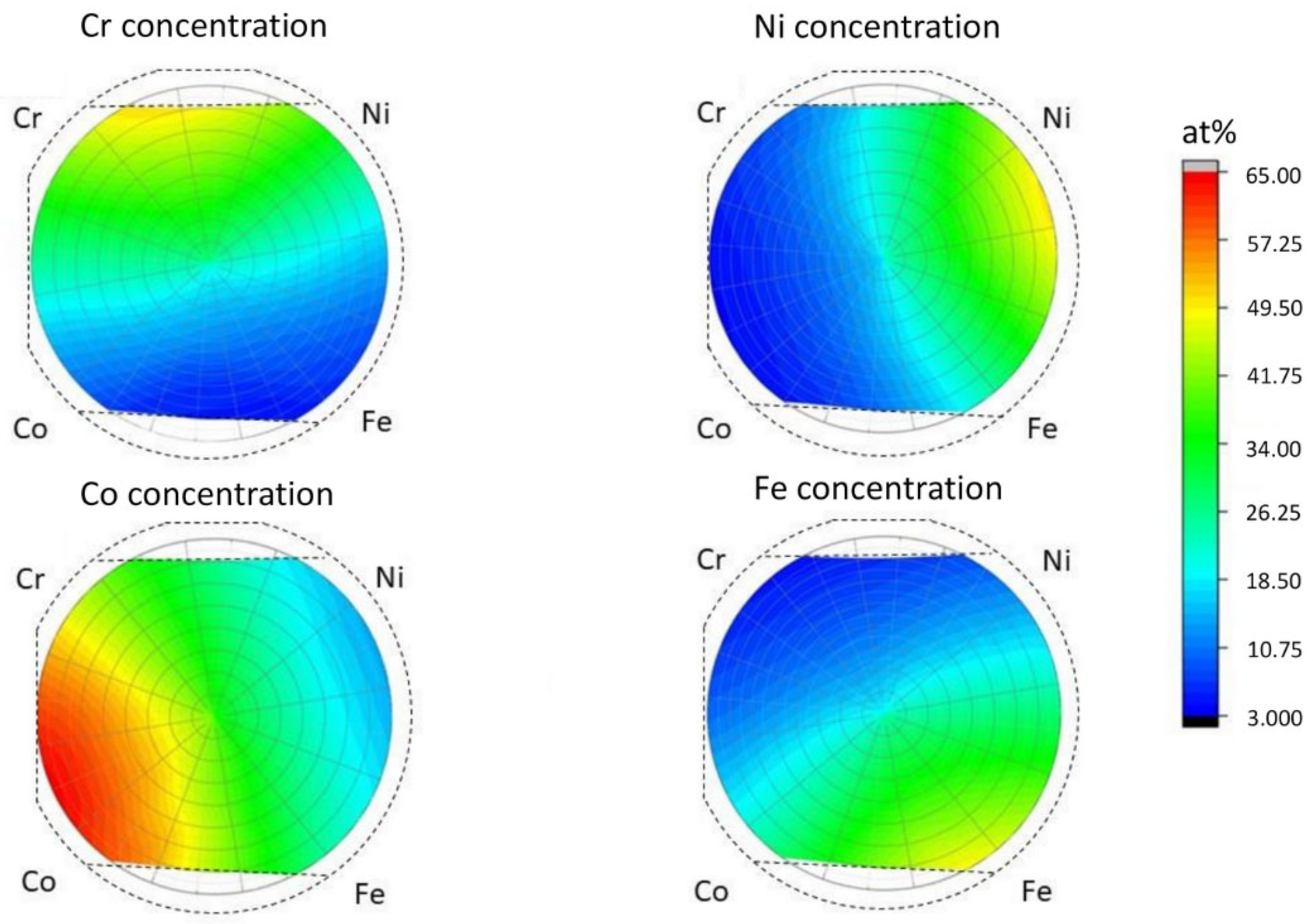
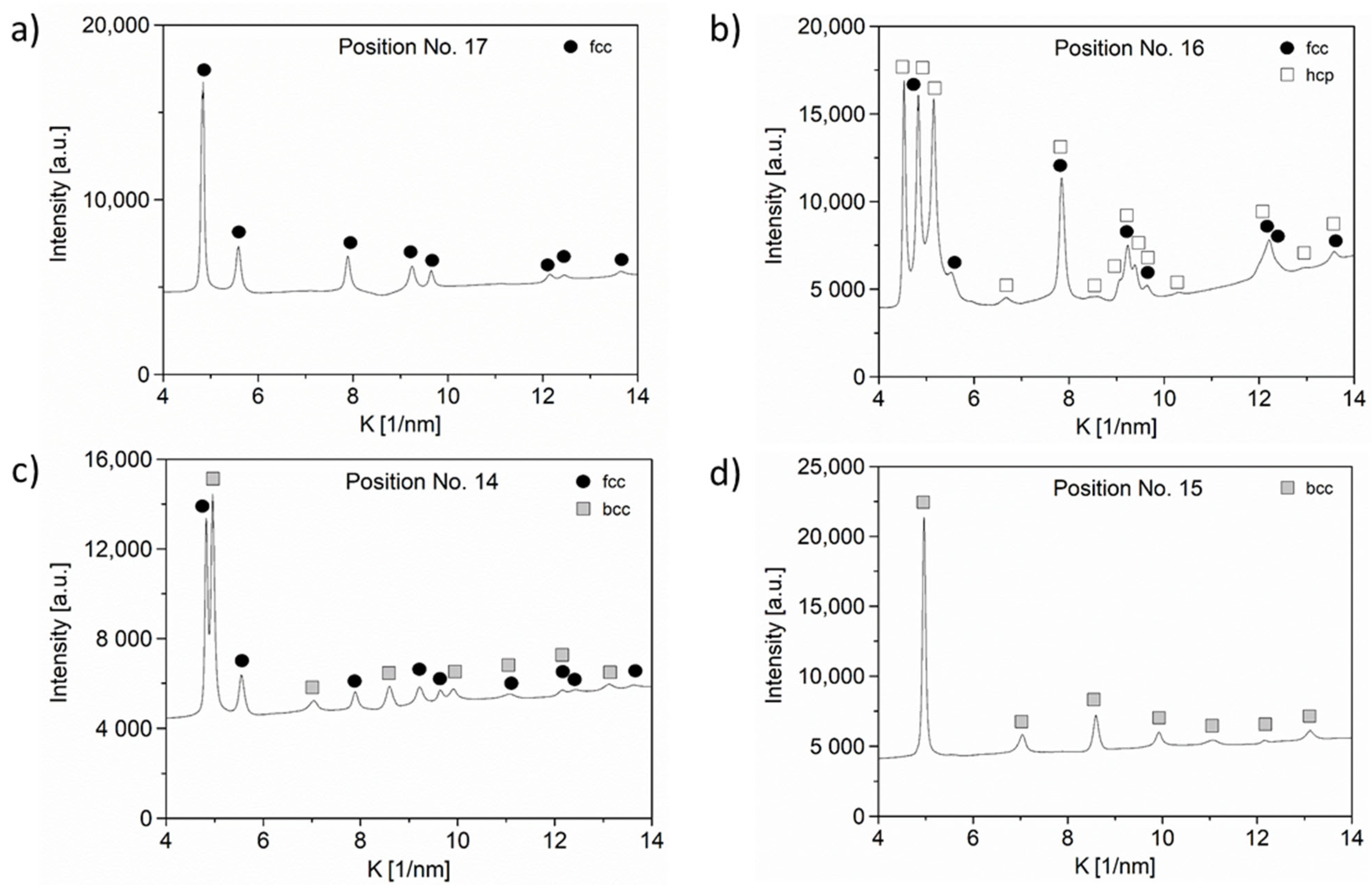




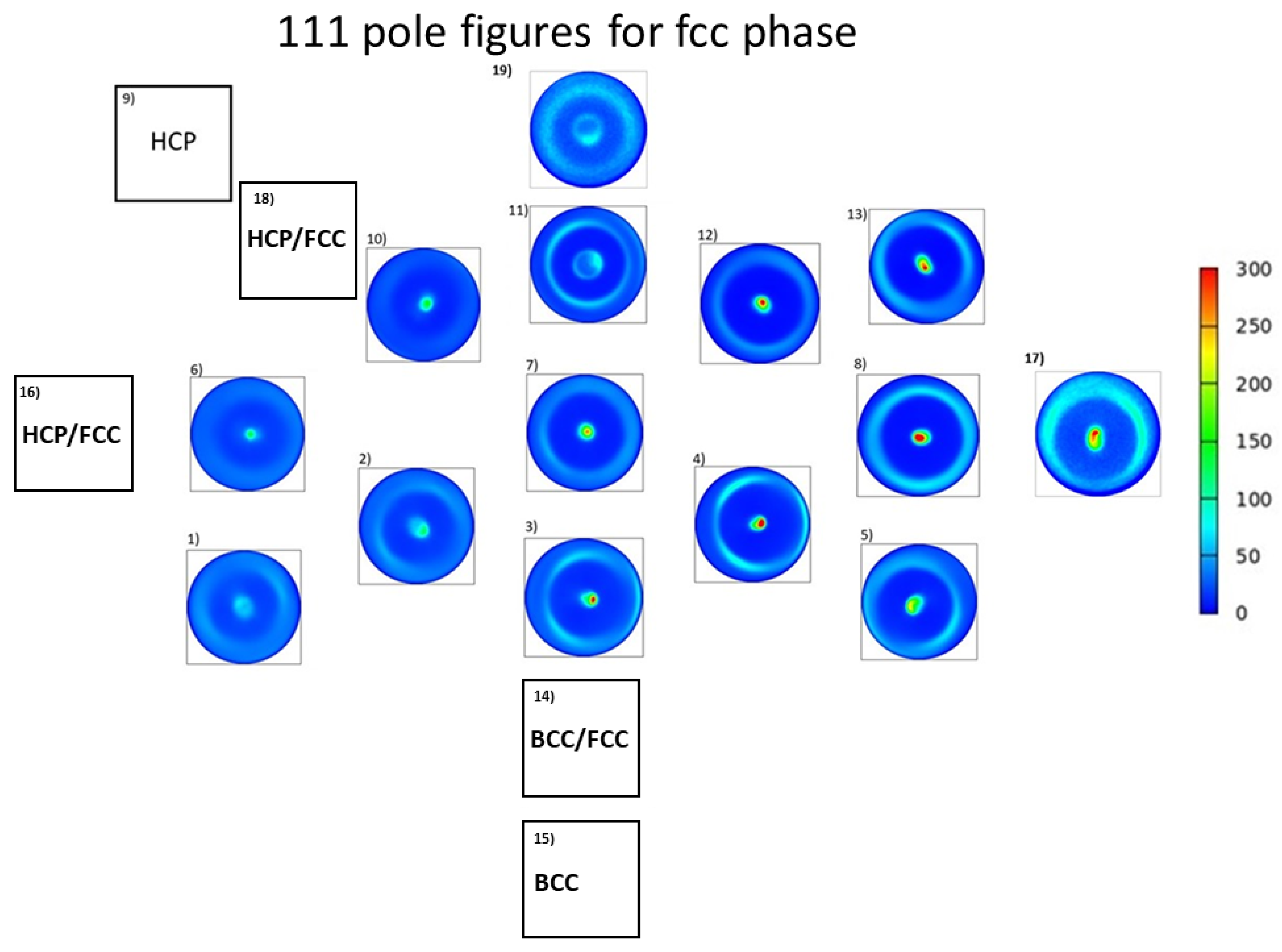

| No. of Position | y | z | Composition from XRF [at.%] | Phase Composition | Lattice Constant [nm] | |||
|---|---|---|---|---|---|---|---|---|
| Co | Cr | Fe | Ni | |||||
| 1 | −1.596 | 82 | 61 | 10 | 24 | 5 | fcc | 0.360 ± 0.001 |
| 2 | −0.524 | 70 | 51 | 15 | 24 | 10 | fcc | 0.360 ± 0.001 |
| 3 | 0.548 | 76 | 39 | 11 | 35 | 15 | fcc | 0.360 ± 0.001 |
| 4 | 1.352 | 70 | 24 | 13 | 35 | 28 | fcc | 0.360 ± 0.001 |
| 5 | 2.156 | 84 | 19 | 6 | 46 | 29 | fcc | 0.359 ± 0.001 |
| 6 | −1.06 | 56 | 52 | 23 | 16 | 9 | fcc | 0.360 ± 0.001 |
| 7 | 0.548 | 56 | 31 | 23 | 23 | 23 | fcc | 0.361 ± 0.001 |
| 8 | 2.156 | 56 | 16 | 19 | 27 | 38 | fcc | 0.360 ± 0.001 |
| 9 | −1.596 | 26 | 42 | 45 | 5 | 8 | hcp + (fcc) | a = 0.258 ± 0.001 (hcp) |
| c = 0.417 ± 0.001 (hcp) | ||||||||
| 10 | −0.524 | 42 | 42 | 35 | 11 | 12 | fcc | 0.362 ± 0.001 |
| 11 | 0.548 | 36 | 27 | 40 | 11 | 22 | fcc | 0.362 ± 0.001 |
| 12 | 1.352 | 44 | 23 | 31 | 16 | 30 | fcc | 0.361 ± 0.001 |
| 13 | 2.424 | 30 | 10 | 34 | 12 | 44 | fcc | 0.361 ± 0.001 |
| 14 | 0.548 | 82 | 39 | 8 | 38 | 15 | fcc + bcc | 0.359 ± 0.001 (fcc) |
| 0.285 ± 0.001 (bcc) | ||||||||
| 15 | 0.548 | 90 | 38 | 6 | 41 | 15 | bcc | 0.285 ± 0.001 |
| 16 | −2.132 | 56 | 61 | 21 | 13 | 5 | hcp + fcc | a = 0.254 ± 0.001 (hcp) |
| c = 0.413 ± 0.001 (hcp) | ||||||||
| 17 | 2.96 | 56 | 10 | 14 | 27 | 49 | fcc | 0.359 ± 0.001 |
| 18 | −0.792 | 30 | 40 | 39 | 9 | 12 | fcc + (hcp) | 0.363 ± 0.001 (fcc) |
| n. a. | ||||||||
| 19 | 0.548 | 12 | 29 | 43 | 9 | 19 | fcc | 0.365 ± 0.001 |
| No. of Position | <x>area [nm] | ρ [1014 m−2] | β [%] | dTEM [nm] |
|---|---|---|---|---|
| 1-fcc | 27 ± 4 | 110 ± 10 | 4.4 ± 0.5 | |
| 2-fcc | 15 ± 2 | 180 ± 20 | 1.2 ± 0.1 | |
| 3-fcc | 11 ± 2 | 100 ± 10 | 1.2 ± 0.1 | 14 ± 2 |
| 4-fcc | 10 ± 2 | 60 ± 10 | 0 ± 0.1 | |
| 5-fcc | 14 ± 2 | 140 ± 20 | 0.9 ± 0.1 | |
| 6-fcc | 14 ± 2 | 200 ± 20 | 3.9 ± 0.4 | |
| 7-fcc | 11 ± 2 | 230 ± 30 | 1.6 ± 0.2 | |
| 8-fcc | 11 ± 2 | 150 ± 20 | 1.1 ± 0.1 | |
| 9-hcp | 19 ± 3 | 90 ± 10 | n.a. | |
| 10-fcc | 16 ± 2 | 200 ± 20 | 2.5 ± 0.3 | 13 ± 2 |
| 11-fcc | 19 ± 3 | 140 ± 20 | 4.6 ± 0.5 | |
| 12-fcc | 11 ± 2 | 250 ± 30 | 2.1 ± 0.2 | |
| 13-fcc | 12 ± 2 | 160 ± 20 | 2.6 ± 0.3 | |
| 14-bcc | 12 ± 2 | 280 ± 30 | n.a. | 15 ± 2 |
| 14-fcc | 28 ± 4 | 220 ± 30 | 1.1 ± 0.1 | |
| 15-bcc | 20 ± 3 | 260 ± 30 | n.a. | 11 ± 2 |
| 16-hcp | 11 ± 2 | 90 ± 10 | n.a. | |
| 17-fcc | 15 ± 2 | 150 ± 20 | 1.9 ± 0.2 | |
| 18-fcc | 7 ± 2 | 120 ± 20 | 3.8 ± 0.4 | 8 ± 2 |
| 19-fcc | 18 ± 3 | 180 ± 20 | 4.6 ± 0.5 |
| No. of Position | H [GPa] | E [GPa] |
|---|---|---|
| 1 | 8.4 ± 0.4 | 199 ± 8 |
| 2 | 10.0 ± 0.4 | 239 ± 5 |
| 3 | 9.3 ± 0.5 | 224 ± 5 |
| 4 | 9.4 ± 0.5 | 226 ± 6 |
| 5 | 8.5 ± 0.5 | 212 ± 7 |
| 6 | 11.0 ± 0.5 | 241 ± 6 |
| 7 | 10.3 ± 0.4 | 208 ± 5 |
| 8 | 10.6 ± 0.6 | 234 ± 6 |
| 9 | 11.8 ± 1.2 | 237 ± 12 |
| 10 | 9.6 ± 1.2 | 182 ± 14 |
| 11 | 10.2 ± 0.5 | 222 ± 7 |
| 12 | 11.1 ± 0.5 | 232 ± 6 |
| 13 | 10.5 ± 0.9 | 237 ± 10 |
| 14 | 8.5 ± 0.5 | 184 ± 5 |
| 15 | 9.2 ± 0.9 | 191 ± 8 |
| 16 | 10.9 ± 1.4 | 204 ± 11 |
| 17 | 9.6 ± 0.9 | 201 ± 9 |
| 18 | 10.4 ± 0.4 | 191 ± 5 |
| 19 | 10 ± 0.7 | 184 ± 9 |
| No. of Position | Experimental Phase Composition | Equilibrium Phase Composition |
|---|---|---|
| 1 | fcc | n.a. |
| 2 | fcc | n.a. |
| 3 | fcc | fcc + bcc |
| 4 | fcc | fcc + bcc |
| 5 | fcc | fcc + bcc |
| 6 | fcc | n.a. |
| 7 | fcc | fcc |
| 8 | fcc | fcc |
| 9 | hcp + fcc | hcp + bcc |
| 10 | fcc | n.a. |
| 11 | fcc | n.a. |
| 12 | fcc | fcc |
| 13 | fcc | n.a. |
| 14 | fcc + bcc | fcc + bcc |
| 15 | bcc | fcc + bcc |
| 16 | hcp + fcc | n.a. |
| 17 | fcc | fcc |
| 18 | fcc + hcp | n.a. |
| 19 | fcc | n.a. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nagy, P.; Rohbeck, N.; Widmer, R.N.; Hegedűs, Z.; Michler, J.; Pethö, L.; Lábár, J.L.; Gubicza, J. Combinatorial Study of Phase Composition, Microstructure and Mechanical Behavior of Co-Cr-Fe-Ni Nanocrystalline Film Processed by Multiple-Beam-Sputtering Physical Vapor Deposition. Materials 2022, 15, 2319. https://doi.org/10.3390/ma15062319
Nagy P, Rohbeck N, Widmer RN, Hegedűs Z, Michler J, Pethö L, Lábár JL, Gubicza J. Combinatorial Study of Phase Composition, Microstructure and Mechanical Behavior of Co-Cr-Fe-Ni Nanocrystalline Film Processed by Multiple-Beam-Sputtering Physical Vapor Deposition. Materials. 2022; 15(6):2319. https://doi.org/10.3390/ma15062319
Chicago/Turabian StyleNagy, Péter, Nadia Rohbeck, Remo N. Widmer, Zoltán Hegedűs, Johann Michler, László Pethö, János L. Lábár, and Jenő Gubicza. 2022. "Combinatorial Study of Phase Composition, Microstructure and Mechanical Behavior of Co-Cr-Fe-Ni Nanocrystalline Film Processed by Multiple-Beam-Sputtering Physical Vapor Deposition" Materials 15, no. 6: 2319. https://doi.org/10.3390/ma15062319
APA StyleNagy, P., Rohbeck, N., Widmer, R. N., Hegedűs, Z., Michler, J., Pethö, L., Lábár, J. L., & Gubicza, J. (2022). Combinatorial Study of Phase Composition, Microstructure and Mechanical Behavior of Co-Cr-Fe-Ni Nanocrystalline Film Processed by Multiple-Beam-Sputtering Physical Vapor Deposition. Materials, 15(6), 2319. https://doi.org/10.3390/ma15062319








