Theoretical Analysis Method of Variable Thickness GFRP Tray
Abstract
:1. Introduction
2. Test Methods
2.1. Test Materials
2.1.1. GFRP Bar
2.1.2. Tray and Conical Nut
2.2. Tensile Strength Test of GFRP Bars
2.3. Nut-Tray Anchorage Tests
2.3.1. Anchoring of GFRP Bars
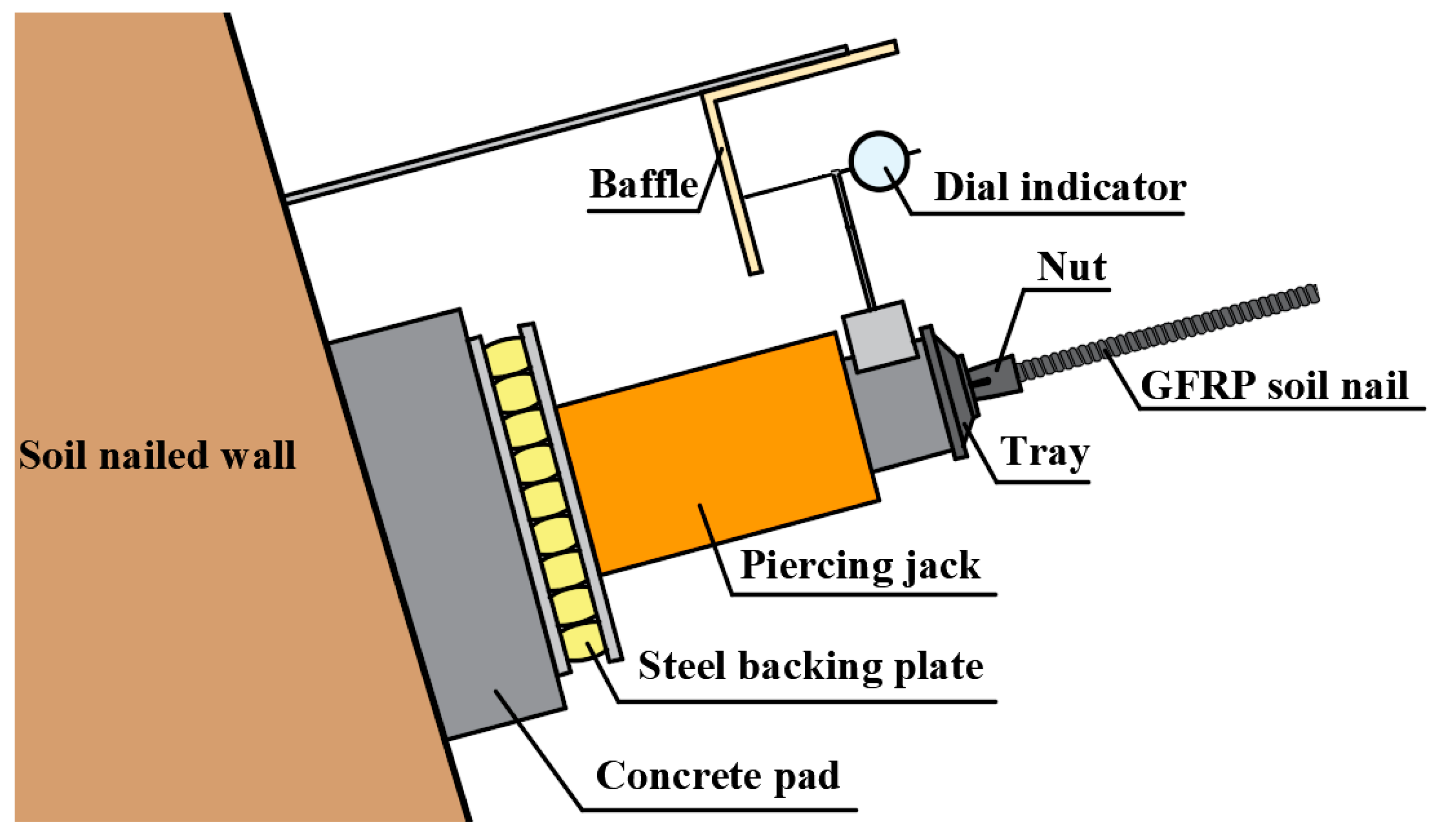
2.3.2. Test Device
2.3.3. Test Method
3. Test Results and Analysis
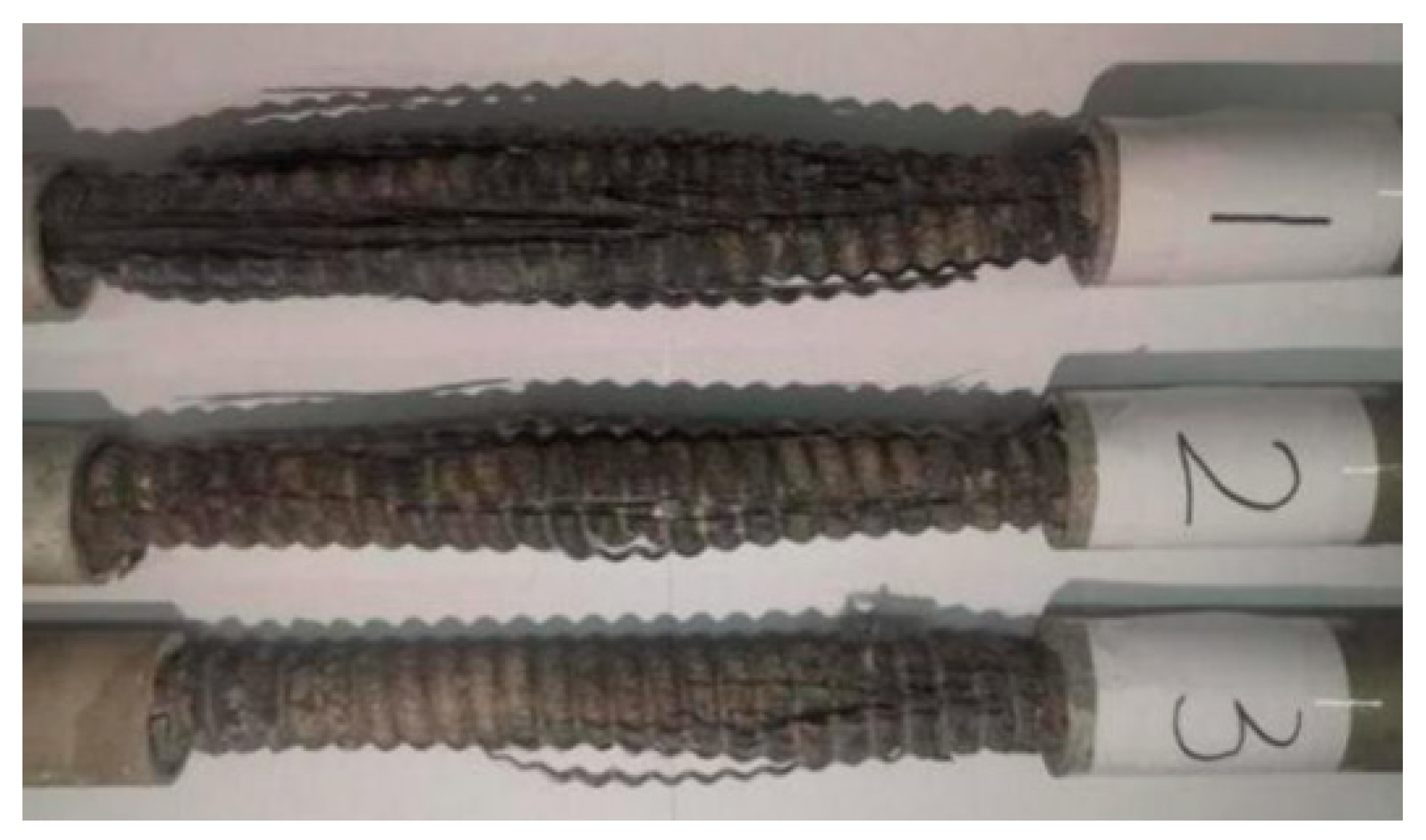
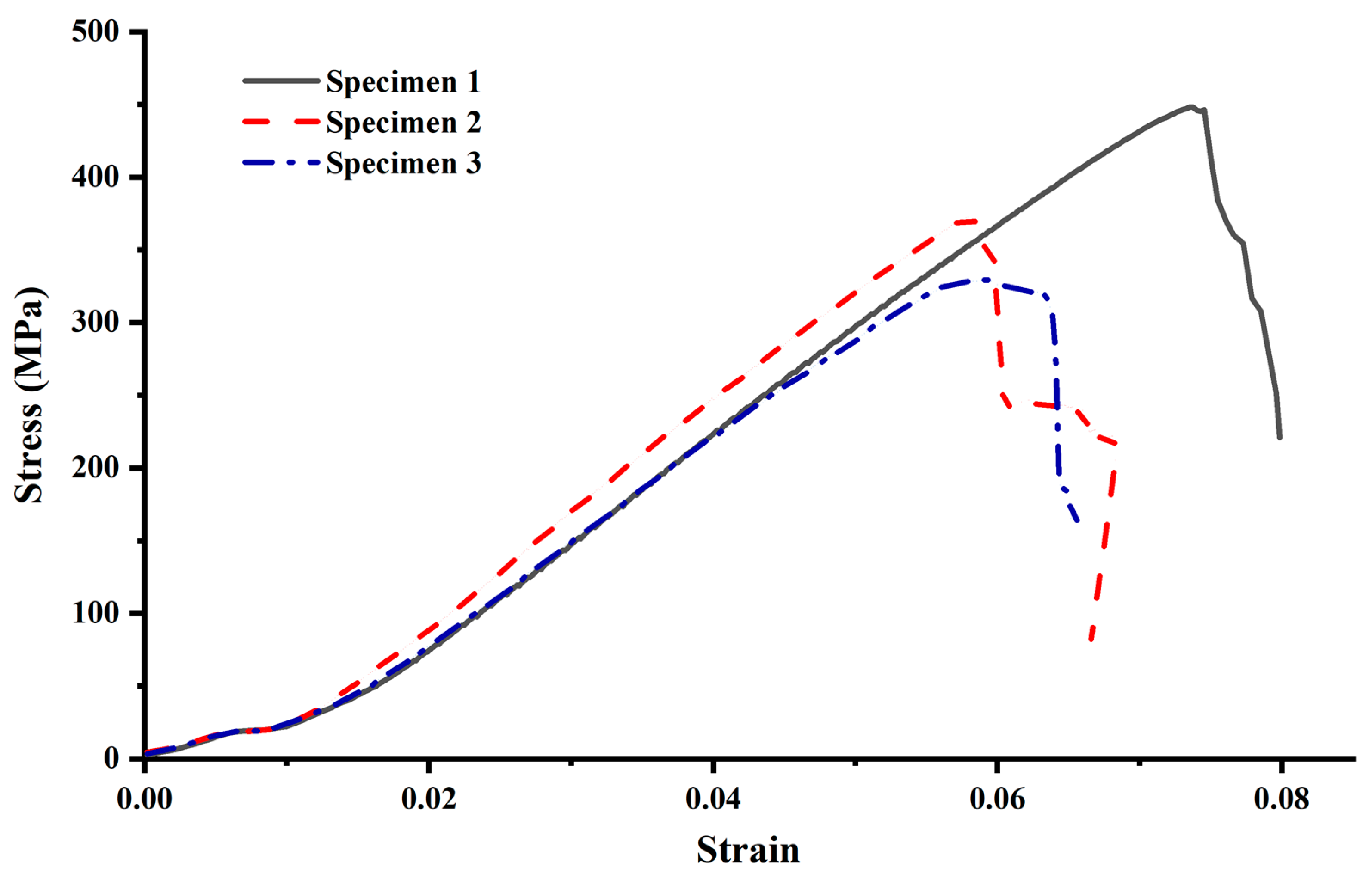
3.1. Results Analysis of GFRP Bars Tensile Strength Test
3.2. Analysis of Nut-Tray Anchorage Test Results
4. Theoretical Analysis on Tray Stress
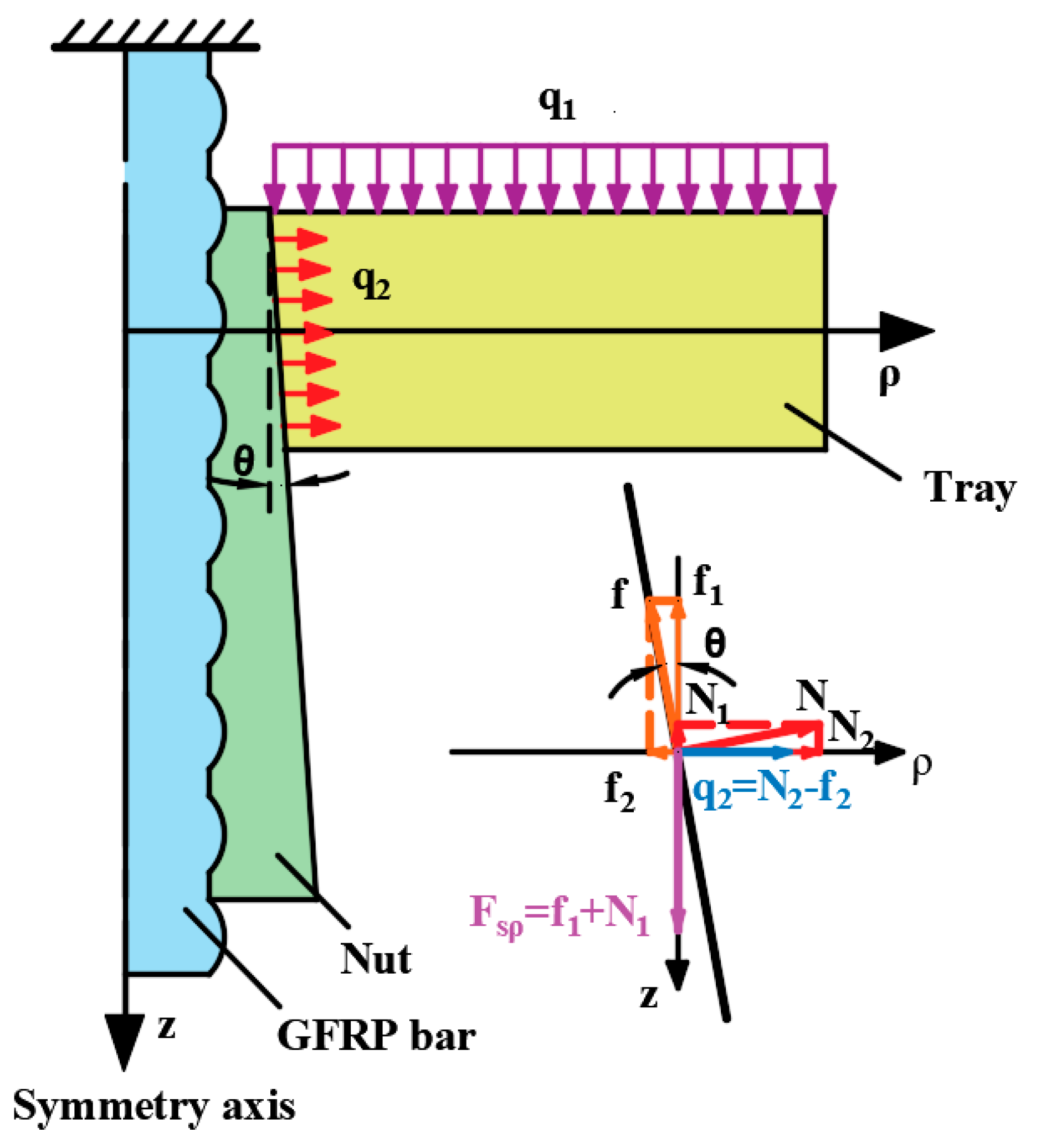
4.1. Force Analysis of Tray Bending under Transverse Load
4.2. Influence of Nut Extrusion on the Tray Internal Force
4.3. Superposition of Tray Internal Force
5. Tray Force Analysis of the Numerical Simulation
5.1. Rationality Verification of the Numerical Simulation Parameters
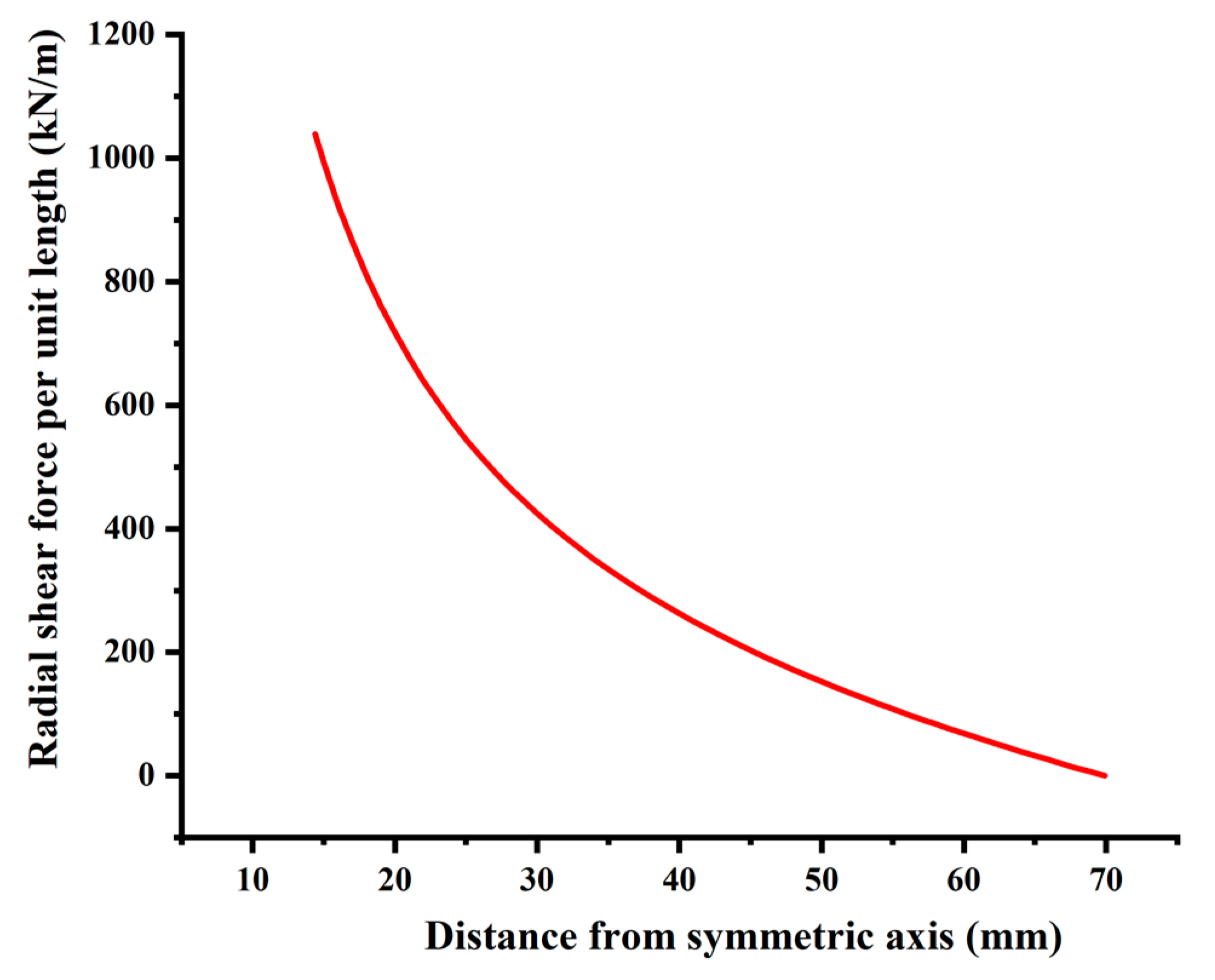
5.2. Numerical Simulation Results of the Tray
6. Discussion
6.1. Comparison of Theoretical Calculation and Numerical Simulation
6.2. Ultimate Strength of Tray Failure
6.3. Potential Strategy to Prevent Failure of Trays
- (1)
- Increase the glass fiber content of the tray, and improve the strength and deformation resistance of the tray from the perspective of materials.
- (2)
- Optimize the appearance shape of the free surface of the tray and reduce the stress concentration caused by the sudden change of the thickness of the tray, so as to improve the stiffness of the tray and reduce the radial deformation of the stressed surface.
- (3)
- Increase the width of the small circular surface of the free surface of the tray and improve the radial restraint ability of the central orifice of the tray free surface to the nut.
- (4)
- Optimize the cone angle of the nut and reasonably distribute the extrusion and shear capacity of the nut.
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, S.G.; Zhang, X.D.; Li, Y.J. Research on fiber rigid plastic anchor rod and its engineering application. J. China Coal Soc. 2002, 27, 619–622. [Google Scholar] [CrossRef]
- Zou, C.F.; Ye, Y.C.; Wang, W.J.; Wang, S.P.; Jin, H.-C. Monitoring analysis on deformation of the roadway bolting by GFRP of Jinshandian Iron Mine. Met. Mine 2011, 40, 41–44. [Google Scholar]
- Zhu, H.M.; Mei, Q.L.; Chen, Q.Y.; Zhu, W.C. Engineering mechanical characteristics and application of anchorage FRP anchor rod support. J. Wuhan Inst. Technol. 2014, 36, 65–69. [Google Scholar] [CrossRef]
- Wang, W.J.; Wan, H. Mechanical characteristics analysis of fully grouted GFRP rock bolts in highly stressed soft rock tunnels. J. Min. Saf. Eng. 2019, 36, 482–490. [Google Scholar] [CrossRef]
- Huang, L.M.; Huang, Z.H.; Li, W.C.; Li, G.W. Application test of GFRP reinforced material substituting steel for anchoring high slope. J. China Foreign Highw. 2005, 025, 144–147. [Google Scholar] [CrossRef]
- Li, G.W.; Liu, C.Q.; Huang, Z.H.; Cai, Y.Q. In-situ test of glass fiber reinforced polymer anchor on highway slope reinforcement. Chin. J. Rock Mech. Eng. 2010, 29, 4056–4062. [Google Scholar]
- Jia, X. Research on Bond Mechanism of GFRP Bolt. Master’s Thesis, Tongji University, Shanghai, China, 2005. [Google Scholar]
- Zhang, M.Y.; Kou, H.L.; Bai, X.Y.; Zhang, Z.Q. Experimental study and mechanism analysis of the anti-pulling behavior of glass fiber reinforced polymer anti-float anchor. Rock Soil Mech. 2014, 35, 1069–1076. [Google Scholar] [CrossRef]
- Kuang, Z.; Bai, X.Y.; Zhang, M.Y. Calculation for the critical anchorage length of glass fiber reinforced polymer anti-floating anchor. Sci. Technol. Eng. 2019, 19, 244–249. [Google Scholar]
- Bai, X.Y.; Zhang, M.Y.; Kuang, Z.; Wang, Y.H.; Yan, N. Load distribution function model of full-length bond GFRP anti-floating anchor. J. Cent. South Univ. (Sci. Technol.) 2020, 51, 1977–1988. [Google Scholar] [CrossRef]
- Li, G.W.; Liu, C.Q.; Huang, Z.H.; Cai, Y.Q. Field test on the load-bearing character of glass fiber reinforced polymer bolt. Chin. J. Rock Mech. Eng. 2006, 25, 86–92. [Google Scholar]
- Liu, Y.H.; Yong, Y. Experimental research on anchorage performance of full-thread GFRP bonding anchor bolts. Chin. J. Rock Mech. Eng. 2010, 29, 394–400. [Google Scholar]
- Huang, Z.H.; Li, G.W. Design and research of glass fiber reinforced plastic anchor rod. Fiber Reinf. Plast./Compos. 2008, 5, 36–40. [Google Scholar]
- Jia, X.; Yuan, Y.; Li, C.F. Experimental study on bond behavior of new type cement grouted GFRP bolts. Chin. J. Rock Mech. Eng. 2006, 25, 2108–2114. [Google Scholar]
- Huang, Z.H.; Li, G.W.; Wang, S.J.; Li, W.C. Field test on pull-out behaviors of anchorage structures with glass fiber reinforced plastic rods for different surrounding rock masses. Chin. J. Rock Mech. Eng. 2008, 027, 1008–1018. [Google Scholar]
- Zhu, H.H.; Yin, J.H.; Yeung, A.T.; Wei, J. Field Pullout Testing and Performance Evaluation of GFRP Soil Nails. J. Geotech. Geoenviron. Eng. 2011, 137, 633–642. [Google Scholar] [CrossRef]
- Ashrafi, H.; Bazli, M.; Oskouei, A.V.; Bazli, L. Effect of Sequential Exposure to UV R-diation and Water Vapor Condensation and Extreme Temperatures on the Mechanical Properties of GFRP Bars. J. Compos. Constr. 2017, 22, 04017047. [Google Scholar] [CrossRef]
- Zhang, J.K.; Li, K.; Zhang, H.; Wang, N.; Guo, Q.L.; Zhao, L.Y. Research on non-destructive testing method of GFRP bolts based on HHT signal analysis. Chin. J. Rock Mech. Eng. 2021, 40, 1460–1472. [Google Scholar] [CrossRef]
- Zhang, X.; Li, H.Y.; Zhang, Z.Q.; Deng, L. Study on bond performance parameters of GFRP bars based on pull-out test. J. Sichuan Univ. (Nat. Sci. Ed.) 2021, 58, 044005. [Google Scholar] [CrossRef]
- Wang, W.; Fu, K. New anchorages for GFRP bar mechanical property tests. China Civ. Eng. J. 2010, 2, 194–198. [Google Scholar] [CrossRef]
- Carvelli, V.; Fava, G.; Pisani, M.A. Anchor system for tension testing of large diameter GFRP bars. J. Compos. Constr. 2009, 13, 344–349. [Google Scholar] [CrossRef]
- Zhang, M.Y.; Bai, X.Y.; Li, W.W. Experiment on external anchorage performance for nut-pallet anchorage of GFRP anti-floating anchors. J. Cent. South Univ. (Sci. Technol.) 2016, 47, 239–246. [Google Scholar]
- Sun, T.; Zhou, F.Y.; Liu, Q.; Yang, J.J.; Liu, T.C. Experimental study on anchor head of GFRP bolt. J. China Inst. Water Resour. Hydropower Res. 2017, 15, 250–255. [Google Scholar]
- Campbell, T.I.; Shrive, N.G.; Soudki, K.A.; Mayah, A.A.; Keatley, J.P.; Reda, M.M. Design and evaluation of a wedge-type anchor for fibre reinforced polymer tendons. Can. J. Civ. Eng. 2000, 27, 985–992. [Google Scholar] [CrossRef]
- Zhan, J.D.; Du, X.L.; Deng, Z.C. Studies and application on anchorages of prestressed FRP tendons. Ind. Constr. 2006, 36, 65–68. [Google Scholar] [CrossRef]
- American Concrete Institute (ACI). Guide Test Methods for Fiber-Reinforced Polymers (FRPS) for Reinforcing or Strengthening Concrete Structures; ACI: Detroit, MI, USA, 2004. [Google Scholar]
- Fan, Y.Q.; Yu, K.; Niu, G.L.; Jian, W.X. Application study of GFRP bolt in slope protection. Highway 2018, 12, 28–35. [Google Scholar]
- Bai, X.Y.; Zhang, M.Y.; Wang, Y.H.; Kuang, Z.; Yan, N.; Zhu, L. Field test on bond strength between Glass Fiber R-einforcement Polymer anti-floating anchor and concrete floor. J. China Univ. Min. Technol. 2020, 49, 93–102. [Google Scholar] [CrossRef]
- Chen, C.; Xu, D.S.; Xu, X.Y.; Chen, J.W. Stress distribution of glass fiber reinforced polymer bolt in the retaining and protection of foundation excavation. Sci. Technol. Eng. 2020, 20, 13394–13401. [Google Scholar]
- Zheng, C.; Bai, X.Y.; Zhang, M.Y.; Wang, H.G. Research progress on glass fiber reinforced polymer anchors in anti-floating engineering of underground structures. Mater. Rep. 2020, 34, 13194–13202. [Google Scholar] [CrossRef]
- Huang, L.Y.; Liu, F.; Ma, J.J. Ultimate stress and displacement analysis of FRP bolt tray and nut. Low Temp. Archit. Technol. 2017, 039, 107–109. [Google Scholar]
- Jia, X.G.; Li, Y.M.; Meng, X.R.; Wang, Y.L. Failure mechanism analysis and structural optimization of glass fiber reinforced plastics bolting tray based on ANSYS. Saf. Coal Mines 2015, 46, 212–215. [Google Scholar] [CrossRef]
- Gao, Q.; Guo, X.W.; Huang, L.Y. Optimal design of FRP anchor bolt fastening system. Low Temp. Archit. Technol. 2015, 201, 98–100. [Google Scholar]
- Wen, M. The Finite Element Value Simulation of Composite Bolt Threaded Nut Contact and Experimental Study. Master’s Thesis, Taiyuan University of Science and Technology, Taiyuan, China, 2008. [Google Scholar]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Technical Specification for Retaining and Protection of Building Foundation Excavations; Architecture and Building Press: Beijing, China, 2012.
- Xu, Z.L. Elasticity, 5th ed.; Higher Education Press: Beijing, China, 2016; Volume II. [Google Scholar]
- Huang, J.G.; Wang, Q. Research on mechanical and friction properties of glass fiber reinforced polyethylene composite. Acata Mater. Compos. Sin. 1997, 14, 19–25. [Google Scholar] [CrossRef]
- Ge, S.R.; Wang, W.H. Study on the tribological properties of glass fiber reinforced nylon 1010 composite. Tribology 2000, 20, 427–430. [Google Scholar] [CrossRef]
- Ma, Y.Y.; Wang, W.H.; Cheng, X.H. On the friction and wear of short glass fiber reinforced nylon. Mech. Sci. Technol. 2003, 22, 994–995. [Google Scholar] [CrossRef]
- Jia, J.H.; Chen, J.S.; Cheng, J.M.; Zhou, H.D.; Yang, S.Y. Tribological behaviors of fibers reinforced polyimide composites. J. Mater. Sci. Eng. 2008, 26, 832–836. [Google Scholar] [CrossRef]
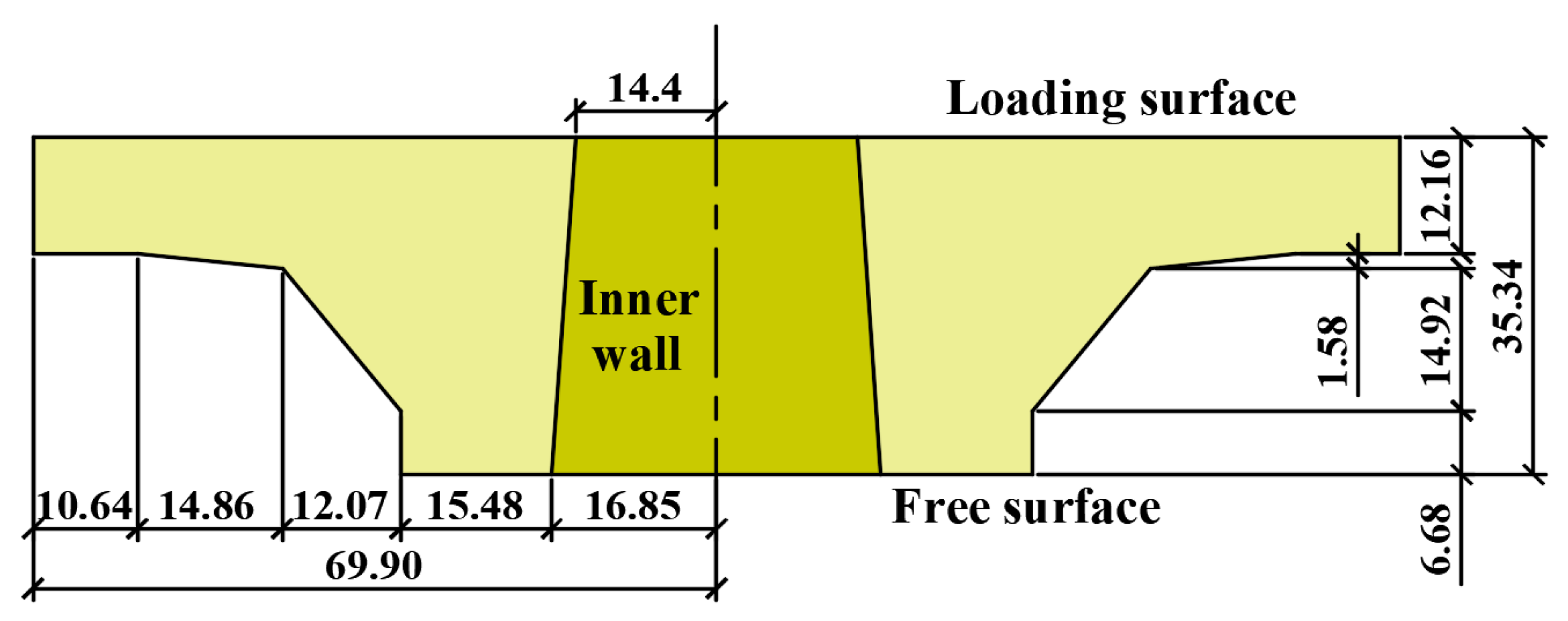




| Diameter (mm) | Rib Height (mm) | Rib Width (mm) | Rib Spacing (mm) | Poisson’s Ratio | Density (g/cm3) |
|---|---|---|---|---|---|
| 20 | 1.58 | 7.38 | 21.11 | 0.2 | 2.0 |
| Length | Big End Outside Diameter | Hexagon Flank Height | Hexagon Length | Cone Height |
|---|---|---|---|---|
| 20 | 1.58 | 7.38 | 21.11 | 0.2 |
| Inside Diameter | Small End Outside Diameter | Conical Angle | Gap Length | Gap Width |
| 20 | 32.378 | 6 | 30 | 3.0 |
| Categories | Theoretical Analysis | Numerical Simulation |
|---|---|---|
| Elastic modulus | The tensile strength test of GFRP bars, 7.0 GPa. | |
| Poisson’s ratio | 0.2 | 0.2 |
| Friction coefficient between nut and inner wall | 0.3 | 0.3 |
| Tray thickness characteristics | Equal thickness | Variable thickness |
| Tray radius, (mm) | 69.90 | 69.90 |
| Tray center opening shape | Equivalent diameter round hole | Conical round hole |
| Boundary condition | Same as Section 2.3 | |
| Load type and size | Equivalent uniform load, 6.4 MPa | |
| Analysis basis | According to Section 3.2., the deformation characteristics of the tray under maximum loading are as follows: the damage of the tray is the local cracking of the inner wall, and the deformation of the tray surface is a recoverable small deformation. | |
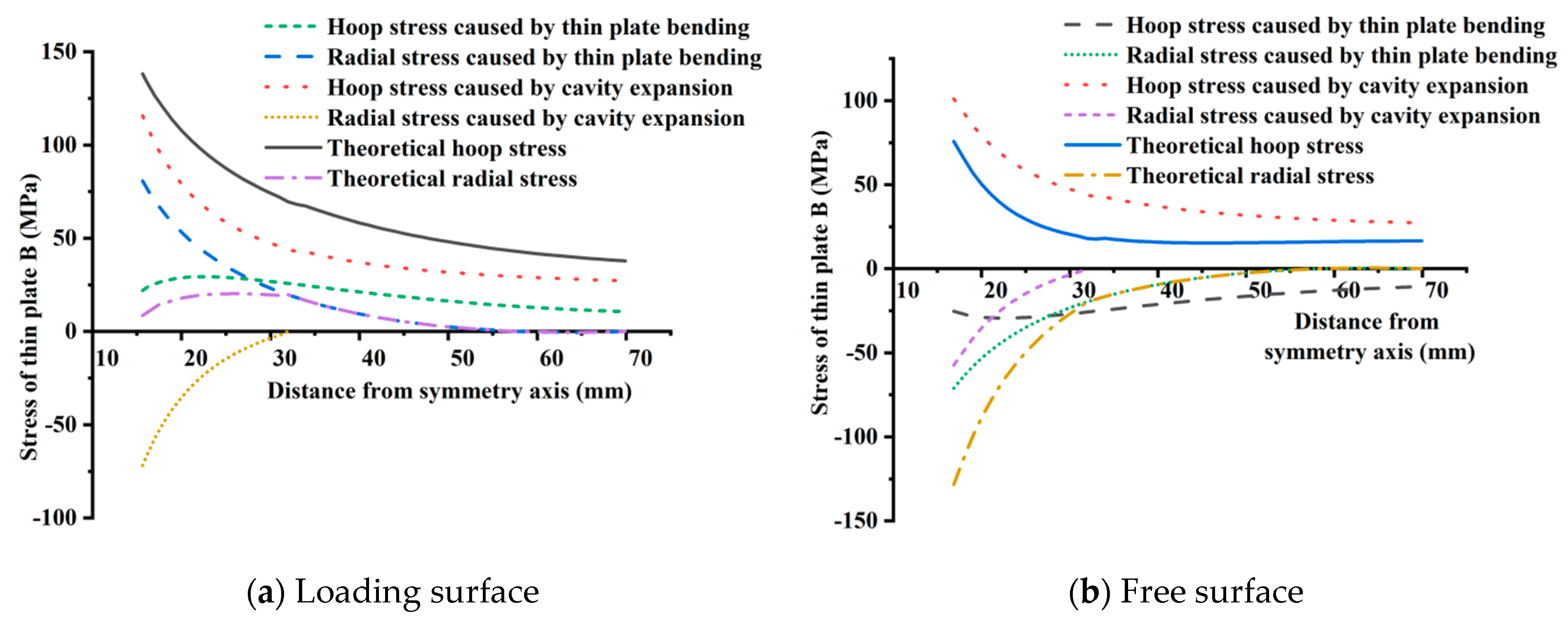
| Analysis method | Superposition of calculation results of thin plate bending and cavity expansion | Linear static analysis |
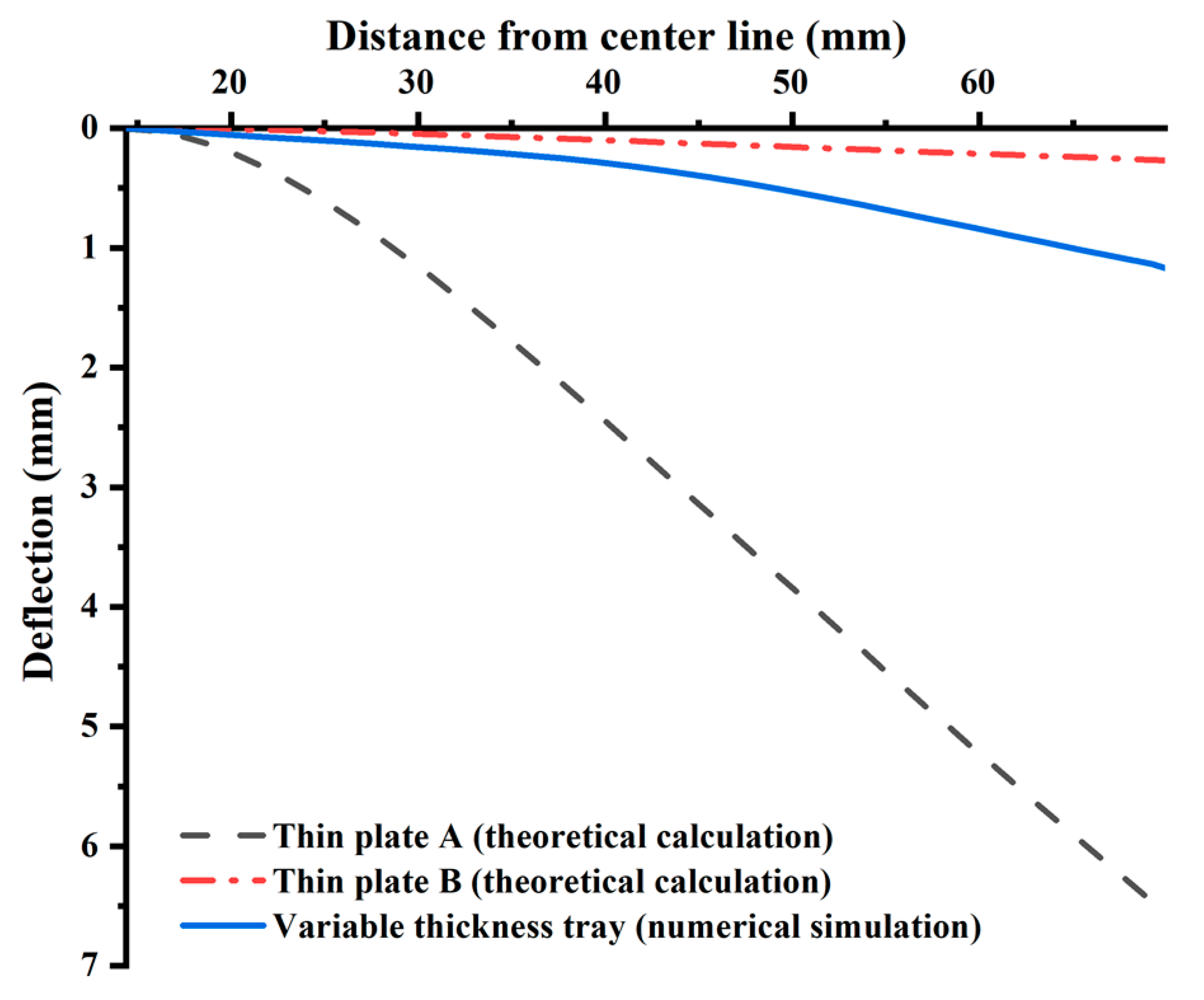
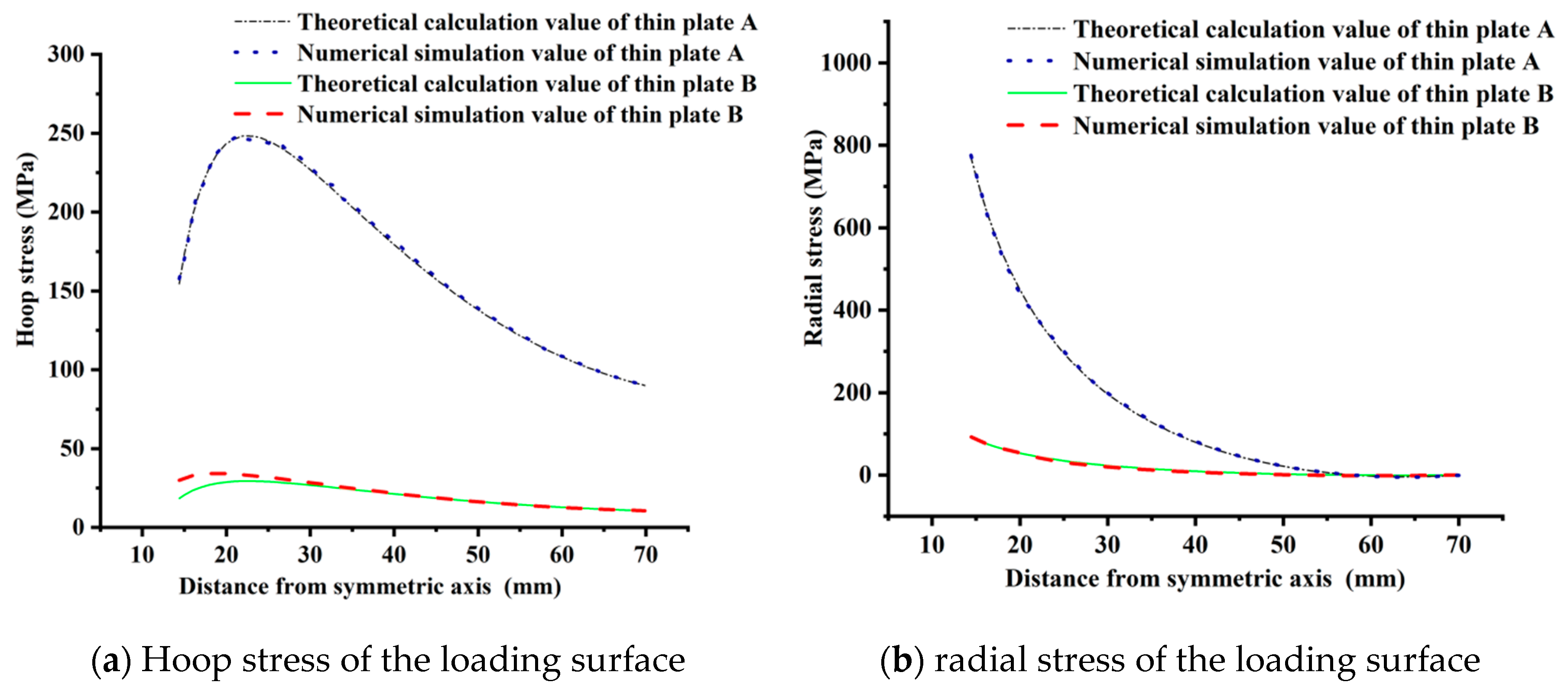
| Radial deflection characteristics of the tray | Theoretical calculation value of plate A > numerical simulation value > Theoretical calculation value of plate B, see Figure 9. | |
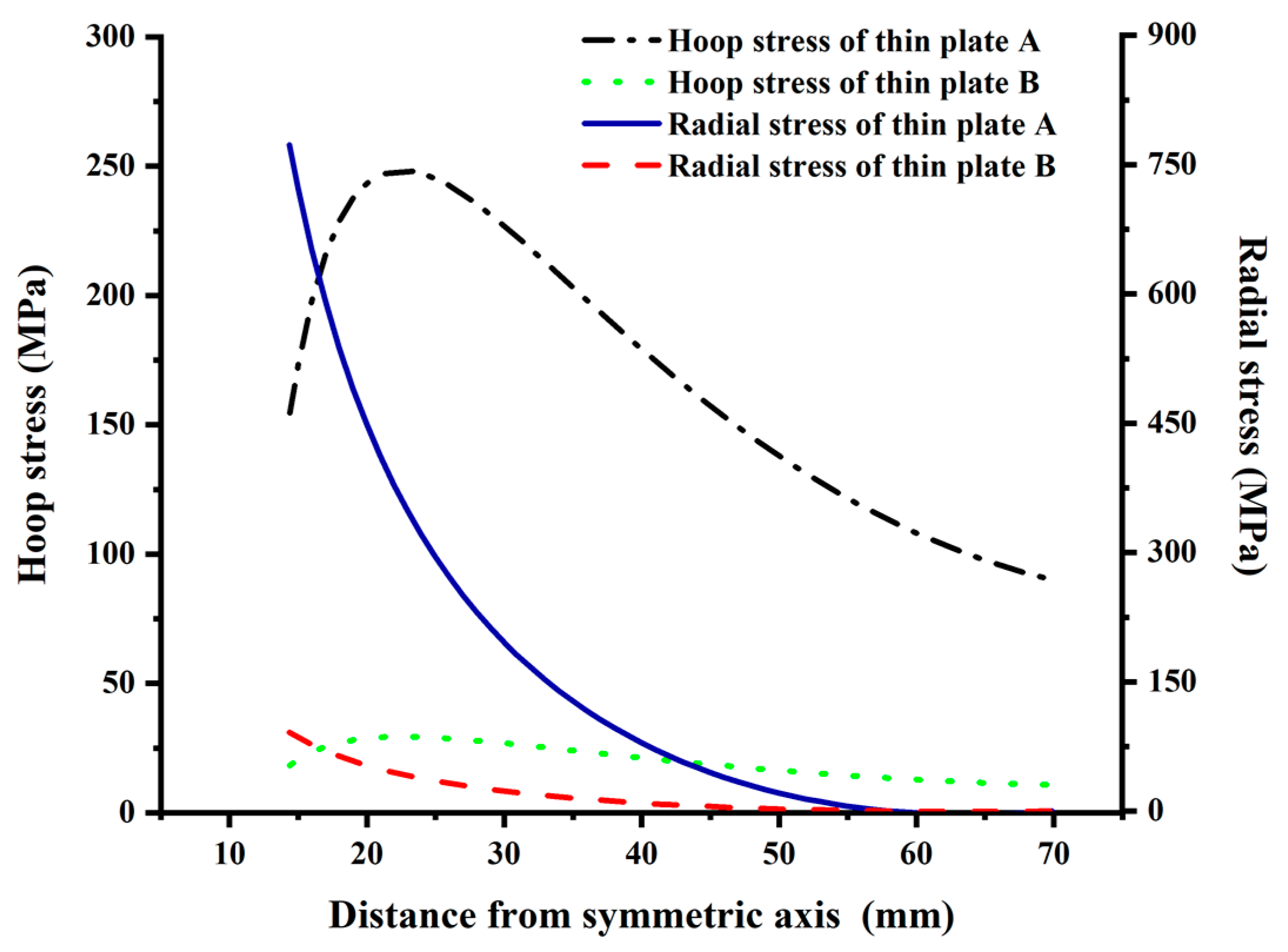
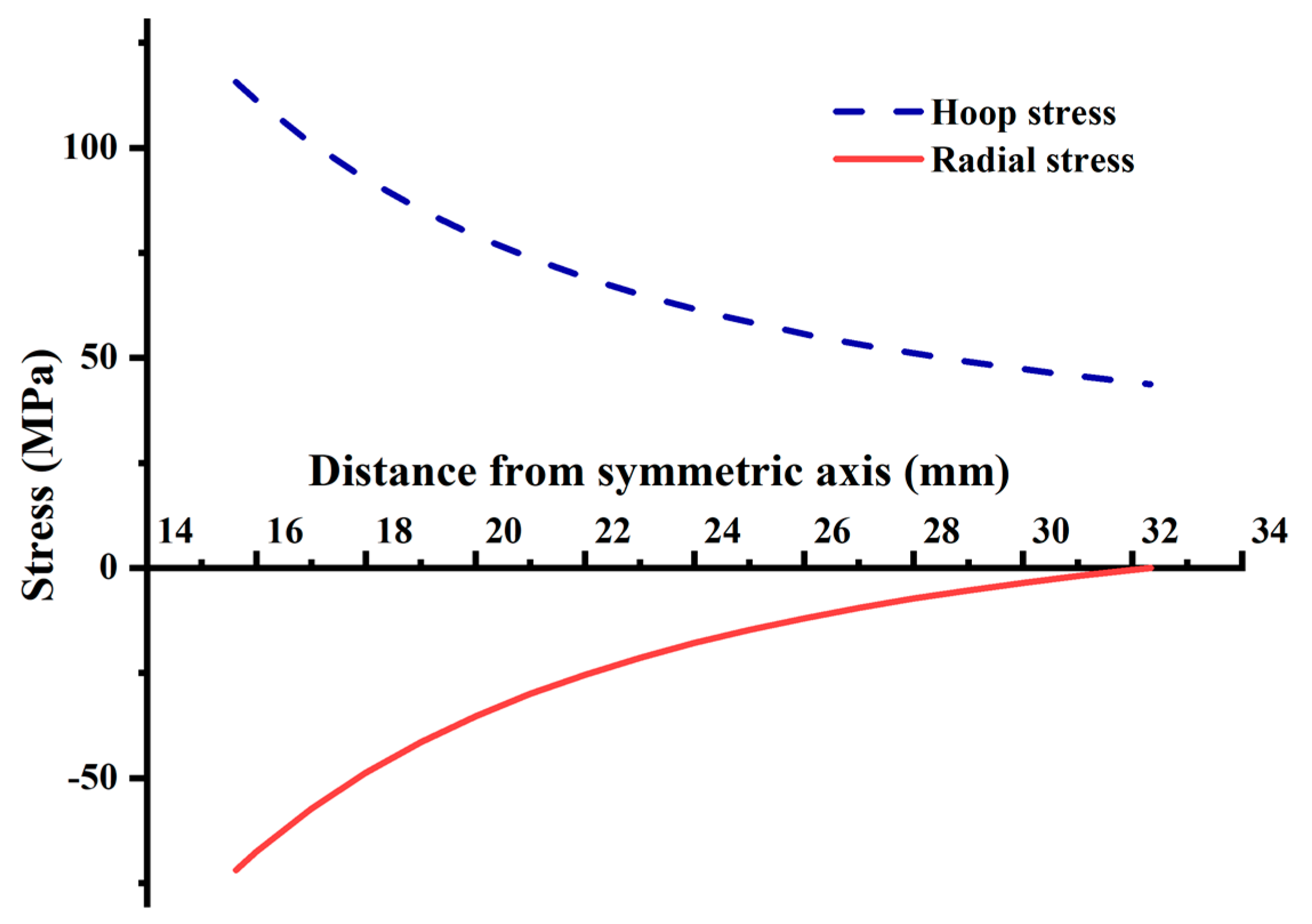
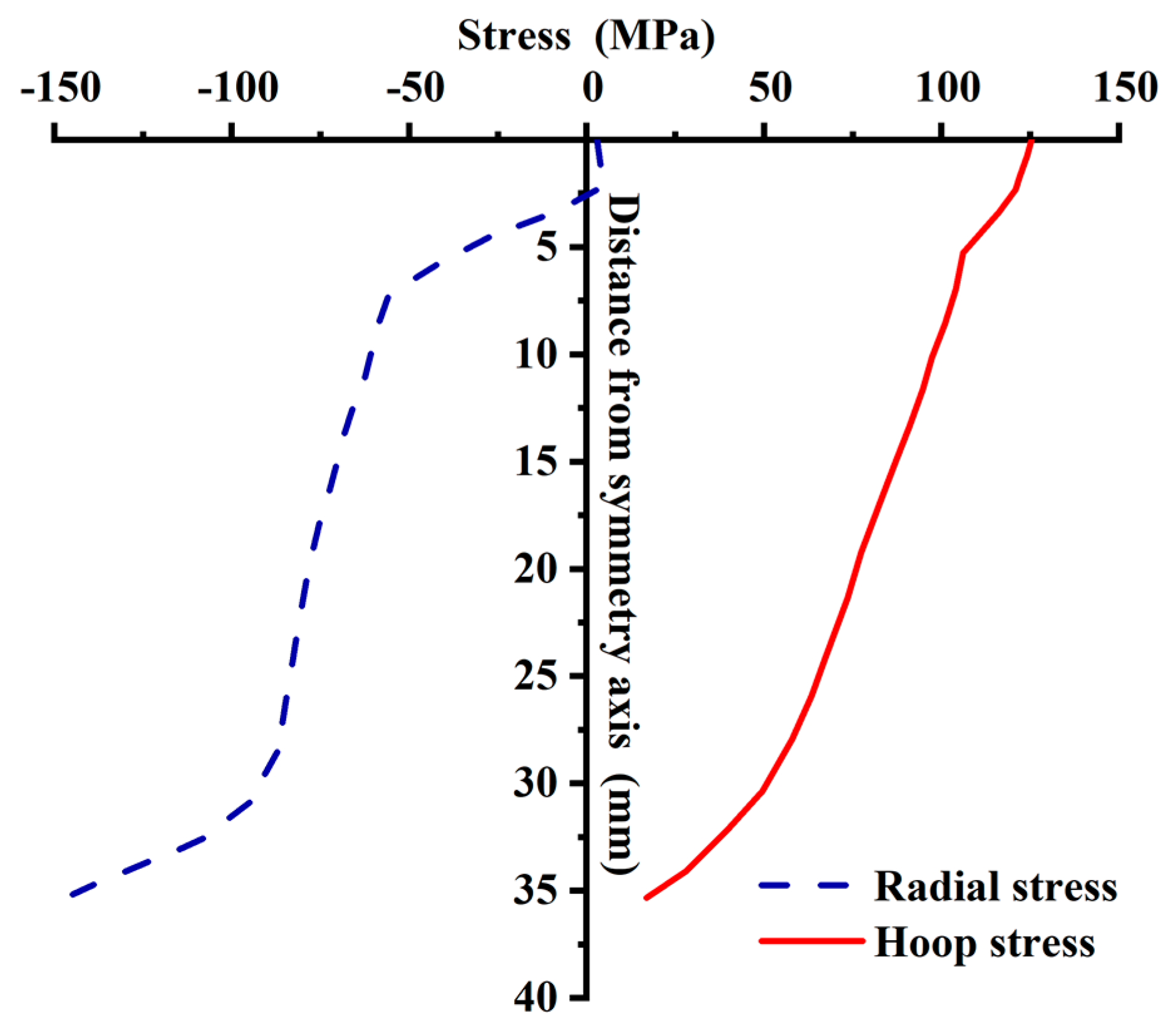
| Hoop stress characteristics of the loading surface of the tray | Controlled by hoop compressive stress, size: Theoretical calculation value of plate A > numerical simulation value ≈ Theoretical calculation value of plate B, see Figure 17. | |
| Radial stress characteristics of the free surface of the tray | Controlled by radial tensile stress, size: Theoretical calculation value of plate A > numerical simulation value ≈ Theoretical calculation value of plate B, see Figure 17. | |
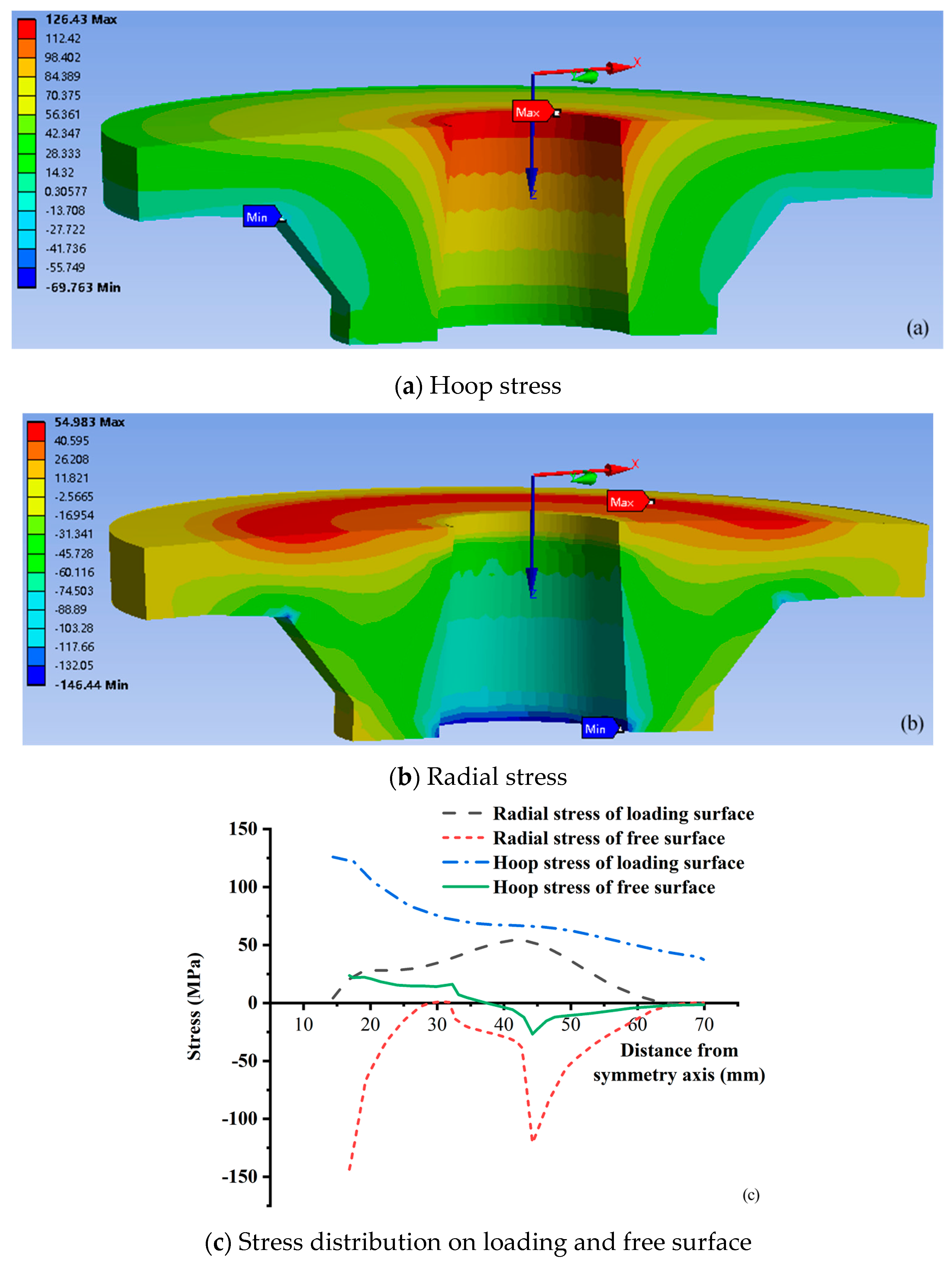
| Radial stress of the inner wall of the tray, (MPa) | 71.83 (plate B) | 67.62 (mean value) |
| Hoop stress of inner wall of the tray, (MPa) | 115.51 (plate B) | 85.44 (mean value) |
| Maximum tensile stress of the free surface inner wall, (MPa) | 207.50 (plate B) | 190.98 |
| Comparative conclusions | (1) The radial deflection, radial stress, and hoop stress calculated by equal thickness plate B are the same as the numerical simulation results. (2) The tensile stress of the inner wall of the free surface of the tray is the largest, which is the weakest part of the tray, and the above analysis conclusion is the same as the damage location of the tray measured in the nut-tray anchorage test. | |
| Position of Strength Calculation | Theoretical Calculation Value of Thin Plate B | Numerical Simulation Value of the Tray | |||
|---|---|---|---|---|---|
| Equivalent Inner Wall of Loading Surface | Inner Wall of Free Surface | Equivalent Inner Wall of Loading Surface | Inner Wall of Free Surface | Thickness Turning Area of Free Surface | |
| σ1 (MPa) | 138.09 | −128.37 | 124.65 | −146.44 | −120.57 |
| σ2 (MPa) | 8.51 | 75.77 | 13.03 | 23.67 | −26.81 |
| σ3 (MPa) | −6.4 | 0 | −6.4 | 0 | 0 |
| σt (MPa) | 171.74 | 207.50 | 154.21 | 190.98 | 140.18 |
| σt/σr(%) | 43.87 | 53.00 | 39.39 | 48.78 | 35.81 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Du, Z.; Geng, S.; Han, W.; Wu, Y.; Feng, H. Theoretical Analysis Method of Variable Thickness GFRP Tray. Materials 2022, 15, 2346. https://doi.org/10.3390/ma15072346
Li J, Du Z, Geng S, Han W, Wu Y, Feng H. Theoretical Analysis Method of Variable Thickness GFRP Tray. Materials. 2022; 15(7):2346. https://doi.org/10.3390/ma15072346
Chicago/Turabian StyleLi, Jianjun, Zhaolong Du, Shaobo Geng, Wenmei Han, Yuxuan Wu, and Hao Feng. 2022. "Theoretical Analysis Method of Variable Thickness GFRP Tray" Materials 15, no. 7: 2346. https://doi.org/10.3390/ma15072346
APA StyleLi, J., Du, Z., Geng, S., Han, W., Wu, Y., & Feng, H. (2022). Theoretical Analysis Method of Variable Thickness GFRP Tray. Materials, 15(7), 2346. https://doi.org/10.3390/ma15072346






