On the Comparative Analysis of Different Phase Coexistences in Mesoporous Materials
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
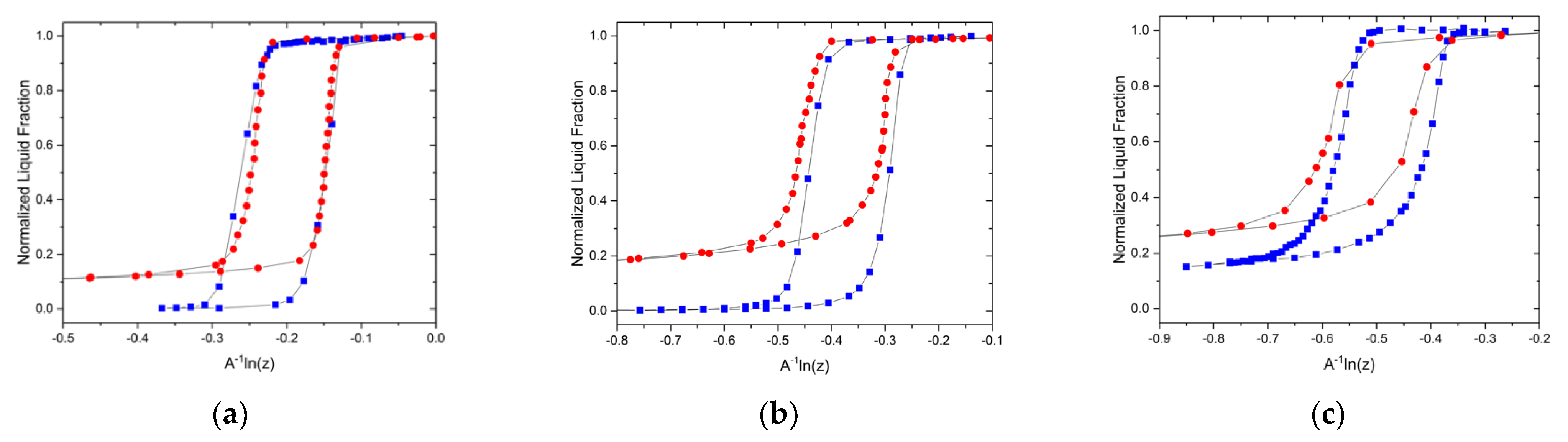
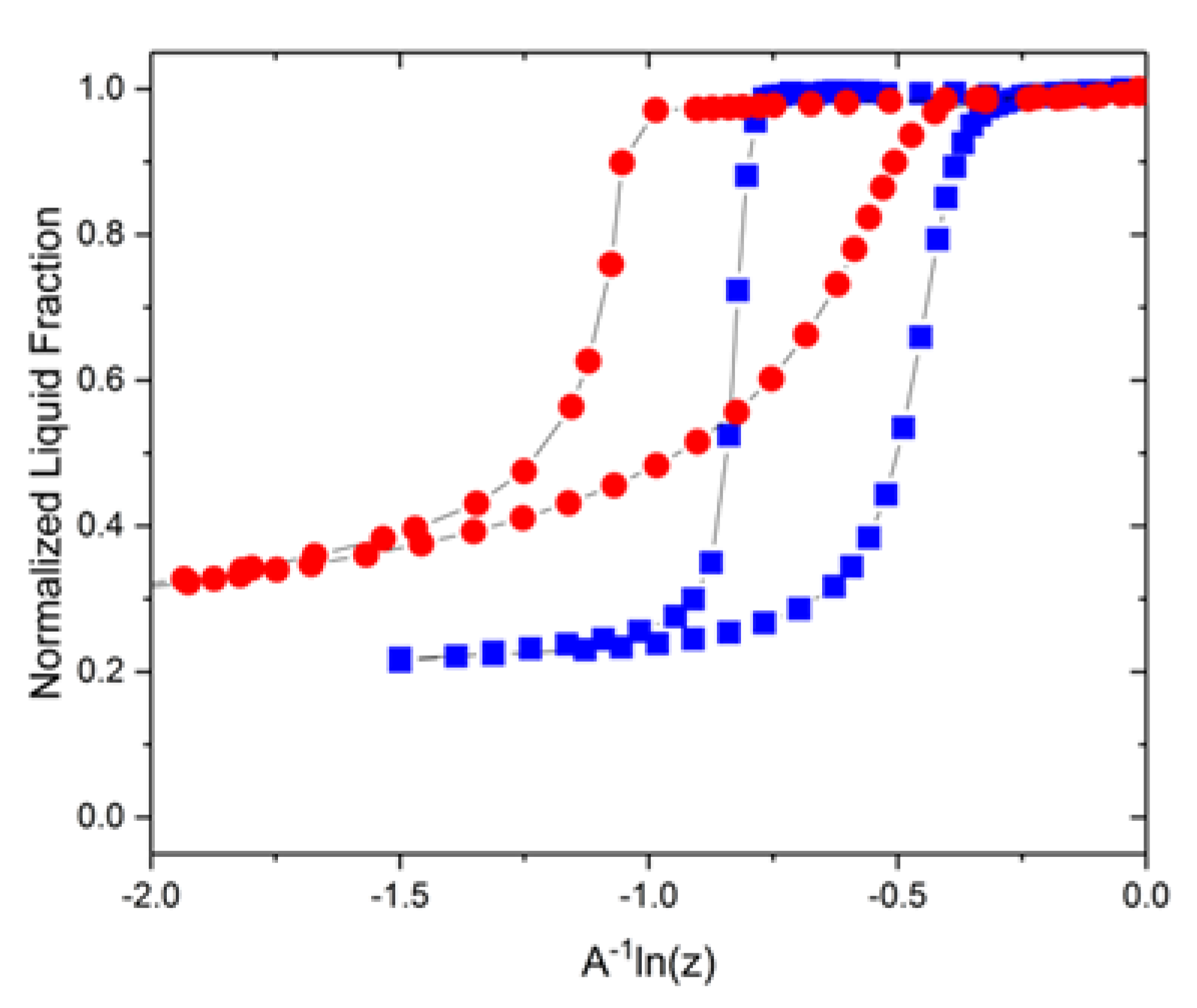
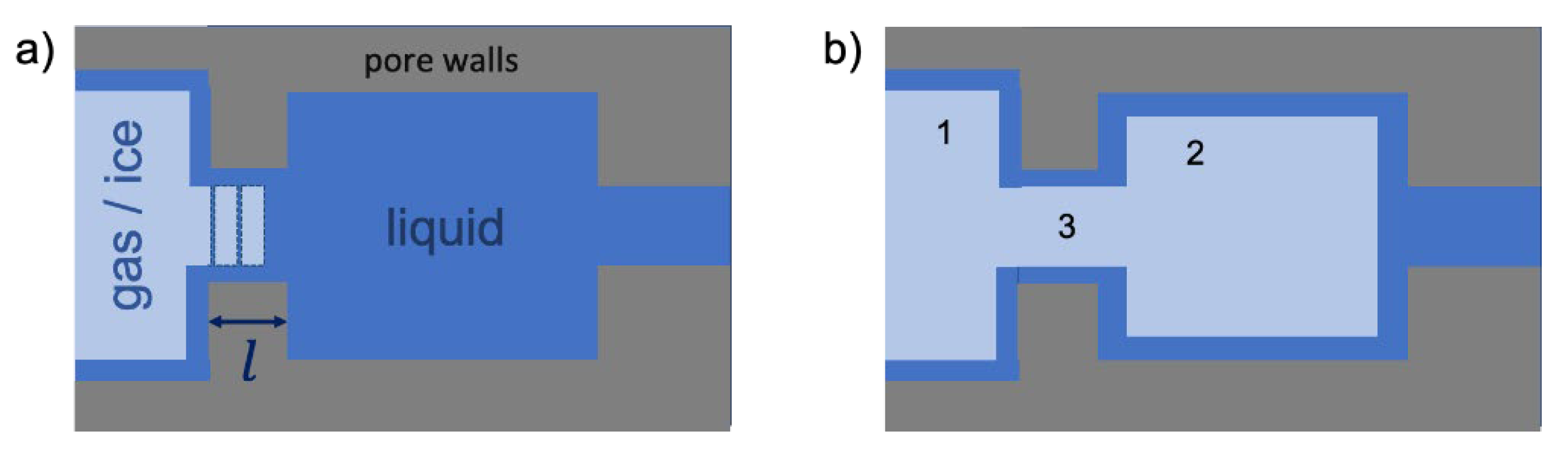
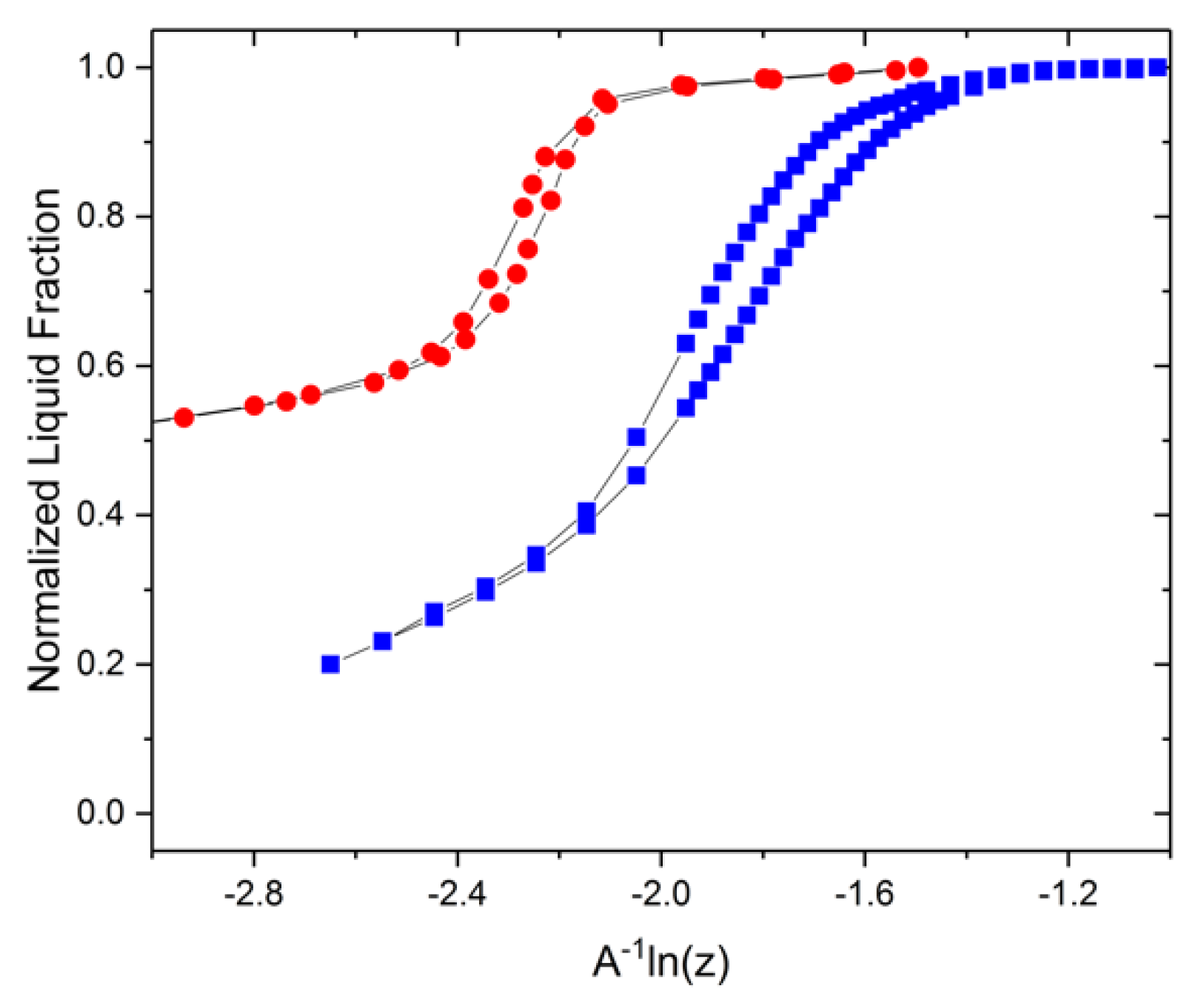
3.1. A Unified Coordinate System for Analysis
3.2. Experimental Visualizations
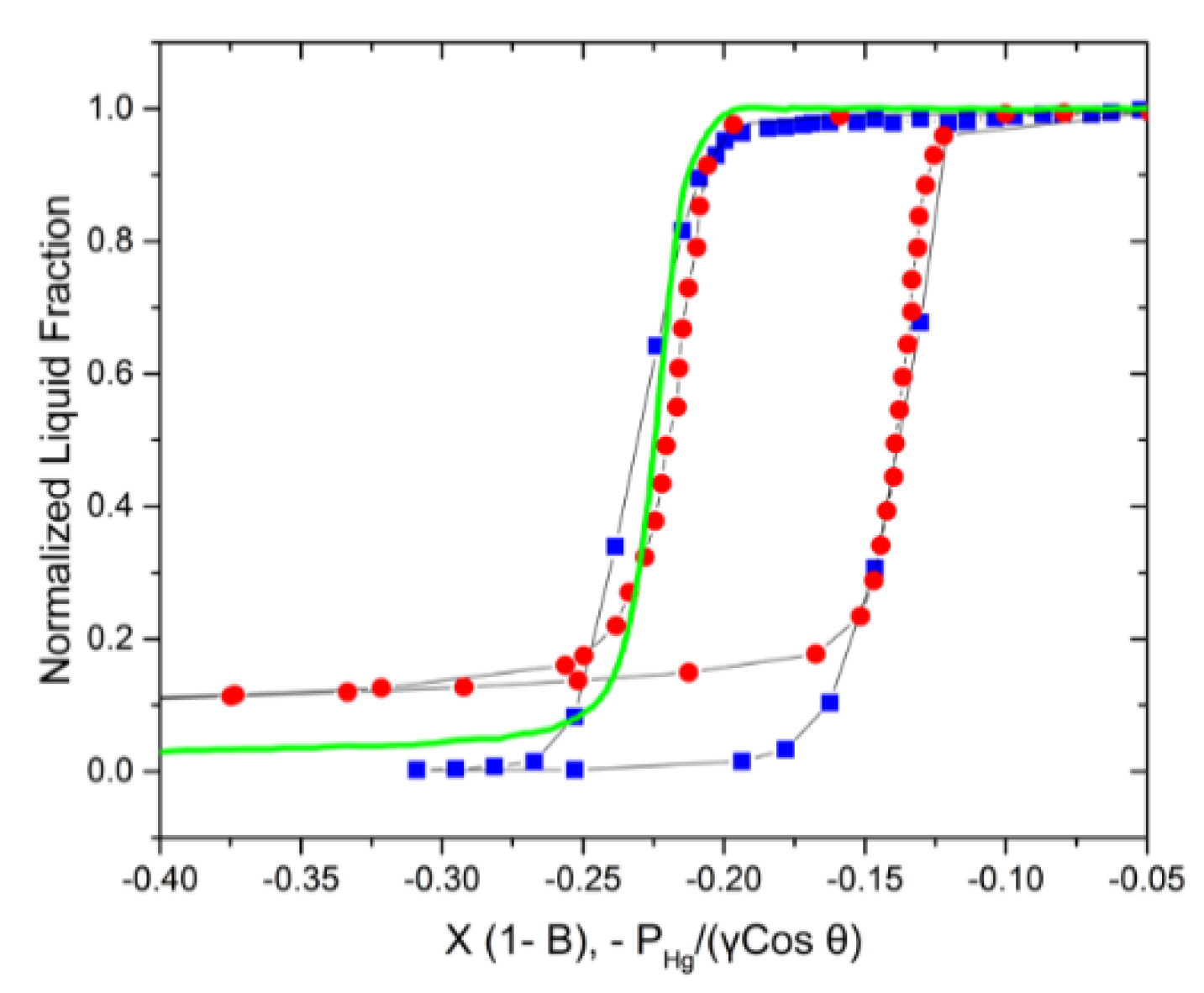
3.3. Adjustment for Mercury Porosimetry
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Christenson, H.K. Confinement effects on freezing and melting. J. Phys. Condens. Matter 2001, 13, R95–R133. [Google Scholar] [CrossRef]
- Alba-Simionesco, C.; Coasne, B.; Dosseh, G.; Dudziak, G.; Gubbins, K.; Radhakrishnan, R.; Sliwinska-Bartkowiak, M. Effects of confinement on freezing and melting. J. Phys. Condens. Matter 2006, 18, R15–R68. [Google Scholar] [CrossRef] [PubMed]
- Sandoval, D.R.; Yan, W.; Michelsen, M.L.; Stenby, E.H. Influence of Adsorption and Capillary Pressure on Phase Equilibria inside Shale Reservoirs. Energy Fuels 2018, 32, 2819–2833. [Google Scholar] [CrossRef] [Green Version]
- Barsotti, E.; Piri, M. Effect of Pore Size Distribution on Capillary Condensation in Nanoporous Media. Langmuir 2021, 37, 2276–2288. [Google Scholar] [CrossRef]
- Campbell, J.M.; Christenson, H.K. Nucleation- and Emergence-Limited Growth of Ice from Pores. Phys. Rev. Lett. 2018, 120, 165701. [Google Scholar] [CrossRef] [Green Version]
- David, R.O.; Marcolli, C.; Fahrni, J.; Qiu, Y.; Sirkin, Y.A.P.; Molinero, V.; Mahrt, F.; Bruhwiler, D.; Lohmann, U.; Kanji, Z.A. Pore condensation and freezing is responsible for ice formation below water saturation for porous particles. Proc. Natl. Acad. Sci. USA 2019, 116, 8184. [Google Scholar] [CrossRef] [Green Version]
- Čejka, J.; Mintova, S. Perspectives of Micro/Mesoporous Composites in Catalysis. Catal. Rev. 2007, 49, 457–509. [Google Scholar] [CrossRef]
- Popat, A.; Hartono, S.B.; Stahr, F.; Liu, J.; Qiao, S.Z.; Lu, G.Q. Mesoporous silica nanoparticles for bioadsorption, enzyme immobilisation, and delivery carriers. Nanoscale 2011, 3, 2801–2818. [Google Scholar] [CrossRef] [Green Version]
- Davis, M.E. Ordered porous materials for emerging applications. Nature 2002, 417, 813–821. [Google Scholar] [CrossRef]
- Kärger, J.; Valiullin, R. Mass transfer in mesoporous materials: The benefit of microscopic diffusion measurement. Chem. Soc. Rev. 2013, 42, 4172–4197. [Google Scholar] [CrossRef]
- Thommes, M.; Kaneko, K.; Neimark, A.V.; Olivier, J.P.; Rodriguez-Reinoso, F.; Rouquerol, J.; Sing, K.S. Physisorption of gases, with special reference to the evaluation of surface area and pore size distribution (IUPAC Technical Report). Pure Appl. Chem. 2015, 87, 1051–1069. [Google Scholar] [CrossRef] [Green Version]
- Brun, M.; Lallemand, A.; Quinson, J.-F.; Eyraud, C. A new method for the simultaneous determination of the size and shape of pores: The thermoporometry. Thermochim. Acta 1977, 21, 59–88. [Google Scholar] [CrossRef]
- Rouquerol, J.; Rouquerol, F.; Llewellyn, P.; Maurin, G.; Sing, K.S. Adsorption by Powders and Porous Solids: Principles, Methodology and Applications; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Strange, J.H.; Rahman, M.; Smith, E.G. Characterization of porous solids by NMR. Phys. Rev. Lett. 1993, 71, 3589–3591. [Google Scholar] [CrossRef]
- Kondrashova, D. Freezing and Melting Transitions of Liquids in Mesoporous Solids. Ph.D. Thesis, Leipzig University, Leipzig, Germany, 2017. [Google Scholar]
- Jackson, C.L.; McKenna, G.B. The melting behavior of organic materials confined in porous solids. J. Chem. Phys. 1990, 93, 9002–9011. [Google Scholar] [CrossRef]
- Beurroies, I.; Denoyel, R.; Llewellyn, P.; Rouquerol, J. A comparison between melting-solidification and capillary condensation hysteresis in mesoporous materials: Application to the interpretation of thermoporometry data. Thermochim. Acta 2004, 421, 11–18. [Google Scholar] [CrossRef]
- Denoyel, R.; Llewellyn, P.; Beurroies, I.; Rouquerol, J.; Rouquerol, F.; Luciani, L. Comparing the basic phenomena involved in three methods of pore-size characterization: Gas adsorption, liquid intrusion and thermoporometry. Part. Part. Syst. Charact. 2004, 21, 128–137. [Google Scholar] [CrossRef]
- Thommes, M.; Morell, J.; Cychosz, K.A.; Fröba, M. Combining Nitrogen, Argon, and Water Adsorption for Advanced Characterization of Ordered Mesoporous Carbons (CMKs) and Periodic Mesoporous Organosilicas (PMOs). Langmuir 2013, 29, 14893–14902. [Google Scholar] [CrossRef]
- Cychosz, K.A.; Guillet-Nicolas, R.; García-Martínez, J.; Thommes, M. Recent advances in the textural characterization of hierarchically structured nanoporous materials. Chem. Soc. Rev. 2017, 46, 389–414. [Google Scholar] [CrossRef]
- Gelb, L.D.; Gubbins, K.; Radhakrishnan, R.; Sliwinska-Bartkowiak, M. Phase separation in confined systems. Rep. Prog. Phys. 1999, 62, 1573–1659. [Google Scholar] [CrossRef] [Green Version]
- Morishige, K.; Shikimi, M. Adsorption hysteresis and pore critical temperature in a single cylindrical pore. J. Chem. Phys. 1998, 108, 7821–7824. [Google Scholar] [CrossRef]
- Morishige, K.; Ishino, M. Lower Closure Point of Adsorption Hysteresis in Ordered Mesoporous Silicas. Langmuir 2007, 23, 11021–11026. [Google Scholar] [CrossRef] [PubMed]
- Enninful, H.R.; Schneider, D.; Kohns, R.; Enke, D.; Valiullin, R. A novel approach for advanced thermoporometry characterization of mesoporous solids: Transition kernels and the serially connected pore model. Microporous Mesoporous Mater. 2020, 309, 110534. [Google Scholar] [CrossRef]
- Enninful, H.R.N.B.; Schneider, D.; Hoppe, A.; König, S.; Fröba, M.; Enke, D.; Valiullin, R. Comparative Gas Sorption and Cryoporometry Study of Mesoporous Glass Structure: Application of the Serially Connected Pore Model. Front. Chem. 2019, 7, 230. [Google Scholar] [CrossRef] [PubMed]
- Rouquerol, J.; Baron, G.; Denoye, L.R.; Giesche, H.; Groen, J.; Klobes, P.; Levitz, P.; Neimark, A.V.; Rigby, S.; Skudas, R.; et al. Liquid intrusion and alternative methods for the characterization of macroporous materials (IUPAC Technical Report). Pure Appl. Chem. 2011, 84, 107–136. [Google Scholar] [CrossRef]
- Enninful, H.R.N.B.; Schneider, D.; Enke, D.; Valiullin, R. Impact of Geometrical Disorder on Phase Equilibria of Fluids and Solids Confined in Mesoporous Materials. Langmuir 2021, 37, 3521–3537. [Google Scholar] [CrossRef] [PubMed]
- Jackson, K.A. Kinetic Processes: Crystal Growth, Diffusion, and Phase Transitions in Materials; Wiley-VCH: Weinheim, Germany, 2004. [Google Scholar]
- Kondrashova, D.; Valiullin, R. Improving structural analysis of disordered mesoporous materials using NMR cryoporometry. Microporous Mesoporous Mater. 2013, 178, 15–19. [Google Scholar] [CrossRef]
- Kondrashova, D.; Valiullin, R. Freezing and Melting Transitions under Mesoscalic Confinement: Application of the Kossel–Stranski Crystal-Growth Model. J. Phys. Chem. C 2015, 119, 4312–4323. [Google Scholar] [CrossRef]
- Enninful, H.R.N.B.; Schneider, D.; Rudolph, B.; Meyer, A.; Mascotto, S.; Valiullin, R. Nuclear Magnetic Resonance Cryoporometry Study of Solid–Liquid Equilibria in Interconnected Spherical Nanocages. J. Phys. Chem. C 2021, 125, 26916–26926. [Google Scholar] [CrossRef]
| Material | ||
|---|---|---|
| Ice | 6.0 | 273 |
| Nitrogen | 2.8 | 77 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Enninful, H.R.N.B.; Enke, D.; Valiullin, R. On the Comparative Analysis of Different Phase Coexistences in Mesoporous Materials. Materials 2022, 15, 2350. https://doi.org/10.3390/ma15072350
Enninful HRNB, Enke D, Valiullin R. On the Comparative Analysis of Different Phase Coexistences in Mesoporous Materials. Materials. 2022; 15(7):2350. https://doi.org/10.3390/ma15072350
Chicago/Turabian StyleEnninful, Henry R. N. B., Dirk Enke, and Rustem Valiullin. 2022. "On the Comparative Analysis of Different Phase Coexistences in Mesoporous Materials" Materials 15, no. 7: 2350. https://doi.org/10.3390/ma15072350
APA StyleEnninful, H. R. N. B., Enke, D., & Valiullin, R. (2022). On the Comparative Analysis of Different Phase Coexistences in Mesoporous Materials. Materials, 15(7), 2350. https://doi.org/10.3390/ma15072350








