Simulation and Optimization of Connection-Strength Performance of Axial Extrusion Joint
Abstract
:1. Introduction
2. Methods
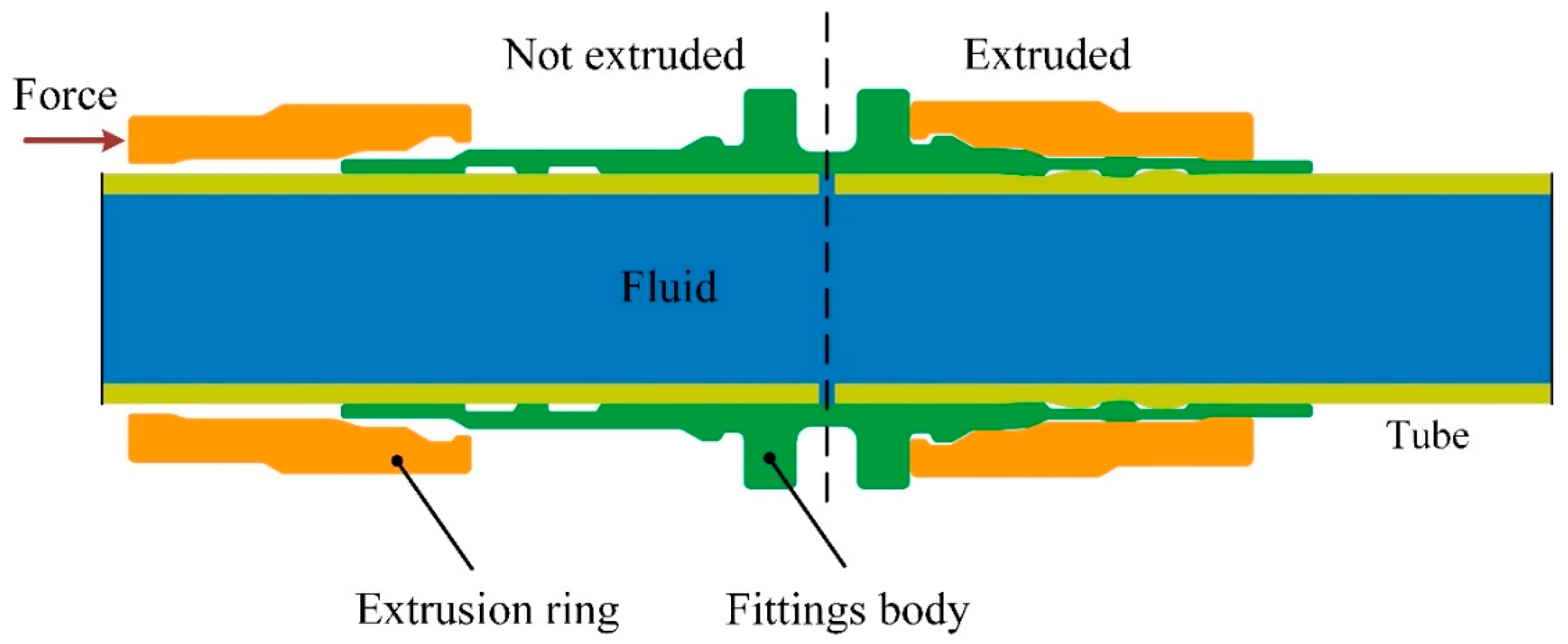
2.1. Experimental Scheme of Joint Strength
2.2. FE Modeling of Joint-Strength Experiment
3. Results and Discussion
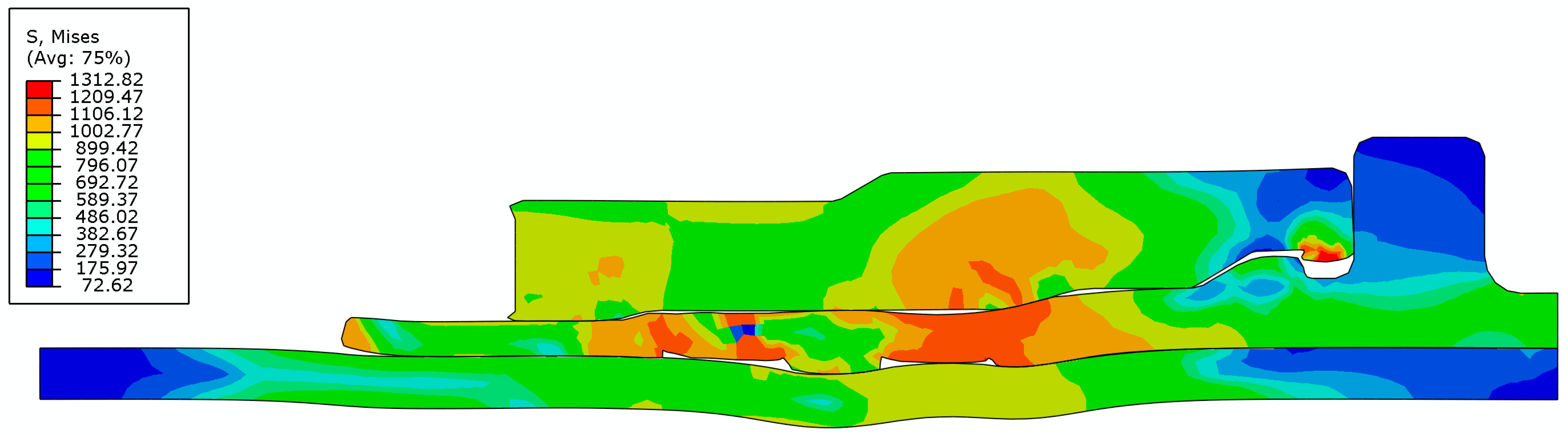
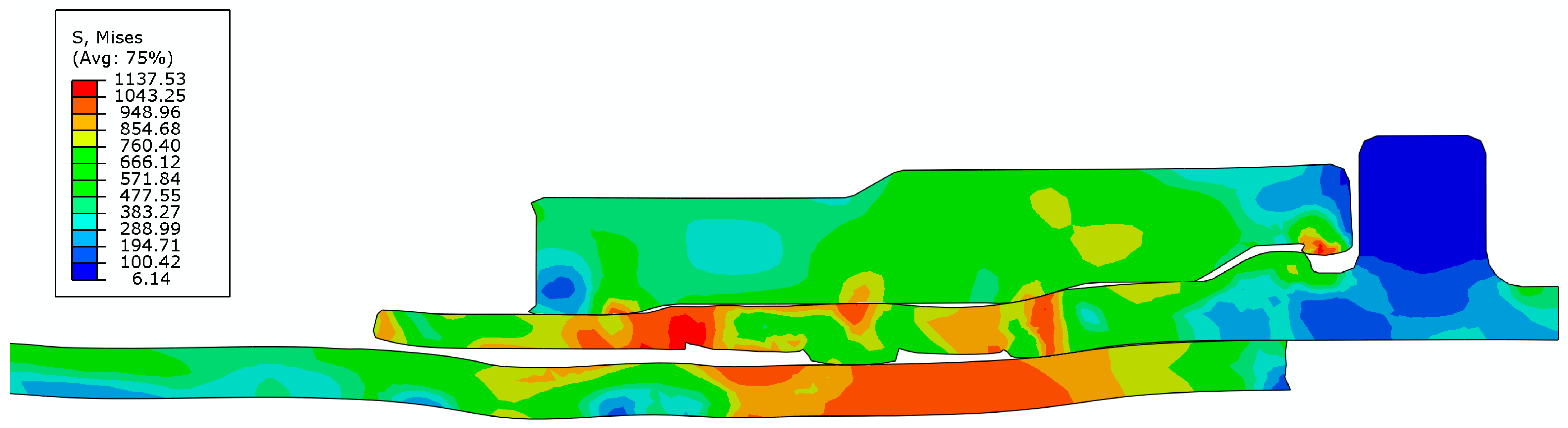
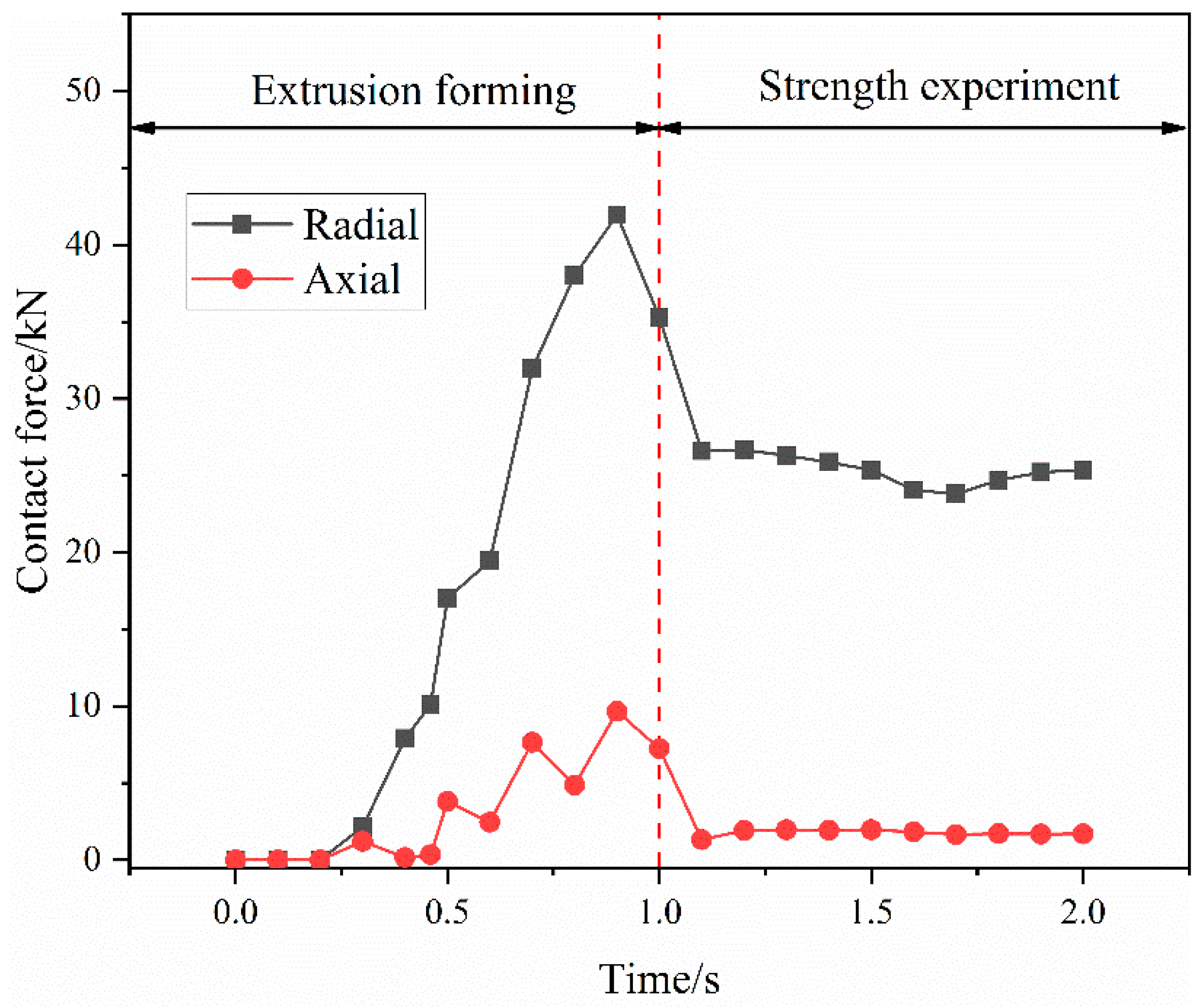
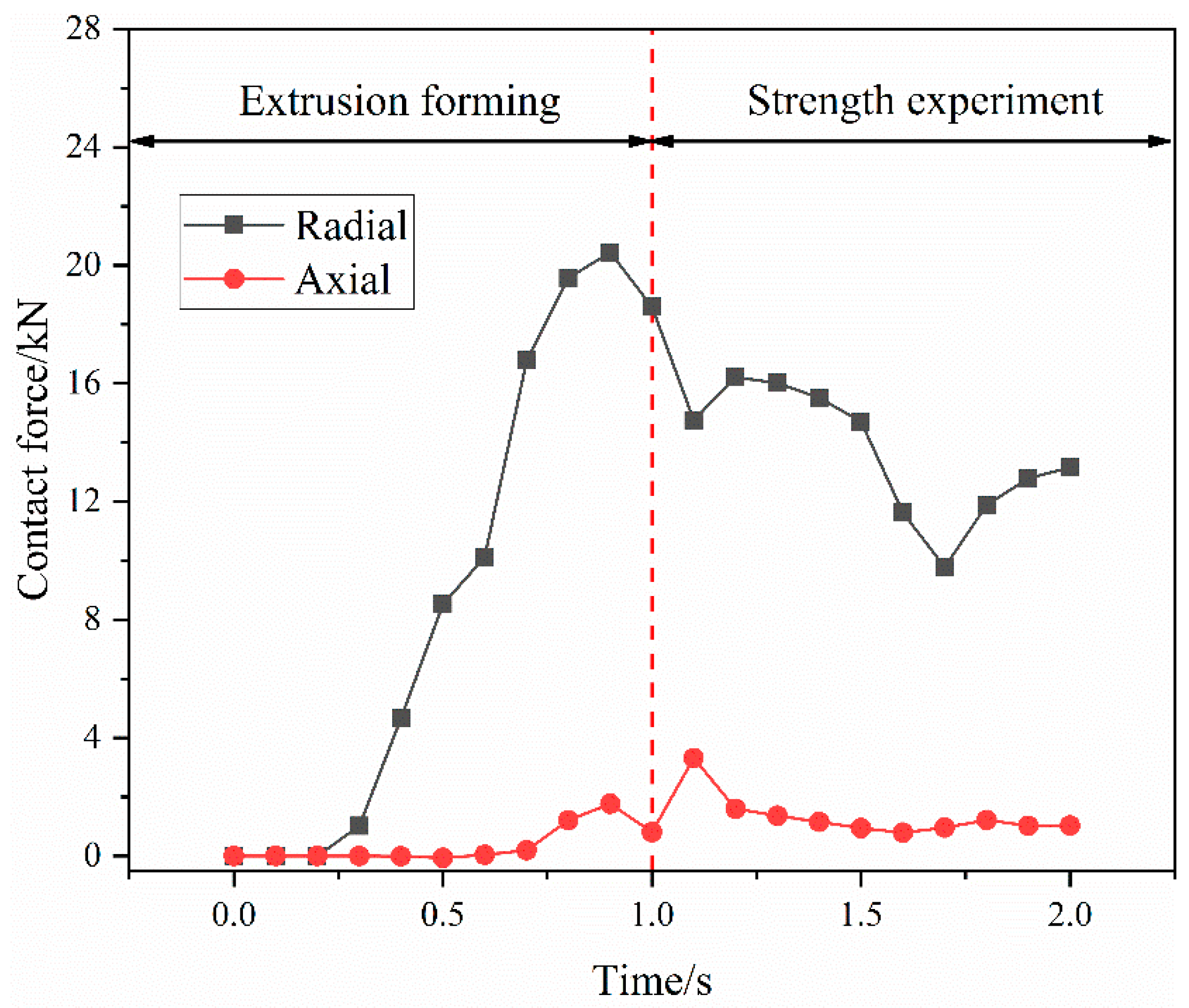
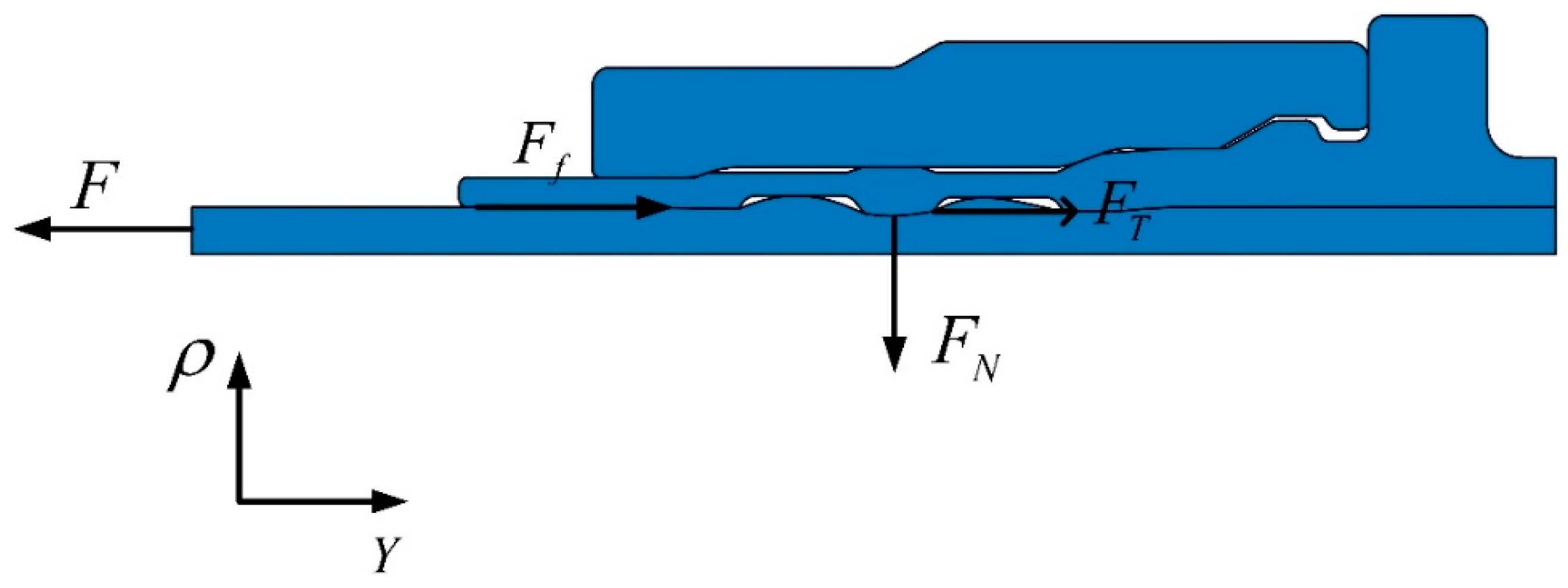
3.1. Joint-Strength Mechanism
3.2. Experimental Design of Influencing Factors on Joint Strength
3.3. Grey Correlation Analysis
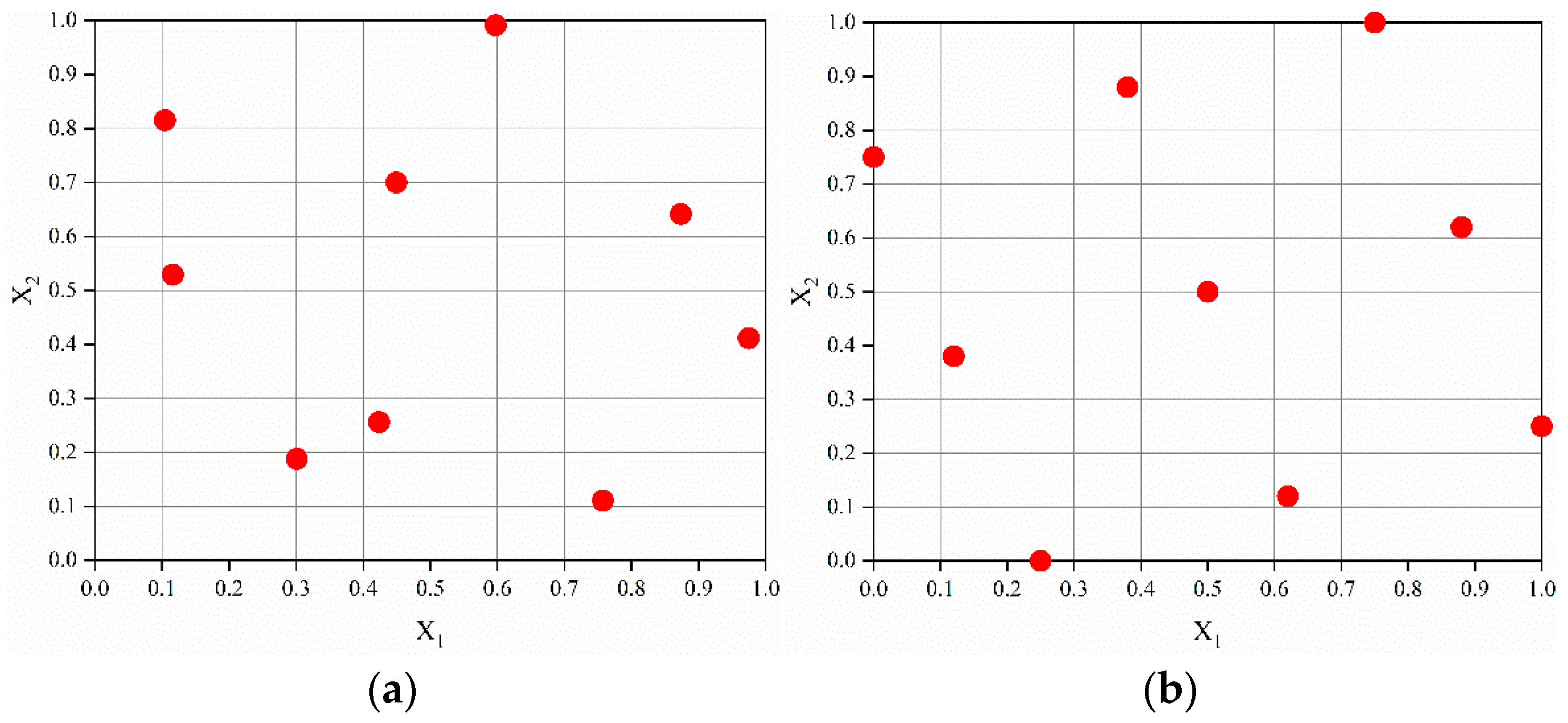
3.4. Optimization of Influencing Factors of Joint Strength
4. Conclusions
- (1)
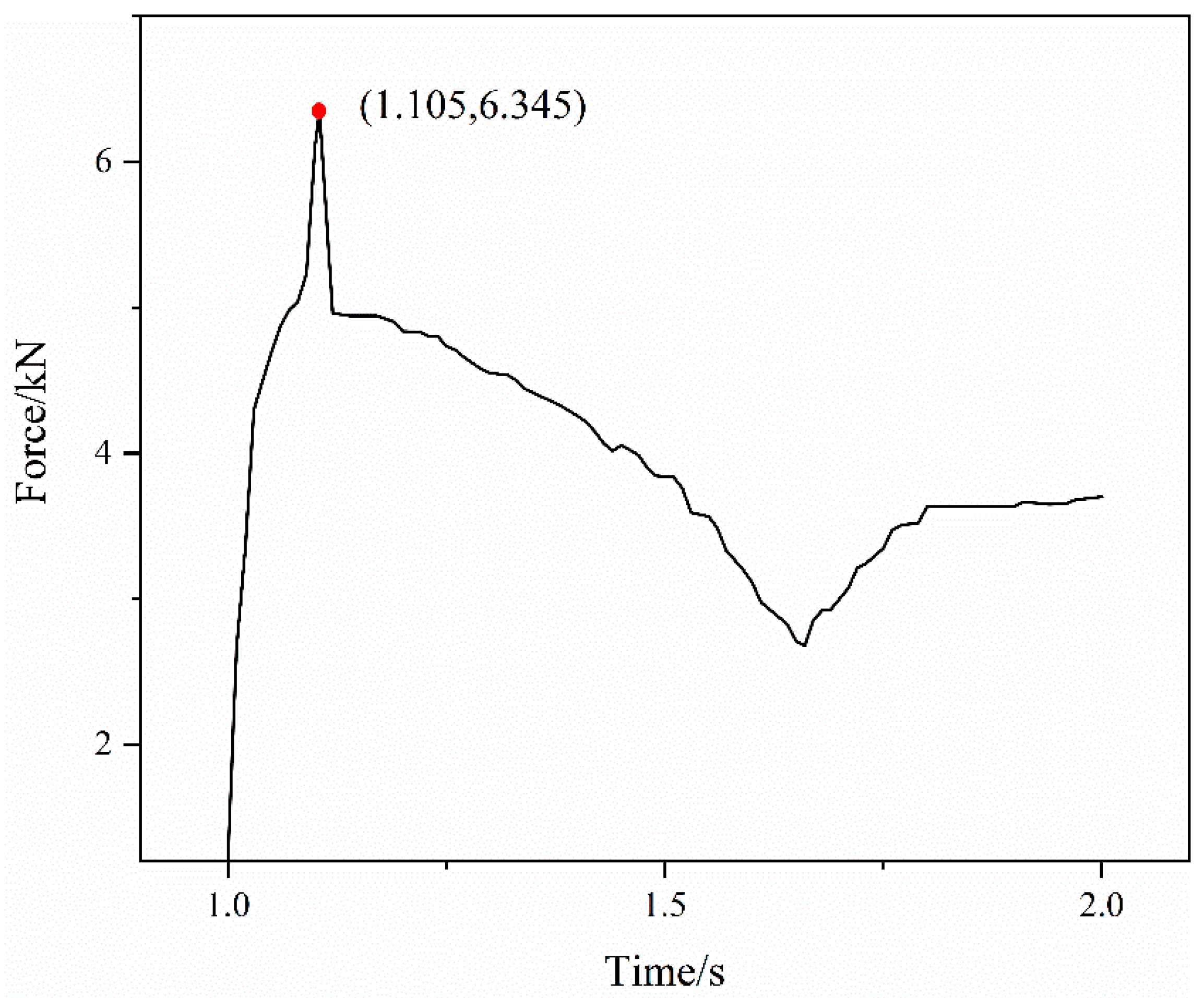
- Based on the joint-strength experimental scheme of the axial extrusion joint, finite-element modeling of the joint was performed using Abaqus to simulate the extrusion-forming and titanium-tube pull-off process of the joint. The forces between the fittings were analyzed and the mechanism of joint-strength generation was analyzed. It is shown that the connection strength of the joint is formed by both the radial contact force between the titanium tube and the fittings body and the axial pull-off resistance of the titanium-tube material embedded in the groove of the joint body. The calculated connection strength of the axial extrusion joint is 6.345 kN.
- (2)
- The factors influencing the joint strength include the angle of the notch ends of the joint body, the extrusion time and the intercomponent friction coefficient. The orthogonal-level test was conducted according to the number and level of the test factors with the joint strength as the target value. Gray correlation analysis was performed on the orthogonal test results to obtain the correlation ranking of each factor on the joint strength. The key factors affecting the joint strength are obtained as the friction coefficient between the extrusion ring and the joint body; the friction coefficient between the titanium tube and the joint body; and the angle of the left end of the groove.
- (3)
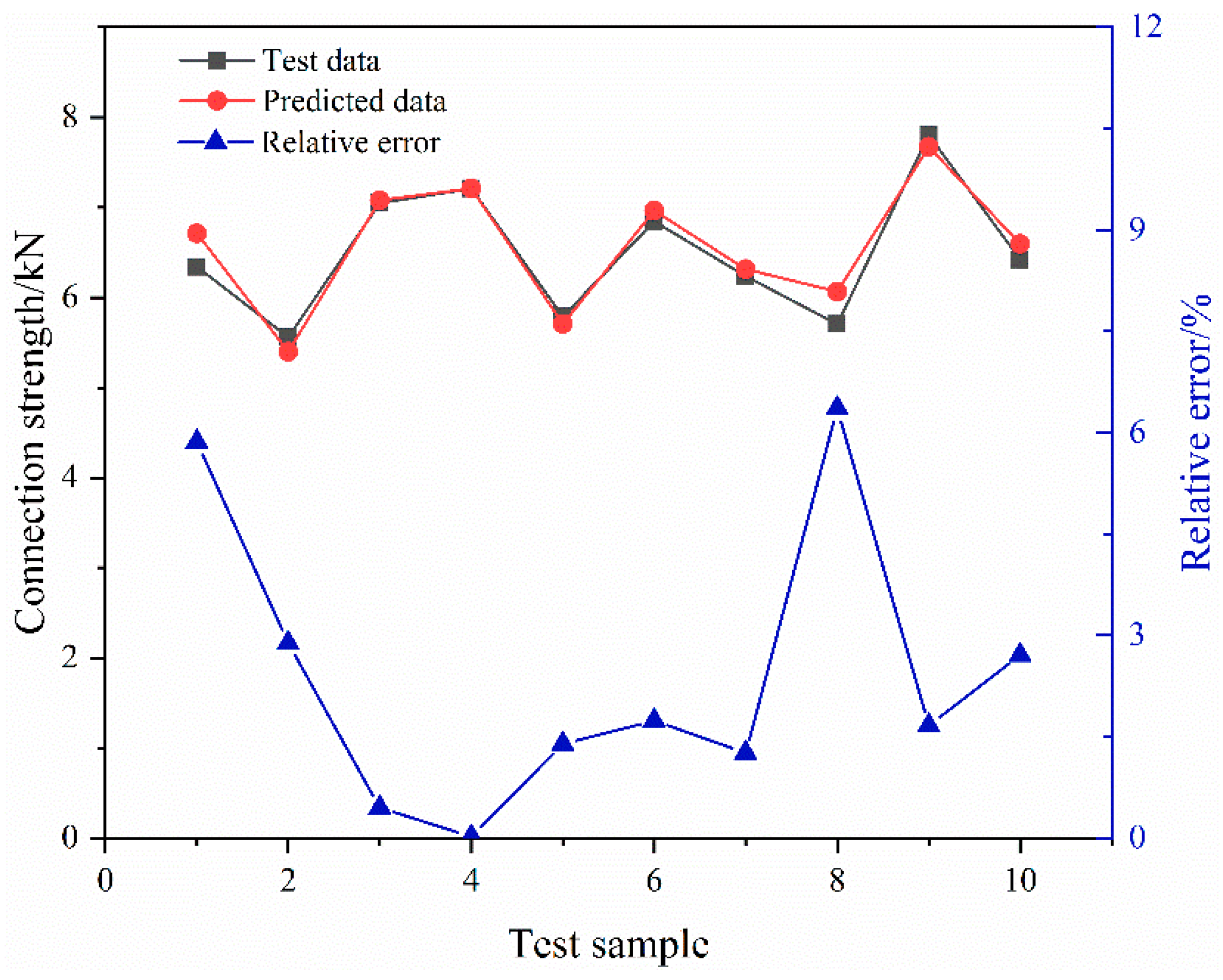
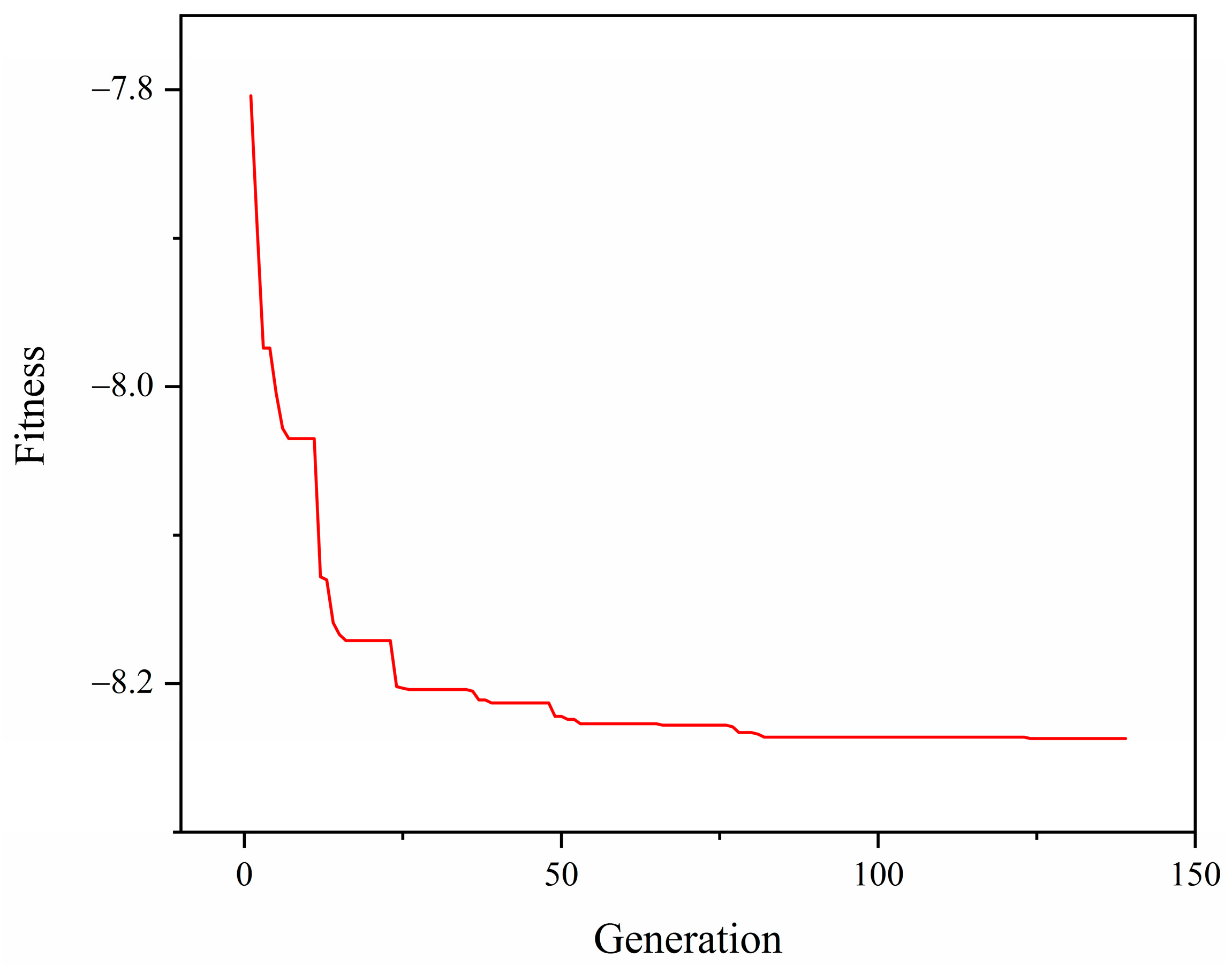
- In order to optimize the connection strength of the axial extrusion joint, the optimized Latin hypercube-sampling method was used to sample the three key influencing factors. The BP neural-network algorithm was used to establish a mathematical model of pipe joint strength. The mean square error of the model is 0.03702 and the regression value is 0.956, indicating that the neural network has high prediction accuracy. The genetic algorithm was used to optimize the neural-network model. The optimal connection strength is 8.237 kN and the optimal combination of influencing factors is 0.2, 0.4 and 76.8°. Compared with the prediction results of the neural-network genetic algorithm, the relative error of the finite element results is 3.9%, indicating that the method has high accuracy.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mori, K.; Bay, N.; Fratini, L.; Micari, F.; Tekkaya, A.E. Joining by plastic deformation. CIRP Ann. 2013, 62, 673–694. [Google Scholar] [CrossRef]
- Yang, H.; Li, H.; Zhang, Z.; Zhan, M.; Liu, J.; Li, G. Advances and Trends on Tube Bending Forming Technologies. Chin. J. Aeronaut. 2012, 25, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Zhang, B.; Du, Y.; Liu, M.; Bai, R.; Si, Y.; Liu, B.; Jung, D.; Osaka, A. Constitutive Model Parameter Identification Based on Optimization Method and Formability Analysis for Ti6Al4V Alloy. Materials 2022, 15, 1748. [Google Scholar] [CrossRef] [PubMed]
- Yi, S.; Yang, Z.; Xie, H. Hot Deformation and Constitutive Modeling of TC21 Titanium Alloy. Materials 2022, 15, 1923. [Google Scholar] [CrossRef]
- Yang, H.; Li, H.; Ma, J.; Wei, D.; Chen, J.; Fu, M.W. Temperature dependent evolution of anisotropy and asymmetry of α-Ti in thermomechanical working: Characterization and modeling. Int. J. Plast. 2020, 127, 102650. [Google Scholar] [CrossRef]
- Groche, P.; Wohletz, S.; Brenneis, M.; Pabst, C.; Resch, F. Joining by forming—A review on joint mechanisms, applications and future trends. J. Mater. Process. Technol. 2014, 214, 1972–1994. [Google Scholar] [CrossRef]
- Xiaoping, O.; Xu, F.; Ying, Z.; Kai, W.; Huayong, Y. Overview of Aviation Hydraulic Fittings. China Mech. Eng. 2015, 26, 2262. [Google Scholar]
- Yang, J.; Li, H.; Huang, D.; Li, G. Deformation-based joining for high-strength Ti-3Al-2.5V tubular fittings based on internal roller swaging. Int. J. Mech. Sci. 2020, 171, 105367. [Google Scholar] [CrossRef]
- Gies, S.; Weddeling, C.; Marré, M.; Kwiatkowski, L.; Tekkaya, A.E. Analytic Prediction of the Process Parameters for Form-Fit Joining by Die-Less Hydroforming. Key Eng. Mater. 2012, 504–506, 393–398. [Google Scholar] [CrossRef]
- Wang, Z.; Qiu, M.; Wang, J. Sealing performance of pipeline connection under the tensile load. J. Aerosp. Power 2011, 26, 5. [Google Scholar]
- Alves, L.M.; Silva, C.M.A.; Martins, P.A.F. End-to-end joining of tubes by plastic instability. J. Mater. Process. Technol. 2014, 214, 1954–1961. [Google Scholar] [CrossRef]
- Yan, Y.; Zhai, J.; Gao, P.; Han, Q. A multi-scale finite element contact model for seal and assembly of twin ferrule pipeline fittings. Tribol. Int. 2018, 125, 100–109. [Google Scholar] [CrossRef]
- Kang, Z.; Zhou, B.; Xue, S. Finite Element Numerical Simulation on Thermo-mechanical Coupling Behavior in Shape Memory Alloy Pipe Connection. J. Mech. Eng. 2018, 54, 68–75. [Google Scholar] [CrossRef]
- Zhou, B.; Liu, F.S. Finite Element Analysis of Removable Shape Memory Alloy Pipe Joint’s Cone Sealing Performance. Mater. Sci. Forum 2015, 817, 685–689. [Google Scholar] [CrossRef]
- Chang, K.H.; Jang, G.C.; Shin, Y.E.; Han, J.G.; Kim, J.M. The behavior of welded joint in steel pipe members under monotonic and cyclic loading. Int. J. Press. Vessel. Pip. 2006, 83, 846–852. [Google Scholar] [CrossRef]
- Jeon, J.-Y.; Kim, B.-T. A Study on Contact Characteristics by the Geometry Variation of Beam Seal Fitting of an Aircraft Fuel Hose. J. Korean Soc. Manuf. Process Eng. 2013, 12, 101–108. [Google Scholar]
- Prodan, V.D.; Bozhko, G.V.; Pogodin, V.K. Design of conical sealed joints. Chem. Pet. Eng. 2010, 45, 707–714. [Google Scholar] [CrossRef]
- Zhang, Q.; Jin, K.; Mu, D. Tube/tube joining technology by using rotary swaging forming method. J. Mater. Process. Technol. 2014, 214, 2085–2094. [Google Scholar] [CrossRef]
- Yamamoto, Y.; Fujita, K.; Iwamoto, T. An Experimental Study on Axial Joint Strength Made of Fe-28Mn-6Si-5Cr Shape Memory Alloy at Various Deformation Speeds. Key Eng. Mater. 2016, 725, 99–104. [Google Scholar] [CrossRef]
- Marré, M.; Gies, S.; Maevus, F.; Tekkaya, A.E. Joining of lightweight frame structures by die-less hydroforming. Int. J. Mater. Form. 2010, 3, 1031–1034. [Google Scholar] [CrossRef]
- Yu, H.; Li, J.; He, Z. Formability assessment of plastic joining by compression instability for thin-walled tubes. Int. J. Adv. Manuf. Technol. 2018, 97, 3423–3430. [Google Scholar] [CrossRef]
- Henriksen, J.; Nordhagen, H.O.; Hoang, H.N.; Hansen, M.R.; Thrane, F.C. Numerical and experimental verification of new method for connecting pipe to flange by cold forming. J. Mater. Process. Technol. 2015, 220, 215–223. [Google Scholar] [CrossRef]
- Agrawal, A.K.; Narayanan, R.G. Experimental and numerical studies on joining steel tubes by end forming. J. Constr. Steel Res. 2020, 167, 105792. [Google Scholar] [CrossRef]
- Weddeling, C.; Woodward, S.T.; Marré, M.; Nellesen, J.; Psyk, V.; Tekkaya, A.E.; Tillmann, W. Influence of groove characteristics on strength of form-fit joints. J. Mater. Process. Technol. 2011, 211, 925–935. [Google Scholar] [CrossRef]
- Zeng, Y.S. Finite Element Simulation and Experimental Research on the Internal Rolling Connection for Titanium Alloy Tubes. Mater. Sci. Forum 2005, 475–479, 3287–3290. [Google Scholar] [CrossRef]
- Liu, S.F.; Forrest, J. The current developing status on grey system theory. J. Grey Syst. 2007, 19, 111–123. [Google Scholar]
- Li, D.C.; Chang, C.J.; Chen, C.C.; Chen, W.C. A grey-based fitting coefficient to build a hybrid forecasting model for small data sets. Appl. Math. Model. 2012, 36, 5101–5108. [Google Scholar] [CrossRef]
- Jin, R.; Chen, W.; Sudjianto, A. An efficient algorithm for constructing optimal design of computer experiments. J. Stat. Plan. Inference 2005, 134, 268–287. [Google Scholar] [CrossRef]
- Hunter, D.; Yu, H.; Pukish, M.S.; Kolbusz, J.; Wilamowski, B.M. Selection of Proper Neural Network Sizes and Architectures-A Comparative Study. IEEE Trans. Ind. Inform. 2012, 8, 228–240. [Google Scholar] [CrossRef]
- Ding, S.F.; Su, C.Y.; Yu, J.Z. An optimizing BP neural network algorithm based on genetic algorithm. Artif. Intell. Rev. 2011, 36, 153–162. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef]


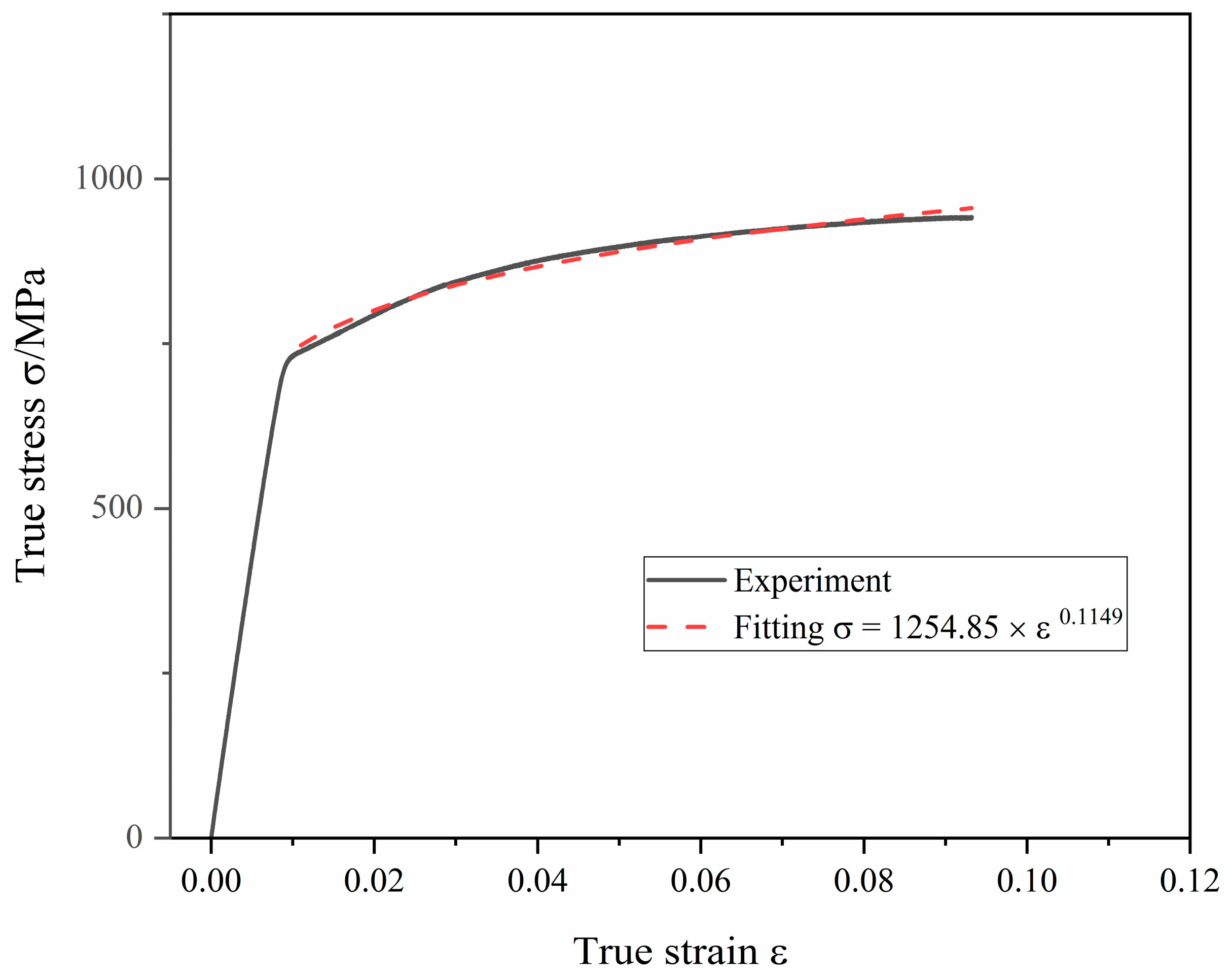






| Materials | Elastic Moduli (GPa) | Yield Strength (MPa) | Tensile Strength (MPa) | Elongation (%) |
|---|---|---|---|---|
| Extrusion ring | 122.11 | 1053 | 1143 | 15.7 |
| Fittings body | 116.54 | 950 | 1010 | 6.9 |
| Tube | 103 | 730 | 864 | 12 |
| Level | Time/s | ||||
|---|---|---|---|---|---|
| Level 1 | 0.05 | 0.2 | 0.1 | 50 | 50 |
| Level 2 | 0.08 | 0.25 | 0.25 | 60 | 60 |
| Level 3 | 0.1 | 0.3 | 0.5 | 70 | 70 |
| Level 4 | 0.15 | 0.35 | 0.75 | 80 | 80 |
| Level 5 | 0.2 | 0.4 | 1 | 90 | 90 |
| Test Number | Time/s | F/kN | ||||
|---|---|---|---|---|---|---|
| 1 | 0.05 | 0.2 | 0.1 | 50 | 50 | 4.9117 |
| 2 | 0.05 | 0.25 | 0.25 | 60 | 60 | 5.3649 |
| 3 | 0.05 | 0.3 | 0.5 | 70 | 70 | 6.6833 |
| 4 | 0.05 | 0.35 | 0.75 | 80 | 80 | 7.0905 |
| 5 | 0.05 | 0.4 | 1 | 90 | 90 | 6.9565 |
| 6 | 0.08 | 0.2 | 0.25 | 70 | 80 | 5.0455 |
| 7 | 0.08 | 0.25 | 0.5 | 80 | 90 | 6.4287 |
| 8 | 0.08 | 0.3 | 0.75 | 90 | 50 | 6.0699 |
| 9 | 0.08 | 0.35 | 1 | 50 | 60 | 6.5218 |
| 10 | 0.08 | 0.4 | 0.1 | 60 | 70 | 7.0614 |
| 11 | 0.1 | 0.2 | 0.5 | 90 | 60 | 6.3271 |
| 12 | 0.1 | 0.25 | 0.75 | 50 | 70 | 5.5689 |
| 13 | 0.1 | 0.3 | 1 | 60 | 80 | 6.1745 |
| 14 | 0.1 | 0.35 | 0.1 | 70 | 90 | 6.7317 |
| 15 | 0.1 | 0.4 | 0.25 | 80 | 50 | 7.2050 |
| 16 | 0.15 | 0.2 | 0.75 | 60 | 90 | 5.3123 |
| 17 | 0.15 | 0.25 | 1 | 70 | 50 | 6.3642 |
| 18 | 0.15 | 0.3 | 0.1 | 80 | 60 | 7.1325 |
| 19 | 0.15 | 0.35 | 0.25 | 90 | 70 | 7.3789 |
| 20 | 0.15 | 0.4 | 0.5 | 50 | 80 | 7.2457 |
| 21 | 0.2 | 0.2 | 1 | 80 | 70 | 6.2761 |
| 22 | 0.2 | 0.25 | 0.1 | 90 | 80 | 6.6211 |
| 23 | 0.2 | 0.3 | 0.25 | 50 | 90 | 6.3385 |
| 24 | 0.2 | 0.35 | 0.5 | 60 | 50 | 7.3973 |
| 25 | 0.2 | 0.4 | 0.75 | 70 | 60 | 7.9805 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Zhai, J.; Yan, Y.; Lin, H.; Chen, S.; Luo, J. Simulation and Optimization of Connection-Strength Performance of Axial Extrusion Joint. Materials 2022, 15, 2433. https://doi.org/10.3390/ma15072433
Wu J, Zhai J, Yan Y, Lin H, Chen S, Luo J. Simulation and Optimization of Connection-Strength Performance of Axial Extrusion Joint. Materials. 2022; 15(7):2433. https://doi.org/10.3390/ma15072433
Chicago/Turabian StyleWu, Jianguo, Jingyu Zhai, Yangyang Yan, Hongwei Lin, Siquan Chen, and Jianping Luo. 2022. "Simulation and Optimization of Connection-Strength Performance of Axial Extrusion Joint" Materials 15, no. 7: 2433. https://doi.org/10.3390/ma15072433
APA StyleWu, J., Zhai, J., Yan, Y., Lin, H., Chen, S., & Luo, J. (2022). Simulation and Optimization of Connection-Strength Performance of Axial Extrusion Joint. Materials, 15(7), 2433. https://doi.org/10.3390/ma15072433





