Band Structure Studies of the R5Rh6Sn18 (R = Sc, Y, Lu) Quasiskutteridite Superconductors
Abstract
:1. Introduction
2. Experimental and Computational Details
3. Electronic Structure of RhSn ( = Sc, Y, Lu): Experiment and Ab Initio Calculations
4. Metallicity or Semimetallicity of RhSn ( = Sc, Y, Lu; ) and the Electronic Structure
5. Band Structure of the System of RRhSn Compounds, Comparison
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Thomas, E.L.; Lee, H.-O.; Bankston, A.N.; MaQuilon, S.; Klavins, P.; Moldovan, M.; Young, D.P.; Fisk, Z.; Chan, J.Y. Crystal growth transport, and magnetic properties of Ln3Co4Sn13 (Ln = La, Ce) with a perovskite-like structure. J. Solid State Chem. 2006, 179, 1642–1649. [Google Scholar] [CrossRef] [Green Version]
- Lue, C.S.; Liu, H.F.; Hsu, S.-L.; Chu, M.W.; Liao, H.Y.; Kuo, Y.K. Observation of a possible charge-density-wave transition in cubic Ce3Co4Sn13. Phys. Rev. B 2012, 85, 205120. [Google Scholar] [CrossRef] [Green Version]
- Klintberg, L.E.; Goh, S.K.; Alireza, P.L.; Saines, P.J.; Tompsett, D.A.; Logg, P.W.; Yang, J.; Chen, B.; Yoshimura, K.; Grosche, F.M. Pressure-and composition-induced structural quantum phase transition in the cubic superconductor (Sr, Ca)3Ir4Sn13. Phys. Rev. Lett. 2012, 109, 237008. [Google Scholar] [CrossRef] [PubMed]
- Köhler, U.; Pikul, A.P.; Oeschler, N.; Westerkamp, T.; Strydom, A.M.; Steglich, F. Low-temperature study of the strongly correlated compound Ce3Rh4Sn13. J. Phys. Condens. Matter 2007, 19, 386207. [Google Scholar] [CrossRef]
- Kalinowski, L.; Kądziołka-Gaweł, M.; Ślebarski, A. Cluster spin-glass-like behavior in heavy-fermion-filled cage Ce3Co4Sn13 doped with Fe: Magnetic and Mössbauer effect studies. Phys. Rev. B 2018, 98, 245140. [Google Scholar] [CrossRef]
- Remeika, J.P.; Espinosa, G.P.; Cooper, A.S.; Barz, H.; Rowel, J.M.; McWhan, D.B.; Vandenberg, J.M.; Moncton, D.E.; Fizk, Z.; Woolf, L.D.; et al. A new family of ternary intermetallic superconducting/magnetic stannides. Sol. State Commun. 1980, 34, 923–926. [Google Scholar] [CrossRef] [Green Version]
- Hodeau, J.L.; Marezio, M.; Remeika, J.P. The structure of [Er(1)1-x,Sn(1)x]Er(2)4Rh6Sn(2)4Sn(3)12Sn(4)2, a ternary reentrant superconductor. Acta Cryst. B 1984, 40, 26–38. [Google Scholar] [CrossRef]
- Kase, N.; Kittaka, S.; Sakakibara, T.; Akimitsu, J. Superconducting gap structure of the cage compound Sc5Rh6Sn18. J. Phys. Soc. Jpn. 2012, 81, SB016. [Google Scholar] [CrossRef] [Green Version]
- Bhattacharyya, A.; Adroja, D.T.; Kase, N.; Hillier, A.D.; Strydom, A.M.; Akimitsu, J. Unconventional superconductivity in the cage-type compound Sc5Rh6Sn18. Phys. Rev. B 2018, 98, 024511. [Google Scholar] [CrossRef] [Green Version]
- Kase, N.; Inoue, K.; Hayamizu, H.; Akimitsu, J. Highly anisotropic gap function in a nonmagnetic superconductor Y5Rh6Sn18. J. Phys. Soc. Jpn. 2011, 80, SA112. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, Y.; Kuo, C.N.; Hong, X.C.; Wang, M.X.; Cai, P.L.; Dong, J.K.; Lue, C.S.; Li, S.Y. Nodeless superconducting gap in the caged-type superconductors Y5Rh6Sn18 and Lu5Rh6Sn18. Supercond. Sci. Technol. 2015, 28, 105008. [Google Scholar] [CrossRef]
- Wang, A.; Nie, Z.Y.; Du, F.; Pang, G.M.; Kase, N.; Akimitsu, J.; Chen, Y.; Gutmann, M.J.; Adroja, D.T.; Perry, R.S.; et al. Nodeless superconductivity in Lu5-xRh6Sn18+x with broken time reversal symmetry. Phys. Rev. B 2021, 103, 024503. [Google Scholar] [CrossRef]
- Ślebarski, A.; Fijałkowski, M.; Maśka, M.M.; Mierzejewski, M.; White, B.D.; Maple, M.B. Superconductivity of La3Co4Sn13 and La3Rh4Sn13: A comparative study. Phys. Rev. B 2014, 89, 125111. [Google Scholar] [CrossRef] [Green Version]
- Ślebarski, A.; Maśka, M.M.; Fijałkowski, M.; McElroy, C.A.; Maple, M.B. Superconductivity in the presence of disorder in skutterudite-related La3Co4Sn13 and La3Ru4Sn13 compounds: Electrical transport and magnetic studies. J. Alloys Compd. 2015, 646, 866–872. [Google Scholar] [CrossRef] [Green Version]
- Ślebarski, A.; Fijałkowski, M.; Zajdel, P.; Maśka, M.M.; Deniszczyk, J.; Zubko, M.; Pavlosiuk, O.; Sasmal, K.; Maple, M.B. Enhancing superconductivity of Y5Rh6Sn18 by atomic disorder. Phys. Rev. B 2020, 102, 054514. [Google Scholar] [CrossRef]
- Ślebarski, A.; Fijałkowski, M.; Maśka, M.M.; Deniszczyk, J.; Zajdel, P.; Trump, B.; Yakovenko, A. Enhancing superconductivity of Lu5Rh6Sn18 by atomic disorder. Phys. Rev. B 2021, 103, 155133. [Google Scholar] [CrossRef]
- Fijałkowski, M.; Maśka, M.M.; Deniszczyk, J.; Ślebarski, A. Magnetic field induced reentrance of superconductivity in the cage-type superconductor Y5Rh6Sn18. Phys. Rev. B 2021, 104, 165306. [Google Scholar] [CrossRef]
- Ślebarski, A.; Zajdel, P.; Fijałkowski, M.; Maśka, M.M.; Witas, P.; Goraus, J.; Fang, Y.; Arnold, D.C.; Maple, M.B. The effective increase in atomic scale disorder by doping and superconductivity in Ca3Rh4Sn13. New J. Phys. 2018, 20, 103020. [Google Scholar] [CrossRef]
- Miraglia, S.; Hodeau, J.L.; Bergevin, F.; Marezio, M. Structural studies by electron and X-ray diffraction of the disordered phases II′: (Sn1-xTbx)Tb4Rh6Sn18 and (Sn1-xDyx)Dy4Os6Sn18. Acta Crystallogr. Sect. B 1987, 43, 76–83. [Google Scholar] [CrossRef]
- Feig, M.; Akselrud, L.; Schnelle, W.; Dyadkin, V.; Chernyshov, D.; Ormeci, A.; Simon, P.; Leithe-Jasper, A.; Gumeniuk, R. Crystal structure, chemical bonding, and electrical and thermal transport in Sc5Rh6Sn18. Dalton Trans. 2020, 49, 6832–6841. [Google Scholar] [CrossRef] [Green Version]
- Baue, E.D.; Ślebarski, A.; Dickey, R.P.; Freeman, E.J.; Sirvent, C.; Zapf, V.S.; Dilley, N.R.; Maple, M.B. Electronic and magnetic investigation of the filled skutterudite compound CeRu4Sb12. J. Phys. Condens. Matter 2001, 13, 5183–5193. [Google Scholar]
- Singh, D.J.; Nordstrom, L. Plane Waves, Pseudopotentials, and the LAPW Method, 2nd ed.; Springer Science: New York, NY, USA, 2006; ISBN 978-0-387-28780-5. [Google Scholar]
- Blaha, P.; Schwarz, K.; Madsen, G.K.H.; Kvasnicka, D.; Luitz, J.; Laskowski, R.; Tran, F.; Marks, L.D. WIEN2k: An Augmented Plane Wave + Local Orbitals Program for Calculating Crystal Properties; Schwarz, K., Ed.; Technischen Universität Wien: Vienna, Austria, 2001; ISBN 3-9501031-1-2. [Google Scholar]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Anisimov, V.I.; Zaanen, J.; Andersen, O.K. Band theory and Mott insulators: Hubbard U instead of Stoner I. Phys. Rev. B 1991, 44, 943–954. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Anisimov, V.I.; Solovyev, I.V.; Korotin, M.A.; Zyk, M.T.C.; Sawatzky, G.A. Density-functional theory and NiO photoemission spectra. Phys. Rev. B 1993, 48, 16929–16934. [Google Scholar] [CrossRef]
- Ślebarski, A.; Zajdel, P.; Maśka, M.M.; Deniszczyk, J.; Fijałkowski, M. Superconductivity of Y5Rh6Sn18; Coexistence of the high temperature thermal lattice relaxation process and superconductivity. J. Alloys Compd. 2020, 819, 152959. [Google Scholar] [CrossRef]
- Ślebarski, A.; Goraus, J.; Witas, P. Electrical resistivity of the heavy-fermion-filled cage compound Ce3M4Sn13(M = Co,Rh,Ru) under high pressure. Phys. Rev. B 2015, 92, 155136. [Google Scholar] [CrossRef]
- Mott, N.F. The transition to the metallic state. Philos. Mag. 1961, 6, 287–309. [Google Scholar] [CrossRef]
- Levytskyi, V.; Feig, M.; Akselrud, L.; Schnelle, W.; Leithe-Jasper, A.; Dyakin, V.; Chernysov, D.; Gumeniuk, R. Crystal structure and superconducting properties of Sc5Ir6Sn18. J. Phys. Condens. Matter 2019, 31, 445603. [Google Scholar] [CrossRef]
- Ślebarski, A.; Maśka, M.M. Enhancing superconductivity of the nonmagnetic quasiskutterudites by atomic disorder. Materials 2020, 13, 5830. [Google Scholar] [CrossRef]
- Kumar, D.; Kuo, C.N.; Astuti, F.; Shang, T.; Lee, M.K.; Lue, C.S.; Watanabe, I.; Barker, J.A.T.; Shiroka, T.; Chang, L.J. Nodeless superconductivity in the cage-type superconductor Sc5Ru6Sn18 with preserved timereversal symmetry. J. Phys. Condens. Matter 2018, 30, 315803. [Google Scholar] [CrossRef] [Green Version]
- Feig, M.; Schnelle, W.; Maisuradze, A.; Amon, A.; Baines, C.; Nicklas, M.; Seiro, S.; Hovald, L.; Khasanov, R.; Leithe-Jasper, A.; et al. Conventional isotropic s-wave superconductivity with strong electron-phonon coupling in Sc5Rh6Sn18. Phys. Rev. B 2020, 102, 024508. [Google Scholar] [CrossRef]
- Gastiasoro, M.N.; Andersen, B.M. Enhancing superconductivity by disorder. Phys. Rev. B 2018, 98, 184510. [Google Scholar] [CrossRef] [Green Version]
- Wejgaard, W. Effect of pressure on the superconducting transition temperature of iridium. Phys. Lett. A 1969, 29, 396–397. [Google Scholar] [CrossRef]
- Seiden, P.E. Pressure dependence of the superconducting transition temperature. Phys. Rev. 1969, 179, 458–462. [Google Scholar] [CrossRef]
- McMillan, W.L. Transition temperature of strong-coupled superconductors. Phys. Rev. 1968, 167, 331–344. [Google Scholar] [CrossRef]
- Morel, P.; Anderson, P.W. Calculation of the superconducting state parameters with retarded electron-phonon interaction. Phys. Rev. 1962, 125, 1263–1271. [Google Scholar] [CrossRef]
- Hopfield, J.J. Angular momentum and transition-metal superconductivity. Phys. Rev. 1969, 186, 443–451. [Google Scholar] [CrossRef]
- Ślebarski, A.; Goraus, J.; Deniszczyk, J.; Skoczeń, Ł. Electronic structure, magnetic properties and electrical resistivity of the Fe2V1-xTixAl Heusler alloys: Experiment and calculation. J. Phys. Condens. Matter 2006, 18, 10319–10334. [Google Scholar] [CrossRef]
- Mott, N.F. Metal-Insulator Transitions; Taylor and Francis Ltd.: London, UK, 1974. [Google Scholar]
- Mott, N.F. The electrical properties of liquid mercury. Philos. Mag. 1966, 13, 989–1014. [Google Scholar] [CrossRef]
- Aliev, F.G.; Brandt, N.B.; Moshchalkov, V.V.; Kozyrkov, V.V.; Skolozdra, R.V.; Belogorokhov, A.I. Gap at the Fermi level in the intermetallic vacancy system RNiSn (R = Ti, Zr, Hf). Z. Phys. B 1989, 75, 167–171. [Google Scholar] [CrossRef]
- Ślebarski, A.; Jezierski, A.; Zygmunt, A.; Mähl, S.; Neumann, M. Suppression of the gap energy in Zr-Ni-Sn and Ti-Ni-Sn by partial substitution of Zr and Ti by Ce. Phys. Rev. B 1998, 57, 9544–9595. [Google Scholar] [CrossRef]
- Ślebarski, A.; Jezierski, A.; Lütkehoff, S.; Neumann, M. Electronic structure of X2ZrSn- and XZrSn-type Heusler alloys with X = Co or Ni. Phys. Rev. B 1998, 57, 6408–6412. [Google Scholar] [CrossRef]
- Skornia, P.; Goraus, J.; Fijałkowski, M.; Ślebarski, A. Electronic structure and magnetic properties of the magnetically ordered intermediate valent Ce5RuGe2. J. Alloys Compd. 2018, 767, 512–521. [Google Scholar] [CrossRef]
- Young, S.M.; Zaheer, S.; Teo, J.C.Y.; Kane, C.L.; Mele, E.J.; Rappe, A.M. Dirac semimetal in three dimensions. Phys. Rev. Lett. 2012, 108, 140405. [Google Scholar] [CrossRef]
- Young, S.M.; Kane, C.L. Dirac semimetals in two dimensions. Phys. Rev. Lett. 2015, 115, 126803. [Google Scholar] [CrossRef] [Green Version]
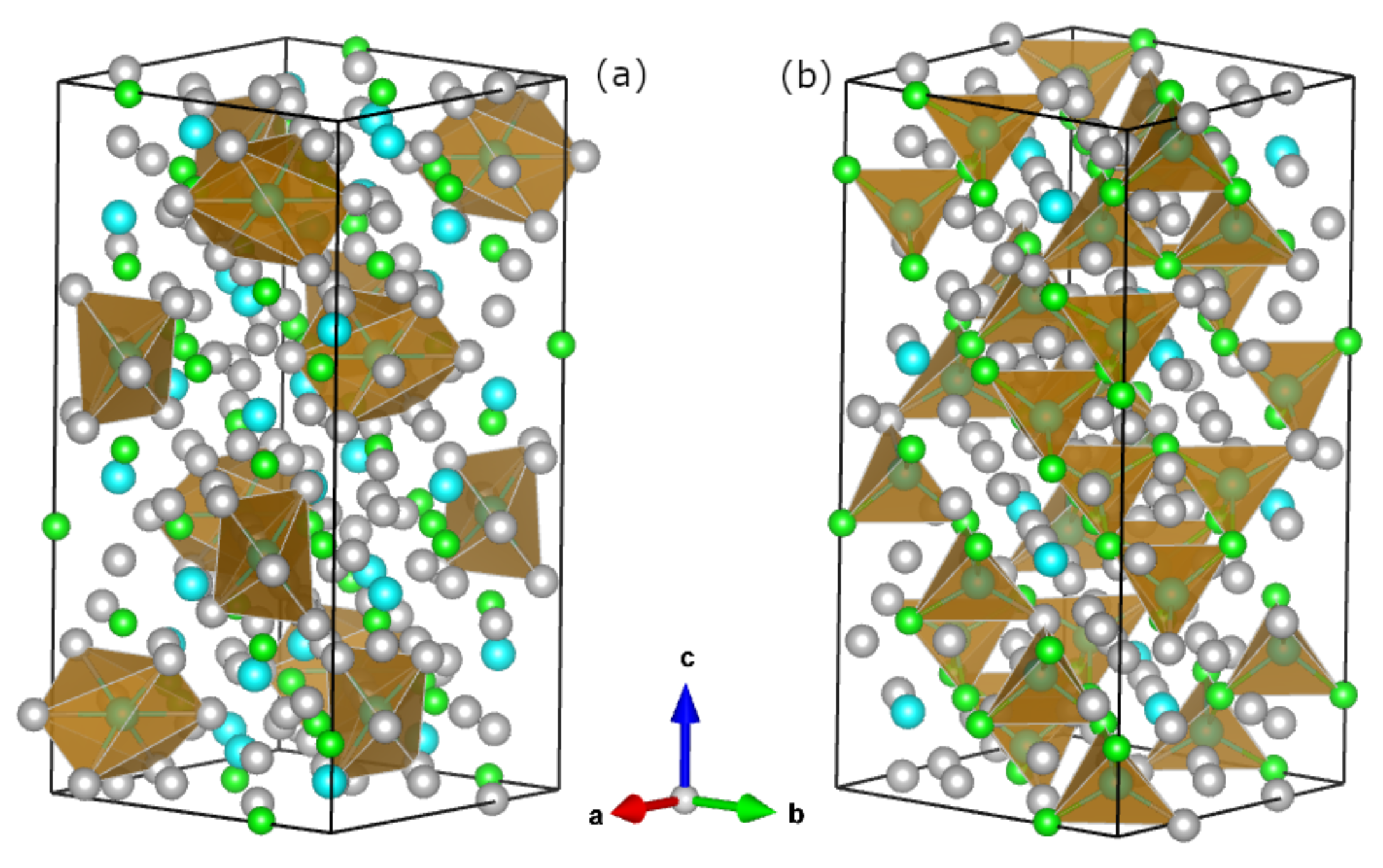
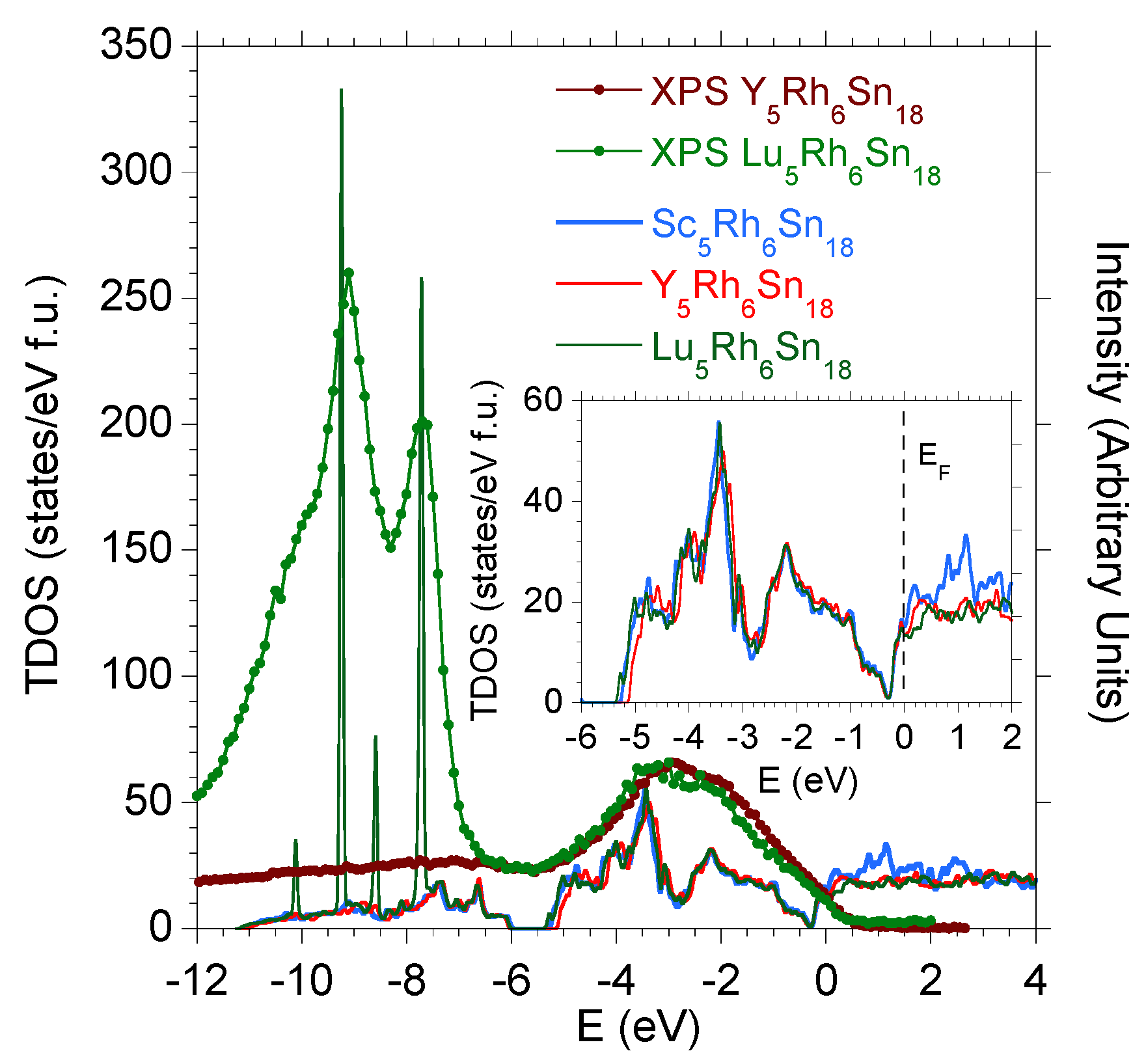
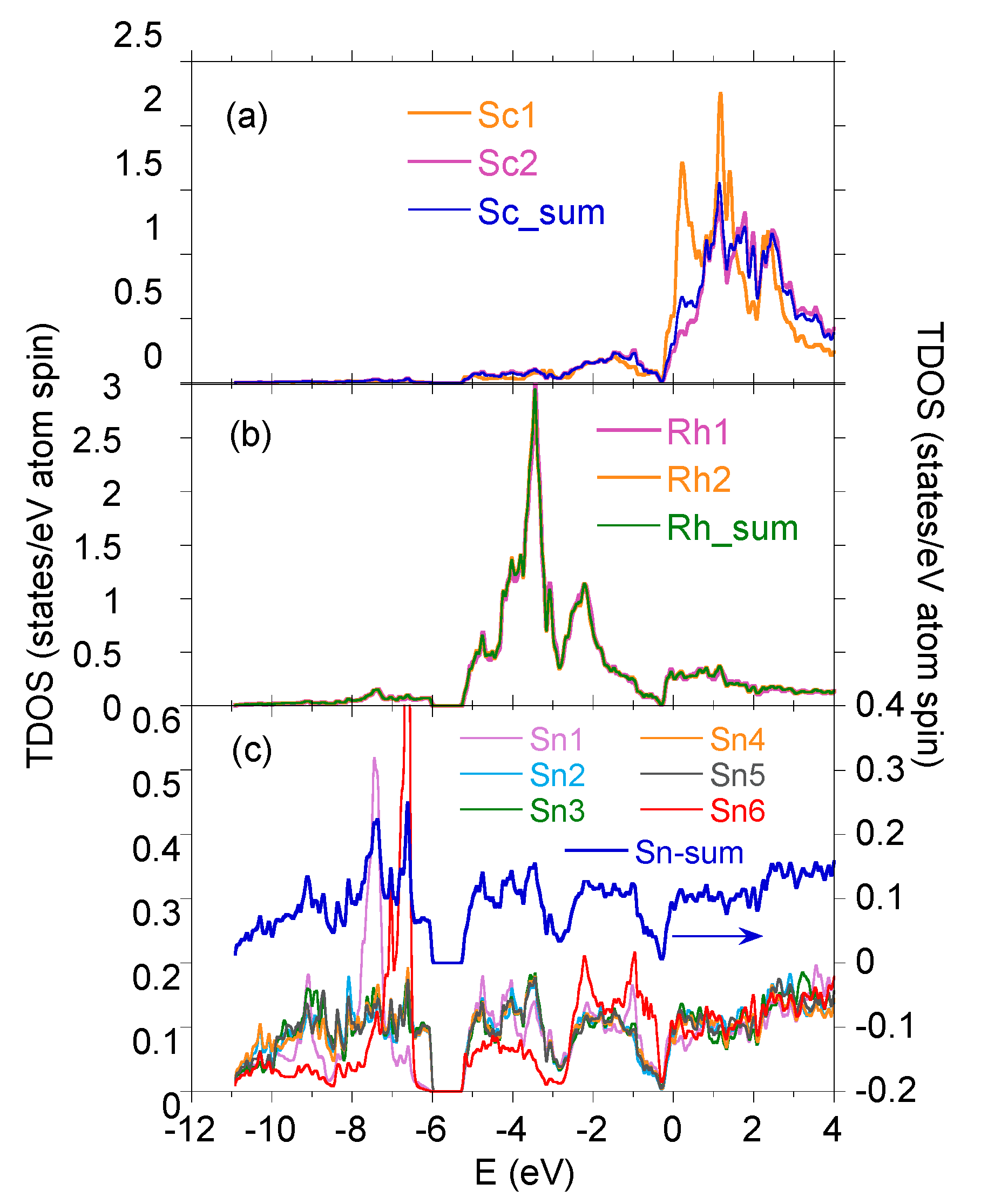
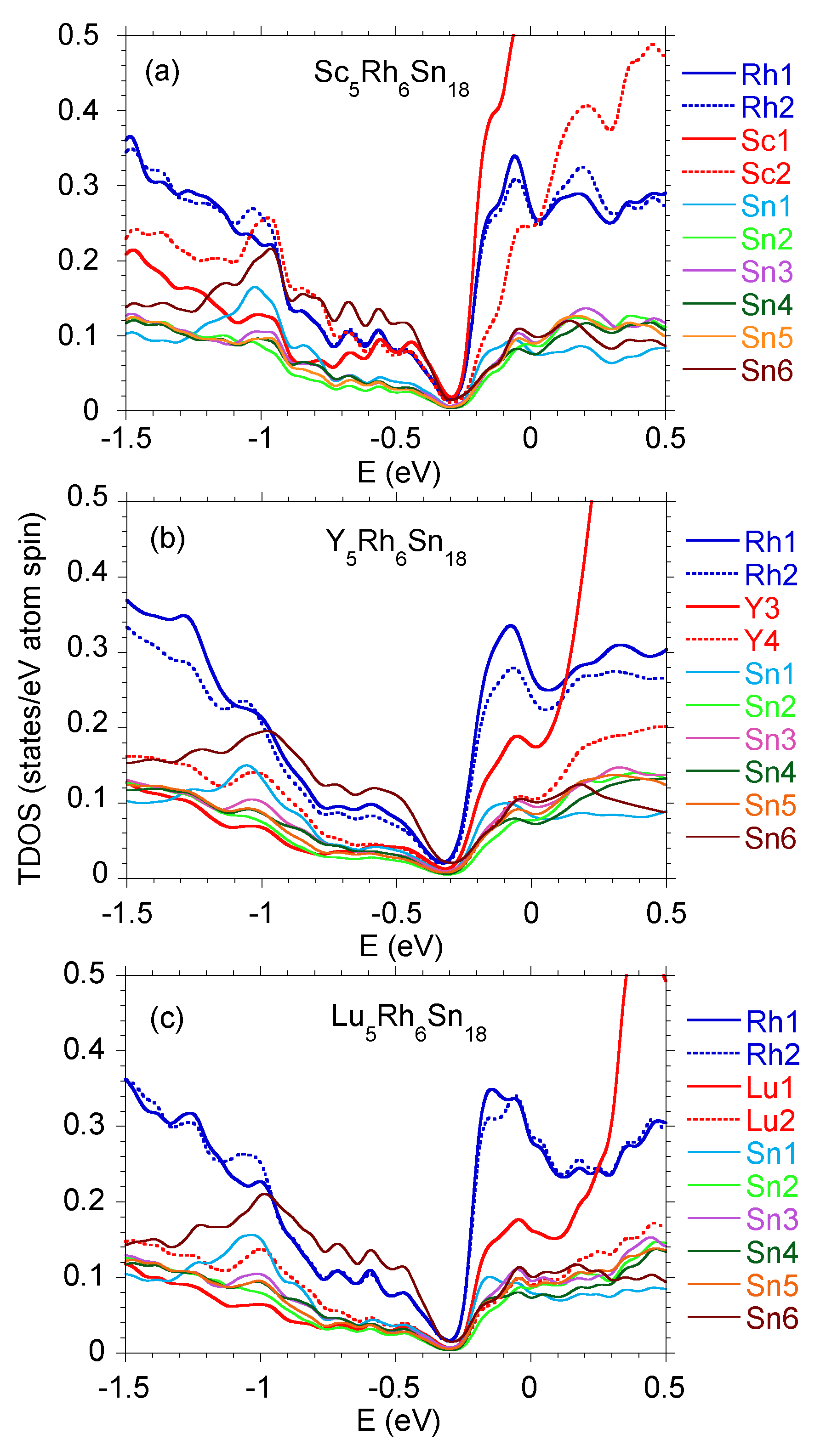

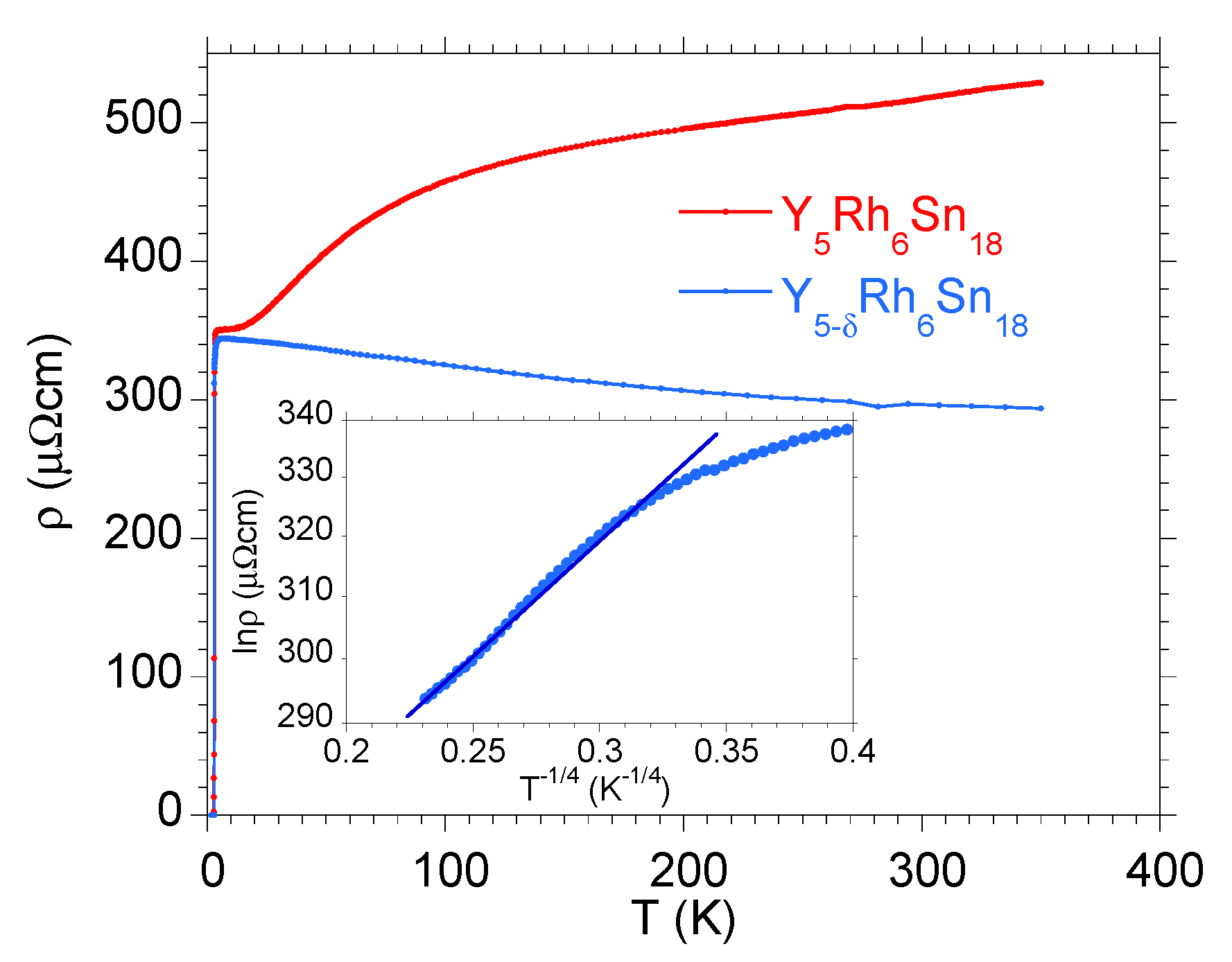
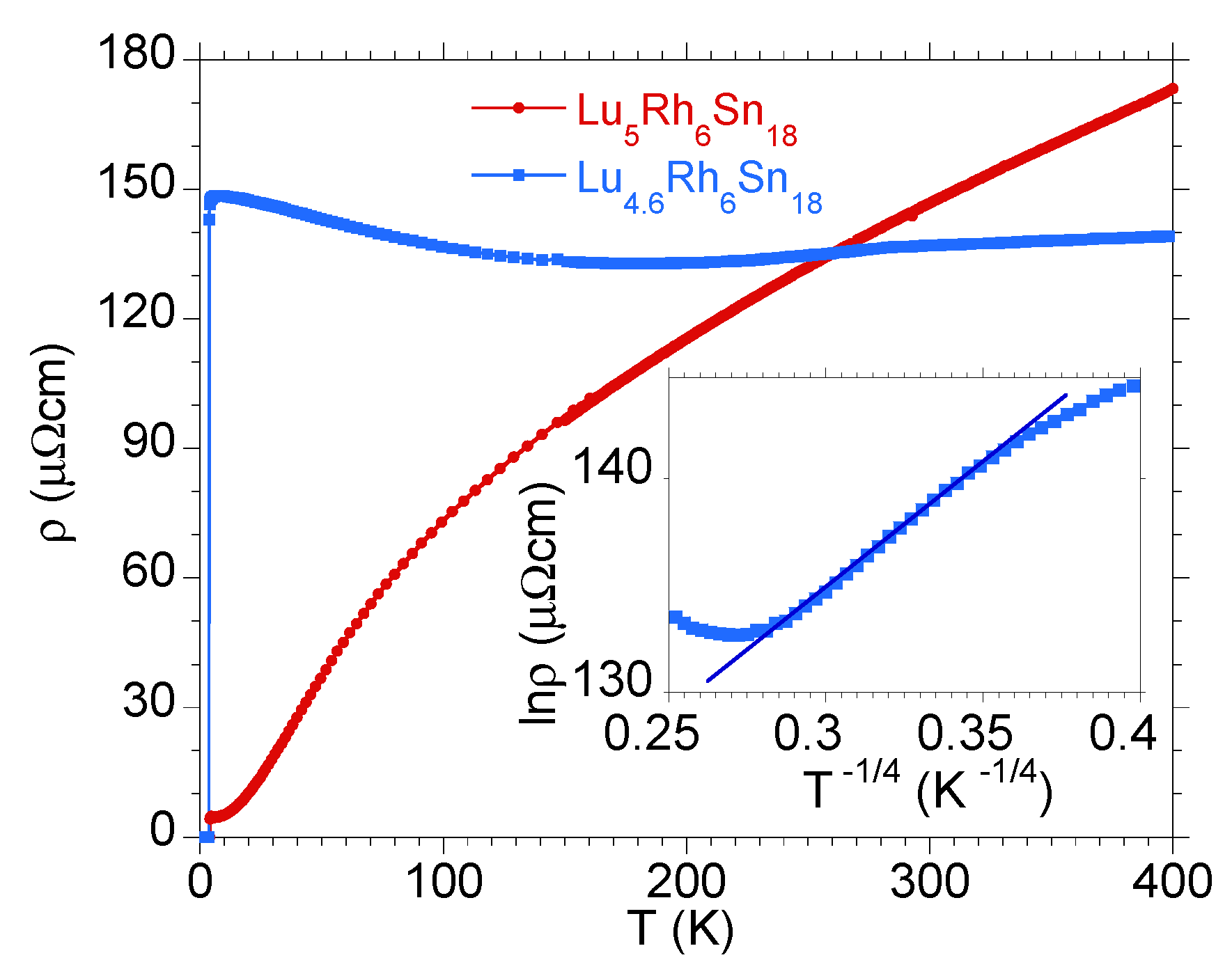
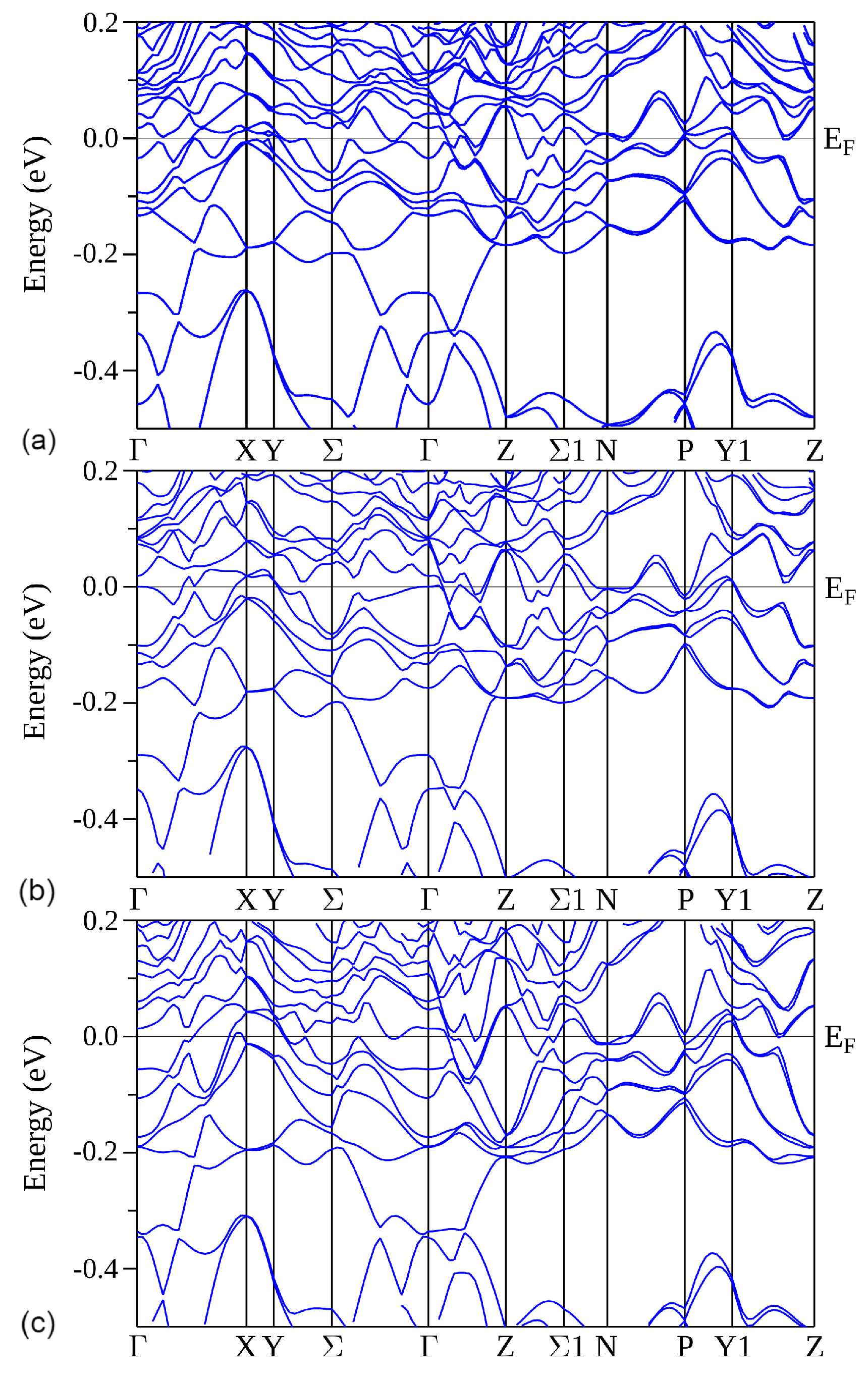
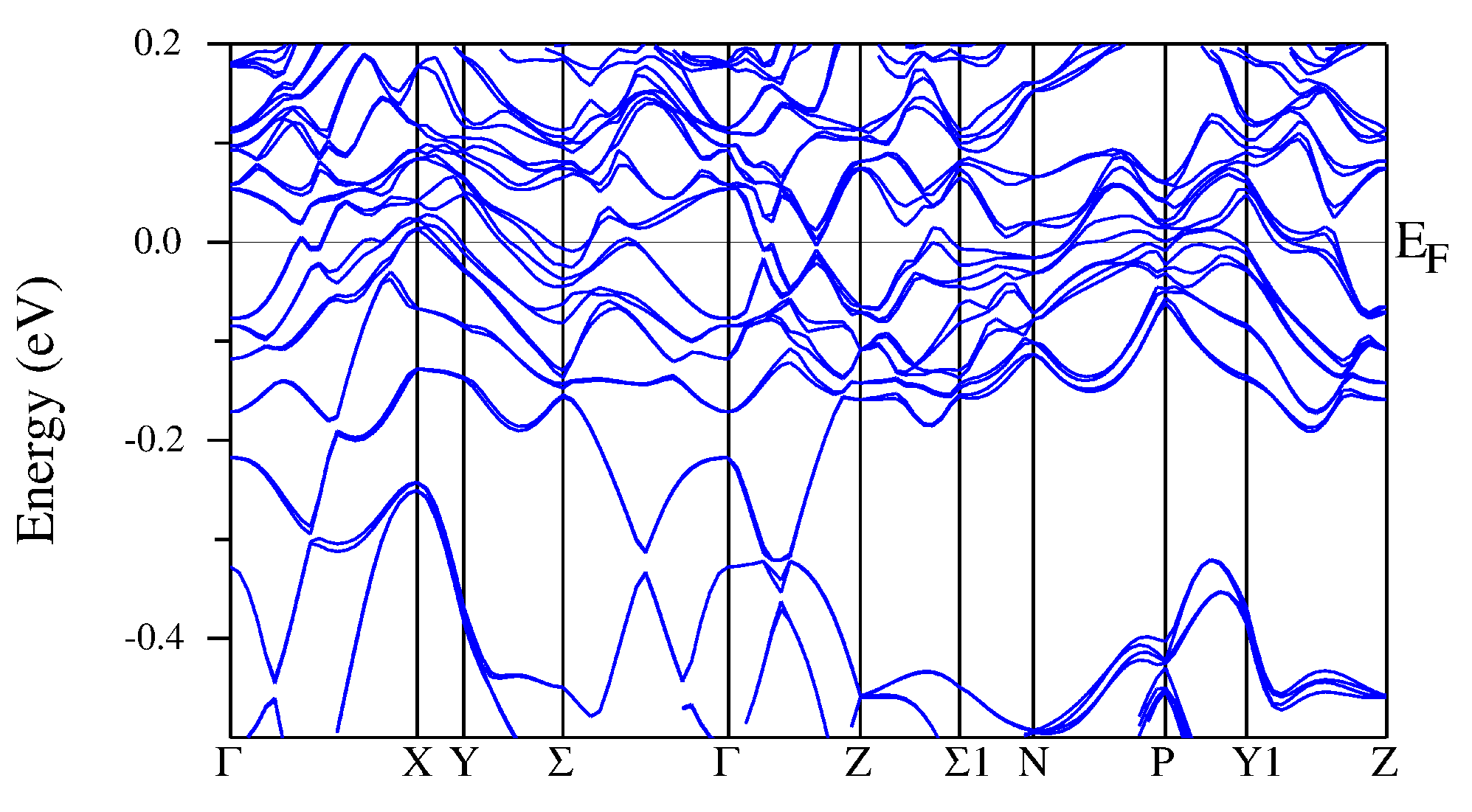
| Atom | ScRhSn | YRhSn | LuRhSn | |||||
|---|---|---|---|---|---|---|---|---|
| Type | Position No. Ref. [27] | Label | (Å) | (e) | (Å) | (e) | (Å) | (e) |
| Rh | 1 | Rh | 2.62 (Sn) | 1.283 | 2.65 | 1.319 | 2.64 | 1.300 |
| Rh | 2 | Rh | 2.62 (Sn) | 1.282 | 2.63 | 1.316 | 2.63 | 1.300 |
| Sc/Y/Lu | 3 | 3.33 (Sn) | 2.009 | 3.38 | 2.630 | 3.36 | 2.617 | |
| Sc/Y/Lu | 4 | 2.95 (Rh) | 1.910 | 3.00 | 2.520 | 2.99 | 2.497 | |
| Sn | 5 | Sn | 2.69 (Rh) | 2.306 | 2.74 | 2.323 | 2.72 | 2.305 |
| Sn | 6 | Sn | 2.62 (Rh) | 2.306 | 2.64 | 2.314 | 2.64 | 2.308 |
| Sn | 7 | Sn | 2.62 (Rh) | 2.304 | 2.66 | 2.311 | 2.64 | 2.305 |
| Sn | 8 | Sn | 2.62 (Rh) | 2.295 | 2.65 | 2.302 | 2.64 | 2.296 |
| Sn | 9 | Sn | 2.62 (Rh) | 2.305 | 2.63 | 2.312 | 2.63 | 2.306 |
| Sn | 10 | Sn | 3.01 (R) | 2.359 | 3.065 | 2.348 | 3.05 | 2.344 |
| YRhSn | ScRhSn | LuRhSn | |
|---|---|---|---|
| a (Å) | 13.7601 [17] | 13.5826 [30] | 13.7590 [16] |
| c (Å) | 27.5412 [17] | 27.1504 [30] | 27.4747 [16] |
| DOS at (1/eV f.u.) | 13.20 | 14.81 | 11.50 |
| (mJ/mol K) () | 31.2 | 34.90 | 27.20 |
| (mJ/mol K) ( T) | 39 (24) [27] | (35.2) [30] | 36 (47) [16] |
| (mJ/mol K) () | 12.1 (9) [31] | (∼7) [32] | 18 (5.5) [31] |
| (mJ/mol K) | 19.4 (14.4) | (11.2) | 28.8 (8.8) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deniszczyk, J.; Ślebarski, A. Band Structure Studies of the R5Rh6Sn18 (R = Sc, Y, Lu) Quasiskutteridite Superconductors. Materials 2022, 15, 2451. https://doi.org/10.3390/ma15072451
Deniszczyk J, Ślebarski A. Band Structure Studies of the R5Rh6Sn18 (R = Sc, Y, Lu) Quasiskutteridite Superconductors. Materials. 2022; 15(7):2451. https://doi.org/10.3390/ma15072451
Chicago/Turabian StyleDeniszczyk, Józef, and Andrzej Ślebarski. 2022. "Band Structure Studies of the R5Rh6Sn18 (R = Sc, Y, Lu) Quasiskutteridite Superconductors" Materials 15, no. 7: 2451. https://doi.org/10.3390/ma15072451
APA StyleDeniszczyk, J., & Ślebarski, A. (2022). Band Structure Studies of the R5Rh6Sn18 (R = Sc, Y, Lu) Quasiskutteridite Superconductors. Materials, 15(7), 2451. https://doi.org/10.3390/ma15072451






