A Mixing Model for Describing Electrical Conductivity of a Woven Structure
Abstract
:1. Introduction
2. Materials
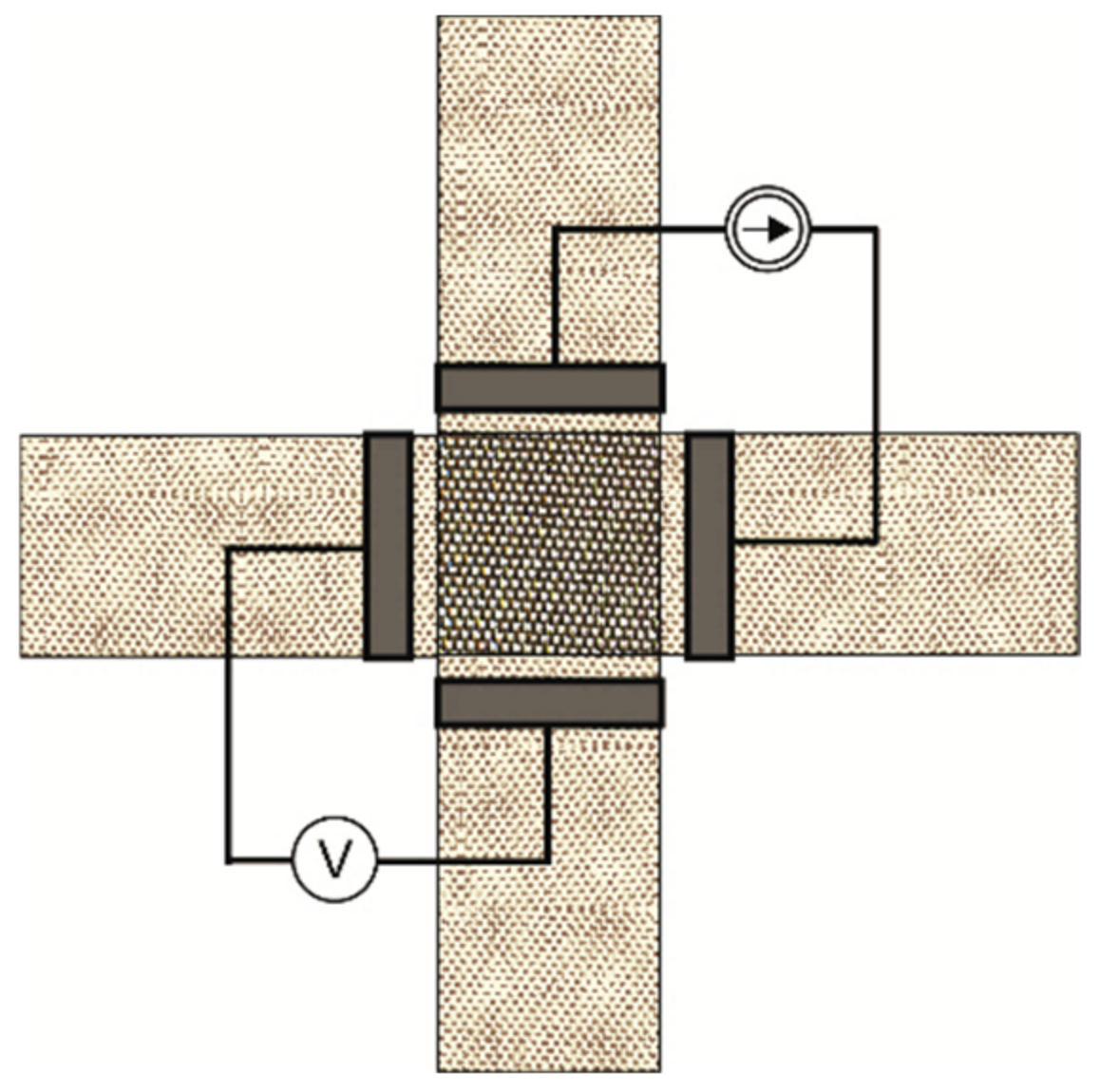
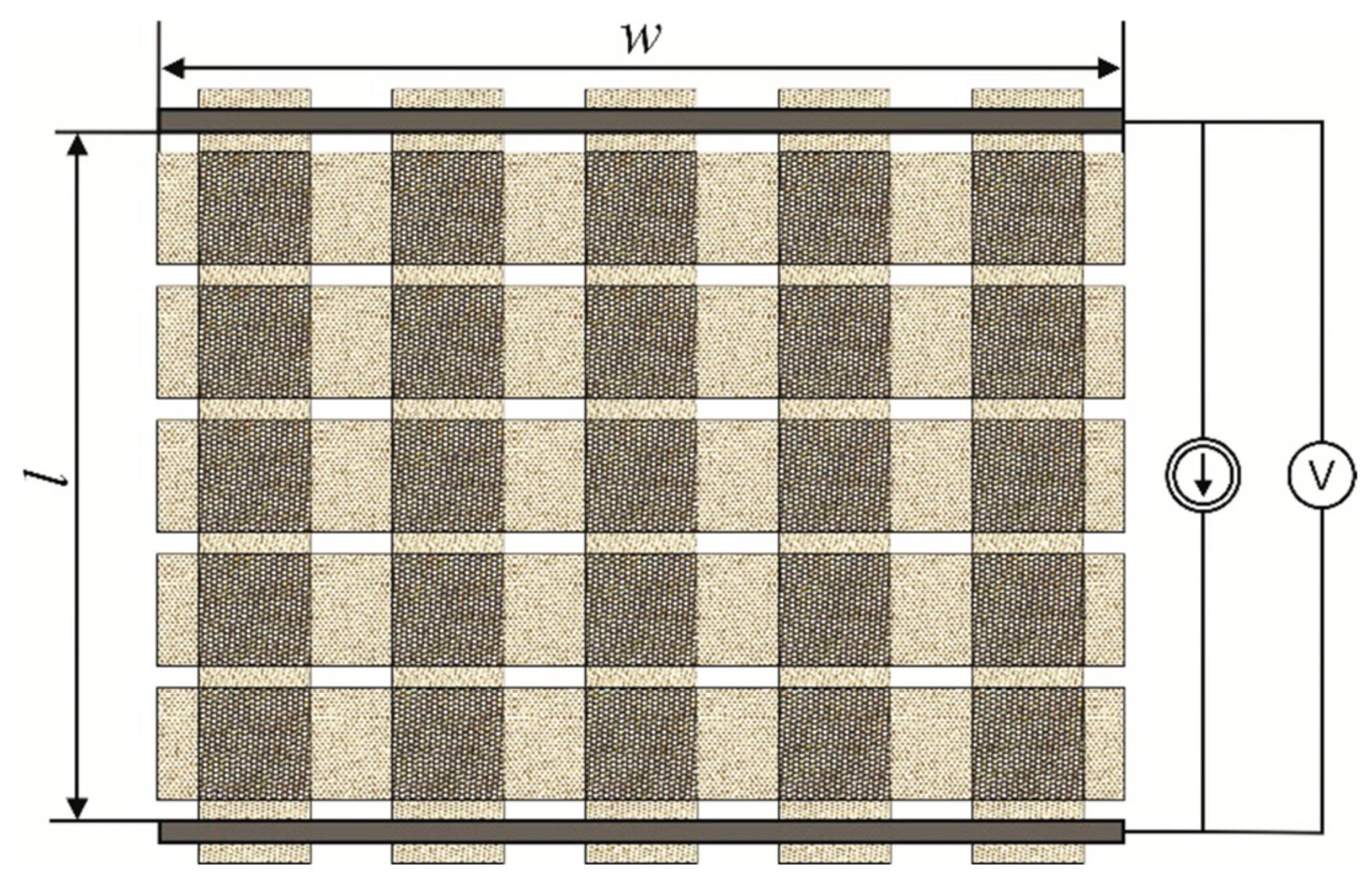
3. Methods
4. Results and Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tyurin, I.N.; Getmantseva, V.V.; Andreeva, E.G. Van der Pauw method for measuring the electrical conductivity of smart textiles. Fibre Chem. 2019, 51, 139–146. [Google Scholar] [CrossRef]
- Castano, L.M.; Flatau, A.B. Smart fabric sensors and e-textile technologies: A review. Smart Mater. Struct. 2014, 23, 053001–053027. [Google Scholar] [CrossRef]
- Gonçalves, C.; da Silva, A.F.; Gomes, J.; Simoes, R. Wearable e-textile technologies: A review on sensors, actuators and control elements. Inventions 2018, 3, 14. [Google Scholar] [CrossRef] [Green Version]
- Korzeniewska, E.; Krawczyk, A.; Mróz, J.; Wyszyńska, E.; Zawiślak, R. Applications of smart textiles in post-stroke rehabilitation. Sensors 2020, 20, 2370. [Google Scholar] [CrossRef] [Green Version]
- Tokarska, M.; Frydrysiak, M.; Zięba, J. Electrical properties of flat textile material as inhomogeneous and anisotropic structure. J. Mater. Sci. Mater. Electron. 2013, 24, 5061–5068. [Google Scholar] [CrossRef] [Green Version]
- Neruda, M.; Vojtech, L. Verification of surface conductance model of textile material. J. Appl. Res. Technol. 2012, 10, 578–584. [Google Scholar] [CrossRef]
- Liu, S.; Tong, J.; Yang, C.; Li, L. Smart e-textile: Resistance properties of conductive knitted fabric—Single pique. Text. Res. J. 2017, 87, 1669–1684. [Google Scholar] [CrossRef]
- Gunnarsson, E.; Karlsteen, M.; Berglin, L.; Stray, J. A novel technique for direct measurements of contact resistance between interlaced conductive yarns in a plain weave. Text. Res. J. 2015, 85, 499–511. [Google Scholar] [CrossRef]
- Kazani, I.; De Mey, G.; Hertleer, C.; Banaszczyk, J.; Schwarz, A.; Guxho, G.; Van Langenhove, L. Van Der Pauw method for measuring resistivities of anisotropic layers printed on textile substrates. Text. Res. J. 2011, 81, 2117–2124. [Google Scholar] [CrossRef]
- Tokarska, M. New concept in assessing compactness of woven structure in terms of its resistivity. J. Mater. Sci. Mater. Electron. 2016, 27, 7335–7341. [Google Scholar] [CrossRef] [Green Version]
- Jiyong, H.; Xiaofeng, Z.; Guohao, L.; Xudong, Y.; Xin, D. Electrical properties of PPy-coated conductive fabrics for human joint motion monitoring. Autex Res. J. 2016, 16, 7–12. [Google Scholar] [CrossRef] [Green Version]
- Tokarska, M.; Gniotek, K. Anisotropy of the electroconductive properties of flat textiles. J. Text. Inst. 2015, 106, 9–18. [Google Scholar] [CrossRef]
- Vasile, S.; Deruck, F.; Hertleer, C.; De Raeve, A.; Ellegiers, T.; De Mey, G. Study of the contact resistance of interlaced stainless steel yarns embedded in hybrid woven fabrics. Autex Res. J. 2017, 17, 170–176. [Google Scholar] [CrossRef] [Green Version]
- Tokarska, M. Mathematical model for predicting the resistivity of an electroconductive woven structure. J. Electron. Mater. 2017, 46, 1497–1503. [Google Scholar] [CrossRef] [Green Version]
- Hertleer, C.; Meul, J.; De Mey, G.; Vasile, S.; Odhiambo, S.A.; Van Langenhove, L. Mathematical model predicting the heat and power dissipated in an electroconductive contact in a hybrid woven fabric. Autex Res. J. 2020, 20, 133–139. [Google Scholar] [CrossRef]
- McLachlan, D.S. Equations for the conductivity of macroscopic mixtures. J. Phys. C Solid State Phys. 1986, 19, 1339–1354. [Google Scholar] [CrossRef]
- McLachlan, D. An equation for the conductivity of binary mixtures with anisotropic grain structures. J. Phys. C Solid State Phys. 1987, 20, 865–877. [Google Scholar] [CrossRef]
- Archie, G.E. Electrical resistivity log as an aid in determining some reservoir characteristics. Trans. AIME 1942, 146, 54–62. [Google Scholar] [CrossRef]
- Glover, P.W.J. A generalized Archie’s law for n phases. Geophysics 2010, 75, E247–E265. [Google Scholar] [CrossRef] [Green Version]
- Glover, P.W.J.; Walker, E. Grain-size to effective pore-size transformation derived from an electrokinetic theory. Geophysics 2009, 74, E17–E29. [Google Scholar] [CrossRef]
- Glover, P.W.J.; Hole, M.J.; Pous, J. A modified Archie’s law for two conducting phases. Earth Planet. Sci. Lett. 2000, 180, 369–383. [Google Scholar] [CrossRef]
- Verwer, K.; Eberli, G.P.; Weger, R.J. Effect of pore structure on electrical resistivity in carbonates. AAGP Bull. 2011, 95, 175–190. [Google Scholar] [CrossRef]
- Kennedy, W.D.; Herrick, D.C. Conductivity models for Archie rocks. Geophysics 2012, 77, WA109–WA128. [Google Scholar] [CrossRef]
- Cai, J.; Wei, W.; Hu, X.; Wood, D.A. Electrical conductivity models in saturated porous media: A review. Earth Sci. Rev. 2017, 171, 419–433. [Google Scholar] [CrossRef]
- Tokarska, M. Modeling of electro-conductive properties of woven structure based on mixing model. Commun. Dev. Assem. Text. Prod. 2020, 1, 12–19. [Google Scholar]
- Glover, P.W.J. A new theoretical interpretation of Archie’s saturation exponent. Solid Earth 2017, 8, 805–816. [Google Scholar] [CrossRef] [Green Version]
- Berrezueta, E.; González-Menéndez, L.; Ordóñez-Casado, B.; Olaya, P. Pore network quantification of sandstones under experimental CO2 injection using image analysis. Comput. Geosci. 2015, 77, 97–110. [Google Scholar] [CrossRef]
- ISO/IEC Guide 98-3:2008(En). Uncertainty of Measurement—Part 3: Guide to the Expression of Uncertainty in Measurement (GUM:1995). Available online: https://www.iso.org/obp/ui/#iso:std:iso-iec:guide:98:-3:ed-1:v2:en (accessed on 14 December 2021).
- Tokarska, M. Characterization of electro-conductive textile materials by its biaxial anisotropy coefficient and resistivity. J. Mater. Sci. Mater. Electron. 2019, 30, 4093–4103. [Google Scholar] [CrossRef] [Green Version]
- Kostajnšek, K.; Urbas, R.; Dimitrovski, K. A new simplified model for predicting the UV-protective properties of monofilament pet fabrics. Autex Res. J. 2019, 19, 263–270. [Google Scholar] [CrossRef] [Green Version]
- EN 16812:2016; Textiles and Textile Products—Electrically Conductive Textiles—Determination of the Linear Electrical Resistance of Conductive Tracks. European Committee for Standardization: Brussels, Belgium. Available online: https://standards.iteh.ai/catalog/standards/cen/6a8bc45e-d439-493d-ba92-58698b5ce97b/en-16812-2016 (accessed on 14 December 2021).
- Meul, J. Study of Electro-Conductive Contacts in Hybrid Woven Fabrics. Master’s Thesis, Ghent University, Ghent, Belgium, 2015. Available online: https://lib.ugent.be/catalog/rug01:002224697 (accessed on 14 December 2021).
- AATCC 76; Test Method for Electrical Surface Resistivity of Fabrics. American Association of Textile Chemists and Colorists (AATCC): Research Triangle Park, NC, USA. Available online: https://global.ihs.com/doc_detail.cfm?document_name=AATCC%2076&item_s_key=00156638 (accessed on 14 December 2021).
- ISO 139:2005. Textiles—Standard Atmospheres for Conditioning and Testing. Available online: https://www.iso.org/obp/ui/#iso:std:iso:139:ed-2:v1:en (accessed on 14 December 2021).
- Corder, G.W.; Foreman, D.I. Nonparametric Statistics for Non-Statisticians: A Step-By-Step Approach; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]


| Woven Fabric | S1 | S2 | S3 |
|---|---|---|---|
| Raw material composition | 100% polyamide woven fabric; nickel and copper metalised | 100% polyester woven fabric; nickel metalised | 100% polyester woven fabric; nickel metalised |
| Weave | Plain | Plain | Twill |
| Microscopic image with total visual magnification 30× ↓ the warp direction → the weft direction |  |  |  |
| Woven Fabric | Thickness (mm) | Areal Density (g/m2) | Bulk Density (kg/m3) | Warp Density (Yarns/1 cm) | Weft Density (Yarns/1 cm) |
|---|---|---|---|---|---|
| S1 | 0.124 (10.5%) | 86 (2.3%) | 694 (10.8%) | 57.0 (1.7%) | 41.0 (1.2%) |
| S2 | 0.078 (15.4%) | 75 (2.7%) | 966 (15.8%) | 40.0 (1.2%) | 30.0 (1.7%) |
| S3 | 0.270 (5.6%) | 152 (2.6%) | 564 (5.8%) | 47.5 (1.9%) | 34.0 (1.7%) |
| dwa = dwe | k × k | Awa (cm) | Pore Width 1 (cm) | Awe (cm) | Pore Length 2 (cm) |
|---|---|---|---|---|---|
| 1.5 cm | 5 × 5 | 1.80 | 0.30 | 2.60 | 1.10 |
| 4 × 4 | 2.25 | 0.75 | 3.25 | 1.75 | |
| 3 × 3 | 3.00 | 1.50 | 4.33 | 2.83 | |
| 1.0 cm | 5 × 5 | 1.80 | 0.80 | 2.60 | 1.60 |
| 4 × 4 | 2.25 | 1.25 | 3.25 | 2.25 | |
| 3 × 3 | 3.00 | 2.00 | 4.33 | 3.33 |
| dwa = dwe | k × k | Fraction of Strips Cth (-) | Fraction of Strip Contacts Ccont (-) | Fraction of Pores Cp (-) | Percentage Surface Cover Cstr (%) 1 |
|---|---|---|---|---|---|
| 1.5 cm | 5 × 5 | 0.449 | 0.481 | 0.070 | 93 |
| 4 × 4 | 0.513 | 0.308 | 0.179 | 82 | |
| 3 × 3 | 0.500 | 0.173 | 0.327 | 67 | |
| 1.0 cm | 5 × 5 | 0.513 | 0.214 | 0.273 | 73 |
| 4 × 4 | 0.479 | 0.137 | 0.384 | 62 | |
| 3 × 3 | 0.410 | 0.077 | 0.513 | 49 |
| Group | Sample | ϕth (-) | σth (Ω cm)−1 | ϕcont (-) | σcont (Ω cm)−1 | σstr (Ω cm)−1 |
|---|---|---|---|---|---|---|
| A1 | S1 5 × 5_1.5 | 0.483 | 2909.3 (6%) | 0.517 | 2489.0 (30%) | 1170.7 (9%) |
| S2 5 × 5_1.5 | 0.483 | 617.5 (16%) | 0.517 | 2202.8 (24%) | 263.6 (8%) | |
| S3 5 × 5_1.5 | 0.483 | 140.7 (6%) | 0.517 | 138.2 (38%) | 61.3 (4%) | |
| A2 | S1 5 × 5_1.0 | 0.706 | 2291.1 (4%) | 0.294 | 3200.2 (17%) | 911.4 (5%) |
| S2 5 × 5_1.0 | 0.706 | 712.1 (6%) | 0.294 | 3338.7 (13%) | 286.1 (7%) | |
| S3 5 × 5_1.0 | 0.706 | 150.3 (9%) | 0.294 | 145.8 (11%) | 67.9 (4%) | |
| B1 | S1 4 × 4_1.5 | 0.625 | 2909.3 (6%) | 0.375 | 2489.0 (30%) | 1203.2 (3%) |
| S2 4 × 4_1.5 | 0.625 | 617.5 (16%) | 0.375 | 2202.8 (24%) | 270.3 (2%) | |
| S3 4 × 4_1.5 | 0.625 | 140.7 (6%) | 0.375 | 138.2 (38%) | 60.9 (3%) | |
| B2 | S1 4 × 4_1.0 | 0.778 | 2291.1 (4%) | 0.222 | 3200.2 (17%) | 966.7 (4%) |
| S2 4 × 4_1.0 | 0.778 | 712.1 (6%) | 0.222 | 3338.7 (13%) | 285.7 (7%) | |
| S3 4 × 4_1.0 | 0.778 | 150.3 (9%) | 0.222 | 145.8 (11%) | 69.6 (9%) | |
| C1 | S1 3 × 3_1.5 | 0.743 | 2909.3 (6%) | 0.257 | 2489.0 (30%) | 1271.6 (2%) |
| S2 3 × 3_1.5 | 0.743 | 617.5 (16%) | 0.257 | 2202.8 (24%) | 268.3 (3%) | |
| S3 3 × 3_1.5 | 0.743 | 140.7 (6%) | 0.257 | 138.2 (38%) | 65.1 (1%) | |
| C2 | S1 3 × 3_1.0 | 0.842 | 2291.1 (4%) | 0.158 | 3200.2 (17%) | 1032.2 (7%) |
| S2 3 × 3_1.0 | 0.842 | 712.1 (6%) | 0.158 | 3338.7 (13%) | 302.3 (2%) | |
| S3 3 × 3_1.0 | 0.842 | 150.3 (9%) | 0.158 | 145.8 (11%) | 69.4 (1%) |
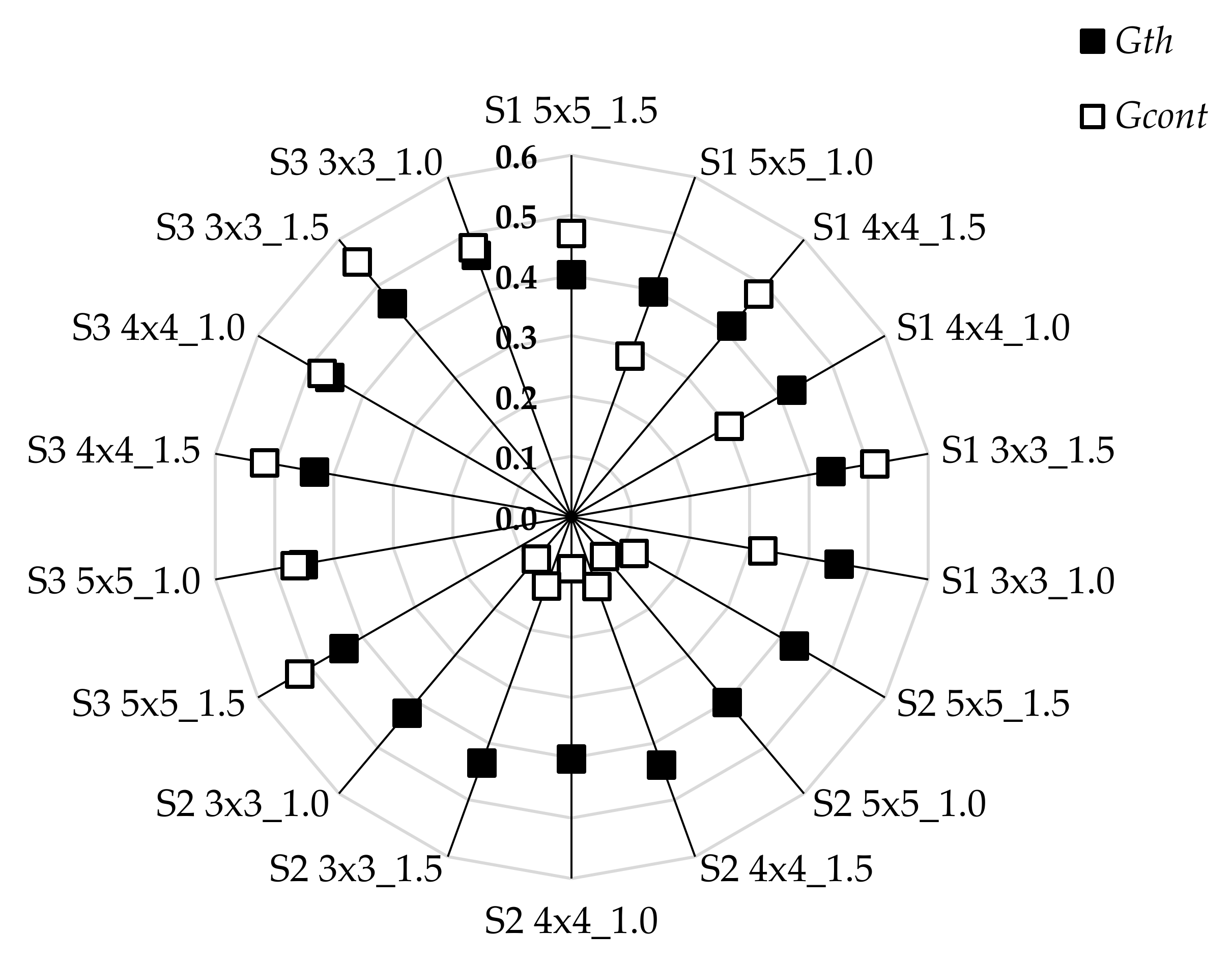
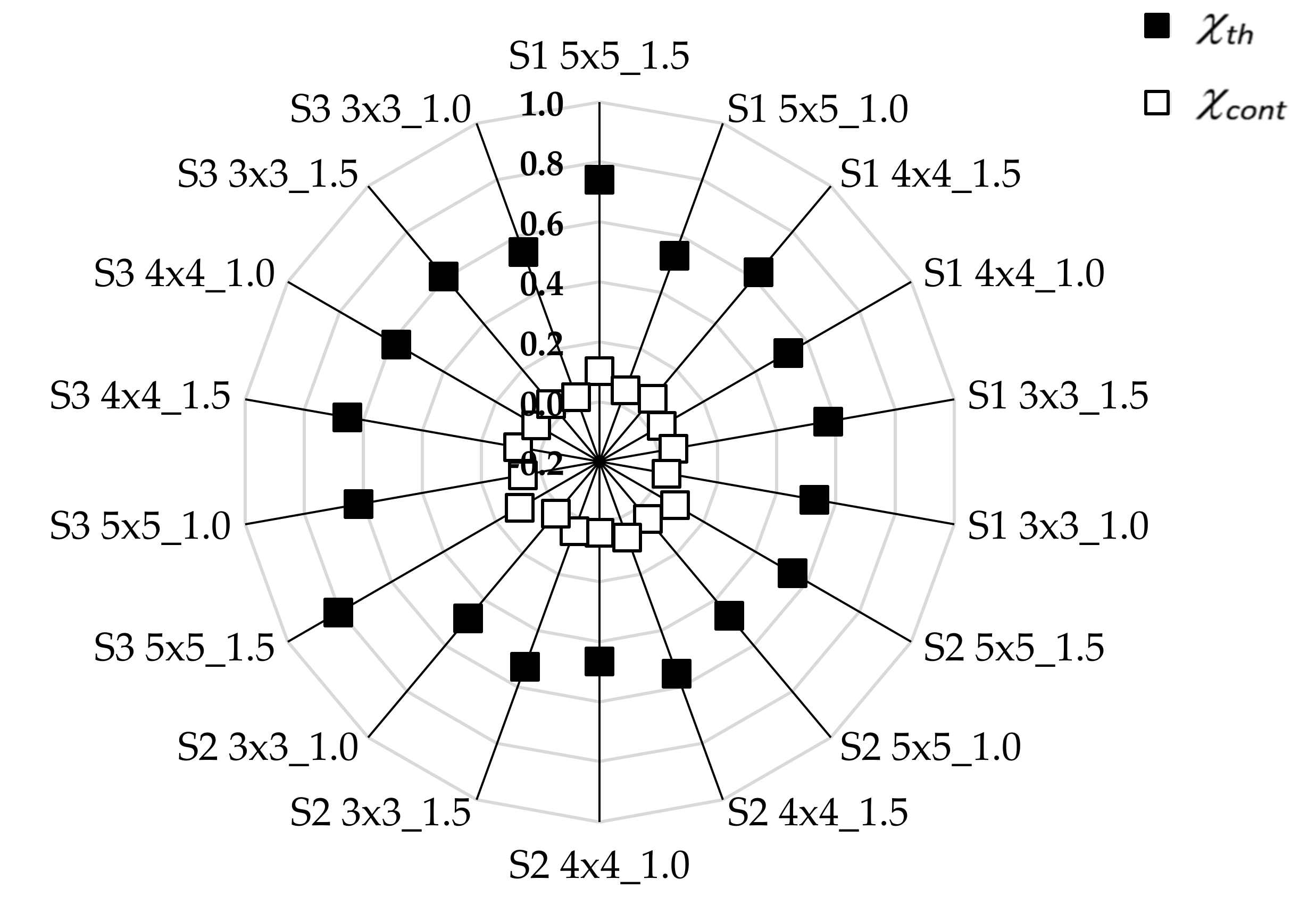
| Group | Sample | mth (-) | Gth (-) | χth (-) | mcont (-) | Gcont (-) | χcont (-) |
|---|---|---|---|---|---|---|---|
| A1 | S1 5 × 5_1.5 | 1.414 | 0.402 | 0.740 | 4.453 | 0.470 | 0.103 |
| S2 5 × 5_1.5 | 1.840 | 0.427 | 0.542 | 4.659 | 0.120 | 0.089 | |
| S3 5 × 5_1.5 | 1.297 | 0.436 | 0.806 | 4.379 | 0.521 | 0.108 | |
| A2 | S1 5 × 5_1.0 | 2.814 | 0.398 | 0.532 | 3.388 | 0.285 | 0.054 |
| S2 5 × 5_1.0 | 3.161 | 0.402 | 0.471 | 3.445 | 0.086 | 0.050 | |
| S3 5 × 5_1.0 | 2.393 | 0.452 | 0.616 | 3.305 | 0.466 | 0.059 | |
| B1 | S1 4 × 4_1.5 | 2.002 | 0.414 | 0.624 | 3.653 | 0.483 | 0.074 |
| S2 4 × 4_1.5 | 2.262 | 0.438 | 0.553 | 3.725 | 0.123 | 0.069 | |
| S3 4 × 4_1.5 | 1.904 | 0.433 | 0.654 | 3.622 | 0.517 | 0.076 | |
| B2 | S1 4 × 4_1.0 | 3.559 | 0.422 | 0.526 | 3.140 | 0.302 | 0.040 |
| S2 4 × 4_1.0 | 4.037 | 0.401 | 0.467 | 3.195 | 0.086 | 0.037 | |
| S3 4 × 4_1.0 | 3.147 | 0.463 | 0.583 | 3.085 | 0.477 | 0.043 | |
| C1 | S1 3 × 3_1.5 | 2.867 | 0.437 | 0.574 | 3.210 | 0.511 | 0.050 |
| S2 3 × 3_1.5 | 3.154 | 0.434 | 0.527 | 3.256 | 0.122 | 0.047 | |
| S3 3 × 3_1.5 | 2.678 | 0.462 | 0.607 | 3.177 | 0.553 | 0.052 | |
| C2 | S1 3 × 3_1.0 | 4.722 | 0.451 | 0.527 | 2.951 | 0.323 | 0.027 |
| S2 3 × 3_1.0 | 5.245 | 0.425 | 0.482 | 2.993 | 0.091 | 0.025 | |
| S3 3 × 3_1.0 | 4.546 | 0.462 | 0.543 | 2.936 | 0.476 | 0.028 |
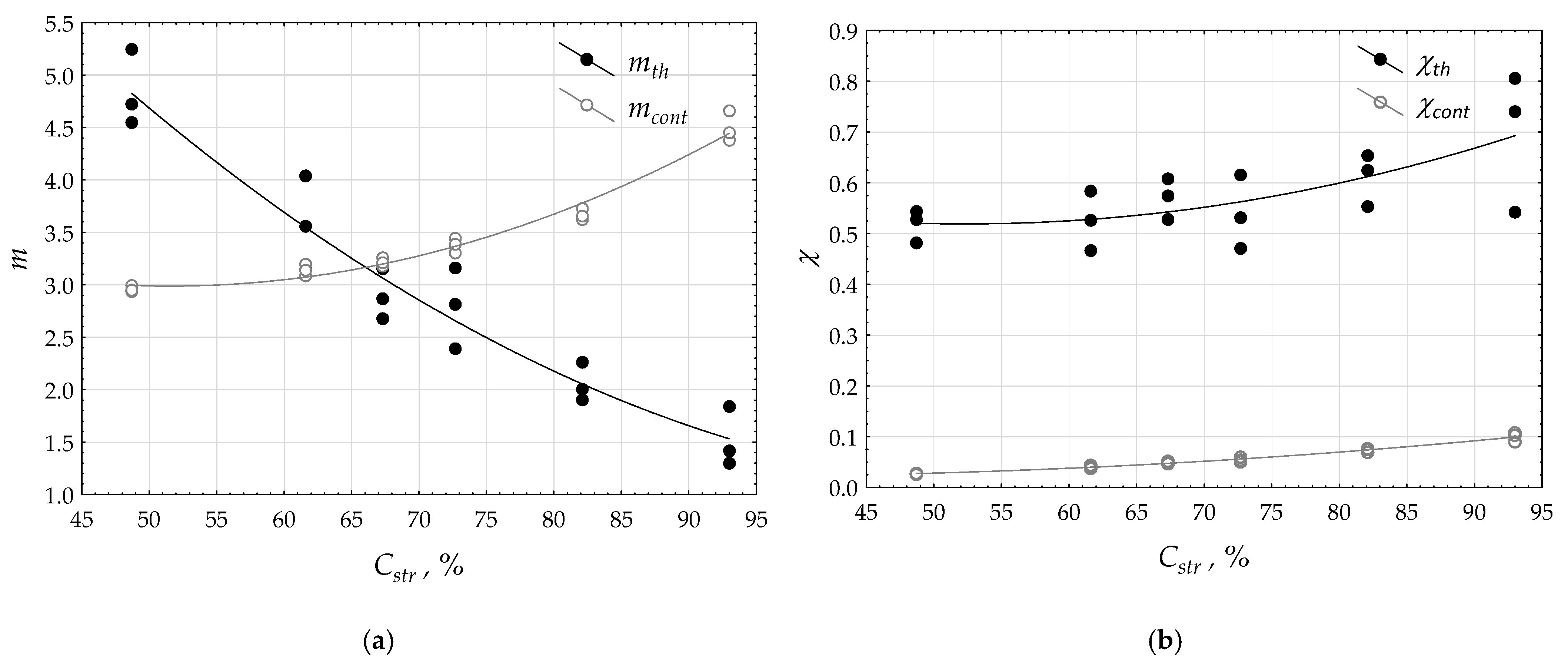
| Gth | Gcont | mth | ϕth | χth | mcont | ϕcont | χcont | Cstr | σth | σcont | σstr | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Gth | 1.000 | 0.459 | 0.160 | 0.318 | 0.134 | −0.342 | −0.318 | −0.243 | −0.350 | −0.473 | −0.717 | −0.435 |
| Gcont | 0.459 | 1.000 | −0.374 | −0.141 | 0.716 | 0.027 | 0.141 | 0.284 | 0.141 | 0.105 | −0.684 | 0.110 |
| mth | 0.160 | −0.374 | 1.000 | 0.903 | −0.738 | −0.804 | −0.903 | −0.933 | −0.953(3) | −0.043 | 0.352 | −0.020 |
| mcont | −0.342 | 0.027 | −0.804 | −0.979 | 0.602 | 1.000 | 0.979 | 0.938 | 0.924(3) | 0.054 | −0.074 | 0.030 |
| χth | 0.134 | 0.716 | −0.738(2) | −0.688(2) | 1.000 | 0.602 | 0.688 | 0.797 | 0.646(3) | 0.025 | −0.568 | 0.014 |
| χcont | −0.243 | 0.284 | −0.933 | −0.985 | 0.797 | 0.938(2) | 0.985(2) | 1.000 | 0.967(3) | 0.048 | −0.267 | 0.024 |
| ϕth | 0.318 | −0.141 | 0.903 | 1.000 | −0.688 | −0.979 | −1.000 | −0.985 | −0.978(3) | −0.055 | 0.162 | −0.029 |
| ϕcont | −0.318 | 0.141 | −0.903 | −1.000 | 0.688 | 0.979 | 1.000 | 0.985 | 0.978(3) | 0.055 | −0.162 | 0.029 |
| Cstr | −0.350 | 0.141 | −0.953 | −0.978 | 0.646 | 0.924 | 0.978 | 0.967 | 1.000 | 0.055 | −0.163 | 0.027 |
| σth | −0.473 | 0.105 | −0.043 | −0.055 | 0.025 | 0.054 | 0.055 | 0.048 | 0.055 | 1.000 | 0.623 | 0.998 |
| σcont | −0.717 | −0.684 | 0.352 | 0.162 | −0.568 | −0.074 | −0.162 | −0.267 | −0.163 | 0.623 | 1.000 | 0.619 |
| σstr | −0.435 | 0.110 | −0.020 | −0.029 | 0.014 | 0.030 | 0.029 | 0.024 | 0.027 | 0.998(1) | 0.619(1) | 1.000 |
| Parameter | K–W Test | Post Hoc Test | p-Value | |
|---|---|---|---|---|
| Gth | Value of test statistic p-value | 7.3801 0.0250 | S1–S2 2 S1–S3 2 S2–S3 2 | 1.0000 0.0520 0.0602 |
| Gcont | Value of test statistic p-value | 12.7836 0.0017 | S1–S2 2 S1–S3 2 S2–S3 2 | 0.0602 0.7026 0.0013 |
| Parameter | K–W Test | Post Hoc Test | p-Value | |
|---|---|---|---|---|
| mth | Value of test statistic p-value | 6.2222 0.0446 | 3 × 3–4 × 4 2 3 × 3–5 × 5 2 4 × 4–5 × 5 2 | 0.8384 0.0386 0.4792 |
| mcont | Value of test statistic p-value | 8.8538 0.0120 | 3 × 3–4 × 4 2 3 × 3–5 × 5 2 4 × 4–5 × 5 2 | 0.4792 0.0088 0.3505 |
| χth | Value of test statistic p-value | 1.0643 0.5873 | 3 × 3–4 × 4 2 3 × 3–5 × 5 2 4 × 4–5 × 5 2 | – – – |
| χcont | Value of test statistic p-value | 7.9064 0.0192 | 3 × 3–4 × 4 2 3 × 3–5 × 5 2 4 × 4–5 × 5 2 | 0.4792 0.0148 0.4792 |
| Phase Exponent | mth (-) | mth (-) | mcont (-) | mcont (-) | |
|---|---|---|---|---|---|
| Width of strip | 1.0 cm | 1.5 cm | 1.0 cm | 1.5 cm | |
| 3 × 3 | 4.84 (8%) | 2.90 (8%) | 2.96 (1%) | 3.21 (1%) | |
| Structure type | 4 × 4 | 3.58 (12%) | 2.06 (9%) | 3.14 (2%) | 3.67 (1%) |
| 5 × 5 | 2.79 (14%) | 1.52 (19%) | 3.38 (2%) | 4.50 (3%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tokarska, M. A Mixing Model for Describing Electrical Conductivity of a Woven Structure. Materials 2022, 15, 2512. https://doi.org/10.3390/ma15072512
Tokarska M. A Mixing Model for Describing Electrical Conductivity of a Woven Structure. Materials. 2022; 15(7):2512. https://doi.org/10.3390/ma15072512
Chicago/Turabian StyleTokarska, Magdalena. 2022. "A Mixing Model for Describing Electrical Conductivity of a Woven Structure" Materials 15, no. 7: 2512. https://doi.org/10.3390/ma15072512
APA StyleTokarska, M. (2022). A Mixing Model for Describing Electrical Conductivity of a Woven Structure. Materials, 15(7), 2512. https://doi.org/10.3390/ma15072512






