Abstract
The static and dynamic magnetic properties and the specific heat of K2Ni2TeO6 and Li2Ni2TeO6 were examined and it was found that they undergo a long-range ordering at TN = 22.8 and 24.4 K, respectively, but exhibit a strong short-range order. At high temperature, the magnetic susceptibilities of K2Ni2TeO6 and Li2Ni2TeO6 are described by a Curie–Weiss law, with Curie-Weiss temperatures Θ of approximately −13 and −20 K, respectively, leading to the effective magnetic moment of about 4.46 ± 0.01 μB per formula unit, as expected for Ni2+ (S = 1) ions. In the paramagnetic region, the ESR spectra of K2Ni2TeO6 and Li2Ni2TeO6 show a single Lorentzian-shaped line characterized by the isotropic effective g-factor, g = 2.19 ± 0.01. The energy-mapping analysis shows that the honeycomb layers of A2Ni2TeO6 (A = K, Li) and Li3Ni2SbO6 adopt a zigzag order, in which zigzag ferromagnetic chains are antiferromagnetically coupled, because the third nearest-neighbor spin exchanges are strongly antiferromagnetic while the first nearest-neighbor spin exchanges are strongly ferromagnetic, and that adjacent zigzag-ordered honeycomb layers prefer to be ferromagnetically coupled. The short-range order of the zigzag-ordered honeycomb lattices of K2Ni2TeO6 and Li2Ni2TeO6 is equivalent to that of an antiferromagnetic uniform chain, and is related to the short-range order of the ferromagnetic chains along the direction perpendicular to the chains.
1. Introduction
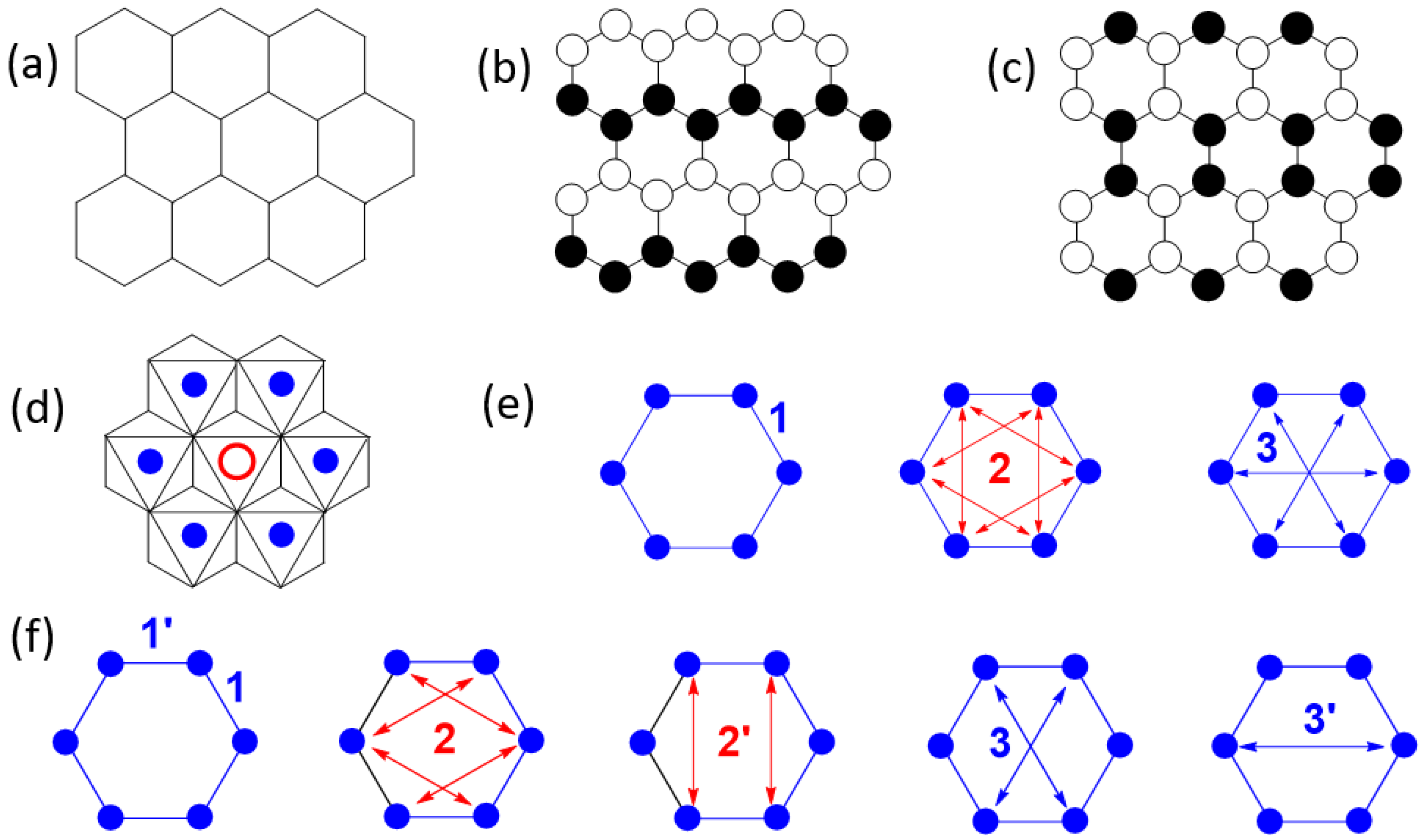
Compounds with honeycomb layers of magnetic ions attracted much attention in the field of low-dimensional magnetism [1], owing in part to Kitaev’s conjecture [2] that they can have gapped and gapless liquid-like ground states in a certain range of spin exchange parameters. It has been elusive to find honeycomb-layered (Figure 1a) magnetic systems confirming Kitaev’s conjecture because of the inevitable interlayer interactions, which can lead to a three-dimensional (3D) long-range ordering. In real honeycomb-layered materials, anisotropic in-plane Kitaev interactions compete with isotropic Heisenberg interactions. The ordering of magnetic moments in honeycomb layers can be zigzag (Figure 1b) or stripy (Figure 1c) [3]. Kitaev’s conjecture was originally analyzed for the spin S = 1/2 case, but it has subsequently been extended to S > 1/2 systems (in particular, S = 1), although these systems are not exactly solvable [4]. It was shown that the bond-dependent Kitaev interaction model can be realized in two-dimensional (2D) Mott insulators if there exists strong Hund coupling of electrons at the cation sites and strong spin-orbit coupling at the anion sites [4]. The iridate Na2IrO3 with honeycomb layers of low-spin Ir4+ (d5, S = 1/2) ions [5,6,7] and the ruthenium chloride α-RuCl3 with honeycomb layers of low-spin Ru3+ (d5, S = 1/2) ions [8,9,10] were examined as the S = 1/2 systems that can capture the basics of Kitaev magnetism. The iridate β-Li2IrO3 has also been examined for Kitaev magnetism, but its Ir4+ ions form a 3D framework rather than honeycomb layers [11,12]. The magnetic structure in the honeycomb layers of Na2IrO3 is consistent with a zigzag order (i.e., FM zigzag chains of Ir4+ ions are antiferromagnetically coupled, Figure 1b) or a stripy order (i.e., AFM zigzag chains of Ir4+ ions are ferromagnetically coupled, Figure 1c) [6]. The magnetic structure of α-RuCl3 is more consistent with a zigzag order than with a stripy order [9]. The layered-phase A3Ni2SbO6 (A = Li, Na) [13,14] consists of honeycomb layers of S = 1 ions (i.e., Ni2+ ions). Each honeycomb layer consists of edge-sharing NiO6 octahedra each containing a Ni2+ ion, in which every hexagon of Ni2+ ions has its center occupied by a Sb5+ cation to form a SbO6 octahedron (Figure 1d). The magnetic structure of A3Ni2SbO6 (A = Li, Na) in the honeycomb layers of Ni2+ ions is described by a zigzag order [13], similar to the one found for the S = 1/2 systems Na2IrO3 and α-RuCl3.
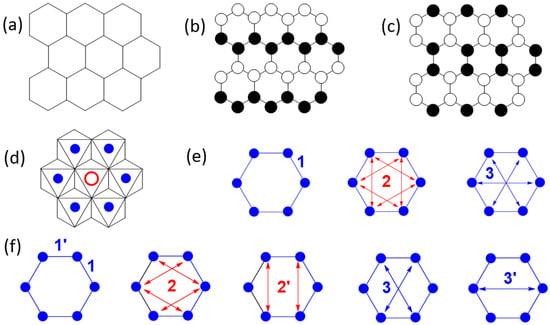
Figure 1.
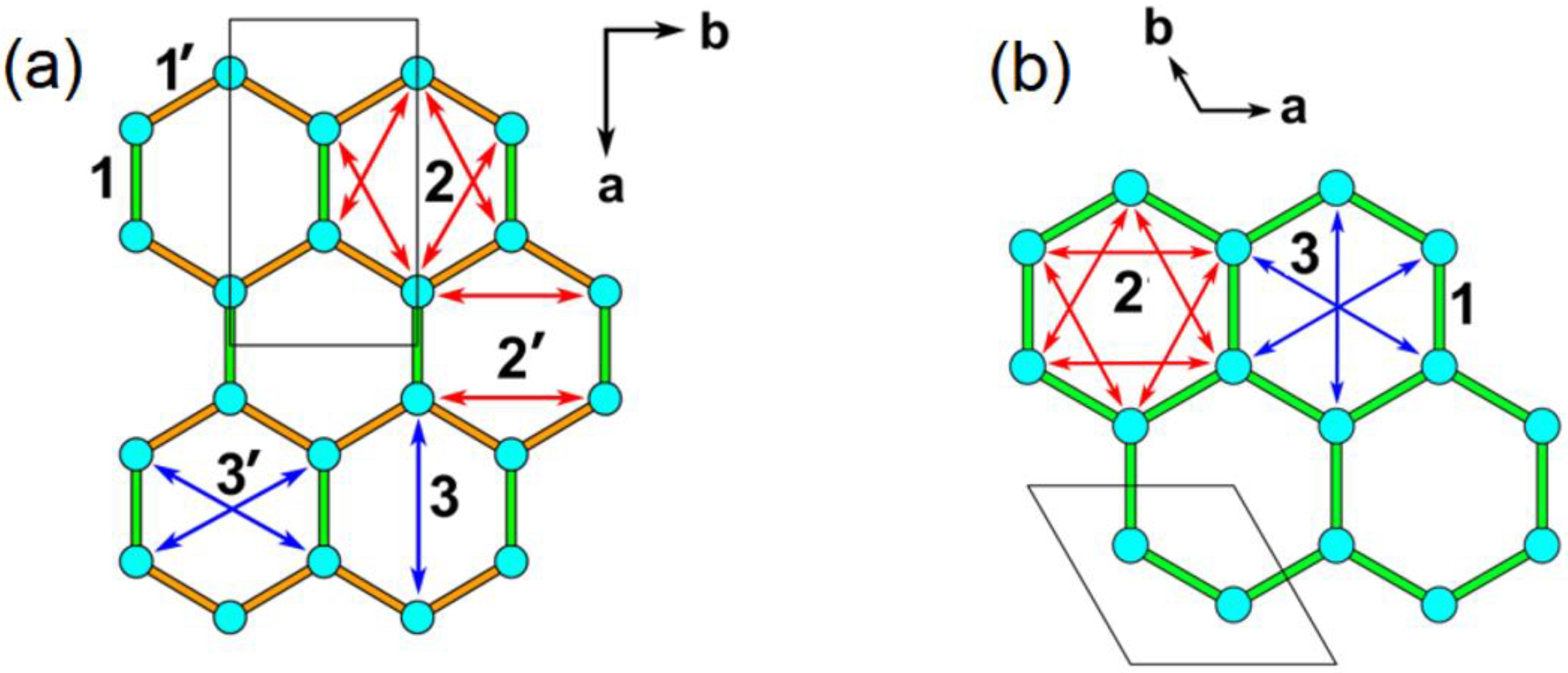
(a) A simplified view of a honeycomb layer made up of magnetic ions. (b) A zigzag order of magnetic moments in a honeycomb layer. (c) A stripy order of magnetic moments in a honeycomb layer. (d) A honeycomb layer of magnetic ions (solid blue circles) in which the center of every hexagon of magnetic ions is occupied by a cation (e.g., Na+ in Na2IrO3, Sb5+ in A3Ni2SbO6, Te6+ in A2Ni2TeO6, (P-P)8+ dimer in NiPS3). (e) First NN spin exchange (J1), second NN spin exchange (J2), and third NN spin exchange (J3) in a honeycomb layer made up of regular hexagons of magnetic ions. (f) First NN spin exchange (J1 and J1′), second NN spin exchange (J2 and J2′), and third NN spin exchange (J3 and J3′) in a honeycomb layer made up of slightly distorted hexagons of magnetic ions (e.g., 2-fold rotational symmetry).
So far, it is not clear why the honeycomb layers of these magnetic systems form a zigzag order, namely, why they adopt FM zigzag chains that are antiferromagnetically coupled. To understand the cause for this ordering, it is necessary to know the spin exchanges between the first, second, and third nearest-neighbor (NN) magnetic ions, which are J1, J2, and J3 depicted in Figure 1e, respectively, when a honeycomb layer is made up of regular hexagons of magnetic ions. However, when these hexagons are lower in symmetry (e.g., 2-fold rotational symmetry), the first, second, and third NN spin exchanges are each split into two different ones, as depicted in Figure 1f. Zvereva et al. evaluated three spin exchanges of A3Ni2SbO6 (A = Li, Na) [13] (namely, the first NN exchanges J1 and J1′ as well as the third NN exchanges J3 and J3′, Figure 1f), and found that J1 is AFM, J1′ is FM, while the third NN spin exchanges J3 and J3′ are practically zero. Although this is consistent with a zigzag order in A3Ni2SbO6 (A = Li, Na), we note that a zigzag order also occurs in the honeycomb layers of M2+ (M = Fe, Co, Ni) ions in the sulfides MPS3, in which each hexagon of M2+ ions has its center occupied by a P2S64− ion (Figure 1d) to form MS6 octahedra. The strongest spin exchange of NiPS3 was found to be the third NN exchanges (J3 and J3′), which are strongly AFM, while the first NN spin exchanges (J1 and J1′) are FM and are weaker than the third NN exchanges by a factor greater than three [15]. Thus, the zigzag order of NiPS3 is caused by the strongly AFM third NN spin exchanges. This finding makes it necessary to check if the third NN spin exchanges vanish in A3Ni2SbO6 (A = Li, Na) as reported [13].
Honeycomb layers of Ni2+ ions similar to those of A3Ni2SbO6 (A = Li, Na) are also present in A2Ni2TeO6 (A = K, Li) [16,17,18,19]. Formally, A2Ni2TeO6 results from A3Ni2SbO6 by replacing the Sb5+ ion with a Te6+ ion, by removing one cation A+ to satisfy the charge balance requirement, and by changing the layer stacking mode leading to trigonal prismatic and tetrahedral coordination for K+ and Li+, respectively. In the present work, we probed the static and dynamic magnetic properties of A2Ni2TeO6 (A = K, Li) and found that they are very similar to those of A3Ni2SbO6 (A = Li, Na), and we determined the spin exchanges (Figure 1f) of A2Ni2TeO6 using the energy-mapping analysis [20,21] to show that the honeycomb layers of not only A2Ni2TeO6 but also A3Ni2SbO6 have a zigzag magnetic order for the same reason as found for NiPS3. Thus, the cause for the zigzag order of not only A2Ni2TeO6 (A = K, Li) but also A3Ni2SbO6 (A = Li, Na) is the third NN spin exchange, which is strongly AFM, as found for NPS3.
Both static and dynamic magnetic properties of A2Ni2TeO6 (A = K, Li) evidence the behavior inherent in a magnet with reduced dimensionality, and the long-range order in these compounds is preceded by a short-range order. These observations are fully supported by specific heat measurements, which reveal sharp λ-type singularities establishing the occurrence of a Néel order. We show that the honeycomb layers of A2Ni2TeO6 (A = K, Li) and Li3Ni2SbO6 adopt a zigzag order, in which zigzag ferromagnetic chains are antiferromagnetically coupled, and that the short-range order of Li2Ni2TeO6 and K2Ni2TeO6 arises from the short-range order of the ferromagnetic chains along the direction perpendicular to the chains.
2. Sample Preparation and X-ray Diffraction
2.1. K2Ni2TeO6
Light-green samples of K2Ni2TeO6 were prepared by conventional solid-state synthesis. Since the material is highly hygroscopic, it was necessary to protect it from the atmospheric moisture (see the Supplementary Materials for details). In agreement with the previous data [18], the XRD pattern (Supplementary Figure S1) shows that our sample of K2Ni2TeO6 represents a hexagonal superlattice of the P2 type, space group P63/mcm, with only weak extra reflections. Least squares refinements resulted in the lattice parameters a = 5.258(3), c = 12.417(1) Å, and c/a = 2.362, which are consistent with the literature data [18]. The small differences in the absolute values are systematic and may hence be due to uncertainties in our refined sample displacement and/or in the wavelengths used. Thus, it is important to compare the axial ratios. Masese et al. [18] reported a slightly higher c/a ratio of 2.370, together with the dark green color of their sample, which suggests the presence of some Ni3+ ions, presumably due to potassium deficiency. Chemical analysis of our light-green sample by reverse redox titration [22] yielded the oxidation state of 2.01 ± 0.01 for Ni, thus confirming the stoichiometry. In contrast, our potassium-deficient samples were black, containing a considerable amount of Ni3+ ions and exhibiting much larger c/a ratios. This is a common feature of the present class of structures: the oxidation of an octahedral cation results in the a-axis contraction, and the loss of the interlayer alkali ions, in the c-axis expansion. However, the deviation from stoichiometry in the reported structure [18] is evidently small and the reported structure is quite reasonable, so we did not attempt a re-refinement.
2.2. Li2Ni2TeO6
We prepared Li2Ni2TeO6 from Na2Ni2TeO6 by an ion-exchange reaction [16] (see the Supplementary Materials for details). Previously, the XRD powder pattern (Supplementary Figure S2) was indexed in the space group Cmca by analogy with T2-Li2NiMn2O6 [23]. The same preparation route and the same space group were adopted by Grundish et al. [17], and the orthorhombic lattice parameters are in reasonable agreement (Table 1). Li2Ni2TeO6 is not isostructural with its sodium precursor (P63/mcm) because small Li+ ions cannot be accommodated in the trigonal prismatic sites (i.e., Na+ ion sites), so the adjacent honeycomb (Ni2TeO6)2− layers are shifted to provide tetrahedral interlayer sites suitable for Li+ ions, as found in T2-Li2NiMn2O6 [23]. Unfortunately, crystal structure refinement of the T2-type Li2Ni2TeO6 [17] resulted in unrealistic bond lengths and bond valence sums (BVSs) (Table 2), and our refinement results were not better. The reasons for this might be: (i) Admixture of foreign phase(s): the zoomed-in view of the XRD pattern (Figure 5 in [17]) reveals a strong unindexed reflection at 2Θ ≈ 17.53°. Visually, it might seem to be the α2 component of the strongest reflection (2Θ ≈ 17.38°), but their separation is three times larger than the doublet separation. Much weaker shoulders are seen in our patterns as well (Figure S2). (ii) The powder patterns are diffuse in nature arising from the stacking faults due to the layer gliding, which is induced by the ion-exchange transforming the space group of the crystal structure from P63/mcm to Cmca. (iii) X-ray diffraction measurements have a low sensitivity to the positions of light atoms (Li and O) in the presence of heavy elements (Te and Ni). Thus, in the X-ray crystal structure reported for Li2Ni2TeO6 [17], some Li, O1, and O2 positions are known only in three decimal places. Thus, it is important to have more accurate atomic positions. The crystal structure of Li2Ni2TeO6 was optimized by DFT calculations [17], but the resulting atomic positions were not reported. Thus, we optimized the crystal structure of Li2Ni2TeO6 by DFT + U calculations with Ueff = 4 eV, and the optimized atomic positions are summarized in Supplementary Table S1.

Table 1.
Lattice parameters of Li2Ni2TeO6 (Cmca) from different sources.

Table 2.
Average lengths of the Li-O, Ni-O, and Te-O bonds and oxidation states of Li, Ni, Te, and O of Li2Ni2TeO6 expected.
The average Li-O, Ni-O, and Te-O bond lengths of Li2Ni2TeO6, determined from the X-ray diffraction and our DFT + U optimized structures, are compared in Table 2, and so are the oxidations states for the Li, Ni, Te, and O atoms of Li2Ni2TeO6 obtained from bond valence sum (BVS) calculations based on the two crystal structures. According to the optimized crystal structure, the oxidation states of Li and Ni are very close to those expected from the ionic electron counting scheme (+1 and +2, respectively). In contrast, the oxidation state of Te is considerably smaller than expected from the ionic electron counting scheme (i.e., +5.29 vs. +6), while that of O is considerably higher than expected (i.e., −1.72/−1.87 vs. −2).
3. Results and Discussion
3.1. Magnetic Properties
3.1.1. Magnetic Susceptibility and Magnetization
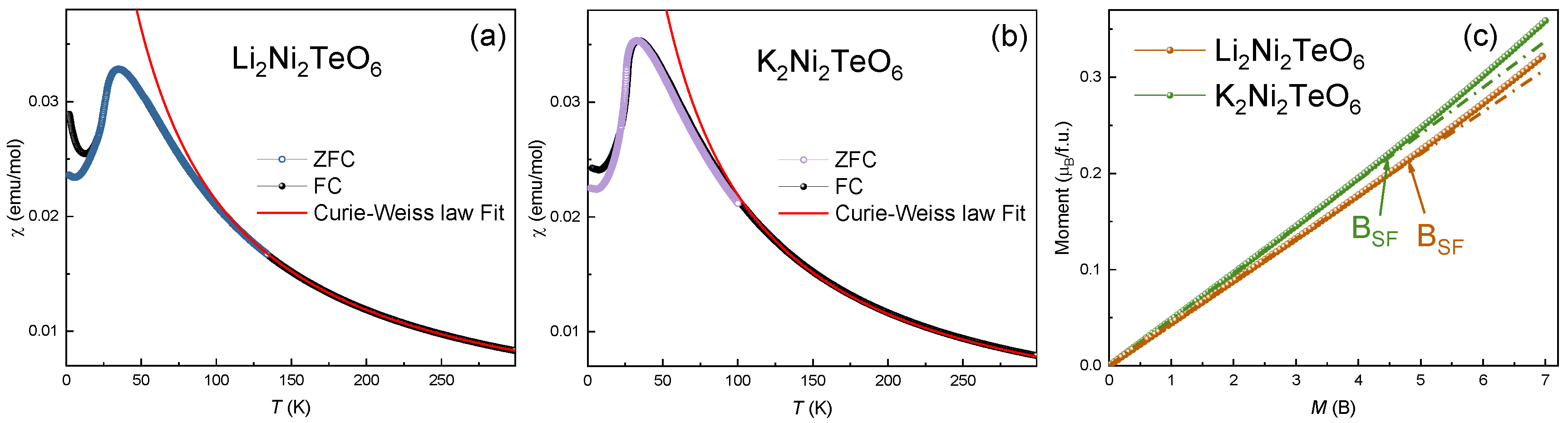
The magnetic susceptibilities, χ(T), of Li2Ni2TeO6 and K2Ni2TeO6 were measured at B = 0.1 T in the temperature range of 2–300 K using a Quantum Design PPMS-9T system, and their isothermal magnetizations, M(B), using a Quantum Design MPMS-7T SQUID-VSM magnetometer under an external field up to 7 T at various temperatures after cooling the sample at zero magnetic field. Results of zero-field-cooled (ZFC) and field-cooled (FC) measurements carried out for Li2Ni2TeO6 and K2Ni2TeO6 as well as magnetization curves are shown in Figure 2a–c. A small divergence between the results of ZFC and FC measurements indicates the presence of a modest spin disorder, due most likely to impurity-related effects. On lowering the temperature, the magnetic susceptibilities of both Li2Ni2TeO6 and K2Ni2TeO6 exhibit a broad maximum, χmax, at Tmax ≈ 34 K, then the value drops by about one third of χmax. The values of the Néel temperatures, TN, deduced as the temperature, T, at which the derivative dχ(T)/dT shows a maximum (not shown), are ~22.8 K for K2Ni2TeO6 and ~24.4 K for Li2Ni2TeO6. These TN values are considerably lower than Tmax, signaling the presence of strong short-range correlations. We note that AFM uniform chains exhibit a broad magnetic susceptibility maximum due to their short-range magnetic order. The occurrence of a magnetic susceptibility maximum in A2Ni2TeO6 (A = Li, K) and A3Ni2SbO6 (A = Li, Na) [13,14] suggests that their magnetic properties possess a one-dimensional (1D) character, although their honeycomb magnetic lattices are 2D in nature.
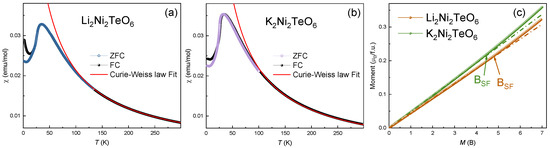
Figure 2.
ZFC and FC magnetic susceptibilities of (a) Li2Ni2TeO6 and (b) K2Ni2TeO6 taken at B = 0.1 T. The solid lines are the fits by the Curie–Weiss law, dashed green lines—Rushbrook–Wood model fit. (c) Magnetizations of Li2Ni2TeO6 and K2Ni2TeO6 at T = 2 K. The fields of the spin–flop transition, Bsf, are marked by arrows.
The high-temperature magnetic susceptibility can be fitted by the Curie–Weiss law plus a temperature-independent term, χ0:
where Θ is the Weiss temperature, and C is the Curie constant, C = NAμeff2μB2/3kB (μeff is the effective magnetic moment, while NA, μB, and kB are Avogadro’s number, Bohr magneton, and Boltzmann constant, respectively). The diamagnetic contributions of K2Ni2TeO6 and Li2Ni2TeO6 were estimated to be χ0 = −1.38 10−4 and −1.1 10−4 emu/mol, respectively, by summing the Pascal’s constants [26]. The χ0 values were fixed to reduce the number of variable parameters during the fitting analysis. From this analysis, it was found that Θ = −13 K for K2Ni2TeO6 and −20 K for Li2Ni2TeO6, implying the presence of dominant antiferromagnetic interactions while, per formula unit (f.u.), μeff = 4.45 μB for K2Ni2TeO6 and 4.47μB for Li2Ni2TeO6. The effective g-factor obtained from ESR data (see below) is about g ≈ 2.2. The result hence well agrees with the theoretical estimate of the effective magnetic moment equal to 4.4 μB/f.u. for both compounds, where n is the number of Ni2+ ions per formula unit, assuming Ni2+ in a high-spin configuration (S = 1).
The magnetic susceptibility of A2Ni2TeO6 (A = K, Li) can be analyzed on the basis of the high-temperature series expansion (HTSE) approach for a 2D planar honeycomb lattice using the Rushbrook and Wood model [27]. Then, the χ(T) curve in the paramagnetic region can be described by:
where x = |J|/kT, A = 4, B = 7.333, C = 7.111, D = –5.703, E = –22.281, and F = 51.737.27 Fitting the χ(T) curve by Equation (3) in the range of 50–300 K yields J = −8 ± 1 K for both compounds. The magnetization isotherms, M(B), taken at 2 K (Figure 2c) demonstrate upward deviations from the linear dependences, suggesting spin–flop transitions at BSF ≈ 4.7 T and 4.4 T for Li2Ni2TeO6 and K2Ni2TeO6, respectively. Table 3 summarizes the parameters describing the magnetic subsystems of A2Ni2TeO6 (A = Li, K), obtained from the magnetic susceptibility and magnetization measurements.

Table 3.
Parameters describing the magnetic subsystems of A2Ni2TeO6 (A = K, Li) tellurates.
3.1.2. Electron Spin Resonance
Electron spin resonance (ESR) studies were carried out using an X-band ESR spectrometer CMS 8400 (ADANI) (f ≈ 9.4 GHz, B ≤ 0.7 T), equipped with a low-temperature mount, operating in the range of T = 6–300 K. The effective g-factors were calculated using an external reference for the resonance field, i.e., BDPA (a,g-bisdiphenylene-b-phenylallyl), for which get = 2.00359. The ESR data in the paramagnetic phase (T > TN) show a single broad Lorentzian line-shape ascribable to Ni2+ ions in octahedral coordination [28] for both K2Ni2TeO6 and Li2Ni2TeO6 (Supplementary Figure S10). The main ESR parameters (effective g-factor, the ESR linewidth, and the integral ESR intensity) were deduced by fitting the experimental spectra with the Lorentzian profile [29]:
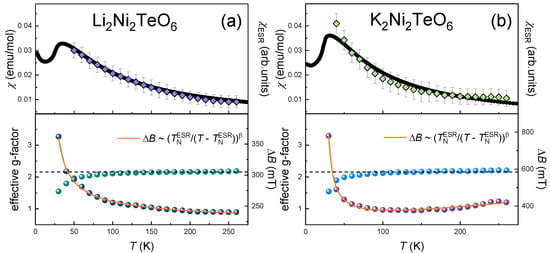
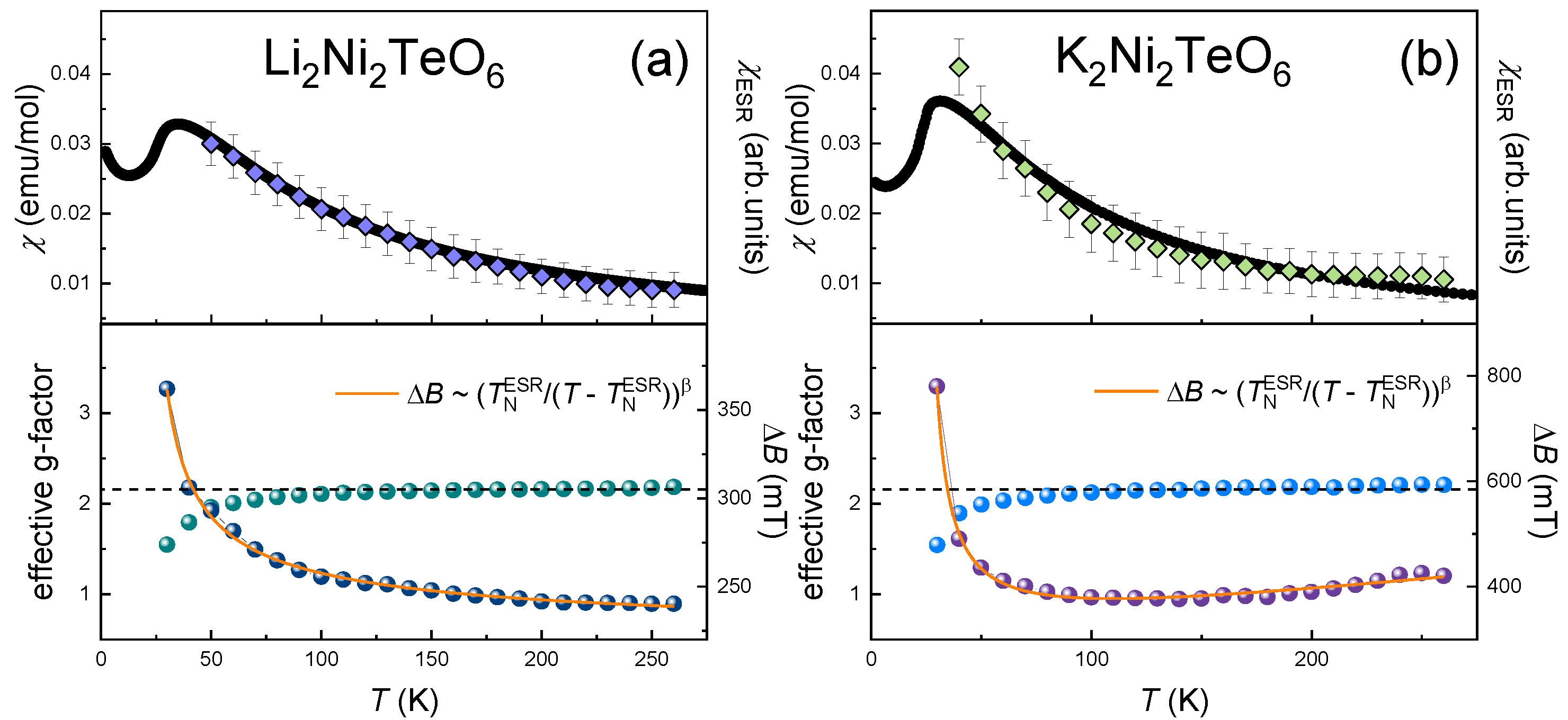
Figure 3.
The temperature dependence of the main ESR parameters of (a) K2Ni2TeO6 and (b) Li2Ni2TeO6 derived from fitting the absorption line with the Lorentzian profile: the integral ESR intensity is shown in the upper panel, and the effective g-factor and the ESR linewidth, ΔB, in the lower panel. The orange solid curves represent an approximation in accordance with a modified Huber theory (Equation (5)), as described in the text for (a), and in the framework of Kawasaki–Mori–Huber theory (Equation (6)) for (b).
The average effective g-factor of 2.20 ± 0.03 remains almost temperature-independent in the paramagnetic phase down to ~100 K (lower panels of Figure 3), and then the visible shift of the resonant field to higher magnetic fields begins upon approaching the Néel temperature from above. This behavior implies the presence of strong short-range correlations at temperatures noticeably higher than TN, which is characteristic of the systems with spin frustration and low dimensionality [29].
The linewidth, ΔB, of K2Ni2TeO6 shows three different dynamic regimes: It decreases weakly and almost linearly on lowering the temperature down to ~150 K, then remains constant down to ~100 K. Upon a further decrease in the temperature, the absorption line broadens significantly and the ESR signal vanishes in the vicinity of the Néel temperature, indicating the opening of an energy gap for resonance excitations, e.g., due to the occurrence of a long-range order. Similar spin dynamics were observed recently for A3Ni2SbO6 (A = Li, Na) with a honeycomb lattice of Ni2+ ions [13]. Following the same procedure, we treated ΔB(T) in the frame of the critical broadening model using the modified Huber’s formula [30,31,32,33] with the third linear term to account for the ΔB(T) behavior over the whole temperature range:
where the first term ΔB* describes the exchange narrowed linewidth, which is temperature-independent. The second term describes the critical behavior, with TNESR as the temperature of the order–disorder transition and β as the critical exponent. The third term relates to the temperature-linear spin-lattice relaxation term. The solid line on the lower panel of Figure 3a represents a least-squares-fitting of ΔB(T). The best fitting was obtained with ΔB* = 290 ± 5 mT, β ≈ 1 ± 0.05, and D = 0.4 mT/K. Clearly, is in good agreement with TN. According to Kawasaki’s approach [25,26], the absolute value of the critical exponent can be expressed as β = [(7 + η)ν/2 − 2(1 − ζ)], where ν describes the divergence of the spin-correlation length, η is a critical exponent for the divergence of static correlations, and ζ reflects the divergence of the specific heat. Using the values η = ζ = 0 and ν = 2/3 for 3D antiferromagnets in the Heisenberg model, β becomes 1/3. Thus, the value of β ≈ 1 extracted for K2Ni2TeO6 is noticeably higher than 1/3 but is still below the value expected for pure 2D antiferromagnets (i.e., β ≈ 3/2) [34,35], but it is quite comparable to the β reported for other related quasi-2D Ni2+ compounds A3Ni2SbO6 (A = Li, Na) [13] and Li4NiTeO6 [36]. According to Kawasaki–Mori–Huber theory, the temperature variation of ΔB of Li2Ni2TeO6 can be described as:
The best agreement by the least square method was obtained with the following parameters: ∆B* = 217 ± 5 mT and β = 0.60 ± 0.05. Thus, the analysis of spin dynamics supports the picture of rather a 2D character of magnetic correlations for both K2Ni2TeO6 and Li2Ni2TeO6. Spin-dynamic parameters of the studied compounds are summarized in Table 4.

Table 4.
The spin-dynamic parameters in A2Ni2TeO6 (A = K and Li) tellurates.
3.1.3. Specific Heat
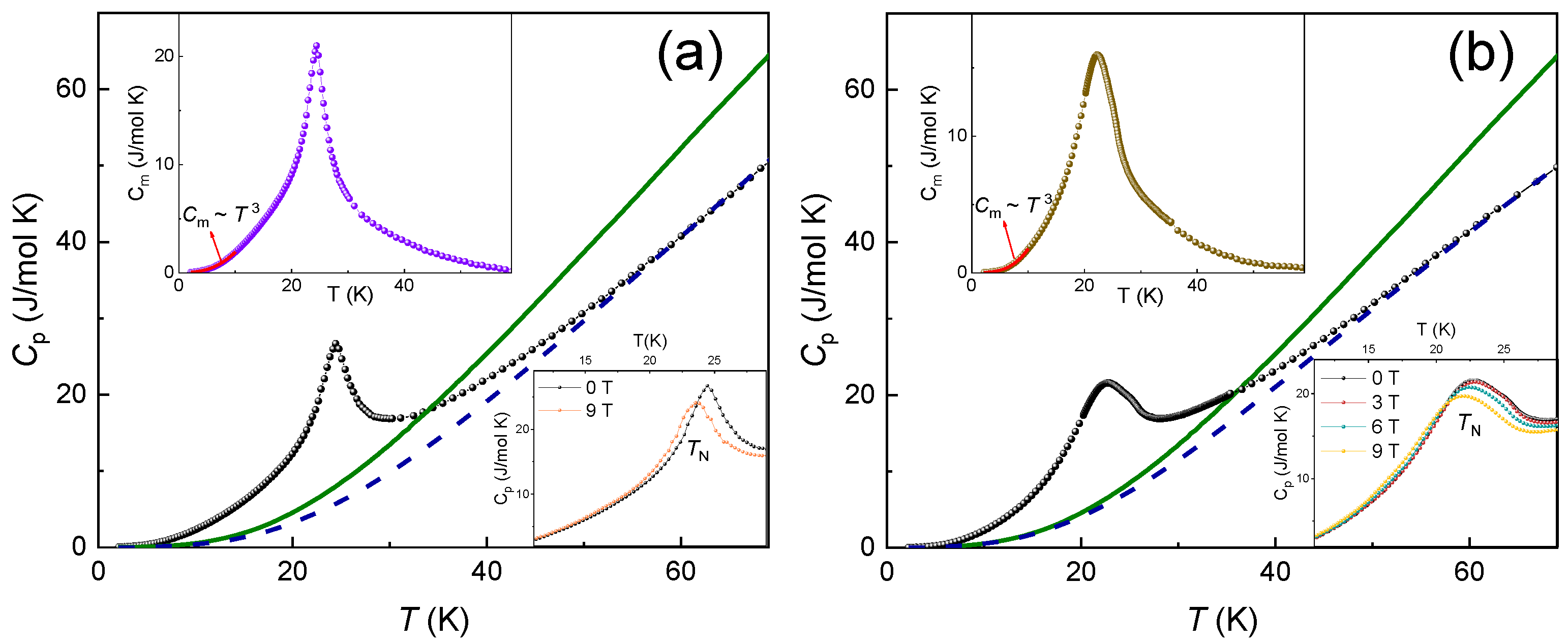
The specific heat, Cp(T), of A2Ni2TeO6 (A = Li, K) has been measured using a relaxation method of a Quantum Design PPMS-9T. The data were collected at the zero magnetic field as well as under applied fields of 3, 6, and 9 T in the temperature range of 2–70 K. The Cp(T) vs. T plots for K2Ni2TeO6 and Li2Ni2TeO6 are shown in Figure 4a,b. A λ-type peak is observed at TN for both K2Ni2TeO6 and A2Ni2TeO6, which clearly shows an occurrence of long-range antiferromagnetic order. These ordering temperatures, TN, coincide with the temperatures at which the peaks of the d(χT)/dT vs. T plot occur (i.e., the Fisher specific heat) [37,38], which is characteristic of low-dimensional antiferromagnets with strong short-range correlations. The positions of TN slightly shift toward the lower temperatures in the applied external magnetic field, as shown in the lower insets in Figure 4a,b, which is typical for antiferromagnetic compounds. To examine the magnetic contribution to specific heat in the title compounds, the Cp(T) curve has been measured for the isostructural non-magnetic system Na2Zn2TeO6. Application of the scaling procedure [39] allows extracting magnetic specific heat, Cm(T), as shown in the upper insets in Figure 4a,b. According to these data, the magnetic entropy, Sm, released below TN is 6.74 and 5.71 J/mol·K for Li- and K-compounds, respectively. These values are to be compared with the thermodynamic limit Sm = nRln(2S + 1) = 18.27 J/mol·K at n = 2 and S = 1, meaning that the dominant part of the magnetic entropy is released above TN.
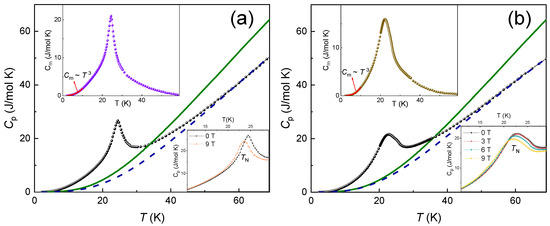
Figure 4.
Temperature dependences of the specific heat in Li2Ni2TeO6 (a) and K2Ni2TeO6 (b). The data for Na2Zn2TeO6 are shown by solid lines. The dashed lines represent the reference curves obtained through the scaling procedure [39]. Lower insets represent Cp(T) curves measured at various magnetic fields. Upper insets represent temperature dependences of magnetic specific heat, Cm.
3.2. Spin Exchanges Leading to a Zigzag Magnetic Order
3.2.1. Computational Details
To extract the values of the spin exchanges in A2Ni2TeO6 (A = K, Li) and Li3Ni2SbO6 (A = Li, Na), we carried out spin-polarized DFT calculations by using the frozen-core projector augmented plane wave met [40,41], encoded in the Vienna ab initio simulation package [42], and the PBE exchange-correlation functionals [43]. The electron correlation associated with the 3d states of Ni was taken into consideration by performing the DFT + U calculations [44] with the effective on-site repulsion Ueff = U − J on magnetic ions. All our DFT calculations used the plane wave cutoff energy of 450 eV and the threshold of 10−6 eV for self-consistent-field energy convergence. To relax the atom positions, DFT + U calculations (with Ueff = 4 eV) were performed using a set of (4 × 6 × 4) k-points with the criterion of 5 × 10−4 eV/Å for the relaxation of the atom positions. Our DFT + U calculations employed a set of (4 × 4 × 4) k-points for Li2Ni2TeO6, (5 × 5 × 3) k-points for K2Ni2TeO6, and (4 × 2 × 4) k-points for Li3Ni2SbO12. As a representative example for the A3Ni2SbO6 (A = Li, Na) family, we examined Li3Ni2SbO12 because Li3Ni2SbO12 is isostructural and isoelectronic with Na3Ni2SbO12, and because A3Ni2SbO6 (A = Li, Na) has already been studied [13]. In our DFT + U calculations, we employed the Ueff values of 3 and 4 eV, which lead to similar trends (see below).
3.2.2. Spin Exchanges and Zigzag Order
The first, second, and third NN intralayer spin exchanges to consider for Li2Ni2TeO6 and Li3Ni2SbO6 are presented in Figure 5a, and those for K2Ni2TeO6 in Figure 5b. We evaluate these spin exchanges by using the energy-mapping analysis based on DFT calculations [15,20,21]. The three spin exchanges of K2Ni2TeO6 (Figure 5b) were determined using the four ordered spin states of Supplementary Figure S3. Similarly, the six intralayer spin exchanges of Li2Ni2TeO6 and Li3Ni2SbO6 (Figure 5a) were determined using the seven ordered spin states of Supplementary Figures S4 and S5, respectively. In the energy-mapping analysis, we determined the relative energies of the ordered spin states by DFT + U calculations (Supplementary Tables S2–S4), expressed the energies of these states in terms of the spin exchanges (Supplementary Tables S5–S7), and finally mapped the relative energies of the DFT + U calculations to the corresponding relative energies expressed in terms of the spin exchanges to find the values of the spin exchanges.
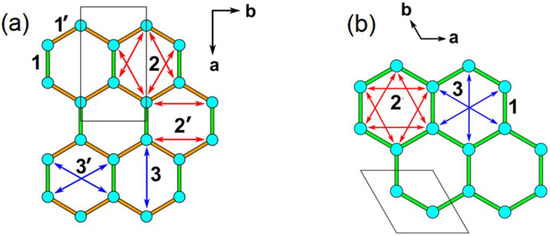
Figure 5.
Intralayer spin exchanges defined for Li2Ni2TeO6 and Li3Ni2SbO6 in (a), and for K2Ni2TeO6 in (b).
The spin exchanges of A2Ni2TeO6 (A = K, Li) and Li3Ni2SbO6 obtained from the energy-mapping analysis are summarized in Table 5 and Table 6, from which we note the following trends: (1) the first NN spin exchanges are all strongly FM, (2) the second NN spin exchanges are all negligible, and (3) the third NN spin exchanges are all strongly AFM. The magnetic order that accommodates these three factors is a zigzag order, as depicted in Figure 1b, which is what has been experimentally observed for A2Ni2TeO6 (A = Li, K) and A3Ni2SbO6 (A = Li, Na) [13,14]. To understand the occurrence of a short-range magnetic order in these materials, one might consider every FM chain of their zigzag-ordered honeycomb lattices as a pseudo-spin unit. Then, each zigzag-ordered honeycomb lattice is equivalent to an AFM uniform chain, so the short-range order of the zigzag-ordered honeycomb lattice becomes equivalent to that of an AFM uniform chain. Namely, the short-range order in the zigzag-ordered honeycomb lattices of A2Ni2TeO6 (A = Li, K) and A3Ni2SbO6 (A = Li, Na) is associated with short-range ordering of the FM chains along the direction perpendicular to the chains.

Table 5.
Experimental Ni…Ni distances (in Å) and calculated spin exchanges (in K), obtained from DFT + U computations, of Li2Ni2TeO6 and Li3Ni2SbO6.

Table 6.
Experimental Ni…Ni distances (in Å) and calculated spin exchanges (in K), obtained from DFT + U computations, of K2Ni2TeO6.
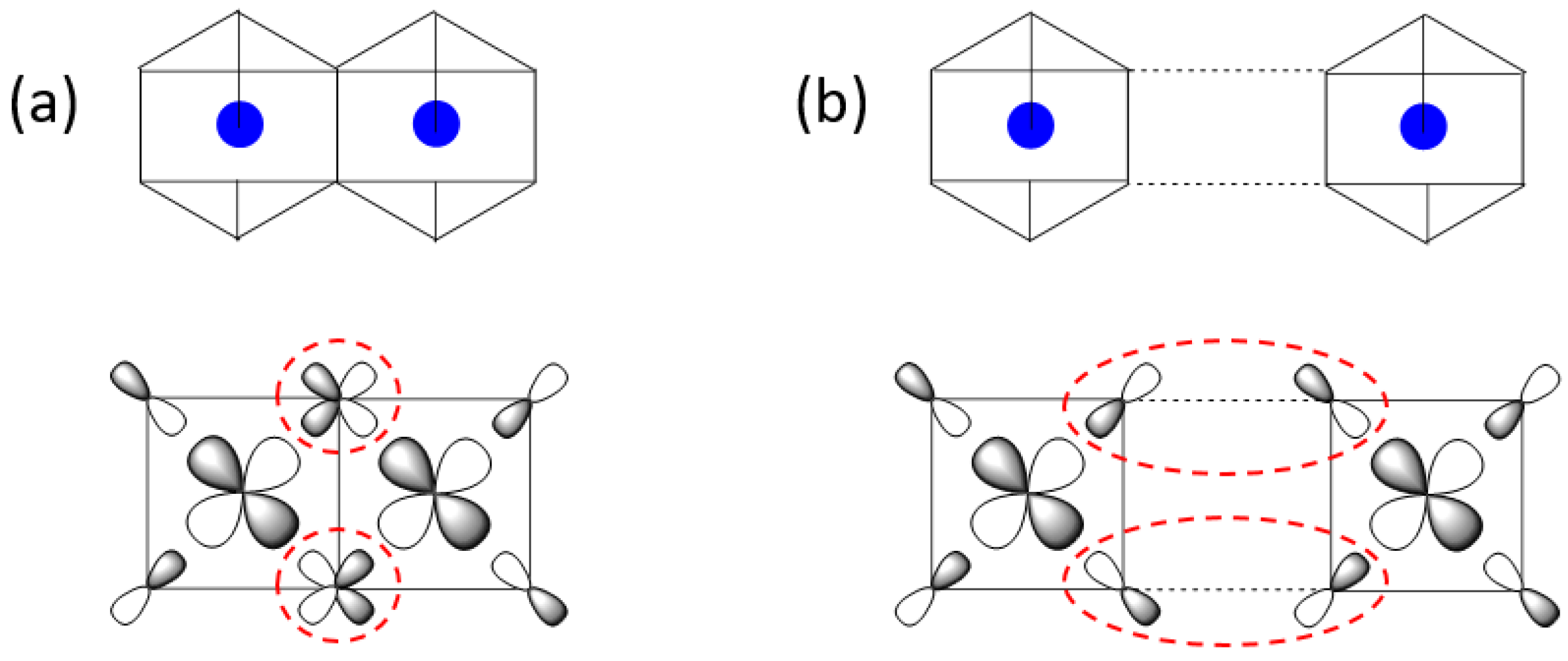
It is of interest to examine why the zigzag order arises in the honeycomb lattices of A2Ni2TeO6 (A = Li, K) and A3Ni2SbO6 (A = Li, Na). The magnetic orbitals of the Ni2+ ion in a NiO6 octahedron are the eg states, namely, the x2 − y2 and 3z2 − r2 states, which are combined out-of-phase with the 2p orbitals of the surrounding oxygen ligands. Of the two, the x2 − y2 state can have a substantial interaction in the first and third NN exchange paths, as depicted in Figure 6a,b, respectively, because the NiO4 square planes containing these orbitals can be coplanar. The first NN exchange consists of two Ni-O-Ni paths, in which the two x2 − y2 states have their p-orbitals orthogonally arranged at the shared oxygen atoms (Figure 6a). Thus, between the two magnetic orbitals, the overlap integral is zero while the overlap density is nonzero. As a result, the first NN exchange becomes FM [15,20,21,45]. The third NN exchange consists of two Ni-O⋅⋅⋅O-Ni paths, in which the p-orbital tails of the two x2 − y2 states are arranged such that the overlap integral is nonzero while the overlap density is practically zero. As a result, the third NN exchange becomes AFM. For the second NN exchange, the NiO4 square planes containing the x2 − y2 states cannot be coplanar (see Supplementary Figure S6). Thus, neither the overlap integral nor the overlap density between the two x2 − y2 states can be substantial, so the second NN exchange is weak.
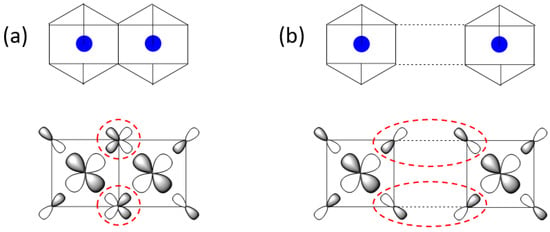
Figure 6.
Arrangement of two x2 − y2 magnetic orbitals (a) in the first NN exchange path and (b) in the third NN exchange path in a honeycomb lattice of magnetic ions. In (a,b), the two magnetic orbitals interact through their p-orbital tails in the circled regions. The NiO6 octahedra are presented to emphasize the square planes containing the x2 − y2 magnetic orbitals.
Finally, we examined the effective interlayer spin exchanges in A2Ni2TeO6 (A = K, Li) and Li3Ni2SbO6. What matters in a long-range magnetic ordering in these systems at low temperature is whether the zigzag-ordered honeycomb layers become ferromagnetically or antiferromagnetically ordered (Supplementary Figures S7–S9). Results of these calculations are summarized in Table 7, which predicts that the honeycomb layers should be ferromagnetically coupled. This is in agreement with the experiment for Li3Ni2SbO6 [13]. The preference for the FM interlayer coupling is much stronger for Li2Ni2TeO6 than for K2Ni2TeO6. This reflects that the interlayer distance is shorter for Li2Ni2TeO6, which strengthens the interlayer interaction. This result is consistent with the observation that the long-range ordering temperature, TN, which involves the ordering between the zigzag-ordered honeycomb layers, is greater for Li2Ni2TeO6 than for K2Ni2TeO6 (~24.4 vs. ~22.8 K).

Table 7.
Relative energies (in K per formula unit), calculated from DFT + U computations, of the FM and AFM arrangements between the zigzag-ordered layers in A2Ni2TeO6 (A = K, Li) and Li3Ni2SbO6.
4. Concluding Remarks
The static magnetic susceptibility along with specific heat data showed the onset of antiferromagnetic order at TN ≈ 22.8 and 24.4 K for K2Ni2TeO6 and Li2Ni2TeO6, respectively, which is preceded by a short-range order. The high-temperature magnetic susceptibility data exhibited Curie–Weiss behavior, with Weiss temperatures Θ of approximately −13 and −20 K for K2Ni2TeO6 and Li2Ni2TeO6, respectively. The effective magnetic moment was estimated to be about 4.46 μB per formula unit and agrees with the theoretical value expected for Ni2+ (S = 1) ions. If we were to describe the high-temperature magnetic portion of the susceptibilities of A2Ni2TeO6 (A = K, Li), they can be described by a honeycomb with spin exchange J ≈ −8 ± 1 K. ESR spectra in the paramagnetic phase showed a single Lorentzian-shaped line, which was attributed to Ni2+ ions at octahedral sites, which were characterized by the isotropic effective g-factor 2.20 ± 0.01. In addition, our ESR data indicated an extended region of short-range order correlations, typical of low-dimensional or frustrated magnets. The intralayer spin exchanges evaluated for A2Ni2TeO6 (A = K, Li) and Li3Ni2SbO6 showed that the honeycomb layers of these magnets adopted a zigzag order, largely because the third nearest-neighbor spin exchanges are strongly antiferromagnetic and because the first nearest-neighbor spin exchanges are strongly ferromagnetic. This finding arises largely from the fact that the spin exchanges between adjacent Ni2+ ions are governed largely by their x2 − y2 magnetic orbitals. Adjacent zigzag-ordered honeycomb layers prefer to be ferromagnetically than antiferromagnetically coupled. The short-range order of the zigzag-ordered honeycomb lattice is equivalent to that of an antiferromagnetic uniform chain, and arises from the short-range ordering of the ferromagnetic chains along the direction perpendicular to the zigzag chains.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/ma15072563/s1, Section S1 on the crystal structure of A2Ni2TeO6, Section S2 on the intralayer spin exchanges, and Section S3 on the intralayer spin exchanges. It includes Figures S1–S10 and Tables S1–S7. References [16,22,46] are cited in the supplementary materials.
Author Contributions
Conceptualization, A.V. and M.-H.W.; methodology, V.N.; formal analysis, J.-S.L. and H.-J.K.; investigation, T.V. and M.E.; writing—original draft preparation, V.N. and M.-H.W.; writing—review and editing, A.V. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the grant 14-03-01122 from the Russian Foundation for Basic Research (VBN), by the Russian Scientific Foundation through Grant No. 22-42-08002, and by the Mega-grant program of the Government of Russian Federation through the project 075-15-2021-604. The work at KHU was financially supported by the Basic Science Research Program through the National Research Foundation (NRF) of Korea, which was funded by the Ministry of Education (2020R1A6A1A03048004).
Data Availability Statement
The original data are available on the request.
Conflicts of Interest
No conflicts of interests are declared.
References
- Vasiliev, A.; Volkova, O.; Zvereva, E.; Markina, M. Milestones of low-D quantum magnetism. NPG Quantum Mater. 2018, 3, 18–30. [Google Scholar] [CrossRef]
- Kitaev, A. Anyons in an exactly solved model and beyond. Ann. Phys. 2006, 321, 2–111. [Google Scholar] [CrossRef]
- Singh, Y.; Manni, S.; Reuther, J.; Berlijn, T.; Thomale, R.; Ku, W.; Trebst, S.; Gegenwart, P. Relevance of the Heisenberg-Kitaev model for the honeycomb lattice iridates A2IrO7. Phys. Rev. Lett. 2012, 108, 127203. [Google Scholar] [CrossRef] [PubMed]
- Stavropoulos, P.P.; Pereira, D.; Kee, H.Y. Microscopic mechanism for a higher-spin Kitaev Model. Phys. Rev. Lett. 2019, 123, 037203. [Google Scholar] [CrossRef]
- Singh, Y.; Gegenwart, P. Antiferromagnetic Mott insulating state in single crystals of the honeycomb lattice material Na2IrO3. Phys. Rev. B 2010, 82, 064412. [Google Scholar] [CrossRef]
- Ye, F.; Chi, S.; Cao, H.; Chakoumakos, B.C.; Fernandez-Baca, J.A.; Custelceanu, R.; Qi, T.F.; Korneta, O.B.; Cao, G. Direct evidence of a zigzag spin-chain structure in the honeycomb lattice: A neutron and x-ray diffraction investigation of single-crystal Na2IrO3. Phys. Rev. B 2012, 85, 180403. [Google Scholar] [CrossRef]
- Liu, X.; Berlijn, T.; Yin, W.-G.; Ku, W.; Tsvelik, A.; Kim, Y.J.; Gretarsson, H.; Singh, Y.; Gegenwart, P.; Hill, J.P. Long-range magnetic ordering in Na2IrO3. Phys. Rev. B 2011, 83, 220403. [Google Scholar] [CrossRef]
- Sandilands, L.J.; Tian, Y.; Plumb, K.W.; Kim, Y.J.; Burch, K.S. Scattering Continuum and Possible Fractionalized Excitations in α-RuCl3. Phys. Rev. Lett. 2015, 114, 147201. [Google Scholar] [CrossRef]
- Sears, J.A.; Songvilay, M.K.; Plumb, W.; Clancy, J.P.; Qiu, Y.; Zhao, Y.; Parshall, D.; Kim, Y.J. Magnetic order in α-RuCl3: A honeycomb-lattice quantum magnet with strong spin-orbit coupling. Phys. Rev. B 2015, 91, 144420. [Google Scholar] [CrossRef]
- Kasahara, Y.; Ohnishi, T.; Mizukami, Y.; Tanaka, O.; Ma, S.; Sugii, K.; Kurita, N.; Tanaka, H.; Nasu, J.; Motome, Y.; et al. Majorana quantization and half-integer thermal quantum Hall effect in a Kitaev spin liquid. Nature 2018, 559, 227–231. [Google Scholar] [CrossRef]
- Takayama, T.; Kato, A.; Dinnebier, R.; Nuss, J.; Kono, H.; Veiga, L.S.I.; Fabbris, G.; Haskel, D.; Takagi, H. Hyperhoneycomb Iridate β-Li2IrO3 as a platform for Kitaev magnetism. Phys. Rev. Lett. 2015, 114, 077202. [Google Scholar] [CrossRef] [PubMed]
- Katukuri, V.M.; Yadav, R.; Hozoi, L.; Nishimoto, S.; van den Brink, J. The vicinity of hyper-honeycomb β-Li2IrO3 to a three-dimensional Kitaev spin liquid state. Sci. Rep. 2016, 6, 29585. [Google Scholar] [CrossRef]
- Zvereva, E.A.; Stratan, M.I.; Ovchenkov, Y.A.; Nalbandyan, V.B.; Lin, J.-Y.; Vavilova, E.L.; Iakovleva, M.F.; Abdel-Hafiez, M.; Silhanek, A.V.; Chen, X.-J.; et al. Zigzag antiferromagnetic quantum ground state in monoclinic honeycomb lattice antimonates A3Ni2SbO6 (A = Li, Na). Phys. Rev. B 2015, 92, 144401. [Google Scholar] [CrossRef]
- Kurbakov, A.I.; Korshunov, A.N.; Podchezertsev, S.Y.; Malyshev, A.L.; Evstigneeva, M.A.; Damay, F.; Park, J.; Koo, C.; Klingeler, R.; Zvereva, E.A.; et al. Zigzag spin structure in layered honeycomb Li3Ni2SbO6: A combined diffraction and antiferromagnetic resonance study. Phys. Rev. B 2017, 96, 024417. [Google Scholar] [CrossRef]
- Koo, H.-J.; Kremer, R.; Whangbo, M.-H. Unusual Spin Exchanges Mediated by the Molecular Anion P2S64−: Theoretical Analyses of the Magnetic Ground States, Magnetic Anisotropy and Spin Exchanges of MPS3 (M = Mn, Fe, Co, Ni). Molecules 2021, 26, 1410. [Google Scholar] [CrossRef]
- Powder Diffraction File; International Centre for Diffraction Data: Newtown Square, PA, USA, 2009; entry 00-059-0445.
- Grundish, N.S.; Seymour, I.D.; Henkelman, G.; Goodenough, J.B. Electrochemical Properties of Three Li2Ni2TeO6 Structural Polymorphs. Chem. Mater. 2019, 31, 9379–9388. [Google Scholar] [CrossRef]
- Masese, T.; Yoshii, K.; Yamaguchi, Y.; Okumura, T.; Huang, Z.-D.; Kato, M.; Kubota, K.; Furutani, J.; Orikasa, Y.; Senoh, H.; et al. Rechargeable potassium-ion batteries with honeycomb-layered tellurates as high voltage cathodes and fast potassium-ion conductors. Nat. Comm. 2018, 9, 3823–3835. [Google Scholar] [CrossRef]
- Matsubara, N.; Nocerino, E.; Forslund, O.K.; Zubayer, A.; Papadopoulos, K.; Andreica, D.; Sugiyama, J.; Palm, R.; Guguchia, Z.; Cottrell, S.P.; et al. Magnetism and ion diffusion in honeycomb layered oxide K2Ni2TeO6. Sci. Rep. 2020, 10, 18305–18318. [Google Scholar] [CrossRef]
- Xiang, H.J.; Lee, C.; Koo, H.-J.; Gong, X.; Whangbo, M.-H. Magnetic properties and energy-mapping analysis. Dalton Trans. 2013, 42, 823–853. [Google Scholar] [CrossRef]
- Whangbo, M.-H.; Xiang, H.J. Magnetic Properties from the Perspectives of Electronic Hamiltonian: Spin Exchange Parameters, Spin Orientation and Spin-Half Misconception. In Handbook in Solid State Chemistry, Volume 5: Theoretical Descriptions; Wiley: Hoboken, NJ, USA, 2017; pp. 285–343. [Google Scholar]
- Evstigneeva, M.A.; Nalbandyan, V.B.; Petrenko, A.A.; Medvedev, B.S.; Kataev, A.A. A New Family of Fast Sodium Ion Conductors: Na2M2TeO6 (M = Ni, Co, Zn, Mg). Chem. Mater. 2011, 23, 1174–1181. [Google Scholar] [CrossRef]
- Paulsen, J.M.; Donaberger, R.A.; Dahn, J.R. Layered T2-, O6-, O2-, and P2-Type A2/3[M’2+1/3M4+2/3]O2 Bronzes, A = Li, Na; M’ = Ni, Mg; M = Mn, Ti. Chem. Mater. 2000, 12, 2257–2267. [Google Scholar] [CrossRef]
- Shannon, R. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Cryst. 1976, A32, 751–767. [Google Scholar] [CrossRef]
- Gagné, O.; Hawthorne, F. Comprehensive derivation of bond-valence parameters for ion pairs involving oxygen. Acta Cryst. 2015, B71, 562–578. [Google Scholar] [CrossRef] [PubMed]
- Bain, G.A.; Berry, J.F. Diamagnetic Corrections and Pascal’s Constants. J. Chem. Educ. 2008, 85, 532–536. [Google Scholar] [CrossRef]
- Rushbrook, G.S.; Wood, P.J. On the Curie points and high temperature susceptibilities of Heisenberg model ferromagnetics. Mol. Phys. 1958, 1, 257–283. [Google Scholar] [CrossRef]
- Abragam, A.; Bleaney, B. Electron Paramagnetic Resonance of Transition Ions; Clarendon Press: Oxford, UK, 1970; 700p. [Google Scholar]
- Joshi, J.P.; Bhat, S.V. On the analysis of broad Dysonian electron paramagnetic resonance spectra. J. Magn. Reson. 2004, 168, 284–287. [Google Scholar] [CrossRef]
- Kawasaki, K. Anomalous Spin Relaxation near the Magnetic Transition. Prog. Theor. Phys. 1968, 39, 285–311. [Google Scholar] [CrossRef][Green Version]
- Kawasaki, K. Ultrasonic attenuation and ESR linewidth near magnetic critical points. Phys. Lett. A 1968, 26A, 543. [Google Scholar] [CrossRef]
- Mori, H.; Kawasaki, K. Antiferromagnetic Resonance Absorbtion. Prog. Theor. Phys. 1962, 28, 971–987. [Google Scholar] [CrossRef]
- Huber, D.L. Critical-Point Anomalies in the Electron-Paramagnetic-Resonance Linewidth and in the Zero-Field Relaxation Time of Antiferromagnets. Phys. Rev. B 1972, 6, 3180–3186. [Google Scholar] [CrossRef]
- Richards, P.M. Critical exponents for NMR and ESR linewidths in a two-dimensional antiferromagnet. Solid State Commun. 1973, 13, 253–256. [Google Scholar] [CrossRef]
- Anders, A.G.; Volotski, S.V. EPR in 1-d and 2-d antiferromagnetic systems. J. Magn. Magn. Mater. 1983, 31–34, 1169–1170. [Google Scholar] [CrossRef]
- Zvereva, E.A.; Savelieva, O.A.; Titov, Y.D.; Evstigneeva, M.A.; Nalbandyan, V.B.; Kao, C.N.; Lin, J.-Y.; Presniakov, I.A.; Sobolev, A.V.; Ibragimov, S.A.; et al. A new layered triangular antiferromagnet Li4FeSbO6: Spin order, field-induced transitions and anomalous critical behavior. Dalton Trans. 2013, 42, 1550–1566. [Google Scholar] [CrossRef] [PubMed]
- Fisher, M.E. Lattice statistics in a magnetic field, I. A two-dimensional super-exchange antiferromagnet. Proc. R. Soc. Lond. Ser. A 1960, 254, 66–85. [Google Scholar]
- Fisher, M.E. Relation between the specific heat and susceptibility of an antiferromagnet. Philos. Mag. 1962, 7, 1731–1743. [Google Scholar] [CrossRef]
- Losee, D.B.; McElearney, J.N.; Shankle, G.E.; Carlin, R.L.; Cresswell, P.J.; Robinson, W.T. An anisotropic low-dimensiomal Izing system, [(CH3)3NH]CoCl32H2O: Its structure and canted antiferromagnetic behavior. Phys. Rev. B 1973, 8, 2185–2199. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Dudarev, S.L.; Botton, G.A.; Savrasov, S.Y.; Humphreys, C.J.; Sutton, A.P. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study. Phys. Rev. B 1998, 57, 1505. [Google Scholar] [CrossRef]
- Whangbo, M.-H.; Koo, H.-J.; Kremer, R.K. Spin Exchanges between Transition Metal Ions Governed by the Ligand p-Orbitals in Their Magnetic Orbitals. Molecules 2021, 26, 531. [Google Scholar] [CrossRef] [PubMed]
- Sudorgin, N.G.; Nalbandyan, V.B. Quantitative X-ray monitoring of electrode processes in sealed cells. Reduction of zirconium β-molybdate by lithium. Soviet Electrochem. 1992, 28, 100–102. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).