Influence of Process Parameters on the Height and Performance of Magnesium Alloy AZ91D Internal Thread by Assisted Heating Extrusion
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Experimental Method
3. Determination of Experimental Conditions
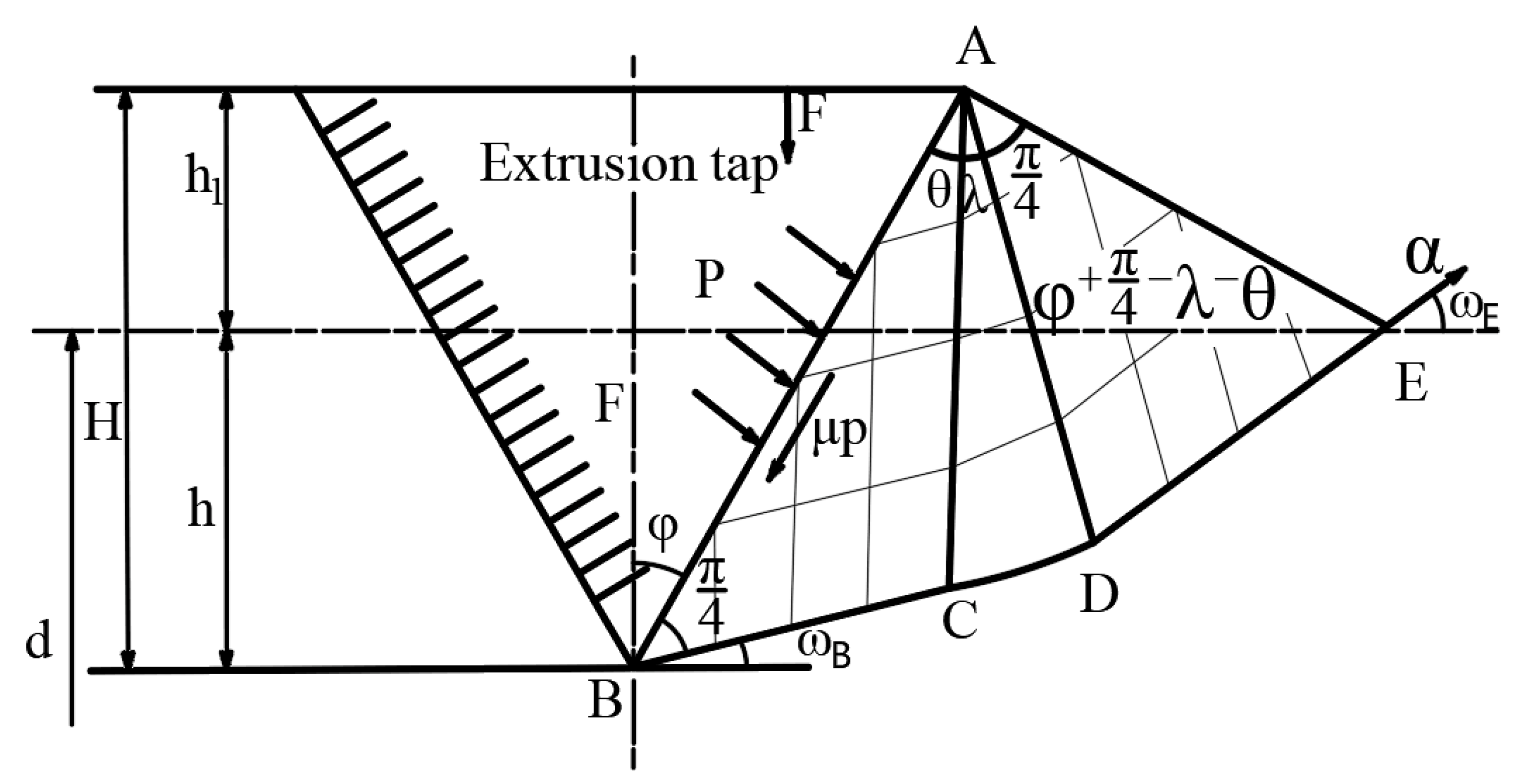
3.1. Auxiliary Heating Temperature
Equivalent Stress and Strain in Forming Process
3.2. Hole Diameter
3.3. Machine Tool Speed
4. Determination of Experimental Conditions
4.1. Response Surface Modeling Method
4.2. Box-Behnken Experimental Design Method
4.3. Establish Regression Model
5. Results and Discussion
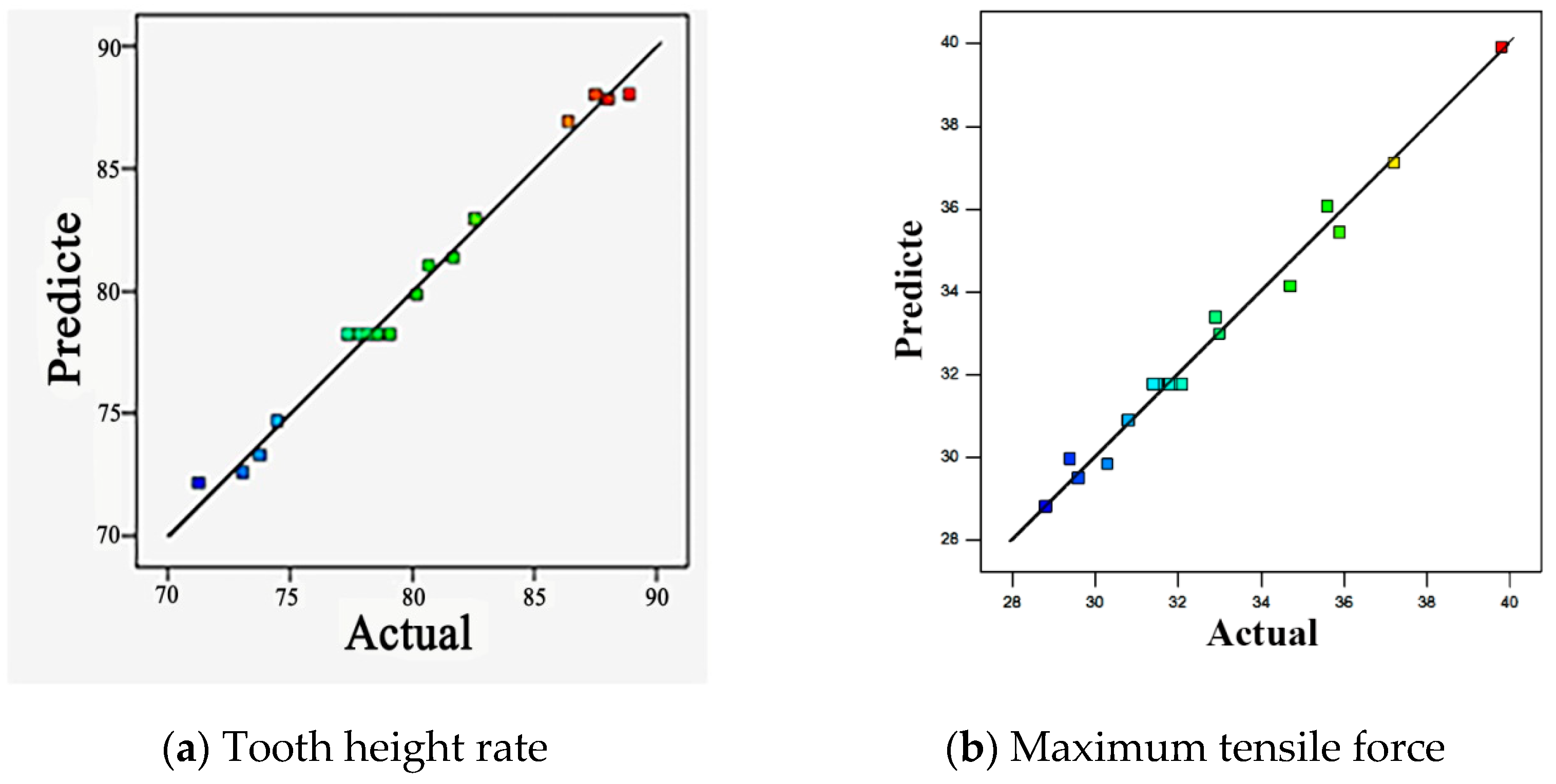
5.1. Regression Model
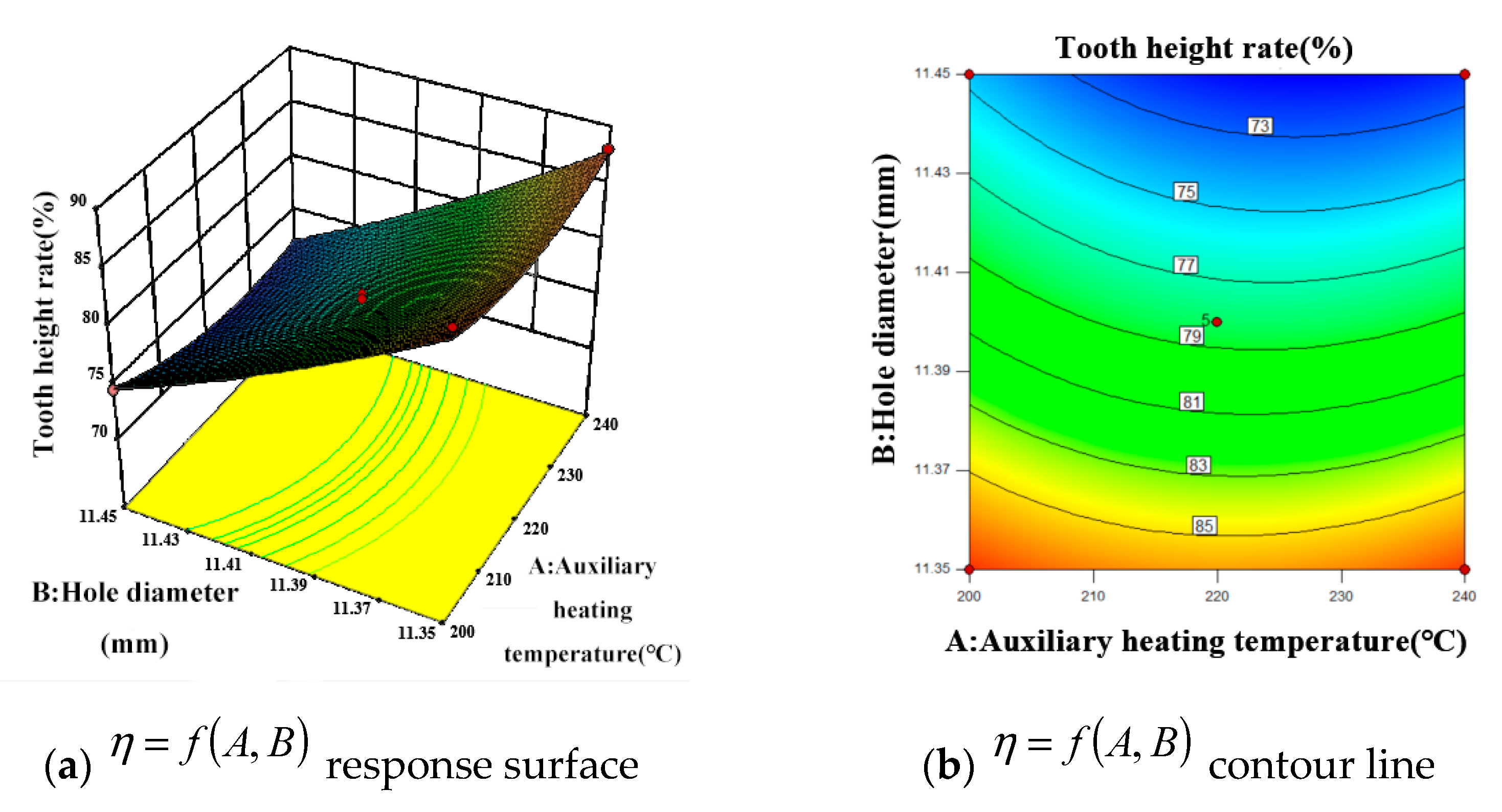
5.2. Response Surface Analysis
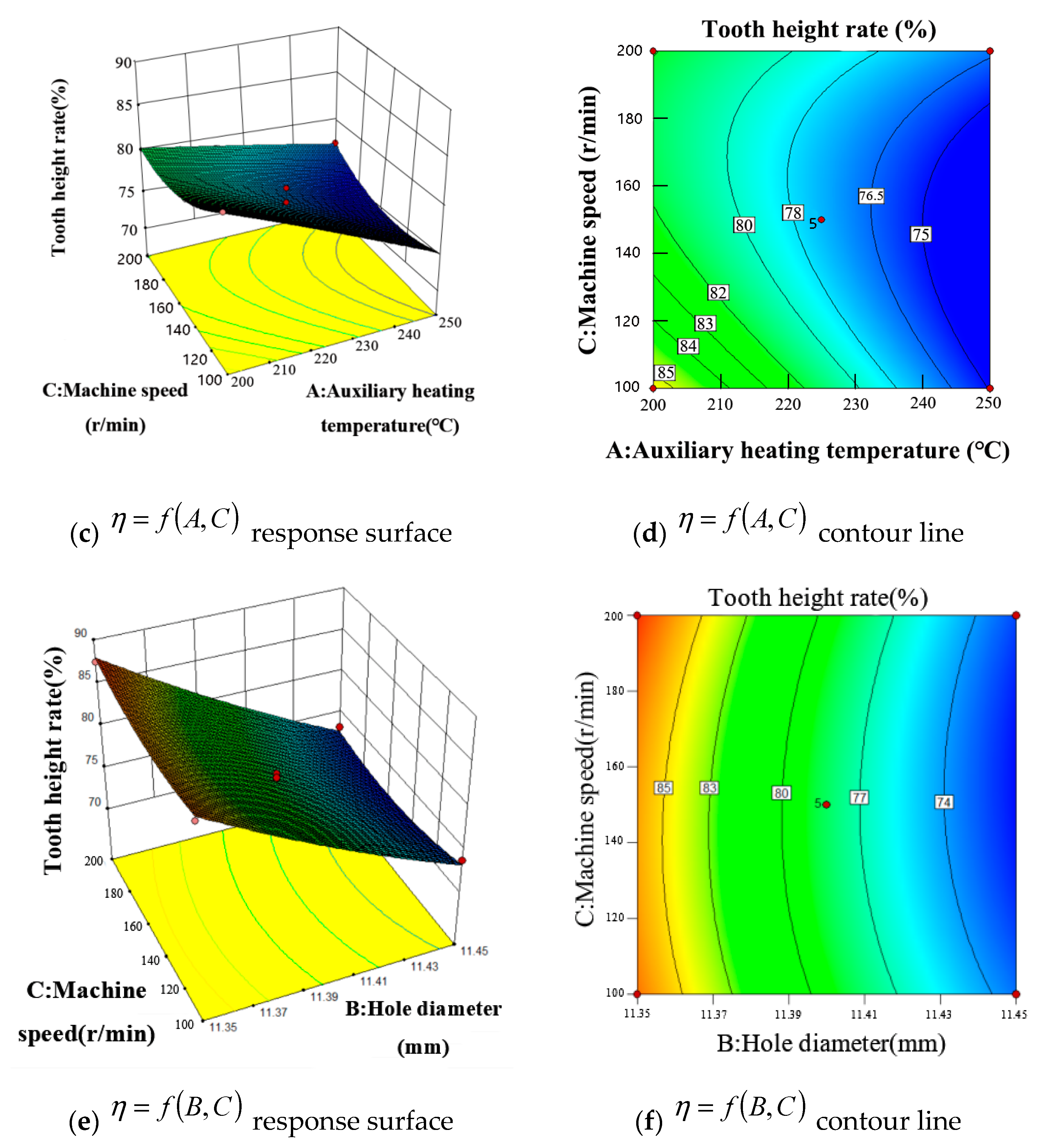
5.2.1. Tooth Height Rate
5.2.2. Maximum Tensile Force
5.3. Optimization Results and Verification
5.4. Optimized Thread Morphology
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Korin, I.; Ipina, J.P. Experimental evaluation of fatigue life and fatigue crack growth in a tension bolt-nut threaded connection. Int. J. Fatigue 2011, 33, 166–175. [Google Scholar] [CrossRef]
- Lauderbaugh, L.K. Analysis of the effects of process parameters on exit burrs in drilling using a combined simulation and experimental approach. J. Mater. Process. Technol. 2009, 209, 1909–1919. [Google Scholar] [CrossRef]
- Aghion, E.; Bronfin, B.; Eliezer, D. The role of the magnesium industry in protecting the environment. J. Mater. Process. Technol. 2001, 117, 381–385. [Google Scholar] [CrossRef]
- Liu, M.; Ji, Z.; Fan, R.; Wang, X. Finite Element Analysis of Extrusion Process for Magnesium Alloy Internal Threads with Electromagnetic Induction-Assisted Heating and Thread Performance Research. Materials 2020, 13, 2170. [Google Scholar] [CrossRef]
- Xu, J.H.; Wang, M.; Jin, W.L. Study on cold extrusion of 300M steel internal thread. Acta Aeronaut. Et Astronaut. Sin. 1993, 10, 557–559. [Google Scholar]
- Xu, J.H.; Wang, M. Research on cold extrusion strengthening of internal thread in high strength steel. J. Mater. Eng. 2000, 4, 41–44. [Google Scholar]
- Miao, H.; Zuo, D.W.; Zhang, R.H. Cold extrusion test of internal thread of Q460 high strength steel. J. Mech. Eng. 2011, 47, 160–166. [Google Scholar] [CrossRef]
- Bierla, A.; Fromentin, G.; Martin, J.M.; Le Mogne, T.; Genet, N. Tribological aspect of lubrication in form tapping of high-strength steel. Lubr. Sci. 2008, 20, 269–281. [Google Scholar] [CrossRef] [Green Version]
- Stéphan, P.; Mathurin, F.; Guillot, J. Analytical study of maximal tapping torque during forming screw process. J. Mater. Process. Technol. 2011, 211, 212–221. [Google Scholar] [CrossRef]
- Stéphan, P.; Mathurin, F.; Guillot, J. Experimental study of forming and tightening processes with thread forming screws. J. Mater. Process. Technol. 2012, 212, 766–775. [Google Scholar] [CrossRef]
- Bierla, A.; Fromentin, G.; Minfray, C.; Martin, J.M.; Le Mogne, T.; Genet, N. Mechanical and physico-chemical study of sulfur additives effect in milling of high strength steel. Wear 2012, 286, 116–123. [Google Scholar] [CrossRef] [Green Version]
- Fromentin, G.; Poulachon, G.; Moisan, A.; Julien, B.; Giessler, J. Precision and surface integrity of threads obtained by form tapping. CIRP Ann. 2005, 54, 519–522. [Google Scholar] [CrossRef]
- Tang, L.L.; Zhao, L.P. Study on the influence of workpiece thickness on cold extrusion molding of internal thread. Mech. Eng. Autom. 2019, 6, 152–153. [Google Scholar]
- Pereira, I.C.; Silva, M. Study of the internal thread process with cut and form taps according to secondary characteristics of the process. Int. J. Adv. Manuf. Technol. 2017, 93, 2357–2368. [Google Scholar] [CrossRef]
- Ribeiro Filho, M.; Luiz, S.; de Oliveira, J.A.; Arruda, E.M.; Brandao, L.C. Analysis of burr formation in form tapping in 7075 aluminum alloy. Int. J. Adv. Manuf. Technol. 2016, 84, 957–967. [Google Scholar] [CrossRef]
- De Carvalho, A.O.; Brandão, L.C.; Panzera, T.H.; Lauro, C.H. Analysis of form threads using fluteless taps in cast magnesium alloy (AM60). J. Mater. Process. Technol. 2012, 212, 1753–1760. [Google Scholar] [CrossRef] [Green Version]
- Chen, B.L. Optimization Theory and Algorithm, 2nd ed.; Tsinghua University Press: Beijing, China, 2005. [Google Scholar]
- Li, X.; Jia, R.; Li, P.; Ang, S. Response surface analysis for enzymatic decolorization of Congo red by manganese peroxidase. J. Mol. Catal. B Enzym. 2009, 56, 1–6. [Google Scholar] [CrossRef]
- Hill, W.J.; Hunter, W.G. A review of response surface methodology: A literature survey. Technometrics 1966, 8, 571–590. [Google Scholar] [CrossRef]
- Huang, D.N.; Wu, N.; Dong, R.F. Optimization of extrusion mold structure for AZ91D magnesium alloy radiator profiles. Forg. Stamp. Technol. 2019, 44, 131–138. [Google Scholar]
- Chen, Z.H.; Xia, W.J.; Yan, H.G. Principles and Technologies of Plastic Deformation for Magnesium Alloys. Chem. Ind. Eng. Prog. 2004, 23, 127–135. [Google Scholar]
- Mathurin, F.; Guillot, J.; Stéphan, P.; Daidié, A. 3D Finite Element Modeling of an Assembly Process With Thread Forming Screw. J. Manuf. Sci. Eng. 2009, 131, 4. [Google Scholar] [CrossRef]
- Challen, J.M. Plastic Deformation of a Metal Surface in Sliding Contact with a Hard Wedge: Its Relation to Friction and Wear. Proc. R. Soc. A Math. 1984, 394, 161–181. [Google Scholar]
- Roux, W.J.; Stander, N.; Haftka, R.T. Response surface approximations for structural optimization. Int. J. Numer. Methods Eng. 2015, 42, 517–534. [Google Scholar] [CrossRef]
- Da-gang, L.U.; Ming-ming, J.I.A.; Gang, L. Uniform design pesponse surface method for structural reliability analysis. Eng. Mech. 2011, 28, 109–116. [Google Scholar]
- Kaymaz, I.; Mcmahon, C.A. A response surface method based on weighted regression for structural reliability analysis. Probab. Eng. Mech. 2005, 20, 11–17. [Google Scholar] [CrossRef]
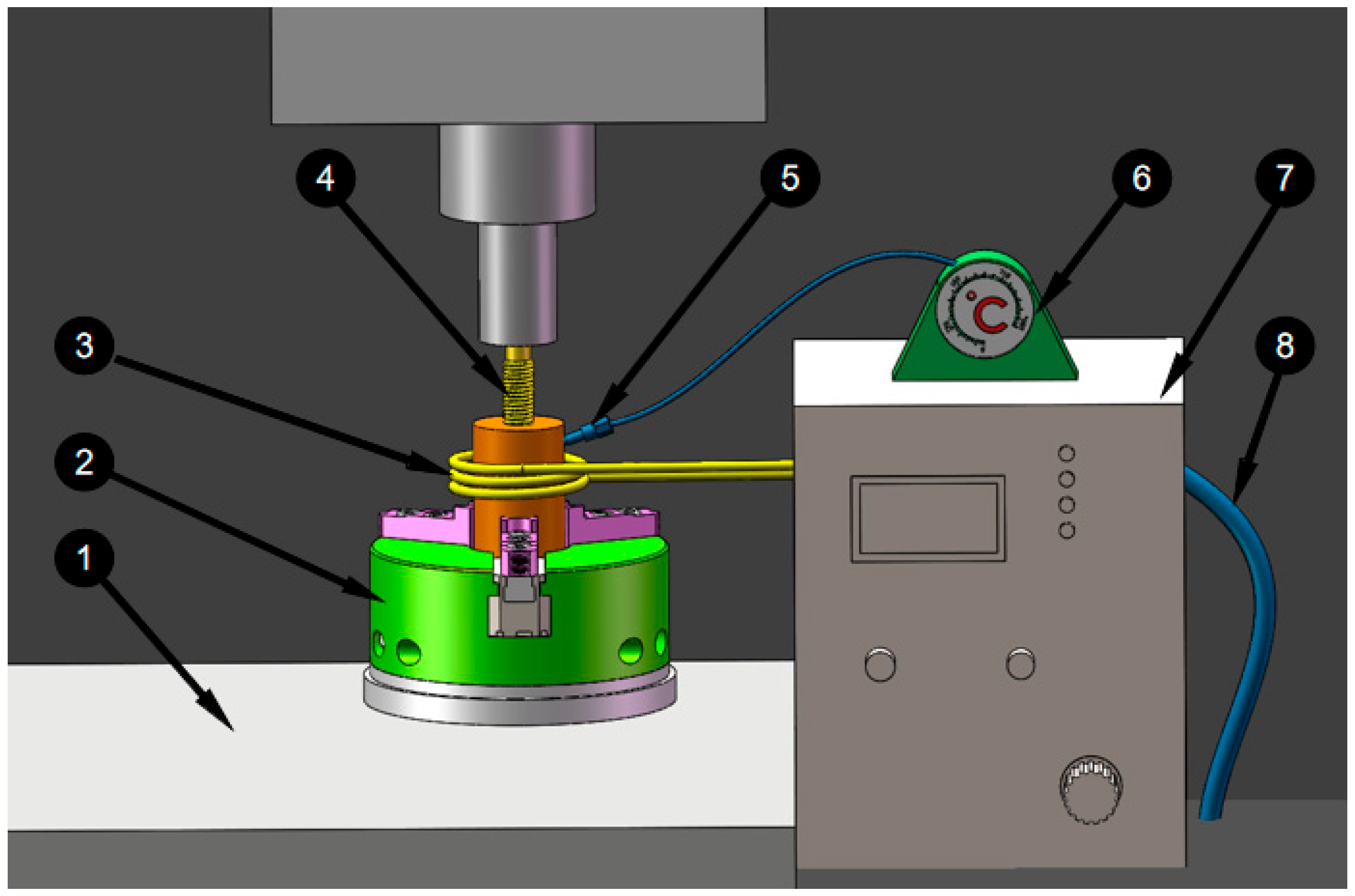




| Al | Zn | Mn | Si | Cu | Ni | Fe | Mg |
|---|---|---|---|---|---|---|---|
| 8.5–9.5 | 0.45–0.90 | 0.17–0.4 | ≤0.05 | ≤0.025 | ≤0.001 | ≤0.004 | Bal. |
| h | 0.43 | 0.41 | 0.38 | 0.37 | 0.35 | 0.33 | 0.30 | 0.26 |
| H | 1.08 | 1.03 | 0.97 | 0.92 | 0.87 | 0.81 | 0.76 | 0.65 |
| d | 11.14 | 11.18 | 11.24 | 11.26 | 11.30 | 11.34 | 11.40 | 11.48 |
| Factor | Level | ||
|---|---|---|---|
| −1 | 0 | 1 | |
| A: Auxiliary heating temperature/°C | 200 | 220 | 240 |
| B: Hole diameter/mm | 11.35 | 11.40 | 11.45 |
| C: Machine tool speed/(r/min) | 100 | 150 | 200 |
| Serial Number | Auxiliary Heating Temperature °C | Hole Diameter [mm] | Machine Tool Speed [r/min] | ||
|---|---|---|---|---|---|
| 1 | 1 (240) | −1 (11.35) | 0 (150) | 73.1 | 29.4 |
| 2 | 0 (220) | 0 (11.40) | 0 (150) | 88.9 | 37.6 |
| 3 | 0 (220) | 0 (11.40) | 0 (150) | 80.7 | 35.6 |
| 4 | −1 (200) | 1 (11.45) | 0 (150) | 77.9 | 31.4 |
| 5 | 0 (220) | 1 (11.45) | −1 (100) | 81.7 | 31.8 |
| 6 | −1 (200) | −1 (11.35) | 0 (150) | 88.0 | 38.8 |
| 7 | 1 (240) | 0 (11.40) | −1 (100) | 78.6 | 31.8 |
| 8 | 1 (240) | 1 (11.45) | 0 (150) | 87.5 | 33.0 |
| 9 | 0 (220) | −1 (11.35) | −1 (100) | 86.4 | 34.7 |
| 10 | 1 (240) | 0 (11.40) | 1 (200) | 78.2 | 32.0 |
| 11 | 0 (220) | 0 (11.40) | 0 (150) | 71.3 | 26.9 |
| 12 | 0 (220) | 0 (11.40) | 0 (150) | 82.6 | 37.2 |
| 13 | 0 (220) | 0 (11.40) | 0 (150) | 74.5 | 28.9 |
| 14 | 0 (220) | −1 (11.35) | 1 (200) | 77.4 | 32.1 |
| 15 | −1 (200) | 0 (11.40) | 1 (200) | 80.2 | 30.3 |
| 16 | 0 (220) | 1 (11.45) | 1 (200) | 82.1 | 32.9 |
| 17 | −1 (200) | 0 (11.40) | −1 (100) | 79.1 | 30.5 |
| Type | Tooth Height Rate | Maximum Tensile Force | ||||||
|---|---|---|---|---|---|---|---|---|
| Sum of Spuares | F | p | Significance | Sum of Spuares | F | p | Significance | |
| Model | 455.06 | 75.23 | <0.0001 | ** | 141.34 | 57.27 | <0.0001 | ** |
| A | 3.78 | 5.63 | 0.0495 | * | 77.50 | 282.63 | <0.0001 | ** |
| B | 421.95 | 627.84 | <0.0001 | ** | 34.86 | 127.13 | <0.0001 | ** |
| C | 0.080 | 0.12 | 0.7402 | 0.000 | 0.000 | 1.0000 | ||
| AB | 1.32 | 1.97 | 0.2034 | 0.090 | 0.33 | 0.5846 | ||
| AC | 2.89 | 4.30 | 0.0768 | 1.10 | 4.02 | 0.0850 | ||
| BC | 0.81 | 1.21 | 0.3086 | 1.32 | 4.82 | 0.0641 | ||
| A2 | 13.15 | 19.57 | 0.0031 | ** | 24.15 | 88.08 | <0.0001 | ** |
| B2 | 1.88 | 2.79 | 0.1387 | 0.66 | 2.40 | 0.1656 | ||
| C2 | 7.03 | 10.47 | 0.0143 | * | 1.95 | 7.10 | 0.0323 | * |
| Lack of fit | 4.70 | 2.37 | 0.2111 | Not significant | 1.92 | 5.55 | 0.0657 | Not significant |
| 3.01 | 0.9898 | 1.55 | 0.9866 | |||||
| 1.69 | 0.9766 | 0.37 | 0.9694 | |||||
| CV/% | 1.02 | 1.60 | ||||||
| Auxiliary Heating Temperature [°C] | Hole Diameter /mm | Machine Tool Speed [r/min] | Tooth Height Rate [%] | Maximum Tensile Force [KN] | |
|---|---|---|---|---|---|
| Optimal design variable (Forecast) | 200 | 11.35 | 198.349 | 90.741 | |
| 200 | 11.35 | 186.307 | 39.901 | ||
| Modified design variable (Actual) | 200 | 11.35 | 200 | 89.056 | 38.824 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Ji, Z.; Bao, L.; Li, X. Influence of Process Parameters on the Height and Performance of Magnesium Alloy AZ91D Internal Thread by Assisted Heating Extrusion. Materials 2022, 15, 2747. https://doi.org/10.3390/ma15082747
Liu M, Ji Z, Bao L, Li X. Influence of Process Parameters on the Height and Performance of Magnesium Alloy AZ91D Internal Thread by Assisted Heating Extrusion. Materials. 2022; 15(8):2747. https://doi.org/10.3390/ma15082747
Chicago/Turabian StyleLiu, Meng, Zesheng Ji, Li Bao, and Xuemei Li. 2022. "Influence of Process Parameters on the Height and Performance of Magnesium Alloy AZ91D Internal Thread by Assisted Heating Extrusion" Materials 15, no. 8: 2747. https://doi.org/10.3390/ma15082747
APA StyleLiu, M., Ji, Z., Bao, L., & Li, X. (2022). Influence of Process Parameters on the Height and Performance of Magnesium Alloy AZ91D Internal Thread by Assisted Heating Extrusion. Materials, 15(8), 2747. https://doi.org/10.3390/ma15082747





