Development and Analysis of Coding and Tailored Metamaterial for Terahertz Frequency Applications
Abstract
:1. Introduction
2. Coding Metamaterial Construction
3. Results and Discussion
3.1. Element “1” Metamaterial
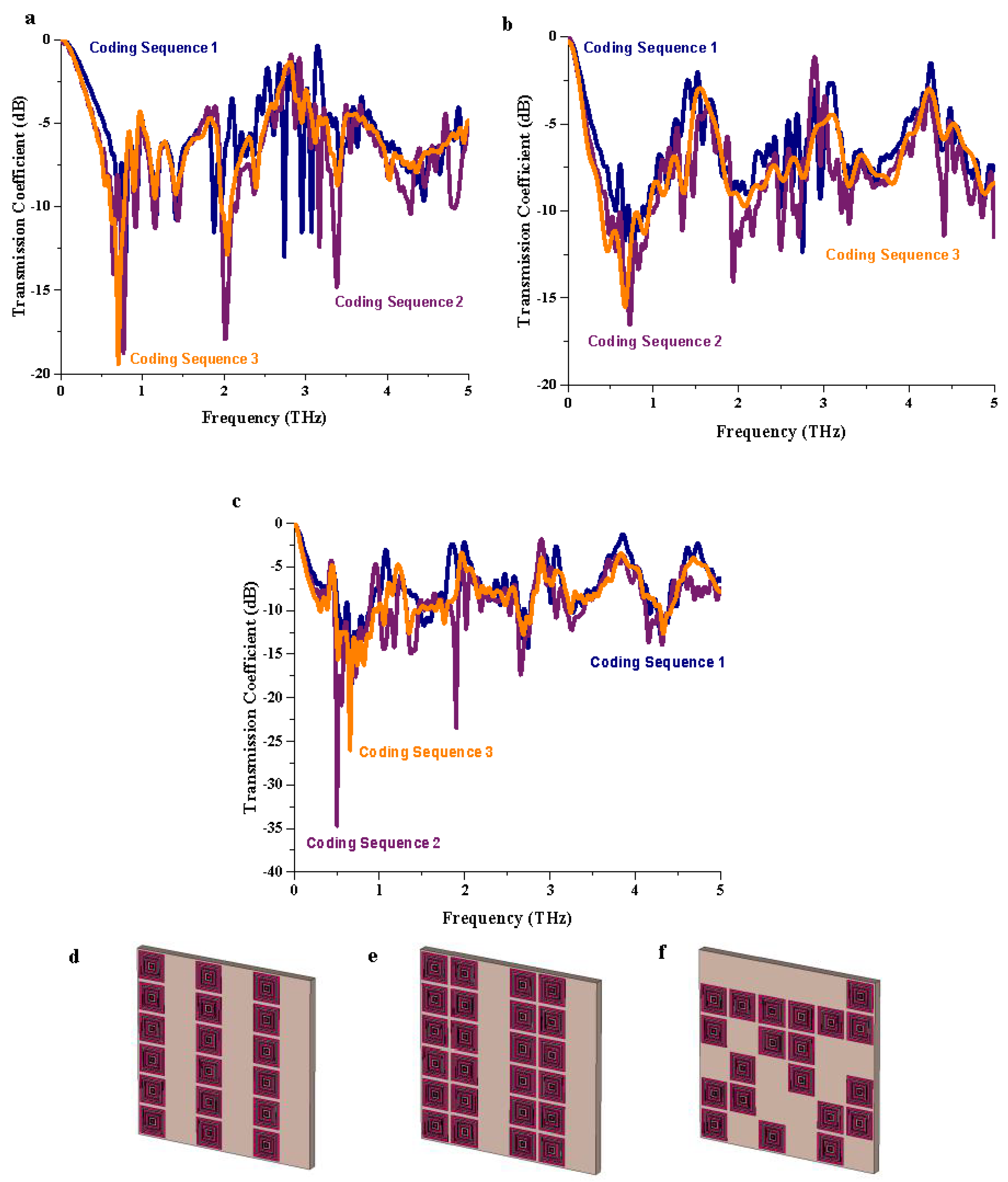
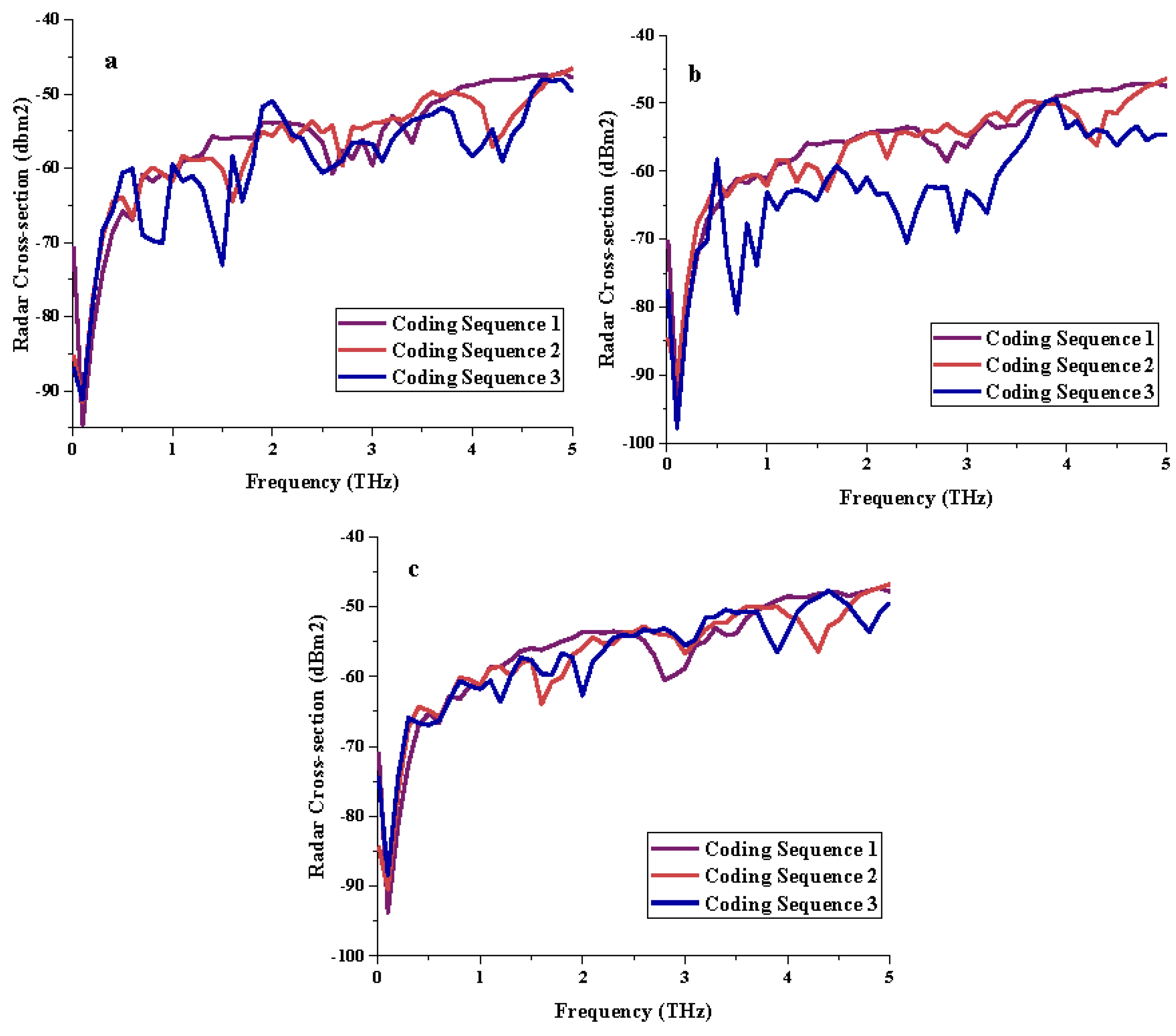
3.2. Coding Metamaterial Sequence
3.2.1. Transmission Coefficient
3.2.2. RCS Reduction
3.3. Tailored Metamaterial Structure
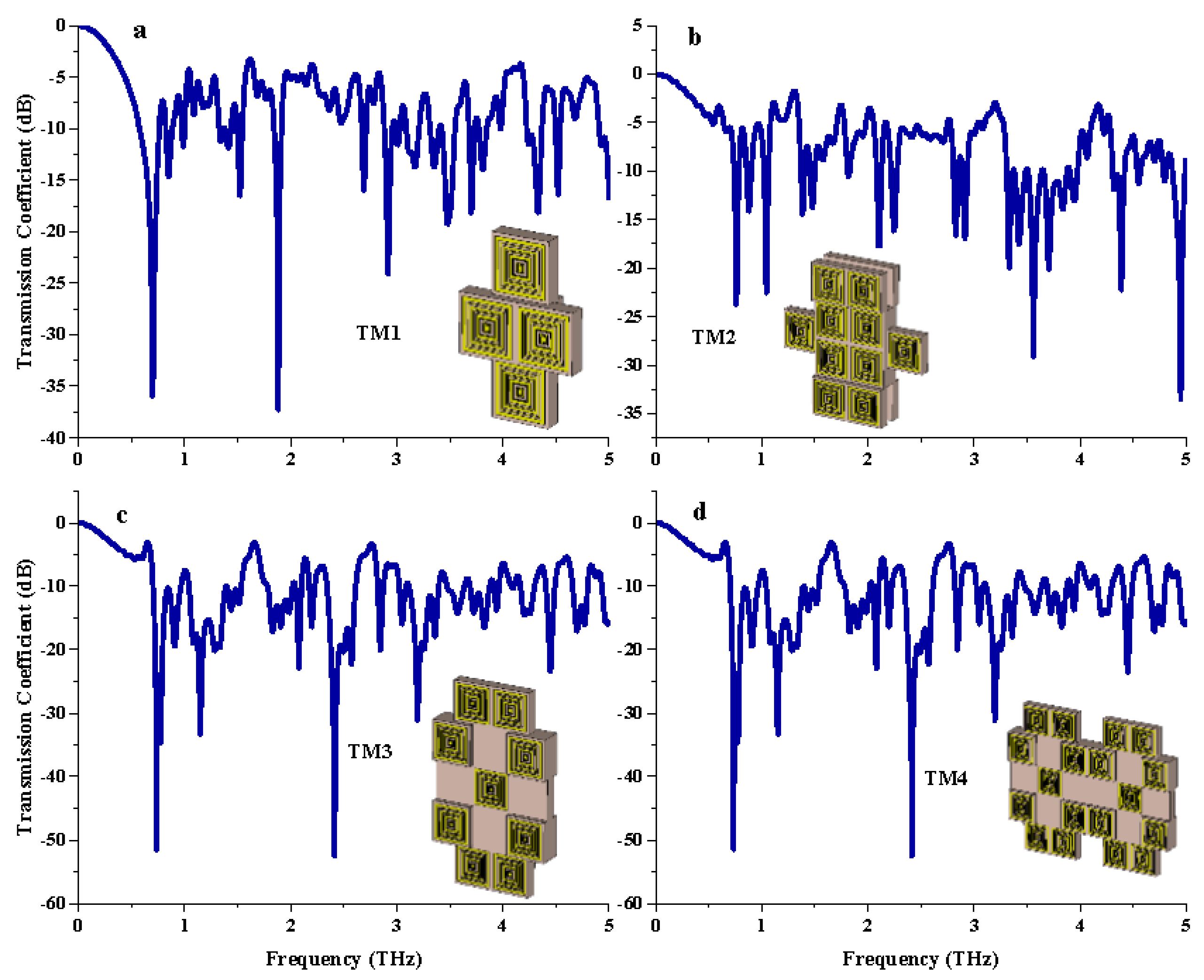
3.3.1. Transmission Coefficient
3.3.2. RCS Reduction
3.4. Scattering Pattern Comparison
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ramachandran, T.; Faruque, M.R.I.; Ahamed, E.; Abdullah, S. Specific absorption rate reduction of multi split square ring metamaterial for L- and S-band application. Results Phys. 2019, 15, 102668. [Google Scholar] [CrossRef]
- Ramachandran, T.; Faruque, M.; Siddiky, A.M.; Islam, M. Reduction of 5G cellular network radiation in wireless mobile phone using an asymmetric square shaped passive metamaterial design. Sci. Rep. 2021, 11, 2619. [Google Scholar] [CrossRef]
- Abdulkarim, Y.I.; Deng, L.; Luo, H.; Huang, S.; Karaaslan, M.; Altıntaş, O.; Bakır, M.; Muhammadsharif, F.F.; Awl, H.N.; Sabah, C.; et al. Design and study of a metamaterial based sensor for the application of liquid chemicals detection. J. Mater. Res. Technol. 2020, 9, 10291–10304. [Google Scholar] [CrossRef]
- Ramachandran, T.; Faruque, M.R.; Islam, M. A Compact Square-shaped Left-handed Passive Metamaterial with Optimized Quintuple Resonance Frequencies for Satellite Applications. Chin. J. Phys. 2020, 67, 360–375. [Google Scholar] [CrossRef]
- Hu, J.; Bandyopadhyay, S.; Liu, Y.; Shao, L. A Review on Metasurface: From Principle to Smart Metadevices. Front. Phys. 2021, 8, 502. [Google Scholar] [CrossRef]
- Ding, F.; Pors, A.; Bozhevolnyi, S.I. Gradient metasurfaces: A review of fundamentals and applications. Rep. Prog. Phys. 2017, 81, 26401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, N.; Capasso, F. Flat optics with designer metasurfaces. Nat. Mater. 2014, 13, 139–150. [Google Scholar] [CrossRef] [PubMed]
- Cui, T.; Qi, M.Q.; Wan, X.; Zhao, J.; Cheng, Q. Coding metamaterials, digital metamaterials and programmable metamaterials. Light Sci. Appl. 2014, 3, e218. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, S.; Cui, T.-J. Theory and application of coding metamaterials. Chin. Opt. 2017, 10, 1–12. [Google Scholar] [CrossRef]
- Wu, H.; Liu, S.; Wan, X.; Zhang, L.; Wang, D.; Li, L.; Cui, T. Controlling Energy Radiations of Electromagnetic Waves via Frequency Coding Metamaterials. Adv. Sci. 2017, 4, 1700098. [Google Scholar] [CrossRef] [PubMed]
- Cuong, M.; Pham, V.; Ho, T.; Nguyen, T.; Do, H.; Bui, X.K.; Tung, B.; Tuyen, D.; Phạm, L.; Vu, D. Broadband microwave coding metamaterial absorbers. Sci. Rep. 2020, 10, 1810. [Google Scholar]
- Iwaszczuk, K.; Heiselberg, H.; Jepsen, P.U. Terahertz radar cross section measurements. Opt. Express 2010, 18, 26399–26408. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, S.; Cui, T.; Xu, Q.; Bao, D.; Du, L.; Wan, X.; Tang, W.; Ouyang, C.; Zhou, X.; Yuan, H.; et al. Polarization-controlled anisotropic coding metamaterials at terahertz frequencies. arXiv 2015, arXiv:1509.03692. [Google Scholar]
- Lui, H.S.; Taimre, T.; Bertling, K.; Lim, Y.L.; Dean, P.; Khanna, S.P.; Lachab, M.; Valavanis, A.; Indjin, D.; Linfield, E.H.; et al. Terahertz radar cross-section characterisation using laser feedback interferometry with quantum cascade laser. Electron. Lett. 2015, 51, 1774–1776. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Wang, P.; Wu, J.; Yan, X.; Zhang, Y.; Zhang, X. Analysis of Terahertz Wave on Increasing Radar Cross Section of 3D Conductive Model. Electronics 2021, 10, 74. [Google Scholar] [CrossRef]
- Wen, D.; Zhang, J.; Fang, C.; Ding, Q.; Lian, J.; Zhang, Q. Experimental validation of the metamaterial absorber for RCS reduction. In Proceedings of the 2014 3rd Asia-Pacific Conference on Antennas and Propagation, Harbin, China, 26–29 July 2014; pp. 1485–1488. [Google Scholar]
- Zhang, Z.-X.; Zhang, J.-C. RCS reduction for patch antenna based on metamaterial absorber. In Proceedings of the 2016 Progress in Electromagnetic Research Symposium (PIERS), Shanghai, China, 8–11 August 2016; pp. 364–368. [Google Scholar]
- Fan, Y.; Wang, J.; Fu, X.; Li, Y.; Pang, Y.; Zheng, L.; Yan, M.-B.; Zhang, J.; Qu, S. Recent developments of metamaterials/metasurfaces for RCS reduction. EPJ Appl. Metamater. 2019, 6, 15. [Google Scholar] [CrossRef] [Green Version]
- Kong, X.; Jiang, S.; Kong, L.; Wang, Q.; Hu, H.; Zhang, X.; Zhao, X. Transparent Metamaterial Absorber with Broadband RCS Reduction for Solar Arrays. arXiv 2020, arXiv:2003.13005. [Google Scholar]
- Smith, D.R.; Vier, D.C.; Soukoulis, C.M. Electromagnetic parameter retrieval from inhomogeneous metamaterials. Phys. Rev. E 2005, 71, 036617. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Castanié, A.; Mercier, J.; Félix, S.; Maurel, A. Generalized method for retrieving effective parameters of anisotropic metamaterials. Opt. Express 2014, 22, 649–661. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Grzegorczyk, T.M.; Wu, B.; Pacheco, J.; Kong, J.A. Robust method to retrieve the constitutive effective parameters of metamaterials. Phys. Rev. E 2004, 70, 016608. [Google Scholar] [CrossRef] [PubMed] [Green Version]
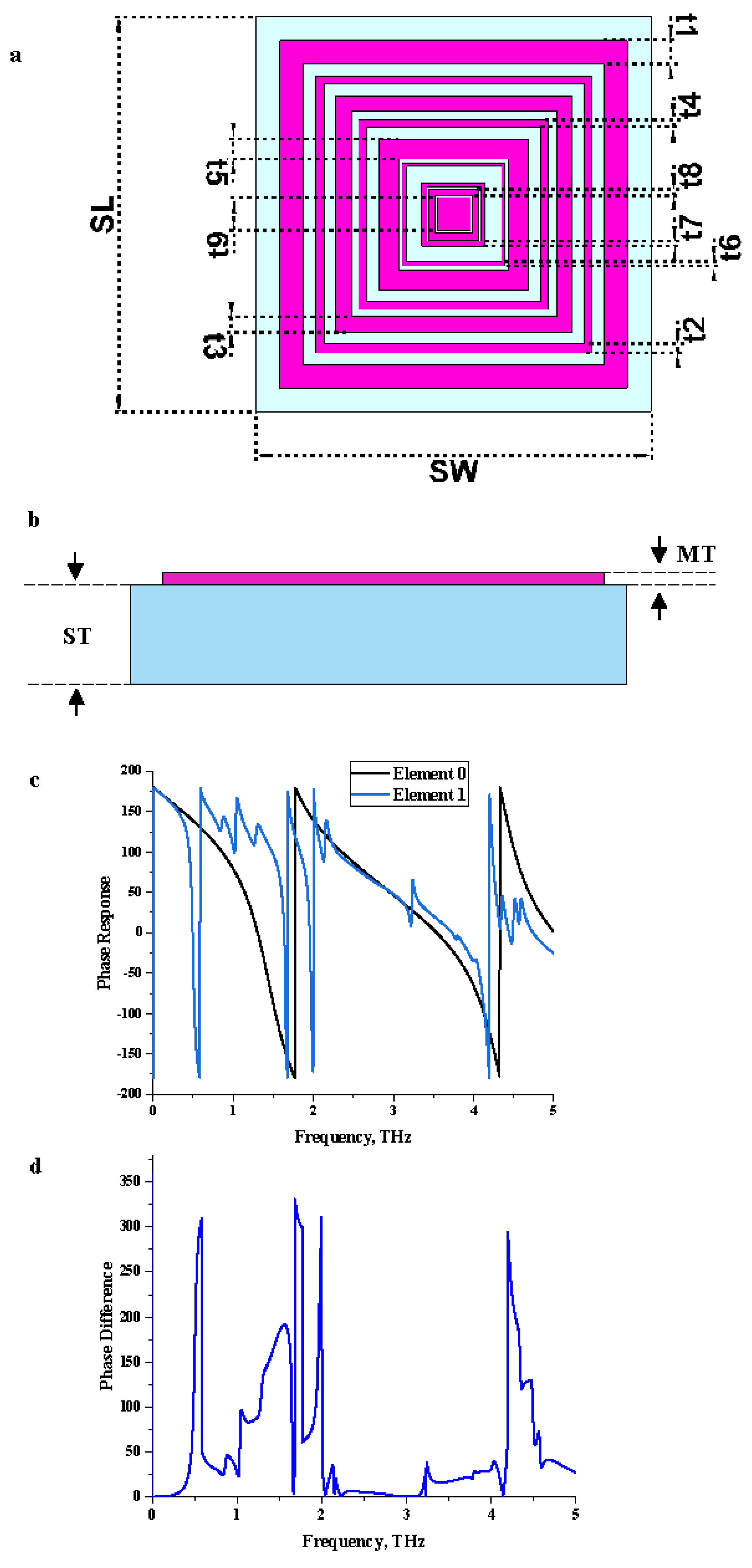
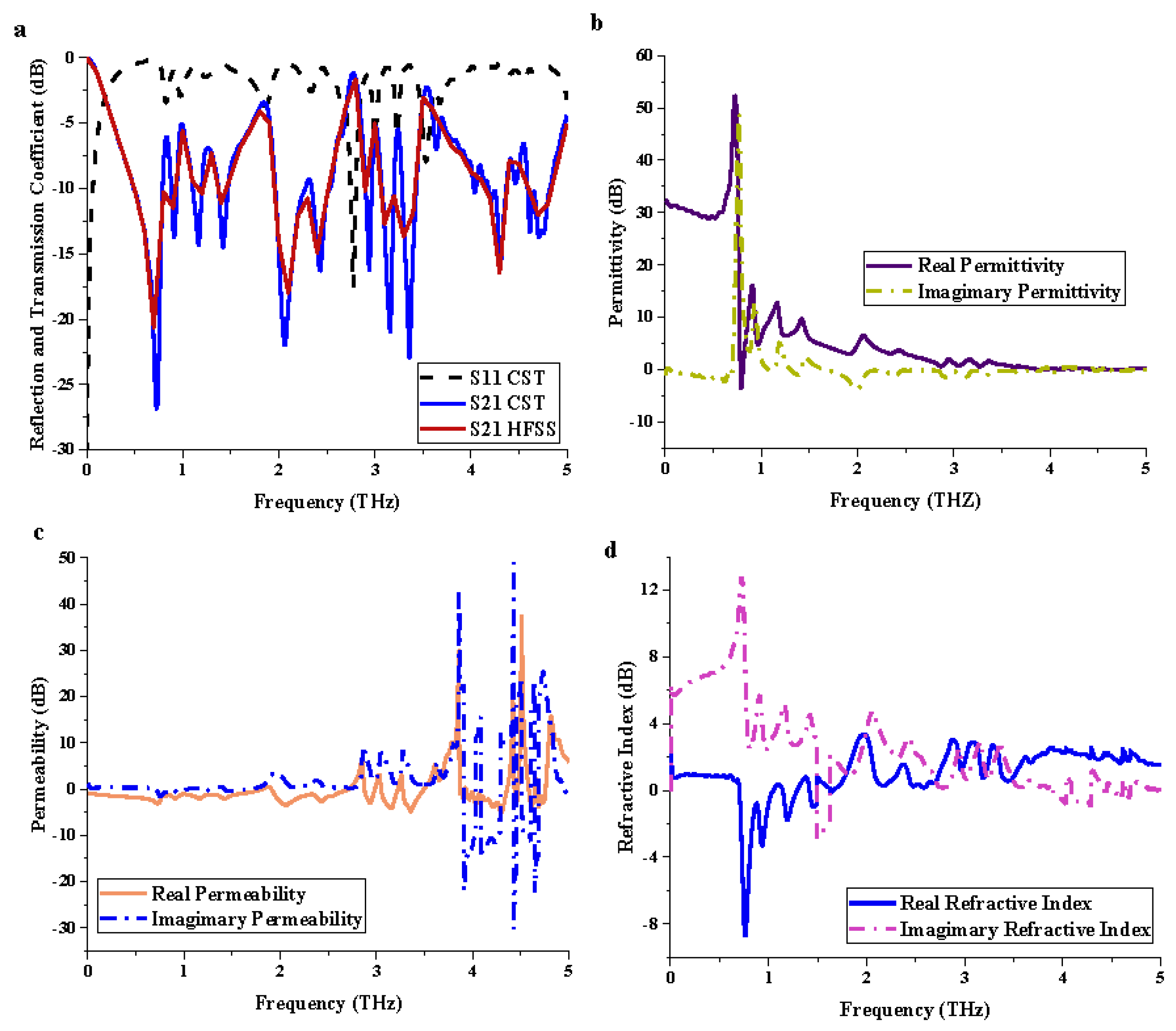

| Descriptions | Dimension (µm) |
|---|---|
| t1 | 3.0 |
| t2 | 0.9 |
| t3 | 2.0 |
| t4 | 1.0 |
| t5 | 2.5 |
| t6 | 0.5 |
| t7 | 0.6 |
| t8 | 0.8 |
| t9 | 4.2 |
| Substrate Length, SL | 50 |
| Substrate Width, SW | 50 |
| Metamaterial Thickness, MT | 0.2 |
| Substrate Thickness, ST | 15 |
| Coding Sequence | Row 1 | Row 2 | Row 3 | Row 4 | Row 5 | Row 6 |
|---|---|---|---|---|---|---|
| 1 | 101010 | 101010 | 101010 | 101010 | 101010 | 101010 |
| 2 | 110110 | 110110 | 110110 | 110110 | 110110 | 110110 |
| 3 | 101010 | 110011 | 010101 | 101100 | 111111 | 000001 |
| Coding Sequences | Single-Layer | Double-Layer | Multi-Layer |
|---|---|---|---|
| 1 | - | - | 0.67 THz |
| 2 | 0.77 and 2.02 THz | 0.73 THz | 0.51, 0.66, 1.90, and 2.66 THz |
| 3 | 0.70 THz | 0.67 THz | 0.65 THz |
| Tailored Metamaterial | Resonance Frequencies |
|---|---|
| TM 1 | 0.70, 1.53, 1.89, 2.69, 3.48, 3.71, 4.34, and 4.52 THz |
| TM 2 | 0.76, 1.05, 2.11, 2.25, 2.83, 2.92, 3.33, 3.43, 3.56, 3.71, and 4.39 THz |
| TM 3 | 0.74, 0.91, 1.15, 2.08, 2.42, 2.85, 3.20, and 4.45 THz |
| TM 4 | 0.74, 0.78, 1.15, 2.08, 2.42, 3.20, and 4.45 THz |
| Coding Metamaterial | |||
|---|---|---|---|
| Coding Sequence 1 | Coding Sequence 2 | Coding Sequence 3 | |
| Single-layer | 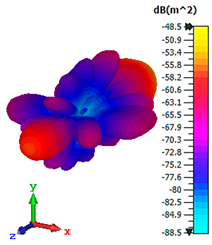 | 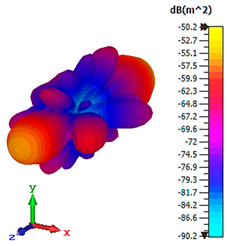 |  |
| Double-layer | 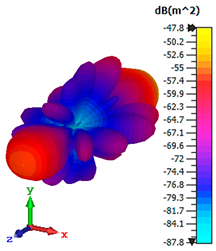 | 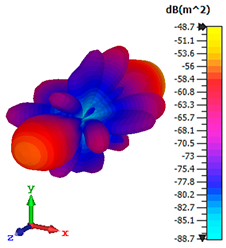 | 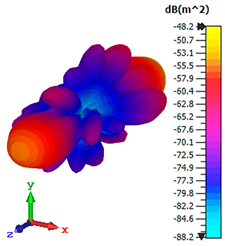 |
| Triple-layer | 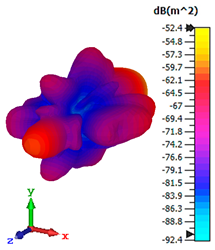 | 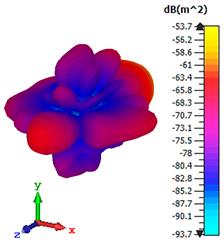 | 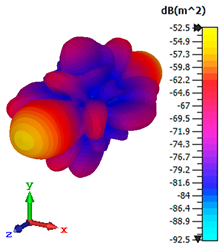 |
| Tailored Metamaterial | |||
|---|---|---|---|
| TM 1 | TM 2 | TM 3 | TM 4 |
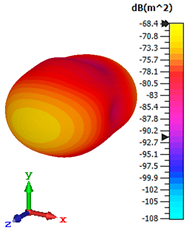 | 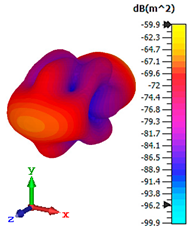 |  |  |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramachandran, T.; Faruque, M.R.I.; Islam, M.T.; Khandaker, M.U.; Alqahtani, A.; Bradley, D.A. Development and Analysis of Coding and Tailored Metamaterial for Terahertz Frequency Applications. Materials 2022, 15, 2777. https://doi.org/10.3390/ma15082777
Ramachandran T, Faruque MRI, Islam MT, Khandaker MU, Alqahtani A, Bradley DA. Development and Analysis of Coding and Tailored Metamaterial for Terahertz Frequency Applications. Materials. 2022; 15(8):2777. https://doi.org/10.3390/ma15082777
Chicago/Turabian StyleRamachandran, Tayaallen, Mohammad Rashed Iqbal Faruque, Mohammad Tariqul Islam, Mayeen Uddin Khandaker, Amal Alqahtani, and D. A. Bradley. 2022. "Development and Analysis of Coding and Tailored Metamaterial for Terahertz Frequency Applications" Materials 15, no. 8: 2777. https://doi.org/10.3390/ma15082777
APA StyleRamachandran, T., Faruque, M. R. I., Islam, M. T., Khandaker, M. U., Alqahtani, A., & Bradley, D. A. (2022). Development and Analysis of Coding and Tailored Metamaterial for Terahertz Frequency Applications. Materials, 15(8), 2777. https://doi.org/10.3390/ma15082777








