A Numerical Study on the Mesoscopic Characteristics of Ti-6Al-4V by Selective Laser Melting
Abstract
:1. Introduction
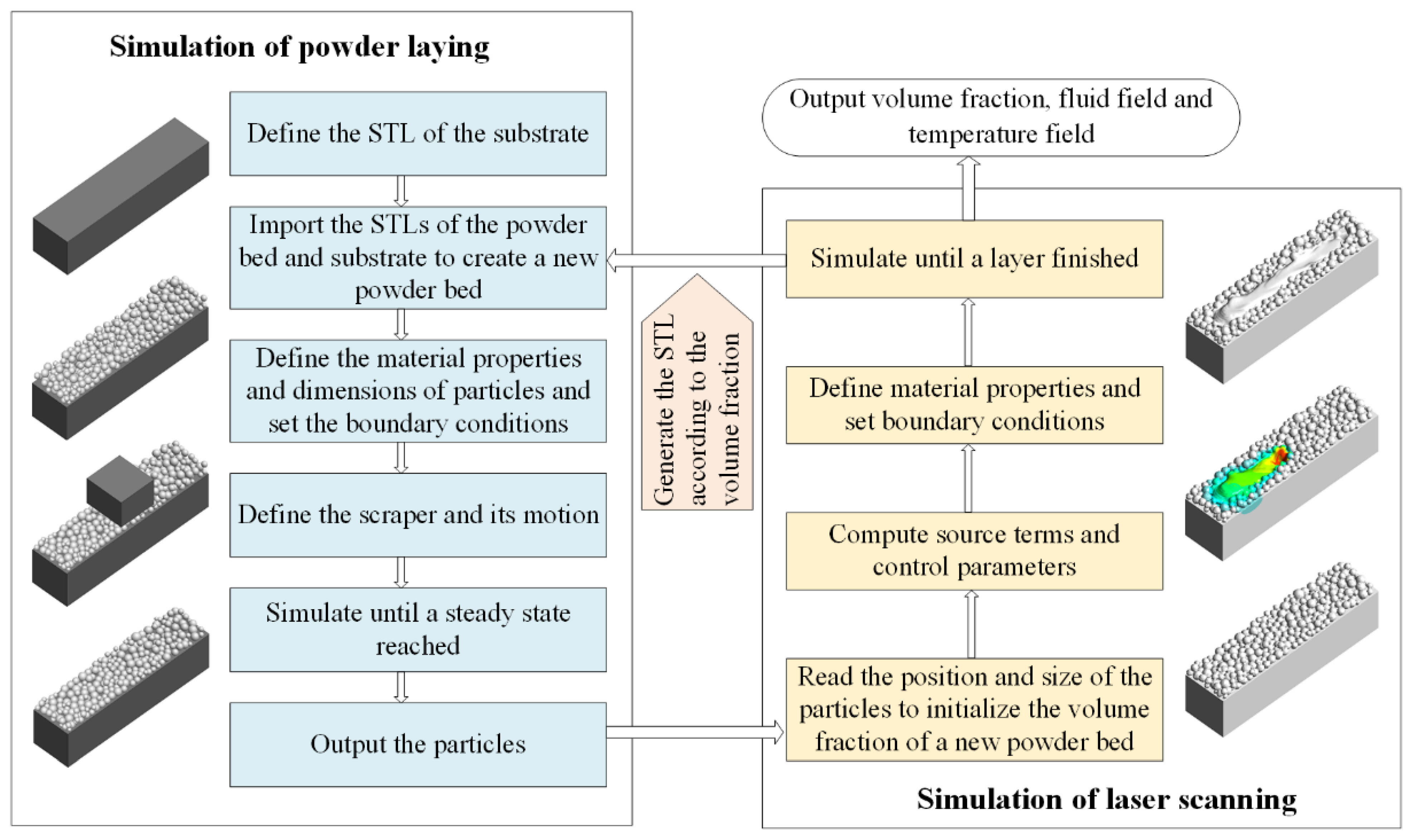
2. Modeling and Simulation Framework
2.1. Discrete-Element Modeling of the Powder-Laying Process
2.2. Multi-Phase and Multi-Physics Coupling Modeling of the Laser-Scanning Process
2.3. Simulation Framework
3. Results and Discussions
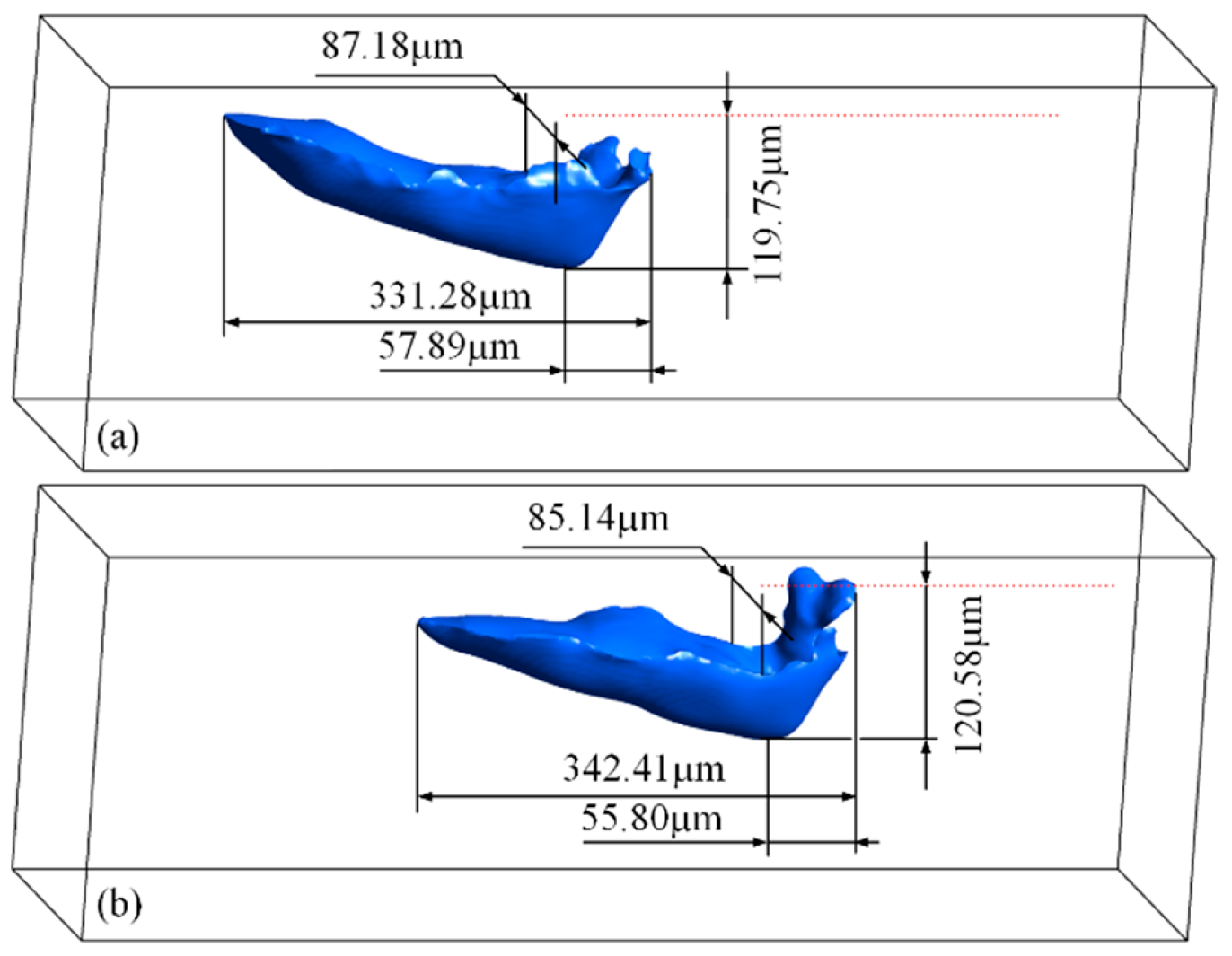
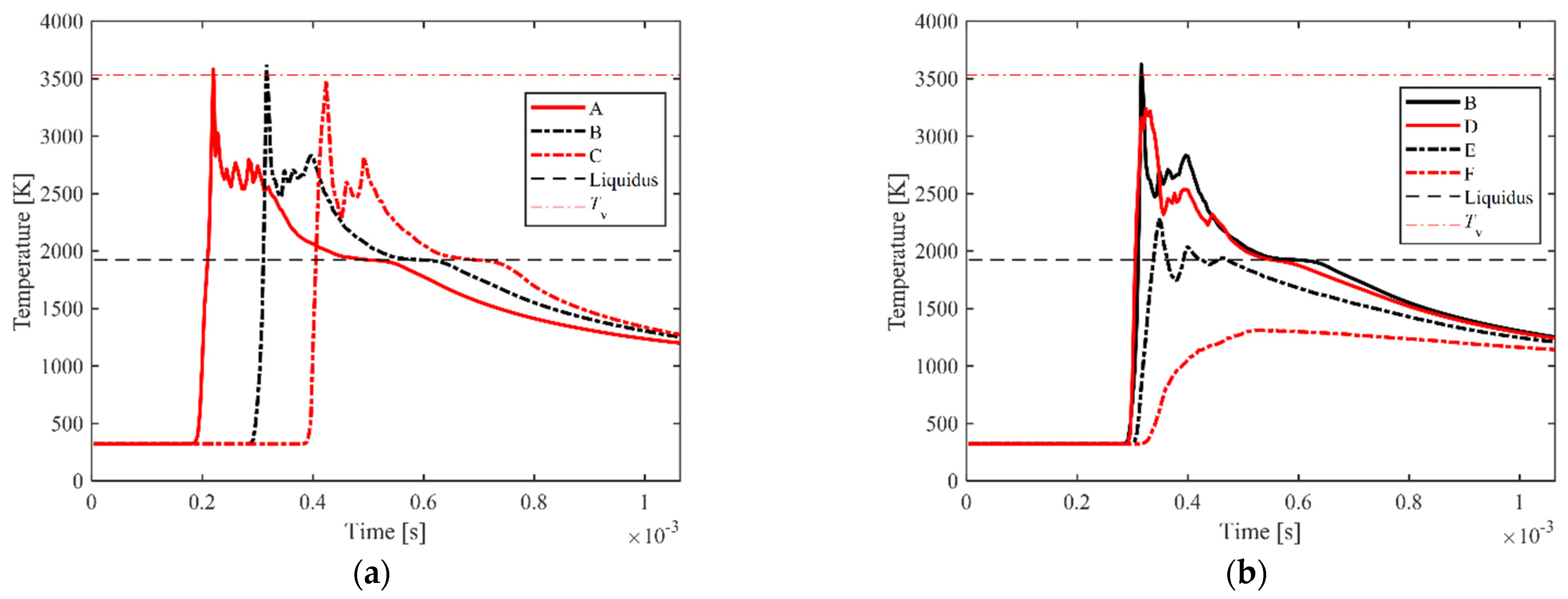
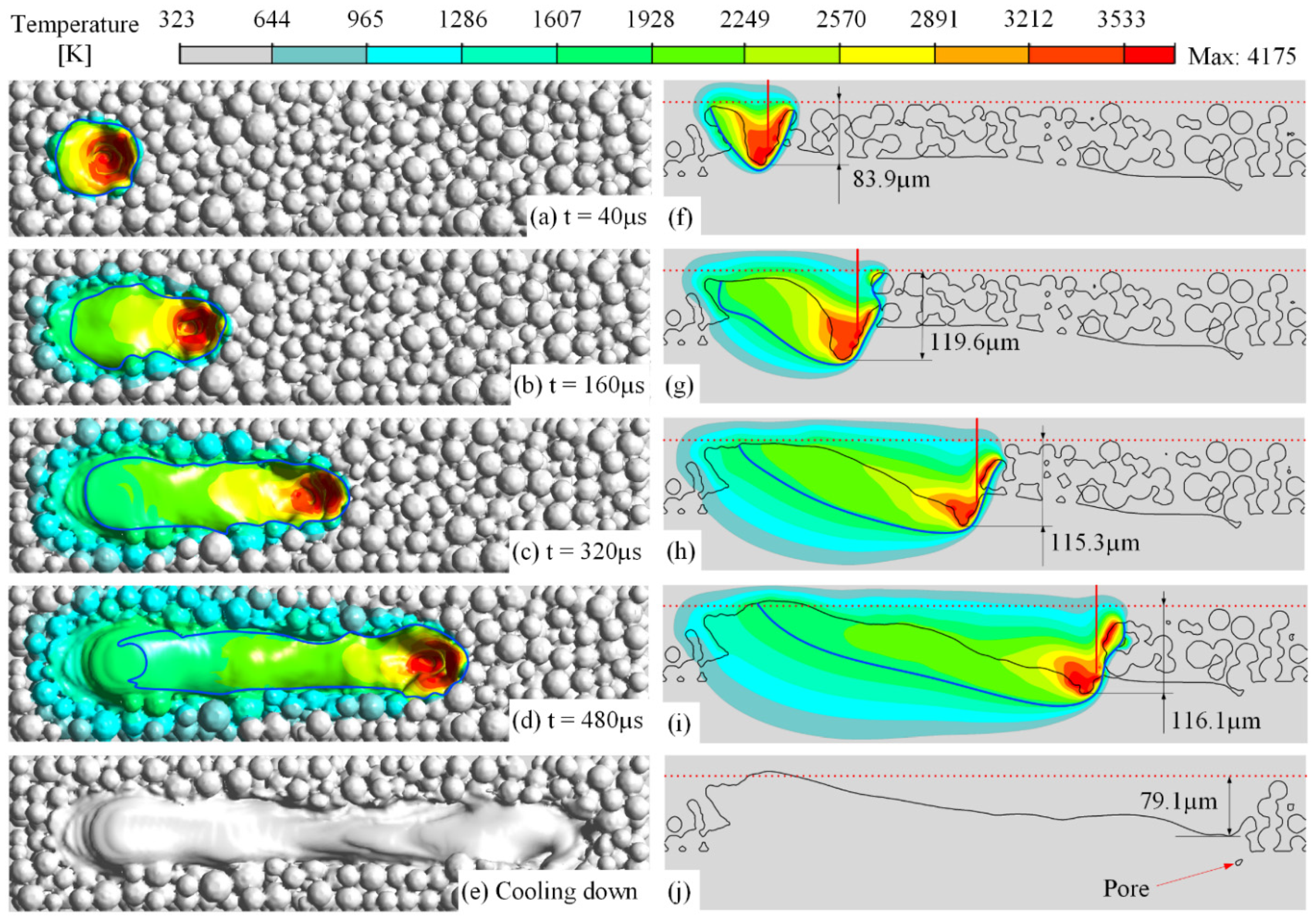
3.1. Application to the Objects with Single and Double Layers
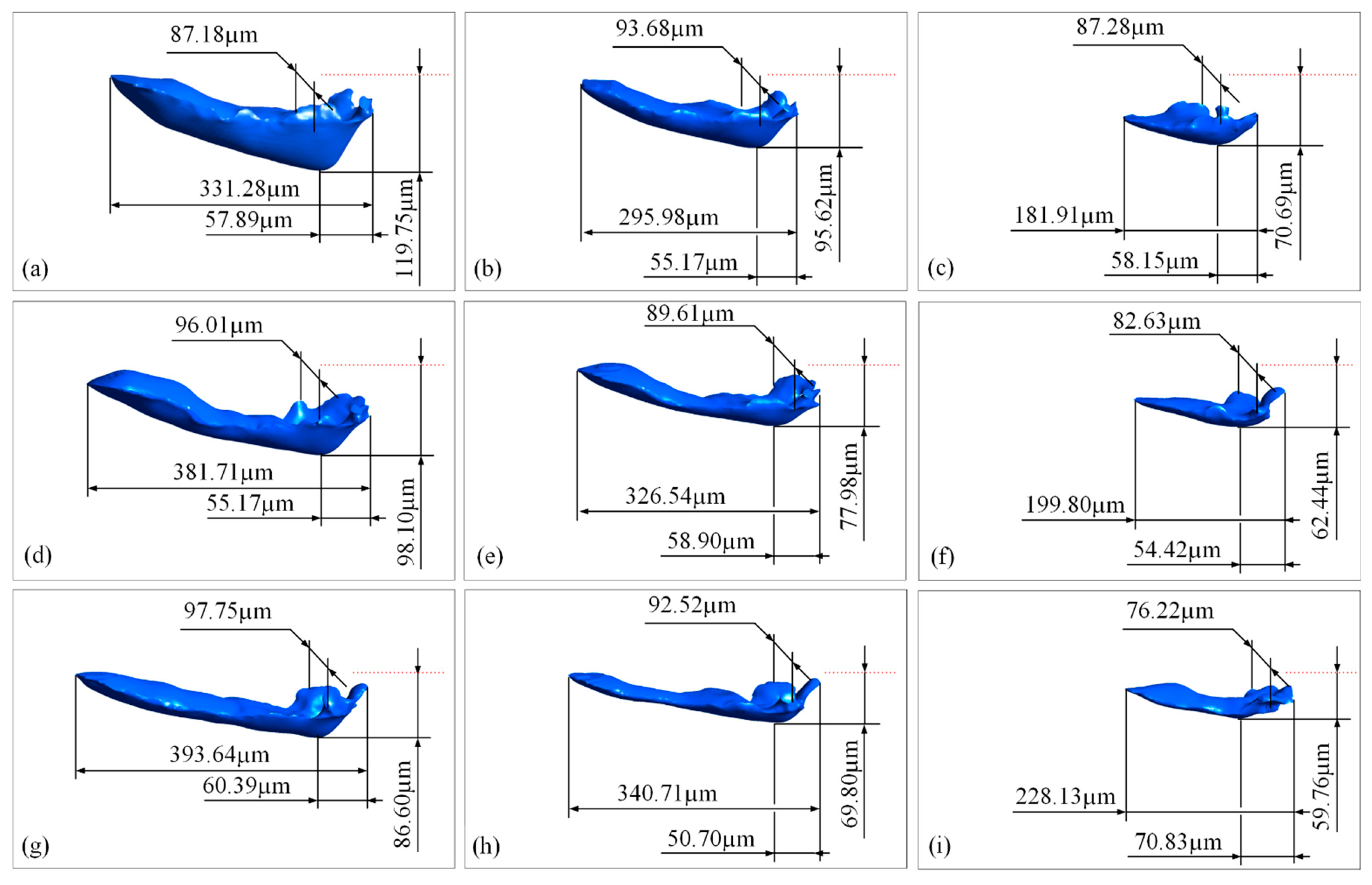
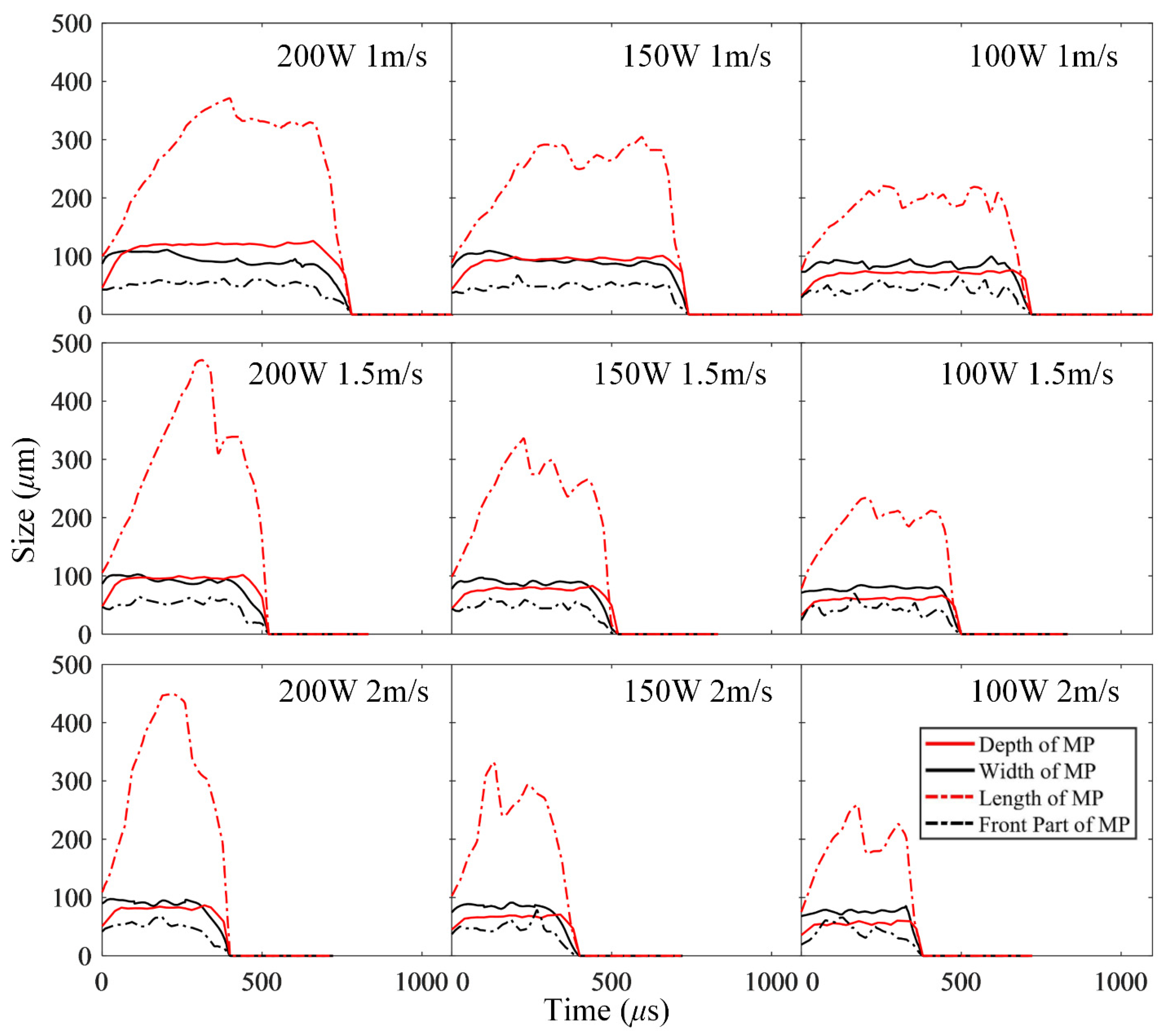
3.2. Effect of Laser Speed and Power
4. Conclusions
- (1)
- This paper introduced a mesoscale DEM and CFD combined simulation framework for the simulation of the SLM process. The application of the framework showed a successful layer-by-layer simulation, which includes the alternate simulations of the power-laying and laser-scanning processes.
- (2)
- The fundamental mesoscopic characteristics of the molten pool of the Ti-6Al-4V powder bed were found. The evolutions of the temperature history, flow field, keyhole, and the morphologies of the molten pool and the solidified track were presented and discussed in detail.
- (3)
- The simulations by varying the laser power and scanning speed showed that as the laser power increases, the solidification bulge at the beginning of the track increases, the depression at its end decreases, the ripples on the top surface of the track gradually decrease and become smoother, and the length and width of the molten pool increase nonlinearly; as the scanning speed increases, the width of the molten pool slightly narrows, and the length increases to a certain extent, but the increment ratio falls far behind that of the scanning speed; there is a big difference in the morphology of the molten pool at the same linear energy density of the laser power; during the laser-scanning process, the stability of the depth of the molten pool is the best, the width and the front distance is the next, and the length is the worst.
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Calignano, F.; Manfredi, D.; Ambrosio, E.P.; Biamino, S.; Lombardi, M.; Atzeni, E.; Salmi, A.; Minetola, P.; Iuliano, L.; Fino, P. Overview on Additive Manufacturing Technologies. Proc. IEEE 2017, 105, 593–612. [Google Scholar] [CrossRef]
- Stolt, R.; Elgh, F. Introducing design for selective laser melting in aerospace industry. J. Comput. Des. Eng. 2020, 7, 489–497. [Google Scholar] [CrossRef]
- Kaya, G.; Yildiz, F.; Hacisalihoğlu, İ. Characterization of the Structural and Tribological Properties of Medical Ti6Al4V Alloy Produced in Different Production Parameters Using Selective Laser Melting. 3D Print. Addit. Manuf. 2019, 6, 253–261. [Google Scholar] [CrossRef]
- Aboulkhair, N.T.; Simonelli, M.; Parry, L.; Ashcroft, I.; Tuck, C.; Hague, R. 3D printing of aluminium alloys: Additive manufacturing of aluminium alloys using selective laser melting. Prog. Mater. Sci. 2019, 106, 100578. [Google Scholar] [CrossRef]
- Guo, Q.; Zhao, C.; Escano, L.I.; Young, Z.; Xiong, L.; Fezzaa, K.; Everhart, W.; Brown, B.; Sun, T.; Chen, L. Transient dynamics of powder spattering in laser powder bed fusion additive manufacturing process revealed by in-situ high-speed high-energy X-ray imaging. Acta Mater. 2018, 151, 169–180. [Google Scholar] [CrossRef]
- Guo, Q.; Zhao, C.; Qu, M.; Xiong, L.; Escano, L.I.; Hojjatzadeh, S.M.H.; Parab, N.D.; Fezzaa, K.; Everhart, W.; Sun, T.; et al. In-situ characterization and quantification of melt pool variation under constant input energy density in laser powder bed fusion additive manufacturing process. Addit. Manuf. 2019, 28, 600–609. [Google Scholar] [CrossRef]
- Wolff, S.J.; Wu, H.; Parab, N.; Zhao, C.; Ehmann, K.F.; Sun, T.; Cao, J. In-situ high-speed X-ray imaging of piezo-driven directed energy deposition additive manufacturing. Sci. Rep. 2019, 9, 962. [Google Scholar] [CrossRef] [Green Version]
- Guo, Q.; Zhao, C.; Qu, M.; Xiong, L.; Hojjatzadeh, S.M.H.; Escano, L.I.; Parab, N.D.; Fezzaa, K.; Sun, T.; Chen, L. In-situ full-field mapping of melt flow dynamics in laser metal additive manufacturing. Addit. Manuf. 2020, 31, 100939. [Google Scholar] [CrossRef]
- Mindt, H.W.; Desmaison, O.; Megahed, M.; Peralta, A.; Neumann, J. Modeling of powder bed manufacturing defects. J. Mater. Eng. Perform. 2018, 27, 32–43. [Google Scholar] [CrossRef]
- He, Q.; Xia, H.; Liu, J.; Ao, X.; Lin, S. Modeling and numerical studies of selective laser melting: Multiphase flow, solidification and heat transfer. Mater. Des. 2020, 196, 109115. [Google Scholar] [CrossRef]
- Ao, X.; Xia, H.; Liu, J.; He, Q. Simulations of microstructure coupling with moving molten pool by selective laser melting using a cellular automaton. Mater. Des. 2020, 185, 108230. [Google Scholar] [CrossRef]
- Chen, H.; Chen, Y.; Liu, Y.; Wei, Q.; Shi, Y.; Yan, W. Packing quality of powder layer during counter-rolling-type powder spreading process in additive manufacturing. Int. J. Mach. Tools Manuf. 2020, 153, 103553. [Google Scholar] [CrossRef]
- Chen, H.; Wei, Q.; Zhang, Y.; Chen, F.; Shi, Y.; Yan, W. Powder-spreading mechanisms in powder-bed-based additive manufacturing: Experiments and computational modeling. Acta Mater. 2019, 179, 158–171. [Google Scholar] [CrossRef]
- Yuan, P.; Gu, D. Molten pool behaviour and its physical mechanism during selective laser melting of TiC/AlSi10Mg nanocomposites: Simulation and experiments. J. Phys. D Appl. Phys. 2015, 48, 035303. [Google Scholar] [CrossRef]
- Yu, G.; Gu, D.; Dai, D.; Xia, M.; Ma, C.; Chang, K. Influence of processing parameters on laser penetration depth and melting/re-melting densification during selective laser melting of aluminum alloy. Appl. Phys. A 2016, 122, 891. [Google Scholar] [CrossRef]
- Xia, M.; Gu, D.; Yu, G.; Dai, D.; Chen, H.; Shi, Q. Porosity evolution and its thermodynamic mechanism of randomly packed powder-bed during selective laser melting of Inconel 718 alloy. Int. J. Mach. Tools Manuf. 2017, 116, 96–106. [Google Scholar] [CrossRef]
- Khairallah, S.A.; Anderson, A. Mesoscopic simulation model of selective laser melting of stainless steel powder. J. Mater. Processing Technol. 2014, 214, 2627–2636. [Google Scholar] [CrossRef]
- Khairallah, S.A.; Anderson, A.T.; Rubenchik, A.; King, W.E. Laser powder-bed fusion additive manufacturing: Physics of complex melt flow and formation mechanisms of pores, spatter, and denudation zones. Acta Mater. 2016, 108, 36–45. [Google Scholar] [CrossRef] [Green Version]
- Tang, C.; Tan, J.L.; Wong, C.H. A numerical investigation on the physical mechanisms of single track defects in selective laser melting. Int. J. Heat Mass Transf. 2018, 126, 957–968. [Google Scholar] [CrossRef]
- Yuan, W.; Chen, H.; Cheng, T.; Wei, Q. Effects of laser scanning speeds on different states of the molten pool during selective laser melting: Simulation and experiment. Mater. Des. 2020, 189, 108542. [Google Scholar] [CrossRef]
- Yan, W.; Ge, W.; Smith, J.; Lin, S.; Kafka, O.; Lin, F.; Liu, W.K. Multi-scale modeling of electron beam melting of functionally graded materials. Acta Mater. 2016, 115, 403–412. [Google Scholar] [CrossRef] [Green Version]
- Yan, W.; Qian, Y.; Ge, W.; Lin, S.; Liu, W.K.; Lin, F.; Wagner, G.J. Meso-scale modeling of multiple-layer fabrication process in Selective Electron Beam Melting: Inter-layer/track voids formation. Mater. Des. 2018, 141, 210–219. [Google Scholar] [CrossRef]
- Yan, W.; Ge, W.; Qian, Y.; Lin, S.; Zhou, B.; Liu, W.K.; Lin, F.; Wagner, G.J. Multi-physics modeling of single/multiple-track defect mechanisms in electron beam selective melting. Acta Mater. 2017, 134, 324–333. [Google Scholar] [CrossRef]
- Cao, L. Numerical simulation of the impact of laying powder on selective laser melting single-pass formation. Int. J. Heat Mass Transf. 2019, 141, 1036–1048. [Google Scholar] [CrossRef]
- Cao, L. Mesoscopic-scale simulation of pore evolution during laser powder bed fusion process. Comput. Mater. Sci. 2020, 179, 109686. [Google Scholar] [CrossRef]
- Bayat, M.; Mohanty, S.; Hattel, J. Multiphysics modelling of lack-of-fusion voids formation and evolution in IN718 made by multi-track/multi-layer L-PBF. Int. J. Heat Mass Transf. 2019, 139, 95–114. [Google Scholar] [CrossRef]
- Bayat, M.; Thanki, A.; Mohanty, S.; Witvrouw, A.; Yang, S.; Thorborg, J.; Tiedje, N.S.; Hattel, J. Keyhole-induced porosities in Laser-based Powder Bed Fusion (L-PBF) of Ti6Al4V: High-fidelity modelling and experimental validation. Addit. Manuf. 2019, 30, 100835. [Google Scholar] [CrossRef]
- Gürtler, F.J.; Karg, M.; Leitz, K.H.; Schmidt, M. Simulation of laser beam melting of steel powders using the three-dimensional volume of fluid method. Phys. Procedia 2013, 41, 881–886. [Google Scholar] [CrossRef] [Green Version]
- Du, Y.; You, X.; Qiao, F.; Guo, L.; Liu, Z. A model for predicting the temperature field during selective laser melting. Results Phys. 2019, 12, 52–60. [Google Scholar] [CrossRef]
- Zhang, T.; Li, H.; Liu, S.; Shen, S.; Xie, H.; Shi, W.; Zhang, G.; Shen, B.; Chen, L.; Xiao, B.; et al. Evolution of molten pool during selective laser melting of Ti–6Al–4V. J. Phys. D Appl. Phys. 2018, 52, 055302. [Google Scholar] [CrossRef]
- Jin, P.; Tang, Q.; Song, J.; Feng, Q.; Guo, F.; Fan, X.; Jin, M.; Wang, F. Numerical investigation of the mechanism of interfacial dynamics of the melt pool and defects during laser powder bed fusion. Opt. Laser Technol. 2021, 143, 107289. [Google Scholar] [CrossRef]
- Jin, P.; Tang, Q.; Li, K.; Feng, Q.; Ren, Z.; Song, J.; Nie, Y.; Ma, S. The relationship between the macro- and microstructure and the mechanical properties of selective-laser-melted Ti6Al4V samples under low energy inputs: Simulation and experiment. Opt. Laser Technol. 2022, 148, 107713. [Google Scholar] [CrossRef]
- Yang, J.; Han, J.; Yu, H.; Yin, J.; Gao, M.; Wang, Z.; Zeng, X. Role of molten pool mode on formability, microstructure and mechanical properties of selective laser melted Ti-6Al-4V alloy. Mater. Des. 2016, 110, 558–570. [Google Scholar] [CrossRef]
- Gorsse, S.; Hutchinson, C.; Gouné, M.; Banerjee, R. Additive manufacturing of metals: A brief review of the characteristic microstructures and properties of steels, Ti-6Al-4V and high-entropy alloys. Sci. Technol. Adv. Mater. 2017, 18, 584–610. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thijs, L.; Verhaeghe, F.; Craeghs, T.; Van Humbeeck, J.; Kruth, J.P. A study of the microstructural evolution during selective laser melting of Ti–6Al–4V. Acta Mater. 2010, 58, 3303–3312. [Google Scholar] [CrossRef]
- Sun, D.; Gu, D.; Lin, K.; Ma, J.; Chen, W.; Huang, J.; Sun, X.; Chu, M. Selective laser melting of titanium parts: Influence of laser process parameters on macro- and microstructures and tensile property. Powder Technol. 2019, 342, 371–379. [Google Scholar] [CrossRef]
- Radjaï, F.; Dubois, F. Discrete-Element Modeling of Granular Materials; Wiley-Iste: London, UK, 2011. [Google Scholar]
- Chen, H.; Yan, W. Spattering and denudation in laser powder bed fusion process: Multiphase flow modelling. Acta Mater. 2020, 196, 154–167. [Google Scholar] [CrossRef]




| Property/Parameter | Value | References |
|---|---|---|
| Density, ρm/kg·m−3 | 4400 | [27] |
| Surface tension coefficient, γ/N·m−1 | 1.53–0.28 × 10−3 (T-1941), T > Tsol | [30] |
| Solidus, Tsol/K | 1877 | [30] |
| Liquidus, Tliq/K | 1923 | [30] |
| Evaporating temperature, Tv/K | 3533 | [30] |
| Thermal conductivity, km/W·m−1·K−1 | [30] | |
| Latent heat of melting, Lm/J·kg−1 | 2.86 × 105 | [30] |
| Latent heat of vaporization, Lv/J·kg−1 | 9.83 × 106 | [30] |
| Saturated vapor pressure at Tv, p0/Pa | 101,325 | - |
| Specific heat capacity, cp/J·K−1·kg−1 | [30] | |
| Radius of the laser spot, ω/μm | 37.5 | - |
| Scanning speed, v/m·s−1 | 1.0–2.0 | - |
| Laser power, P/W | 100–200 | - |
| Absorptivity coefficient, A | 0.4 | [30] |
| Radiation coefficient, ε | 0.4 | [27] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ao, X.; Liu, J.; Xia, H.; Yang, Y. A Numerical Study on the Mesoscopic Characteristics of Ti-6Al-4V by Selective Laser Melting. Materials 2022, 15, 2850. https://doi.org/10.3390/ma15082850
Ao X, Liu J, Xia H, Yang Y. A Numerical Study on the Mesoscopic Characteristics of Ti-6Al-4V by Selective Laser Melting. Materials. 2022; 15(8):2850. https://doi.org/10.3390/ma15082850
Chicago/Turabian StyleAo, Xiaohui, Jianhua Liu, Huanxiong Xia, and Ye Yang. 2022. "A Numerical Study on the Mesoscopic Characteristics of Ti-6Al-4V by Selective Laser Melting" Materials 15, no. 8: 2850. https://doi.org/10.3390/ma15082850
APA StyleAo, X., Liu, J., Xia, H., & Yang, Y. (2022). A Numerical Study on the Mesoscopic Characteristics of Ti-6Al-4V by Selective Laser Melting. Materials, 15(8), 2850. https://doi.org/10.3390/ma15082850







