Impact Resistant Structure Design and Optimization Inspired by Turtle Carapace
Abstract
:1. Introduction
2. Materials and Methods
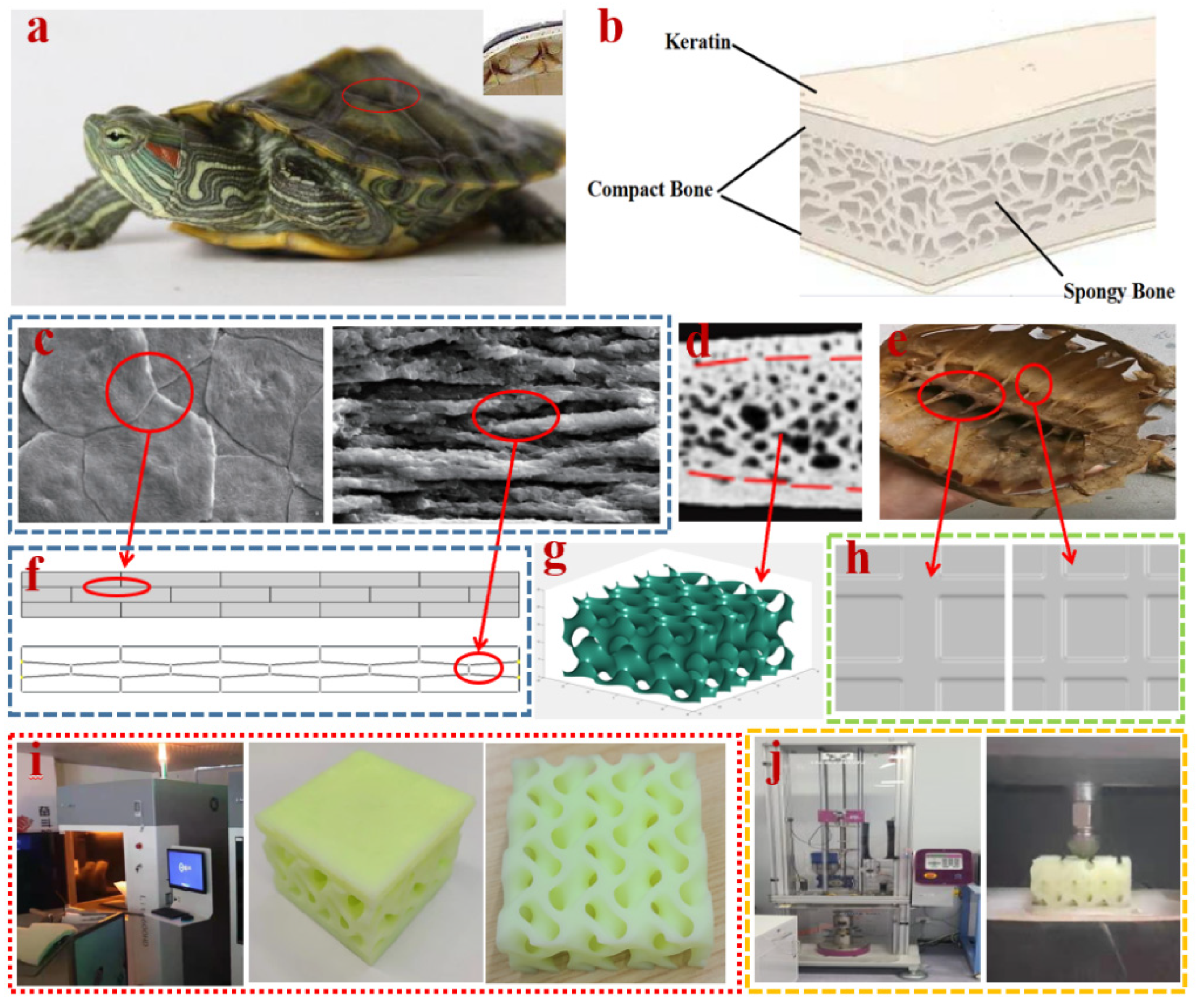
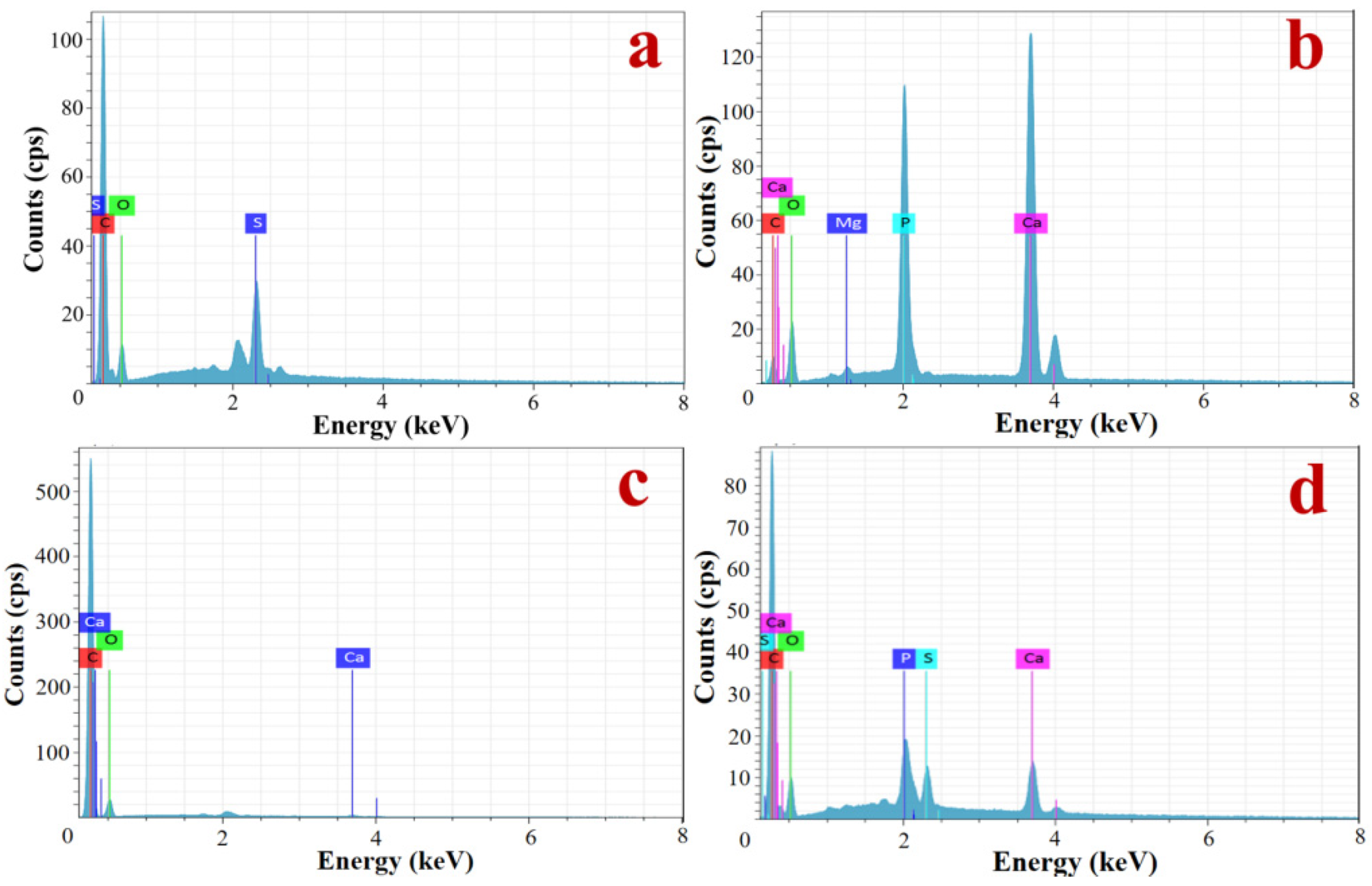
2.1. Elemental Analysis of Turtle Carapace
2.2. Structural Design
2.3. Finite Element Simulations
2.4. Drop-Weight Experiments
3. Results
3.1. Elemental Analysis of Turtle Carapace
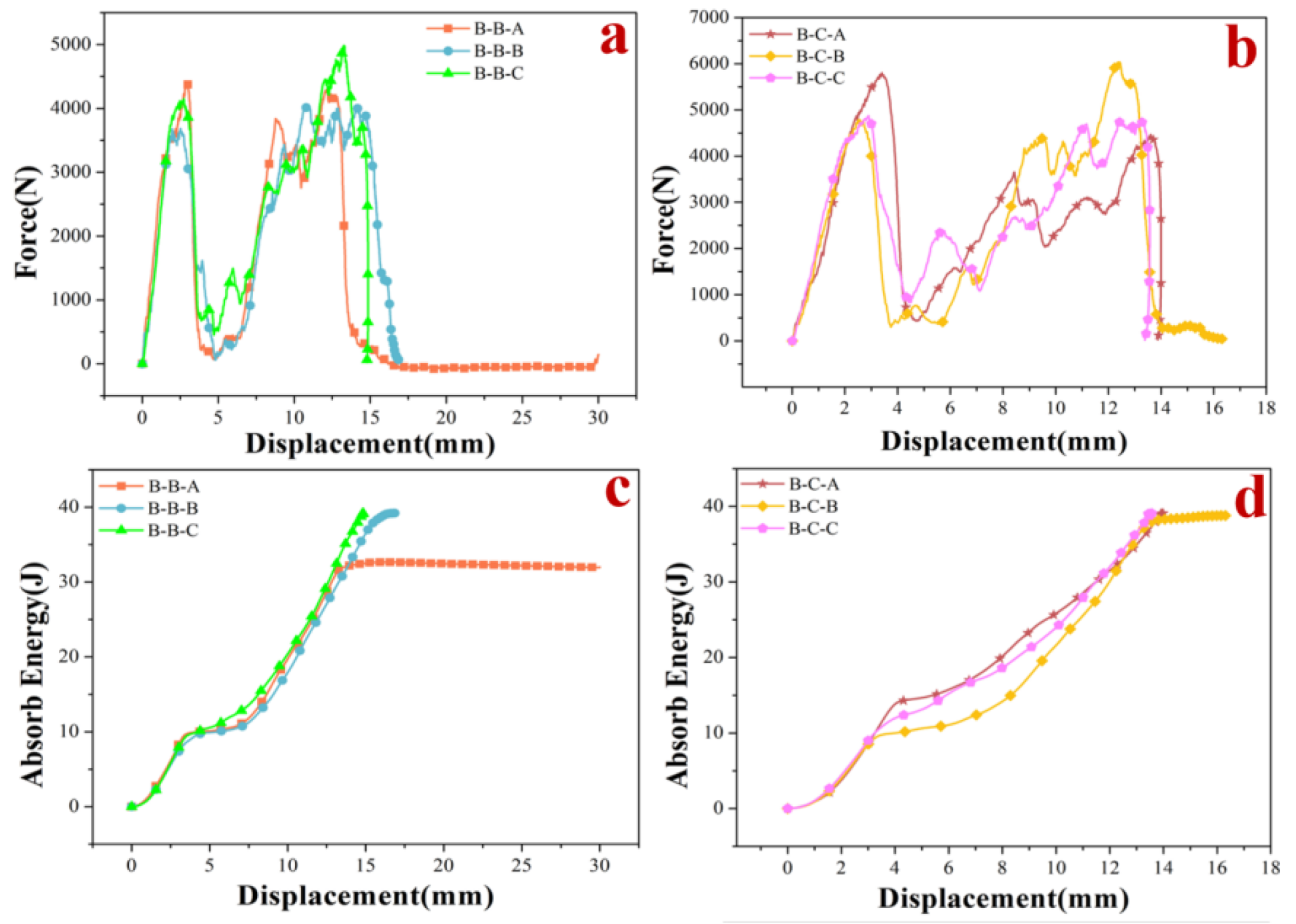
3.2. Numerical Results
3.3. Drop-Weight Impact Experiment
4. Discussion
5. Conclusions
- Cysteine, which contains the element S, chemically binds the keratin in the keratin scutes together, which has great mechanical properties.
- The application of the turtle carapace to the optimization of armor with a typical sandwich composite structure and no variation in mass and volume will significantly increase the impact resistance, and may provide insight into the subsequent development of protective armor for aerospace applications.
- The plate plays a crucial role in absorbing energy, and its increased stiffness and strength can reduce the depth of depression of the core to a greater extent. The use of negative-gradient structures can improve the energy absorption efficiency of the cores.
- A backplate with a reasonable stiffener layout will improve the impact resistance of composite structures when they are not fully penetrated.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Avery, J.G. Design Manual for Impact Damage Tolerant Aircraft Structure; Advisory Group for Aerospace Research and Development Neuilly-Sur-Seine: Neuilly-sur-Seine, France, 1981. [Google Scholar]
- Guo, X.; Dong, X.; Yu, Z.; Zhang, Z.; Xie, X.; Wang, X.; Xin, R.; Yan, W. Study on the Mechanical Properties of Bionic Protection and Self-Recovery Structures. Materials 2020, 13, 389. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guo, Y.; Yuan, M.; Qian, X. Bionic stab-resistant body armor based on triangular pyramid structure. Def. Technol. 2021, 17, 792–799. [Google Scholar] [CrossRef]
- Xiao, G.; He, Y.; Huang, Y.; He, S.; Wang, W.; Wu, Y. Bionic microstructure on titanium alloy blade with belt grinding and its drag reduction performance. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2020, 235, 2073810558. [Google Scholar] [CrossRef]
- Wu, M.L.; Ren, C.Z.; Xu, H.Z.; Zhou, C.L. Fabrication of a bionic microstructure on a C/SiC brake lining surface: Positive applications of surface defects for surface wetting control. Appl. Surf. Sci. 2018, 440, 669–679. [Google Scholar] [CrossRef]
- Huang, H.J.; Wu, Z.; Zhi, L. Architectural Design of Bionic Structure and Biomimetic Materials. Adv. Mater. Res. 2011, 314, 1991–1994. [Google Scholar] [CrossRef]
- Yang, W.; Zhou, F.; Chen, X.; Zhang, Y. Performance analysis of axial air cooling system with shark-skin bionic structure containing phase change material. Energy Convers. Manag. 2021, 250, 114921. [Google Scholar] [CrossRef]
- Feng, D.; Nan, J.; Feng, Y.; Zhang, X.; Yan, Y. Numerical investigation on improving the heat storage and transfer performance of ceramic/D-mannitol composite phase change materials by bionic graded pores and nanoparticle additives. Int. J. Heat Mass Transf. 2021, 179, 121748. [Google Scholar] [CrossRef]
- Chang, L.; Wang, D.; Hu, J.; Li, Y.; Wang, Y.; Hu, Y. Hierarchical Structure Fabrication of IPMC Strain Sensor with High Sensitivity. Front. Mater. 2021, 354. [Google Scholar] [CrossRef]
- Zhang, W.; Wu, C.; Zhang, C.; Chen, Z. Numerical study of the mechanical response of turtle shell. J. Bionic Eng. 2012, 9, 330–335. [Google Scholar] [CrossRef]
- Moustakas Verho, J.E.; Cherepanov, G.O. The integumental appendages of the turtle shell: An evo-devo perspective. J. Exp. Zool. Part B Mol. Dev. Evol. 2015, 324, 221–229. [Google Scholar] [CrossRef] [Green Version]
- Damiens, R.; Rhee, H.; Hwang, Y.; Park, S.J.; Hammi, Y.; Lim, H.; Horstemeyer, M.F. Compressive behavior of a turtle’s shell: Experiment, modeling, and simulation. J. Mech. Behav. Biomed. Mater. 2012, 6, 106–112. [Google Scholar] [CrossRef]
- Achrai, B.; Wagner, H.D. Micro-structure and mechanical properties of the turtle carapace as a biological composite shield. Acta Biomater. 2013, 9, 5890–5902. [Google Scholar] [CrossRef]
- Achrai, B.; Bar-On, B.; Wagner, H.D. Biological armors under impact—effect of keratin coating, and synthetic bio-inspired analogues. Bioinspiration Biomim. 2015, 10, 16009. [Google Scholar] [CrossRef]
- Trukhanov, A.V.; Tishkevich, D.I.; Podgornaya, S.V.; Kaniukov, E.; Darwish, M.A.; Zubar, T.I.; Timofeev, A.V.; Trukhanova, E.L.; Kostishin, V.G.; Trukhanov, S.V. Impact of the Nanocarbon on Magnetic and Electrodynamic Properties of the Ferrite/Polymer Composites. Nanomaterials 2022, 12, 868. [Google Scholar] [CrossRef]
- Almessiere, M.A.; Algarou, N.A.; Slimani, Y.; Sadaqat, A.; Baykal, A.; Manikandan, A.; Trukhanov, S.V.; Trukhanov, A.V.; Ercan, I. Investigation of exchange coupling and microwave properties of hard/soft (SrNi0. 02Zr0. 01Fe11. 96O19)/(CoFe2O4) x nanocomposites. Mater. Today Nano 2022, 18, 100186. [Google Scholar] [CrossRef]
- Han, B.S.; Xu, Y.J.; Guo, E.Y.; Jing, T.; Hou, H.L.; Luo, L.S. Microstructure and Mechanical Properties of Tortoise Carapace Structure Bio-Inspired Hybrid Composite. Acta Met. Sin. 2018, 31, 945–952. [Google Scholar] [CrossRef] [Green Version]
- Tarlochan, F. Sandwich structures for energy absorption applications: A review. Materials 2021, 14, 4731. [Google Scholar] [CrossRef]
- Wang, E.; Gardner, N.; Shukla, A. The blast resistance of sandwich composites with stepwise graded cores—ScienceDirect. Int. J. Solids Struct. 2009, 46, 3492–3502. [Google Scholar] [CrossRef] [Green Version]
- Jing, L.; Zhao, L. Blast resistance and energy absorption of sandwich panels with layered gradient metallic foam cores. J. Sandw. Struct. Mater. 2017, 21, 425909923. [Google Scholar] [CrossRef]
- Huang, W.; Fan, Z.; Zhang, W.; Liu, J.; Zhou, W. Impulsive response of composite sandwich structure with tetrahedral truss core. Compos. Sci. Technol. 2019, 176, 17–28. [Google Scholar] [CrossRef]
- Yang, S.; Qi, C.; Wang, D.; Gao, R.; Hu, H.; Shu, J. A Comparative Study of Ballistic Resistance of Sandwich Panels with Aluminum Foam and Auxetic Honeycomb Cores. Adv. Mech. Eng. 2013, 2013, 496–500. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, W.; Zhou, G.; Wang, C. Analysis and parametric optimization of a novel sandwich panel with double-V auxetic structure core under air blast loading. Int. J. Mech. Sci. 2018, 142, 245–254. [Google Scholar] [CrossRef]
- Hou, S.; Li, T.; Jia, Z.; Wang, L. Mechanical properties of sandwich composites with 3d-printed auxetic and non-auxetic lattice cores under low velocity impact. Mater. Des. 2018, 160, 1305–1321. [Google Scholar] [CrossRef]
- Zhang, J.; Ye, Y.; Zhu, Y.; Yuan, H.; Qin, Q.; Wang, T. On axial splitting and curling behaviour of circular sandwich metal tubes with metal foam core. Int. J. Solids Struct. 2020, 202, 111–125. [Google Scholar] [CrossRef]
- Shelef, Y.; Bar-On, B. Surface protection in bio-shields via a functional soft skin layer: Lessons from the turtle shell. J. Mech. Behav. Biomed. Mater. 2017, 73, 68–75. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Hu, N.; Zhou, C.; Lin, X.; Xie, H.; He, Q. The hierarchical structure and mechanical performance of a natural nanocomposite material: The turtle shell. Colloids Surf. A Physicochem. Eng. Asp. 2017, 520, 97–104. [Google Scholar] [CrossRef]
- Yoo, D.J. Porous scaffold design using the distance field and triply periodic minimal surface models. Biomaterials 2011, 32, 7741–7754. [Google Scholar] [CrossRef]
- Yao, Y.; Yang, S.; Chen, S.; Peng, Z. The microstructure and tensile property of the cuticle of turtle shells. Sci. Sin. Phys. Mech. Astron. 2020, 50, 090012. (In Chinese) [Google Scholar]
- Li, D.; Dai, N.; Tang, Y.; Dong, G.; Zhao, Y.F. Design and optimization of graded cellular structures with triply periodic level surface-based topological shapes. J. Mech. Des. 2019, 141, 071402. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Liao, Z.Q.; Wang, T. Research on aerodynamic characteristic of hollow projectile with 12.7 mm diameter. J. Syst. Simul. 2010, 22, 337–339. [Google Scholar]
- Wang, W.Z.; Zhao, T.Y.; Feng, S.S. Numerical simulation study on penetration of a 12.7 mm kinetic energy bullet into a composite armor. Explos. Shock. Waves 2019, 39, 123301. [Google Scholar]
- Shah, I.A.; Khan, R.; Koloor, S.S.R.; Petru, M.; Badshah, S.; Ahmad, S.; Amjad, M. Finite Element Analysis of the Ballistic Impact on Auxetic Sandwich Composite Human Body Armor. Materials 2022, 15, 2064. [Google Scholar] [CrossRef] [PubMed]
- Slimane, S.A.; Slimane, A.; Guelailia, A.; Boudjemai, A.; Kebdani, S.; Smahat, A.; Mouloud, D. Hypervelocity impact on honeycomb structure reinforced with bi-layer ceramic/aluminum facesheets used for spacecraft shielding. Mech. Adv. Mater. Struct. 2021, 1–19. [Google Scholar] [CrossRef]
- Cicero, S.; Madrazo, V.; Carrascal, I.A. On the Point Method load-bearing capacity predictions in Al7075-T651 structural components containing stress risers. Eng. Fail. Anal. 2012, 26, 129–138. [Google Scholar] [CrossRef]
- Bal, B.; Karaveli, K.K.; Cetin, B.; Gumus, B. The Precise Determination of the Johnson–Cook Material and Damage Model Parameters and Mechanical Properties of an Aluminum 7068-T651 Alloy. J. Eng. Mater. Technol. 2019, 141, 041001. [Google Scholar] [CrossRef]
- Nikawa, M.; Mori, H.; Kitagawa, Y.; Okada, M. FEM simulation for orthogonal cutting of Titanium-alloy considering ductile fracture to Johnson-Cook model. Mech. Eng. J. 2016, 3, 15–536. [Google Scholar] [CrossRef] [Green Version]
- Montroni, D.; Sparla, F.; Fermani, S.; Falini, G. Influence of proteins on mechanical properties of a natural chitin-protein composite. Acta Biomater. 2021, 120, 81–90. [Google Scholar] [CrossRef]
- Li, X.; Zhang, P.; Wang, Z.; Wu, G.; Zhao, L. Dynamic behavior of aluminum honeycomb sandwich panels under air blast: Experiment and numerical analysis. Compos. Struct. 2014, 108, 1001–1008. [Google Scholar] [CrossRef]
- Lin, J.; Wang, Z.; Zhao, L. Response of metallic cylindrical sandwich shells subjected to projectile impact—Experimental investigations. Compos. Struct. 2014, 107, 36–47. [Google Scholar]
- Yu, J.; Wang, E.; Li, J.; Zheng, Z. Static and low-velocity impact behavior of sandwich beams with closed-cell aluminum-foam core in three-point bending. Int. J. Impact Eng. 2008, 35, 885–894. [Google Scholar] [CrossRef]
- Ajdari, A.; Nayeb-Hashemi, H.; Vaziri, A. Dynamic crushing and energy absorption of regular, irregular and functionally graded cellular structures. Int. J. Solids Struct. 2011, 48, 506–516. [Google Scholar] [CrossRef]
- Ajdari, A.; Babaee, S.; Vaziri, A. Mechanical properties and energy absorption of heterogeneous and functionally graded cellular structures. Procedia Eng. 2011, 10, 219–223. [Google Scholar] [CrossRef] [Green Version]
- Almessiere, M.A.; Slimani, Y.; Algarou, N.A.; Vakhitov, M.G.; Klygach, D.S.; Baykal, A.; Zubar, T.I.; Trukhanov, S.V.; Trukhanov, A.V.; Attia, H.; et al. Tuning the Structure, Magnetic, and High Frequency Properties of Sc-Doped Sr0.5Ba0.5ScxFe12−xO19/NiFe2O4 Hard/Soft Nanocomposites. Adv. Electron. Mater. 2022, 8, 2101124. [Google Scholar] [CrossRef]



| Plate Group | Name | Core Group | Name | Backplate Group | Name |
|---|---|---|---|---|---|
| Control | Plate A | Control | Core A | Control | Backplate A |
| Square | Plate B | Negative Gradient | Core B | Three Stiffeners | Backplate B |
| Rhombus | Plate C | Positive Gradient | Core C | Four Stiffeners | Backplate C |
| Sr. No. | Property | Value | Unit |
|---|---|---|---|
| 1 | Strain Rate Correlation | First-Order | |
| 2 | Initial Yield Stress | 835.833 | MPa |
| 3 | Strain-hardening Coefficient | 473.667 | MPa |
| 4 | Strain-hardening Exponent | 0.561 | |
| 5 | Strain Rate Sensitivity | −0.08581 | |
| 6 | Thermal Softening Exponent | 4.2285 | |
| 7 | Melting Temperature | 873 | K |
| 8 | Reference Strain Rate (/sec) | 0.0005 |
| Sr. No. | Property | Value |
|---|---|---|
| 1 | Damage Constant D1 | 0.1009 |
| 2 | Damage Constant D2 | 0.1214 |
| 3 | Damage Constant D3 | −0.9150 |
| 4 | Damage Constant D4 | 0.16789 |
| 5 | Damage Constant D5 | 0.877675 |
| 6 | Melting Temperature | 873 K |
| 7 | Reference Strain Rate (/sec) | 1 |
| Sr. No. | Property | Value | Unit |
|---|---|---|---|
| 1 | Hardness | 85 | Shore D |
| 2 | Flexural modulus | 2692–2775 | Mpa |
| 3 | Flexural strength | 69–74 | Mpa |
| 4 | Tensile modulus | 2589–2695 | Mpa |
| 5 | Tensile strength | 38–56 | Mpa |
| 6 | Elongation at break | 8–12% | |
| 7 | Poisson’s | 0.4–0.44 | |
| 8 | Impact strength notched Izod | 45–55 | J/m |
| 9 | Heat deflection temperature | 38~50 | °C |
| 10 | Coefficient of thermal expansion | 0.000097 | °C |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pei, B.; Guo, L.; Wu, X.; Hu, M.; Wu, S.; Wang, Y. Impact Resistant Structure Design and Optimization Inspired by Turtle Carapace. Materials 2022, 15, 2899. https://doi.org/10.3390/ma15082899
Pei B, Guo L, Wu X, Hu M, Wu S, Wang Y. Impact Resistant Structure Design and Optimization Inspired by Turtle Carapace. Materials. 2022; 15(8):2899. https://doi.org/10.3390/ma15082899
Chicago/Turabian StylePei, Baoqing, Lei Guo, Xueqing Wu, Mengyuan Hu, Shuqin Wu, and Yangwei Wang. 2022. "Impact Resistant Structure Design and Optimization Inspired by Turtle Carapace" Materials 15, no. 8: 2899. https://doi.org/10.3390/ma15082899
APA StylePei, B., Guo, L., Wu, X., Hu, M., Wu, S., & Wang, Y. (2022). Impact Resistant Structure Design and Optimization Inspired by Turtle Carapace. Materials, 15(8), 2899. https://doi.org/10.3390/ma15082899







