Experimental and Numerical Investigations on the Damage Induced in the Shearing Process for QP980 Steel
Abstract
:1. Introduction
2. Material and Methods
2.1. Material
2.2. Methods
2.2.1. Shearing Experiment
2.2.2. Microstructure Characterization
2.2.3. Mechanical Property Tests
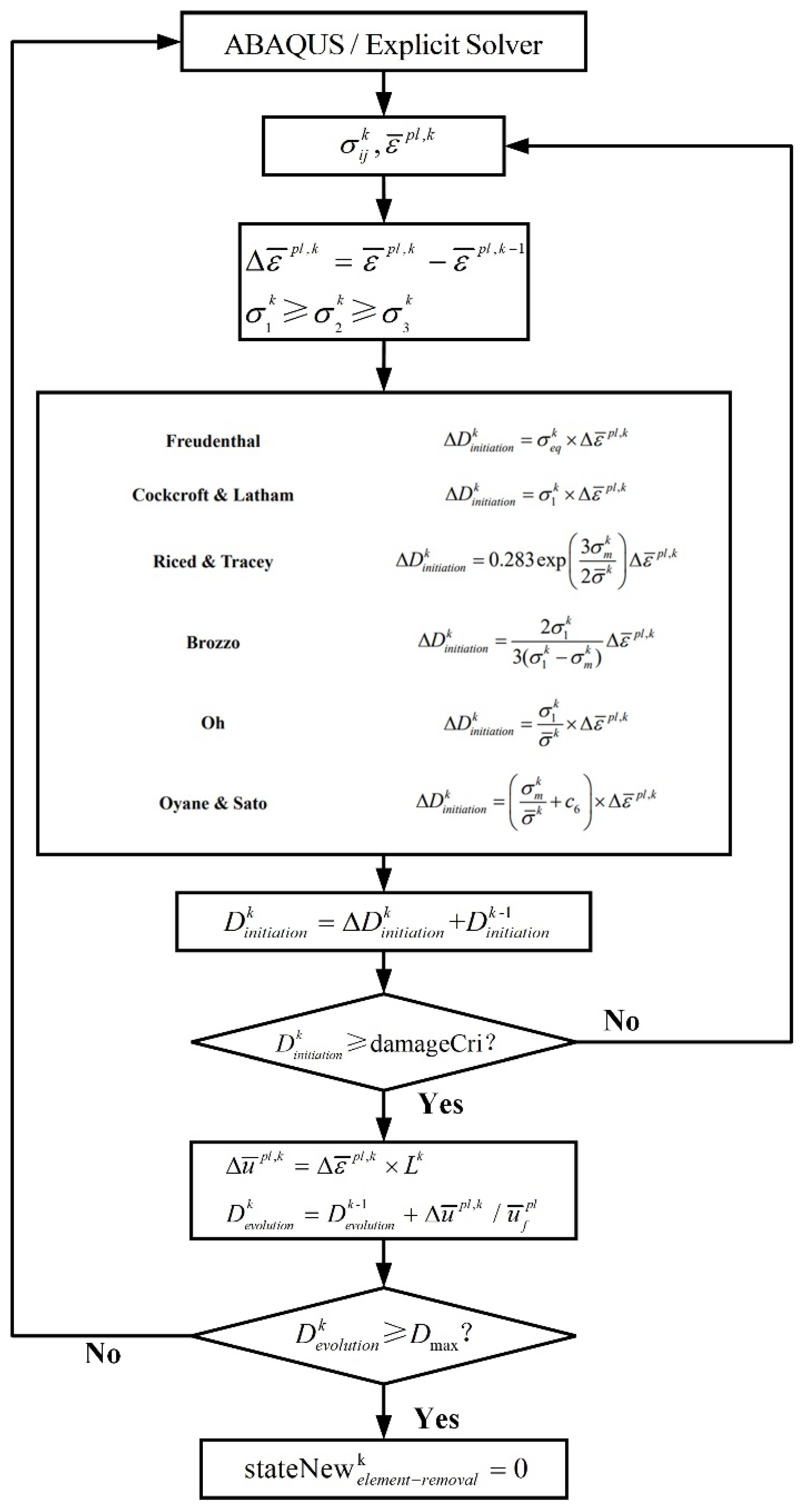
2.2.4. FEM Simulation for the Shearing Process
- Material property
- 2.
- Modeling and meshing
- 3.
- Ductile fracture criteria
| Ductile Fracture Criteria | Equations |
|---|---|
| Freudenthal [44] | |
| Cockcroft and Latham [45] | |
| Rice and Tracey [46] | |
| Brozzo [47] | |
| Oh [48] | |
| Oyane-Sato [49] |
| Material | /MPa | /MPa | /MPa | ||||
|---|---|---|---|---|---|---|---|
| QP980 | 230.53 | 213.49 | 0.089 | 0.19 | 0.20 | 0.17 | 2.08 |
3. Results and Discussion
3.1. Analysis of Deformation and Damage Evolution in the Shearing Process
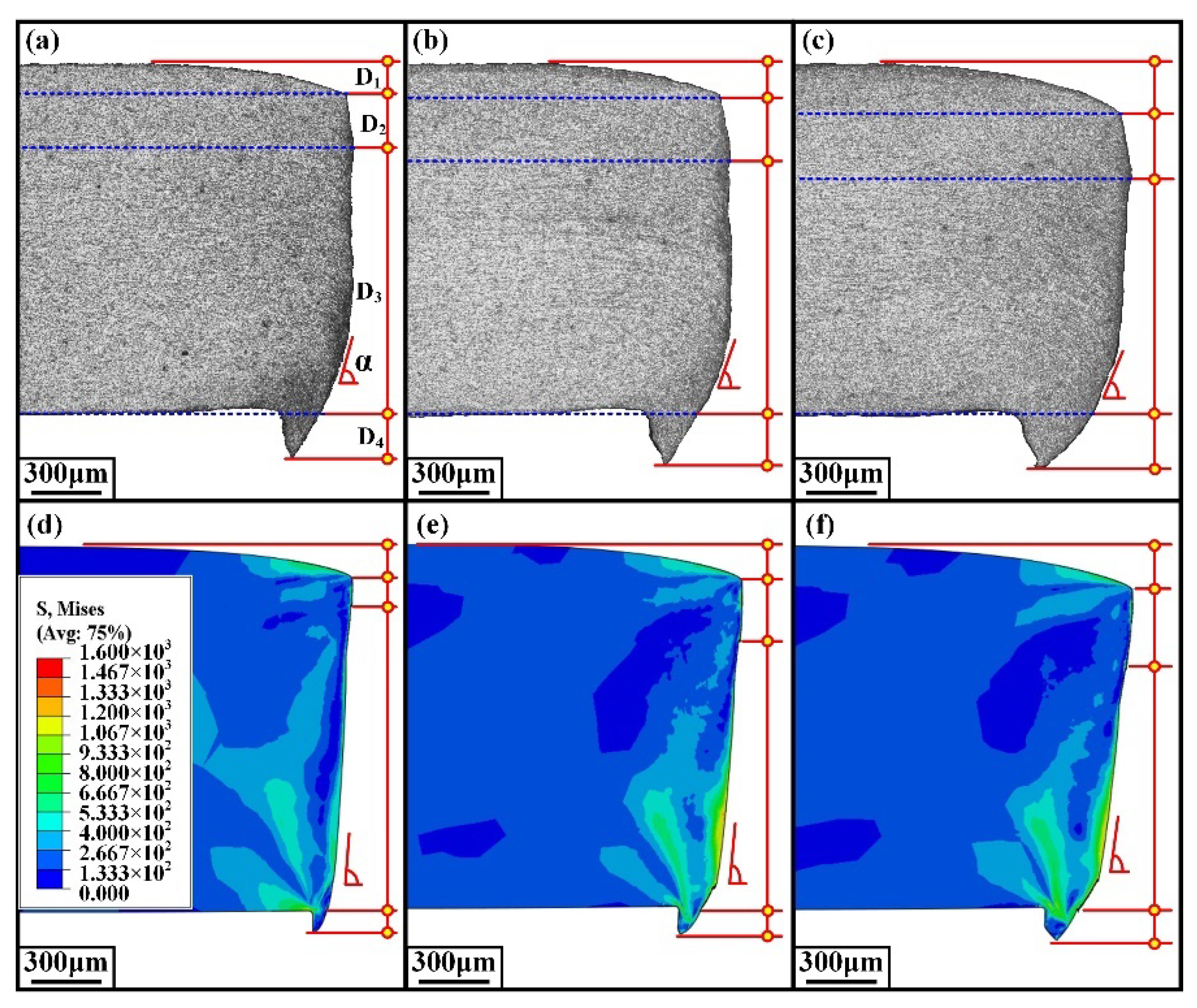
3.1.1. Shearing Deformation
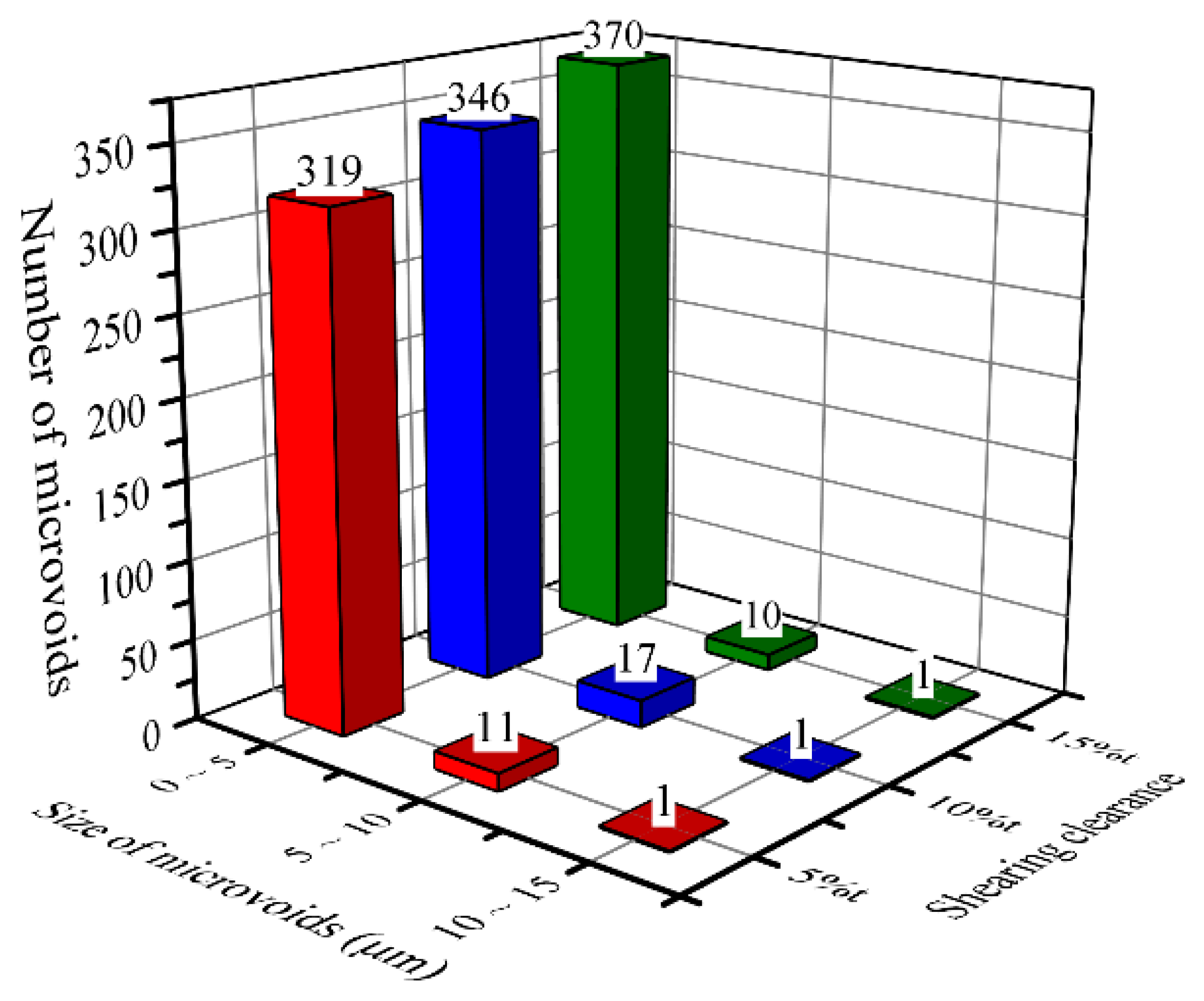
3.1.2. Analysis of Microvoids Generated in the Shearing Process
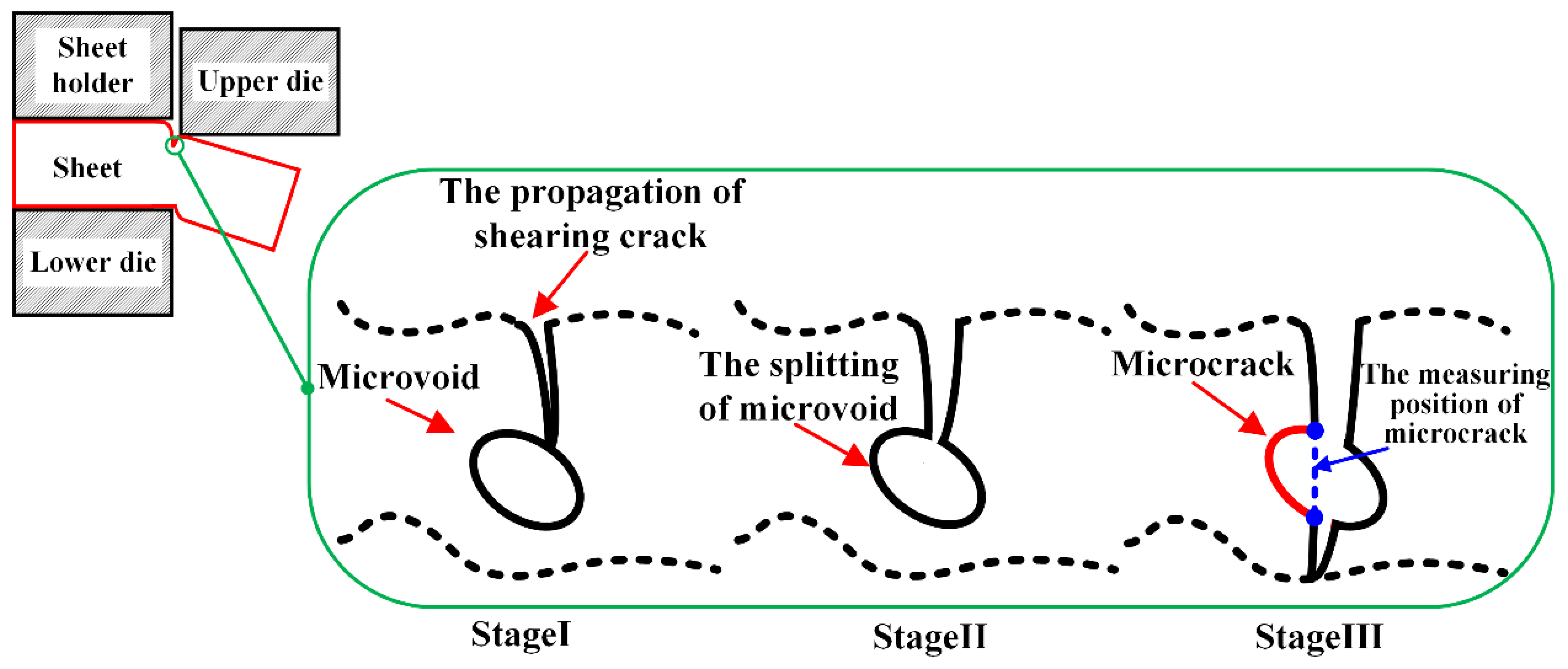
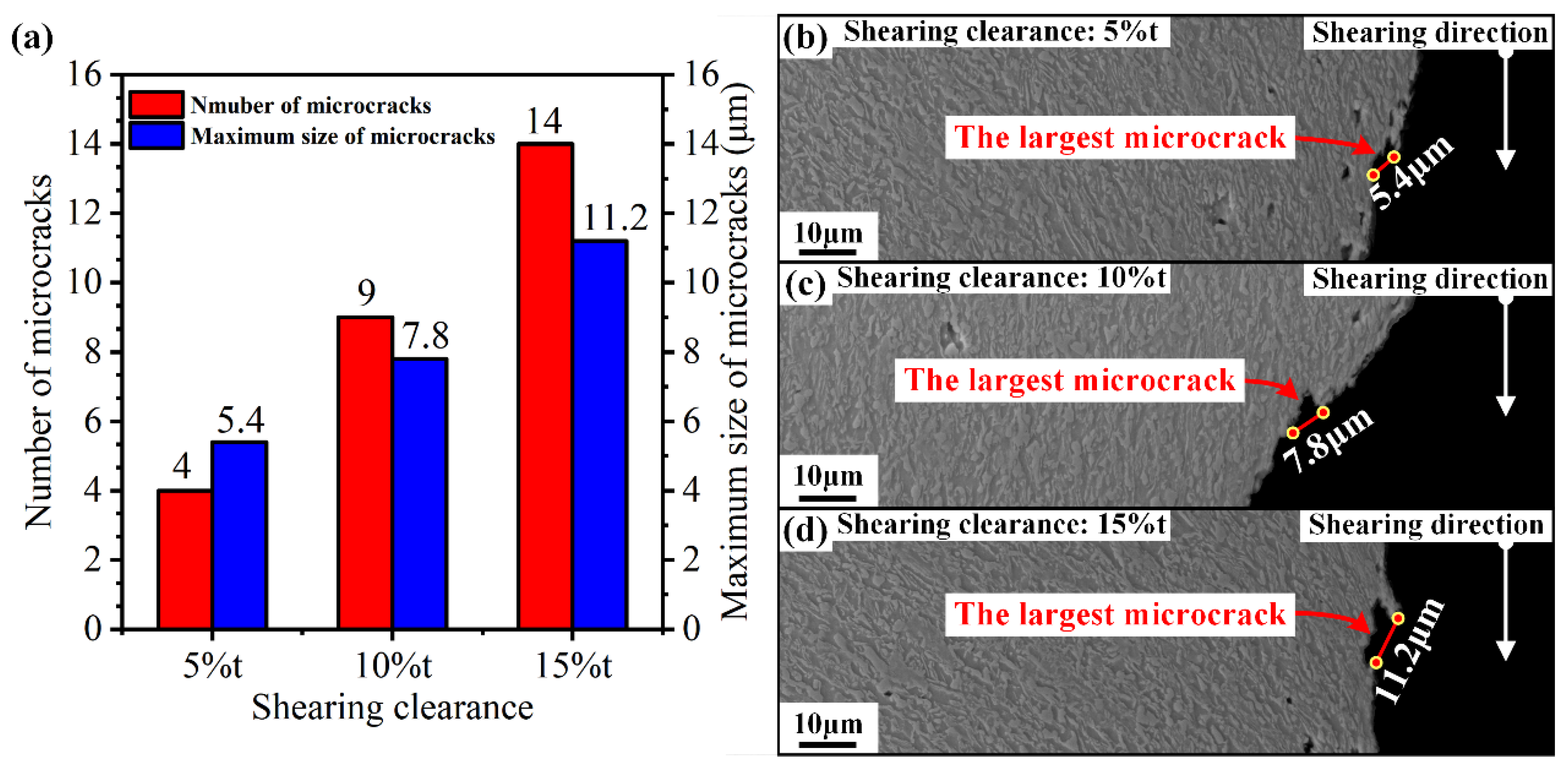
3.1.3. Study of Microcracks Formed in the Shearing Process
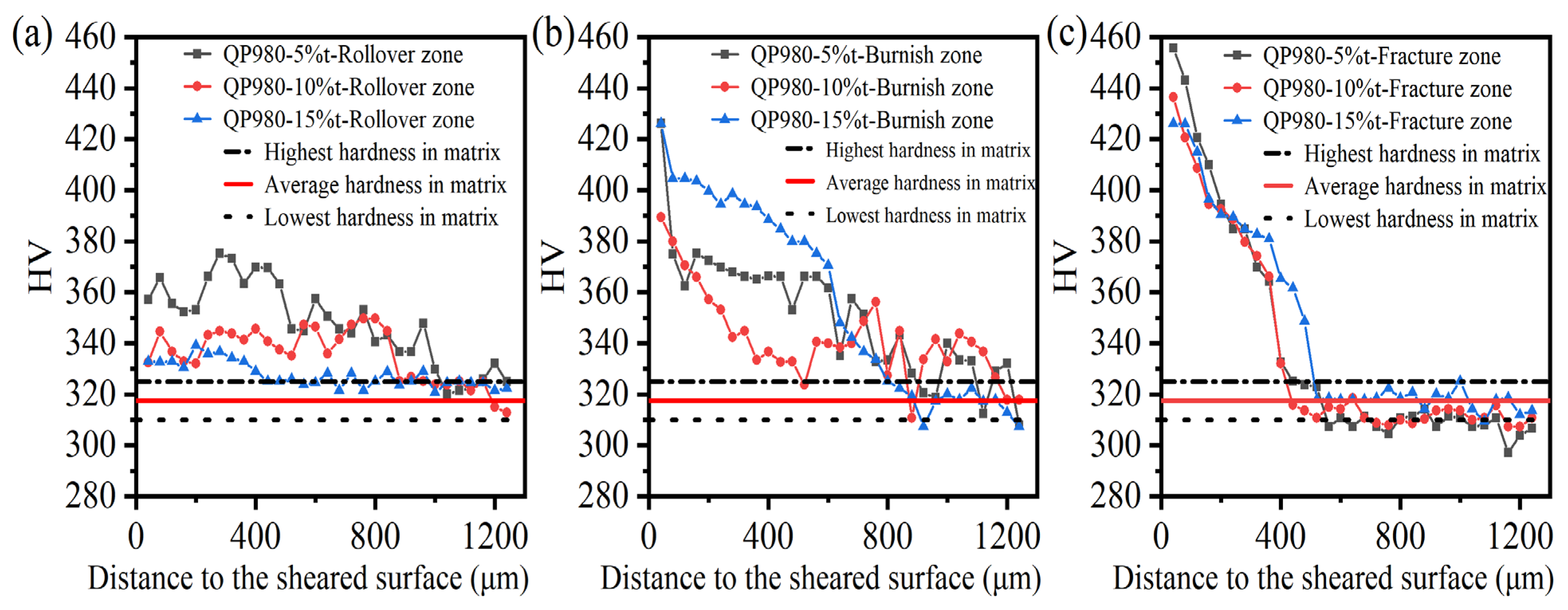
3.1.4. Characterization of Work-Hardening Behavior
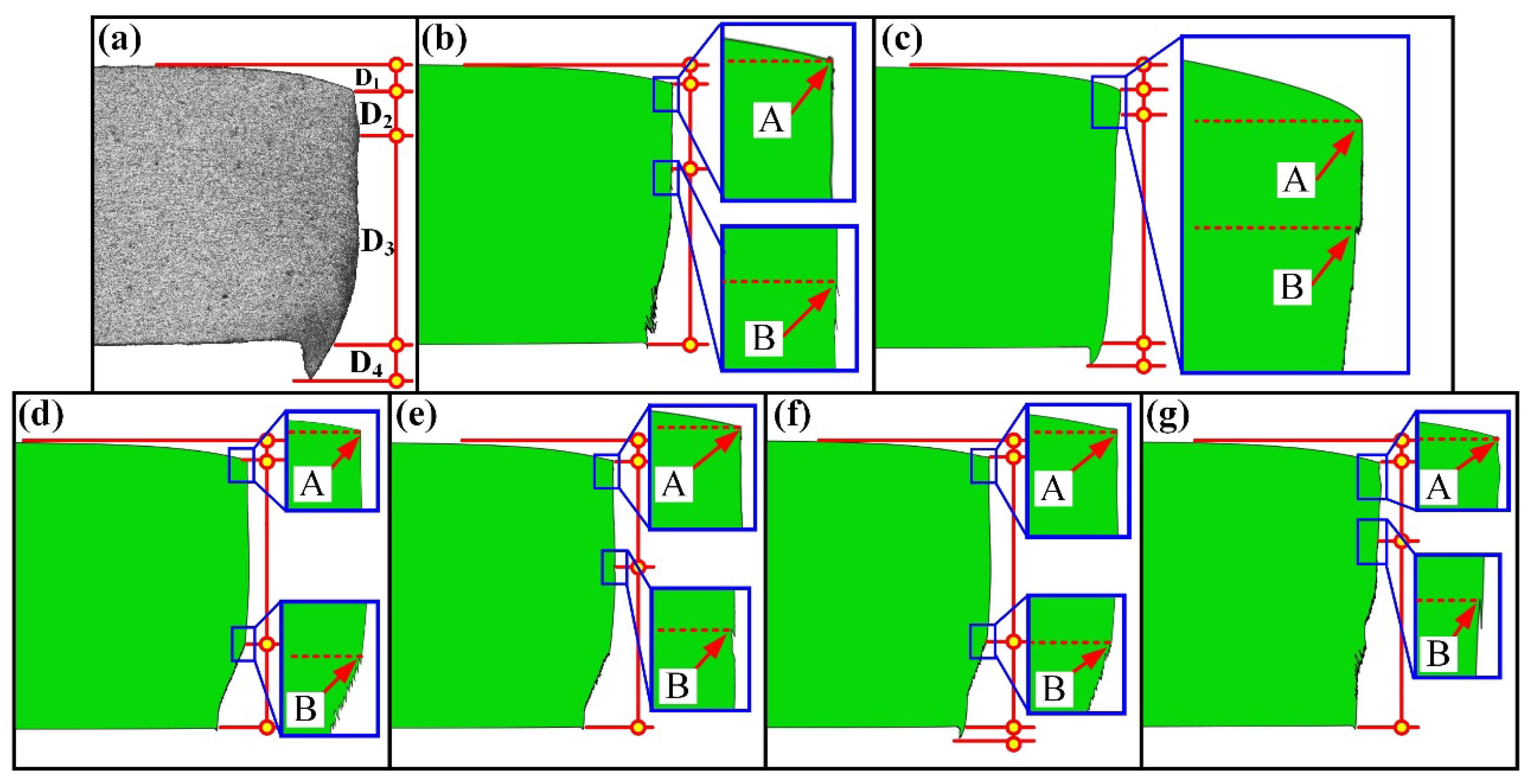
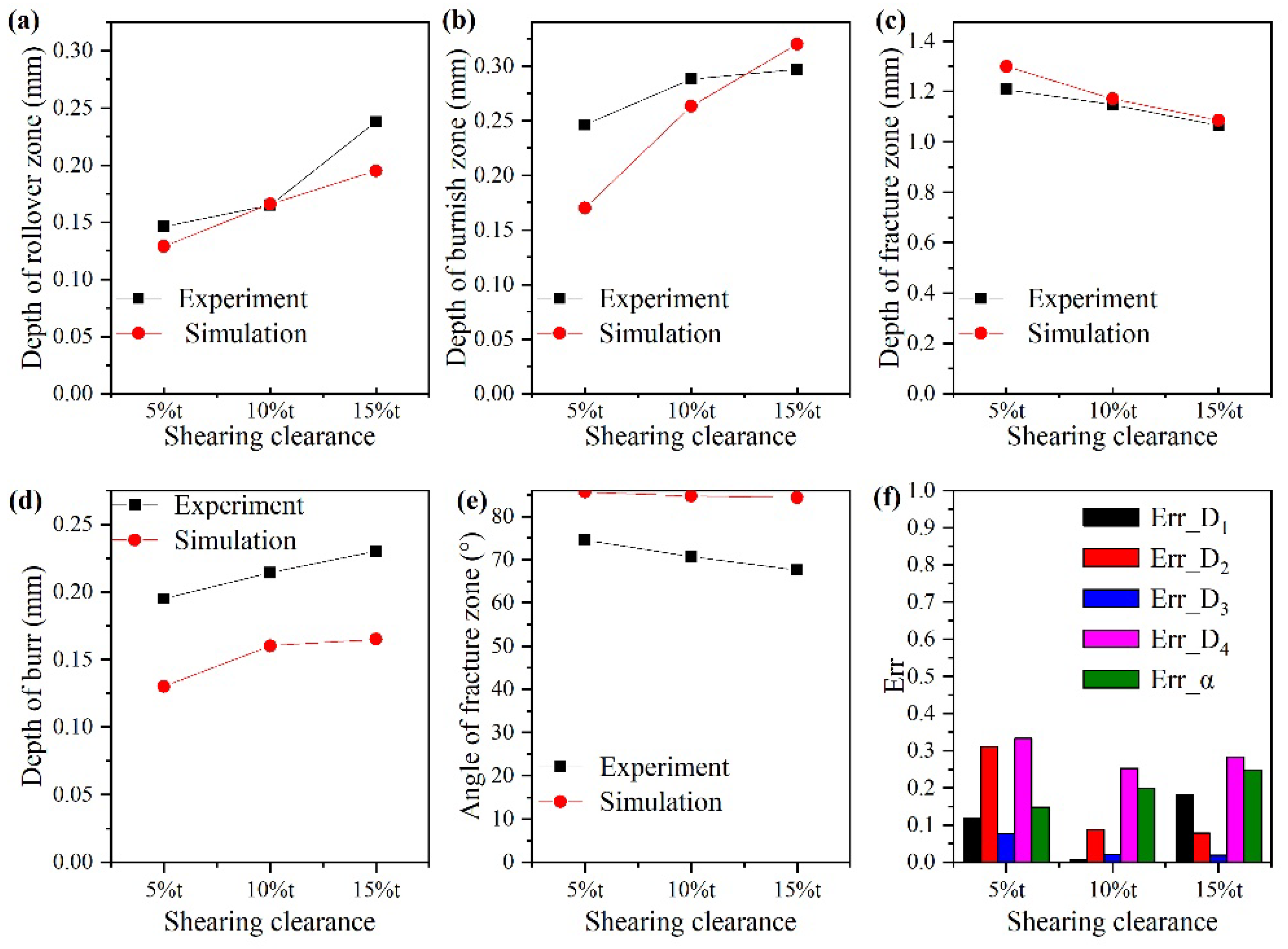
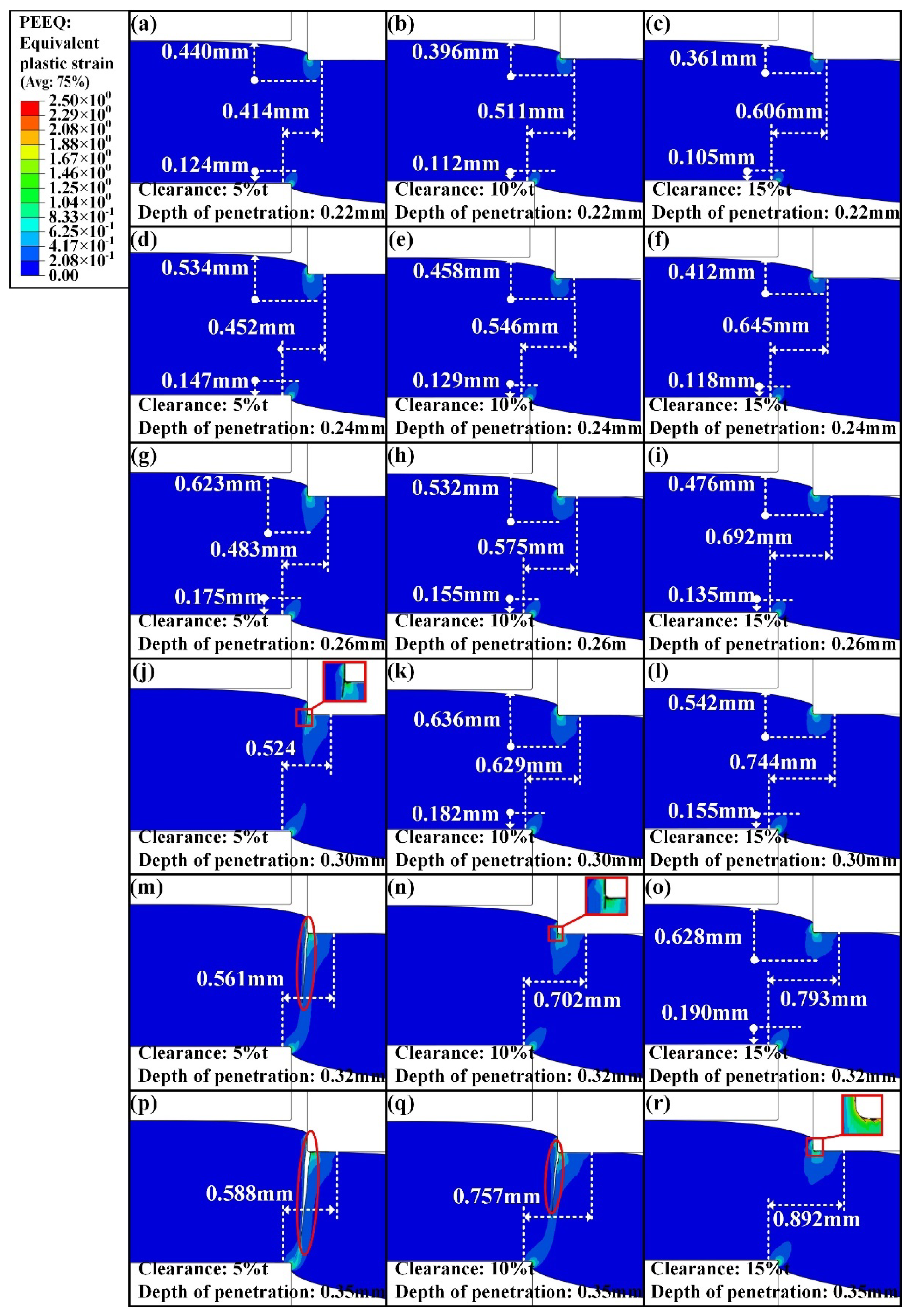
3.2. Finite Element Analysis of Shearing Process
3.3. Evaluation of Tensile Property of Sheared Edge
4. Conclusions
- (1)
- Three kinds of damage generated by mechanical deformation in the shearing process including microvoids, microcracks, and work-hardening behavior were determined, and the damage degree increased with the increasing shearing clearance. The optimum formability of the sheared edge with minimal damage validated by the tensile test was obtained under the shearing clearance of 5%t.
- (2)
- Two different types of microvoids were identified based on the nucleation site. A large number of microvoids with small sizes (≤5 μm) were formed at phase interfaces, and a few microvoids generated from inclusions had large sizes of more than 5 μm. The V-shape microcrack evolved from the microvoid distributed in the sheared surface, which is a crucial factor for it can result in edge failure in the next forming process.
- (3)
- Obvious work-hardening behavior appeared in the sheared edge. The longest work-hardening distance (800 μm) was located in the burnish zone, while the highest microhardness (>420 HV) occurred in the fracture zone, which further increases the risk of sheared-edge cracking. Therefore, reducing the depth of the fracture zone and controlling the damage degree are the key to improving the formability of sheared edges.
- (4)
- Six widely applicated uncoupled ductile fracture models, including Freudenthal, Cockcroft and Latham, Rice and Tracey, Brozzeo, Oh, and Oyane-Sato models, were successfully introduced to simulate the shearing process through developing user-defined subroutine VUSDFLD in Abaqus. The simulation results of the Cockcroft and Latham model agree with experimental results better than others. The determination of suitable ductile fracture criteria for QP980 steel and accurate simulations are useful for engineers to shorten the time and cost of designing an optimum shearing process.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, L.; Speer, J.G. Quenching and partitioning steel heat treatment. Metall. Microstruct. Anal. 2013, 2, 268–281. [Google Scholar] [CrossRef] [Green Version]
- Parthiban, R.; Ray, R.K.; Hari Kumar, K.C.; Sankaran, S. Influence of rolling temperature and strain on the microstructural evolution and mechanical properties in quench and partition (Q&P) steels. Mater. Sci. Eng. A 2021, 825, 141893. [Google Scholar]
- Kim, D.H.; Kang, J.-H.; Gwon, H.; Ryu, J.H.; Kim, S.-J. Counter-balancing effects of Si on C partitioning and stacking fault energy of austenite in 10Mn quenching and partitioning steel. J. Mater. Sci. Technol. 2022, 98, 248–257. [Google Scholar] [CrossRef]
- Kickinger, C.; Suppan, C.; Hebesberger, T.; Schnitzer, R.; Hofer, C. Microstructure and mechanical properties of partially ferritic Q&P steels. Mater. Sci. Eng. A 2021, 815, 141296. [Google Scholar]
- Wang, Y.; Xu, Y.; Liu, R.; Peng, F.; Gu, X.; Zhang, T.; Hou, X.; Sun, W. Microstructure evolution and mechanical behavior of a novel hot-galvanized Q&P steel subjected to high-temperature short-time overaging treatment. Mater. Sci. Eng. A 2020, 789, 139665. [Google Scholar]
- Krbata, M.; Krizan, D.; Eckert, M.; Kaar, S.; Dubec, A.; Ciger, R. Austenite Decomposition of a Lean Medium Mn Steel Suitable for Quenching and Partitioning Process: Comparison of CCT and DCCT Diagram and Their Microstructural Changes. Materials 2022, 15, 1753. [Google Scholar] [CrossRef]
- Chen, X.; Jiang, H.; Cui, Z.; Lian, C.; Lu, C. Hole Expansion Characteristics of Ultra High Strength Steels. Procedia Eng. 2014, 81, 718–723. [Google Scholar] [CrossRef] [Green Version]
- Han, Y.; Chu, X.; Kuang, S.; Li, T.; Xie, C.; Teng, H. Investigation of the edge crack sensitivity of cold rolled hot-dip galvanized DP780 steels. J. Mater. Eng. Perform. 2019, 28, 372–381. [Google Scholar] [CrossRef]
- Matsuno, T.; Nitta, J.; Sato, K.; Mizumura, M.; Suehiro, M. Effect of shearing clearance and angle on stretch-flange formability evaluated by saddle-type forming test. J. Mater. Process. Technol. 2015, 223, 98–104. [Google Scholar] [CrossRef]
- Zhou, M.; Li, Y.; Hu, Q.; Li, X.; Chen, J. Investigations on edge quality and its effect on tensile property and fracture patterns of QP980. J. Manuf. Processes 2019, 37, 509–518. [Google Scholar] [CrossRef]
- Nothhaft, K.; Suh, J.; Golle, M.; Picas, I.; Casellas, D.; Volk, W. Shear cutting of press hardened steel: Influence of punch chamfer on process forces, tool stresses and sheared edge qualities. Prod. Eng. 2012, 6, 413–420. [Google Scholar] [CrossRef]
- Wang, L.; Hu, D.; Chen, M.; Wang, H. Experimental Investigation of the Blanked Surface of C5191 Phosphor Bronze Sheet over a Wide Range of Blanking Speeds. Materials 2020, 13, 3335. [Google Scholar] [CrossRef] [PubMed]
- Choi, H.-S.; Kim, B.-M.; Ko, D.-C. Effect of clearance and inclined angle on sheared edge and tool failure in trimming of DP980 sheet. J. Mech. Sci. Technol. 2014, 28, 2319–2328. [Google Scholar] [CrossRef]
- Akyürek, F.; Yaman, K.; Tekiner, Z. An experimental work on tool wear affected by die clearance and punch hardness. Arab. J. Sci. Eng. 2017, 42, 4683–4692. [Google Scholar] [CrossRef]
- Mori, K.; Abe, Y.; Suzui, Y. Improvement of stretch flangeability of ultra high strength steel sheet by smoothing of sheared edge. J. Mater. Process. Technol. 2010, 210, 653–659. [Google Scholar] [CrossRef]
- Sachnik, P.; Hoque, S.E.; Volk, W. Burr-free cutting edges by notch-shear cutting. J. Mater. Process. Technol. 2017, 249, 229–245. [Google Scholar] [CrossRef]
- Golovashchenko, S.F.; Gillard, A.J.; Mamutov, A.V.; Bonnen, J.F.; Tang, Z. Electrohydraulic trimming of advanced and ultra high strength steels. J. Mater. Process. Technol. 2014, 214, 1027–1043. [Google Scholar] [CrossRef]
- Stahl, J.; Pätzold, I.; Golle, R.; Sunderkötter, C.; Sieurin, H.; Volk, W. Effect of one- and two-stage shear cutting on the fatigue strength of truck frame parts. J. Manuf. Mater. Process. 2020, 4, 52. [Google Scholar] [CrossRef]
- Kim, J.H.; Seo, E.J.; Kwon, M.-H.; Kang, S.; De Cooman, B.C. Effect of quenching temperature on stretch flangeability of a medium Mn steel processed by quenching and partitioning. Mater. Sci. Eng. A 2018, 729, 276–284. [Google Scholar] [CrossRef]
- Karelova, A.; Krempaszky, C.; Werner, E.; Tsipouridis, P.; Hebesberger, T.; Pichler, A. Hole expansion of dual-phase and complex-phase AHS steels—Effect of edge conditions. Steel Res. Int. 2009, 80, 71–77. [Google Scholar]
- Yoon, J.I.; Lee, H.H.; Jung, J.; Kim, H.S. Effect of grain size on stretch-flangeability of twinning-induced plasticity steels. Mater. Sci. Eng. A 2018, 735, 295–301. [Google Scholar] [CrossRef]
- Gwon, H.; Kim, J.H.; Kim, J.-K.; Suh, D.-W.; Kim, S.-J. Role of grain size on deformation microstructures and stretch-flangeability of TWIP steel. Mater. Sci. Eng. A 2020, 773, 138861. [Google Scholar] [CrossRef]
- Achouri, M.; Germain, G.; Dal Santo, P.; Saidane, D. Experimental and numerical analysis of micromechanical damage in the punching process for High-Strength Low-Alloy steels. Mater. Des. 2014, 56, 657–670. [Google Scholar] [CrossRef] [Green Version]
- Lou, Y.; Huh, H.; Lim, S.; Pack, K. New ductile fracture criterion for prediction of fracture forming limit diagrams of sheet metals. Int. J. Solids Struct. 2012, 49, 3605–3615. [Google Scholar] [CrossRef] [Green Version]
- Hubert, C.; Dubar, M.; Dubois, A.; Dubar, L. 3D modeling of edge trimming process. Int. J. Mater. Form. 2009, 2, 837–840. [Google Scholar] [CrossRef]
- Hatanaka, N.; Yamaguchi, K.; Takakura, N. Finite element simulation of the shearing mechanism in the blanking of sheet metal. J. Mater. Process. Technol. 2003, 139, 64–70. [Google Scholar] [CrossRef]
- Hatanaka, N.; Yamaguchi, K.; Takakura, N.; Iizuka, T. Simulation of sheared edge formation process in blanking of sheet metals. J. Mater. Process. Technol. 2003, 140, 628–634. [Google Scholar] [CrossRef]
- Wang, K.; Luo, M.; Wierzbicki, T. Experiments and modeling of edge fracture for an AHSS sheet. Int. J. Fract. 2014, 187, 245–268. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.; Greve, L.; Wierzbicki, T. FE simulation of edge fracture considering pre-damage from blanking process. Int. J. Solids Struct. 2015, 71, 206–218. [Google Scholar] [CrossRef]
- Qian, L.; Ji, W.; Sun, C.; Fang, G.; Lian, J. Prediction of edge fracture during hole-flanging of advanced high-strength steel considering blanking pre-damage. Eng. Fract. Mech. 2021, 248, 107721. [Google Scholar] [CrossRef]
- Wang, C.; Chen, J.; Xia, C.; Ren, F.; Chen, J. A new method to calculate threshold values of ductile fracture criteria for advanced high-strength sheet blanking. J. Mater. Eng. Perform. 2014, 23, 1296–1306. [Google Scholar] [CrossRef]
- Kolanu, N.R.; Raju, G.; Ramji, M. A unified numerical approach for the simulation of intra and inter laminar damage evolution in stiffened CFRP panels under compression. Compos. B Eng. 2020, 190, 107931. [Google Scholar] [CrossRef]
- Rozylo, P. Failure analysis of thin-walled composite structures using independent advanced damage models. Compos. Struct. 2021, 262, 113598. [Google Scholar] [CrossRef]
- Jia, Q.; Guo, W.; Wan, Z.; Peng, Y.; Zou, G.; Tian, Z.; Zhou, Y.N. Microstructure and mechanical properties of laser welded dissimilar joints between QP and boron alloyed martensitic steels. J. Mater. Process. Technol. 2018, 259, 58–67. [Google Scholar] [CrossRef]
- Guo, W.; Wan, Z.; Peng, P.; Jia, Q.; Zou, G.; Peng, Y. Microstructure and mechanical properties of fiber laser welded QP980 steel. J. Mater. Process. Technol. 2018, 256, 229–238. [Google Scholar] [CrossRef]
- Zou, D.Q.; Li, S.H.; He, J.; Gu, B.; Li, Y.F. The deformation induced martensitic transformation and mechanical behavior of quenching and partitioning steels under complex loading process. Mater. Sci. Eng. A 2018, 715, 243–256. [Google Scholar] [CrossRef]
- Guo, W.; Wan, Z.; Jia, Q.; Ma, L.; Zhang, H.; Tan, C.; Peng, P. Laser weldability of TWIP980 with DP980/B1500HS/QP980 steels: Microstructure and mechanical properties. Opt. Laser Technol. 2020, 124, 38. [Google Scholar] [CrossRef]
- Chang, Y.; Han, S.; Li, X.; Wang, C.; Zheng, G.; Dong, H. Effect of shearing clearance on formability of sheared edge of the third-generation automotive medium-Mn steel with metastable austenite. J. Mater. Process. Technol. 2018, 259, 216–227. [Google Scholar] [CrossRef]
- ISO 6507-1:2018; Metallic Materials—Vickers Hardness Test—Part 1: Test Method. International Organization for Standardization: Geneva, Switzerland, 2018; pp. 1–38.
- ISO 6892-1:2016; Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature. International Organization for Standardization: Geneva, Switzerland, 2019; pp. 1–86.
- Park, N.; Huh, H.; Lim, S.J.; Lou, Y.; Kang, Y.S.; Seo, M.H. Fracture-based forming limit criteria for anisotropic materials in sheet metal forming. Int. J. Plast. 2017, 96, 1–35. [Google Scholar] [CrossRef]
- Mu, L.; Zang, Y.; Wang, Y.; Li, X.L.; Araujo Stemler, P.M. Phenomenological uncoupled ductile fracture model considering different void deformation modes for sheet metal forming. Int. J. Mech. Sci. 2018, 141, 408–423. [Google Scholar] [CrossRef]
- Lou, Y.; Huh, H. Prediction of ductile fracture for advanced high strength steel with a new criterion: Experiments and simulation. J. Mater. Process. Technol. 2013, 213, 1284–1302. [Google Scholar] [CrossRef]
- Freudenthal, A.M. The Inelastic Behavior of Engineering Materials and Structures. John Wiley & Sons: New York, NY, USA, 1950. [Google Scholar]
- Cockroft, M.G.; Latham, D.J. Ductility and the workability of metals. J. Met. 1968, 96, 33–39. [Google Scholar]
- Rice, J.R.; Tracey, D.M. On the ductile enlargement of voids in triaxial stress fields. J. Mech. Phys. Solids 1969, 17, 201–217. [Google Scholar] [CrossRef] [Green Version]
- Brozzo, P.; Deluca, B.; Rendina, R. A new method for the prediction of formability limits in metal sheets. In Proceedings of the 7th Biennal Conference IDDR, Amsterdam, The Netherlands, 9–13 October 1972; pp. 9–13. [Google Scholar]
- Oh, S.I.; Chen, C.C.; Kobayashi, S. Ductile Fracture in Axisymmetric Extrusion and Drawing—Part 2: Workability in Extrusion and Drawing. J. Eng. Ind. Trans. ASME 1979, 101, 36–44. [Google Scholar] [CrossRef]
- Oyane, M.; Sato, T.; Okimoto, K.; Shima, S. Criteria for ductile fracture and their applications. J. Mech. Work. Technol. 1980, 4, 65–81. [Google Scholar] [CrossRef]
- Han, X.; Yang, K.; Ding, Y.; Tan, S.; Chen, J. Numerical and experimental investigations on mechanical trimming process for hot stamped ultra-high strength parts. J. Mater. Process. Technol. 2016, 234, 158–168. [Google Scholar] [CrossRef]
- Hillerborg, A.; Modéer, M.; Petersson, P.E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cem. Concr. Res. 1976, 6, 773–781. [Google Scholar] [CrossRef]
- Han, S.; Chang, Y.; Wang, C.Y.; Dong, H. A comprehensive investigation on the damage induced by the shearing process in DP780 steel. J. Mater. Process. Technol. 2022, 299, 117377. [Google Scholar] [CrossRef]
- Zhou, F.L.; Wang, C.Y.; Lei, Z.G.; Cao, W.Q.; Dan, H. Crack propagation behavior of medium manganese automobile steel in 0.13C-5Mn. Iron Steel 2019, 54, 75–80. [Google Scholar]
- Chang, Y.; Han, S.; Li, X.; Wang, C.; Zheng, G.; Dong, H. Effects of Different Cutting Processes on Characteristics of Cut Damage for the Third-Generation Automobile Medium-Mn Steel. Steel Res. Int. 2018, 89, 1700375. [Google Scholar] [CrossRef]

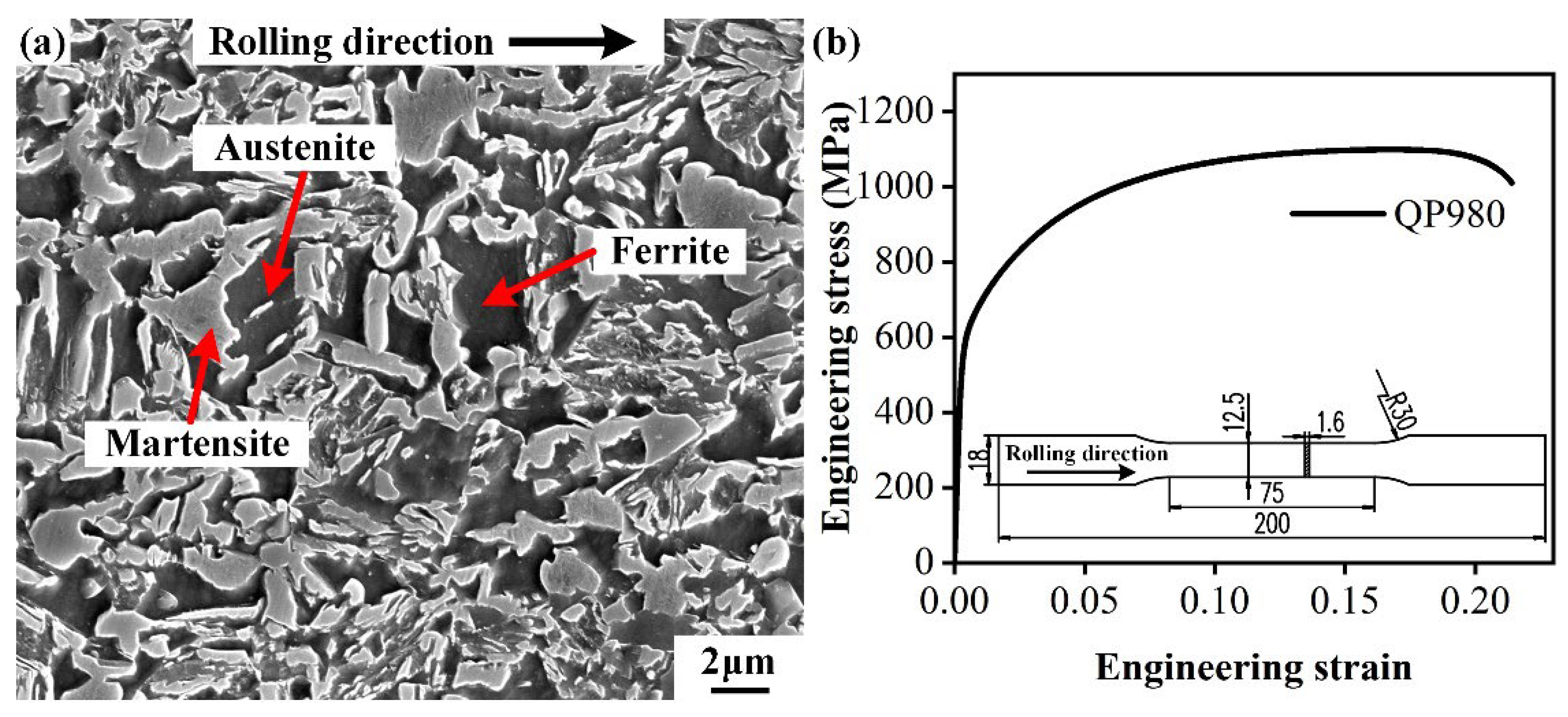

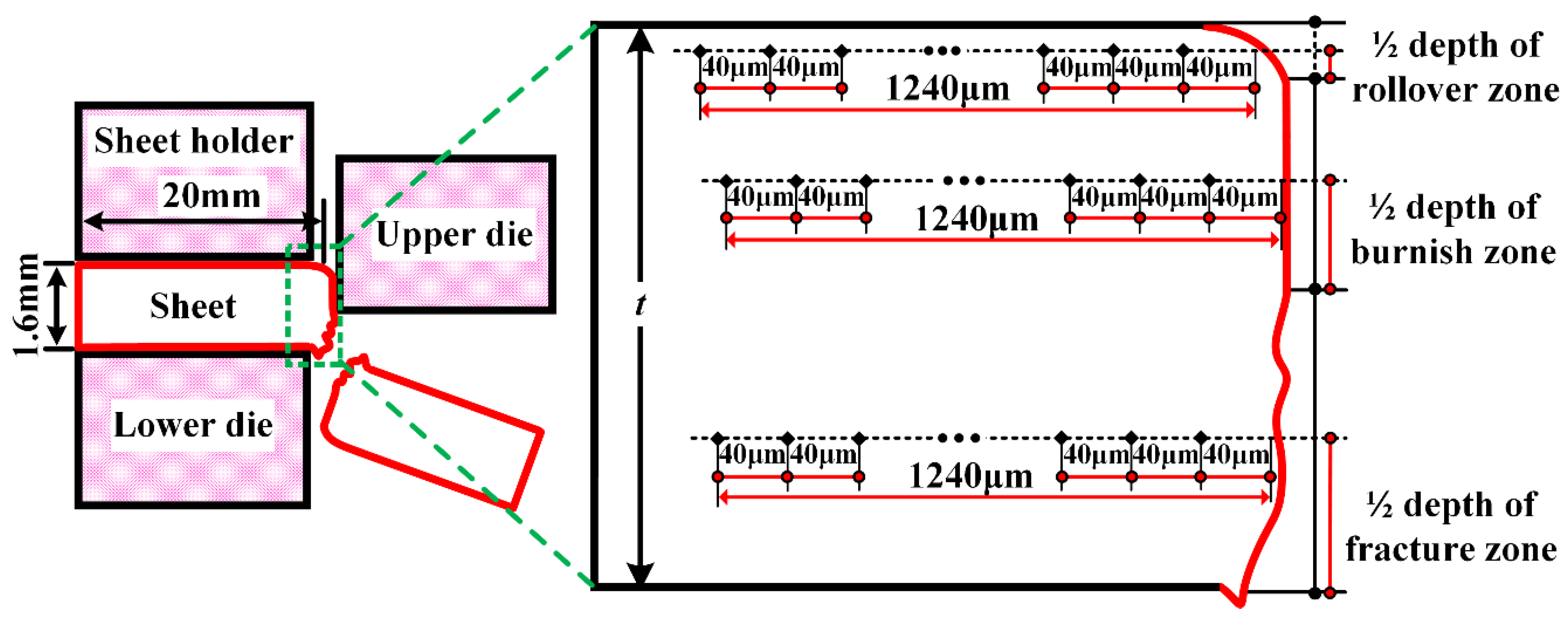
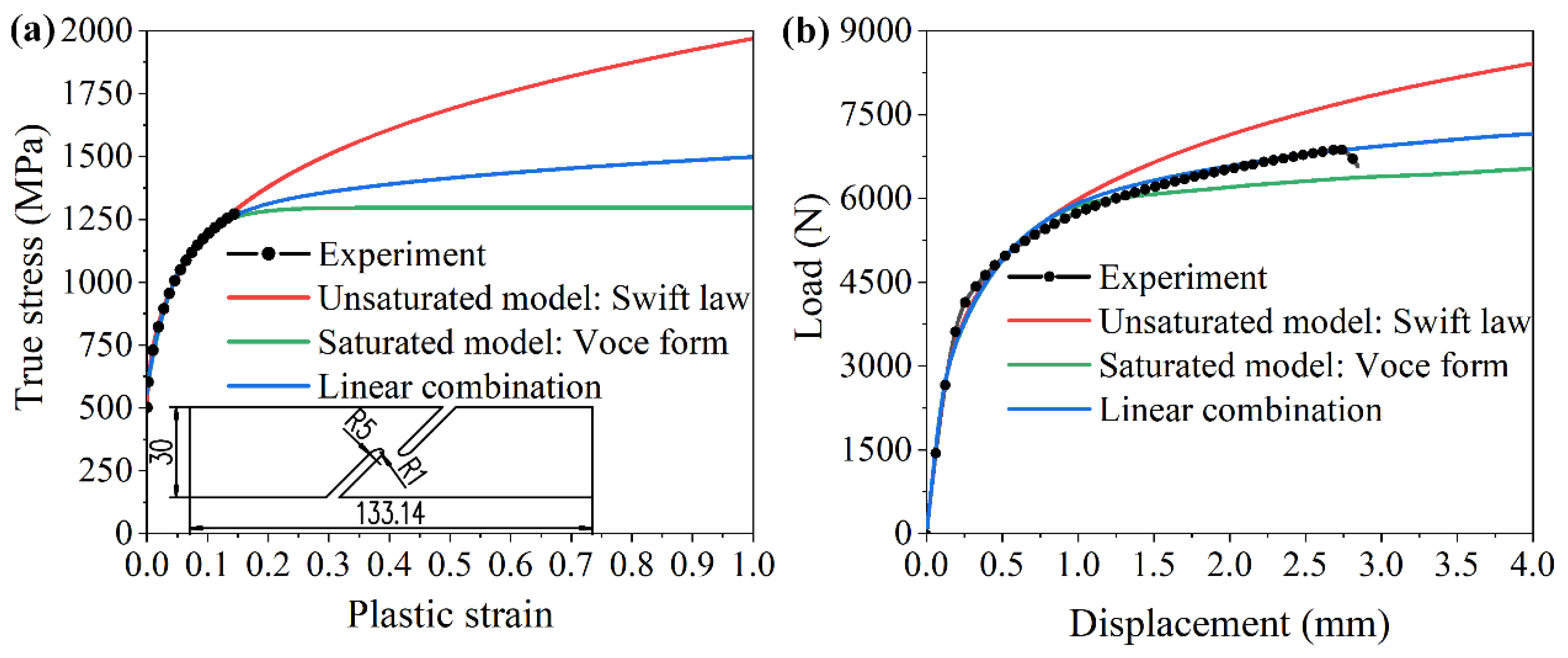
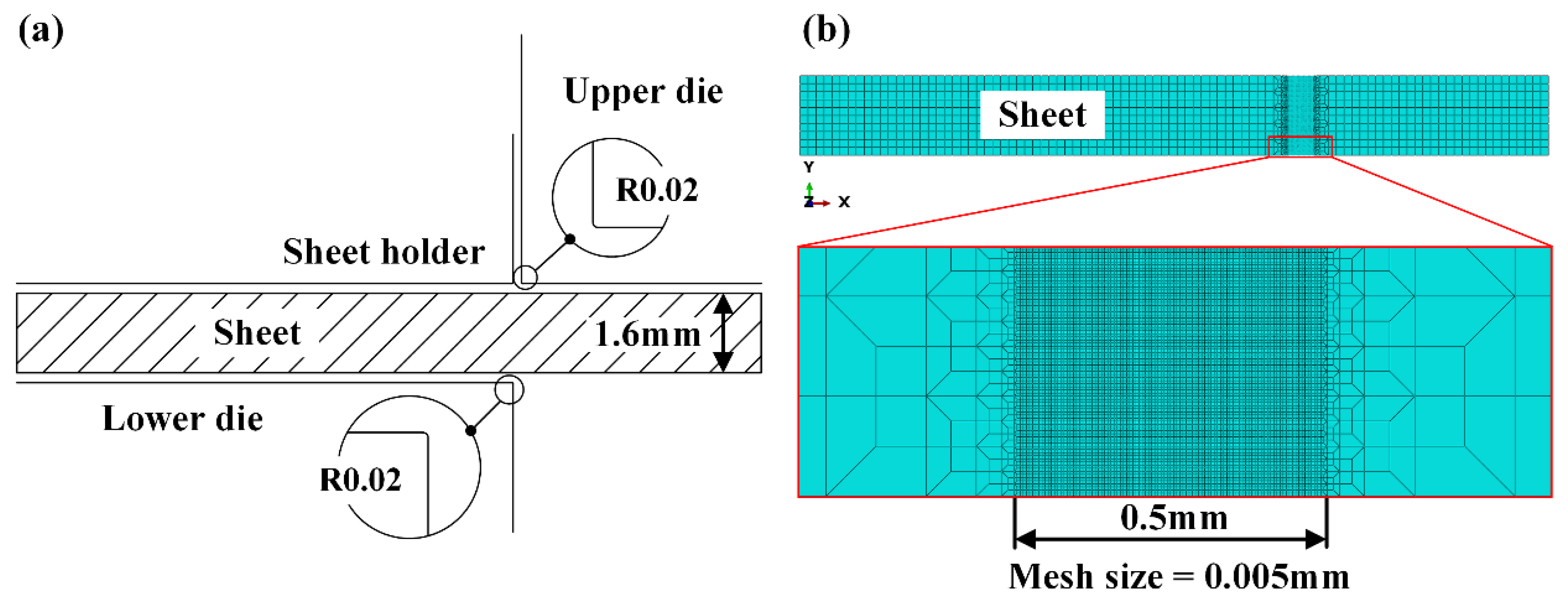













| Material | Thickness/mm | Yield Strength/MPa | Tensile Strength/MPa | Total Elongation/% |
|---|---|---|---|---|
| QP980 | 1.6 | 606.4 | 1098.7 | 21.4 |
| Material | /MPa | /MPa | /MPa | ||||
|---|---|---|---|---|---|---|---|
| QP980 | 1967.75 | 0.0025 | 0.22 | 1296.54 | 576.63 | 25,889.67 | 0.70 |
| Element | Weight (%) | Atomic (%) |
|---|---|---|
| O | 60.15 | 74.19 |
| Al | 14.02 | 10.26 |
| S | 23.02 | 14.17 |
| Ca | 2.81 | 1.38 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, S.; Chang, Y.; Wang, C.; Han, Y.; Dong, H. Experimental and Numerical Investigations on the Damage Induced in the Shearing Process for QP980 Steel. Materials 2022, 15, 3254. https://doi.org/10.3390/ma15093254
Han S, Chang Y, Wang C, Han Y, Dong H. Experimental and Numerical Investigations on the Damage Induced in the Shearing Process for QP980 Steel. Materials. 2022; 15(9):3254. https://doi.org/10.3390/ma15093254
Chicago/Turabian StyleHan, Shuo, Ying Chang, Cunyu Wang, Yun Han, and Han Dong. 2022. "Experimental and Numerical Investigations on the Damage Induced in the Shearing Process for QP980 Steel" Materials 15, no. 9: 3254. https://doi.org/10.3390/ma15093254





