Optimization of WEDM Parameters While Machining Biomedical Materials Using EDAS-PSO
Abstract
:1. Introduction
1.1. Electric Discharge Machining (EDM) of Titanium and Its Alloys
1.2. Optimization Techniques for WEDM Process Parameters
2. Experimental Procedure and Data Collection
3. Methodology Adopted
3.1. Evaluation Based on Distance from Average Solution (EDAS)
3.2. PSO
- Initialize the population by creating random permutations;
- Using the weights, the score of each permutation is evaluated;
- Non-dominated permutations are identified, and archives are updated accordingly;
- In the next step, updating of gbest and pbest take place;
- For each particle, the leader permutation is selected as per the technique;
- The upgraded values are noted for position and velocity of particles and the best values are selected as the solution. In the search space, the velocity and position of the ith particle are shown as wi = (wi1, wi2, …, win) and xi = (xi1, xi2, …, xin), respectively. The values of position and velocity are upgraded using Equations (13) and (14) [36]:
- 7.
- Move the particle according to the Equation (14); if the condition is not satisfied, then the algorithm is repeated from step 2.
4. Results and Discussion
4.1. Analysis for Response Characteristics
4.2. Mean Surface Roughness
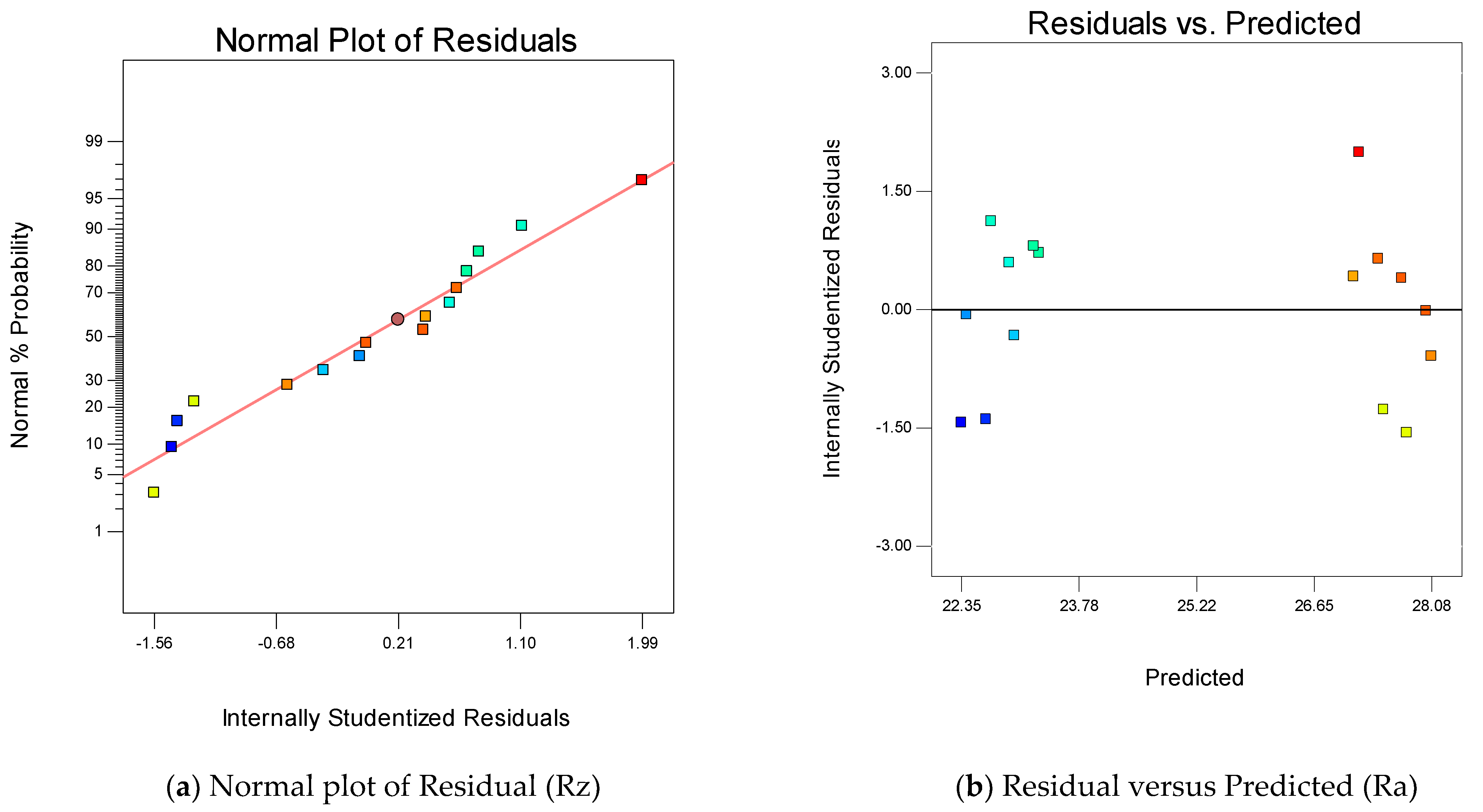
4.3. Mean Roughness Depth
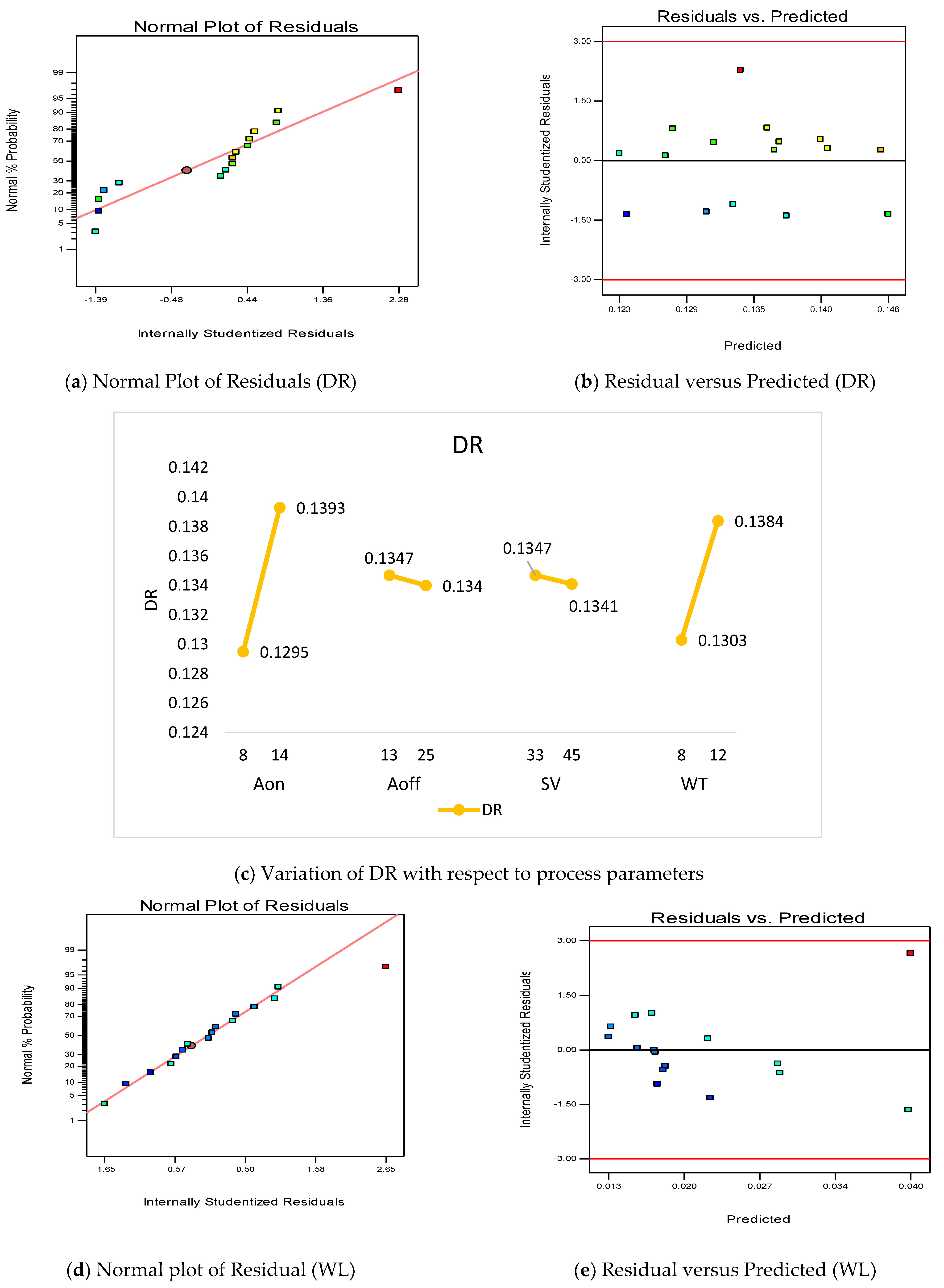
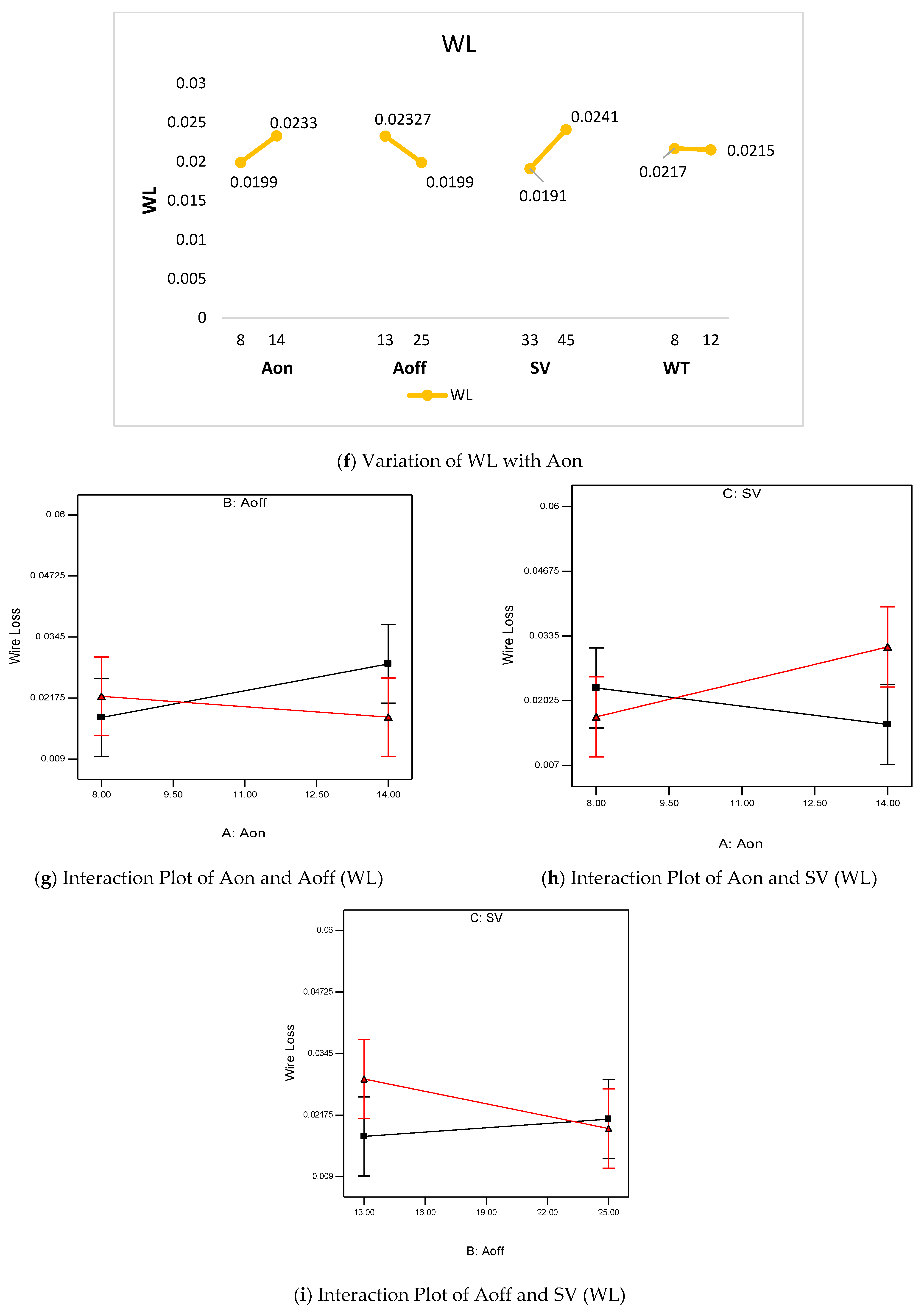
4.4. Wire Loss (WL) and Reduction in Wire Diameter (DR)
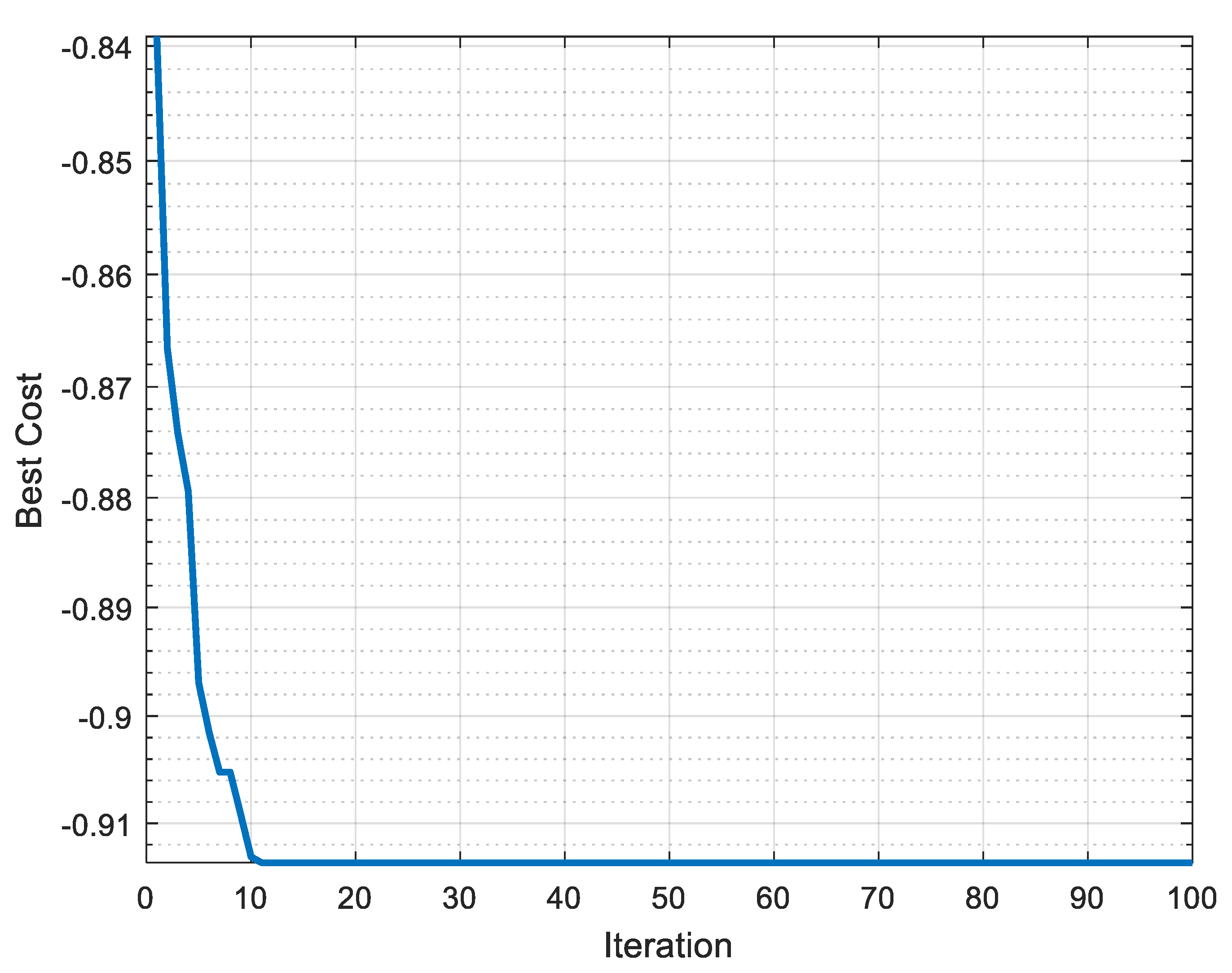
5. EDAS-PSO
6. Morphological Investigations
7. Conclusions
- The pure titanium is machined successfully using WEDM at different parametric settings.
- From the ANOVA, it is found that Aon is the major influencing factor for the evaluation of DA, Ra, Rz, WL and DR. The DA decreases with the increase in Aon value, while Ra, Rz, WL and DR values increases with the increase in Aon value.
- The statistical summary suggests that the models developed for DA, Ra, Rz, WL and DA are significant, while lack of fit are non-significant. These tests verified the presence of a good ANOVA.
- The multi-response optimization for the optimal solution is predicted using the integrated approach of EDAS-PSO. The optimal setting for the machining of Ti is: Aon: 8 μs; Aoff: 13 μs; SV: 45 V; and WT: 8 N. The suggested predicted solution at the optimized setting is: DA: 95%; Ra: 3.163 μm; Rz: 22.99 μm; WL: 0.0182 g; and DR: 0.1277 mm.
- The morphology of the machined surface indicates the presence of deposited lumps, microcracks, sub-surface formation and globules. At the optimized setting suggested by EDAS-PSO, the number of defects on the machined surface is reduced significantly.
- The SEM micrographs show that the more compact structure was obtained at the optimized setting due to smaller grain formation, which forms the more refined material.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviation | Description |
|---|---|
| Aon, Ton | Pulse on-time |
| ANN | Artificial Neural Networks |
| Aoff, Toff | Pulse off-time |
| AS | Appraisal Score |
| BBD | Box-Behnken design |
| DA | Dimensional accuracy |
| df | Degree of freedom |
| DR | Diameter reduction |
| EDAS | Evaluation Based on Distance from Average Solution |
| m | number of alternatives |
| MS | Mean square |
| n | number of attributes |
| NDA | Negative distance from average |
| NSN | Normalized SN |
| NSP | Normalized SP |
| PDA | Positive distance from average |
| Pij | Performance value of the ith alternative corresponding to jth criterion |
| PSO | Particle Swarm Optimization |
| Ra | Average surface roughness |
| RSM | Response surface methodology |
| Rz | Root mean square surface roughness |
| SN | Sum of NDA |
| SP | Sum of PDA |
| SR | Surface roughness |
| SS | Sum of square |
| SV | Servo voltage |
| WEDM | Wire electric discharge machining |
| WF | Wire feed |
| WL | Wire loss |
| WT | Wire tension |
References
- Rack, H.J.; Qazi, J.I. Titanium alloys for biomedical applications. Mater. Sci. Eng. C 2006, 26, 1269–1277. [Google Scholar] [CrossRef]
- Elias, C.N.; Lima, J.H.C.; Valiev, R.; Meyers, M.A. Biomedical applications of titanium and its alloys. J. Miner. 2008, 60, 46–49. [Google Scholar] [CrossRef]
- De Viteri, V.S.; Fuentes, E. Titanium and Titanium Alloys as Biomaterials. Tribol.-Fundam. Adv. 2013, 5, 154–181. [Google Scholar]
- Veiga, C.; Davim, J.P. Review on machinability of titanium alloys: The process perspective. Rev. Adv. Mater. Sci. 2013, 34, 148–164. [Google Scholar]
- Niknam, S.A.; Khettabi, R.; Songmene, V. Machinability and Machining of Titanium Alloys: A Review; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar] [CrossRef]
- Manjaiah, M.; Narendranath, S.; Basavarajappa, S. A review on machining of titanium based alloys. Rev. Adv. Mater. Sci. 2014, 36, 89–111. [Google Scholar]
- Zoya, Z.A.; Krishnamurthy, R. Performance of CBN tools in the machining of titanium alloys. J. Mater. Process. Technol. 2000, 100, 80–86. [Google Scholar] [CrossRef]
- Prengel, H.G.; Pfouts, W.R.; Santhanam, A.T. HtllNOLO I State of the art in hard coatings for carbide cutting tools. Surf. Coat. Technol. 1998, 102, 183–190. [Google Scholar] [CrossRef]
- Mantle, A.L.; Aspinwall, D.K. Surface integrity of a high speed milled gamma titanium aluminide. J. Mater. Process. Technol. 2001, 118, 143–150. [Google Scholar] [CrossRef]
- Sridhar, B.R.; Devananda, G.; Ramachandra, K.; Bhat, R. Effect of machining parameters and heat treatment on the residual stress distribution in titanium alloy IMI-834. J. Mater. Process. Technol. 2003, 139, 628–634. [Google Scholar] [CrossRef]
- Abbas, N.M.; Solomon, D.G.; Bahari, F. A review on current research trends in electrical discharge machining. Int. J. Mach. Tools Manuf. 2007, 47, 1214–1228. [Google Scholar] [CrossRef]
- Kansal, H.K.; Singh, S.; Kumar, P. Technology and research developments in powder mixed electric discharge machining (PMEDM). J. Mater. Process. Technol. 2007, 184, 32–41. [Google Scholar] [CrossRef]
- Annebushan, M.; Marla, D.; Kumar, R. Heliyon Methods and variables in Electrical discharge machining of titanium alloy—A review. Heliyon 2020, 6, e05554. [Google Scholar] [CrossRef]
- Nourbakhsh, F.; Rajurkar, K.P.; Malshe, A.P.; Cao, J. Wire electro-discharge machining of titanium alloy. Procedia-Soc. Behav. Sci. 2013, 5, 13–18. [Google Scholar] [CrossRef] [Green Version]
- Alias, A.; Abdullah, B.; Mohd, N. Influence of machine feed rate in wedm of titanium Ti-6Al-4V with constant current (6A) using brass wire. Procedia Eng. 2012, 41, 1806–1811. [Google Scholar] [CrossRef] [Green Version]
- Sivaprakasam, P.; Hariharan, P.; Gowri, S. Engineering Science and Technology, an International Journal Modeling and analysis of micro-WEDM process of titanium alloy (Ti–6Al–4V) using response surface approach. Eng. Sci. Technol. Int. J. 2014, 17, 227–235. [Google Scholar] [CrossRef] [Green Version]
- Majumder, H.; Maity, K. Performance analysis in WEDM of titanium grade 6 through process capability index. World J. Eng. 2020, 17, 144–151. [Google Scholar] [CrossRef]
- Prasanna, R.; Gopal, P.M.; Uthayakumar, M.; Aravind, S. Multicriteria Optimization of Machining Parameters in WEDM of Titanium Alloy 6242; Springer: Singapore, 2019; ISBN 9789811363740. [Google Scholar]
- Chaudhari, R.; Vora, J.; Vishal, D.M.P.; Sakshum, W. Multi-response Optimization of WEDM Parameters Using an Integrated Approach of RSM–GRA Analysis for Pure Titanium. J. Inst. Eng. Ser. D 2020, 101, 117–126. [Google Scholar] [CrossRef]
- Thangaraj, M.; Annamalai, R.; Moiduddin, K.; Alkindi, M.; Ramalingam, S.; Alghamdi, O. Enhancing the surface quality of micro titanium alloy specimen in WEDM process by adopting TGRA-based optimization. Materials 2020, 13, 1440. [Google Scholar] [CrossRef] [Green Version]
- Srinivasarao, G.; Suneel, D. Parametric Optimization of WEDM on α-β Titanium Alloy using Desirability Approach. Mater. Today Proc. 2018, 5, 7937–7946. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, V.; Kumar, J. Multi-response optimization of process parameters based on response surface methodology for pure titanium using WEDM process. Int. J. Adv. Manuf. Technol. 2013, 68, 2645–2668. [Google Scholar] [CrossRef]
- Raj, D.A.; Senthilvelan, T. Empirical Modelling and Optimization of Process Parameters of machining Titanium alloy by Wire-EDM using RSM. Mater. Today Proc. 2015, 2, 1682–1690. [Google Scholar] [CrossRef]
- Nandakumar, C.; Mohan, B.; Senthilkumar, C.; Vickram, K. Modeling and Optimization of WEDM of Titanium. Appl. Mech. Mater. 2015, 767, 873–877. [Google Scholar] [CrossRef]
- Priyadarshini, M.; Behera, A.; Swain, B.; Patel, S. Materials Today: Proceedings Multi-objective optimization of EDM process for titanium alloy. Mater. Today Proc. 2020, 33, 5526–5529. [Google Scholar] [CrossRef]
- Majumder, H.; Maity, K.P. Predictive Analysis on Responses in WEDM of Titanium Grade 6 Using General Regression Neural Network (GRNN) and Multiple Regression Analysis (MRA). Silicon 2018, 10, 1763–1776. [Google Scholar] [CrossRef]
- Majumder, H.; Maity, K. Optimization of Machining Condition in WEDM for Titanium Grade 6 Using MOORA Coupled with PCA | A Multivariate Hybrid Approach. J. Adv. Manuf. Syst. 2017, 16, 81–99. [Google Scholar] [CrossRef]
- Gupta, N.K.; Somani, N.; Prakash, C.; Singh, R.; Walia, A.S.; Singh, S.; Pruncu, C.I. Revealing the WEDM Process Parameters for the Machining of Pure and Heat-Treated Titanium (Ti-6Al-4V) Alloy. Materials 2021, 14, 2292. [Google Scholar] [CrossRef]
- Goyal, A.; Gautam, N.; Pathak, V.K. An adaptive neuro-fuzzy and NSGA-II-based hybrid approach for modelling and multi-objective optimization of WEDM quality characteristics during machining titanium alloy. Neural Comput. Appl. 2021, 33, 16659–16674. [Google Scholar] [CrossRef]
- Sharma, N.; Gupta, R.D.; Khanna, R.; Sharma, R.C.; Sharma, Y.K. Machining of Ti-6Al-4V biomedical alloy by WEDM: Investigation and optimization of MRR and Rz using grey-harmony search. World J. Eng. 2021. [Google Scholar] [CrossRef]
- Farooq, M.U.; Ali, M.A.; He, Y.; Khan, A.M.; Pruncu, C.I.; Kashif, M.; Ahmed, N.; Asif, N. Curved profiles machining of Ti6Al4V alloy through WEDM: Investigations on geometrical errors. J. Mater. Res. Technol. 2020, 9, 16186–16201. [Google Scholar] [CrossRef]
- Fuse, K.; Dalsaniya, A.; Modi, D.; Vora, J.; Pimenov, D.Y.; Giasin, K.; Prajapati, P.; Chaudhari, R.; Wojciechowski, S. Integration of fuzzy AHP and fuzzy TOPSIS methods for wire electric discharge machining of titanium (Ti6Al4V) alloy using RSM. Materials 2021, 14, 7408. [Google Scholar] [CrossRef]
- Kumar, A.; Sharma, R.; Gujral, R. Investigation of crack density, white layer thickness, and material characterization of biocompatible material commercially pure titanium (grade-2) through a wire electric discharge machining process using a response surface methodology. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2021, 235, 2073–2097. [Google Scholar] [CrossRef]
- Pramanik, A.; Basak, A.K.; Prakash, C. Understanding the wire electrical discharge machining of Ti6Al4V alloy. Heliyon 2019, 5, e01473. [Google Scholar] [CrossRef]
- Sharma, N.; Khanna, R.; Sharma, Y.K.; Gupta, R.D. Multi-quality characteristics optimisation on WEDM for Ti-6Al-4V using Taguchi-grey relational theory. Int. J. Mach. Mach. Mater. 2019, 21, 66–81. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: Perth, Australia, 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Sen, B.; Hussain SA, I.; Gupta, A.D.; Gupta, M.K.; Pimenov, D.Y.; Mikołajczyk, T. Application of type-2 fuzzy AHP-ARAS for selecting optimal WEDM parameters. Metals 2020, 11, 42. [Google Scholar] [CrossRef]
- Garg, M.P.; Jain, A.; Bhushan, G. Modelling and multi-objective optimization of process parameters of wire electrical discharge machining using non-dominated sorting genetic algorithm-II. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2012, 226, 1986–2001. [Google Scholar] [CrossRef]
- Sharma, N.; Khanna, R.; Gupta, R. Multi quality characteristics of WEDM process parameters with RSM. Procedia Eng. 2013, 64, 710–719. [Google Scholar] [CrossRef] [Green Version]
- Goyal, K.K.; Sharma, N.; Dev Gupta, R.; Singh, G.; Rani, D.; Banga, H.K.; Kumar, R.; Pimenov, D.Y.; Giasin, K. A Soft Computing-Based Analysis of Cutting Rate and Recast Layer Thickness for AZ31 Alloy on WEDM Using RSM-MOPSO. Materials 2022, 15, 635. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.H.; Li, X. Study of the surface integrity of the machined workpiece in the EDM of tungsten carbide. J. Mater. Process. Technol. 2003, 139, 315–321. [Google Scholar] [CrossRef]
- Rohilla, V.K.; Goyal, R.; Kumar, A.; Singla, Y.K.; Sharma, N. Surface integrity analysis of surfaces of nickel-based alloys machined with distilled water and aluminium powder-mixed dielectric fluid after WEDM. Int. J. Adv. Manuf. Technol. 2021, 116, 2467–2472. [Google Scholar] [CrossRef]
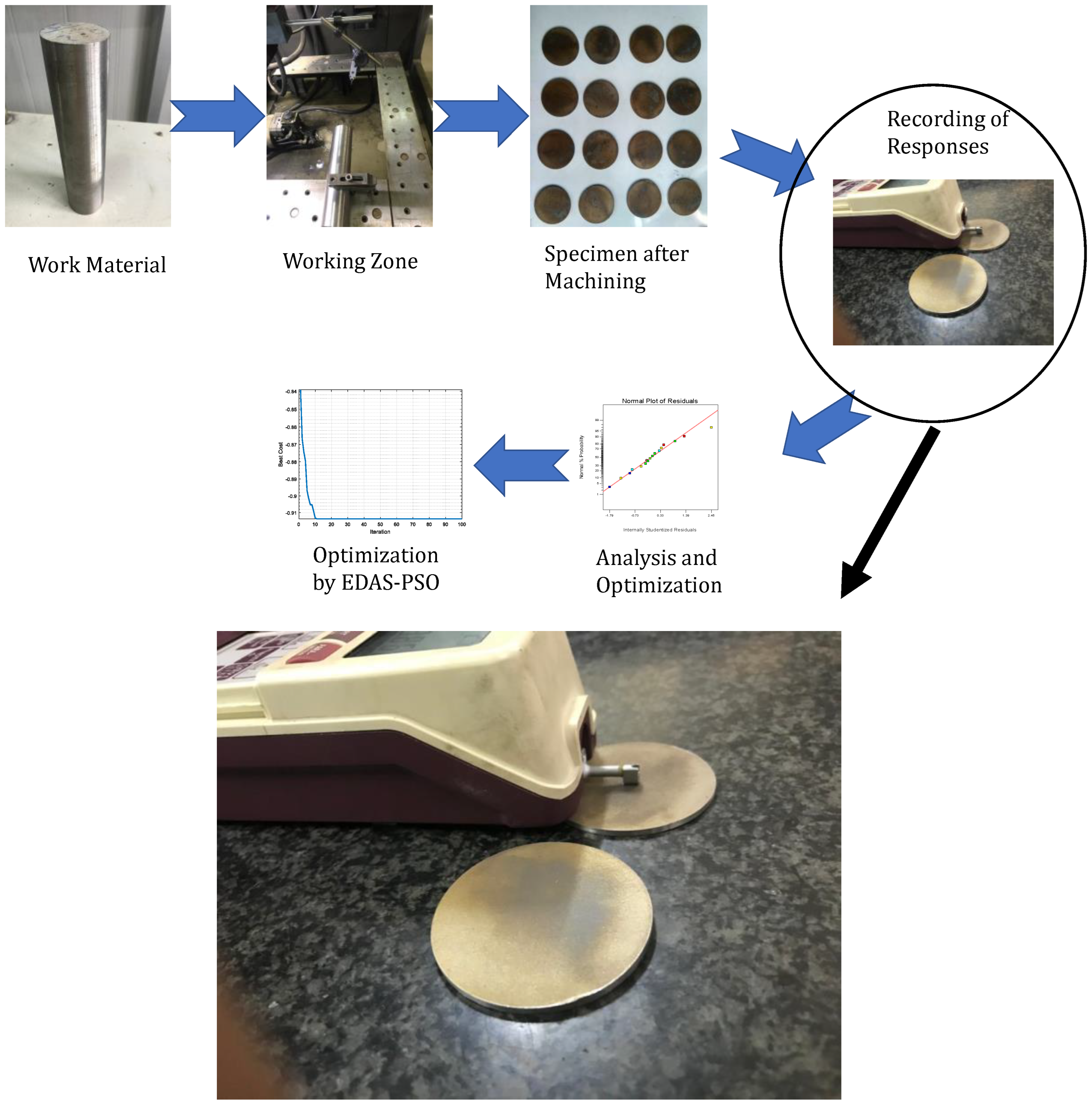
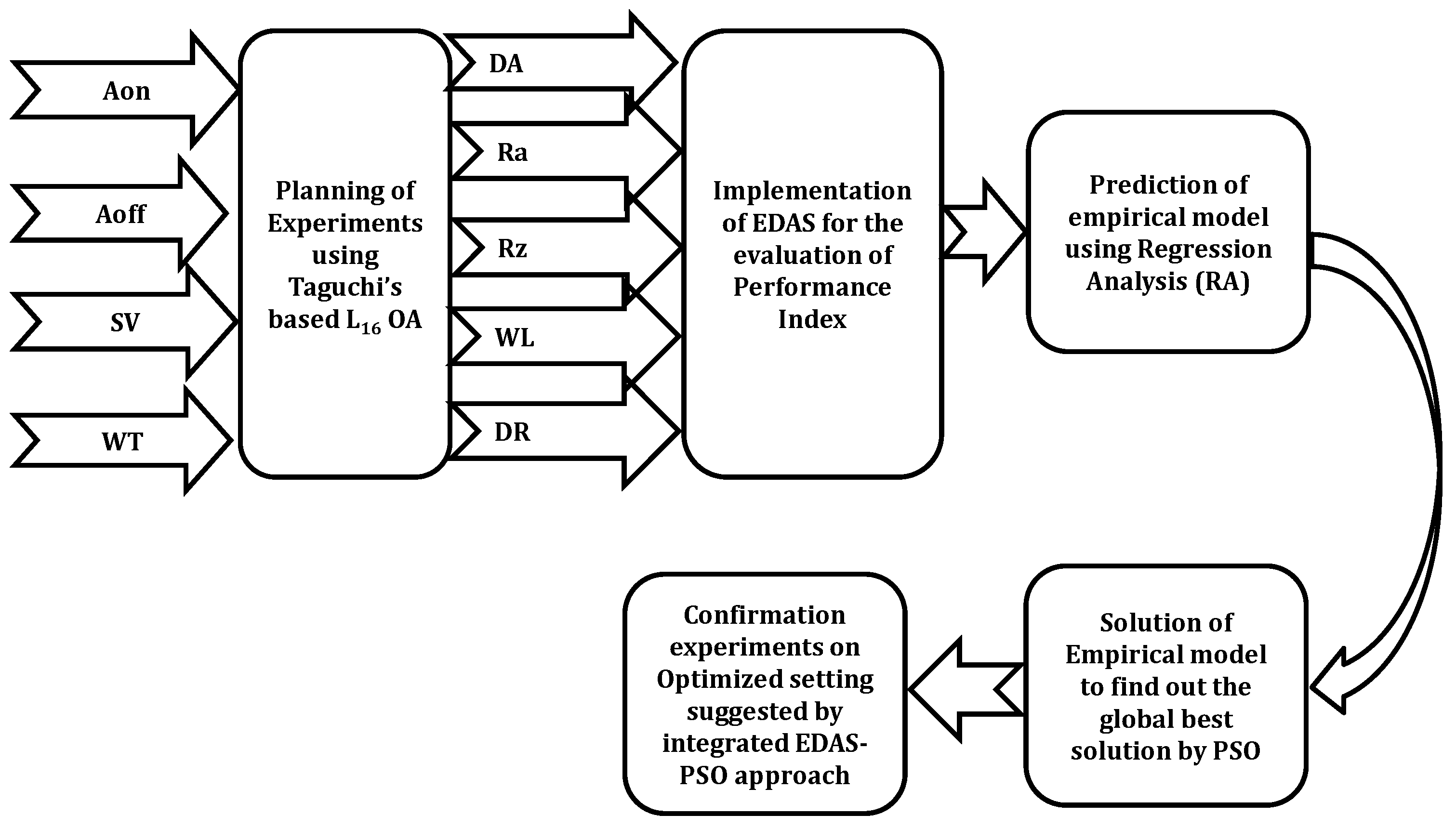
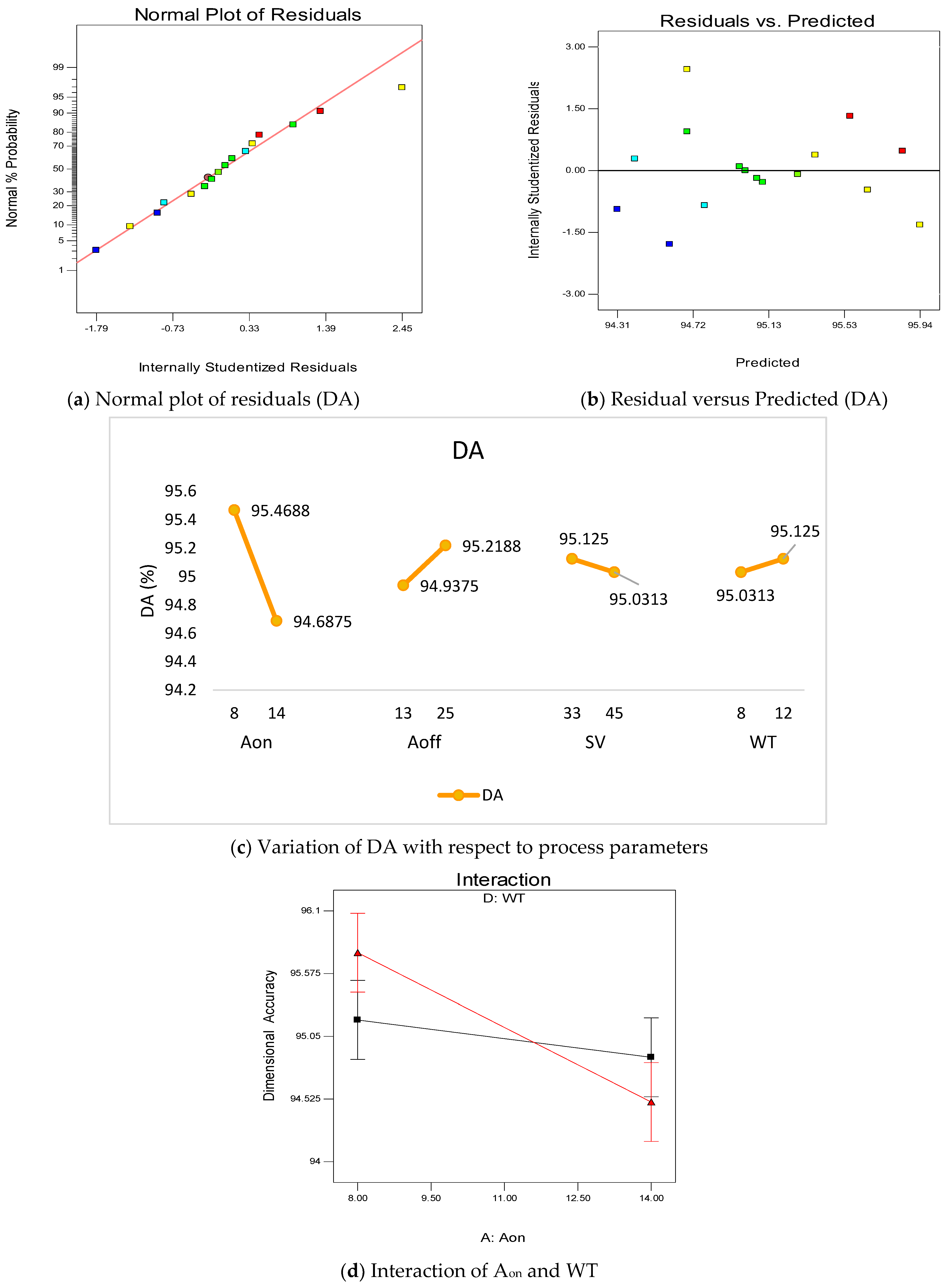
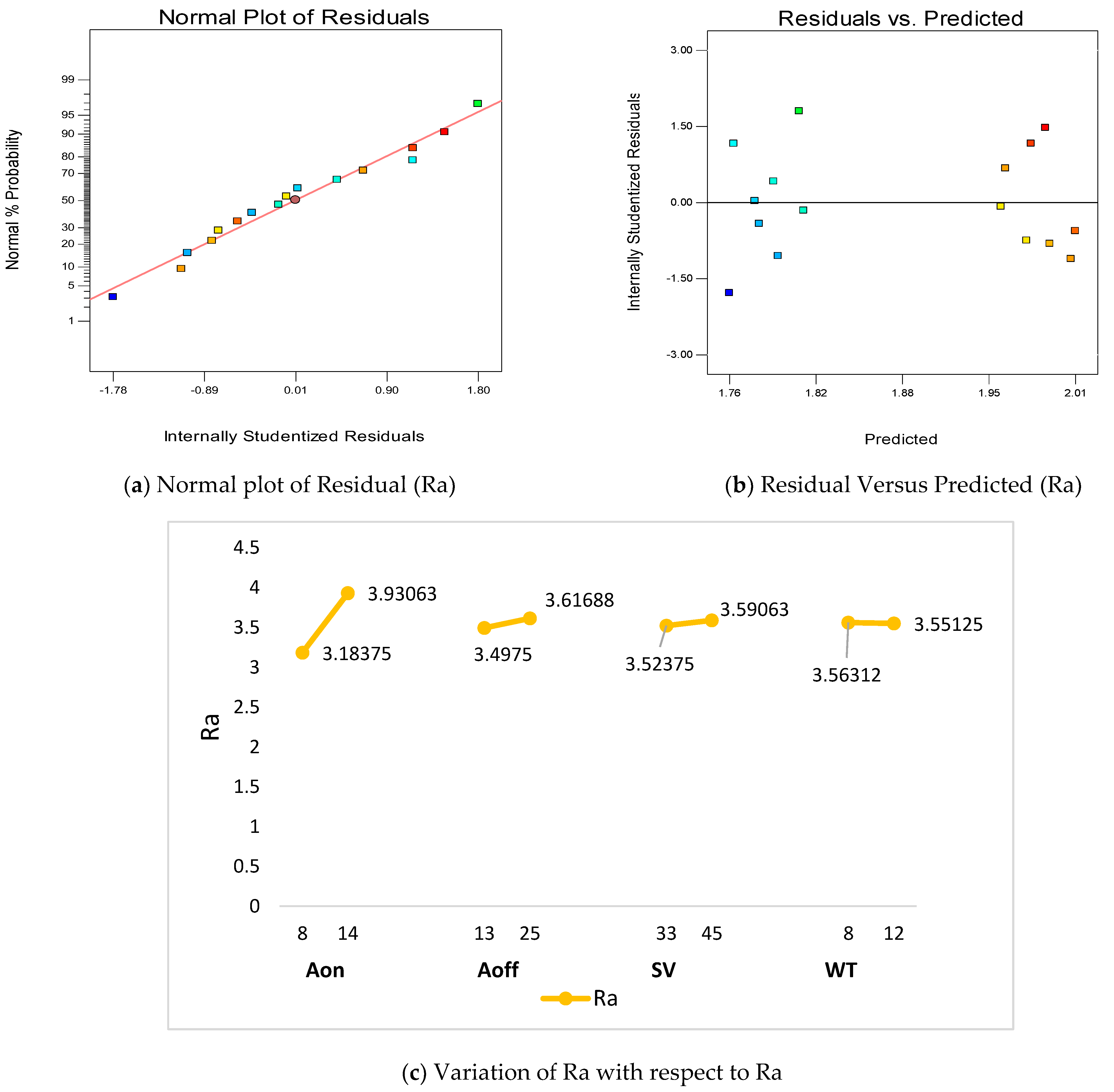


| Sr. No. | Author | Year | Materials | Input Parameters | Output Parameters | Methodology | Finding |
|---|---|---|---|---|---|---|---|
| 1 | Gupta et al. [28] | 2021 | Ti6Al4V | SV, WF, wire tension | CS and surface characterization | RSM | The maximum value of CS 1.75 mm/min |
| 2 | Goyal et al. [29] | 2021 | Ti6Al4V | Ton, Toff, WF, peak current | MRR, wire wear ratio | ANN-NSGA-II | The maximum error between the predicted and actual value is 7.5%. |
| 3 | Thangaraj et al. [20] | 2020 | Titanium (α-β) alloy | gap voltage, duty factor, discharge current | microhardness, WWR, average white layer thickness | TGRA | The optimal settings significantly affect the surface quality. |
| 4 | Chaudhari et al. [19] | 2020 | Pure Titanium | Ton, Toff, discharge current | CR, SR | RSM-GRA | A close agreement between the predicted and actual values has been obtained. |
| 5 | Sharma et al. [30] | 2021 | Ti6Al4V | Ton, Toff, SV | MRR, Rz | Grey-Harmony Search | The optimized value of MRR and Rz at the suggested setting are 6.5 mm3/min and 13.84 um. |
| 6 | Majumdar and Maity [17] | 2020 | Titanium Grade 6 | Ton, Toff, WF and WT | MRR and SR | Taguchi and Process Capability index | With the proposed approach, the cost of item failure decreases. |
| 7 | Farooq et al. [31] | 2020 | Ti6Al4V | SV, WF, Ton, Toff | Corner radii and geometric deviation | Taguchi | At optimized setting, geometric deviation is minimum |
| 8 | Fuse et al. [32] | 2021 | Ti6Al4V | Ton, Toff, current | CS, MRR and SR | Fuzzy AHP and Fuzzy TOPSIS | The use of fuzzy eliminates the uncertainty from the system. |
| 9 | Kumar et al. [33] | 2021 | Ti Grade 2 | Ton, Toff, peak current, SV | White layer thickness, MRR, SR | RSM | The major factors deteriorating the surface are Ton, Toff, SV and peak current. |
| 10 | Pramanik et al. [34] | 2019 | Ti6Al4V | Ton, flushing pressure, WT | MRR, wire degradation, Kerf width, surface generation | Design of Experiments | The recast layer is discontinuous and weak underneath solid layer. |
| 11 | Sharma et al. [35] | 2019 | Ti6Al4V | Ton, Toff, SV | CS, SR | Taguchi Grey relational | The crack intensity increases with the increase in discharge energy. |
| Titanium (Grade 2) | ||||||
|---|---|---|---|---|---|---|
| Element | H | N | C | O | Fe | Ti |
| Content (%) | <0.015 | <0.30 | <0.08 | <0.25 | <0.30 | >98.9 |
| Denotation | Machining Parameter | Level | |
|---|---|---|---|
| Low | High | ||
| AON | Pulse-ON time (µs) | 8 | 14 |
| AOFF | Pulse-OFF time (µs) | 13 | 25 |
| SV | Servo Voltage (V) | 33 | 45 |
| WT | Wire Tension (kg F) | 8 | 12 |
| Work piece material | Titanium (Grade 2) | ||
| Work piece dimensions | Cylindrical (25 mm D × 300 mm L) | ||
| Electrode material | Brass (zinc-coated) | ||
| Electrode dimensions | Wire (0.25 mm diameter) | ||
| Electrolyte | Deionized water | ||
| Sr No. | AON | AOFF | SV | WT | DA (%) | Ra (µm) | Rz (µm) | Weight Loss (g) | DR (mm) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 8 | 13 | 33 | 8 | 95 | 3.205 | 22.365 | 0.01505 | 0.11 |
| 2 | 14 | 13 | 33 | 8 | 94.5 | 3.905 | 28.655 | 0.01695 | 0.156667 |
| 3 | 8 | 25 | 33 | 8 | 95.5 | 3.115 | 23.53 | 0.01085 | 0.125 |
| 4 | 14 | 25 | 33 | 8 | 95 | 3.88 | 26.57 | 0.02845 | 0.121667 |
| 5 | 8 | 13 | 45 | 8 | 95 | 3.125 | 22.755 | 0.01795 | 0.135833 |
| 6 | 14 | 13 | 45 | 8 | 95 | 4.03 | 26.64 | 0.02425 | 0.123333 |
| 7 | 8 | 25 | 45 | 8 | 95.25 | 3.265 | 23.82 | 0.01725 | 0.128333 |
| 8 | 14 | 25 | 45 | 8 | 95 | 3.98 | 27.65 | 0.01295 | 0.141667 |
| 9 | 8 | 13 | 33 | 12 | 95.5 | 2.925 | 21.3 | 0.02415 | 0.139167 |
| 10 | 14 | 13 | 33 | 12 | 94.5 | 3.815 | 27.44 | 0.01575 | 0.1325 |
| 11 | 8 | 25 | 33 | 12 | 95.5 | 3.24 | 21.63 | 0.02575 | 0.144167 |
| 12 | 14 | 25 | 33 | 12 | 95.5 | 4.105 | 27.905 | 0.05925 | 0.148333 |
| 13 | 8 | 13 | 45 | 12 | 96 | 3.155 | 23.365 | 0.01415 | 0.135833 |
| 14 | 14 | 13 | 45 | 12 | 94 | 3.82 | 28.01 | 0.02435 | 0.144167 |
| 15 | 8 | 25 | 45 | 12 | 96 | 3.44 | 23.82 | 0.01615 | 0.1175 |
| 16 | 14 | 25 | 45 | 12 | 94 | 3.91 | 28.005 | 0.02235 | 0.145833 |
| Average | 95.07813 | 3.55719 | 25.21625 | 0.02160 | 0.13438 | ||||
| Source | SS | % Cont. | df | MS | F-Value | p-Value |
|---|---|---|---|---|---|---|
| Model | 3.71 | 5 | 0.74 | 4.22 | 0.0253 | |
| A-Aon | 2.44 | 44.67 | 1 | 2.44 | 13.89 | 0.0039 |
| B-Aoff | 0.32 | 5.86 | 1 | 0.32 | 1.8 | 0.2094 |
| C-SV | 0.035 | 0.64 | 1 | 0.035 | 0.2 | 0.6643 |
| D-WT | 0.035 | 0.64 | 1 | 0.035 | 0.2 | 0.6643 |
| AD | 0.88 | 16.11 | 1 | 0.88 | 5 | 0.0493 |
| Residual | 1.76 | 32.08 | 10 | 0.18 | ||
| Cor Total | 5.46 | 100 | 15 |
| Source | SS | % Cont. | df | MS | F-Value | p-Value |
|---|---|---|---|---|---|---|
| Model | 0.16 | 4 | 0.041 | 41.32 | <0.0001 | |
| A-Aon | 0.16 | 94.11 | 1 | 0.16 | 159.58 | <0.0001 |
| B-Aoff | 4.19 × 10−3 | 2.46 | 1 | 4.19 × 10−3 | 4.24 | 0.0639 |
| C-SV | 1.40 × 10−3 | 0.82 | 1 | 1.40 × 10−3 | 1.41 | 0.2599 |
| D-WT | 4.19 × 10−5 | 0.02 | 1 | 4.19 × 10−5 | 0.042 | 0.8406 |
| Residual | 0.011 | 2.59 | 11 | 9.88 × 10−4 | ||
| Cor Total | 0.17 | 100 | 15 |
| Source | SS | % Cont. | df | MS | F-Value | p-Value |
|---|---|---|---|---|---|---|
| Model | 93.37 | - | 4 | 23.34 | 30.04 | <0.0001 |
| A-Aon | 91.63 | 89.9 | 1 | 91.63 | 117.92 | <0.0001 |
| B-Aoff | 0.36 | 0.35 | 1 | 0.36 | 0.46 | 0.5102 |
| C-SV | 1.36 | 1.33 | 1 | 1.36 | 1.75 | 0.2122 |
| D-WT | 0.016 | 0.02 | 1 | 0.016 | 0.021 | 0.8876 |
| Residual | 8.55 | 8.4 | 11 | 0.78 | ||
| Cor Total | 101.92 | 100 | 15 |
| WL | |||||
| Source | SS | df | MS | F-Value | Prob > F |
| Model | 1.10 × 10−3 | 7 | 1.57 × 10−4 | 1.55 | 0.275 |
| A-Aon | 4.69 × 10−5 | 1 | 4.69 × 10−5 | 0.46 | 0.5153 |
| B-Aoff | 4.49 × 10−5 | 1 | 4.49 × 10−5 | 0.44 | 0.5243 |
| C-SV | 9.90 × 10−5 | 1 | 9.90 × 10−5 | 0.98 | 0.3517 |
| D-WT | 1.60 × 10−7 | 1 | 1.60 × 10−7 | 1.58 × 10−3 | 0.9693 |
| AB | 2.42 × 10−4 | 1 | 2.42 × 10−4 | 2.39 | 0.1609 |
| AC | 4.75 × 10−4 | 1 | 4.75 × 10−4 | 4.69 | 0.0622 |
| BC | 1.92 × 10−4 | 1 | 1.92 × 10−4 | 1.89 | 0.206 |
| Residual | 8.10 × 10−4 | 8 | 1.01 × 10−4 | ||
| Cor Total | 1.91 × 10−3 | 15 | |||
| DR | |||||
| Source | SS | df | MS | F-Value | Prob > F |
| Model | 7.35 × 10−4 | 5 | 1.47 × 10−4 | 0.89 | 0.5225 |
| A-Aon | 3.84 × 10−4 | 1 | 3.84 × 10−4 | 2.32 | 0.1584 |
| B-Aoff | 1.56 × 10−6 | 1 | 1.56 × 10−6 | 9.47 × 10−3 | 0.9244 |
| C-SV | 1.56 × 10−6 | 1 | 1.56 × 10−6 | 9.47 × 10−3 | 0.9244 |
| D-WT | 2.64 × 10−4 | 1 | 2.64 × 10−4 | 1.6 | 0.2346 |
| CD | 8.40 × 10−5 | 1 | 8.40 × 10−5 | 0.51 | 0.4919 |
| Residual | 1.65 × 10−3 | 10 | 1.65 × 10−4 | ||
| Cor Total | 2.39 × 10−3 | 15 | |||
| Sr. No. | PDA | NDA | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.00000 | 0.00000 | 0.11307 | 0.30324 | 0.18140 | 0.00082 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| 2 | 0.00000 | 0.09778 | 0.00000 | 0.21528 | 0.00000 | 0.00608 | 0.09778 | 0.13637 | 0.00000 | 0.16589 |
| 3 | 0.00444 | 0.00000 | 0.06687 | 0.49769 | 0.06977 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| 4 | 0.00000 | 0.09075 | 0.00000 | 0.00000 | 0.09457 | 0.00082 | 0.09075 | 0.05369 | 0.31713 | 0.00000 |
| 5 | 0.00000 | 0.00000 | 0.09761 | 0.16898 | 0.00000 | 0.00082 | 0.00000 | 0.00000 | 0.00000 | 0.01085 |
| 6 | 0.00000 | 0.13292 | 0.00000 | 0.00000 | 0.08217 | 0.00082 | 0.13292 | 0.05646 | 0.12269 | 0.00000 |
| 7 | 0.00181 | 0.00000 | 0.05537 | 0.20139 | 0.04496 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| 8 | 0.00000 | 0.11886 | 0.00000 | 0.40046 | 0.00000 | 0.00082 | 0.11886 | 0.09652 | 0.00000 | 0.05427 |
| 9 | 0.00444 | 0.00000 | 0.15531 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.11806 | 0.03566 |
| 10 | 0.00000 | 0.07248 | 0.00000 | 0.27083 | 0.01395 | 0.00608 | 0.07248 | 0.08819 | 0.00000 | 0.00000 |
| 11 | 0.00444 | 0.00000 | 0.14222 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.19213 | 0.07287 |
| 12 | 0.00444 | 0.15400 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.15400 | 0.10663 | 1.74306 | 0.10387 |
| 13 | 0.00970 | 0.00000 | 0.07341 | 0.34491 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.01085 |
| 14 | 0.00000 | 0.07388 | 0.00000 | 0.00000 | 0.00000 | 0.01134 | 0.07388 | 0.11079 | 0.12731 | 0.07287 |
| 15 | 0.00970 | 0.00000 | 0.05537 | 0.25231 | 0.12558 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| 16 | 0.00000 | 0.09918 | 0.00000 | 0.00000 | 0.00000 | 0.01134 | 0.09918 | 0.11059 | 0.03472 | 0.08527 |
| Weighted PDA | SPi | Weighted NDA | SNi | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.00000 | 0.00000 | 0.02261 | 0.06065 | 0.03628 | 0.11954 | 0.00016 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00016 |
| 0.00000 | 0.01956 | 0.00000 | 0.04306 | 0.00000 | 0.06261 | 0.00122 | 0.01956 | 0.02727 | 0.00000 | 0.03318 | 0.08122 |
| 0.00089 | 0.00000 | 0.01337 | 0.09954 | 0.01395 | 0.12775 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| 0.00000 | 0.01815 | 0.00000 | 0.00000 | 0.01891 | 0.03706 | 0.00016 | 0.01815 | 0.01074 | 0.06343 | 0.00000 | 0.09248 |
| 0.00000 | 0.00000 | 0.01952 | 0.03380 | 0.00000 | 0.05332 | 0.00016 | 0.00000 | 0.00000 | 0.00000 | 0.00217 | 0.00233 |
| 0.00000 | 0.02658 | 0.00000 | 0.00000 | 0.01643 | 0.04302 | 0.00016 | 0.02658 | 0.01129 | 0.02454 | 0.00000 | 0.06258 |
| 0.00036 | 0.00000 | 0.01107 | 0.04028 | 0.00899 | 0.06071 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| 0.00000 | 0.02377 | 0.00000 | 0.08009 | 0.00000 | 0.10386 | 0.00016 | 0.02377 | 0.01930 | 0.00000 | 0.01085 | 0.05409 |
| 0.00089 | 0.00000 | 0.03106 | 0.00000 | 0.00000 | 0.03195 | 0.00000 | 0.00000 | 0.00000 | 0.02361 | 0.00713 | 0.03074 |
| 0.00000 | 0.01450 | 0.00000 | 0.05417 | 0.00279 | 0.07145 | 0.00122 | 0.01450 | 0.01764 | 0.00000 | 0.00000 | 0.03335 |
| 0.00089 | 0.00000 | 0.02844 | 0.00000 | 0.00000 | 0.02933 | 0.00000 | 0.00000 | 0.00000 | 0.03843 | 0.01457 | 0.05300 |
| 0.00089 | 0.03080 | 0.00000 | 0.00000 | 0.00000 | 0.03169 | 0.00000 | 0.03080 | 0.02133 | 0.34861 | 0.02077 | 0.42151 |
| 0.00194 | 0.00000 | 0.01468 | 0.06898 | 0.00000 | 0.08560 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00217 | 0.00217 |
| 0.00000 | 0.01478 | 0.00000 | 0.00000 | 0.00000 | 0.01478 | 0.00227 | 0.01478 | 0.02216 | 0.02546 | 0.01457 | 0.07924 |
| 0.00194 | 0.00000 | 0.01107 | 0.05046 | 0.02512 | 0.08859 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| 0.00000 | 0.01984 | 0.00000 | 0.00000 | 0.00000 | 0.01984 | 0.00227 | 0.01984 | 0.02212 | 0.00694 | 0.01705 | 0.06822 |
| Sr. No. | NSPi | NSNi | ASi | Rank |
|---|---|---|---|---|
| 1 | 0.93573 | 0.99961 | 0.96767 | 2 |
| 2 | 0.49010 | 0.80730 | 0.64870 | 9 |
| 3 | 1.00000 | 1.00000 | 1.00000 | 1 |
| 4 | 0.29012 | 0.78061 | 0.53537 | 13 |
| 5 | 0.41735 | 0.99446 | 0.70591 | 8 |
| 6 | 0.33673 | 0.85154 | 0.59414 | 10 |
| 7 | 0.47519 | 1.00000 | 0.73759 | 7 |
| 8 | 0.81302 | 0.87167 | 0.84234 | 4 |
| 9 | 0.25008 | 0.92706 | 0.58857 | 11 |
| 10 | 0.55931 | 0.92088 | 0.74009 | 6 |
| 11 | 0.22960 | 0.87426 | 0.55193 | 12 |
| 12 | 0.24804 | 0.00000 | 0.12402 | 16 |
| 13 | 0.67008 | 0.99485 | 0.83246 | 5 |
| 14 | 0.11566 | 0.81201 | 0.46384 | 15 |
| 15 | 0.69347 | 1.00000 | 0.84674 | 3 |
| 16 | 0.15527 | 0.83815 | 0.49671 | 14 |
| Method | Parametric Setting | Predicted Value | Experimental Value | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AS | DA | Ra | Rz | WL | DR | DA | Ra | Rz | WL | DR | ||
| EDAS-PSO and EDAS | (Aon)8(Aoff)13 (SV)45(WT)8 | 0.9137 | 95 | 3.163 | 22.996 | 0.0182 | 0.1277 | 95 | 3.125 | 22.755 | 0.0179 | 0.135 |
| Trial Run | (Aon)8(Aoff)25 (SV)33(WT)8 | 1 | 95.375 | 3.216 | 22.713 | 0.0286 | 0.1231 | 95.5 | 3.115 | 23.53 | 0.0108 | 0.125 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharma, V.S.; Sharma, N.; Singh, G.; Gupta, M.K.; Singh, G. Optimization of WEDM Parameters While Machining Biomedical Materials Using EDAS-PSO. Materials 2023, 16, 114. https://doi.org/10.3390/ma16010114
Sharma VS, Sharma N, Singh G, Gupta MK, Singh G. Optimization of WEDM Parameters While Machining Biomedical Materials Using EDAS-PSO. Materials. 2023; 16(1):114. https://doi.org/10.3390/ma16010114
Chicago/Turabian StyleSharma, Vishal S., Neeraj Sharma, Gurraj Singh, Munish Kumar Gupta, and Gurminder Singh. 2023. "Optimization of WEDM Parameters While Machining Biomedical Materials Using EDAS-PSO" Materials 16, no. 1: 114. https://doi.org/10.3390/ma16010114
APA StyleSharma, V. S., Sharma, N., Singh, G., Gupta, M. K., & Singh, G. (2023). Optimization of WEDM Parameters While Machining Biomedical Materials Using EDAS-PSO. Materials, 16(1), 114. https://doi.org/10.3390/ma16010114







