Finite Element Modeling of Hot Rolling of 1075 Carbon Steel Process with Variable Cross Section
Abstract
:1. Introduction
2. Mathematical Modeling
3. Numerical Modeling
- Ambient temperature constant was 25 °C.
- Heat transfer coefficient was assumed as 20 W/m2 °C. This value considers cooling in air.
- Friction coefficient was 0.3.
- Isotropic behavior.
- Roll geometries were rigid, therefore the only mesh needed was the resolution of the STL file to improve surface contact conditions.
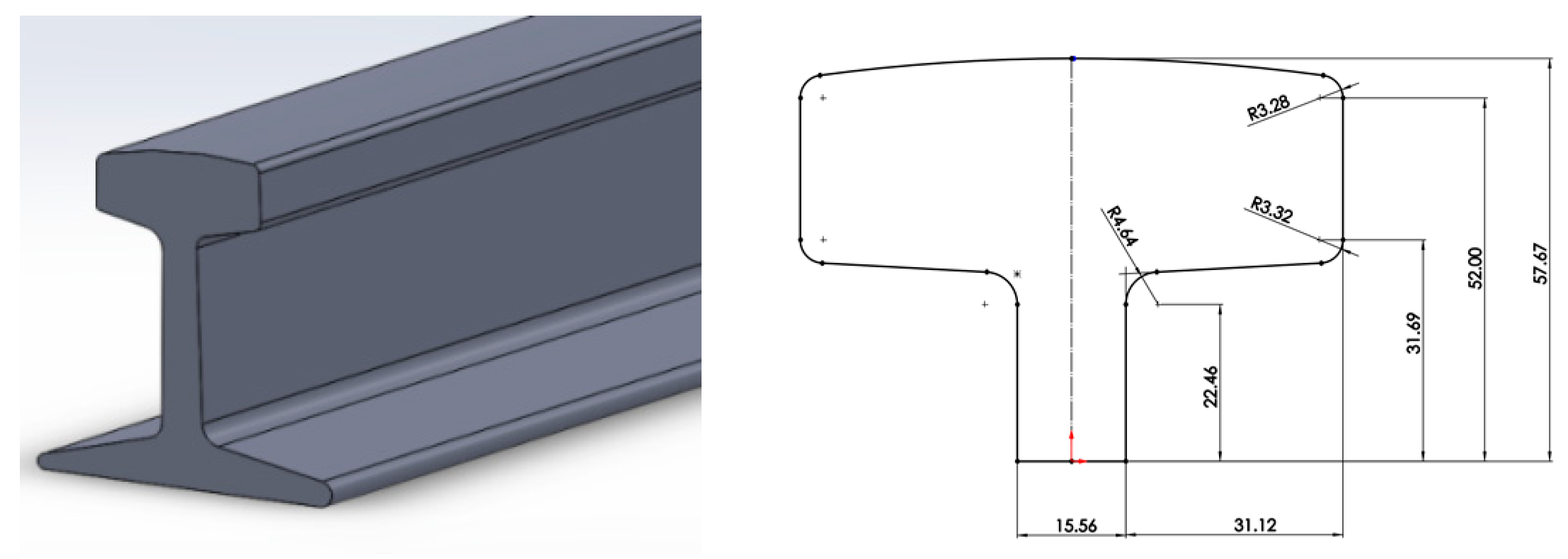
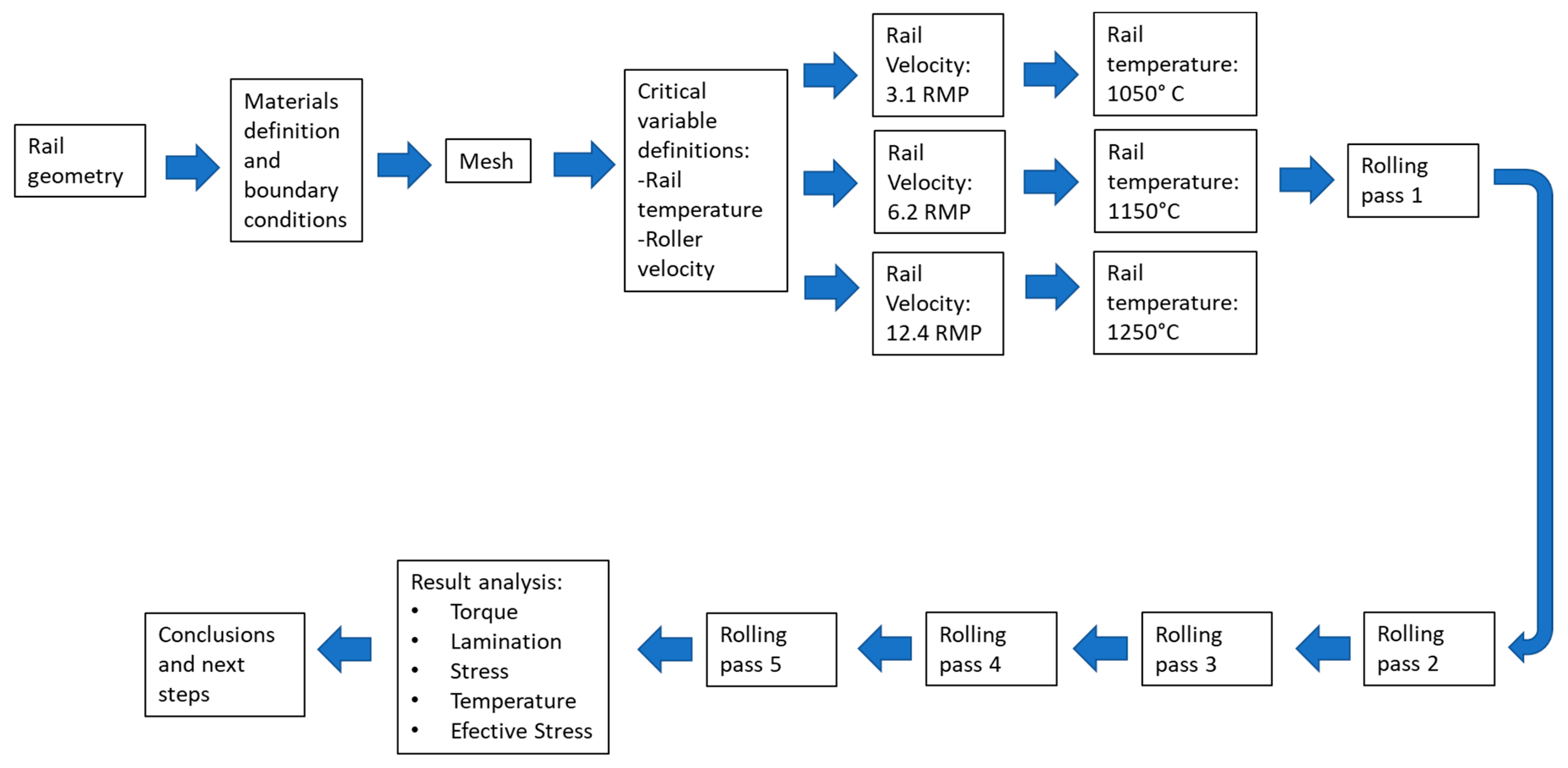
- (A)
- Upper rail part (T shape).
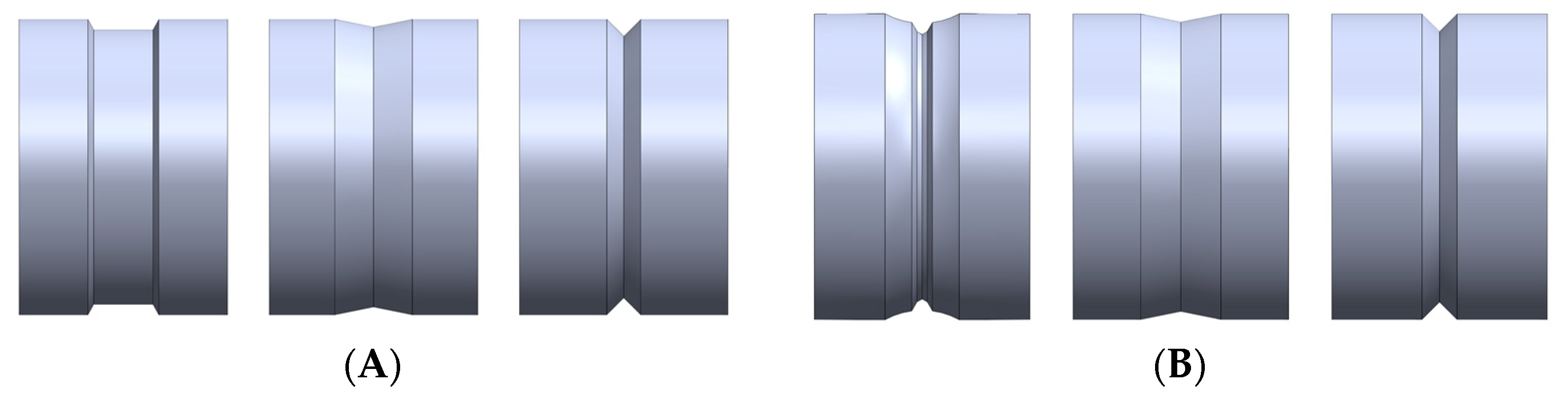
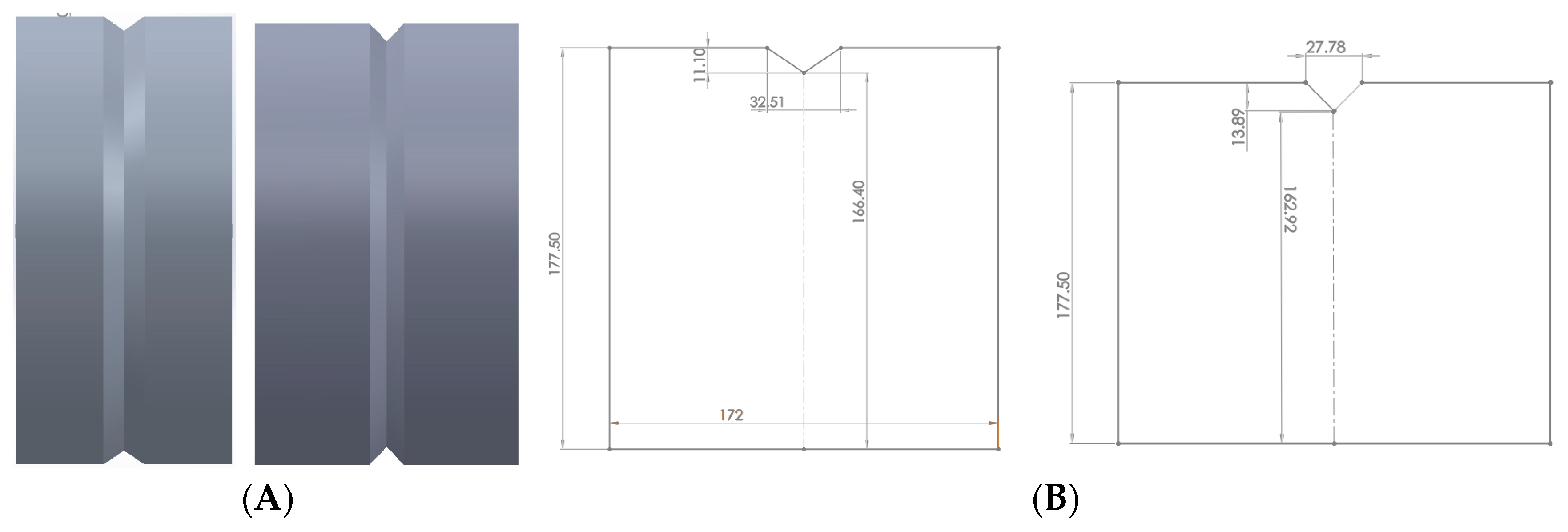
- (B)
- Five rolling passes.
- (A)
- 1050 °C.
- (B)
- 1150 °C.
- (C)
- 1250 °C.
- (A)
- 3.1 RPM.
- (B)
- 6.2 RPM.
- (C)
- 12.4 RPM.
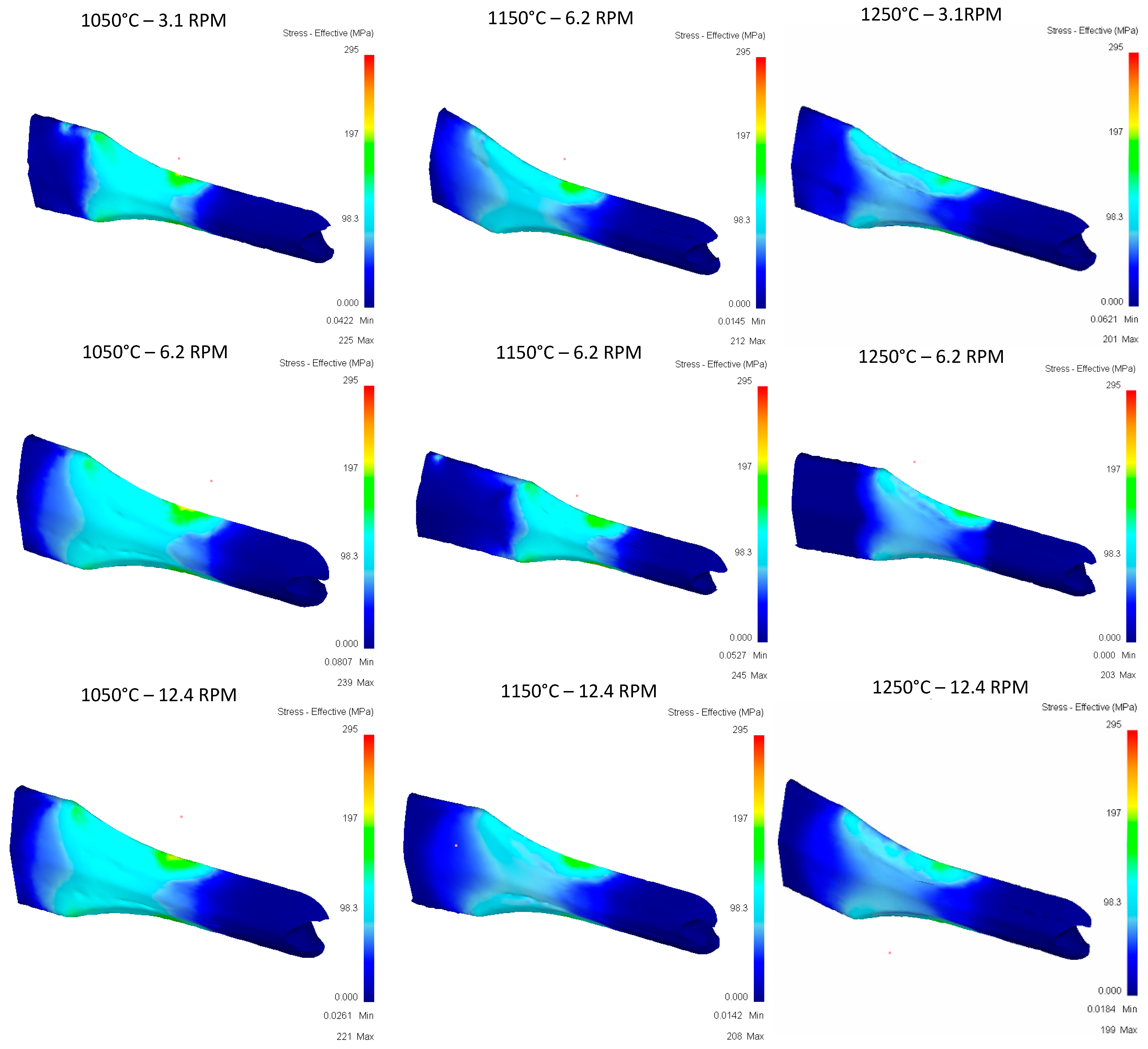
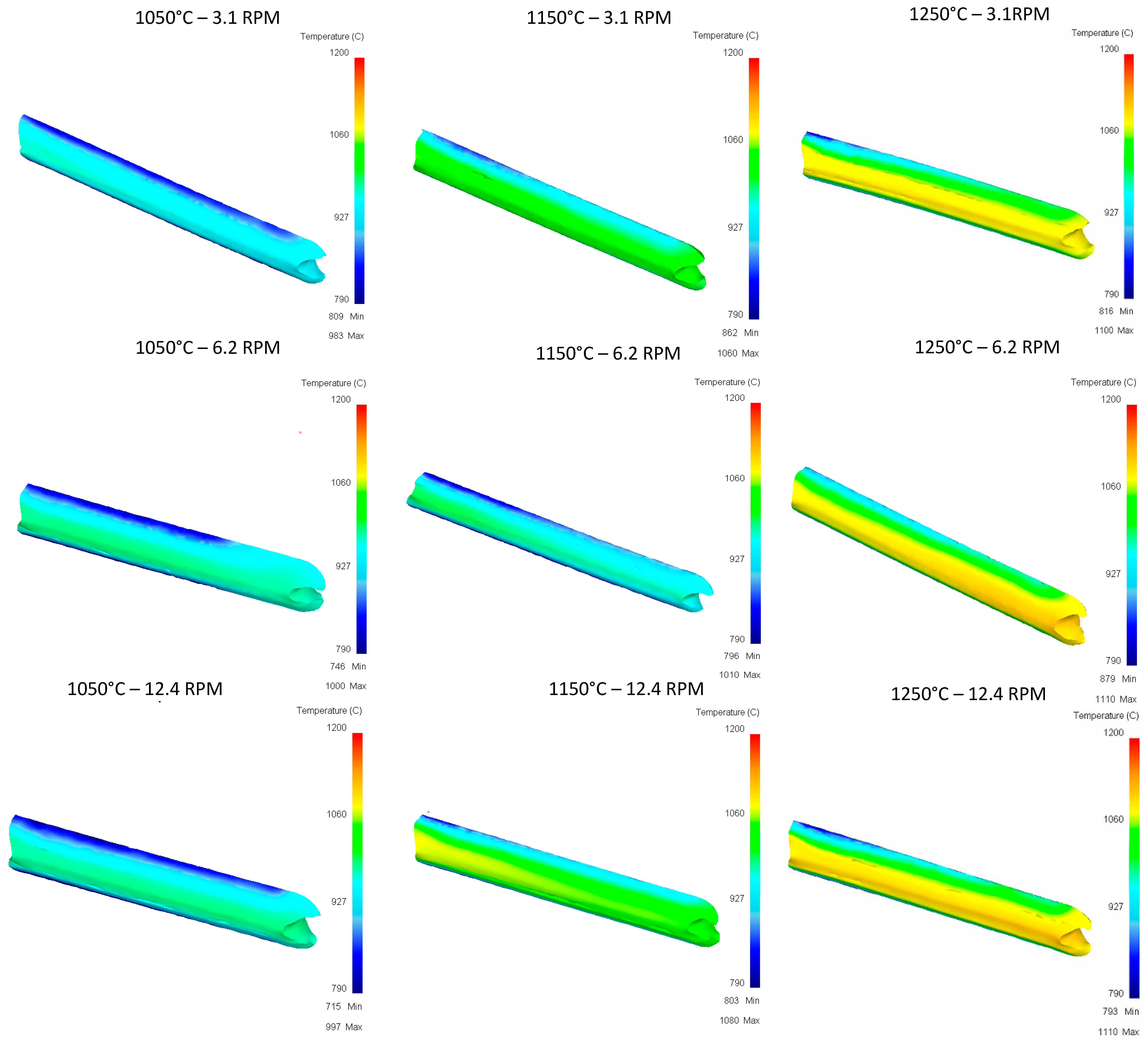
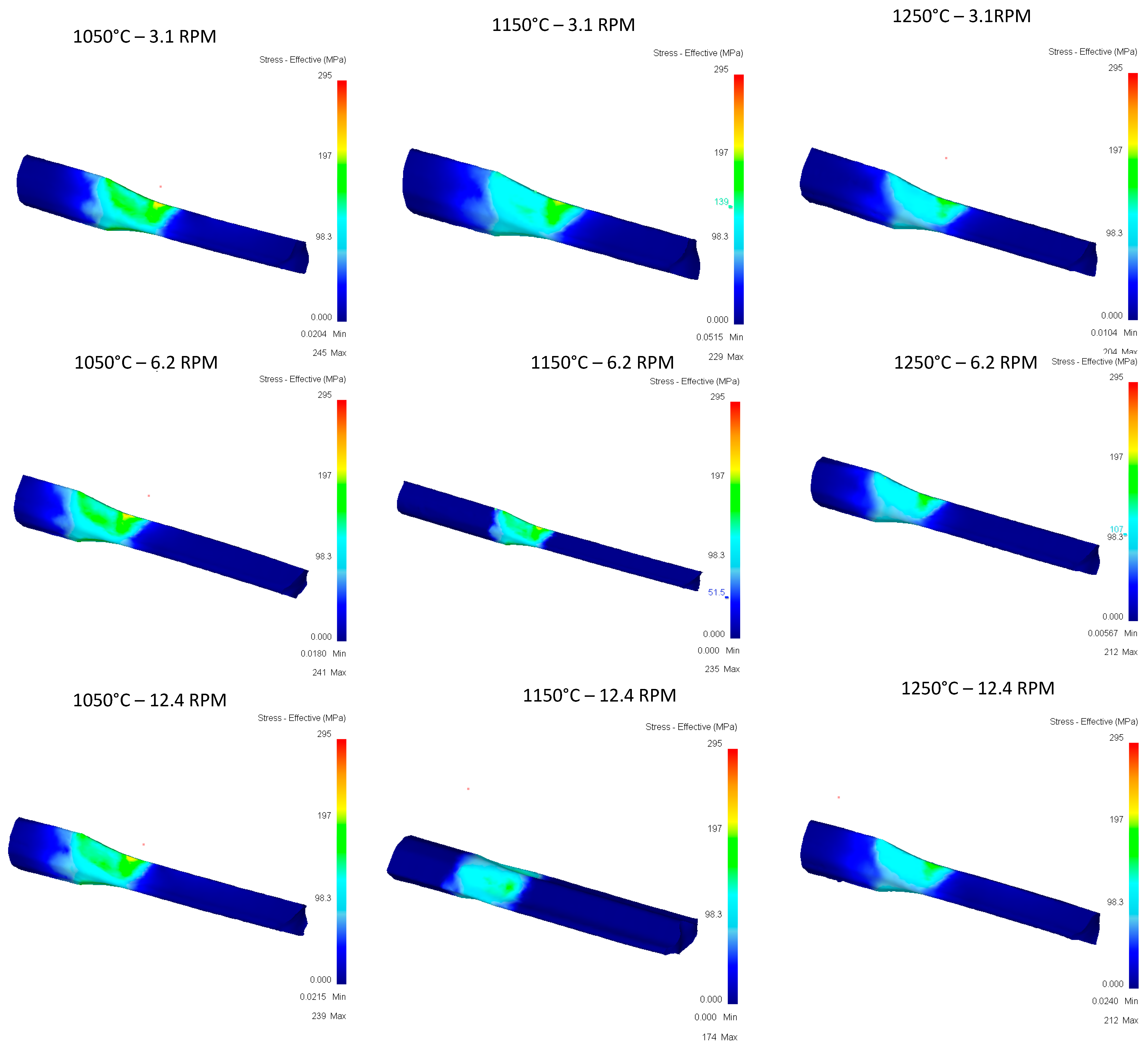
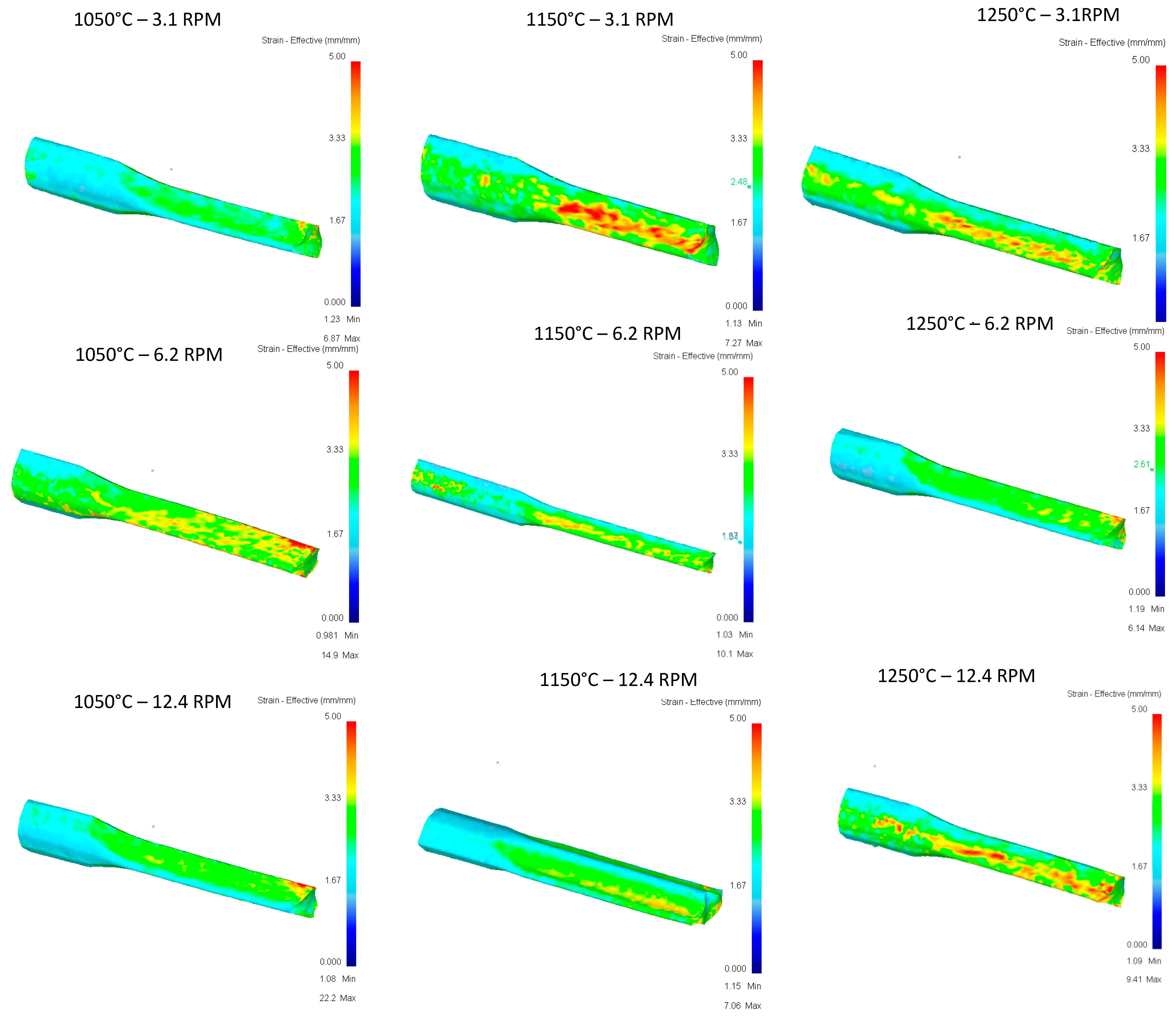
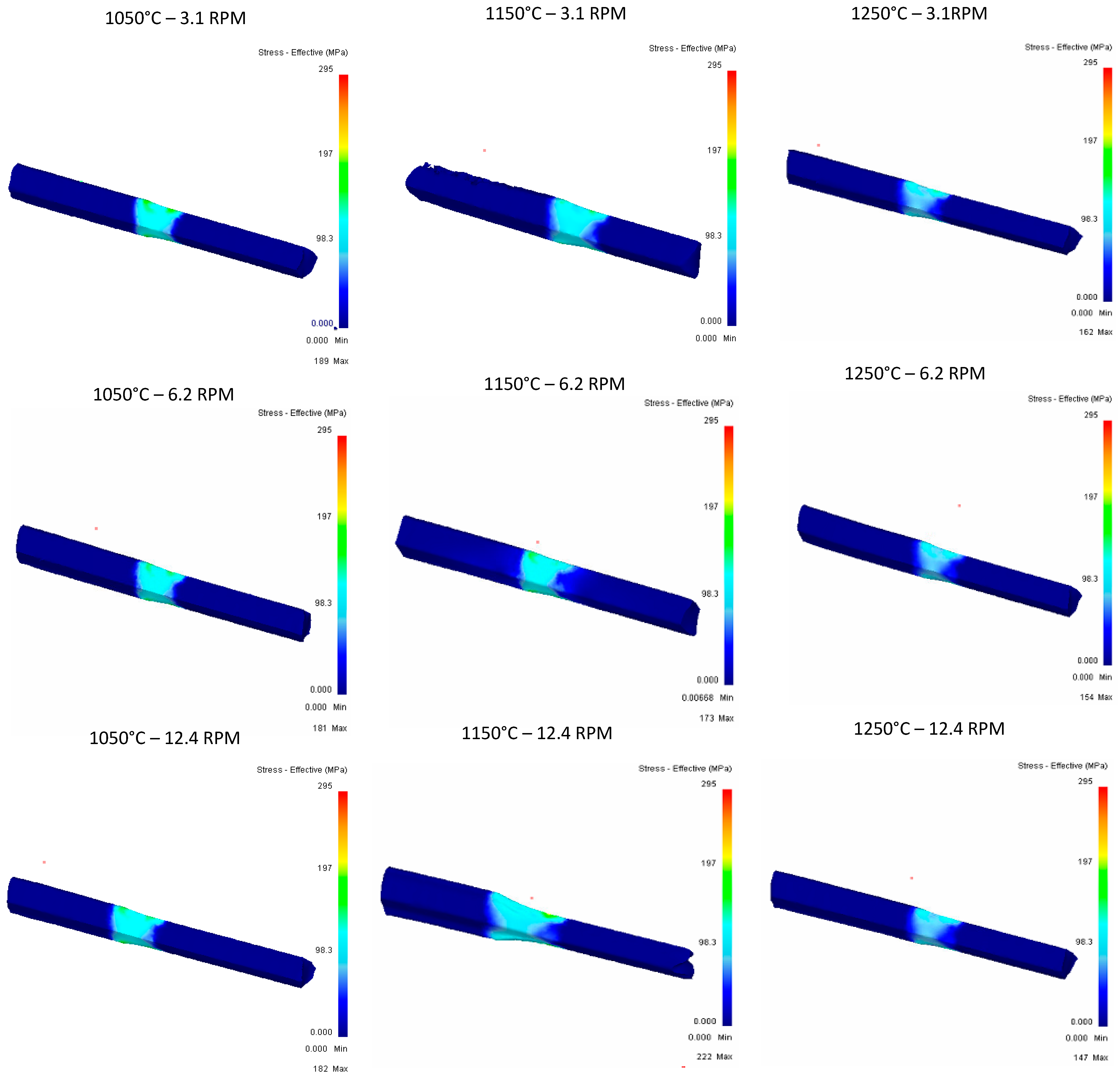
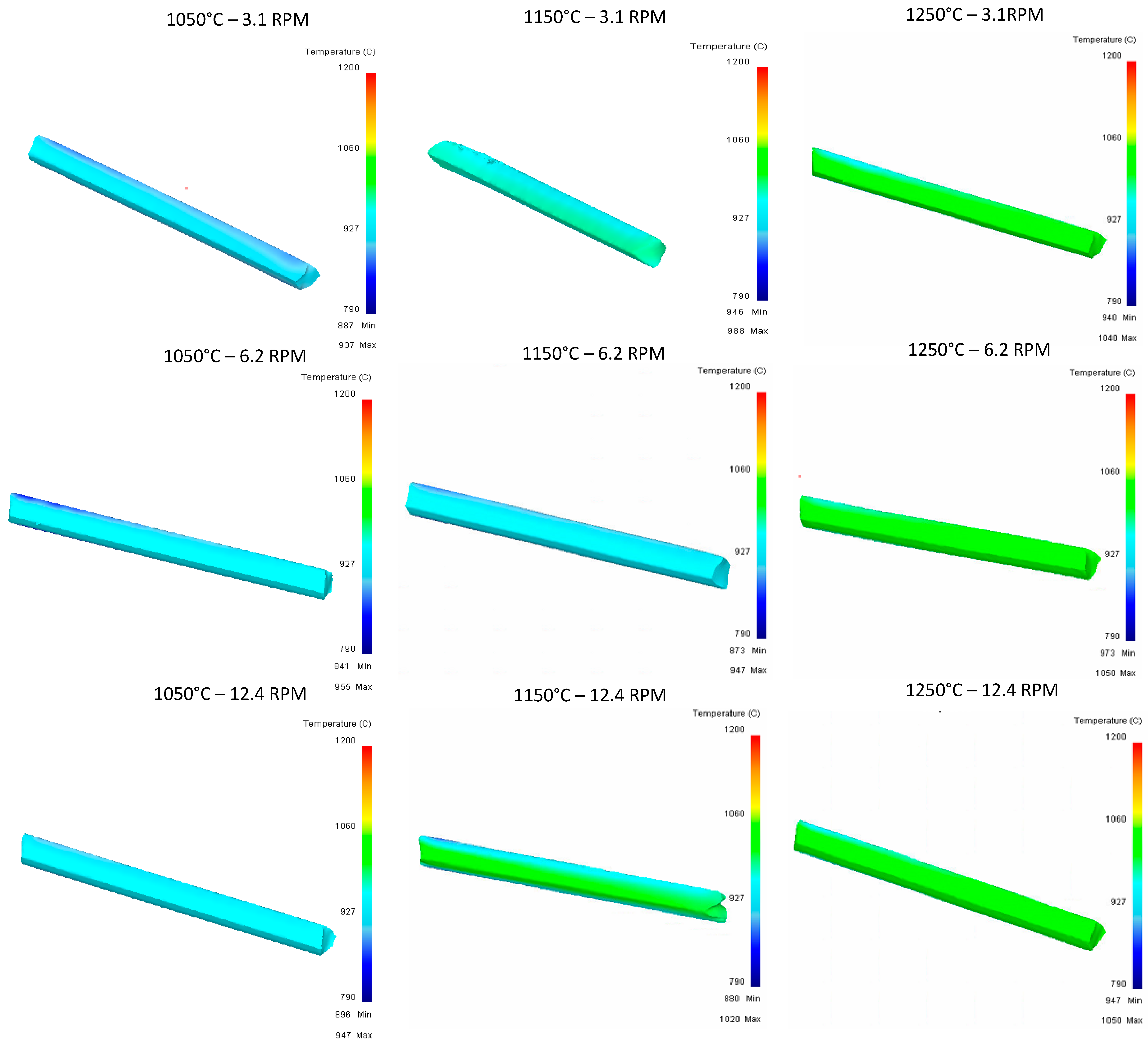
4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Motallebi1, S.R.; Khalili, A. Investigation of Influence Parameters on the Hot Rolling Process Using Finite Element Method. In Proceedings of the 2nd International Conference on Engineering Optimization, Lisbon, Portugal, 6–9 September 2010; pp. 332–338. [Google Scholar]
- Musonda, V.; Akinlabi, E.T. Three-dimensional simulation of a single pass hot rolling of carbon steel: Case of instabilities in steady state region. IOP Conf. Ser. Mater. Sci. Eng. 2018, 423, 012162. [Google Scholar] [CrossRef]
- Fabík, R.; Kliber, J.; Mamuzic, I.; Kubina, T.; Aksenov, S.A. Mathematic al modelling of Flat and long hot rolling based on finite element methods (FEM). Metalurgia 2012, 51, 341–344. [Google Scholar]
- Awaisa, M.; Leea, H.W.; Ima, Y.T.; Kwonb, H.C.; Byonc, S.M.; Parkb, H.D. Defects efects simulation of rolling strip. Mater. Eng. 2009, 16. [Google Scholar]
- Awais, M.; Lee, H.W.; Im, Y.T.; Kwon, H.C.; Byon, S.M.; Park, H.D. Plastic work approach for surface defect prediction in the hot bar rolling process. J. Mater. Process. Technol. 2008, 201, 73–78. [Google Scholar] [CrossRef]
- Kwon, H.-C.; Lee, H.-W.; Kim, H.-Y.; Im, Y.-T.; Park, H.-D.; Lee, D.-L. Surface wrinkle defect of carbon steel in the hot bar rolling process. J. Mater. Process. Technol. 2009, 209, 4476–4483. [Google Scholar] [CrossRef]
- Kainz, A.; Ilie, S.; Parteder, E.; Zeman, K. From Slab Corner Cracks to Edge-Defects in Hot Rolled Strip-Experimental and Numerical Investigations. Steel Res. Int. 2008, 79, 861–867. [Google Scholar] [CrossRef]
- Zambrano, P.C.; Leduc, L.A.; Colás, R. Modelling profile and shape evolution during hot rolling of steel strip. Rev. Metal. 2006, 42, 382–390. [Google Scholar] [CrossRef] [Green Version]
- Zambrano, P.; Guerrero-Mata, M.P.; de la Fuente, M.I.G.; Artigas, A.; Monsalve, A.; Colás, R. Modelación de fenómenos metalúrgicos en laminación en caliente de acero. Rev. Metal. 2008, 44, 74–84. [Google Scholar]
- Suwanpinij, P. Multi-Scale Modelling of Hot Rolled Dual-Phase Steels for Process Design. Master’s Thesis, Facultad de Ingeniería de Georecursos y Materiales, Rheinisch-Westfälische Technische Hochschule Aquisgrán, Aachen, Germany, 2012. [Google Scholar]
- Minutolo, F.C.; Durante, M.; Lambiase, F.; Langella, A. Dimensional analysis of a new type of groove for steel rebar rolling. In Proceedings of the 12th International Scientific Conference Achievements in Mechanical and Materials Engineeeing, Gliwice, Poland, 7–10 December 2003. [Google Scholar]
- Samareh Salavati Pour, H.; Khademhosseini Beheshti, H.; Poursina, M. Prediction of work roll initial crown according to desired strip profile in hot rolling. Int. J. Eng. Trans. C Asp. 2012, 25, 79–88. [Google Scholar] [CrossRef] [Green Version]
- SIMULA. Two-Pass Rolling Simulation. In Abaqus Technology Brief; TB-03-TPRS-1; Dassault Systèmes: Providence, RI, USA, 2007. [Google Scholar]
- Guerrero, A.; Belzunce, J.; Betegón, C.; Jorge, J.; Francisco; Vigil, J. Hot Rolling Process Simulation: Application to UIC-60 Rail Rolling. Recent Pat. Mech. Eng. 2010, 3, 65–71. [Google Scholar]
- Muñiz, A.R. Non-Lineal Finite Method Simulation and Modeling of the Cold and Hot Rolling Processes; Faculty of the Virginia Polytechnic Institute and State University: Blacksburg, VA, USA, 2007. [Google Scholar]
- Cavaliere, M.A.; Goldschmit, M.B.; Dvorkin, E.N. Finite element simulation of the steel plates hot rolling process. Int. J. Numer. Methods Eng. 2001, 52, 1411–1430. [Google Scholar] [CrossRef] [Green Version]
- Nolle, L.; Armstrong, A.; Hopgood, A.; Ware, A. Optimum Work Roll Profile Selection in the Hot Rolling of Wide Steel Strip using Computational Intelligence; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1999; Volume 1625. [Google Scholar]
- Milenin, A.A.; Dyja, H.; Mróz, S. Simulation of metal forming during multi-pass rolling of shape bars. J. Mater. Process. Technol. 2004, 153–154, 108–114. [Google Scholar] [CrossRef]
- Dziedzic, M.; Turczyn, S. Experimental and numerical investigation of strip rolling from dual phase steel. Arch. Civ. Mech. Eng. 2010, 10, 21–30. [Google Scholar] [CrossRef]
- Schafstall, H.; Barth, C. An Innovate Approach to Automated Simulation of Full 3D Ring Rolling Process and Other Incremental Forming Processes. Steel Res. Int. 2010, 81, 202–205. [Google Scholar]
- Lee, Y.; Choi, S.; Kim, H.; Choo, W.Y. An Experimental Study of the Mean Effective Strain in Rod (or Bar) Rolling Process. Met. Mater. 2000, 6, 525–531. [Google Scholar] [CrossRef]
- Hong, H.; Kang, Y. Finite Element Simulation of Hot Continuous Rolling of 37Mn5 Tube Rail and Roll Pass Optimization; School of Materials Science and Engineering, University of Science and Technology Beijing: Beijing, China, 2012. [Google Scholar]
- Kainz, A.; Finstermann, G. A New Eulerian-Lagrangian Hybrid Finite Element Method Gor the Numerical Simulation of Stationary Rolling Processes; VOEST-ALPINE Industrieanlagenbau GmbH: Linz, Austria, 2008. [Google Scholar]
- Hemanth, S.T.; Arunkumar, Y.; Srinath, M.S. Optimize the Rolling Process Parameters for Material AA1100 using Metal Forming Simulation. MATEC Web Conf. 2018, 144, 03005. [Google Scholar] [CrossRef]
- Pérez-Alvarado, A.; Arreola-Villa, S.A.; Calderón-Ramos, I.; Castañeda, R.S.; de la Rosa, L.A.M.; Chattopadhyay, K.; Morales, R. Numerical Simulation of the Hot Rolling Process of Steel Beams. Materials 2021, 14, 7038. [Google Scholar] [CrossRef] [PubMed]
- Hanoglu, U.; Šarler, B. Hot Rolling Simulation System for Steel Based on Advanced Meshless Solution. Metals 2019, 9, 788. [Google Scholar] [CrossRef]
- Klement, S. Incremental Support Vector Regression for Steering Hot Rolling Mills. Diploma Thesis, Instituto de Neuroinformáticay Bioinformática, Universidad de Lübeck, Lübeck, Germany, 2006. [Google Scholar]
- Rios-Gonzalez, J.A.; Garcia-Pastor, F.A. FEM Comparative Between Two Roller Sizes for Hot Shape Rolling of Reinformecent Bars Fabrication; Centro de Investigación y de Estudios Avanzados del IPN Unidad Saltillo: Ramos Arizpe, Mexico, 2014. [Google Scholar]










| Element | Percentage |
|---|---|
| C | 0.7–0.8 |
| Mn | 0.4–0.7 |
| S | <0.05 |
| P | <0.04 |
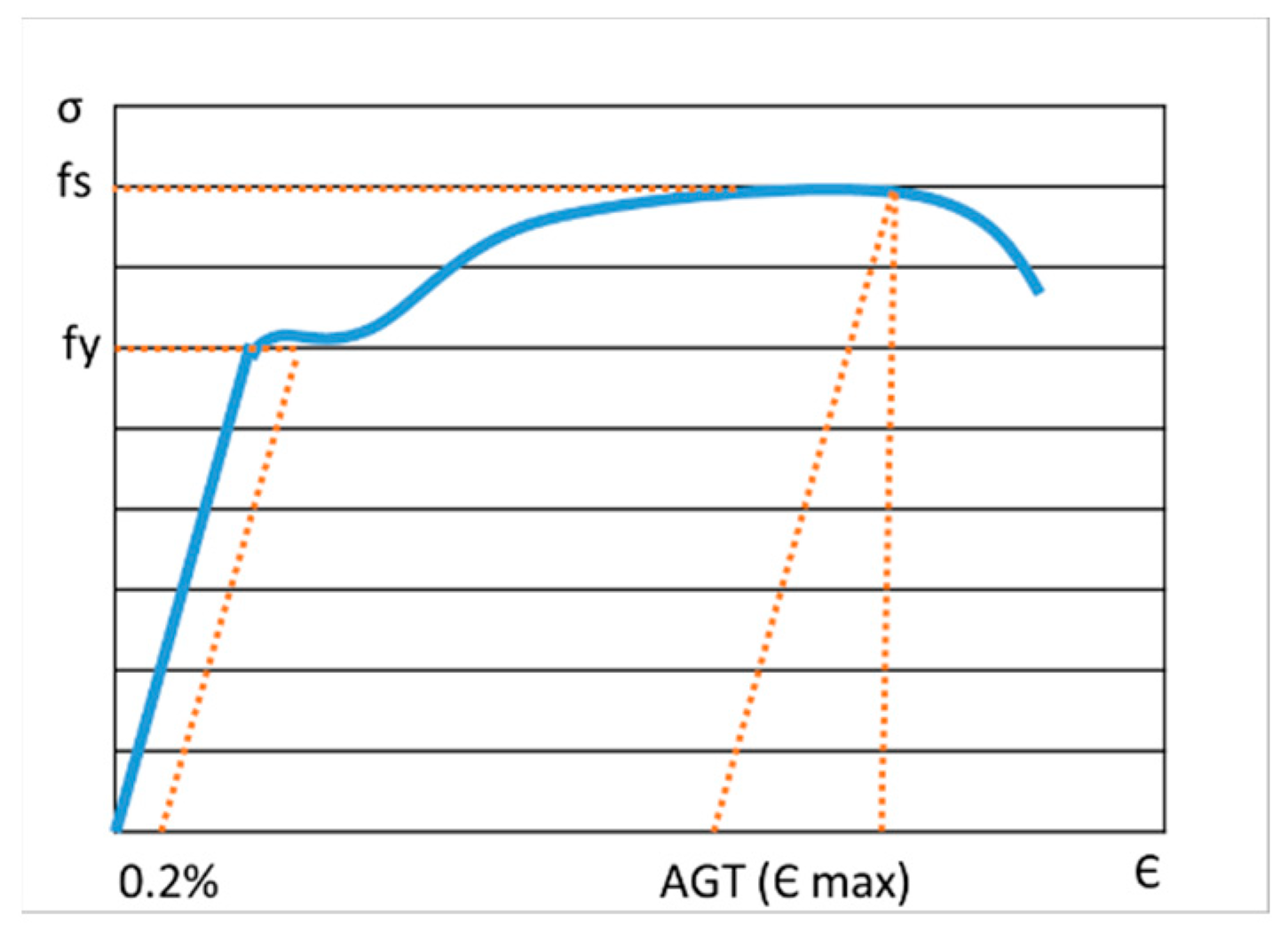
| Young’s modulus (GPa) | 206 |
| Poisson’s ratio | 0.3 |
| Thermal expansion coefficient (°C−1) | 1.2 × 10−5 |
| Density (kg/m3) | 7800 |
| Variable | Pass 0 | Pass 1 | Pass 2 | Pass 3 | Pass 4 | Pass 5 | |
|---|---|---|---|---|---|---|---|
| Railway rail dimensions | Length (mm) | 348.63 | 417.41 | 662.58 | 1001.09 | 1665.32 | 1829.52 |
| Width (mm) | 70.39 | 73.05 | 82.03 | 44.85 | 27.17 | 26.9 | |
| Height (mm) | 57.59 | 41.75 | 24.07 | 29.4 | 37.92 | 32.67 | |
| Top roll diameter (mm) | - | 355 | 355 | 355 | 304.8 | 304.8 | |
| Bottom roll diameter (mm) | - | 355 | 355 | 355 | 304.8 | 304.8 | |
| Average value of deformation (reduction) | - | 16.5% | 32.5% | 32.5% | 36.7% | 18.7% | |
| Deformation velocity (m/s) | version 3.1 RPM | - | 0.07 | 0.09 | 0.09 | 0.08 | 0.06 |
| version 6.2 RPM | - | 0.14 | 0.17 | 0.17 | 0.16 | 0.12 | |
| version 12.4 RPM | - | 0.28 | 0.34 | 0.34 | 0.31 | 0.24 | |
| Machine time (s) | - | 13.4 | 26.2 | 37.9 | 52 | 65.8 | |
| Contact area upper roller vs. pass mm2 | - | 1846 | 1655.8 | 233.1 | 91.6 | 61.9 | |
| Contact area lower roller vs. pass mm2 | - | 334 | 935 | 242 | 89 | 61.9 | |
| Rolling Load (KN) | |||||||||
| T (°C) | 1050 | 1150 | 1250 | ||||||
| Pass\ Ang vel | 3.1 | 6.2 | 12.4 | 3.1 | 6.2 | 12.4 | 3.1 | 6.2 | 12.4 |
| 1 | 200 | 205 | 215 | 145 | 155 | 157 | 130 | 145 | 151 |
| 2 | 500 | 450 | 440 | 370 | 350 | 340 | 310 | 302 | 290 |
| 3 | 190 | 170 | 175 | 150 | 175 | 135 | 125 | 115 | 120 |
| 4 | 220 | 205 | 208 | 155 | 200 | 180 | 150 | 148 | 146 |
| 5 | 58 | 57 | 58 | 49 | 52 | 69 | 40 | 39 | 39 |
| Rolling Torque (KN) | |||||||||
| T (°C) | 1050 | 1150 | 1250 | ||||||
| Pass\ Ang vel | 3.1 | 6.2 | 12.4 | 3.1 | 6.2 | 12.4 | 3.1 | 6.2 | 12.4 |
| 1 | 14 | 10 | 11 | 7.0 | 6.8 | 7.0 | 9.5 | 9.3 | 9.7 |
| 2 | 16 | 14.5 | 12.9 | 11.5 | 11.9 | 11 | 10 | 9.2 | 9.8 |
| 3 | 7.7 | 7.0 | 6.9 | 6.5 | 7.0 | 4.9 | 5.5 | 4.5 | 5.5 |
| 4 | 5 | 5.1 | 4.9 | 4.2 | 5.0 | 3.3 | 4.1 | 3.2 | 3.5 |
| 5 | 0.8 | 0.9 | 1.0 | 0.7 | 0.8 | 1.6 | 0.7 | 0.6 | 0.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montemayor-de la Garza, K.; Zambrano-Robledo, P.d.C.; Zapata-Hernandez, O.J.; Leduc-Lezama, L.A. Finite Element Modeling of Hot Rolling of 1075 Carbon Steel Process with Variable Cross Section. Materials 2023, 16, 2. https://doi.org/10.3390/ma16010002
Montemayor-de la Garza K, Zambrano-Robledo PdC, Zapata-Hernandez OJ, Leduc-Lezama LA. Finite Element Modeling of Hot Rolling of 1075 Carbon Steel Process with Variable Cross Section. Materials. 2023; 16(1):2. https://doi.org/10.3390/ma16010002
Chicago/Turabian StyleMontemayor-de la Garza, Karina, Patricia del Carmen Zambrano-Robledo, Oscar Jesus Zapata-Hernandez, and Luis Adolfo Leduc-Lezama. 2023. "Finite Element Modeling of Hot Rolling of 1075 Carbon Steel Process with Variable Cross Section" Materials 16, no. 1: 2. https://doi.org/10.3390/ma16010002
APA StyleMontemayor-de la Garza, K., Zambrano-Robledo, P. d. C., Zapata-Hernandez, O. J., & Leduc-Lezama, L. A. (2023). Finite Element Modeling of Hot Rolling of 1075 Carbon Steel Process with Variable Cross Section. Materials, 16(1), 2. https://doi.org/10.3390/ma16010002






