The Effect of Particle Necks on the Mechanical Properties of Aerogels
Abstract
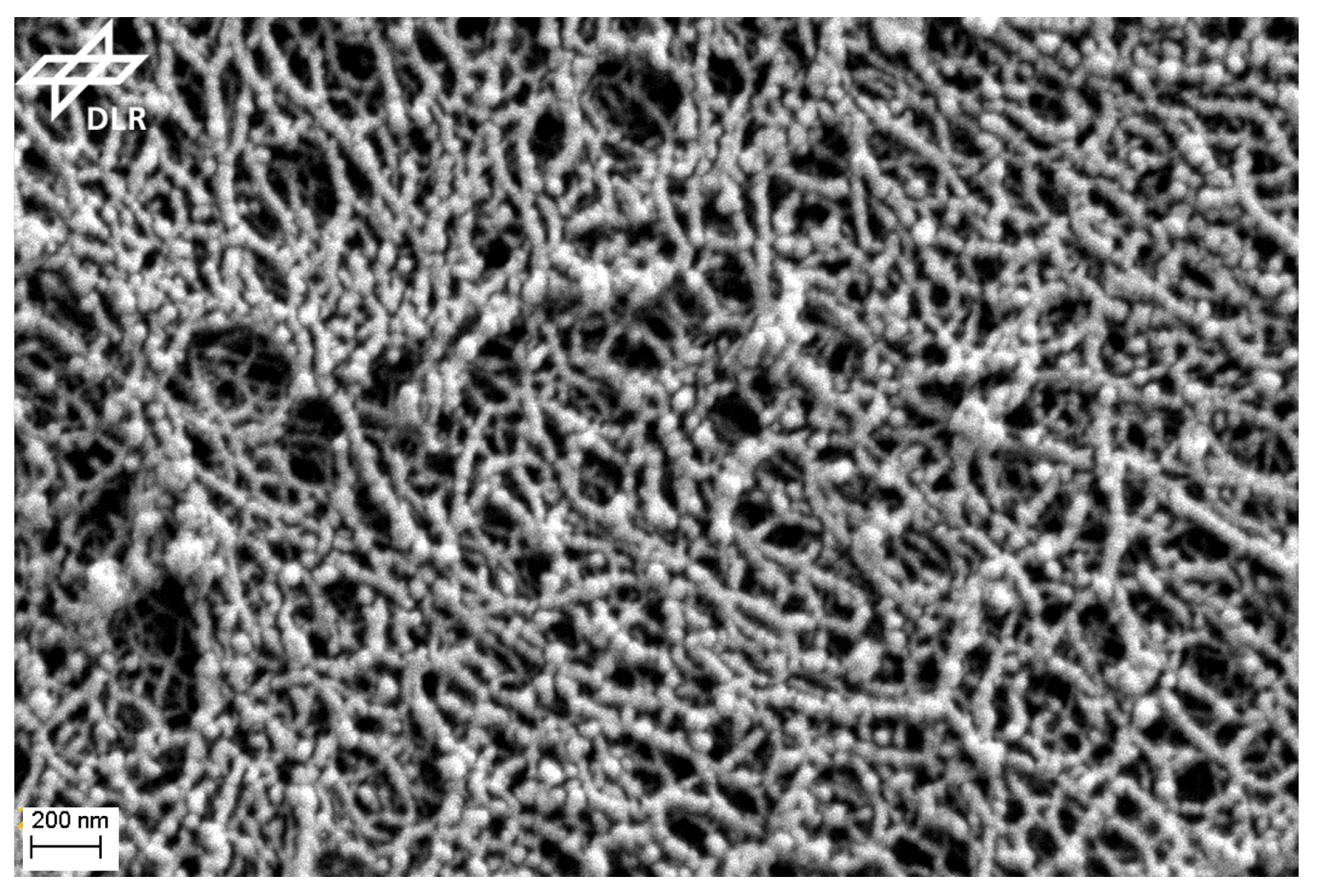
:1. Introduction
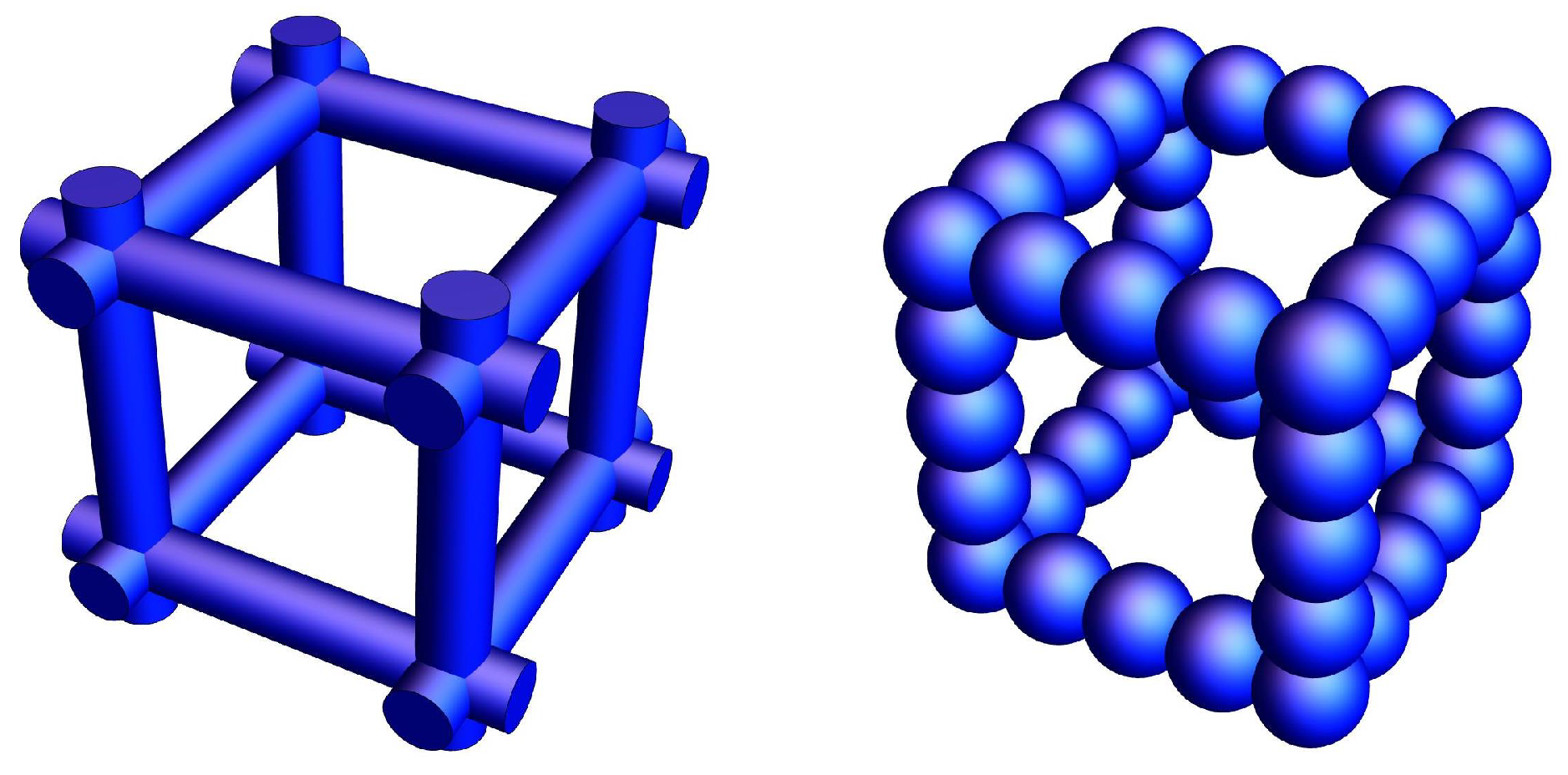
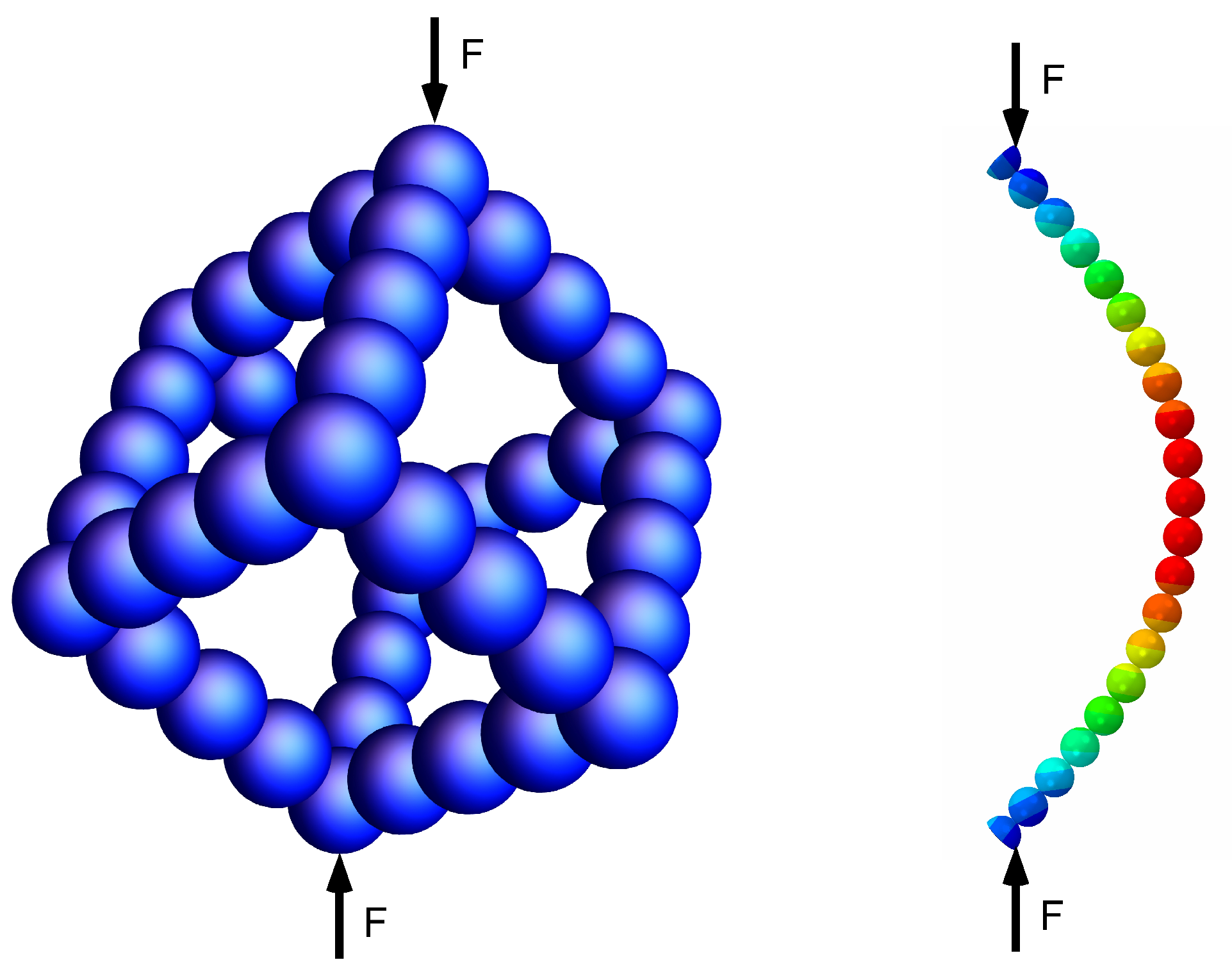
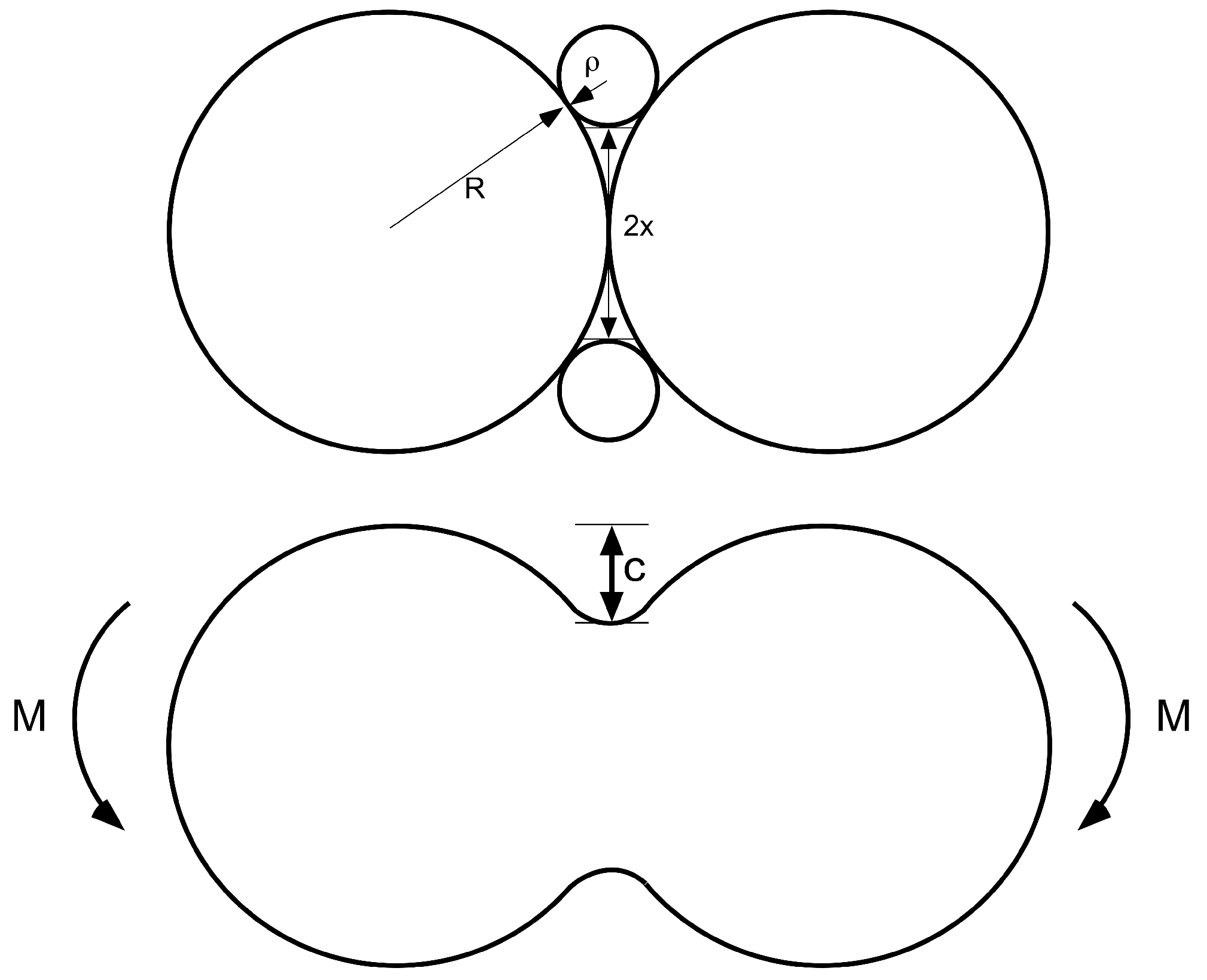
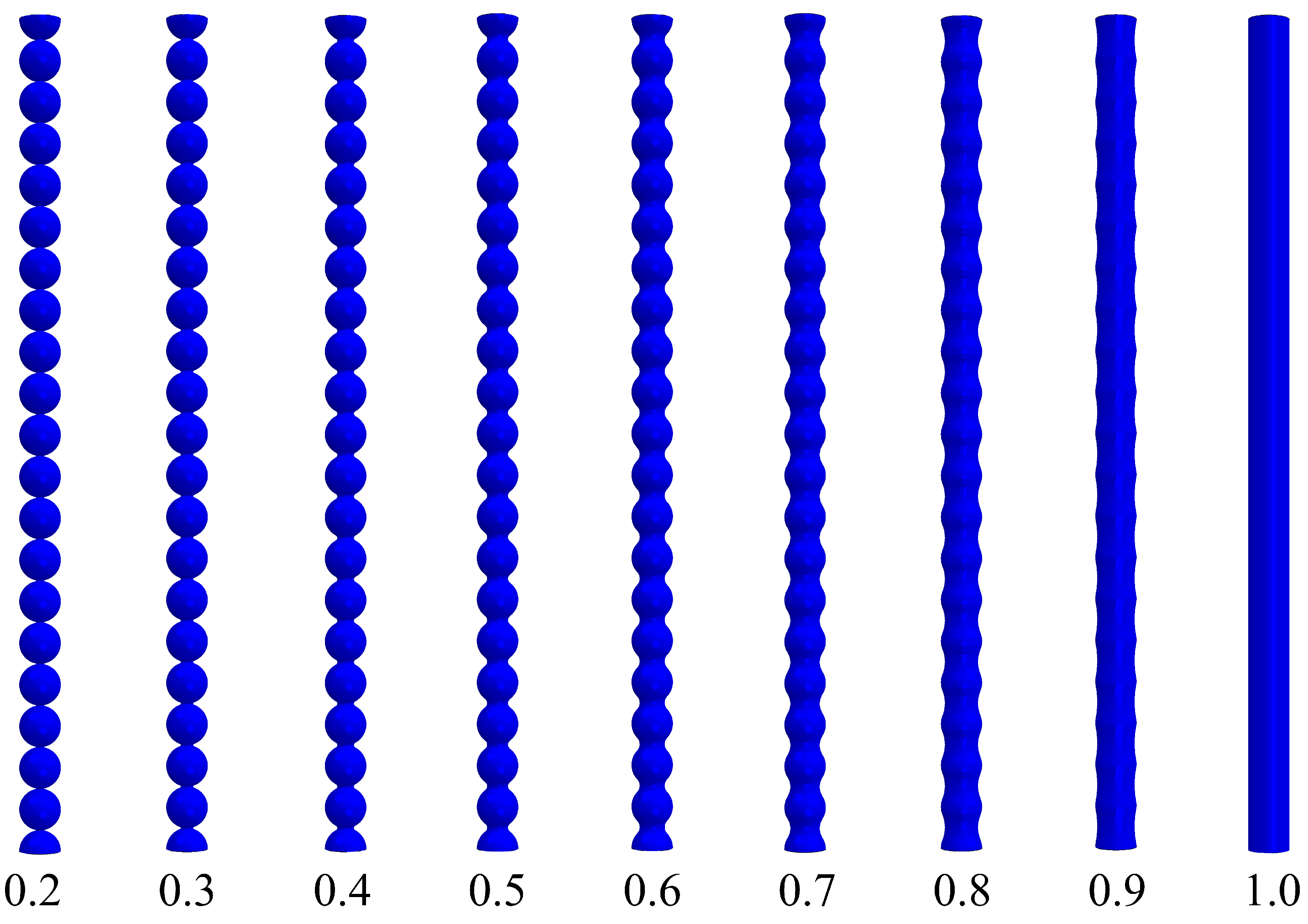
2. Description of Pore Walls as Corrugated Beams
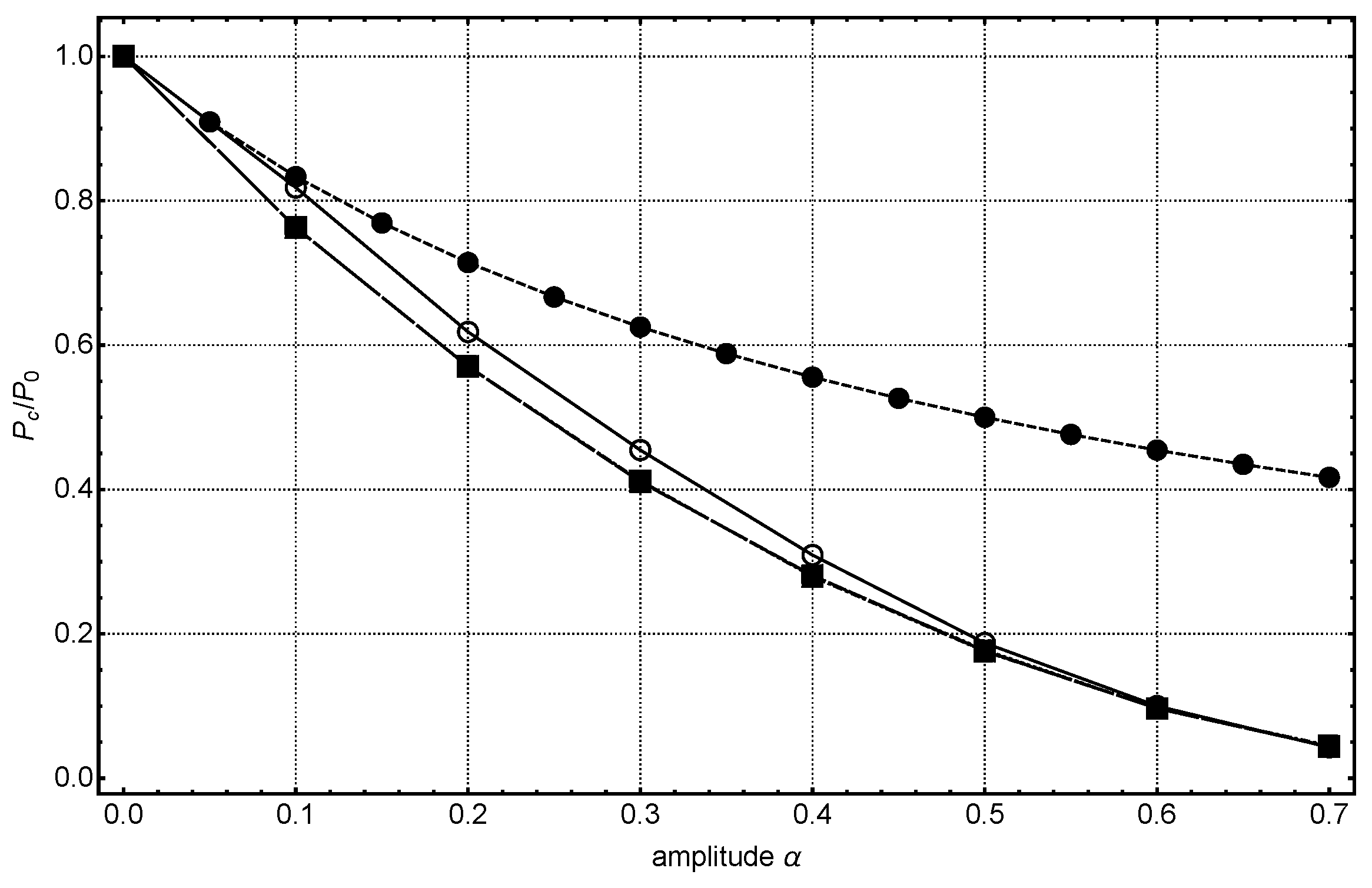
3. A Simple Estimate of Buckling Strength
4. Bending of Corrugated Beams
4.1. Approximate Analytical Solution
4.2. Nonlinear Bending-Numerical Solution
5. Finite Element Modeling of the Pore Walls with Particle Necks
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gibson, L.J.; Ashby, M.F. Cellular Solids, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Aney, S.; Rege, A. The effect of pore sizes on the elastic behaviour of open-porous cellular materials. Math. Mech. Solids 2022. [Google Scholar] [CrossRef]
- Ratke, L.; Gurikov, P. The Chemistry and Physics of Aerogels; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Rege, A.; Aney, S.; Milow, B. Influence of pore-size distributions and pore-wall mechanics on the mechanical behavior of cellular solids like aerogels. Phys. Rev. E 2021, 103, 043001. [Google Scholar] [CrossRef] [PubMed]
- Schwan, M.; Tannert, R.; Ratke, L. New soft and spongy resorcinol–formaldehyde aerogels. J. Supercrit. Fluids 2016, 107, 201–208. [Google Scholar] [CrossRef]
- Lei, J.; Liu, Z. A novel constitutive model for the mechanical properties of silica aerogels. J. Appl. Phys. 2018, 124, 025102. [Google Scholar] [CrossRef]
- Chandrasekaran, R.; Hillgärtner, M.; Ganesan, K.; Milow, B.; Itskov, M.; Rege, A. Computational design of biopolymer aerogels and predictive modelling of their nanostructure and mechanical behaviour. Sci. Rep. 2021, 11, 10198. [Google Scholar] [CrossRef] [PubMed]
- Rege, A. A perspective on methods to computationally design the morphology of aerogels. Adv. Eng. Mater. 2022; accepted. [Google Scholar] [CrossRef]
- Gelb, L.D. Simulating Silica Aerogels with a Coarse-Grained Flexible Model and Langevin Dynamics. J. Phys. Chem. C 2007, 111, 15792–15802. [Google Scholar] [CrossRef]
- Abdusalamov, R.; Scherdel, C.; Itskov, M.; Milow, B.; Reichenauer, G.; Rege, A. Modeling and Simulation of the Aggregation and the Structural and Mechanical Properties of Silica Aerogels. J. Phys. Chem. B 2021, 125, 1944–1950. [Google Scholar] [CrossRef] [PubMed]
- Rege, A.; Aney, S.; Ratke, L. Impact of pearl-necklace-like skeleton on pore sizes and mechanical properties of porous materials: A theoretical view. AIP Adv. 2022, 12, 105108. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, X.; Giuliani, F.; Atkinson, A. Microstructural characteristics and elastic modulus of porous solids. Acta Mater. 2015, 89, 268–277. [Google Scholar] [CrossRef] [Green Version]
- Dargazany, R.; Itskov, M. Yield behavior of colloidal aggregates due to combined tensile-bending loads. Phys. Rev. E 2012, 85, 051406. [Google Scholar] [CrossRef] [PubMed]
- Dargazany, R.; Chen, H.; Lin, J.; Azad, A.I.; Alexander-Katz, A. On the validity of representation of the inter-particle forces of a polymer-colloid cluster by linear springs. Polymer 2017, 109, 266–277. [Google Scholar] [CrossRef]
- Aney, S.; Schettler, J.; Schwan, M.; Milow, B.; Rege, A. Insights into the Micromechanics of Organic Aerogels Based on Experimental and Modeling Results. Adv. Eng. Mater. 2022, 24, 2100095. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, L.; Liu, Y.; Zhang, G.; Zhu, P. Characterization and functional assessment of alginate fibers prepared by metal-calcium ion complex coagulation bath. Carbohydr. Polym. 2020, 232, 115693. [Google Scholar] [CrossRef] [PubMed]
- Beyerlein, G.S. Synthese und Eigenschaften Polyurethanbasierter Aerogele auf Basis Rohstofflich Recycelter Reststoffe. Ph.D. Thesis, RWTH Aachen University, Aachen, Germany, 2021. [Google Scholar]
- Landau, L.; Lifshitz, E. Lehbrbuch der Theoretischen Physik; Akademie Verlag: Berlin, Germany, 1965; Volume VII. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions, 10th printing ed.; Dover Publications: Mineola, NY, USA, 1972. [Google Scholar]
- Oliver, F.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. NIST Handbook of Mathematical Functions; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Luongo, A. Mode Localization in Dynamics and Buckling of Linear Imperfect Continuous Structures. Nonlinear Dyn. 2001, 25, 133–156. [Google Scholar] [CrossRef]
- Hutzler, S.; Mughal, A.; Ryan-Purcell, J.; Irannezhad, A.; Weaire, D. Buckling of a linear chain of hard spheres in a harmonic confining potential: Numerical and analytical results for low and high compression. Phys. Rev. E 2020, 102, 022905. [Google Scholar] [CrossRef] [PubMed]
- Einarsrud, M.A.; Nilsen, E. Strengthening of water glass and colloidal sol based silica gels by aging in TEOS. J. Non-Cryst. Solids 1998, 226, 122–128. [Google Scholar] [CrossRef]
- Einarsrud, M.A.; Nilsen, E.; Rigacci, A.; Pajonk, G.M.; Buathier, S.; Valette, D.; Durant, M.; Chevalier, B.; Nitz, P.; Ehrburger-Dolle, F. Strengthening of silica gels and aerogels by washing and aging processes. J. Non-Cryst. Solids 2001, 285, 1–7. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ratke, L.; Rege, A.; Aney, S. The Effect of Particle Necks on the Mechanical Properties of Aerogels. Materials 2023, 16, 230. https://doi.org/10.3390/ma16010230
Ratke L, Rege A, Aney S. The Effect of Particle Necks on the Mechanical Properties of Aerogels. Materials. 2023; 16(1):230. https://doi.org/10.3390/ma16010230
Chicago/Turabian StyleRatke, Lorenz, Ameya Rege, and Shivangi Aney. 2023. "The Effect of Particle Necks on the Mechanical Properties of Aerogels" Materials 16, no. 1: 230. https://doi.org/10.3390/ma16010230





