Elastic–Plastic Numerical Analysis of the Spinning Process of SA-372 Steel Used in High-Pressure Hydrogen Storage Cylinders (≥100 MPA)
Abstract
:1. Introduction
2. Establishment of the Simulation Model
2.1. Simulation Conditions
2.2. Influence of Spinning Temperature
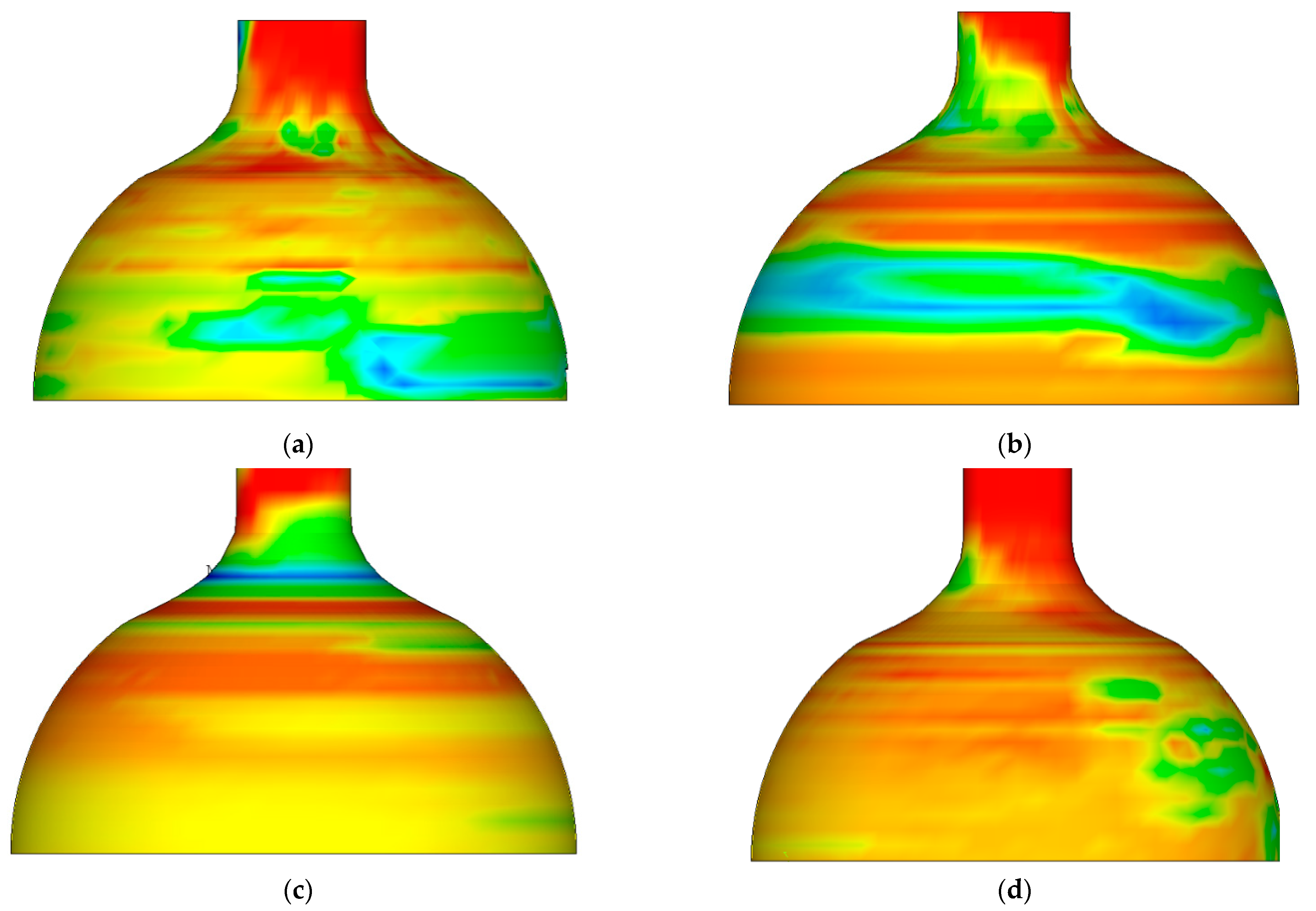
2.2.1. Effect of Spinning Temperature on the Equivalent Effect Distribution
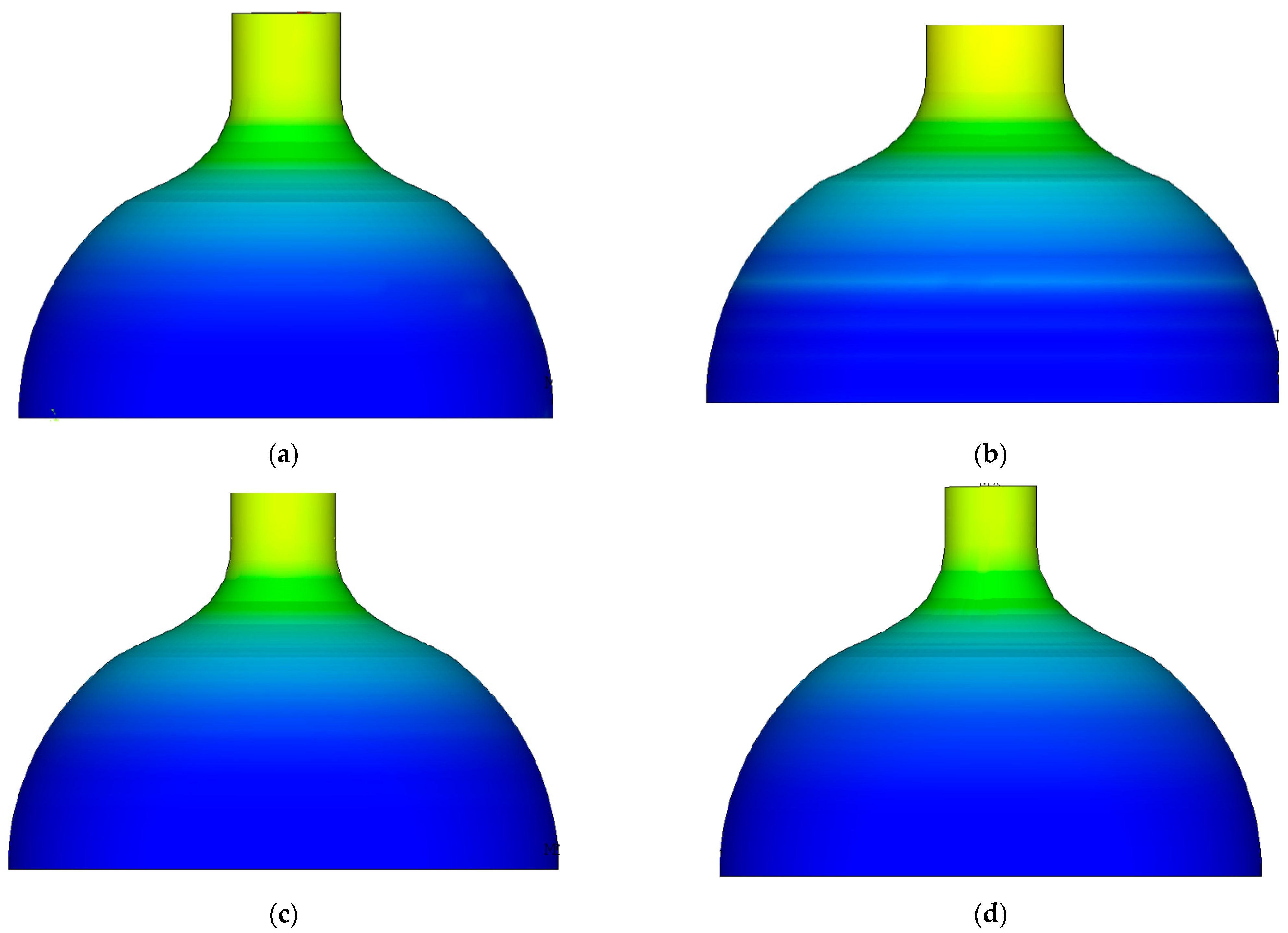
2.2.2. Effect of Spinning Temperature on the Equivalent Strain
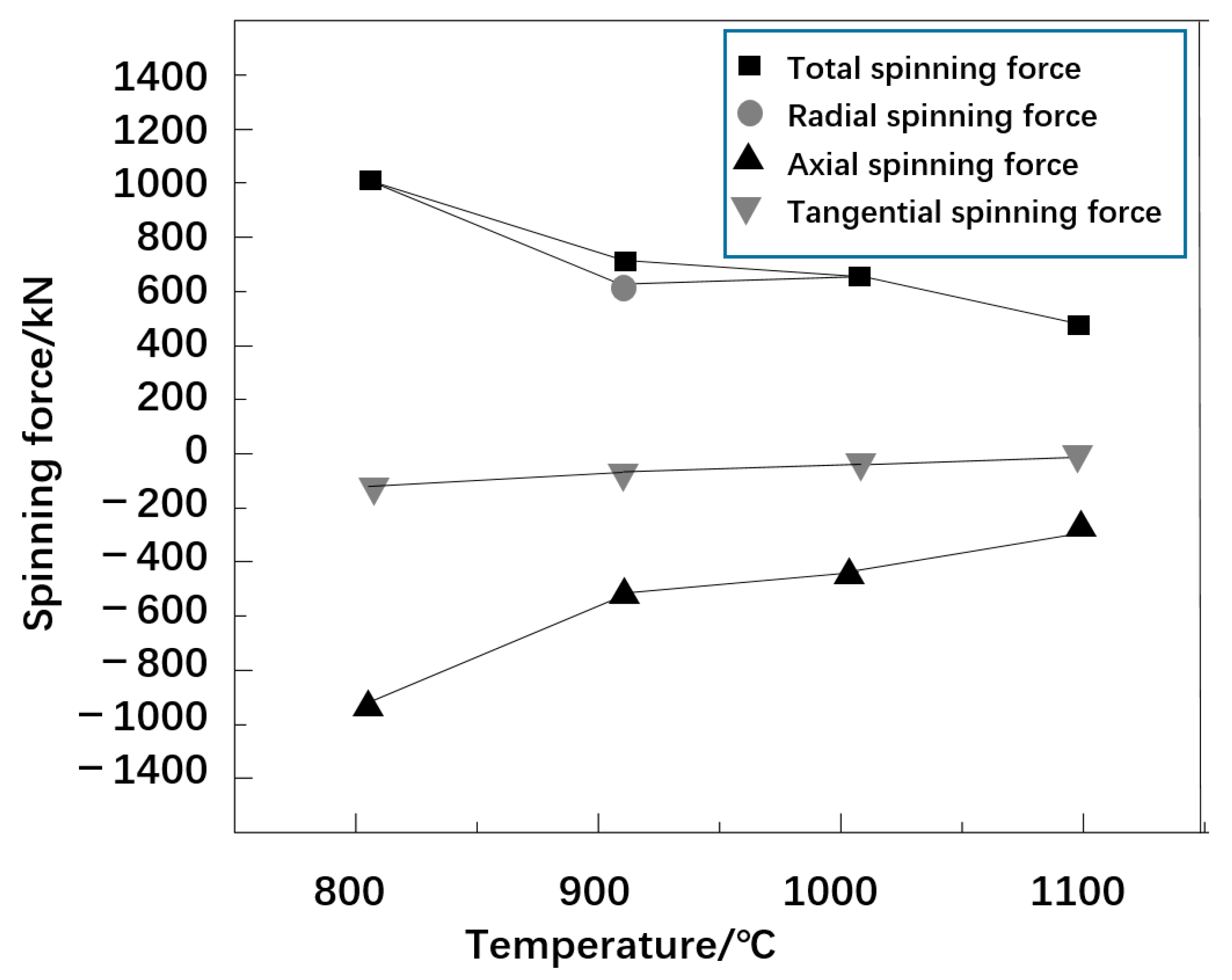
2.2.3. Effect of Spinning Temperature on Spinning Pressure
2.2.4. Influence of Spinning Temperature on the Wall Thickness of a High-Pressure Hydrogen Storage Cylinder
2.3. Effect of Feed Ratio on Spin Forming
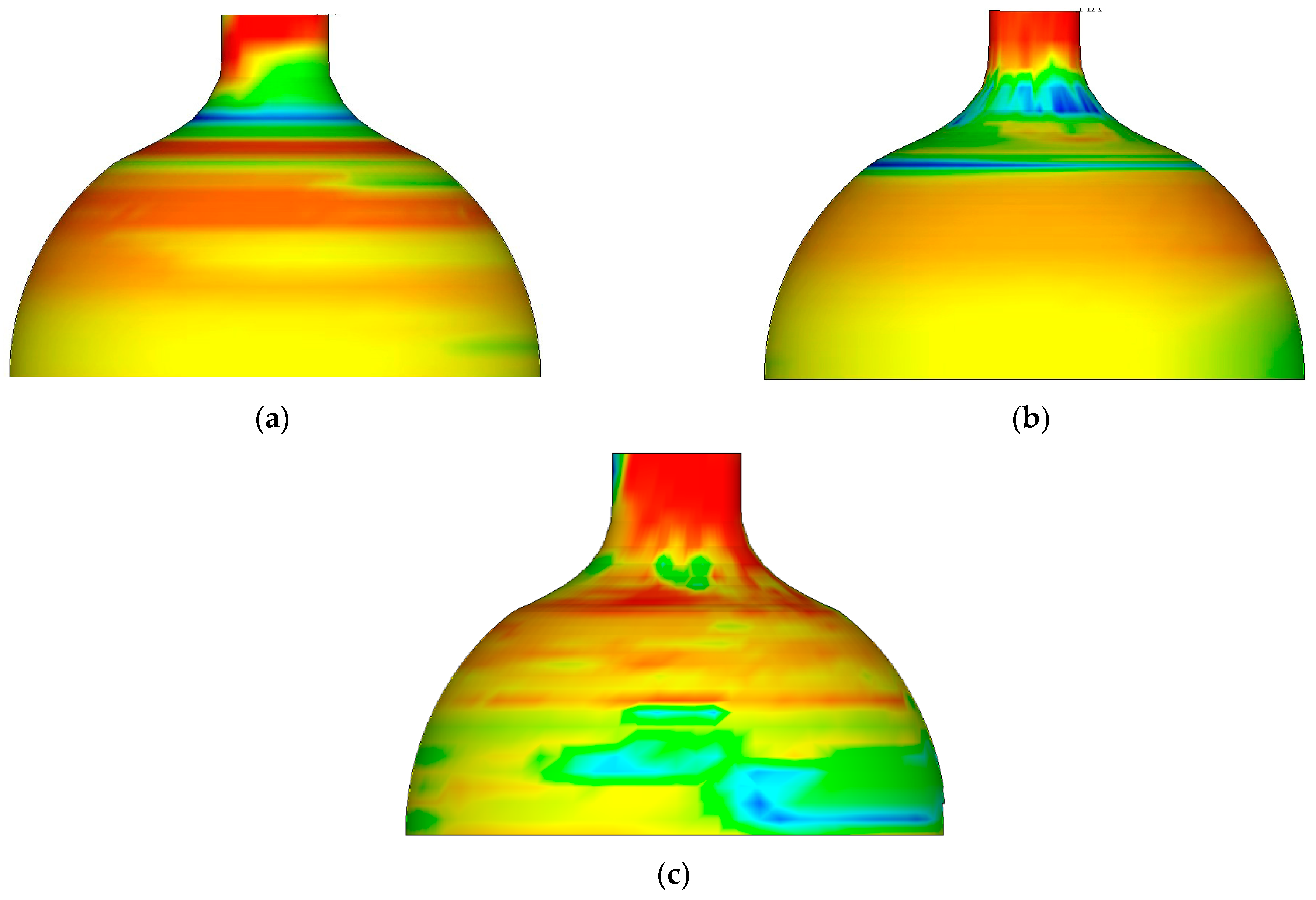
2.3.1. Effect of Feed Ratio on Stress Field Distribution
2.3.2. Influence of Feed Ratio on Strain Field Distribution
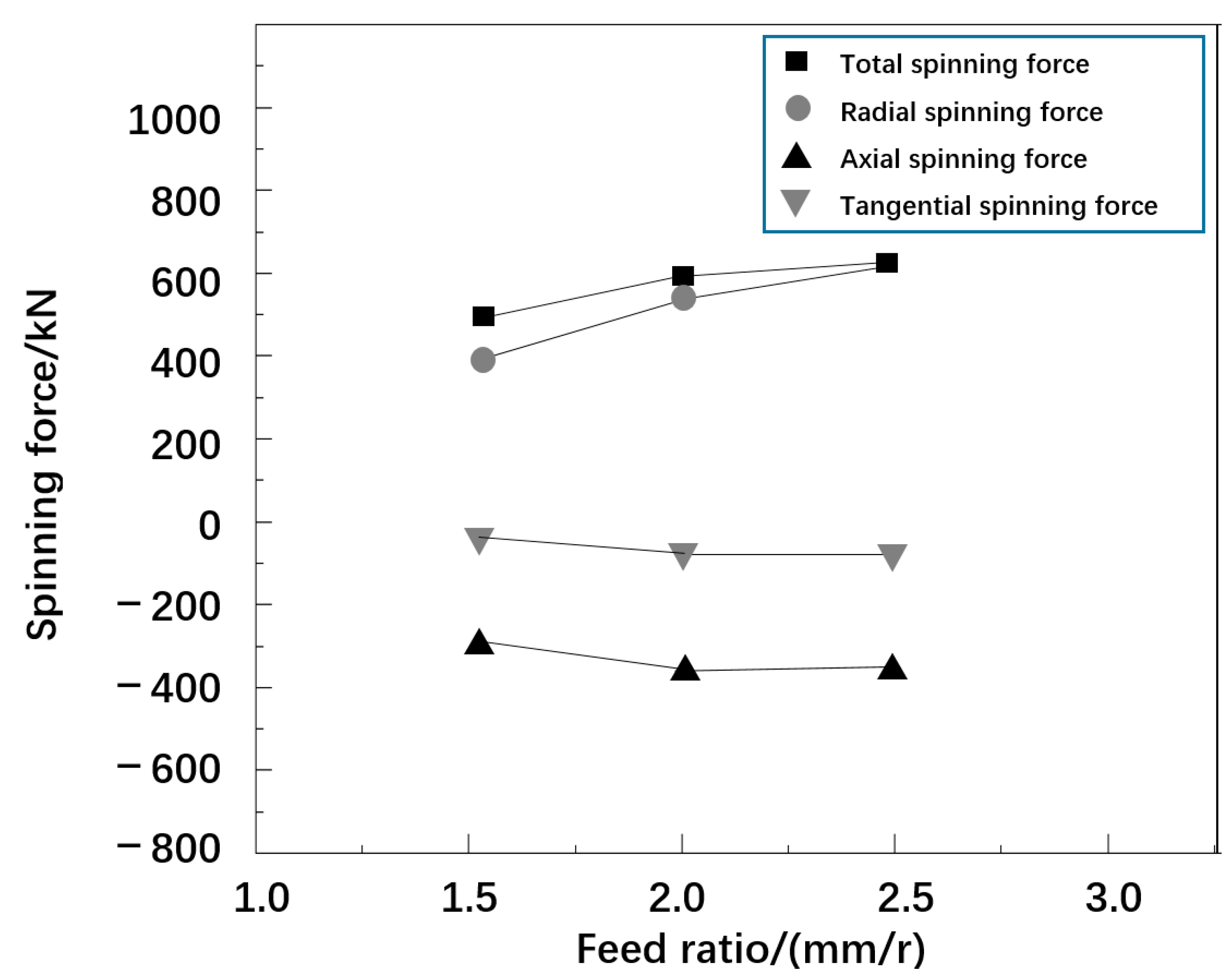
2.3.3. Effect of Feed Ratio on Rotation
2.3.4. Effect of Feed Ratio on Cylinder Wall Thickness
3. Spinning Experiment
4. Hydrogen Embrittlement Test after Spinning
4.1. Test Principle
4.2. Test Conditions and Procedure
4.3. Test Results
5. Conclusions
- With the increase in temperature, the maximum value of the equivalent stress gradually decreases, the maximum value of the equivalent strain gradually increases, and the total rotational pressure, radial, axial and tangential rotational pressure decreases.
- With the increase in feed ratio, the total spin pressure and the three-way spin pressure both show an increasing trend, and the equivalent strain slightly increases.
- The optimized processing parameters were determined based on the numerical analysis results. The pinning temperature and the roller feed ratio were 1000 °C and 2.0 mm/s, respectively.
- The hydrogen embrittlement test after spinning was performed based on the ISO 11114-4:2005 method using the optimized process parameters. The results revealed that the optimized spinning parameters could effectively improve the hydrogen embrittlement resistance of the shoulder of the high-pressure hydrogen storage cylinder.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, Y.Z.; Meng, B.; Chen, L.X.; Wang, G.; Zheng, J.Y.; Gu, C.H.; Zhang, X.; Zhang, J.F. Current situation analysis of hydrogen energy utilization. Chem. Ind. Prog. 2015, 9, 3248–3255. [Google Scholar]
- Zheng, J.Y.; Kai, F.M.; Liu, Z.Q.; Chen, R.; Chen, C.P. High pressure hydrogen storage and transportation equipment and its risk assessment. J. Sol. Energy 2006, 27, 1168–1174. [Google Scholar]
- Chen, R.; Zheng, J.Y.; Xu, P.; Kai, F.M.; Liu, P.F. Research progress of hydrogen embrittlement of metal materials at room temperature and high pressure. Sun Chin. J. Energy 2008, 29, 502–508. [Google Scholar]
- Yamada, E.; Watanabe, S.; Hayashi, A.K.; Tsuboi, N. Numerical analysis on auto-ignition of a high pressure hydrogen jet spouting from a tube. Proc. Combust. Inst. 2009, 32, 2363–2369. [Google Scholar] [CrossRef]
- Schefer, R.W.; Houf, W.G.; Williams, T.C.; Bourne, B.; Colton, J. Characterization of high-pressure, under expanded hydrogen-jet flames. Int. J. Hydrogen Energy 2007, 32, 2081–2093. [Google Scholar] [CrossRef]
- Liang, B.X.; Yang, M.H.; Yang, Y.H.; Xia, Q. Cylinder Spinning Forming Technology. Electromechanical Eng. Technol. 2004, 33, 12–13. [Google Scholar]
- Makhviladze, G.M.; Yakush, S.E. Large-seal unconfined fires and explosion. Proc. Combust. Inst. 2002, 29, 195–210. [Google Scholar] [CrossRef]
- Zhou, D.H.; Tan, Y. Environmental Hydrogen Embrittlement of Metals and Its Test Technology; National Defense Industry Press: Beijing, China, 1998. [Google Scholar]
- Chu, W.Y.; Qiao, L.J.; Chen, Q.Z.; Gao, K.W. Fracture and Environmental Fracture; Science Press: Beijing, China, 2000. [Google Scholar]
- Louthan, M.R.; Bernstein, I.M.; Thompson, A.W. Hydrogen in Metals; ASM: Metals Park, OH, USA, 1974; p. 53. [Google Scholar]
- Yang, J.L. The Multi-passes Spinning Process of TA2 Tube Based on Finite Element Method. J. Plast. Eng. 2010, 2, 39–44. [Google Scholar]
- Mei, Z.; Shang, G.M. The treatment of Relative Motion between Mandrel and Roller in Numerical Simulation for Tube Spinning. J. Netshape Form. Eng. 2011, 6, 107–111. [Google Scholar]
- Song, X.F.; Zhan, M.; Jiang, H.B.; Li, T.; Yang, H. Forming mechanism of defects in spinning of large complicated thin-wall aluminum alloy shells. J. Plast. Eng. 2013, 20, 31–36. [Google Scholar]
- Zhao, L.J.; Zhang, Q.; Nie, J.; Shang, G.; Wen, B.; Kong, Z.J.; Rong, J.W. Simulation Analysis on Spin Forming of Pulleys for Engine Front End Accessory. J. Plast. Eng. 2015, 22, 30–36. [Google Scholar]
- Cao, Z. The Development of Spinning Forming Technology in Future. China Aviat. News 2016, 3, S03. [Google Scholar]
- Dong, S.B.; Lee, J.K.; Lee, S.P.; Son, I.S.; Baek, U.B.; Nahm, S.H.; Lee, J.H. Evaluation on hydrogen embrittlement of material using nondestructive test. Int. J. Precis. Eng. Manuf. 2014, 15, 989–993. [Google Scholar]
- Rosenton, D.F. Production and Progress of Seamless Steel Pipes for High Pressure Cylinders. Steel Pipes 1999, 28, 1–5. [Google Scholar]
- Xu, H.P.; Fan, G.S.; Zhang, S.P. Application and development of spinning equipment and process technology. New Technol. Process 2007, 12, 6–8. [Google Scholar]
- Chi, J.X.; Cai, Z.Y.; Li, L.L. Optimization of spinning process parameters for long thin-walled cylinder of TC11 alloy based on processing map. Int. J. Adv. Manuf. 2018, 97, 1961–1969. [Google Scholar] [CrossRef]
- Li, X.G.; Wang, Y.L.; Liang, W.; Miao, L.Q. Research on influence of spinning process parameters based on simulation and experiment. IOP Conf. Ser. Mater. Sci. Eng. 2018, 397, 012133. [Google Scholar] [CrossRef] [Green Version]
- Lu, Q.Y.; Yan, J. Elastic–Plastic Numerical Analysis of Spinning Forming Process of Major Flywheel on DMFW based on DEFORM. New Technol. New Process 2016, 7, 9–13. [Google Scholar]
- Xi, Q.H.; Fan, W.X.; Lv, W.; Chen, D.B. Parameter Optimization of Power Spinning Forming Process Based on Grey Correlation Degree Hot Working Technology. Int. J. Adv. Manuf. 2016, 45, 129–132. [Google Scholar]
- Zhang, X.X.; Wang, J.; Lu, G.D.; Wang, Y.Y. Spinning of Curvilinear Generatrix Parts without Mandrel based on Main and Auxiliary Rollers Forging & Stamping Technology. J. Plast. Eng. 2017, 42, 86–92. [Google Scholar]
- Li, X.G.; Liang, H.S.; Wang, D.L.; Sui, L.H.; Chen, L.D. Research on Simulation of Spinning of Ta-2.5W Spherical Disc Part. Manuf. Autom. 2014, 36, 43–45. [Google Scholar]
- Shi, M.; Zhao, Y.X.; Kong, Q.S.; Yu, Z.Q. Baffle-Assistant Spinning Method for Thin-walled Aluminum Alloy Seal Head. J. Shanghai Jiaotong Univ. 2015, 49, 1497–1503. [Google Scholar]
- Ying, F.Q.; Zhang, G.C.; Pan, X.Y. Discussion on 3D Finite Element Simulation Technology of Metal Plastic Forming. Forg. Stamp. Technol. 2004, 29, 1–5. [Google Scholar]
- Miao, P.Z.; Zhu, X.B.; Hu, C.I.; Guo, L.G. Finite Element Modeling and Optimization Analysis of Powerful Spinning for Thin-walled Cylinder Parts. Forg. Press. Technol. 2014, 39, 137–142. [Google Scholar]
- Gan, J.K.; Wang, J.L.; Liu, Z.B. Forging & Stamping Branch of Chinese Mechanical Engineering Society. In Forging & Stamping Manual (Impact Volume); Machine Press: Beijing, China, 2002; pp. 480–490. [Google Scholar]





| Outer diameter of cylinder | 406 mm |
| Thickness of cylinder | 38 mm |
| Density | 7750 kg/m3 |
| Poisson’s ratio | 0.3 |
| Elastic modulus | 202 GPa |
| Temperature 1100 °C | Minimum Wall Thickness (mm) | Maximum Wall Thickness (mm) |
|---|---|---|
| 800 | 37.4 | 44.5 |
| 900 | 37.6 | 45.3 |
| 1000 | 38.0 | 46.2 |
| 1100 | 38.4 | 47.5 |
| Feed Ratio (mm/r) | The Minimum Wall Thickness (mm) | The Maximum Wall Thickness (mm) |
|---|---|---|
| 1.5 | 39.2 | 44.1 |
| 2.0 | 38.6 | 46.5 |
| 2.5 | 37.8 | 47.7 |
| Sample No. | A3 | A4 | A5 | B3 | B4 | B5 | C3 | C4 | C5 |
|---|---|---|---|---|---|---|---|---|---|
| Pressure rise rate (bar/min) | 62.2 | 30.1 | 3.7 | 355.4 | 239.2 | 20.0 | 15.1 | 6.0 | 157.4 |
| Corrected helium rupture pressures Pr′He (bar) | 623.9 | 617.0 | 596.7 | 640.7 | 636.9 | 613.0 | 610.4 | 601.5 | 632.9 |
| Corrected hydrogen rupture pressure Pr′H2 (bar) | 380.3 | 379.0 | 450.2 | 546.9 | 428.6 | 328.0 | 347.3 | 332.7 | 478.3 |
| Pr′He/Pr′H2 | 1.6 | 1.6 | 1.3 | 1.2 | 1.5 | 1.9 | 1.8 | 1.8 | 1.3 |
| Acceptance level | Hydrogen embrittlement index ≤ 2 | ||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, R.; Fu, R.; Wei, W.; Gao, J.; Liu, Y.; Ge, S. Elastic–Plastic Numerical Analysis of the Spinning Process of SA-372 Steel Used in High-Pressure Hydrogen Storage Cylinders (≥100 MPA). Materials 2023, 16, 275. https://doi.org/10.3390/ma16010275
Yin R, Fu R, Wei W, Gao J, Liu Y, Ge S. Elastic–Plastic Numerical Analysis of the Spinning Process of SA-372 Steel Used in High-Pressure Hydrogen Storage Cylinders (≥100 MPA). Materials. 2023; 16(1):275. https://doi.org/10.3390/ma16010275
Chicago/Turabian StyleYin, Ruifeng, Ruidong Fu, Wenlong Wei, Jianfu Gao, Yongjiu Liu, and Shuaitao Ge. 2023. "Elastic–Plastic Numerical Analysis of the Spinning Process of SA-372 Steel Used in High-Pressure Hydrogen Storage Cylinders (≥100 MPA)" Materials 16, no. 1: 275. https://doi.org/10.3390/ma16010275
APA StyleYin, R., Fu, R., Wei, W., Gao, J., Liu, Y., & Ge, S. (2023). Elastic–Plastic Numerical Analysis of the Spinning Process of SA-372 Steel Used in High-Pressure Hydrogen Storage Cylinders (≥100 MPA). Materials, 16(1), 275. https://doi.org/10.3390/ma16010275





