Experimental Compaction of a High-Silica Sand in Quasi-Static Conditions
Abstract
:1. Introduction
2. Materials and Methods
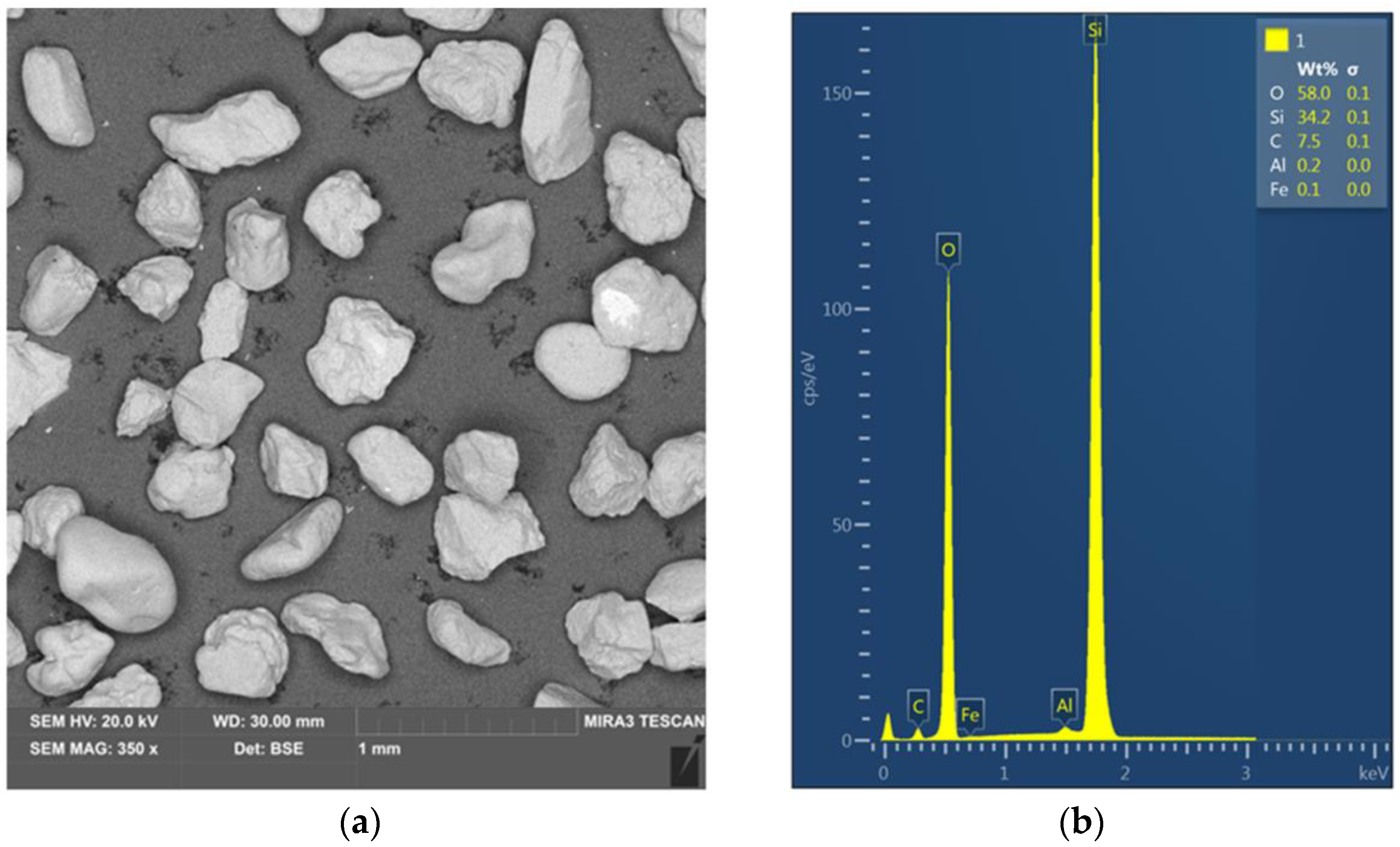
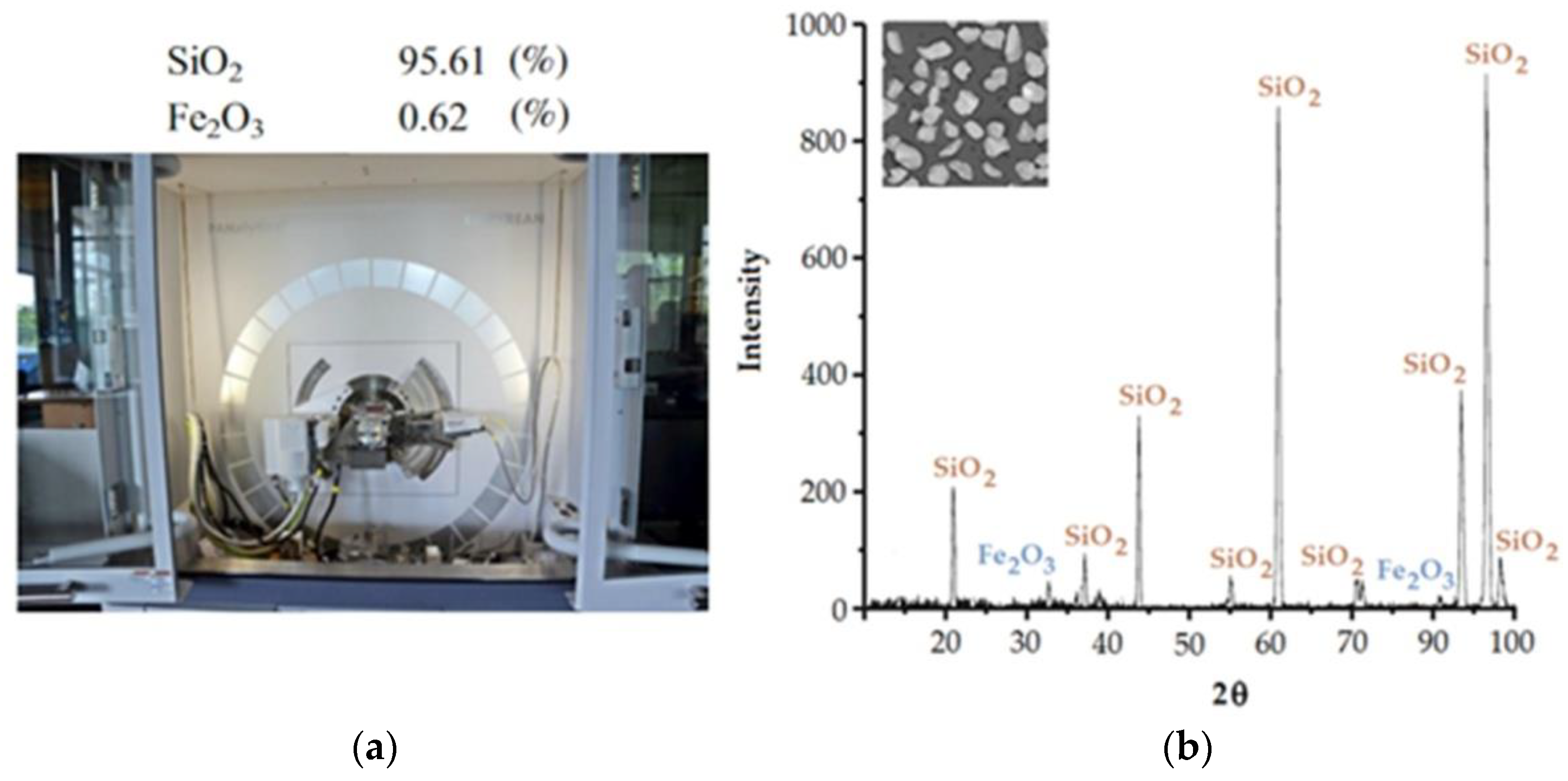
2.1. Material
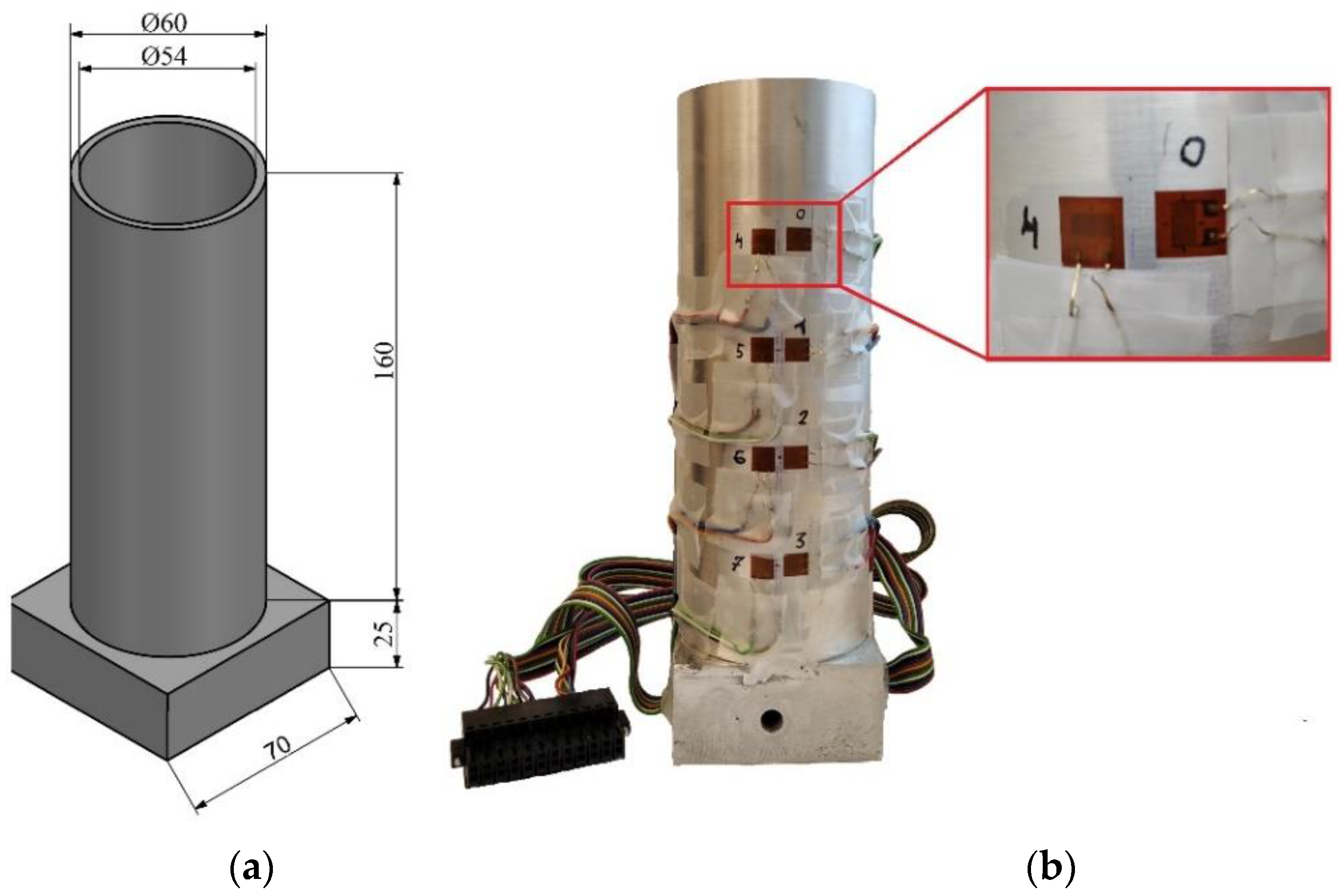
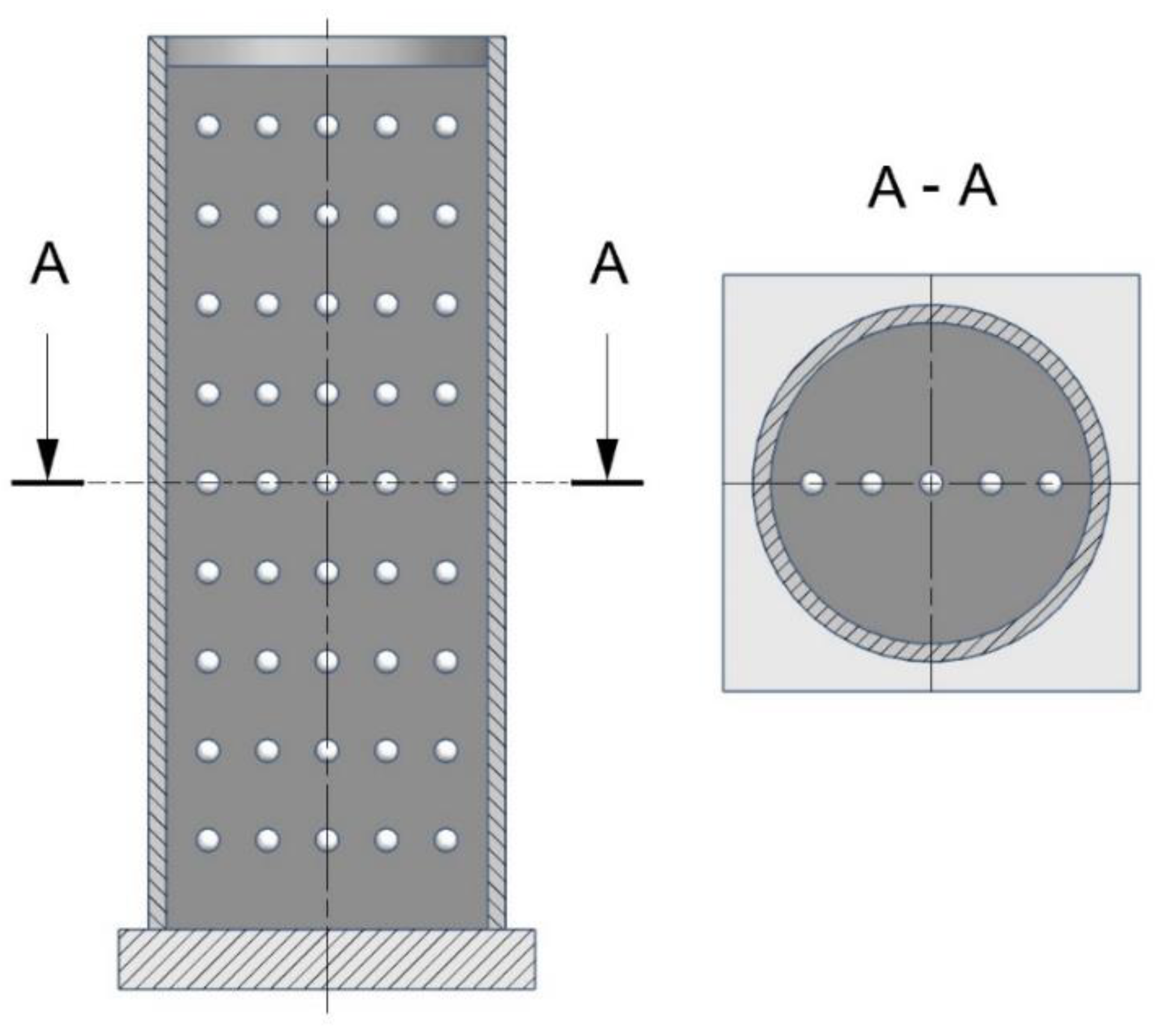
2.2. Compaction Setup
2.3. Surface Roughness Measurement
2.4. Sieve Analysis
3. Results
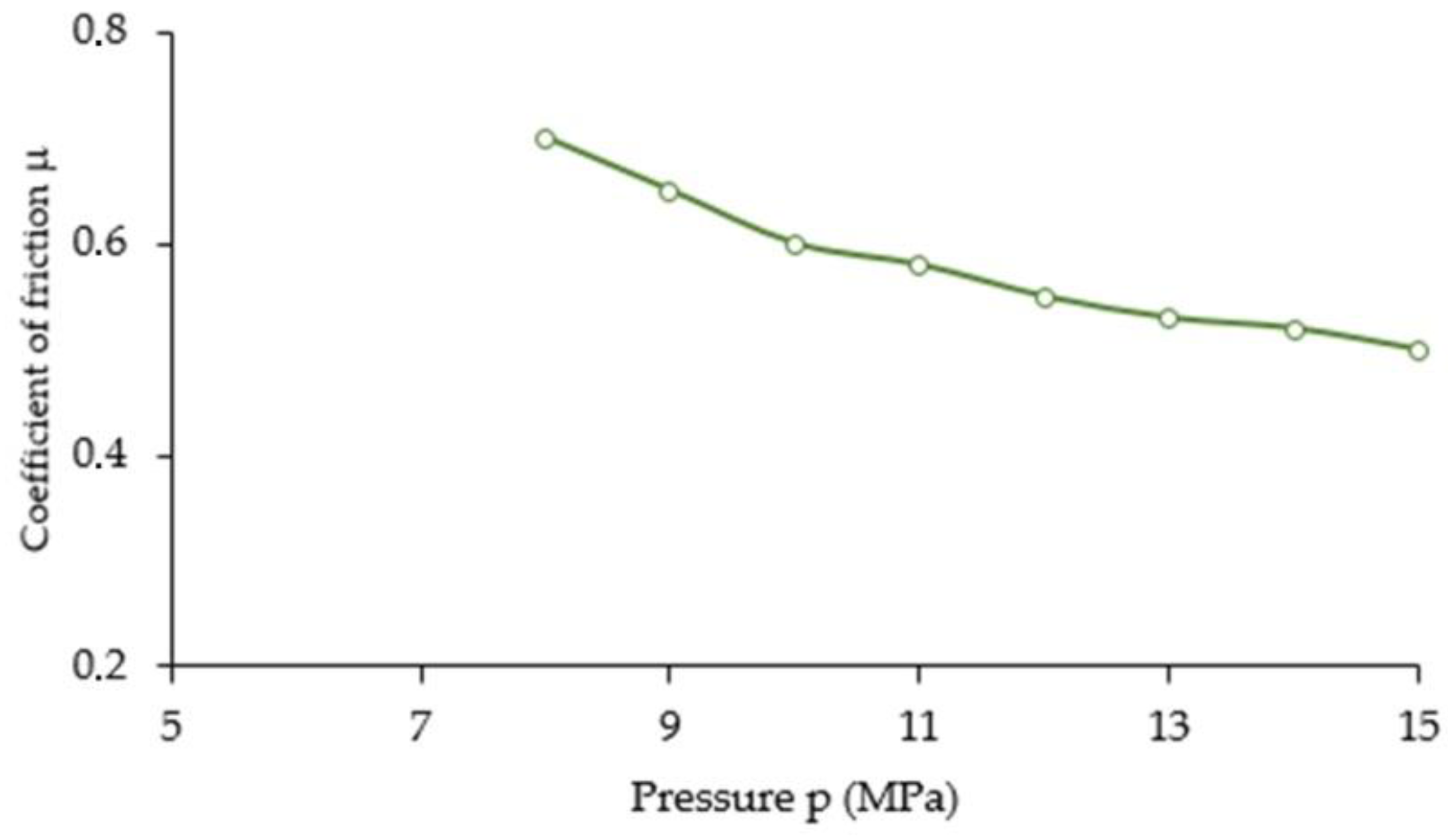
3.1. Coefficient of Friction
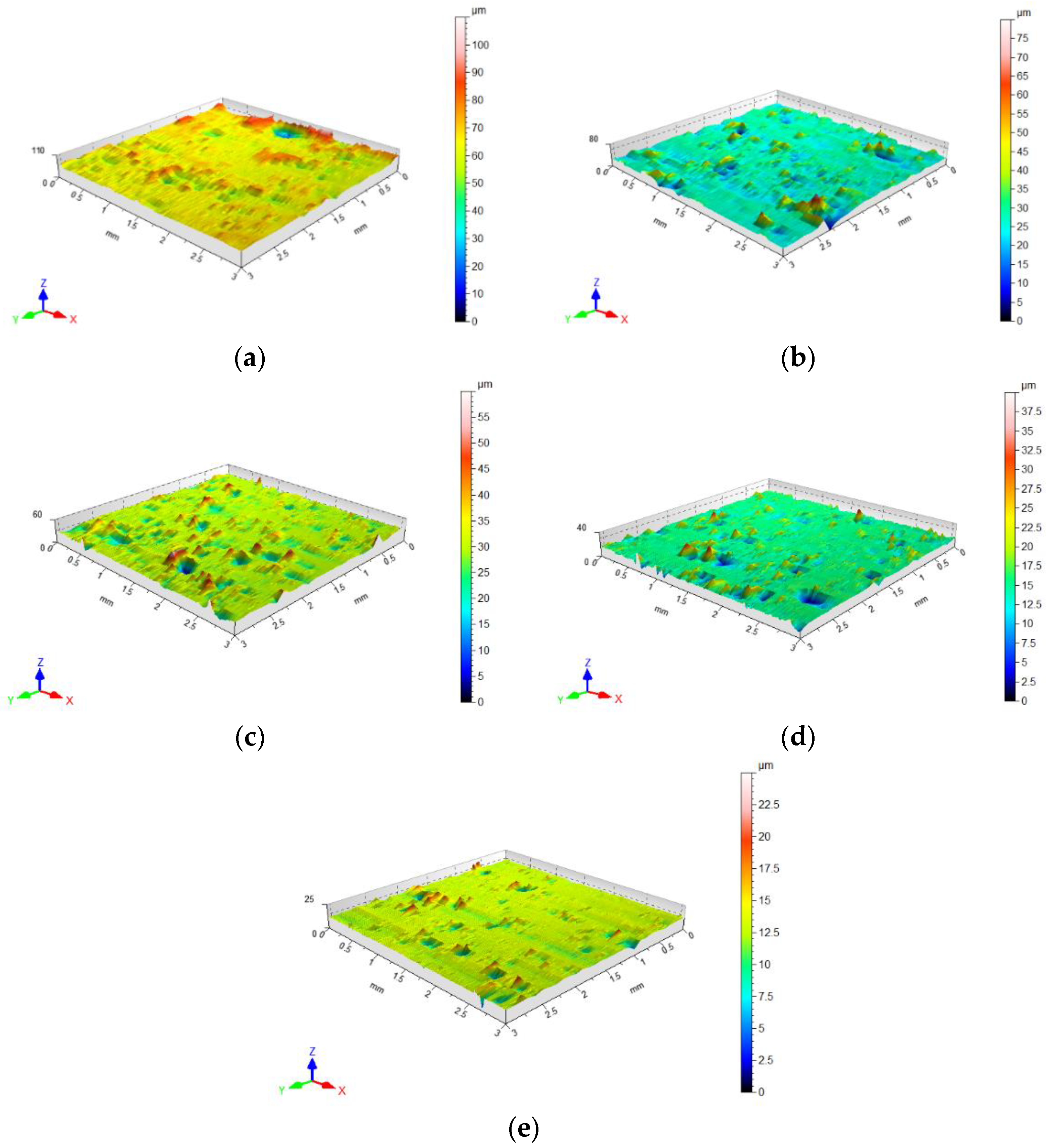
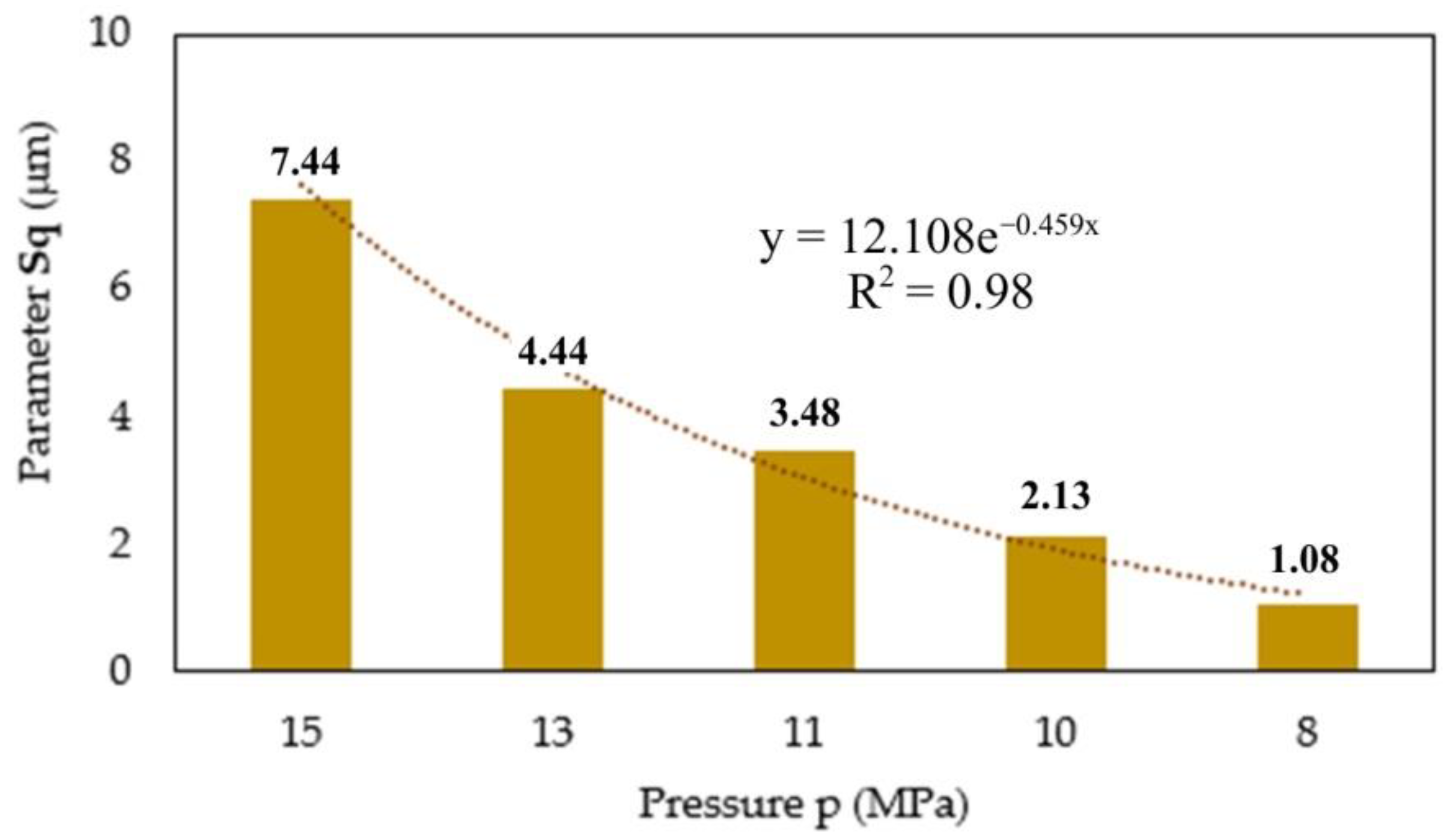
3.2. Surface Topography
4. Conclusions
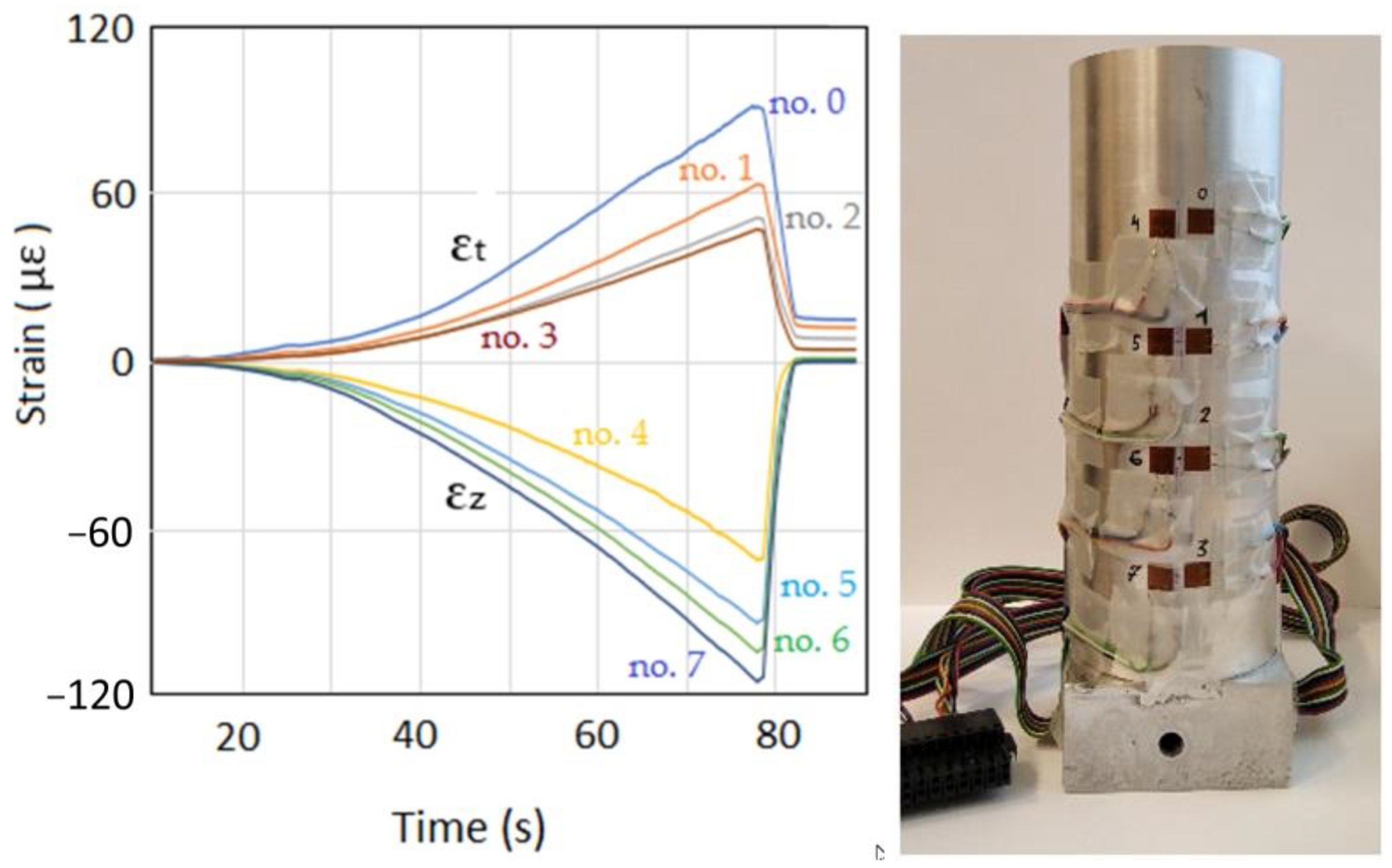
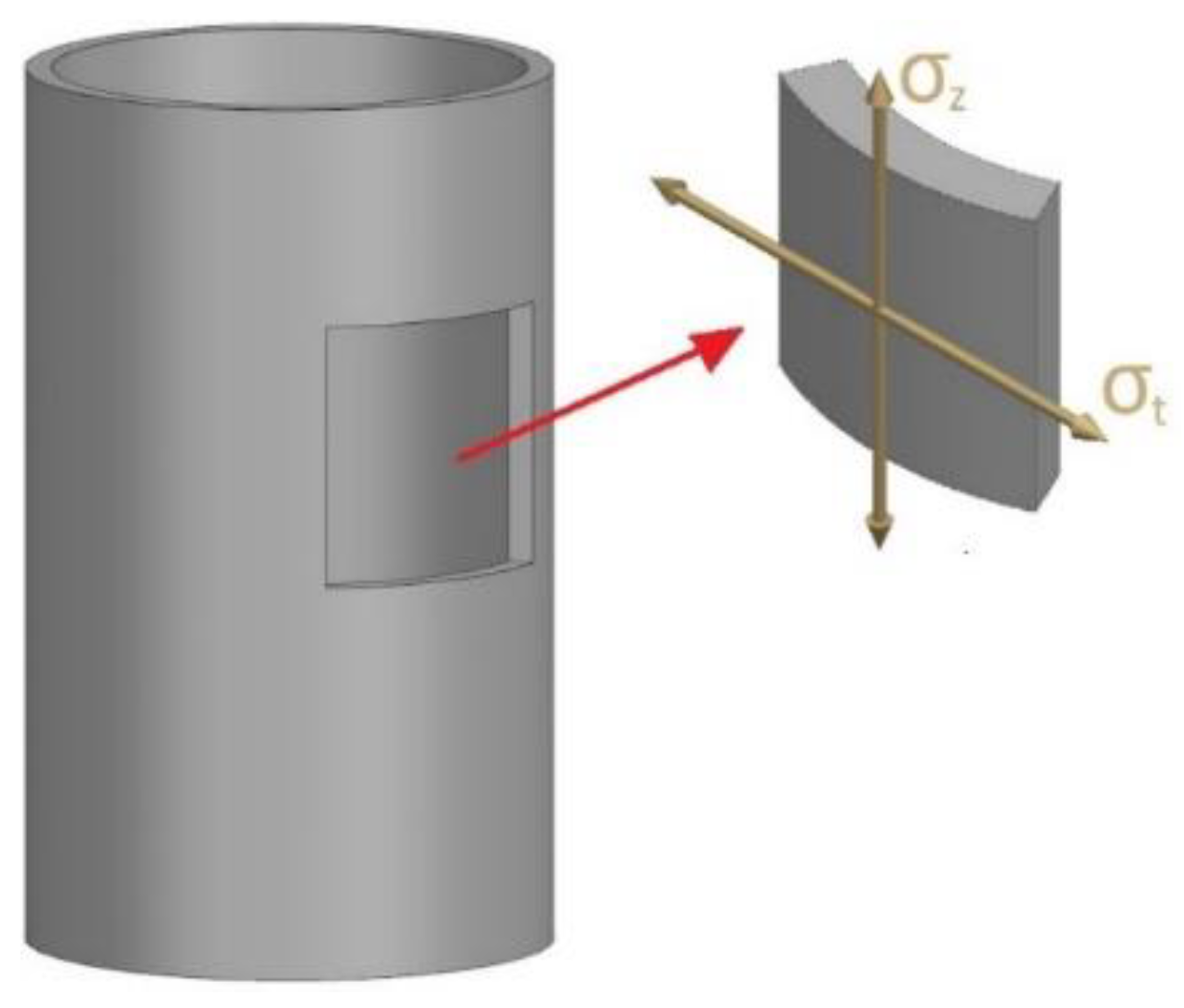
- changes in the value of strains of the external walls of the die (both axial and tangential) are exponential as a function of the distance along the axis of the punch. The greatest tangential strains (εt) were recorded near the surface of the punch. On the other hand, the highest value of axial strain (εz) was achieved in the place farthest from the surface of the punch;
- the compaction of high-silica sand grains along the punch axis can be described by an exponential function. Layers closer to the surface of the punch undergo greater deformation, which results from, among others factors, the lower value of the coefficient of friction between the material to be compacted and the inner wall of the die;
- the tests conducted have shown the usefulness of measuring the deformation on the outer surface of the die for indirect determination of the value of the coefficient of external friction;
- the distribution of the pressure p(z) in the direction of the punch axis during compaction of high-silica sand can be described using X-ray tomography analysis;
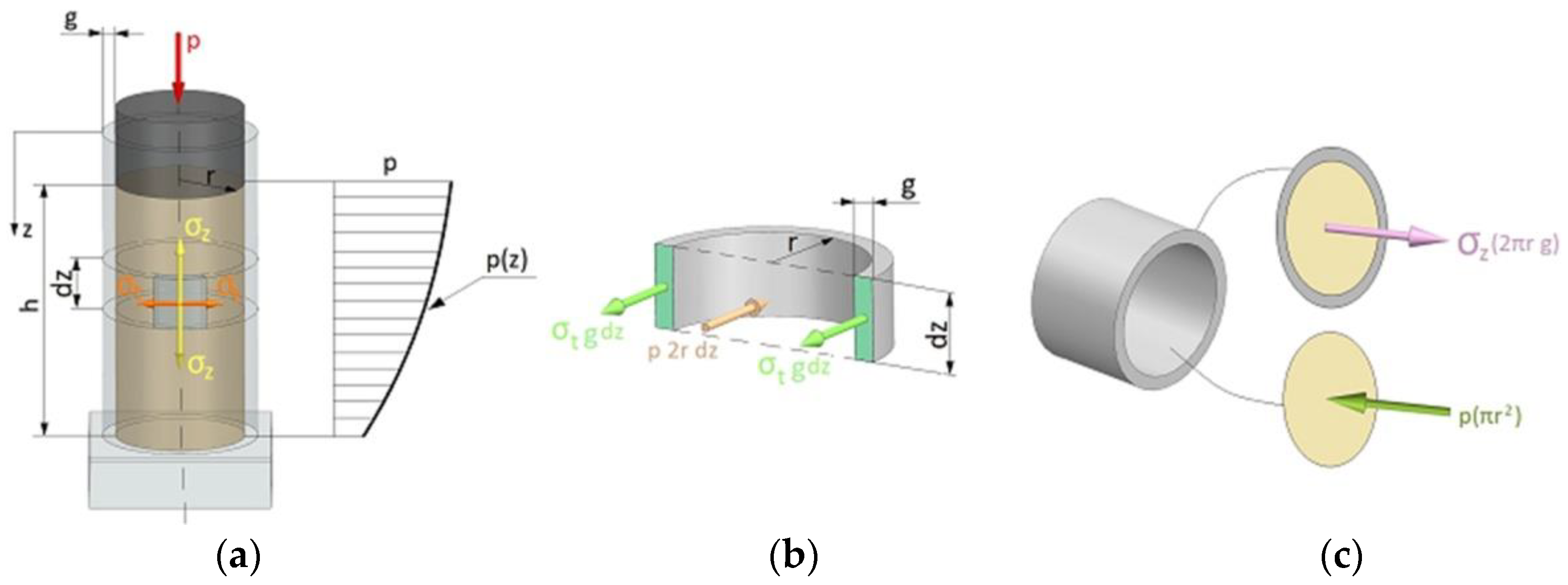
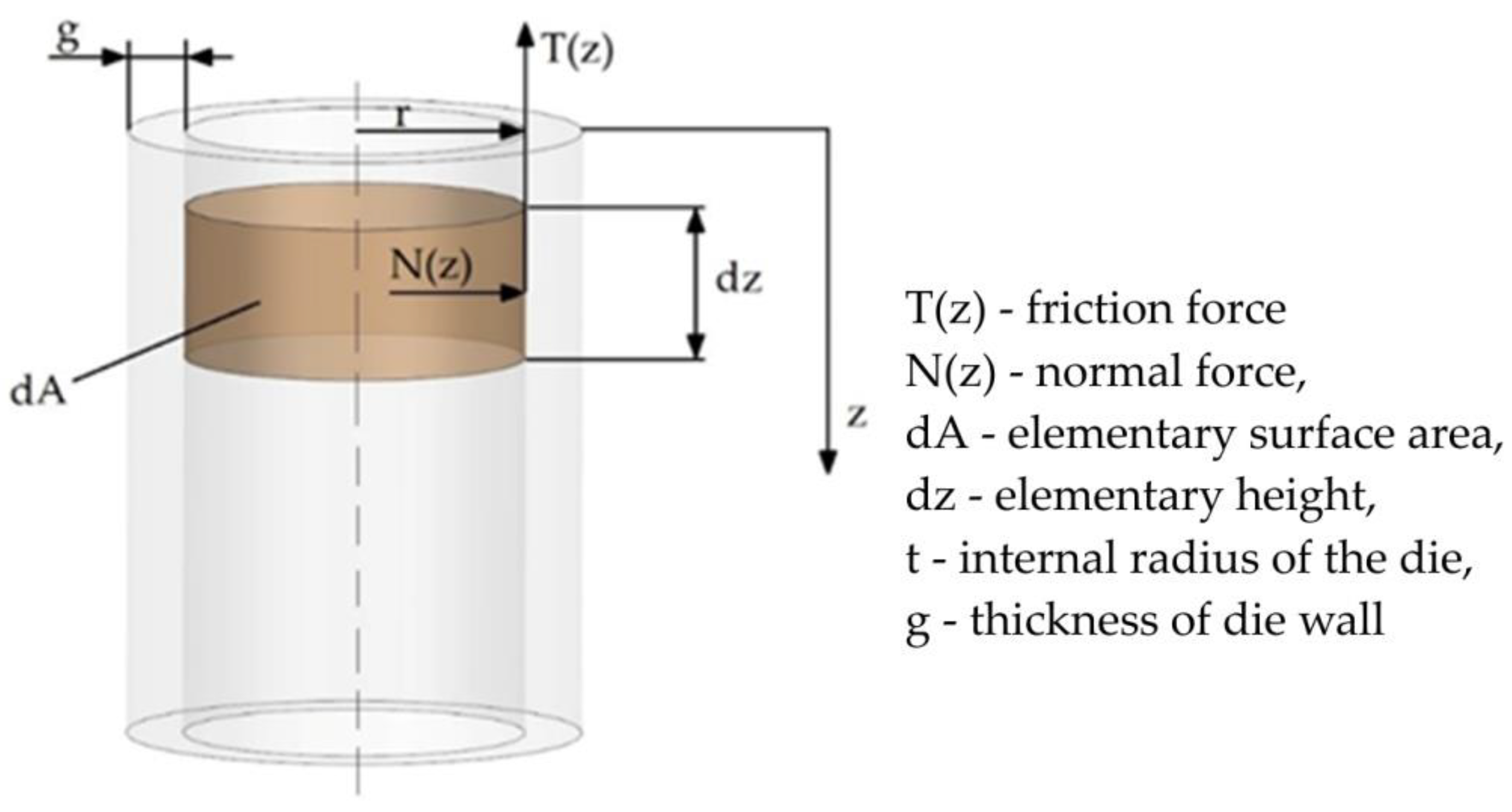
- the friction forces cause a reduction in pressure with increasing distance from the punch surface;
- the value of the coefficient of friction µ(z) decreases with increasing pressure p(z).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ketterhagen, W.R. Modeling the motion and orientation of various pharmaceutical tablet shapes in a film coating pan using DEM. Int. J. Pharm. 2011, 409, 137–149. [Google Scholar] [CrossRef] [PubMed]
- Rogers, A.J.; Hashemi, A.; Ierapetritou, M.G. Modeling of Particulate Processes for the Continuous Manufacture of Solid-Based Pharmaceutical Dosage Forms. Processes 2013, 1, 67–127. [Google Scholar] [CrossRef] [Green Version]
- Chtourou, H.; Guillot, M.; Gakwaya, A. Modeling of the metal powder compaction process using the cap model. Part I. Experimental material characterization and validation. Int. J. Solids Struct. 2002, 39, 1059–1075. [Google Scholar] [CrossRef]
- Martin, C.L. Elasticity, fracture and yielding of cold compacted metal powders. J. Mech. Phys. Solids 2004, 52, 1691–1717. [Google Scholar] [CrossRef]
- Chen, M.L.; Wu, G.J.; Gan, B.R.; Jiang, W.H.; Zhou, J.W. Physical and Compaction Properties of Granular Materials with Artificial Grading behind the Particle Size Distributions. Adv. Mater. Sci. Eng. 2018, 2018, 8093571. [Google Scholar] [CrossRef] [Green Version]
- Styks, J.; Wróbel, M.; Frączek, J.; Knapczyk, A. Effect of Compaction Pressure and Moisture Content on Quality Parameters of Perennial Biomass Pellets. Energies 2020, 13, 1859. [Google Scholar] [CrossRef] [Green Version]
- Pater, Z. Podstawy Metalurgii i Odlewnictwa; Politechnika Lubelska: Lublin, Poland, 2014. [Google Scholar]
- Hardman, J.S.; Lilley, B.A. Mechanisms of compaction of powdered materials. Proc. R. Soc. Lond. A 1973, 333, 183–199. [Google Scholar]
- Lowe, C.A.; Greenaway, M.W. Compaction processes in granular beds composed of different particle sizes. J. Appl. Phys. 2005, 98, 123519. [Google Scholar] [CrossRef]
- Hoffman, K. An Introduction to Measurements Using Strain Gauges; Hottinger Baldwin Messtechnik Gmbh: Darmstadt, Germany, 1989. [Google Scholar]
- Kim, K.; Kim, J.; Jiang, X.; Kim, T. Static Force Measurement Using Piezoelectric Sensors. J. Sens. 2021, 2021, 6664200. [Google Scholar] [CrossRef]
- Paulish, A.G.; Zagubisalo, P.S.; Churilov, S.M.; Barakov, V.N.; Pavlov, M.A.; Poyarkov, A.V. Piezo-Optical Transducers in High Sensitive Strain Measurements. In Optoelectronics; IntechOpen: London, UK, 2020. [Google Scholar] [CrossRef]
- Żaba, K.; Trzepieciński, T.; Rusz, S.; Puchlerska, S.; Balcerzak, M. Full-Field Temperature Measurement of Stainless Steel Specimens Subjected to Uniaxial Tensile Loading at Various Strain Rates. Materials 2021, 14, 5259. [Google Scholar] [CrossRef] [PubMed]
- Słomiński, C.; Niedostatkiewicz, M.; Tejchman-Konarzewski, J. Deformation measurements in granular bodies using a particle image velocimetry technique. Arch. Hydro-Eng. Environ. Mech. 2006, 53, 71–94. [Google Scholar]
- Shooshpasha, I.; Hasanzadeh, A.; Kharun, M. The influence of micro silica on the compaction properties of cemented sand. IOP Conf. Ser. Mater. Sci. Eng. 2019, 675, 012002. [Google Scholar] [CrossRef]
- Humphrens, H.W. A method for controllong compaction of granular materials. Highw. Res. Board Bull. 1957, 159, 41–57. [Google Scholar]
- Chester, J.S.; Lenz, S.C.; Chester, F.M.; Lang, R.A. Mechanisms of compaction of quartz sand at diagenetic conditions. Earth Planet. Sci. Lett. 2004, 220, 435–451. [Google Scholar] [CrossRef]
- Vu, T.L.; Nezamabadi, S.; Mora, S. Compaction of elastic granular materials: Inter-particles friction effects and plastic events. Soft Matter. 2020, 3, 679–687. [Google Scholar] [CrossRef] [PubMed]
- Brzeskovsky, R.H.; Spiers, C.J.; Peach, C.J.; Hangx, S.J.T. Time-independent compaction behavior of quartz sands. J. Geophys. Res. Solid Earth 2014, 119, 936–956. [Google Scholar] [CrossRef] [Green Version]
- Nezamabadi, S.; Nguyen, T.H.; Delenne, J.Y.; Radjai, F. Modeling soft granular materials. Granul. Matter. 2017, 19, 8. [Google Scholar] [CrossRef] [Green Version]
- Nezamabadi, S.; Radjai, F.; Averseng, J.; Delenne, J.Y. Implicit frictional-contact model for soft particie systems. J. Mech. Phys. Solids 2015, 83, 72–87. [Google Scholar] [CrossRef] [Green Version]
- Nezamabadi, S.; Frank, X.; Delenne, J.Y.; Averseng, J.; Radjai, F. Parallel implicit contact algorithm for soft particie systems. Comput. Phys. Commun. 2019, 237, 17–25. [Google Scholar] [CrossRef] [Green Version]
- Munjiza, A.A.; Owen, D.R.J.; Bicanic, N. A combined finite-discrete element method in transient dynamics of fracturing solids. Eng. Comput. 1995, 12, 145–174. [Google Scholar] [CrossRef]
- Munjiza, A.A. The Combined Finite-Discrete Element Method; Wiley: Chichester, UK, 2004. [Google Scholar]
- Ransing, R.S.; Gethin, D.T.; Khoei, A.R.; Mosbah, P.; Lewis, R.W. Powder compaction modelling via the discrete and finite element method. Mater. Des. 2000, 21, 263–269. [Google Scholar] [CrossRef]
- Procopio, A.T.; Zavaliangos, A. Simulation of multi-axial compaction of granular media from loose to high relative densities. J. Mech. Phys. Solids 2005, 53, 1523–1551. [Google Scholar] [CrossRef]
- Güner, F.; Cora, Ö.N.; Safoğlu, H. Numerical modeling of cold powder compaction using multi particle and continuum media approaches. Powder Technol. 2015, 271, 238–247. [Google Scholar] [CrossRef]
- ISO 25178-2; Geometrical Product Specifications (GPS)—Surface Texture: Areal—Part 2: Definitions and Surface Texture Parameters. International Organization for Standardization: Geneva, Switzerland, 2012.









| Property | Unit | Value |
|---|---|---|
| Hardness HB | - | 110 |
| Density | g/cm3 | 2.79 |
| Poisson’s ratio | - | 0.33 |
| Coefficient of thermal expansion | °C−1 | 22.9 × 10−6 |
| Specific resistance | nWm | 51 |
| Young’s modulus | MPa | 72,500 |
| Parameter | Unit | Value |
|---|---|---|
| Resistance | Ω | 350 ± 0.2% |
| Width | mm | 5.0 |
| Length | mm | 8.5 |
| Thickness | µm | 60 |
| Maximum current, mA | mA | 50 |
| Temperature range | °C | −40–200 |
| Fatigue strength | - | n > 107 for ε = 0.1% |
| Maximum strain | % | approx. 4 |
| Strain sensitivity factor k | - | 2.1–2.2 |
| Tolerance of coefficient k, % | % | 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szwajka, K.; Szewczyk, M.; Trzepieciński, T. Experimental Compaction of a High-Silica Sand in Quasi-Static Conditions. Materials 2023, 16, 28. https://doi.org/10.3390/ma16010028
Szwajka K, Szewczyk M, Trzepieciński T. Experimental Compaction of a High-Silica Sand in Quasi-Static Conditions. Materials. 2023; 16(1):28. https://doi.org/10.3390/ma16010028
Chicago/Turabian StyleSzwajka, Krzysztof, Marek Szewczyk, and Tomasz Trzepieciński. 2023. "Experimental Compaction of a High-Silica Sand in Quasi-Static Conditions" Materials 16, no. 1: 28. https://doi.org/10.3390/ma16010028
APA StyleSzwajka, K., Szewczyk, M., & Trzepieciński, T. (2023). Experimental Compaction of a High-Silica Sand in Quasi-Static Conditions. Materials, 16(1), 28. https://doi.org/10.3390/ma16010028








