A Non-Thinning Forming Method with Improvement of Material Properties
Abstract
:1. Introduction
2. Simulation and Experiment
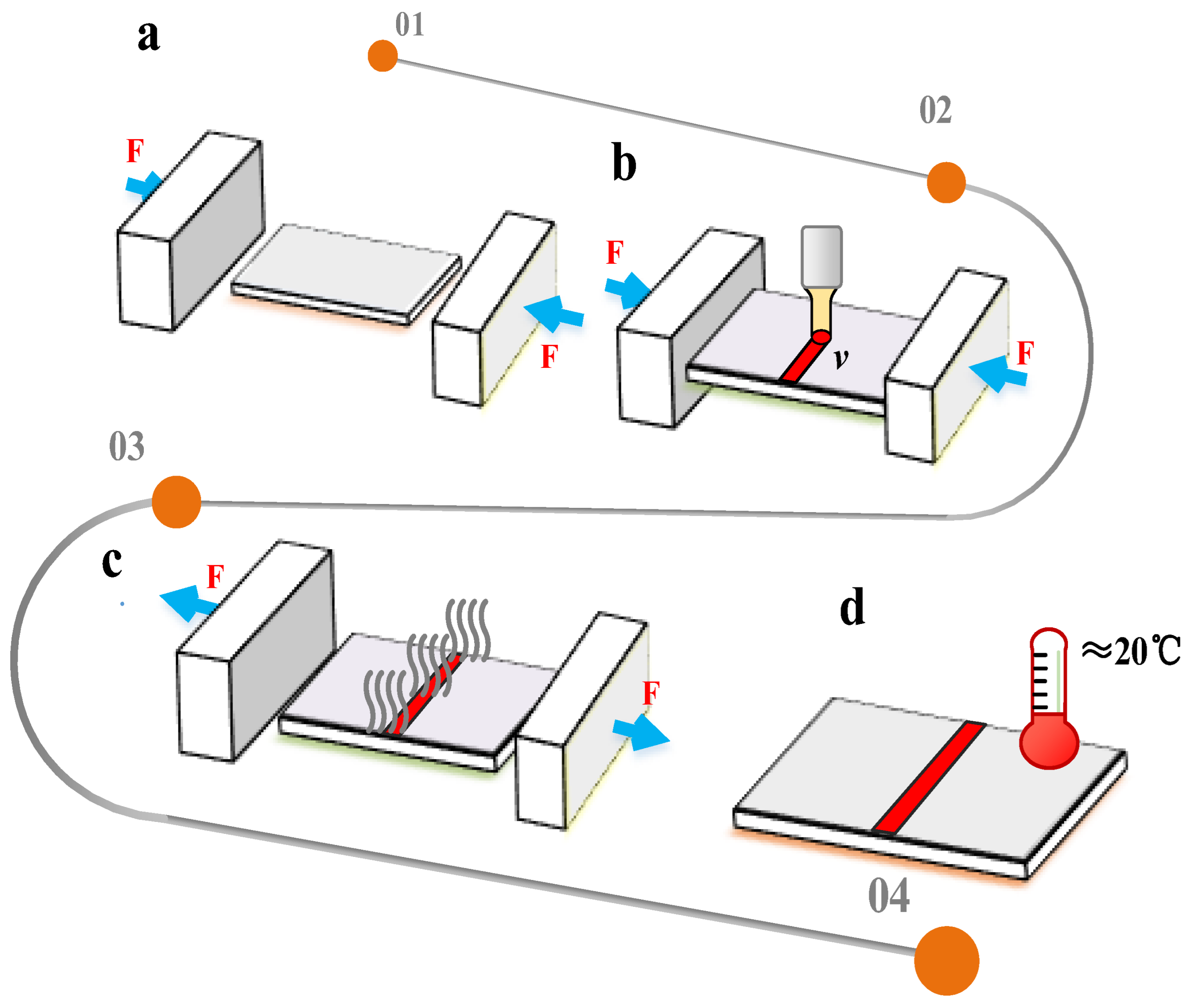
2.1. Specific Steps of BPM
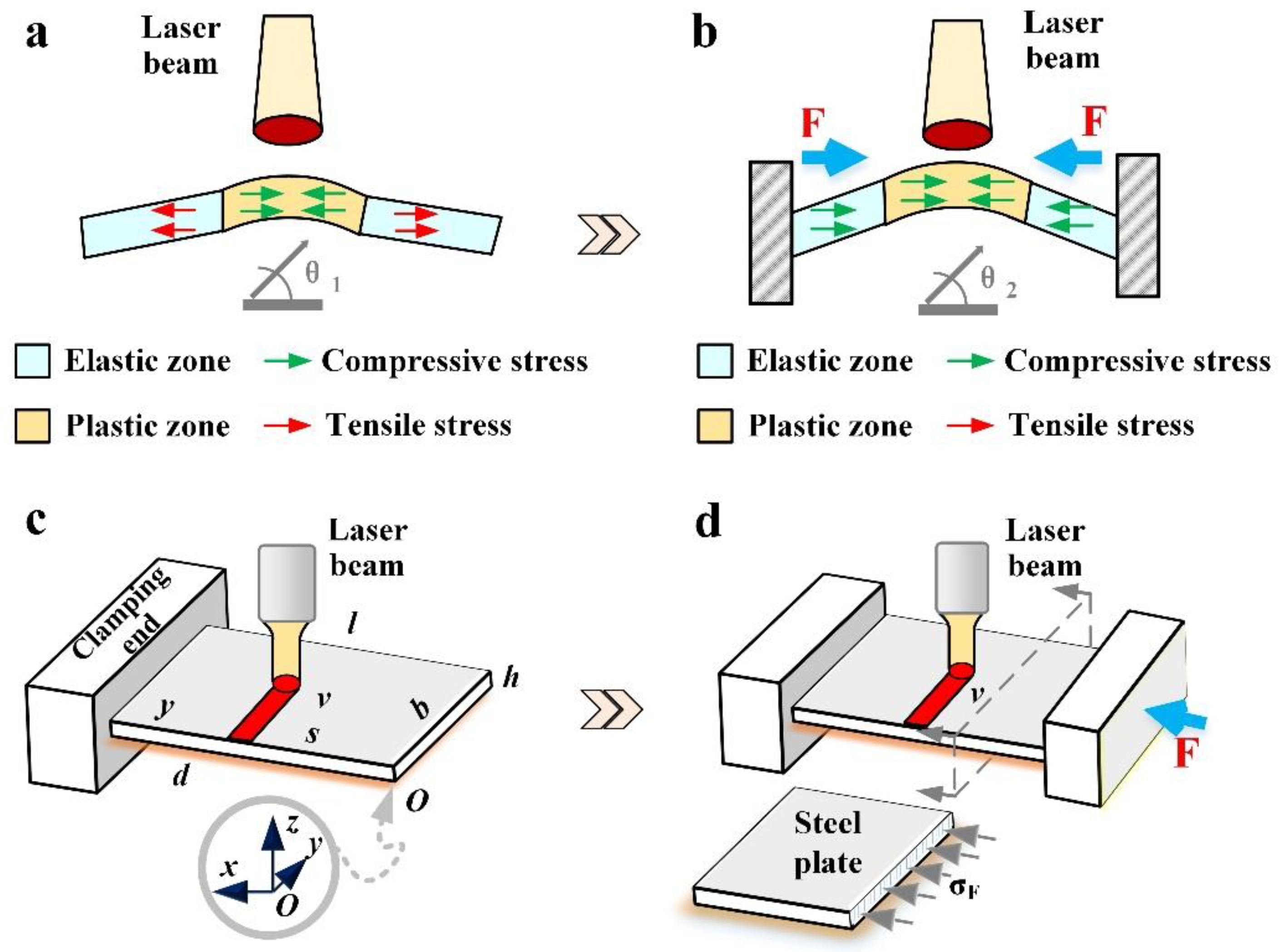
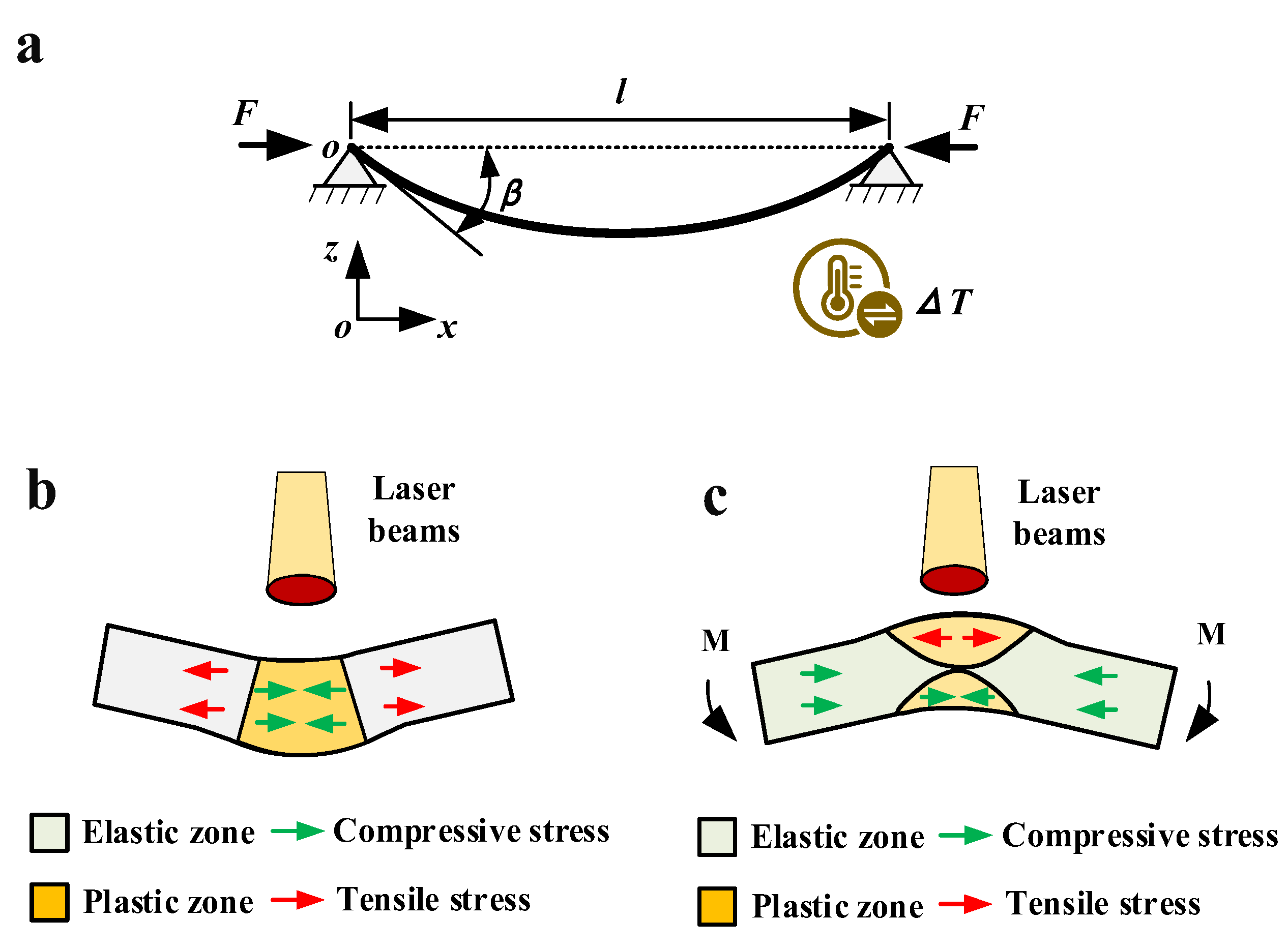
- Before laser scanning, the two ends of the plate are pressured with baffles to keep the plate under pressure (Figure 2a).
- When the laser beam scans the surface of the plate, the heating zone will undergo plastic deformation because of the coupling of thermal stress and pre-stress (Figure 2b).
- After the laser scan is complete, wait for the plate to cool to room temperature and then remove the baffle (Figure 2c,d).
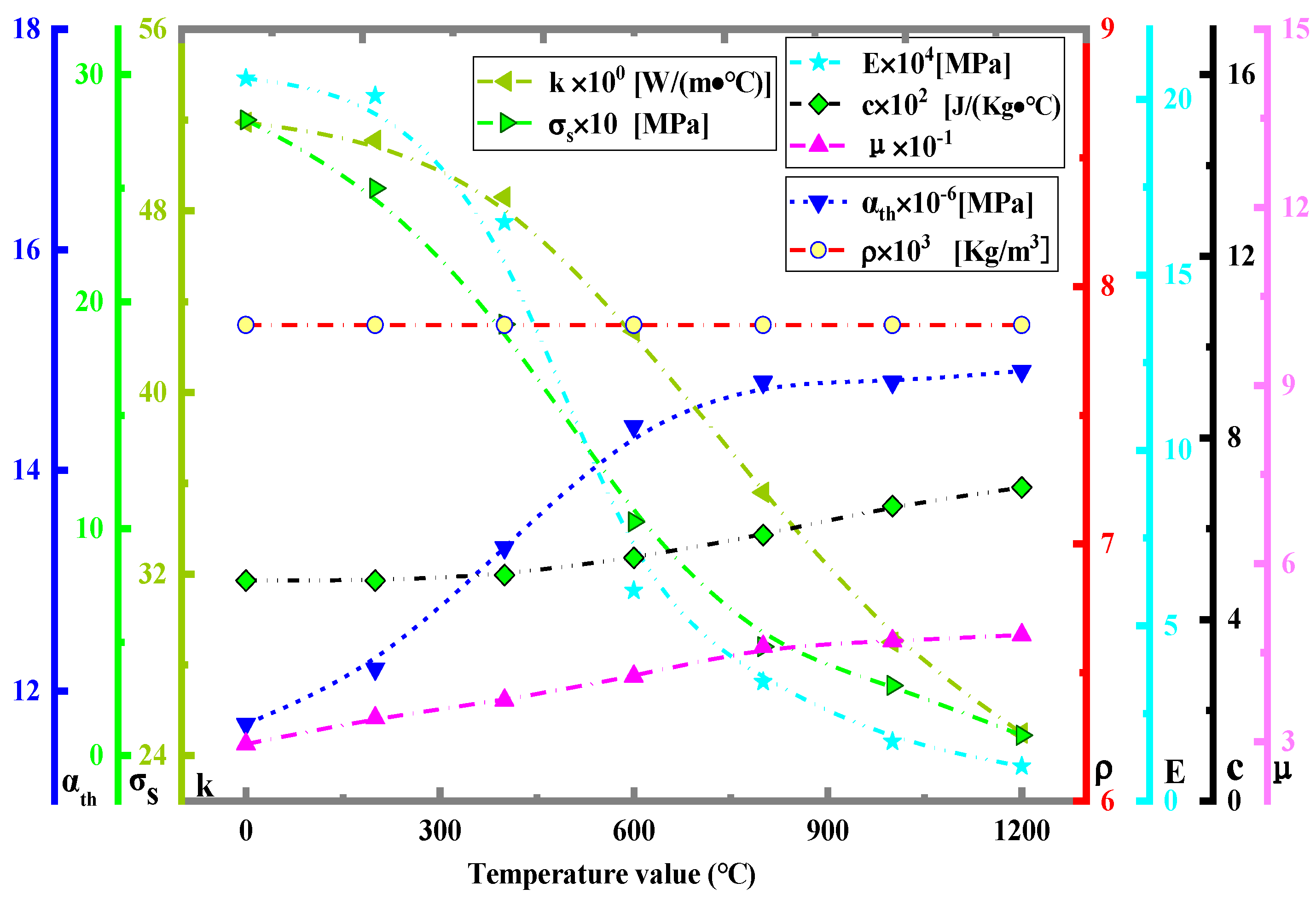
2.2. Meshing and Parameters
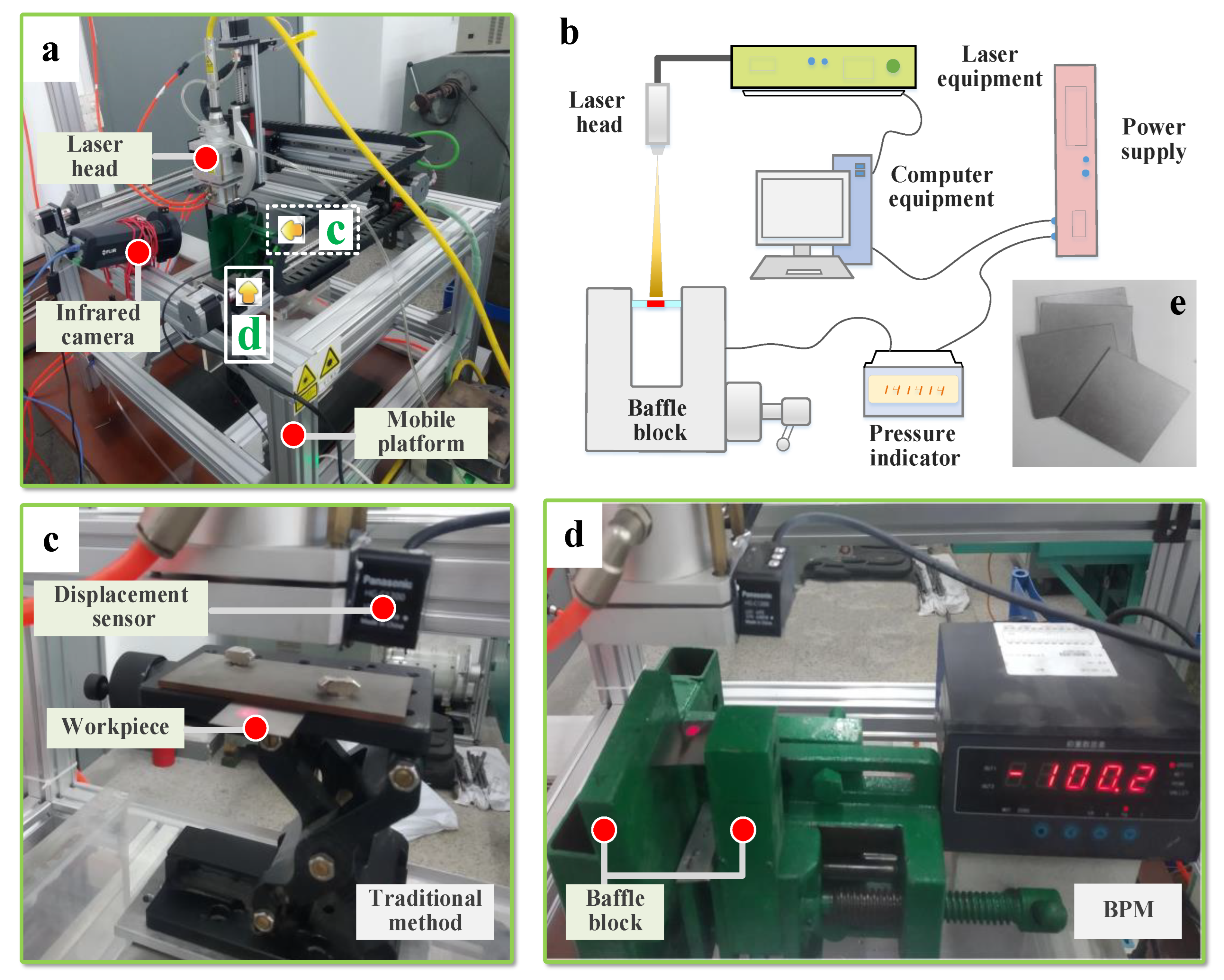
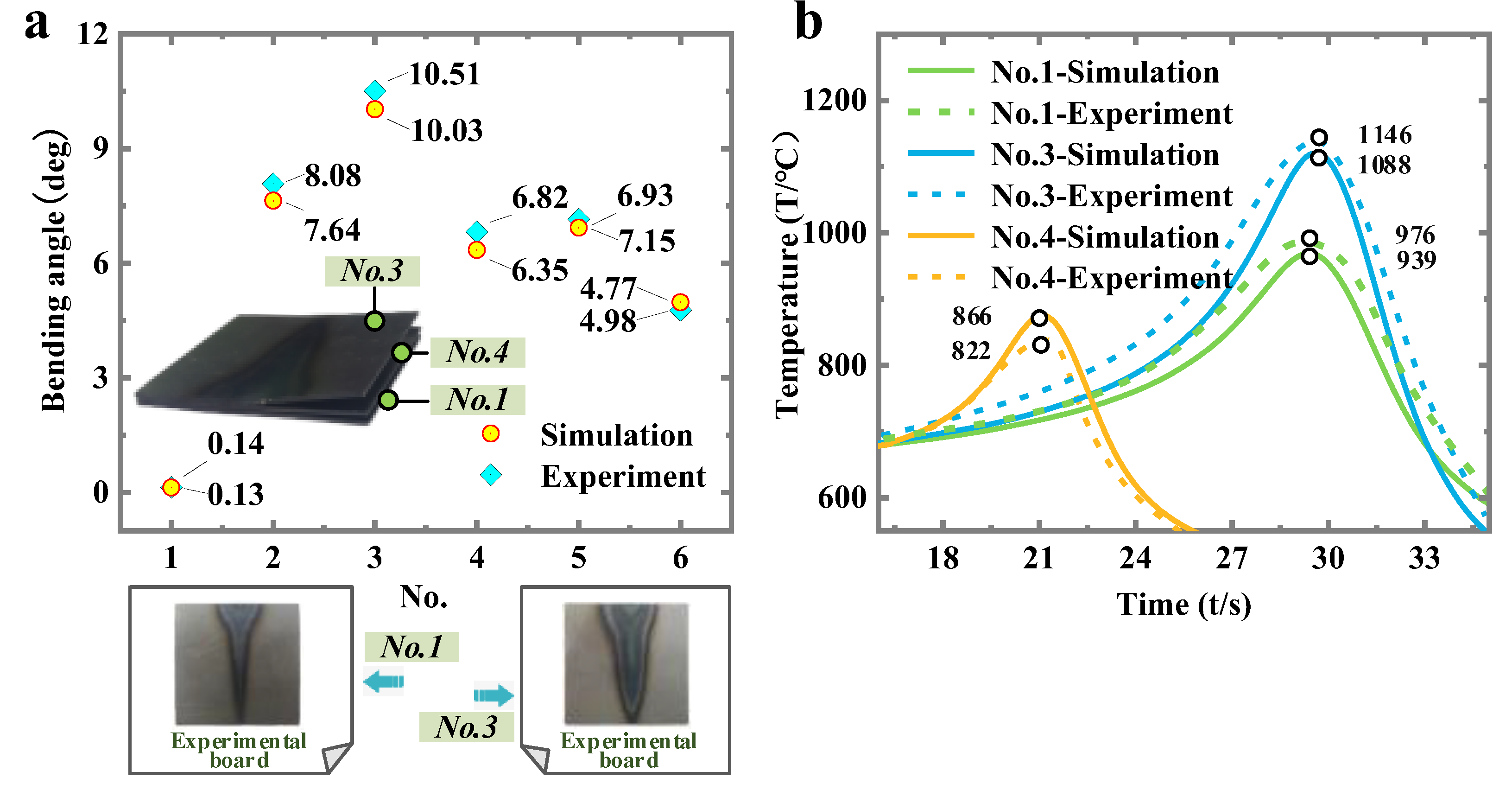
2.3. Experimental Verification
3. Results and Discussion
3.1. Bending Angle
3.1.1. Deformation Mechanism
3.1.2. Pressure and Plate Thickness
3.1.3. Processing Parameters
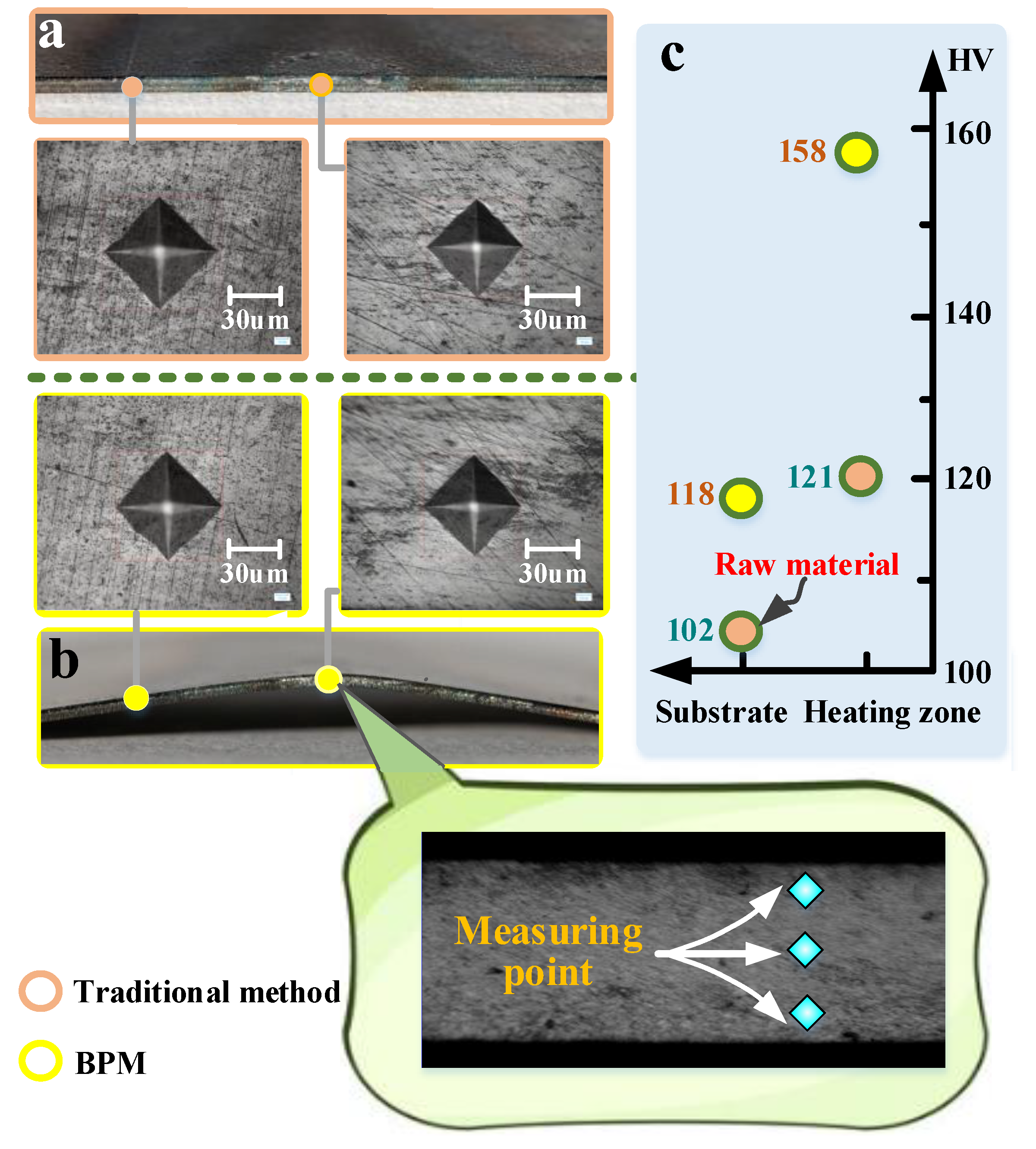
3.2. Grain Size and Microhardness
3.2.1. Grain Size
3.2.2. Microhardness
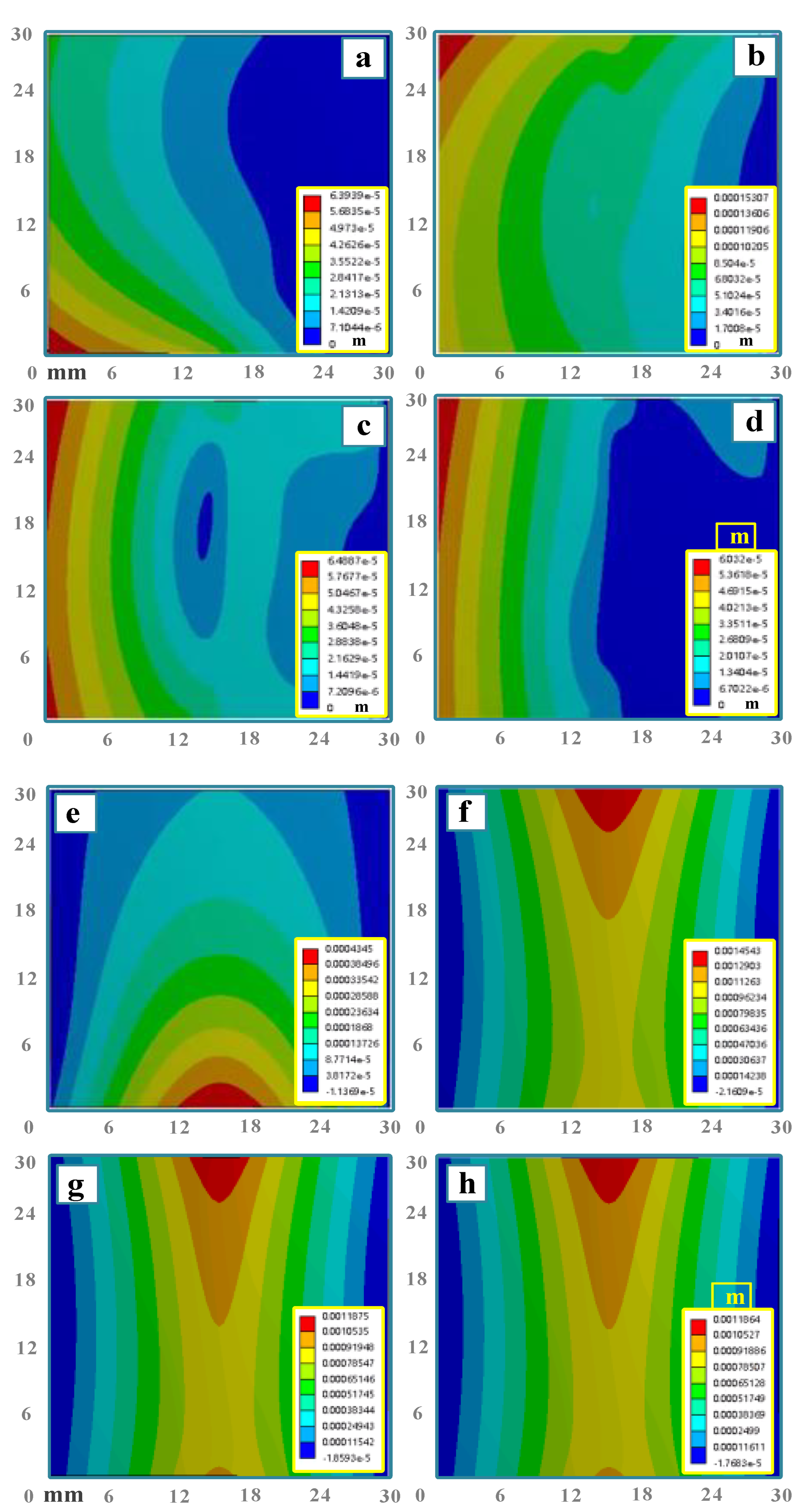
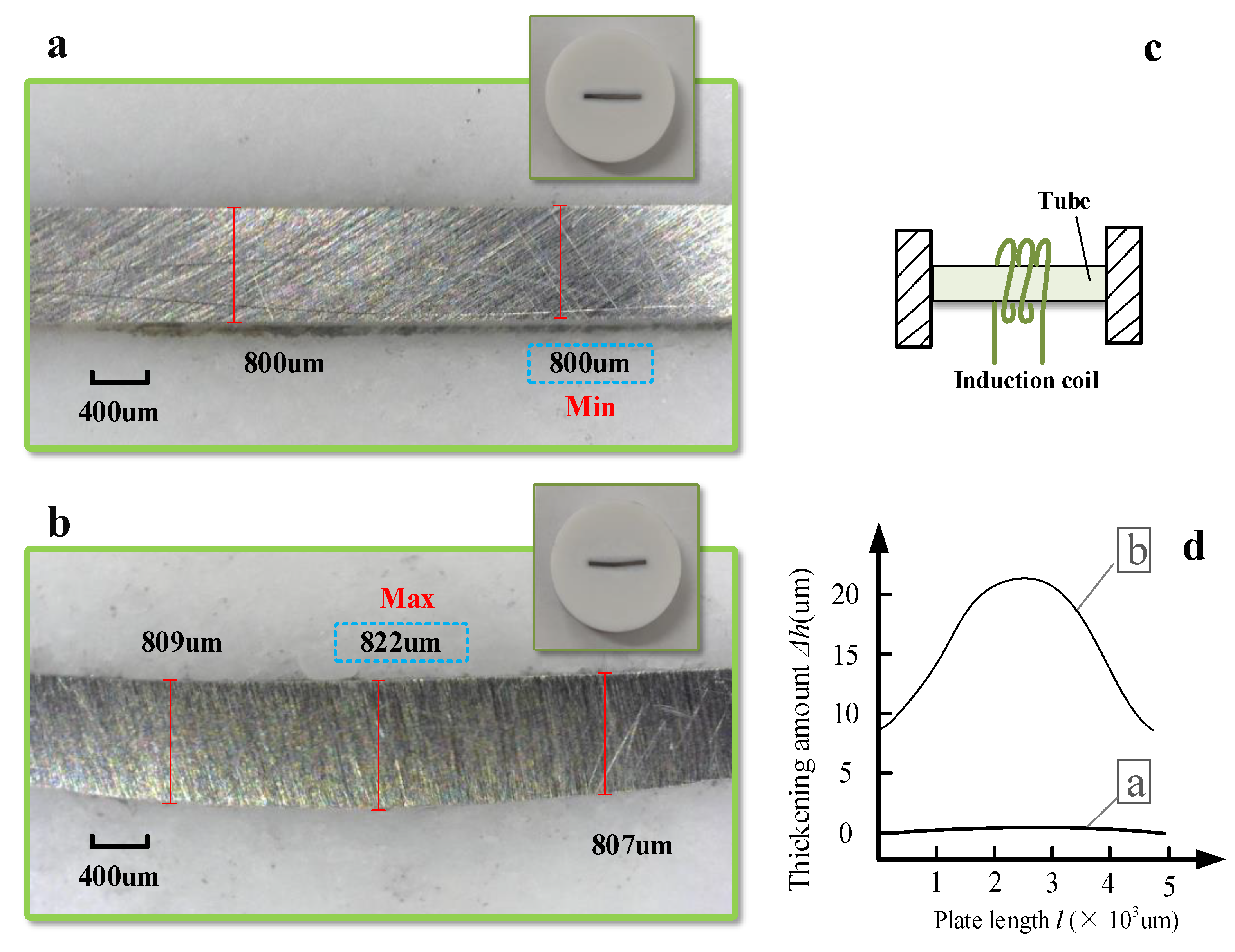
3.2.3. Thickness Variation
4. Conclusions
- Compared with the traditional method, BPM can improve the bending angle by 57.71 times. The bending angle can be effectively improved by BPM. The bending angle of the traditional method is determined by thermal buckling. In contrast, the BPM is determined by both thermal buckling and baffle, but the baffle plays a major role.
- In the BPM method, the bending angle will increase as the pressure and laser power increase. In contrast, the bending angle decreases with the increase of the plate thickness, scanning speed and laser diameter.
- Compared with the traditional method, BPM can refine the grain size and increase the microhardness by 1.31 times. BPM has a certain effect on improving material properties. In addition, BPM can thicken the heating zone by about 2.75%, which can obtain a better bending without thinning effect.
- The analytical equation of beam bending with laser as heat source is established, which further enriches and develops the basic theory of beam thermoplastic bending, and has certain reference and significance for other plate bending with laser as heat source.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Parsa, M.H.; Mohammadi, S.V.; Mohseni, E. Thickness change and springback of cold roll bonded aluminum/copper clad sheets in air bending process. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2017, 231, 675–689. [Google Scholar] [CrossRef]
- Fang, J.; Ouyang, F.; Lu, S.; Wang, K.; Min, X.; Xiao, B. Wall thinning behaviors of high strength 0Cr21Ni6Mn9N tube in numerical control bending considering variation of elastic modulus. Adv. Mech. Eng. 2021, 13, 177–183. [Google Scholar] [CrossRef]
- Ben Said, L. The incremental sheet forming; technology, modeling and formability: A brief review. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2022, 236, 09544089221093306. [Google Scholar] [CrossRef]
- Choi, H.; Lee, C. A mathematical model to predict thickness distribution and formability of incremental forming combined with stretch forming. Robot. Comput. Integr. Manuf. 2019, 55, 164–172. [Google Scholar] [CrossRef]
- Jia, B.B.; Chen, G.; Wang, W.W.; Shen, Y.; Gu, Y. Deformation characteristics and forming force limits of multi-point forming with individually controlled force–displacement. Int. J. Adv. Manuf. Technol. 2022, 123, 1565–1576. [Google Scholar] [CrossRef]
- Ma, X.P.; Wang, X.Y.; Xu, W.J.; Guo, D. Study on the thickening phenomenon in the laser bending zone of stainless steel-carbon steel laminates. China Laser 2014, 41, 8. [Google Scholar]
- Li, J.H.; Su, C.Z.; Yao, F.P. Application of BP neural network in laser bending forming of aluminum alloy plate. Hot. Work. Technol. 2017, 46, 58–165. [Google Scholar]
- Fu, S.C.; Yang, L.J.; Zhang, H.Z. Analyses of effects of process parameters on laser bending of stiffened panels. Int. J. Precis. Eng. Manuf. 2018, 19, 593–604. [Google Scholar] [CrossRef]
- Nejad, R.M.; Shojaati, Z.; Wheatley, G.; Ghahremani-Moghadam, D. On the bending angle of aluminum-copper two-layer sheets in laser forming process. Opt. Laser Technol. 2021, 142, 107233. [Google Scholar] [CrossRef]
- Abedinzadeh, R.; Sattari, M.; Toghraie, D. Experimental Analysis on Bending Behavior of Non-Alloy Carbon Steel Sheets Using Laser-Forming Process. Steel Res. Int. 2022, 93, 2200011. [Google Scholar] [CrossRef]
- Hussain, M.; Gupta, A.; Kumar, P.; Hussain, M.; Das, A.K. Experimental study and statistical analysis of bending titanium alloy sheet with continuous wave fiber laser. Arch. Civ. Mech. Eng. 2022, 22, 110. [Google Scholar] [CrossRef]
- Shi, Y.J. Study on Laser Thermal Deformation Mechanism and Thermal Forming Process Planning of Complex Curved Panel; Shanghai Jiaotong University: Shangai, China, 2007. [Google Scholar]
- Mjali, K.V.; Els-Botes, A.; Mashinini, P.M. The effects of laser and mechanical forming on the hardness and microstructural layout of commercially pure grade 2 titanium alloy plates. In Proceedings of the ASME 2017 12th International Manufacturing Science and Engineering Conference, Los Angeles, CA, USA, 4–8 June 2017. [Google Scholar]
- Kant, R.; Joshi, S.N. A Numerical Investigation into the Effect of Forced Convection Cooling on the Performance of Multi-scan Laser Bending Process. In Application of Lasers in Manufacturing; Springer: Singapore, 2019. [Google Scholar]
- Lambiase, F.; Ilio, A.D.; Paoletti, A. Productivity in multi-pass laser forming of thin AISI 304 stainless steel sheets. J. Adv. Manuf. Technol. 2016, 86, 259–268. [Google Scholar] [CrossRef]
- Kalvettukaran, P.; Das, S.; Marimuthu, S.; Misra, D. Increment in laser bending angle by forced bottom cooling. J. Adv. Manuf. Technol. 2018, 94, 2137–2147. [Google Scholar]
- Otsu, M.; Ito, Y.; Ishii, A.; Miura, H.; Takashima, K. Effect of heat treatment and transformation on bending angle in laser forming of titanium foils. Key Eng. Mater. 2007, 344, 243–250. [Google Scholar] [CrossRef]
- Safari, M. A comparative study on laser bending process with linear and curved irradiating schemes. Optik 2022, 264, 169426. [Google Scholar] [CrossRef]
- Wang, H.; Wang, K.; Wang, W. Microstructure and Mechanical Properties of Low-Carbon Q235 Steel Welded Using Friction Stir Welding. Acta Metall. Sin. 2020, 33, 1556–1570. [Google Scholar] [CrossRef]
- Guan, Y.J.; Sun, S. Study on buckling mechanism of laser bending of sheet metal. Laser Technol. 2001, 025, 11–14. [Google Scholar]
- Shen, H. Accuracy Control Study of Laser Bending Forming; Shanghai Jiaotong University: Shanghai, China, 2007. [Google Scholar]
- Vollertsen, F.; Komel, I.; Kals, R. The laser bending of steel foils for microparts by the buckling mechanism-a model. Model. Simul. Mater. Sci. Eng. 1995, 3, 107–119. [Google Scholar] [CrossRef]
- Chen, J.K.; He, W. Thermal buckling analysis of statically indeterminate elastic rods. J. Yangzhou Univ. 1995, 16, 73–77. [Google Scholar]
- Wu, J.D.; Zhao, X.G.; Qiu, G.J. Calculation of Large Deflection Buckling of Elastic Rod during Thermal Expansion. J. Shenyang Univ. Chem. Technol. 1997, 000, 37–46. [Google Scholar]
- Shi, Y.J.; Yao, Z.Q.; Shen, H. Analysis of angular deformation in laser thermal stress sheet forming. J. Nanjing Univ. Aeronaut. Astronaut. 2005, 37, 99–103. [Google Scholar]
- Li, W.M.; Lu, X.C. Influence rule of sheet thickness in laser bending process. Chin. J. Nonferrous Met. 1999, 9, 6. [Google Scholar]
- Sun, Y.L.; Ma, H.H.; Yang, M. Research on Interface Characteristics and Mechanical Properties of 6061 Al Alloy and Q235a Steel by Hot Melt-Explosive Compression Bonding. Coatings 2020, 10, 1031. [Google Scholar] [CrossRef]
- Muhammad, S.; Lothar, W. Influence of extrusion parameters on microstructure and texture developments, and their effects on mechanical properties of the magnesium alloy AZ80. Mat. Sci. Eng. A Struct. 2009, 506, 141–147. [Google Scholar]
- Song, J.L.; Li, D.Z.; Bai, S.B. Microstructure and deformation mechanism of TWIP Steel under static tension at room temperature. J. Iron Steel Res. Int. 2015, 27, 61–66. [Google Scholar]
- Meng, M.; Zhao, X.; Zhang, Z. Effects of Compression-pass on microstructure and mechanical properties of AZ80 Alloy. J. Mater. Eng. Perform. 2014, 23, 3407–3411. [Google Scholar] [CrossRef]
- Zhang, S.H.; Luo, C.X.; Liu, J.A. Effect of extrusion process on grain size of alloy bars. J. Cent. South Univ. Technol. 2001, 32, 77–81. [Google Scholar]




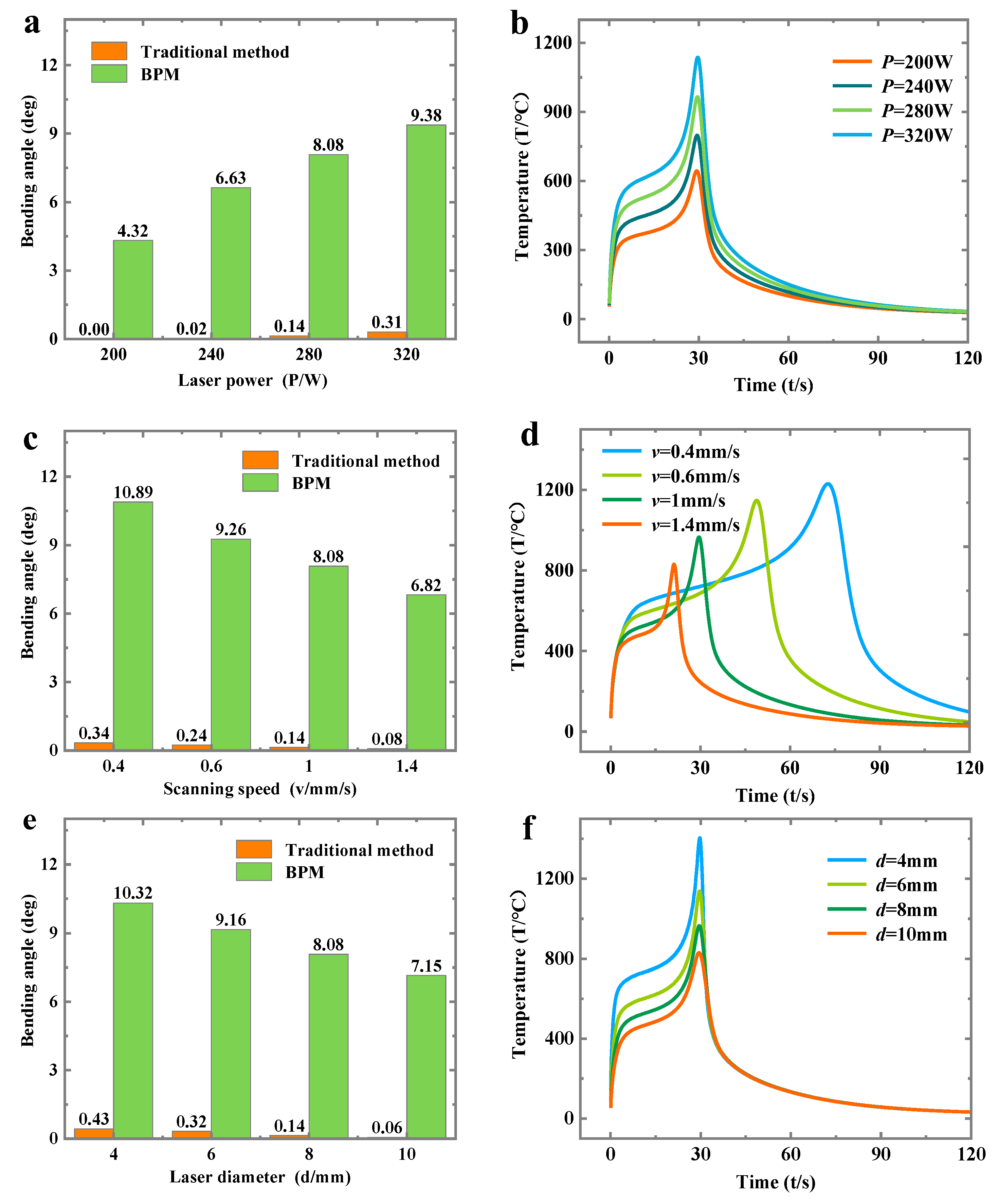

| Case | Laser Power (P/W) | Scanning Speed (v/mm·s−1) | Spot Diameter (d/mm) | Plate Thickness (h/mm) | Scanning Position (y/mm) | Pressure (q/Pa) |
|---|---|---|---|---|---|---|
| Different plate thickness | 280 | 1 | 8 | 0.6, 0.8, 1, 1.2 | 15 | 1.5 × 107 |
| Different pressure values | 280 | 1 | 8 | 0.8 | 15 | Traditional, 0.75 × 107, 1.5 × 107, 2.25 × 107 |
| Different laser power | 200, 240, 280, 320 | 1 | 8 | 0.8 | 15 | 1.5 × 107 |
| Different scanning speed | 280 | 0.6, 1, 1.4, 1.8 | 8 | 0.8 | 15 | 1.5 × 107 |
| Different spot diameters | 280 | 1 | 7, 8, 9, 10 | 0.8 | 15 | 1.5 × 107 |
| Brand | Model | Frequency (kHz) | Maximum Power (kW) | Central Wavelength |
|---|---|---|---|---|
| Chuangxin | MFSC-2000 | 0–50 | 2 | 1080 (nm) |
| Operation mode | Core diameter (µm) | Beam quality (mm × rad) | Cooling mode | |
| CW modulation | 100 | BPP = 2.8 | Water-cooling |
| Brand | Model | Measurement Range (°C) | Time Response (ms) | Spatial Resolution (mrad) |
|---|---|---|---|---|
| Flir | A-615 | −50~2000 | 8 | 0.68 |
| Measurement error (%) | ||||
| ±2 |
| Brand | Model | Measurement Range (mm) |
|---|---|---|
| Panasonic | HG-C1400 | ±200 |
| No. | Laser Power (P/W) | Scanning Speed (v/mm·s−1) | Spot Diameter (d/mm) | Plate Thickness (h/mm) | Pressure (q/Pa) |
|---|---|---|---|---|---|
| 1 | 280 | 1 | 8 | 0.8 | / |
| 2 | 280 | 1 | 8 | 0.8 | 1.5 × 107 |
| 3 | 320 | 1 | 8 | 0.8 | 1.5 × 107 |
| 4 | 280 | 1.4 | 8 | 0.8 | 1.5 × 107 |
| 5 | 280 | 1 | 10 | 0.8 | 1.5 × 107 |
| 6 | 280 | 1 | 8 | 1.2 | 1.5 × 107 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Shi, Y.; Guo, F. A Non-Thinning Forming Method with Improvement of Material Properties. Materials 2023, 16, 407. https://doi.org/10.3390/ma16010407
Guo Y, Shi Y, Guo F. A Non-Thinning Forming Method with Improvement of Material Properties. Materials. 2023; 16(1):407. https://doi.org/10.3390/ma16010407
Chicago/Turabian StyleGuo, Yankuo, Yongjun Shi, and Feng Guo. 2023. "A Non-Thinning Forming Method with Improvement of Material Properties" Materials 16, no. 1: 407. https://doi.org/10.3390/ma16010407
APA StyleGuo, Y., Shi, Y., & Guo, F. (2023). A Non-Thinning Forming Method with Improvement of Material Properties. Materials, 16(1), 407. https://doi.org/10.3390/ma16010407






