Influence of Repair Welding on the Fatigue Behavior of S355J2 T-Joints
Abstract
1. Introduction
2. Experimental Procedure
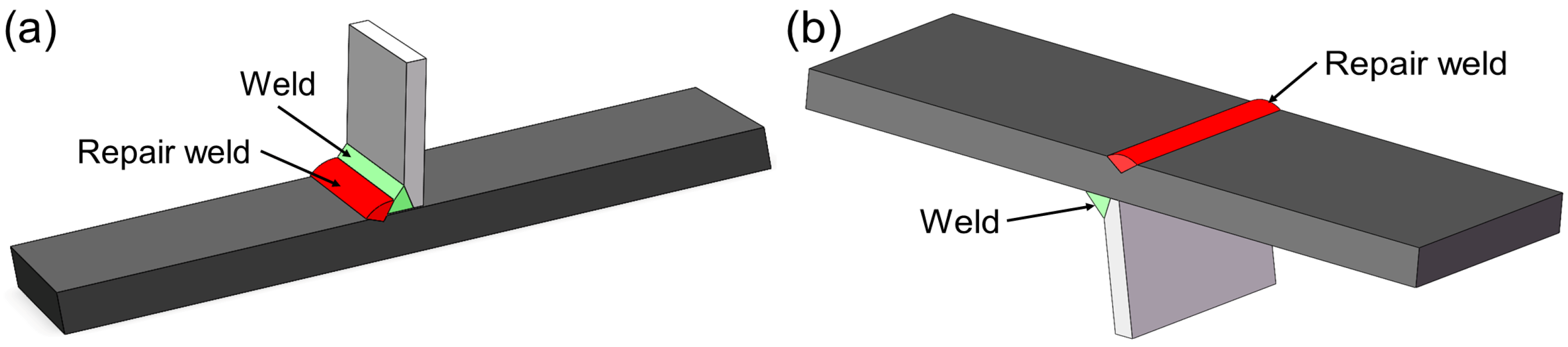
2.1. Materials and Test Specimen Preparation
2.2. Experiments
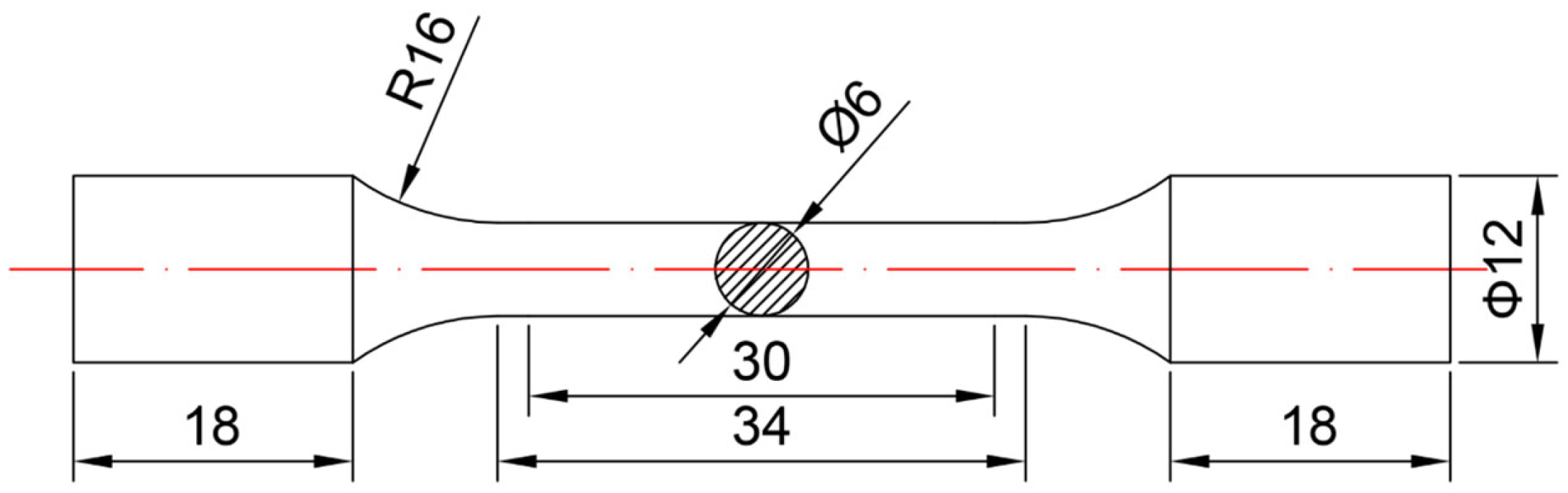
2.2.1. Microstructure and Mechanical Properties Test
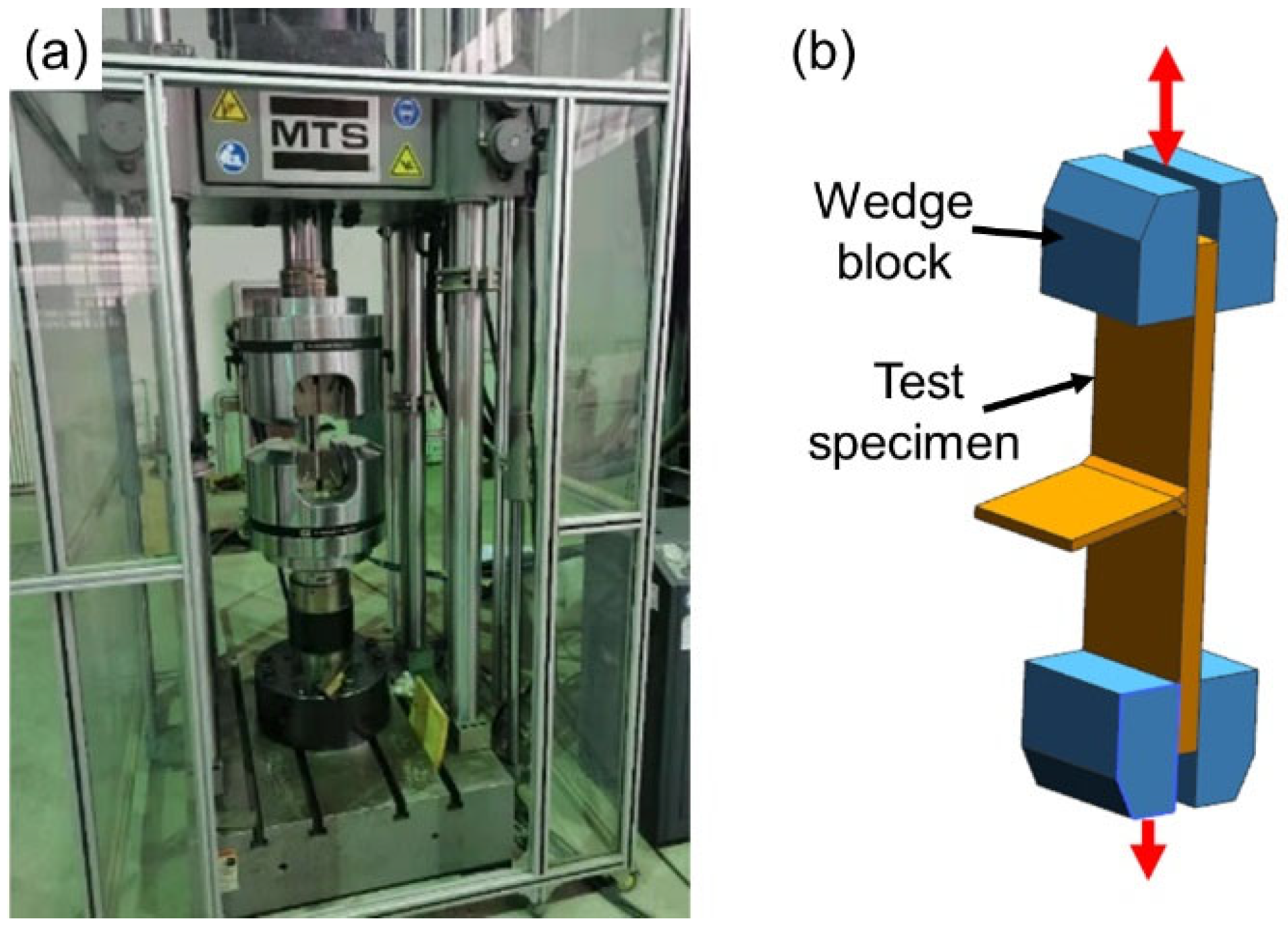
2.2.2. High Cycle Fatigue Test
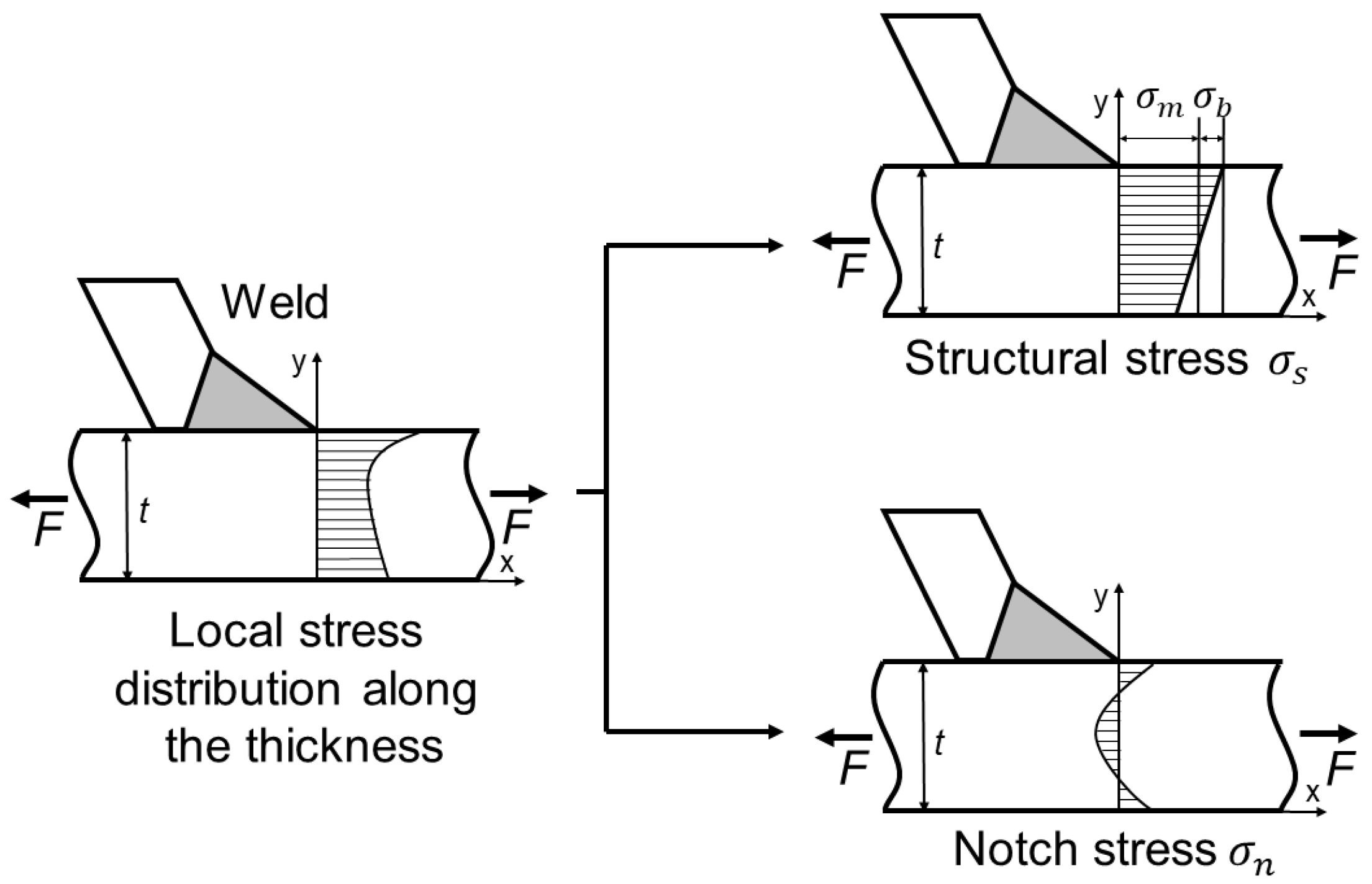
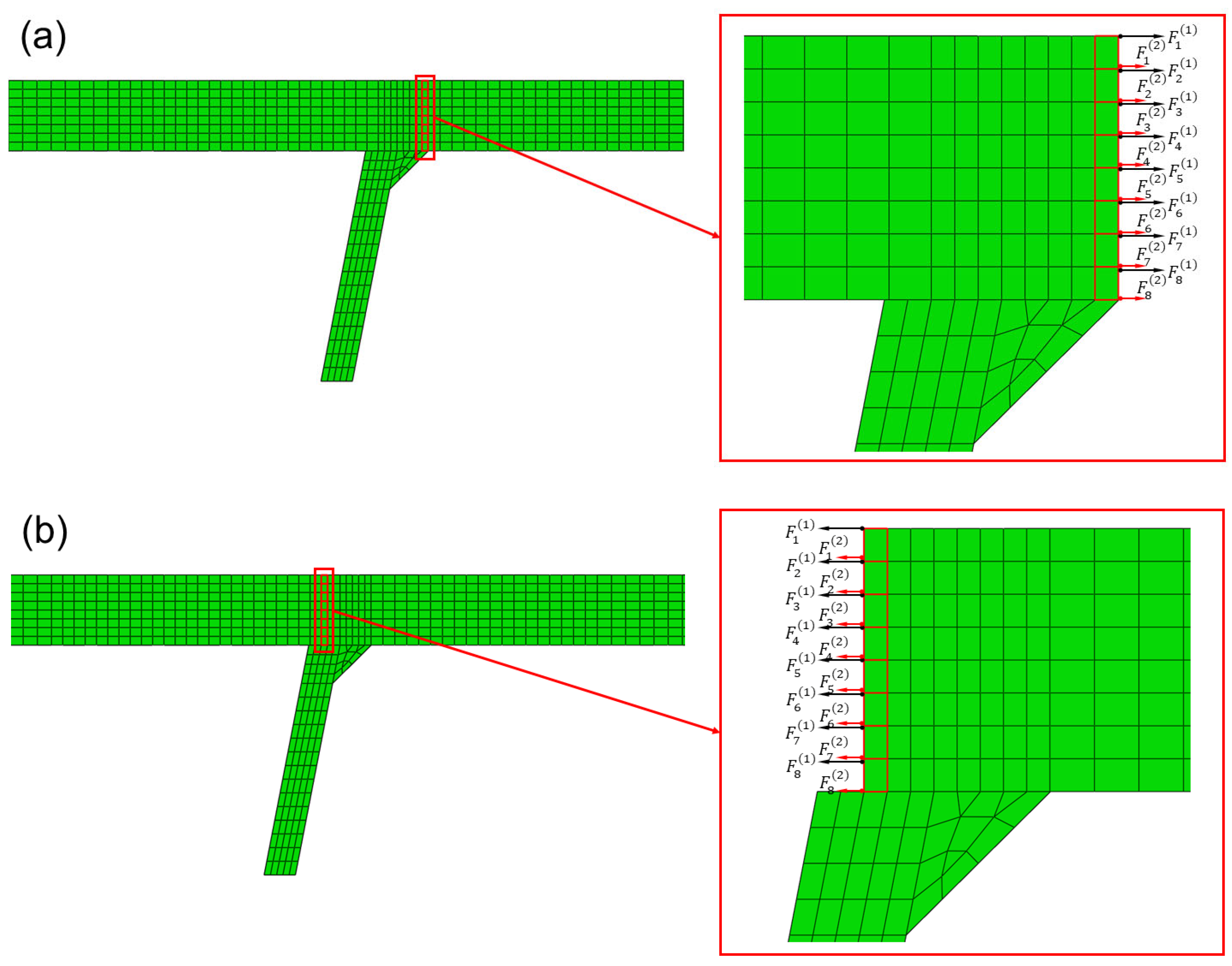
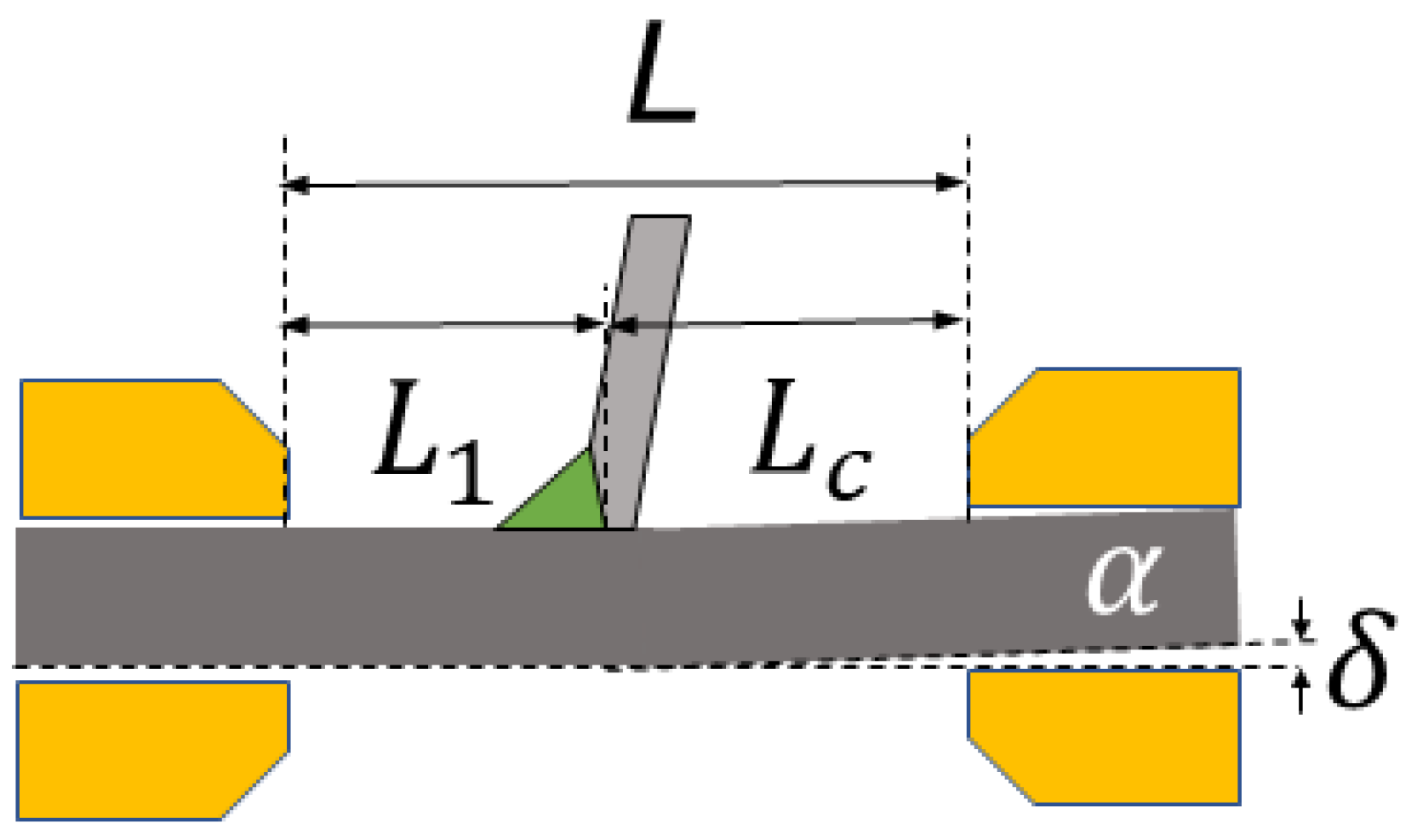
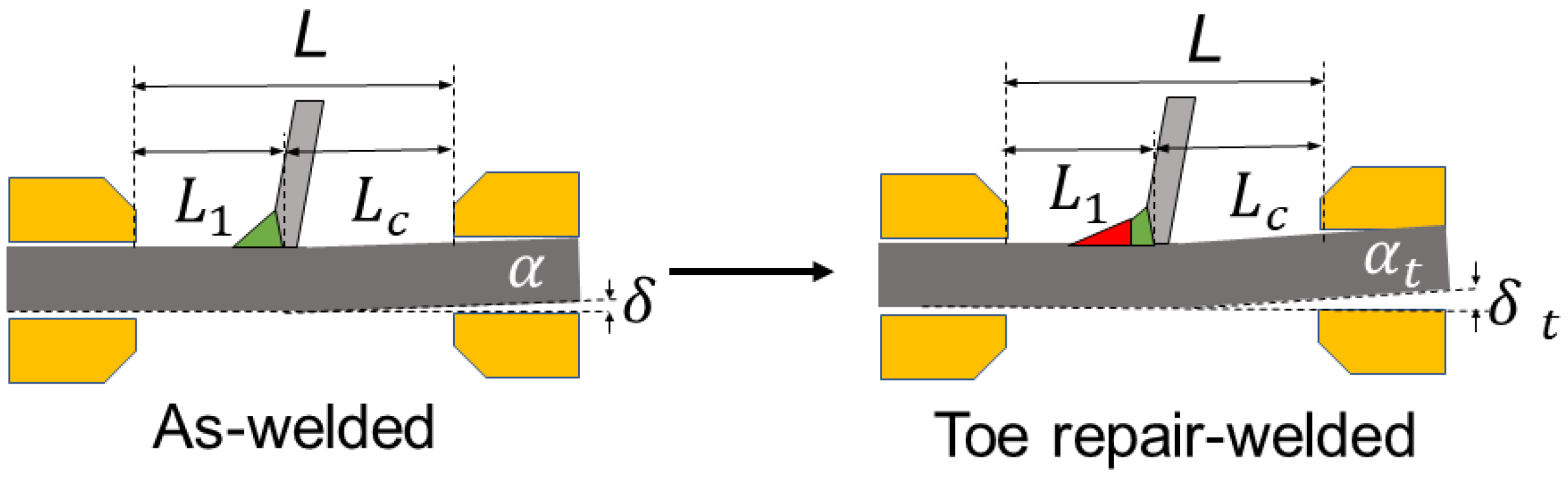
2.3. Traction Structural Stress Method
3. Microstructure and Mechanical Properties
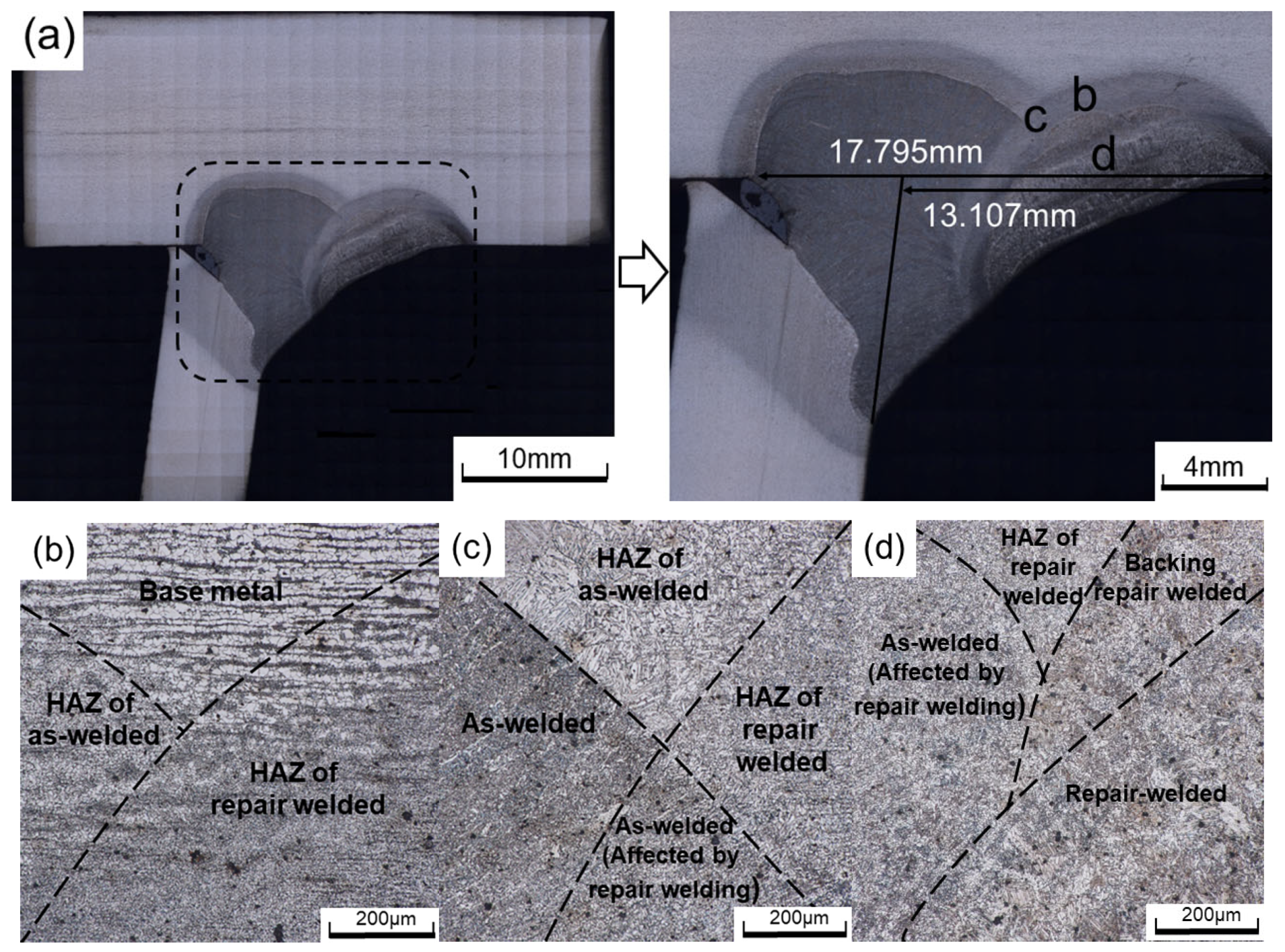
3.1. Microstructure
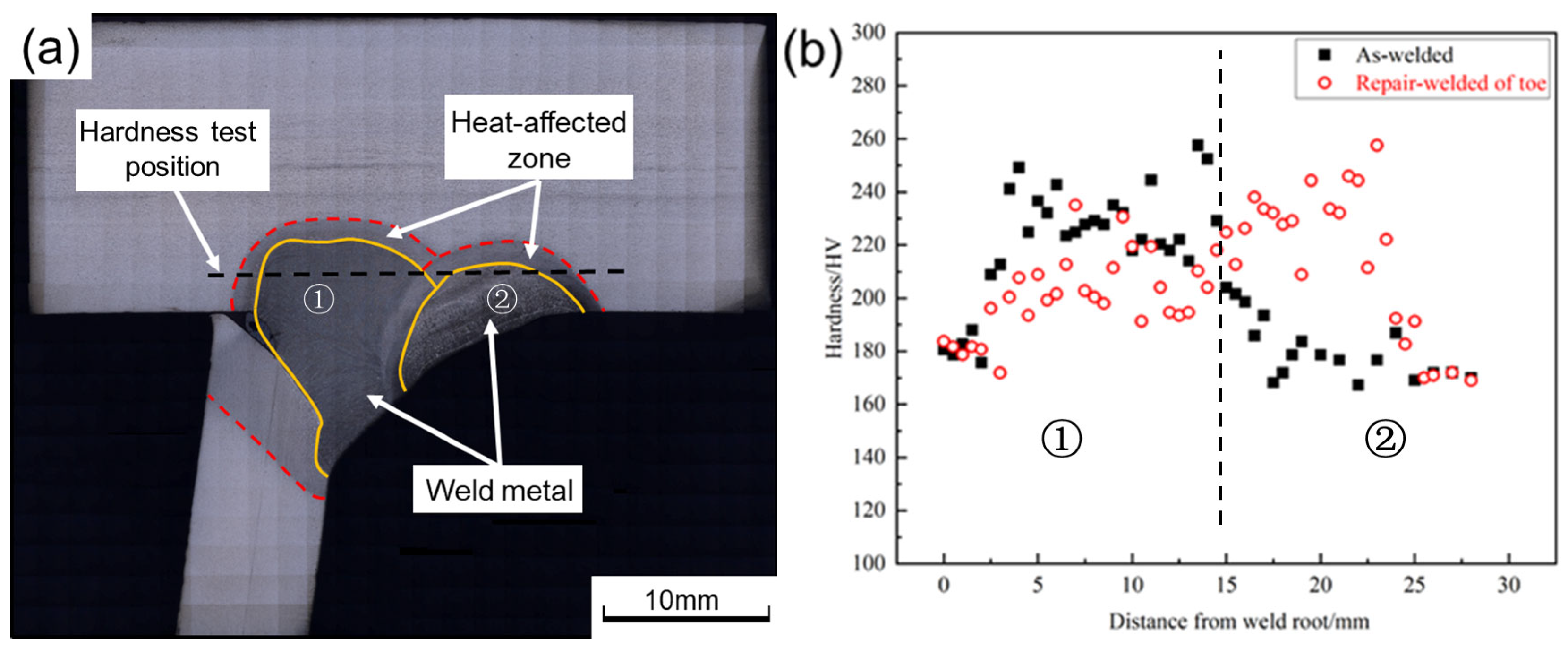
3.2. Microhardness
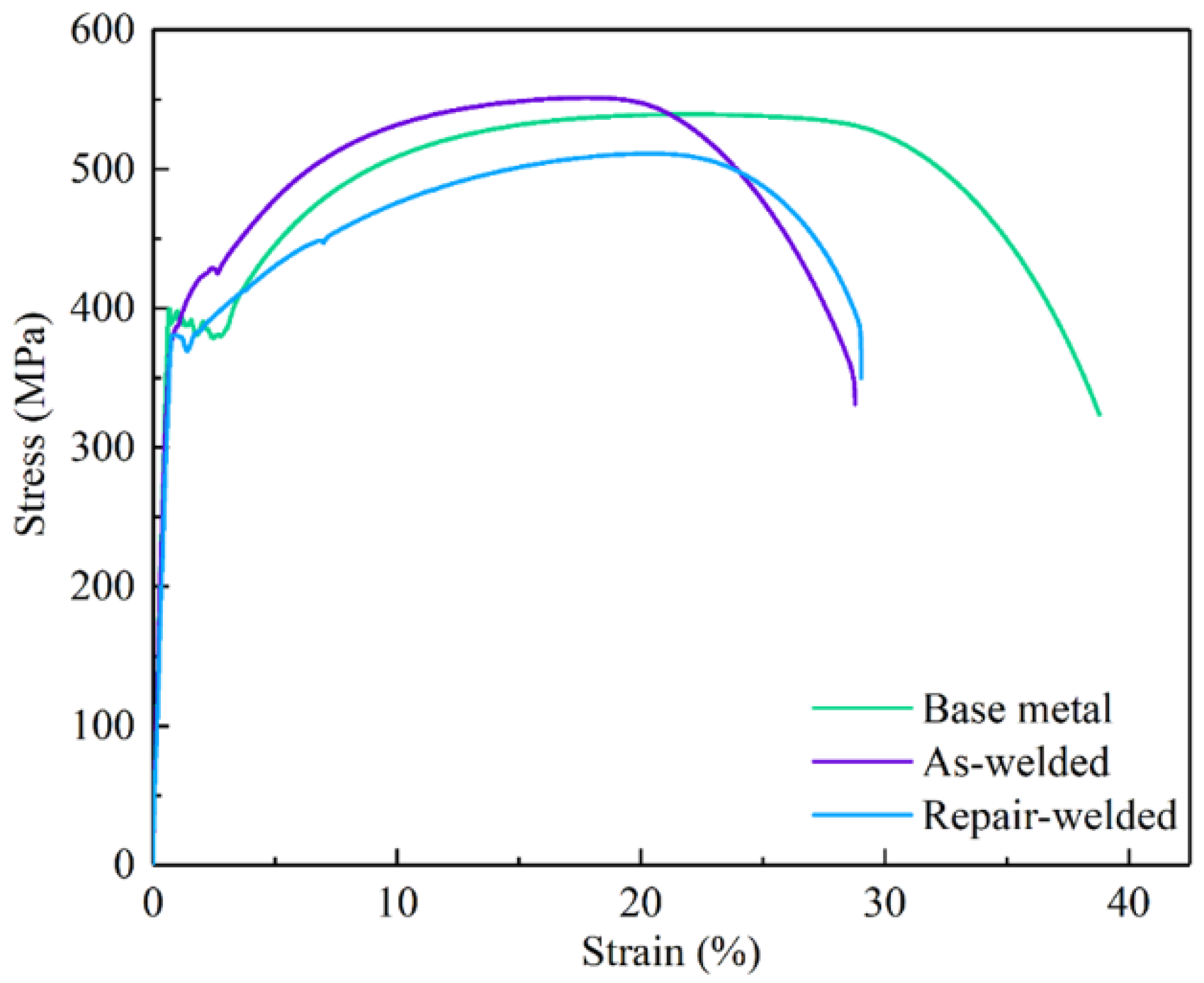
3.3. Tensile
4. HCF Behavior of T-Joints
4.1. Fatigue Test Results
4.2. Fracture Characteristics
4.3. Fatigue Life Assessment Based on Equivalent Traction Structural Stress
5. Conclusions
- Repair welding increases the grain size of WM and HAZ, which reduces the hardness of WM by about 30 HV. The tensile strength of the welded joint is the same as that of the base metal, while the tensile strength of the repair-welded joint is reduced by about 20 MPa. Compared with the base metal, the elongation of the welded and repair-welded joint decreases by about 25%.
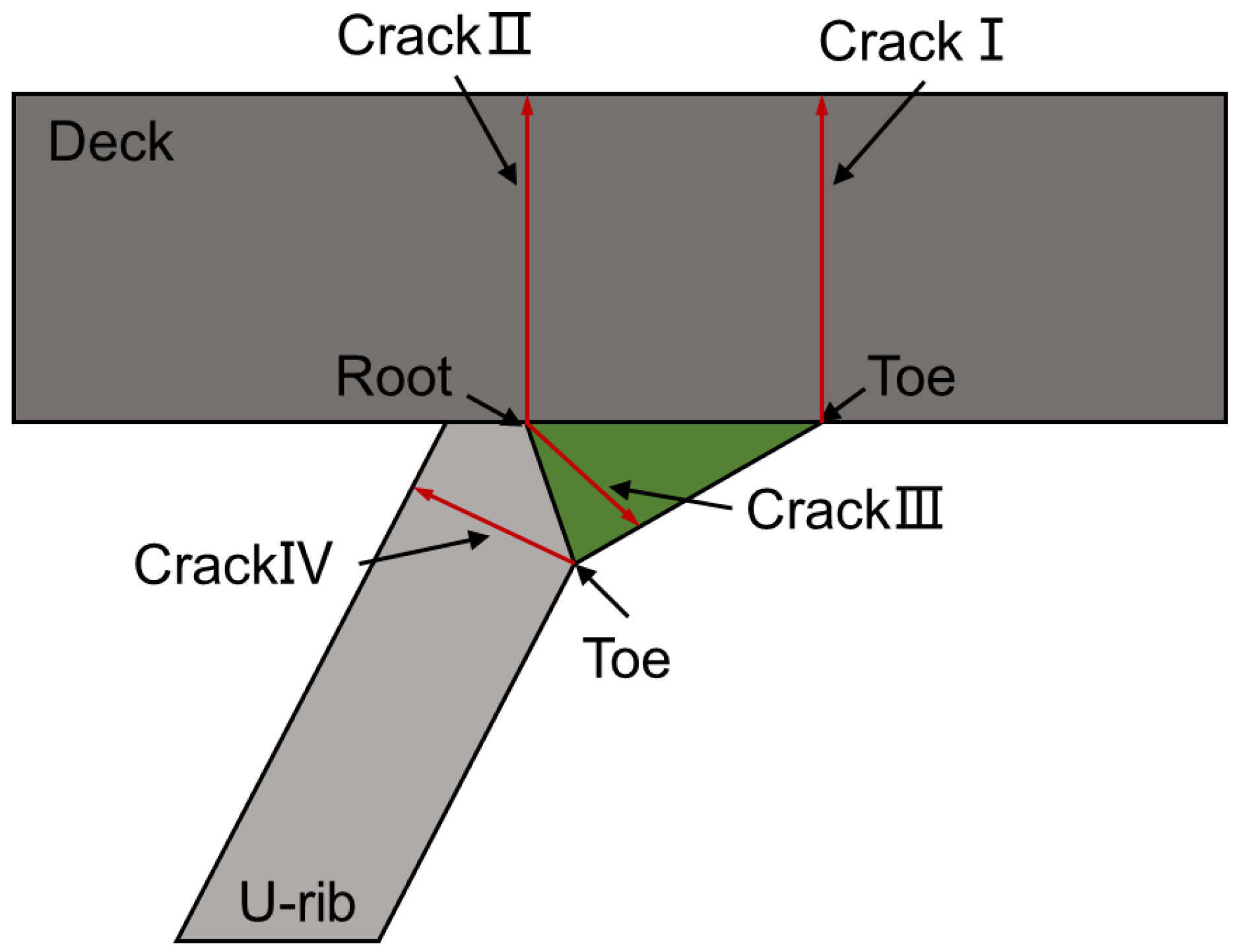
- The fracture positions of the welded joints are both weld toe and root, and the ratio is even, which is the same for deck repair-welded joints cracking. However, all of toe repair-welded joints fracture at the weld root. The macro-fracture characteristics of the root surface show that the fatigue cracks initiate on the surface of the specimen and propagate along the thickness of the deck, while the cracks of the toe surface initiate at the middle of the weld toe and propagate to both sides.
- The fatigue data with and without AM are all within the ±95% confidence interval of the master S-N curve, while the data considering AM is less discrete to the main curve.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A



References
- Li, J.; Zhang, Q.H.; Bao, Y.; Zhu, J.Z.; Chen, L.; Bu, Y.Z. An equivalent structural stress-based fatigue evaluation framework for rib-to-deck welded joints in orthotropic steel deck. Eng. Struct. 2019, 196, 109304. [Google Scholar] [CrossRef]
- Zeng, Y.; He, H.W.; Qu, Y.; Sun, X.D.; Tan, H.M.; Zhou, J.T. Numerical Simulation of Fatigue Cracking of Diaphragm Notch in Orthotropic Steel Deck Model. Materials 2023, 16, 457. [Google Scholar]
- Cheng, C.; Xie, X.; Yu, W.T. Investigation of the Fatigue Stress of Orthotropic Steel Decks Based on an Arch Bridge with the Application of the Arlequin Method. Materials 2021, 14, 7653. [Google Scholar] [CrossRef]
- Jiang, F.; Fu, Z.; Ji, B.; Wan, L. Fatigue life evaluation of deck to U-rib welds in orthotropic steel deck integrating weldment size effects on welding residual stress. Eng. Fail. Anal. 2021, 124, 105359. [Google Scholar] [CrossRef]
- Wang, D.L.; Xiang, C.; Ma, Y.H.; Chen, A.R.; Wang, B.J. Experimental study on the root-deck fatigue crack on orthotropic steel decks. Mater. Des. 2021, 203, 109601. [Google Scholar] [CrossRef]
- Ji, B.H.; Liu, R.; Chen, C.; Maeno, H.F.; Chen, X.F. Evaluation on root-deck fatigue of orthotropic steel bridge deck. J. Constr. Steel Res. 2013, 90, 174–183. [Google Scholar] [CrossRef]
- Kolstein, M.H. Fatigue Classification of Welded Joints in Orthotropic Steel Bridge Decks; Delft University of Technology: Delft, The Netherlands, 2007. [Google Scholar]
- Sim, H.B.; Uang, C.M. Stress analyses and parametric study on full-scale fatigue tests of rib-to-deck welded joints in steel orthotropic decks. J. Bridge Eng. 2012, 17, 765–773. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Q.H.; Guo, Y.W.; Bu, Y.Z. Comparison of Different Design Codes on Fatigue Assessment of Typical Welded Joints in Orthotropic Steel Bridge Decks. In Proceedings of the 40th IABSE Symposium, Nantes, France, 19–21 September 2018. [Google Scholar]
- Sakagami, T.; Izumi, Y.L.; Kubo, S. Application of infrared thermography to structural integrity evaluation of steel bridges. J. Mod. Opt. 2010, 57, 1738–1746. [Google Scholar] [CrossRef]
- Yuriok, N.; Horii, Y. Recent developments in repair welding technologies in Japan. Sci. Technol. Weld. Join. 2006, 11, 255. [Google Scholar] [CrossRef]
- AghaAli, I.; Farzam, M.; Golozar, M.A.; Danaee, I. The effect of repeated repair welding on mechanical and corrosion properties of stainless steel 316L. Mater. Des. 2014, 54, 331–341. [Google Scholar] [CrossRef]
- Luo, Y.; Gu, W.B.; Peng, W.; Jin, Q.; Qin, Q.L.; Yi, C.M. A study on microstructure, residual stresses and stress corrosion cracking of repair welding on 304 stainless steel: Part i-effects of heat input. Materials 2020, 13, 2416. [Google Scholar] [CrossRef]
- Katsas, S.; Papadimitriou, J.N. Microstructural changes accompanying repair welding in 5xxx aluminium alloys and their effect on the mechanical properties. Mater. Des. 2006, 27, 968–975. [Google Scholar] [CrossRef]
- Shojaati, M.; Bozorg, S.F.K.; Vatanara, M.; Yazdizadeh, M.; Abbasi, M. The heat affected zone of X20Cr13 martensitic stainless steel after multiple repair welding: Microstructure and mechanical properties assessment. Int. J. Press. Vessel. Pip. 2020, 188, 104205. [Google Scholar] [CrossRef]
- Dong, P.S. On repair weld residual stresses and significance to structural integrity. Weld. World 2018, 62, 351–362. [Google Scholar] [CrossRef]
- Wang, Y.X.; Ji, B.H.; Fu, Z.Q.; Yao, Y. Fatigue repairing craftsmanship of deck-to-vertical stiffener weld in the steel bridge deck. Adv. Steel Constr. 2019, 15, 232–241. [Google Scholar]
- Seo, J.W.; Kwon, S.J.; Lee, C.W.; Lee, D.F.; Goo, B.C. Fatigue strength and residual stress evaluation of repair welding of bogie frame for railway vehicles. Eng. Fail. Anal. 2020, 119, 104980. [Google Scholar] [CrossRef]
- Savaidis, G.; Vormwald, M. Hot-spot stress evaluation of fatigue in welded structural connections supported by finite element analysis. Int. J. Fatigue 2000, 22, 85–91. [Google Scholar] [CrossRef]
- Lee, J.M.; Seo, J.K.; Kim, M.H.; Shin, S.B.; Han, M.S.; Park, J.S.; Mahendran, M. Comparison of hot spot stress evaluation methods for welded structures. Int. J. Nav. Archit. Ocean Eng. 2010, 2, 200–210. [Google Scholar] [CrossRef]
- Zamzami, I.A.; Davison, B.; Susmel, L. Nominal and local stress quantities to design aluminium-to-steel thin welded joints against fatigue. Int. J. Fatigue 2019, 123, 279–295. [Google Scholar]
- Fricke, W. Fatigue analysis of welded joints: State of development. Mar. Struct. 2003, 16, 185–200. [Google Scholar] [CrossRef]
- Dong, P.S. A robust structural stress method for fatigue analysis of offshore/marine structures. Offshore Mech. Arct. Eng. 2005, 127, 68. [Google Scholar] [CrossRef]
- ASME:2007; Sec VIII, Div. 2 (ASME BPVC-VIII-2 e2007). American Society of Mechanical Engineers: New York, NY, USA, 2007.
- ISO 6892-1:2009; Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature. ISO: Berlin, Germany, 2009.
- Chen, Z.H.; Yu, B.L.; Wang, P.; Qian, H.L.; Dong, P.S. Fatigue behaviors of aluminum alloy butt joints with backing plates: Experimental testing and traction stress modeling. Int. J. Fatigue 2022, 163, 107040. [Google Scholar] [CrossRef]
- Wang, P.; Pei, X.J.; Dong, P.S.; Song, S.P. Traction structural stress analysis of fatigue behaviors of rib-to-deck joints in orthotropic bridge deck. Int. J. Fatigue 2019, 125, 11–22. [Google Scholar] [CrossRef]
- Dong, P.S. A structural stress definition and numerical implementation for fatigue analysis of welded joints. Int. J. Fatigue 2001, 23, 865–876. [Google Scholar] [CrossRef]
- Veerababu, J.; Goyal, S.; Sandhya, R.; Laha, K. Low cycle fatigue behaviour of Grade 92 steel weld joints. Int. J. Fatigue 2017, 105, 60–70. [Google Scholar] [CrossRef]
- Xing, S.Z.; Dong, P.S.; Wang, P. A Quantitative Weld Sizing Criterion for Fatigue Design of Load-Carrying Fillet-Welded Connections. Int. J. Fatigue 2017, 101, 448–458. [Google Scholar] [CrossRef]
- Xing, S.Z.; Dong, P.S. An analytical SCF solution method for joint misalignments and application in fatigue test data interpretation. Mar. Struct. 2016, 50, 143–161. [Google Scholar] [CrossRef]








| Material | Si | Mn | C | P | S | Ni | Cr | Cu | Fe |
|---|---|---|---|---|---|---|---|---|---|
| S355J2 | 0.50 | 1.70 | 0.18 | 0.025 | 0.025 | 0.50 | 0.30 | 0.30 | Bal. |
| E500T-1 | 0.90 | 1.75 | 0.18 | 0.03 | 0.03 | - | - | - | Bal. |
| Specimen | Length/mm | Width/mm | Deck Thickness/mm | Schematic Diagram of Specimen |
|---|---|---|---|---|
| Post-weld specimen | 1800 | 600 | 18 |  |
| Post-cut specimen | 600 | 300 | 18 | 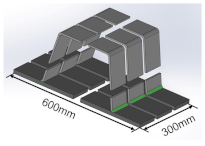 |
| T-joint | 300 | 100 | 18 | 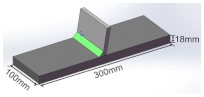 |
| Specimen | Welding State | Loading Frequency/Hz | Minimum/Maximum Load/kN |
|---|---|---|---|
| A-1 | As-welded | 15 | 36/360 |
| A-2 | As-welded | 15 | 40/400 |
| A-3 | As-welded | 15 | 44/440 |
| A-4 | As-welded | 15 | 46/460 |
| B-DZ-1 | Repair-welded of deck | 15 | 36/360 |
| B-DZ-2 | Repair-welded of deck | 15 | 40/400 |
| B-DZ-3 | Repair-welded of deck | 15 | 44/440 |
| B-DZ-4 | Repair-welded of deck | 15 | 46/460 |
| B-D-1 | Repair welded of toe | 15 | 36/360 |
| B-D-2 | Repair welded of toe | 15 | 40/400 |
| B-D-3 | Repair welded of toe | 15 | 44/440 |
| B-D-4 | Repair welded of toe | 15 | 46/460 |
| Specimen |  Beta Angle (°) |  Leg1 (mm) |  Leg2 (mm) |  Throat (mm) |  Toe Angle1 (°) |  Toe Angle2 (°) |
|---|---|---|---|---|---|---|
| Welded joints | 101 | 10.1 | 7.99 | 5.4 | 146 | 120 |
| Repair-welded joints | 99 | 10.0 | 13.1 | 5.9 | 144 | 155 |
| Specimen | Yield Strength σYS/MPa | Ultimate Tensile Strength σUTS/MPa | Tensile Elongation δ/% |
|---|---|---|---|
| Base metal | 393 | 539 | 38.7 |
| As-welded | 401 | 551 | 28.8 |
| Repair-welded | 380 | 511 | 29 |
| Specimen | Minimum/Maximum Load (kN) | Test Cycle | Fracture Location |
|---|---|---|---|
| A-1 | 36/360 | 584,810 | Weld root |
| A-2 | 40/400 | 709,590 | Weld toe |
| A-3 | 44/440 | 356,690 | Weld toe |
| A-4 | 46/460 | 288,464 | Weld toe |
| B-DZ-1 | 36/360 | 202,070 | Weld root |
| B-DZ-2 | 40/400 | 163,023 | Weld root |
| B-DZ-3 | 44/440 | 223,383 | Weld root |
| B-DZ-4 | 46/460 | 125,140 | Weld root |
| B-D-1 | 36/360 | 413,257 | Weld toe |
| B-D-2 | 40/400 | 325,298 | Weld toe |
| B-D-3 | 44/440 | 187,688 | Weld root |
| B-D-4 | 46/460 | 234,109 | Weld root |
| Specimen | Minimum/Maximum Load (kN) | Nominal Stress (MPa) | Stress Concentration Factor of Fracture Interface | Equivalent Traction Structural Stress of Fracture Interface (MPa) |
|---|---|---|---|---|
| A-1 | 36/360 | 180 | 1.687 | 303.61 |
| A-2 | 40/400 | 200 | 1.599 | 319.80 |
| A-3 | 44/440 | 220 | 1.599 | 351.78 |
| A-4 | 46/460 | 230 | 1.599 | 367.77 |
| B-DZ-1 | 36/360 | 180 | 1.679 | 302.18 |
| B-DZ-2 | 40/400 | 200 | 1.679 | 335.76 |
| B-DZ-3 | 44/440 | 220 | 1.679 | 369.34 |
| B-DZ-4 | 46/460 | 230 | 1.679 | 386.12 |
| B-D-1 | 36/360 | 180 | 1.599 | 287.82 |
| B-D-2 | 40/400 | 200 | 1.599 | 319.80 |
| B-D-3 | 44/440 | 220 | 1.687 | 371.10 |
| B-D-4 | 46/460 | 230 | 1.687 | 387.95 |
| Curve | ||
|---|---|---|
| Master curve | 19,930.2 | 0.3195 |
| Upper curve () | 28,626.5 | 0.3195 |
| Lower curve (−) | 13,875.7 | 0.3195 |
| Upper curve () | 34,308.1 | 0.3195 |
| Lower curve (−3) | 11,577.9 | 0.3195 |
| Specimen | L (mm) | Lc (mm) | α (°) | ||
|---|---|---|---|---|---|
| A-1 | 140 | 69.2 | 0.99 | 0.0672 | 322.56 |
| A-2 | 140 | 69.2 | 1.23 | 0.0835 | 344.56 |
| A-3 | 140 | 69.2 | 1.36 | 0.0923 | 381.90 |
| A-4 | 140 | 69.2 | 0.95 | 0.0645 | 389.75 |
| B-DZ-1 | 140 | 69.2 | 2.385 | 0.1618 | 347.61 |
| B-DZ-2 | 140 | 69.2 | 3.273 | 0.2221 | 405.02 |
| B-DZ-3 | 140 | 69.2 | 3.497 | 0.2373 | 450.74 |
| B-DZ-4 | 140 | 69.2 | 2.9 | 0.1968 | 456.70 |
| B-D-1 | 140 | 69.2 | 0.342 | 0.0232 | 294.00 |
| B-D-2 | 140 | 69.2 | 0.303 | 0.0206 | 325.88 |
| B-D-3 | 140 | 69.2 | 0.328 | 0.0223 | 378.76 |
| B-D-4 | 140 | 69.2 | 0.419 | 0.0284 | 398.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, P.; Yu, B.; Wang, P.; Liu, Y.; Song, X. Influence of Repair Welding on the Fatigue Behavior of S355J2 T-Joints. Materials 2023, 16, 3682. https://doi.org/10.3390/ma16103682
Zhao P, Yu B, Wang P, Liu Y, Song X. Influence of Repair Welding on the Fatigue Behavior of S355J2 T-Joints. Materials. 2023; 16(10):3682. https://doi.org/10.3390/ma16103682
Chicago/Turabian StyleZhao, Peng, Banglong Yu, Ping Wang, Yong Liu, and Xiaoguo Song. 2023. "Influence of Repair Welding on the Fatigue Behavior of S355J2 T-Joints" Materials 16, no. 10: 3682. https://doi.org/10.3390/ma16103682
APA StyleZhao, P., Yu, B., Wang, P., Liu, Y., & Song, X. (2023). Influence of Repair Welding on the Fatigue Behavior of S355J2 T-Joints. Materials, 16(10), 3682. https://doi.org/10.3390/ma16103682










