A Modified Bond-Associated Non-Ordinary State-Based Peridynamic Model for Impact Problems of Quasi-Brittle Materials
Abstract
:1. Introduction
2. Methodology
2.1. Brief Review of Peridynamic Models for Quasi-Brittle Materials
2.1.1. Original Non-Ordinary State-Based Peridynamics
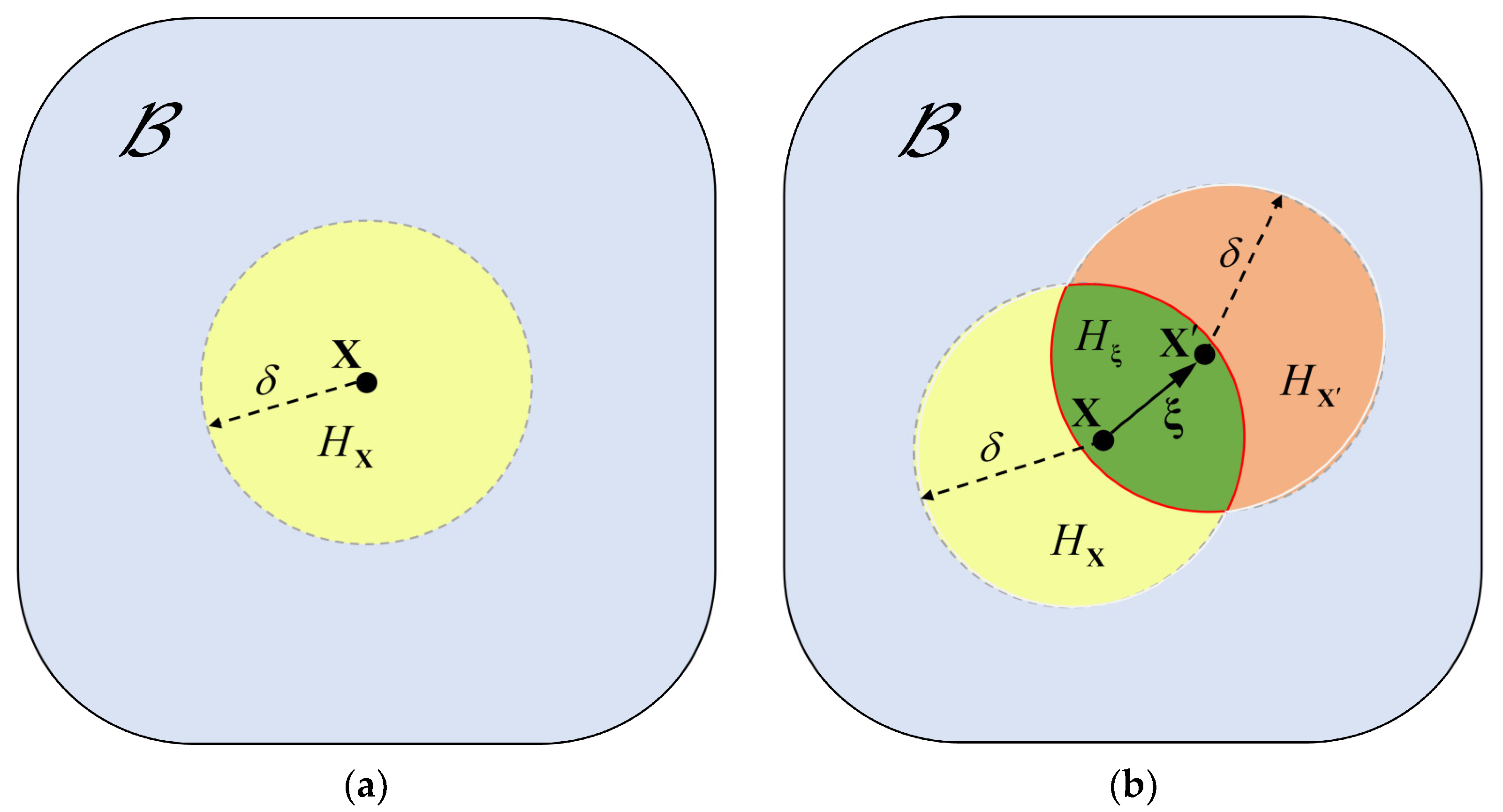
2.1.2. Bond-Associated Non-Ordinary State-Based Peridynamics
2.1.3. JH2 Constitutive Model
2.2. Modified Bond-Associated Non-Ordinary State-Based Peridynamic Model
2.2.1. Bond-Associated Volumetric Strain
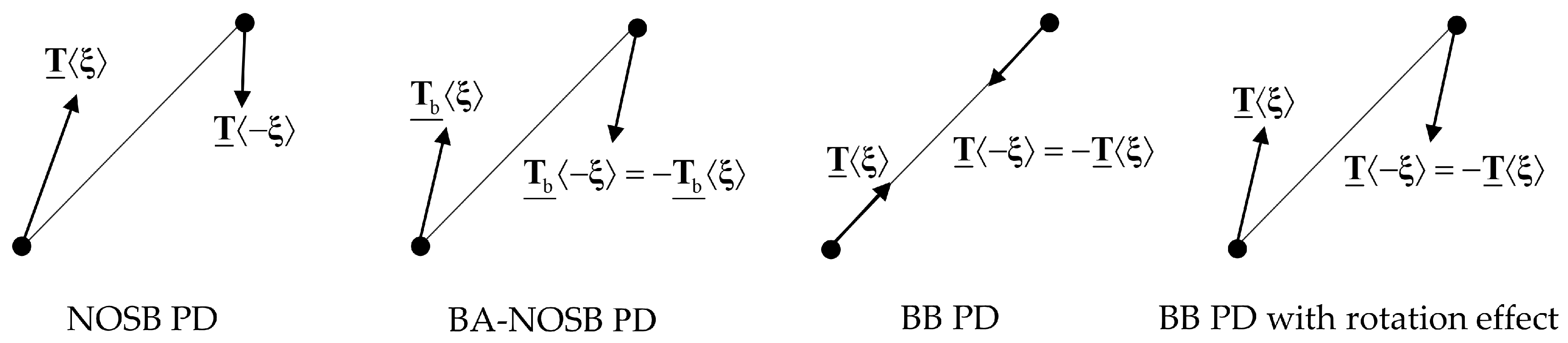
2.2.2. Bond-Breaking Criterion
2.2.3. Treatment Strategy of Broken Bonds
2.3. Constitutive Update Scheme
2.4. Other Zero-Energy Mode Control Schemes
- Control Scheme I:
- Control Scheme II:
- Control Scheme III:
- Control Scheme IV:
2.5. Numerical Discretization and Implementation
2.5.1. Numerical Discretization
2.5.2. Artificial Viscosity
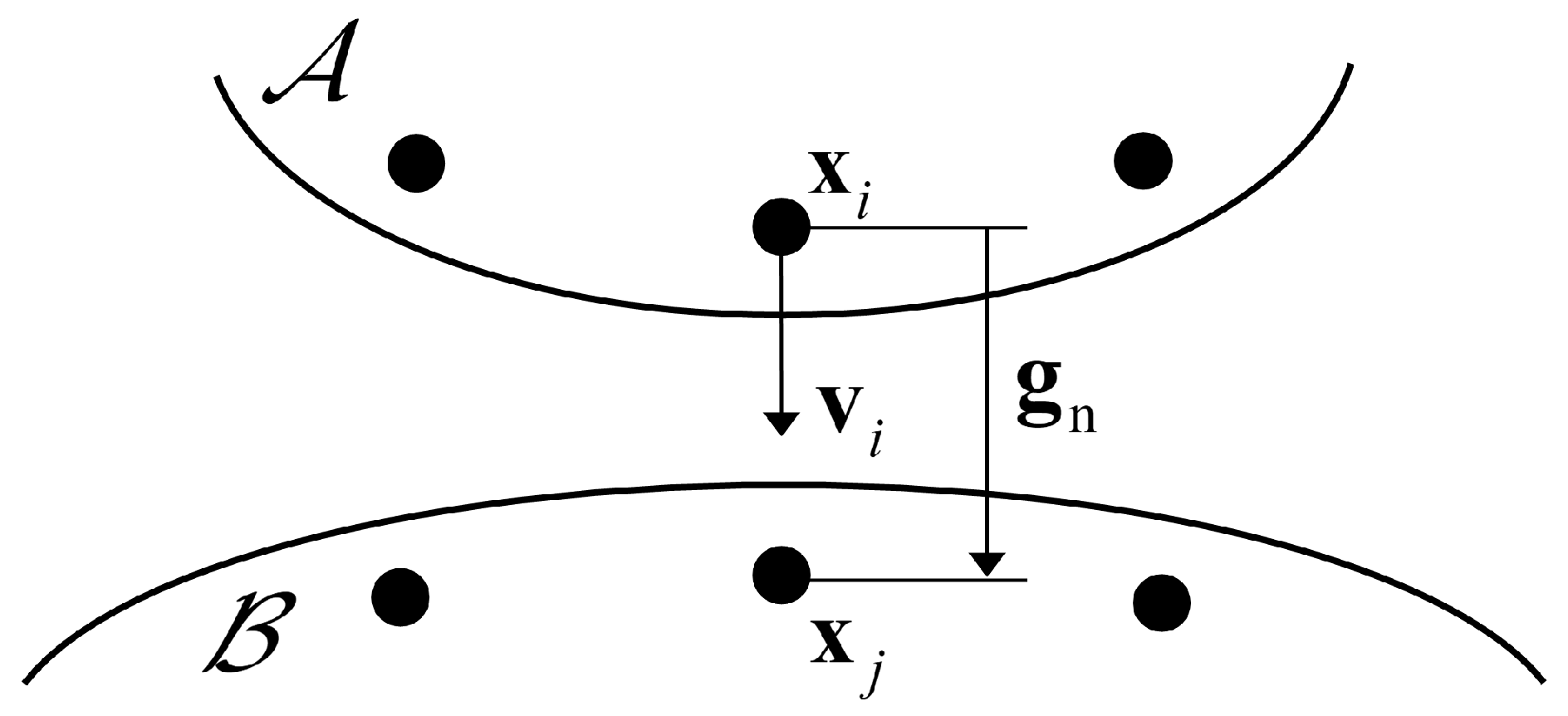
2.5.3. Contact Algorithm
3. Numerical Examples
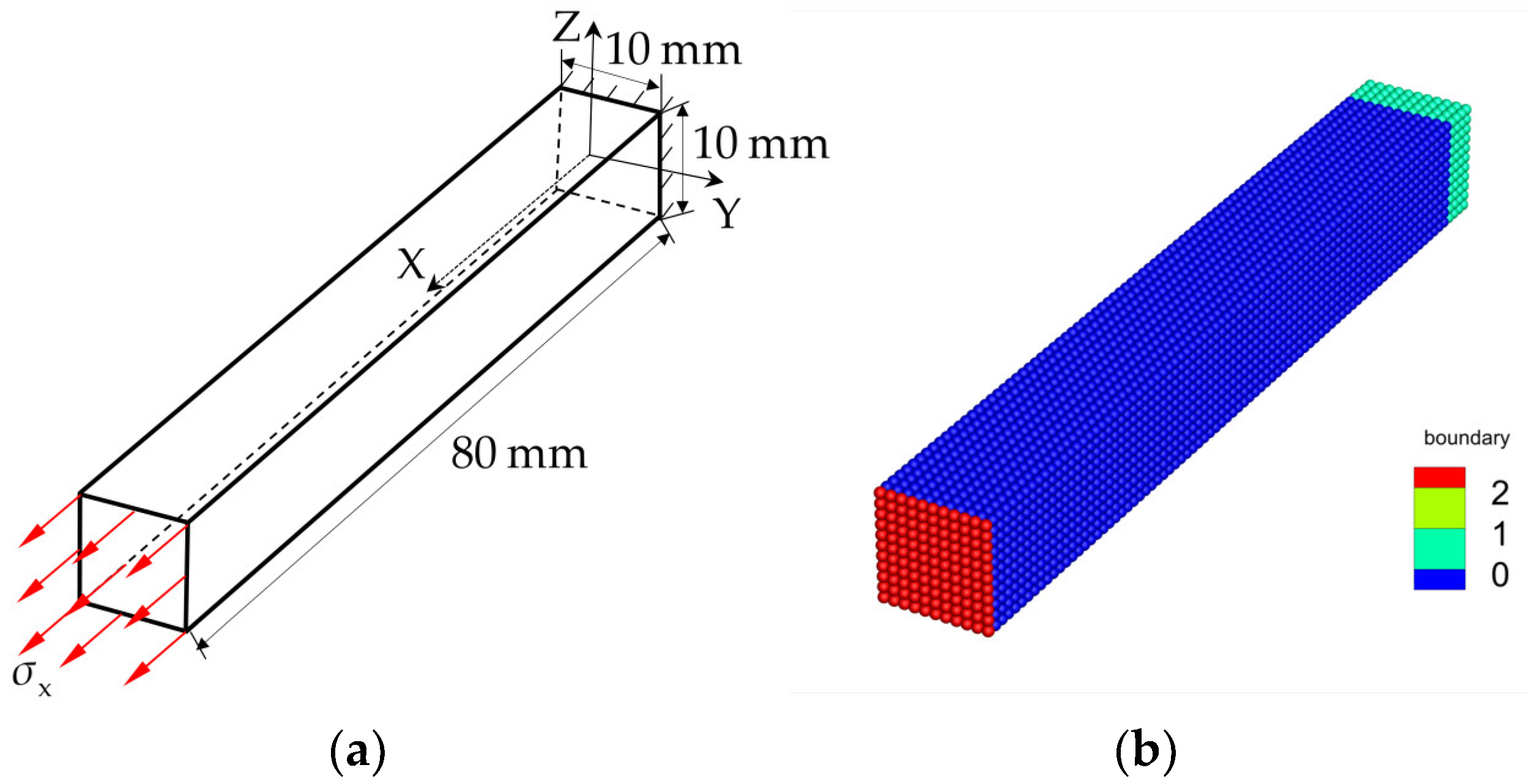
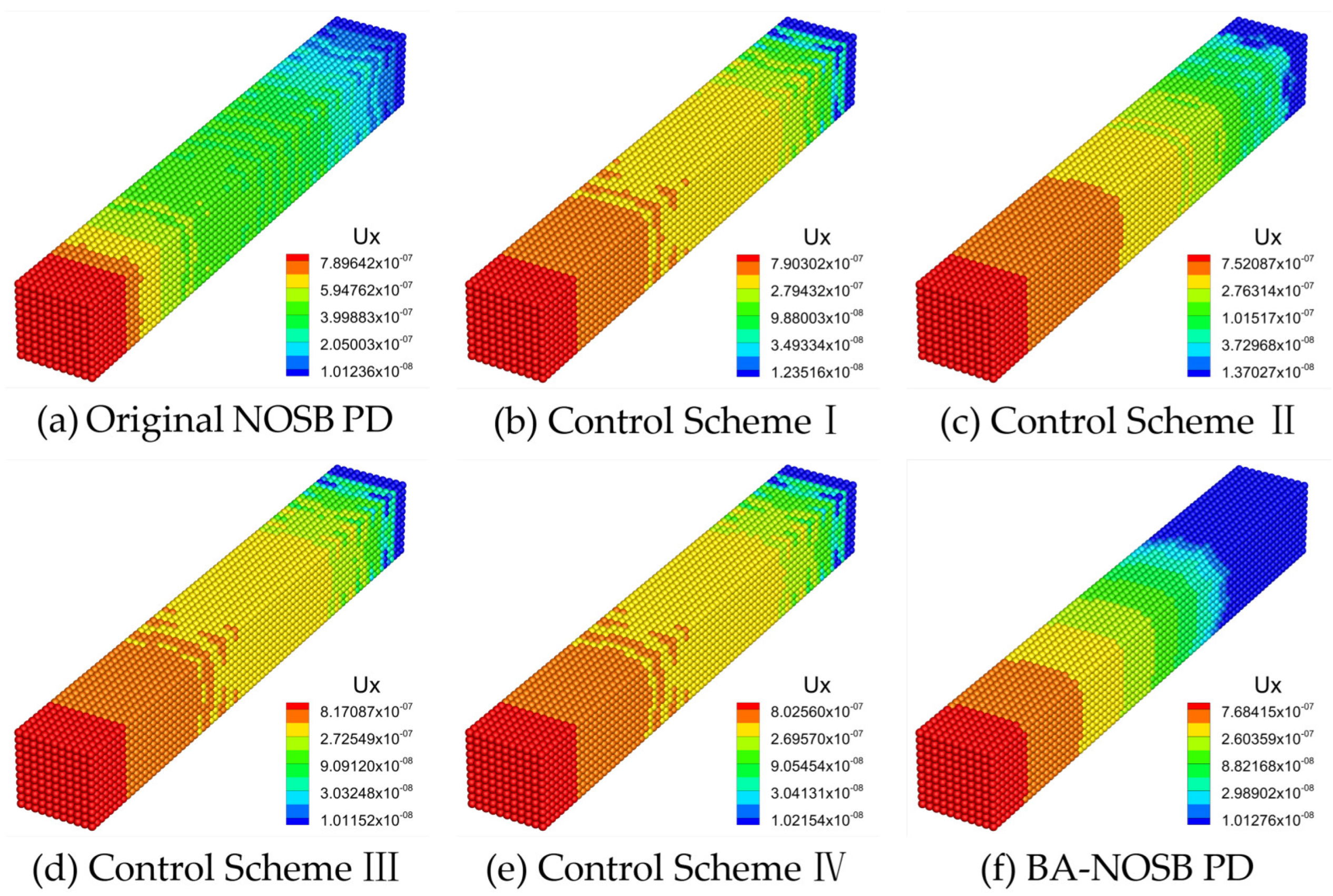
3.1. Uniaxial Tension of an Elastic Bar under Stress Loading
3.2. Uniaxial Tension of an Elastic Bar under Velocity Loading
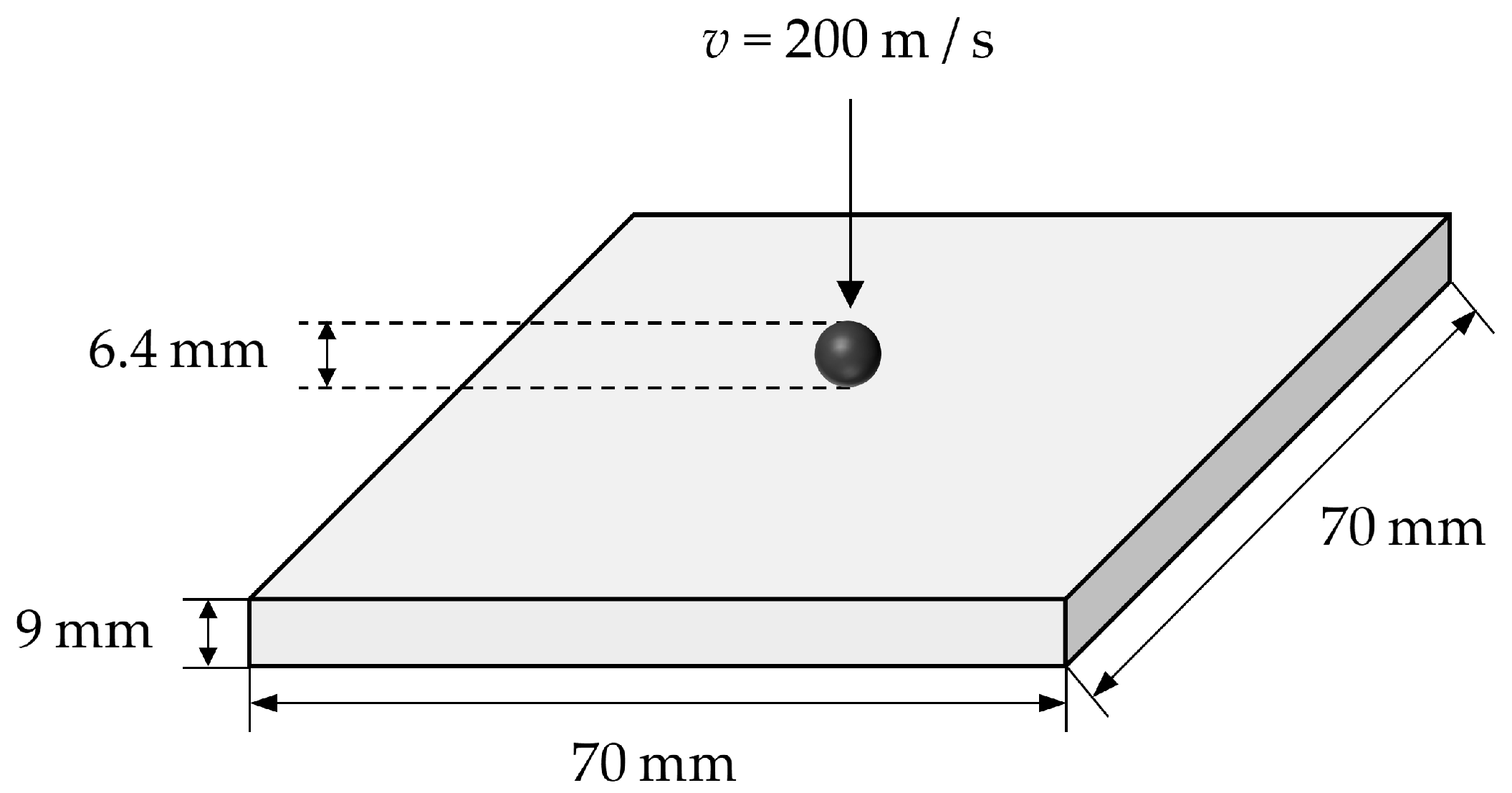
3.3. Edge-On Impact Simulation of Ceramics
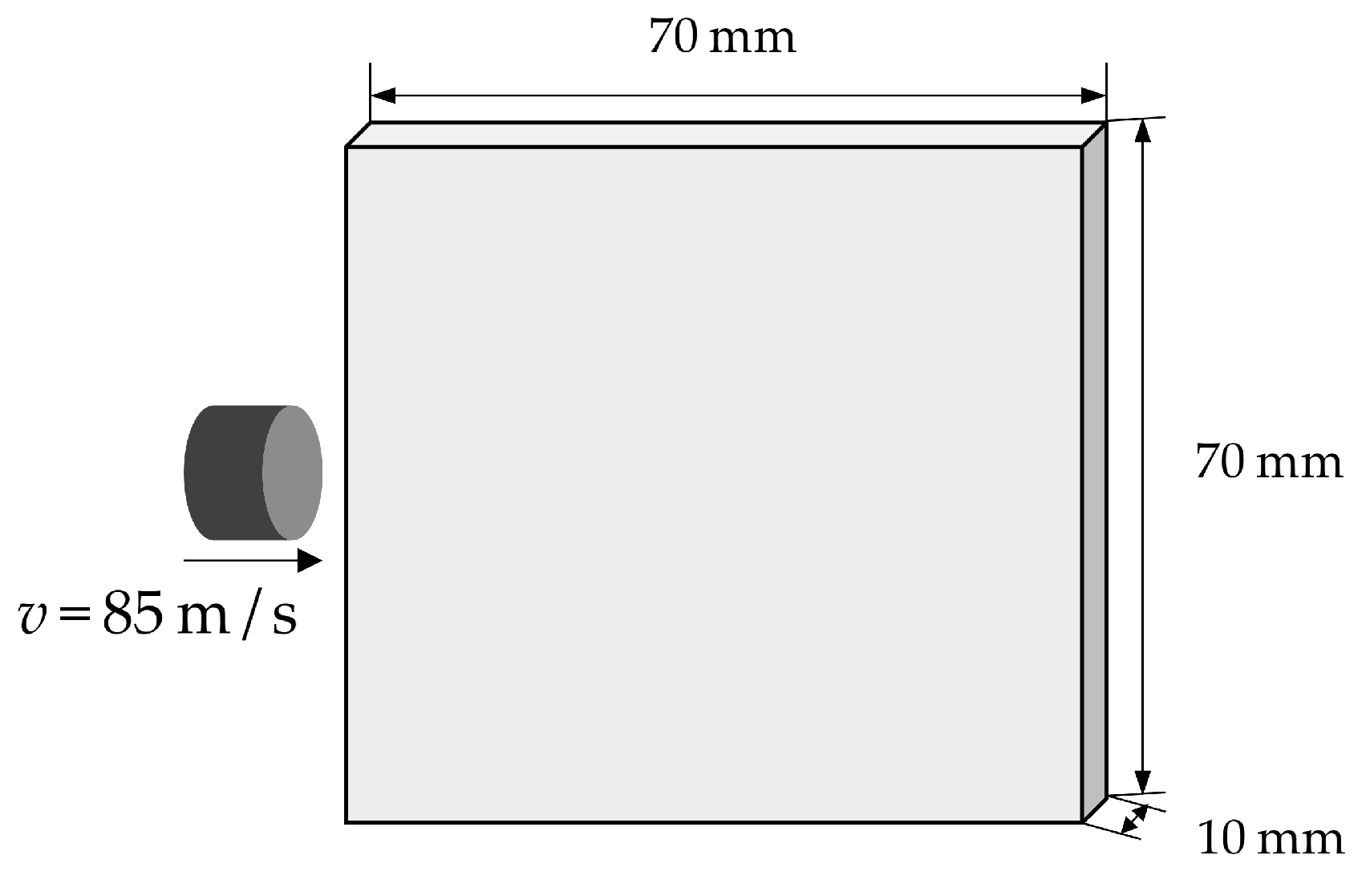
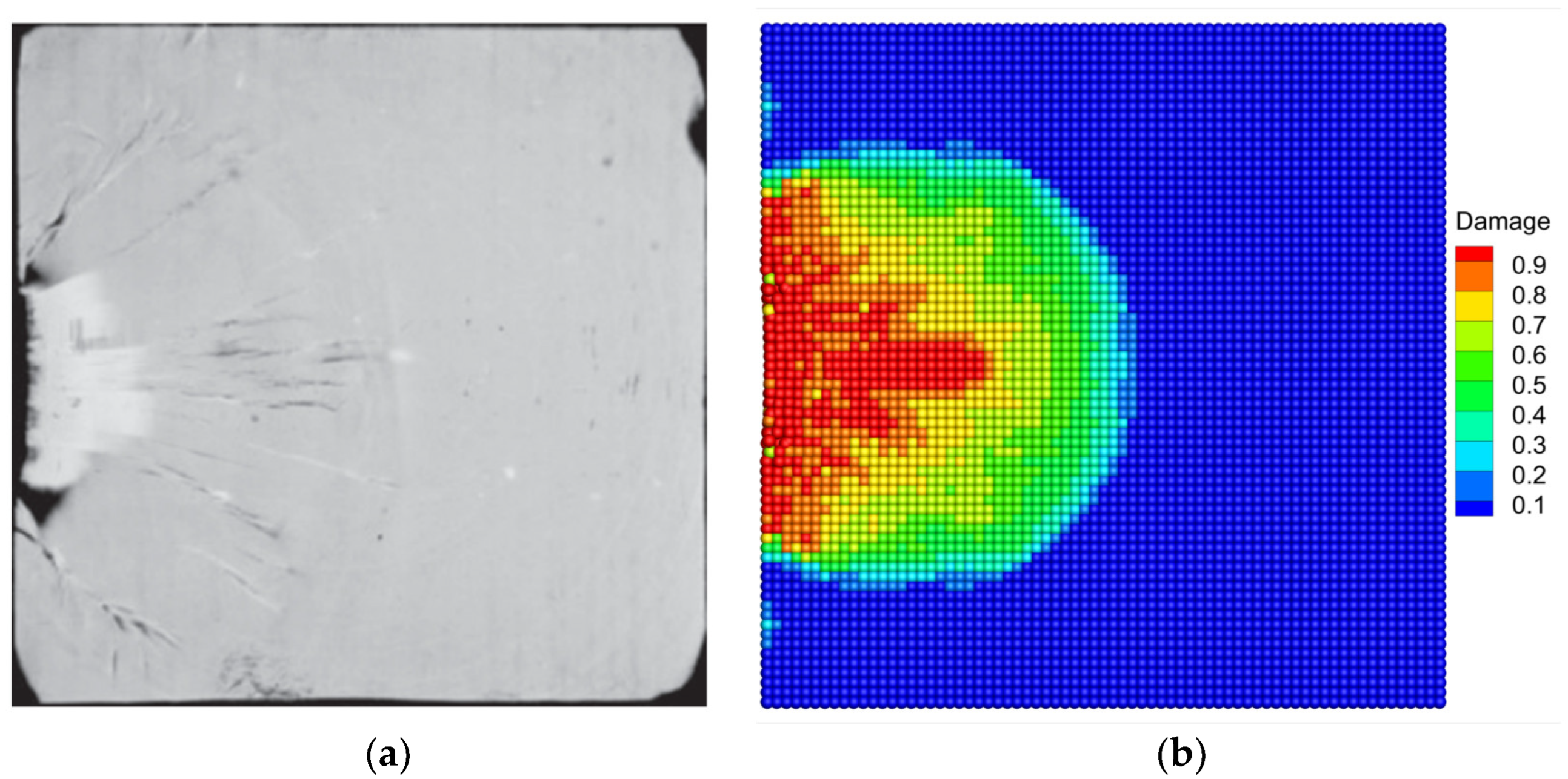
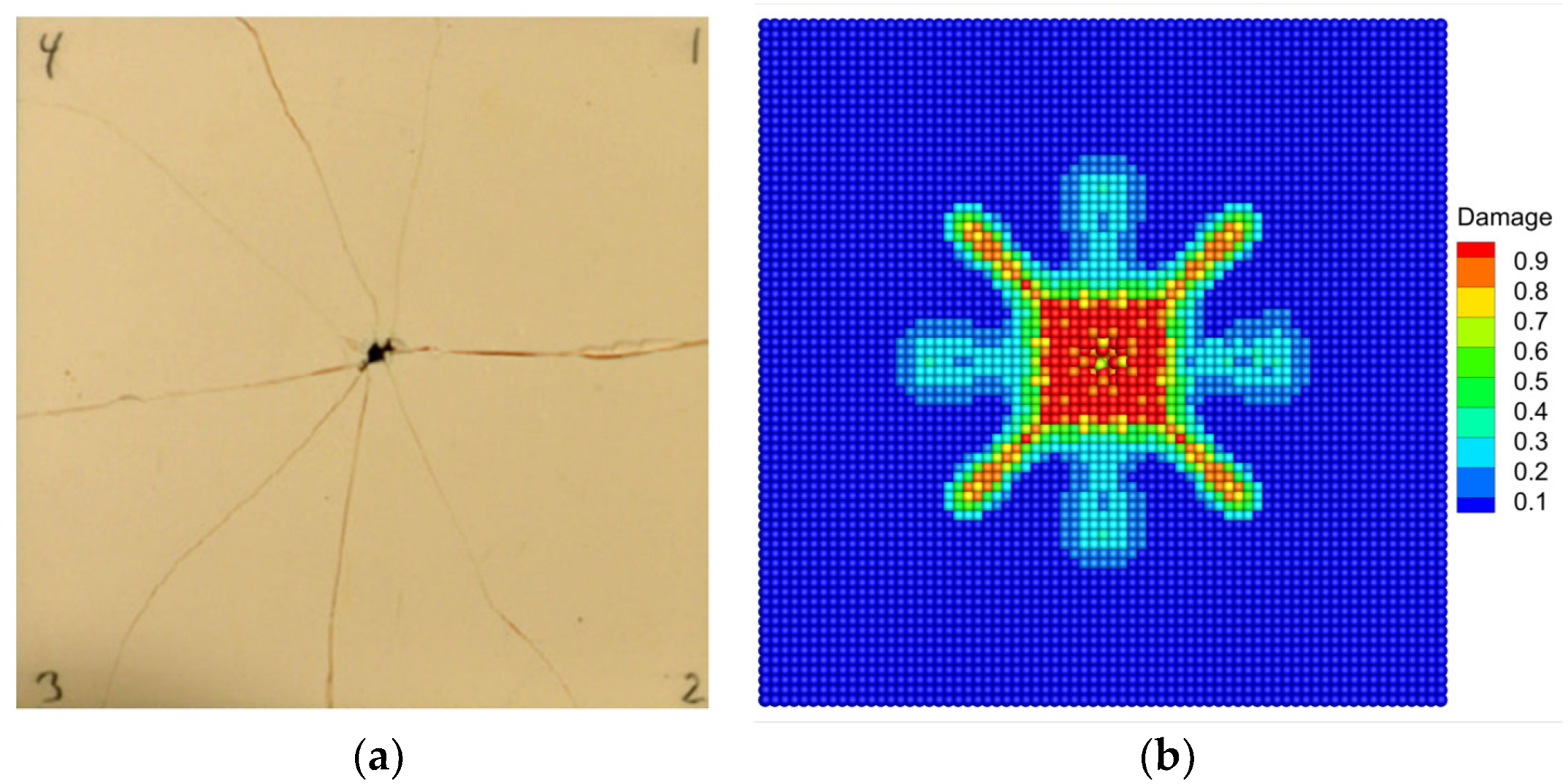
3.4. Normal Impact Simulation of Ceramics
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Walley, S.M. Historical review of high strain rate and shock properties of ceramics relevant to their application in armour. Adv. Appl. Ceram. 2010, 109, 446–466. [Google Scholar] [CrossRef]
- Chen, W.W.; Rajendran, A.M.; Song, B.; Nie, X. Dynamic fracture of ceramics in armor applications. J. Am. Ceram. Soc. 2007, 90, 1005–1018. [Google Scholar] [CrossRef]
- Song, J.H.; Wang, H.; Belytschko, T. A comparative study on finite element methods for dynamic fracture. Comput. Mech. 2008, 42, 239–250. [Google Scholar] [CrossRef]
- Pezzotta, M.; Zhang, Z.L.; Jensen, M.; Grande, T.; Einarsrud, M.A. Cohesive zone modeling of grain boundary microcracking induced by thermal anisotropy in titanium diboride ceramics. Comput. Mater. Sci. 2008, 43, 440–449. [Google Scholar] [CrossRef]
- Krishnan, K.; Sockalingam, S.; Bansal, S.; Rajan, S.D. Numerical simulation of ceramic composite armor subjected to ballistic impact. Compos. B Eng. 2010, 41, 583–593. [Google Scholar] [CrossRef]
- Silling, S.A. Reformulation of elasticity theory for discontinuities and long-range forces. J. Mech. Phys. Solids. 2000, 48, 175–209. [Google Scholar] [CrossRef]
- Silling, S.A. Dynamic Fracture Modeling with a Meshfree Peridynamic Code. In Computational Fluid and Solid Mechanics; Elsevier Science Ltd.: Amsterdam, The Netherlands, 2003; pp. 641–644. [Google Scholar]
- Silling, S.A.; Askari, E. A meshfree method based on the Peridynamic model of solid mechanics. Comput. Struct. 2005, 83, 1526–1535. [Google Scholar] [CrossRef]
- Silling, S.A.; Epton, M.; Weckner, O.; Xu, J.; Askari, E. Peridynamic states and constitutive modeling. J. Elast. 2007, 88, 151–184. [Google Scholar] [CrossRef]
- Ha, Y.D.; Bobaru, F. Studies of dynamic crack propagation and crack branching with Peridynamics. Int. J. Fract. 2010, 162, 229–244. [Google Scholar] [CrossRef]
- Ha, Y.D.; Bobaru, F. Characteristics of dynamic brittle fracture captured with Peridynamics. Eng. Fract. Mech. 2011, 78, 1156–1168. [Google Scholar] [CrossRef]
- Zhu, Q.Z.; Ni, T. Peridynamic formulations enriched with bond rotation effects. Int. J. Eng. Sci. 2017, 121, 118–129. [Google Scholar] [CrossRef]
- Chu, B.F.; Liu, Q.W.; Liu, L.S.; Lai, X.; Mei, H. A rate-dependent Peridynamic model for the dynamic behavior of ceramic materials. CMES-Comp. Model. Eng. Sci. 2020, 124, 151–178. [Google Scholar] [CrossRef]
- Liu, Y.X.; Liu, L.S.; Mei, H.; Liu, Q.W.; Lai, X. A modified rate-dependent Peridynamic model with rotation effect for dynamic mechanical behavior of ceramic materials. Comput. Meth. Appl. Mech. Eng. 2022, 388, 114246. [Google Scholar] [CrossRef]
- Kudryavtsev, O.A.; Sapozhnikov, S.B. Numerical simulations of ceramic target subjected to ballistic impact using combined DEM/FEM approach. Int. J. Mech. Sci. 2016, 114, 60–70. [Google Scholar] [CrossRef]
- Zhang, Y.; Qiao, P.Z. A new bond failure criterion for ordinary state-based Peridynamic mode II fracture analysis. Int. J. Fract. 2019, 215, 105–128. [Google Scholar] [CrossRef]
- Foster, J.T.; Silling, S.A.; Chen, W.W. Viscoplasticity using Peridynamics. Int. J. Numer. Methods Eng. 2010, 81, 1242–1258. [Google Scholar] [CrossRef]
- O’Grady, J.; Foster, J. Peridynamic beams: A non-ordinary, state-based model. Int. J. Solids Struct. 2014, 51, 3177–3183. [Google Scholar] [CrossRef]
- Lai, X.; Ren, B.; Fan, H.F.; Li, S.F.; Wu, C.T.; Regueiro, R.A.; Liu, L.S. Peridynamics simulations of geomaterial fragmentation by impulse loads. Int. J. Numer. Anal. Methods Geomech. 2015, 39, 1304–1330. [Google Scholar] [CrossRef]
- Lai, X.; Liu, L.S.; Li, S.F.; Zeleke, M.; Liu, Q.W.; Wang, Z. A non-ordinary state-based Peridynamics modeling of fractures in quasi-brittle materials. Int. J. Impact Eng. 2018, 111, 130–146. [Google Scholar] [CrossRef]
- Wu, L.W.; Huang, D.; Xu, Y.P.; Wang, L. A non-ordinary state-based Peridynamic formulation for failure of concrete subjected to impacting loads. ES-Comp. Model. Eng. Sci. 2019, 118, 561–581. [Google Scholar] [CrossRef]
- Wang, H.; Xu, Y.P.; Huang, D. A non-ordinary state-based Peridynamic formulation for thermo-visco-plastic deformation and impact fracture. Int. J. Mech. Sci. 2019, 159, 336–344. [Google Scholar] [CrossRef]
- Zhu, F.; Zhao, J.D. Peridynamic modelling of blasting induced rock fractures. J. Mech. Phys. Solids. 2021, 153, 104469. [Google Scholar] [CrossRef]
- Yang, S.Y.; Gu, X.; Zhang, Q.; Xia, X.Z. Bond-associated non-ordinary state-based Peridynamic model for multiple spalling simulation of concrete. Acta Mech. Sin. 2021, 37, 1104–1135. [Google Scholar] [CrossRef]
- Li, S.; Lai, X.; Liu, L.S. Peridynamic Modeling of Brittle Fracture in Mindlin-Reissner Shell Theory. CMES-Comp. Model. Eng. Sci. 2022, 131, 715–746. [Google Scholar] [CrossRef]
- Littlewood, D.J. A Nonlocal Approach to Modeling Crack Nucleation in AA 7075-T651. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Sandia National Laboratory, Albuquerque, NM, USA, 10–18 November 2011. [Google Scholar]
- Silling, S.A. Stability of Peridynamic correspondence material models and their particle discretizations. Comput. Meth. Appl. Mech. Eng. 2017, 322, 42–57. [Google Scholar] [CrossRef]
- Li, P.; Hao, Z.M.; Zhen, W.Q. A stabilized non-ordinary state-based Peridynamic model. Comput. Meth. Appl. Mech. Eng. 2018, 339, 262–280. [Google Scholar] [CrossRef]
- Wan, J.; Chen, Z.; Chu, X.H.; Liu, H. Improved method for zero-energy mode suppression in Peridynamic correspondence model. Acta Mech. Sin. 2019, 35, 1021–1032. [Google Scholar] [CrossRef]
- Yaghoobi, A.; Chorzepa, M.G. Higher-order approximation to suppress the zero-energy mode in non-ordinary state-based Peridynamics. Comput. Struct. 2017, 188, 63–79. [Google Scholar] [CrossRef]
- Luo, J.; Sundararaghavan, V. Stress-point method for stabilizing zero-energy modes in non-ordinary state-based Peridynamics. Int. J. Solids Struct. 2018, 150, 197–207. [Google Scholar] [CrossRef]
- Cui, H.; Li, C.G.; Zheng, H. A higher-order stress point method for non-ordinary state-based Peridynamics. Eng. Anal. Bound. Elem. 2020, 117, 104–118. [Google Scholar] [CrossRef]
- Chen, H.L. Bond-associated deformation gradients for peridynamic correspondence model. Mech. Res. Commun. 2018, 90, 34–41. [Google Scholar] [CrossRef]
- Chen, H.L.; Spencer, B.W. Peridynamic bond-associated correspondence model: Stability and convergence properties. Int. J. Numer. Methods Eng. 2019, 117, 713–727. [Google Scholar] [CrossRef]
- Gu, X.; Zhang, Q.; Madenci, E.; Xia, X.Z. Possible causes of numerical oscillations in non-ordinary state-based Peridynamics and a bond-associated higher-order stabilized model. Comput. Meth. Appl. Mech. Eng. 2019, 357, 112592. [Google Scholar] [CrossRef]
- Li, P.; Hao, Z.M.; Yu, S.R.; Zhen, W.Q. Implicit implementation of the stabilized non-ordinary state-based Peridynamic model. Int. J. Numer. Methods Eng. 2020, 121, 571–587. [Google Scholar] [CrossRef]
- May, S.; Vignollet, J.; De Borst, R. A numerical assessment of phase-field models for brittle and cohesive fracture: Γ-convergence and stress oscillations. Eur. J. Mech. A-Solids 2015, 52, 72–84. [Google Scholar] [CrossRef]
- Wu, J.Y. A unified phase-field theory for the mechanics of damage and quasi-brittle failure. J. Mech. Phys. Solids 2017, 103, 72–99. [Google Scholar] [CrossRef]
- Narayan, S.; Anand, L. A gradient-damage theory for fracture of quasi-brittle materials. J. Mech. Phys. Solids 2019, 129, 119–146. [Google Scholar] [CrossRef]
- Costin, L.S. A microcrack model for the deformation and failure of brittle rock. J. Geophys. Res. 1983, 88, 9485–9492. [Google Scholar] [CrossRef]
- Addessio, F.L.; Johnson, J.N. A constitutive model for the dynamic response of brittle materials. J. Appl. Phys. 1990, 67, 3275–3286. [Google Scholar] [CrossRef]
- Rajendran, A.M.; Grove, D.J. Modeling the shock response of silicon carbide, boron carbide and titanium diboride. Int. J. Impact Eng. 1996, 18, 611–631. [Google Scholar] [CrossRef]
- Zuo, Q.H.; Addessio, F.L.; Dienes, J.K.; Lewis, M.W. A rate-dependent damage model for brittle materials based on the dominant crack. Int. J. Solids Struct. 2006, 43, 3350–3380. [Google Scholar] [CrossRef]
- Zuo, Q.H.; Disilvestro, D.; Richter, J.D. A crack-mechanics based model for damage and plasticity of brittle materials under dynamic loading. Int. J. Solids Struct. 2010, 47, 2790–2798. [Google Scholar] [CrossRef]
- Johnson, G.R.; Holmquist, T.J. A Computational Constitutive Model for Brittle Materials Subjected to Large Strains, High Strain Rates and High Pressures. Shock Wave and High-Strain-Rate Phenomena in Materials; Marcel Dekker Inc.: New York, NY, USA, 1992; pp. 1075–1081. [Google Scholar]
- Johnson, G.R.; Holmquist, T.J. An Improved Computational Constitutive Model for Brittle Materials. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 1994. [Google Scholar]
- Johnson, G.R.; Cook, W.H. A Constitutive Model and Data for Materials Subjected to Large Strains, High Strain Rates, and High Temperatures. In Proceedings of the Seventh International Symposium on Ballistics, The Hague, The Netherlands, 19–21 April 1983. [Google Scholar]
- Johnson, G.R.; Holmquist, T.J.; Beissel, S.R. Response of aluminum nitride (including a phase change) to large strains, high strain rates, and high pressures. J. Appl. Phys. 2003, 94, 1639–1646. [Google Scholar] [CrossRef]
- Rubinstein, R.; Atluri, S.N. Objectivity of incremental constitutive relations over finite time steps in computational finite deformation analyses. Comput. Meth. Appl. Mech. Eng. 1983, 36, 277–290. [Google Scholar] [CrossRef]
- Monaghan, J.J.; Gingold, R.A. Shock simulation by the particle method SPH. J. Comput. Phys. 1983, 52, 374–389. [Google Scholar] [CrossRef]
- Li, S. Smoothed particle hydrodynamics-a meshfree method, by G.R. Liu and M.B. Liu. Comput. Mech. 2004, 33, 491. [Google Scholar] [CrossRef]
- Belytschko, T.; Lin, J.I. A three-dimensional impact-penetration algorithm with erosion. Int. J. Impact Eng. 1987, 5, 111–127. [Google Scholar] [CrossRef]
- Heinstein, M.W.; Attaway, S.W.; Swegle, J.W.; Mello, F.J. A General-Purpose Contact Detection Algorithm for Nonlinear Structural Analysis Codes; Sandia National Labs: Albuquerque, NM, USA, 1993.
- Whirley, R.G.; Engelmann, B.E. Automatic contact algorithm in DYNA3D for crashworthiness and impact problems. Nucl. Eng. Des. 1994, 150, 225–233. [Google Scholar] [CrossRef]
- Bourago, N.G.; Kukudzhanov, V.N. A review of contact algorithms. Mech. Solids 2005, 40, 35–71. [Google Scholar]
- Cronin, D.S.; Bui, K.; Kaufmann, C.; McIntosh, G.; Berstad, T.; Cronin, D. Implementation and Validation of the Johnson-Holmquist Ceramic Material Model in LS-Dyna. In Proceedings of the 4th European LS-DYNA User’s Conference, Ulm, Germany, 22–23 May 2003. [Google Scholar]
- Strassburger, E. Visualization of impact damage in ceramics using the edge-on impact technique. Int. J. Appl. Ceram. Technol. 2004, 1, 235–242. [Google Scholar] [CrossRef]
- Simons, E.C.; Weerheijm, J.; Toussaint, G.; Sluys, L.J. An experimental and numerical investigation of sphere impact on alumina ceramic. Int. J. Impact Eng. 2020, 145, 103670. [Google Scholar] [CrossRef]

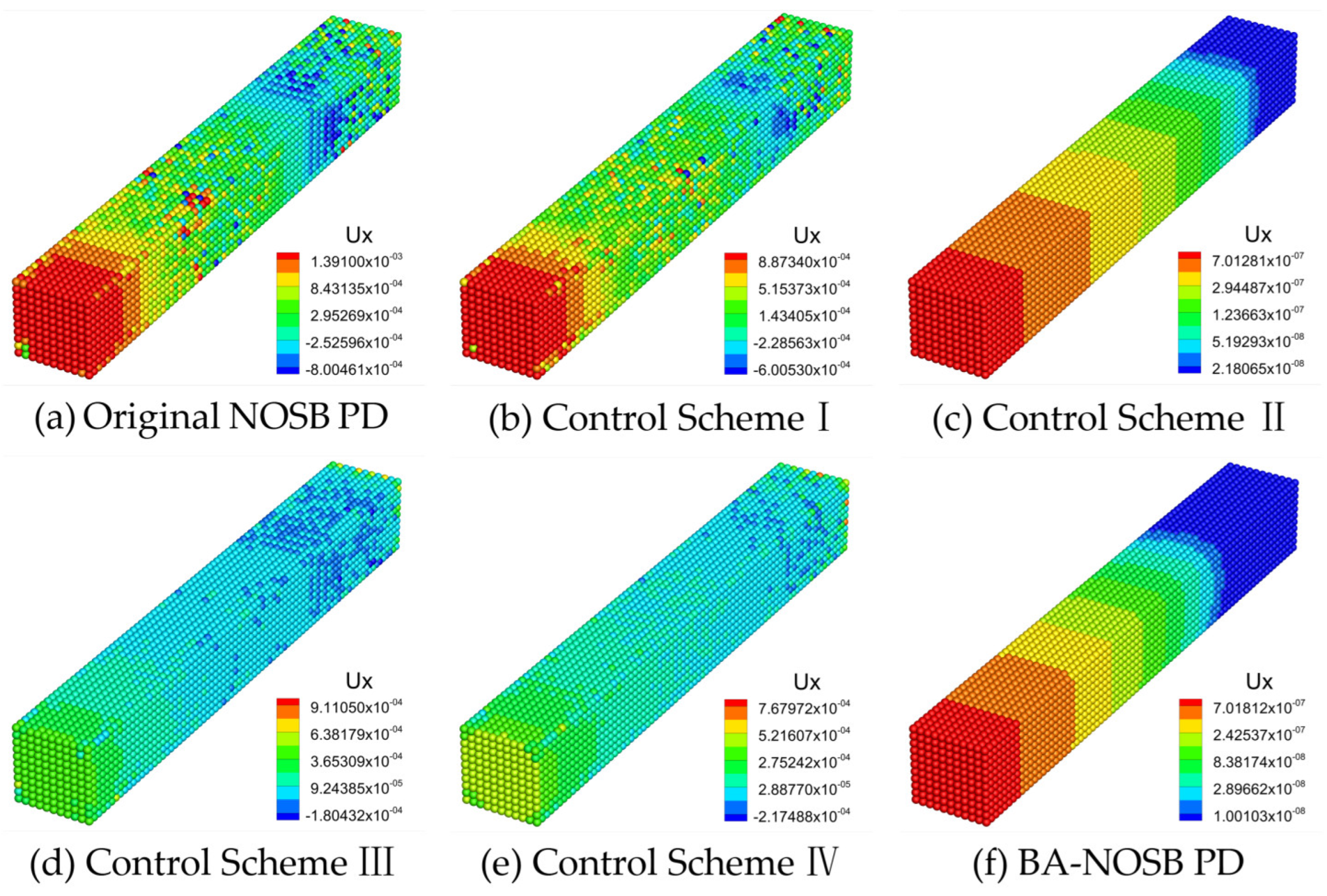
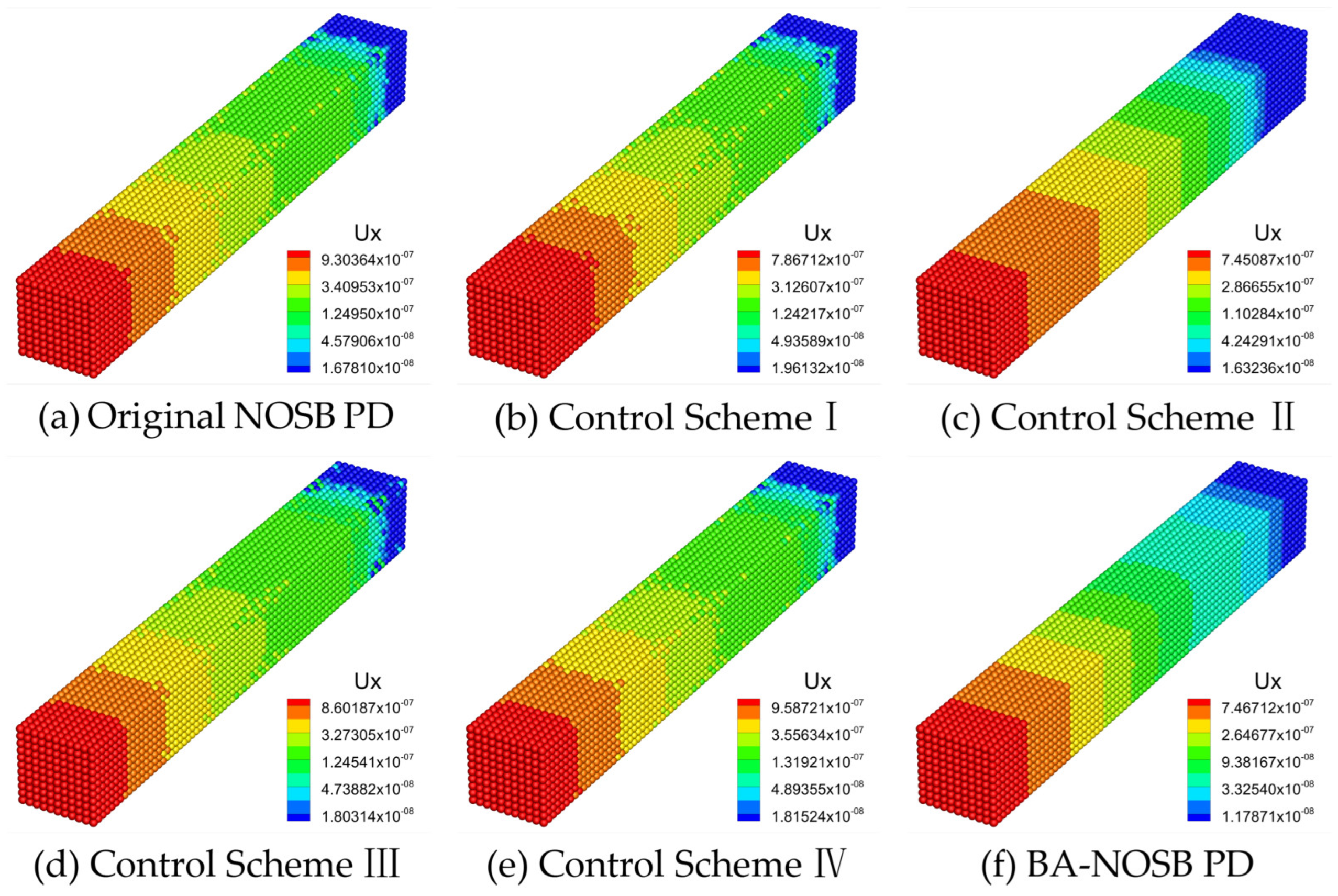
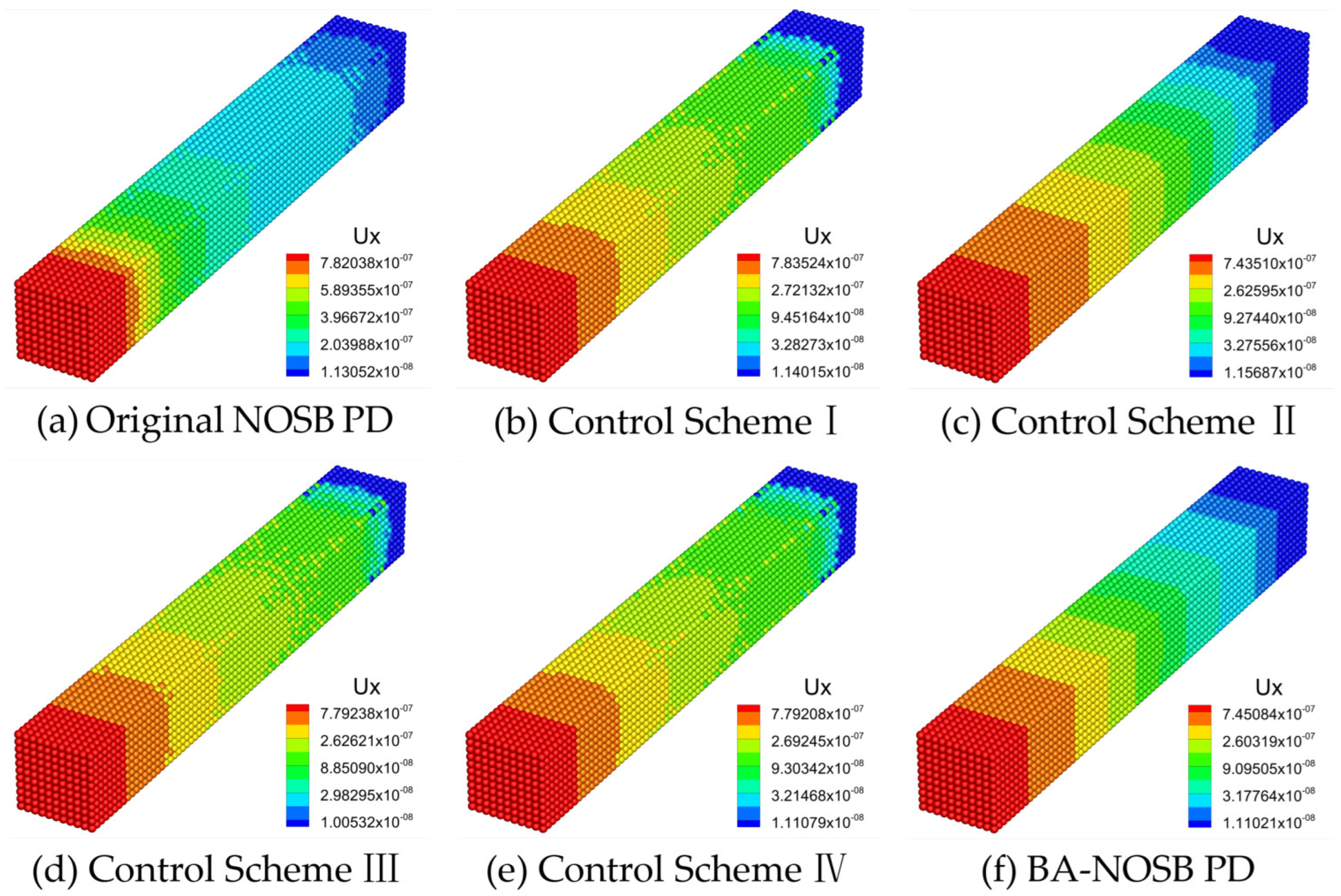
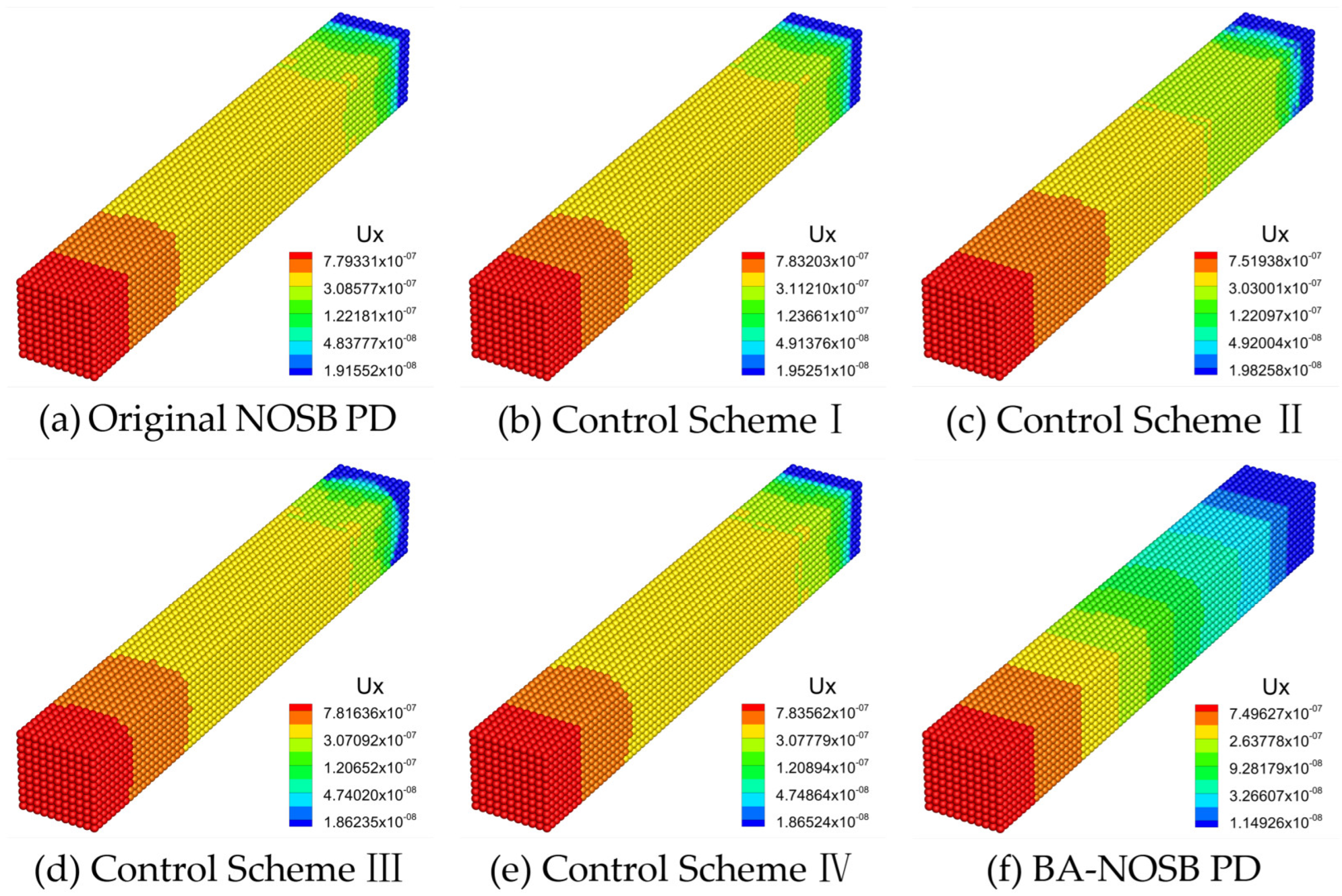



| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Density (kg/m3) | 3700 | T (GPa) | 0.2 |
| Shear modulus G (GPa) | 90.16 | (GPa) | 1.46 |
| Poisson’s ratio | 0.22 | (GPa) | 2.0 |
| A | 0.93 | 0.005 | |
| B | 0.31 | 1.0 | |
| C | 0.0 | (GPa) | 130.95 |
| M | 0.6 | (GPa) | 0.0 |
| N | 0.6 | (GPa) | 0.0 |
| 1.0 | 1.0 |
| Solution A | Solution B | Solution C |
|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Liu, Y.; Lai, X.; Liu, L.; Mei, H.; Liu, X. A Modified Bond-Associated Non-Ordinary State-Based Peridynamic Model for Impact Problems of Quasi-Brittle Materials. Materials 2023, 16, 4050. https://doi.org/10.3390/ma16114050
Zhang J, Liu Y, Lai X, Liu L, Mei H, Liu X. A Modified Bond-Associated Non-Ordinary State-Based Peridynamic Model for Impact Problems of Quasi-Brittle Materials. Materials. 2023; 16(11):4050. https://doi.org/10.3390/ma16114050
Chicago/Turabian StyleZhang, Jing, Yaxun Liu, Xin Lai, Lisheng Liu, Hai Mei, and Xiang Liu. 2023. "A Modified Bond-Associated Non-Ordinary State-Based Peridynamic Model for Impact Problems of Quasi-Brittle Materials" Materials 16, no. 11: 4050. https://doi.org/10.3390/ma16114050





