Out-of-Plane Flexural Behavior of Insulated Wall Panels Constructed with Large Insulation Thicknesses
Abstract
1. Introduction
- The impact of increasing insulation thickness on the double shear test performance of the tie, global flexural behavior of ICSWPs, and local behavior at the vicinity of connectors.
- Comparison of the results of this research to results in the literature and analytical methods for computing tie performance alone and global flexural behavior of large-scale specimens.
- Evaluation of the impact of increasing the insulation thickness on the “percent composite action” of large-scale specimens to assess whether the connector implemented in the study can effectively maintain significant composite action for the panels.
2. Materials and Methods
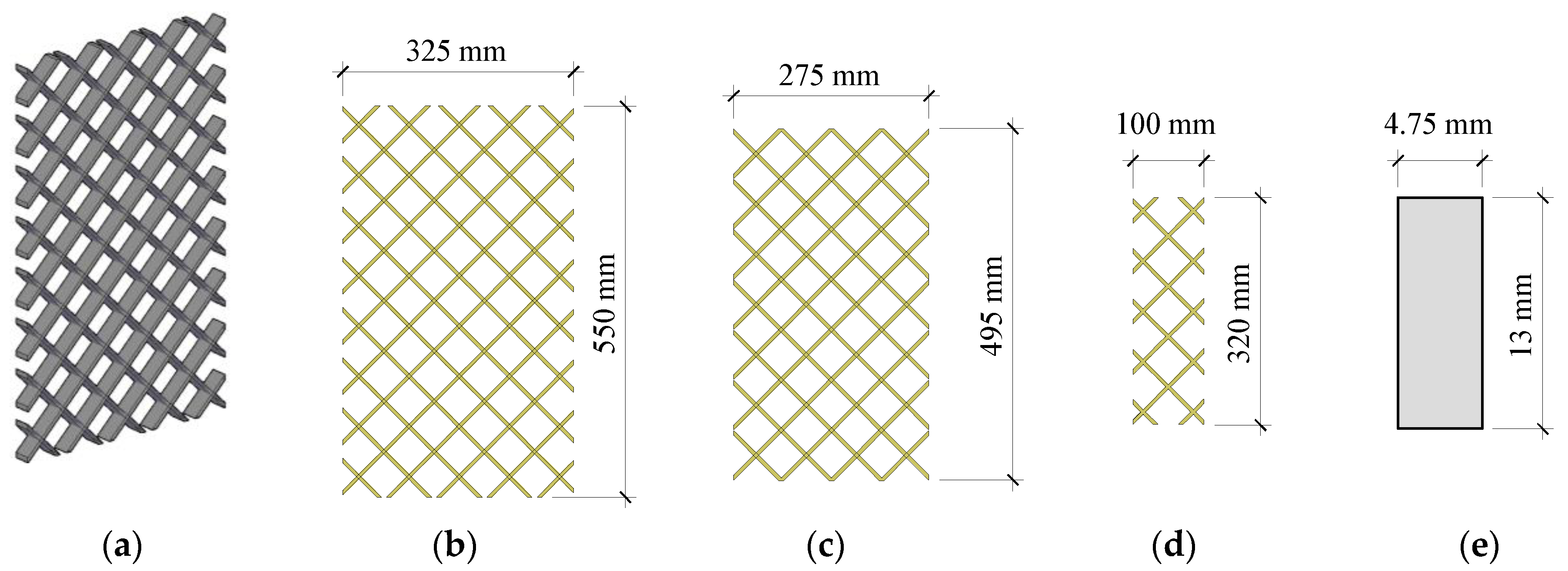
2.1. Double Shear Test: Materials, Specimens, Setup, and Instrumentation
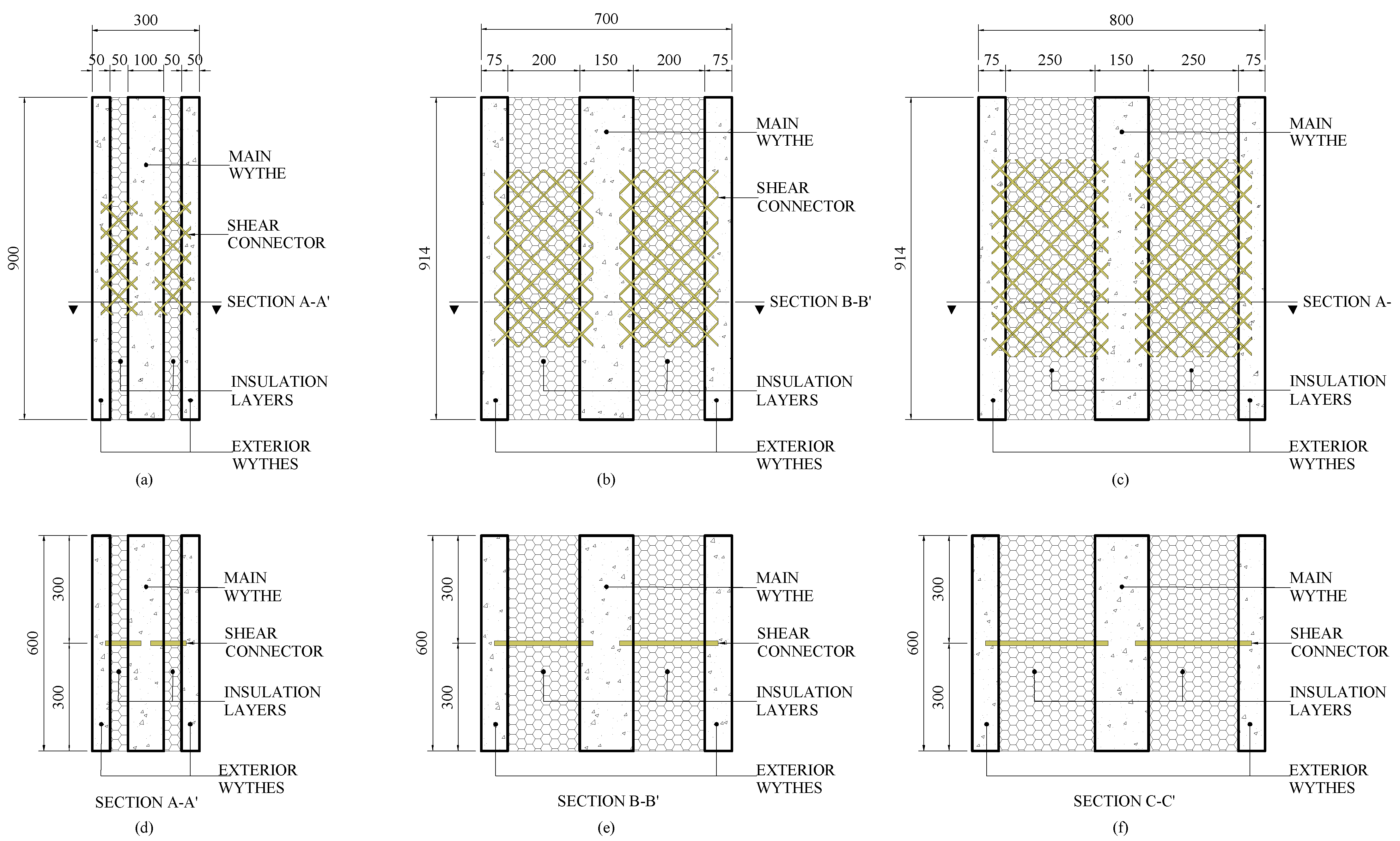
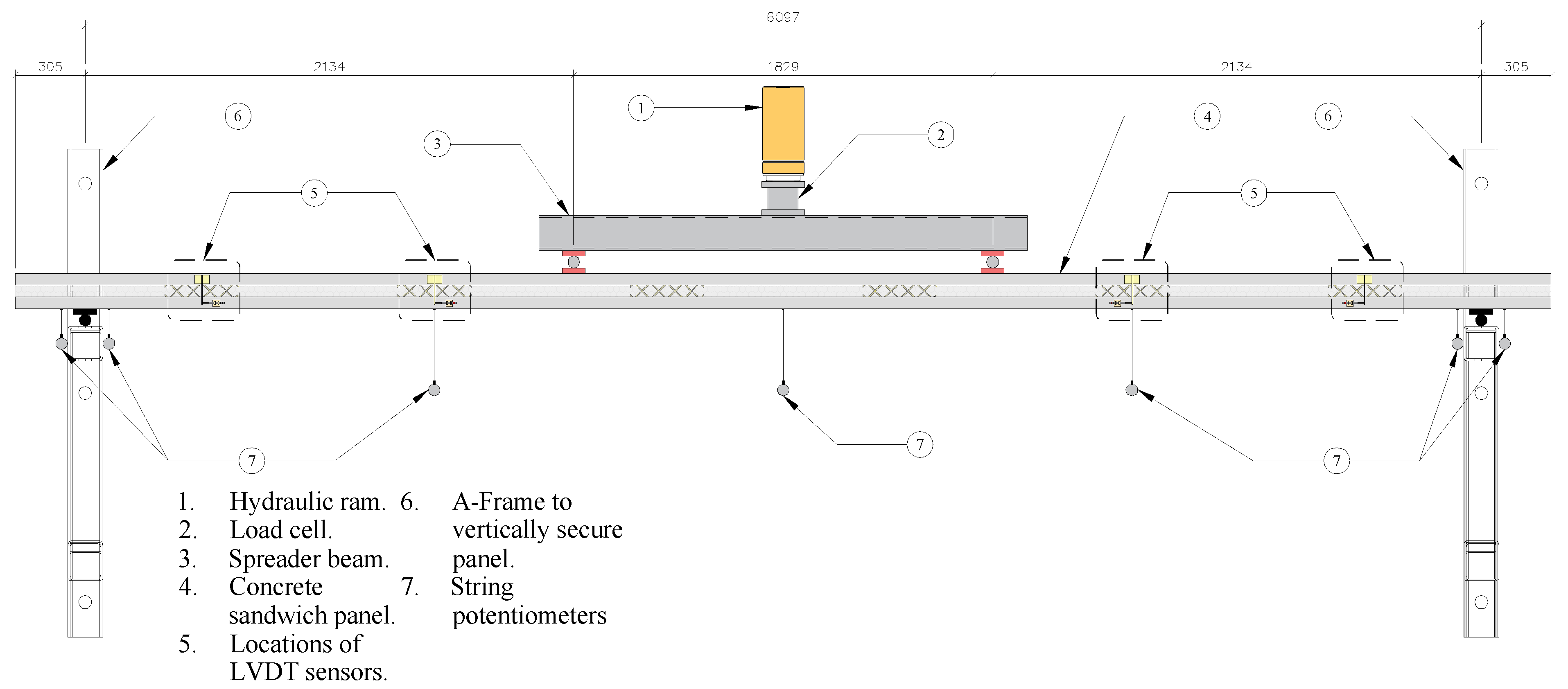
2.2. Large-Scale Test: Materials, Specimens, Setup, and Instrumentation
3. Results
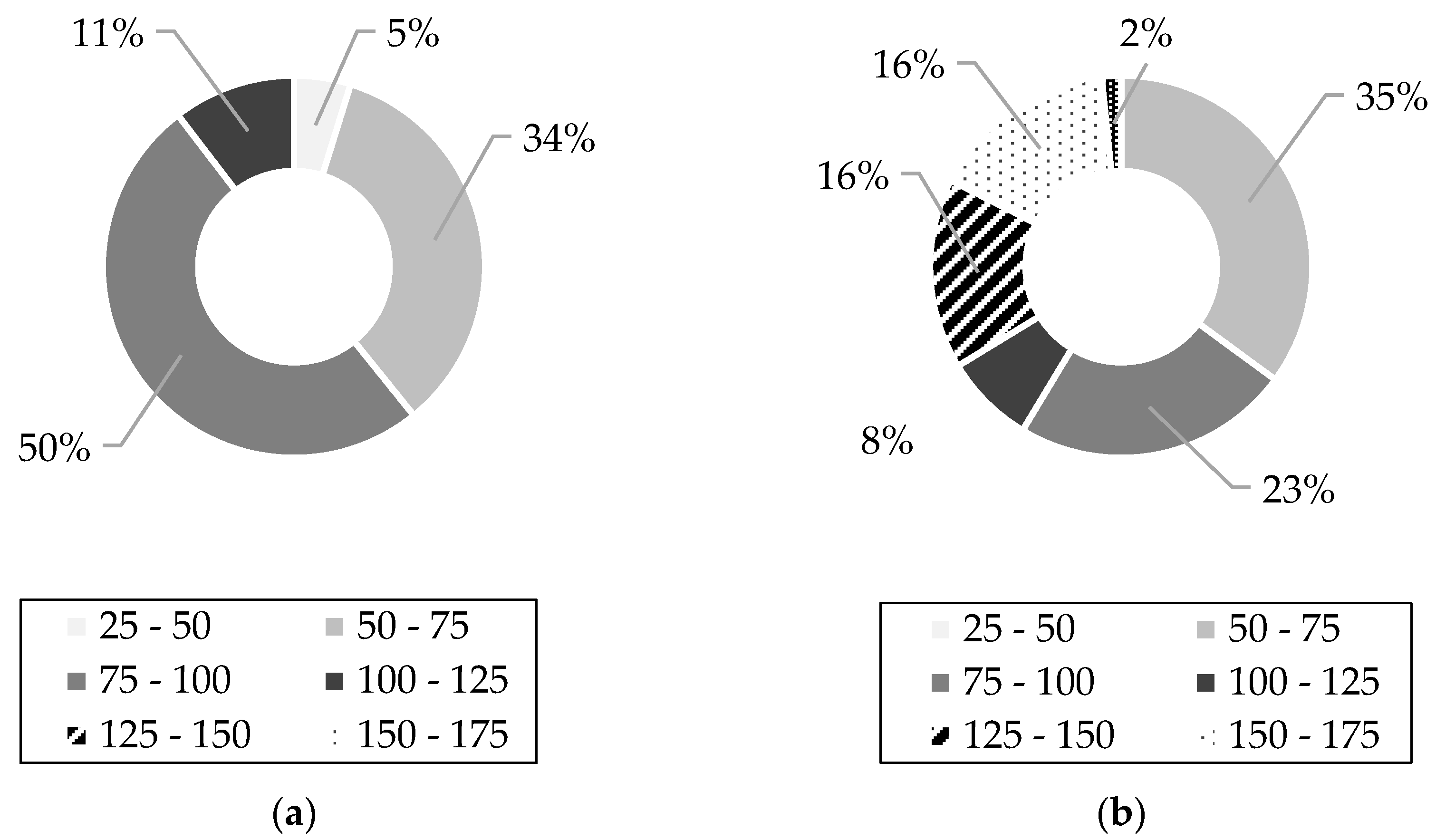
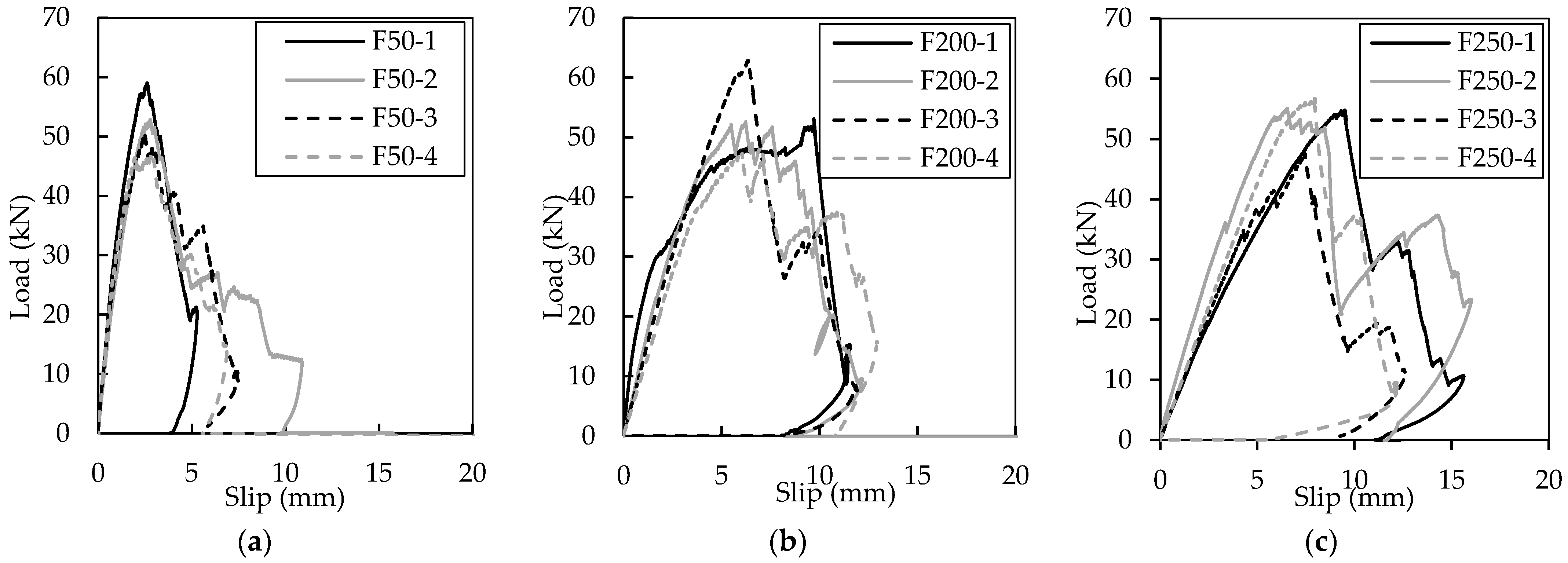
3.1. Double Shear Test Results
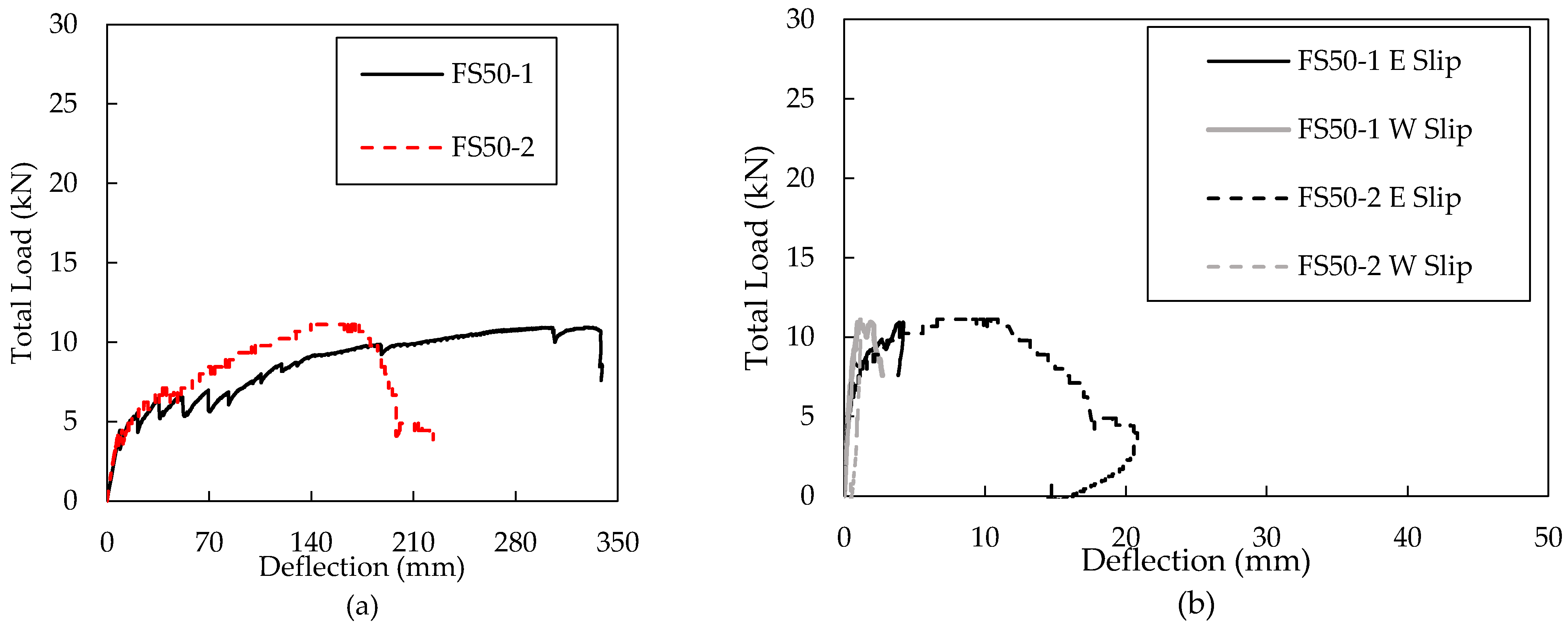
3.2. Large-Scale Test Results
4. Discussion
4.1. Composite Action and Large-Scale Performance
- IExp = Experimental moment of inertia determined from the deflection.
- INC = Non-composite moment of inertia determined as a sum of the moment of inertia of the individual wythes.
- IFC = Fully composite moment of inertia of the composite shape (neglects the foam contribution).
- MExp = Experimental flexural moment.
- MNC = Non-composite flexural moment determined as the sum of moment capacities of the wythes.
- MFC = Fully composite flexural moment.
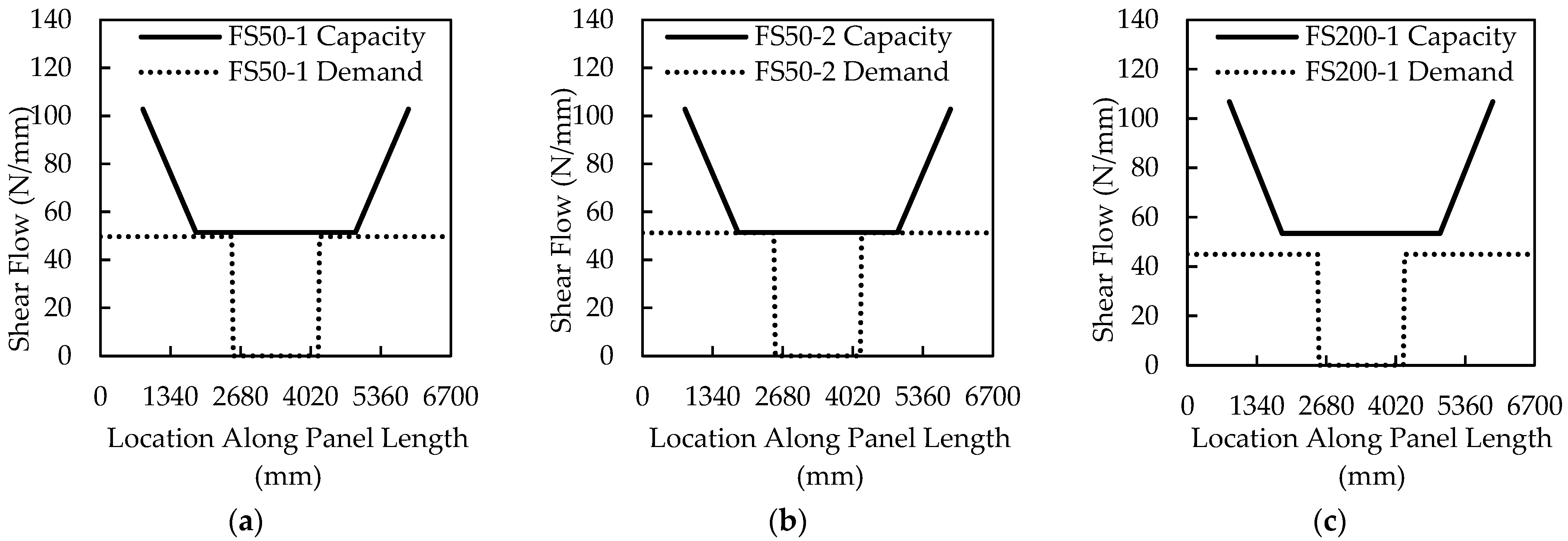
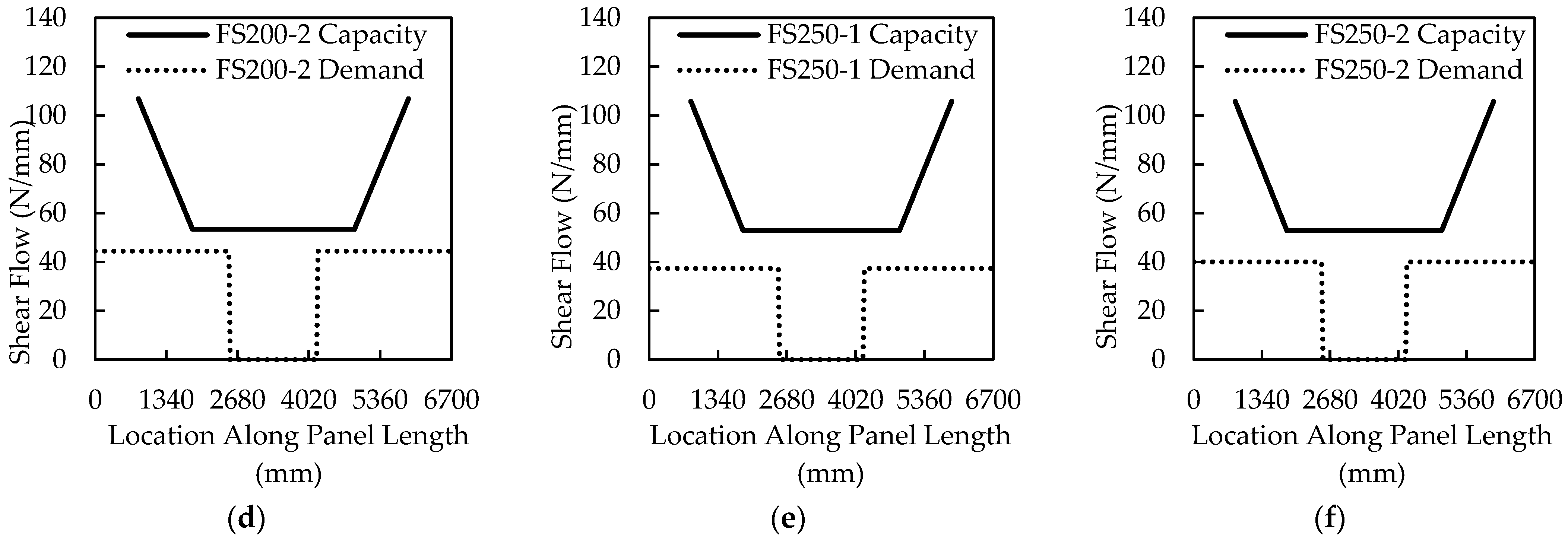
4.2. Horizontal Shear Strength Prediction of Large-Scale Specimens Using the Shear Flow Approach
5. Conclusions
- All three methods used to predict the elastic behavior of the large-scale panels were accurate in their predictions, with their average percentage differences from the measured stiffnesses within 3% for all methods.
- All three methods used to predict the cracking moment of the large-scale panels were accurate in their predictions, with their average percentage differences from the measured cracking moments within 6% for all methods.
- Based on the above bullets, the elastic methods investigated herein are suitable for the prediction of elastic deflections and cracking moments for panels with extreme dimensions in the experimental program.
- The shear flow approach did not accurately predict the ultimate capacity of the thick insulation large-scale panels, significantly overpredicting the shear capacity of the connectors with an average measured ratio of 0.82 with a COV of 0.11.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sorensen, T.J. Reducing Thermal Bridging and Understanding Second-Order Effects in Concrete Sandwich Wall Panels. Ph.D. Thesis, Utah State University, Logan, UT, USA, 2019. [Google Scholar]
- Sorensen, T.; Dorafshan, S.; Maguire, M. Thermal Evaluation of Common Locations of Heat Loss in Sandwich Wall Panels. In Proceedings of the Congress on Technical Advancement 2017, Duluth, MN, USA, 10–13 September 2017. [Google Scholar]
- Maguire, M.; Pozo-Lora, F.F. Partially Composite Concrete Sandwich Wall Panels. Concr. Int. 2020, 42, 47–52. [Google Scholar]
- Holmberg, A.; Plem, E. Behaviour of Load-Bearing Sandwich-Type Structures; Byggforskningen: Stockholm, Sweden, 1965. [Google Scholar]
- Allen, H.G. Analysis and Design of Structural Sandwich Panels; Pergamon Press: London, UK, 1969. [Google Scholar]
- Bai, F.; Davidson, J.S. Theory for Composite Sandwich Structures with Unsymmetrical Wythes and Transverse Interaction. Eng. Struct. 2016, 116, 178–191. [Google Scholar] [CrossRef]
- Olsen, J.; Al-Rubaye, S.; Sorensen, T.; Maguire, M. Developing a General Methodology for Evaluating Composite Action in Insulated Wall Panels; Precast/Prestressed Concrete Institute: Chicago, IL, USA, 2017. [Google Scholar]
- Gombeda, M.J.; Trasborg, P.; Naito, C.J.; Quiel, S.E. Simplified Model for Partially-Composite Precast Concrete Insulated Wall Panels Subjected to Lateral Loading. Eng. Struct. 2017, 138, 367–380. [Google Scholar] [CrossRef]
- Jensen, K.; Al-Rubaye, S.; Thomas, R.J.; Maguire, M. Mechanics-Based Model for Elastic Bending, Axial, Thermal Deformations, and Asymmetry of Concrete Composite Sandwich Wall Panels. Structures 2020, 23, 459–471. [Google Scholar] [CrossRef]
- Pozo-Lora, F.F.; Maguire, M. Flexural Behavior of Continuous Non-Loadbearing Insulated Wall Panels. In Proceedings of the 2019 PCI/NBC; PCI: Chicago, IL, USA, 2019; p. 15. [Google Scholar]
- Bai, F.; Davidson, J.S. Analysis of Partially Composite Foam Insulated Concrete Sandwich Structures. Eng. Struct. 2015, 91, 197–209. [Google Scholar] [CrossRef]
- Al-Rubaye, S.; Sorensen, T.; Maguire, M. Iterative and Simplified Sandwich Beam Theory for Partially Composite Concrete Sandwich Wall Panels. J. Struct. Eng. 2021, 147, 4021143. [Google Scholar] [CrossRef]
- Bunn, W. CFRP Grid/Rigid Foam Shear Transfer Mechanism for Precast, Prestressed Concrete Sandwich Wall Panels; North Carolina State University: Raleigh, NC, USA, 2011. [Google Scholar]
- Al-Rubaye, S.A. Experimental and Simplified Analytical Investigation of Full-Scale Sandwich Panel Walls. Ph.D. Thesis, Utah State University, Logan, UT, USA, 2017. [Google Scholar]
- Al-Rubaye, S.; Sorensen, T.; Thomas, R.J.; Maguire, M. Generalized Beam–Spring Model for Predicting Elastic Behavior of Partially Composite Concrete Sandwich Wall Panels. Eng. Struct. 2019, 198, 109533. [Google Scholar] [CrossRef]
- Tomlinson, D. Behaviour of Partially Composite Precast Concrete Sandwich Panels under Flexural and Axial Loads. Ph.D. Thesis, Queen’s University, Kingston, ON, Canada, 2015. [Google Scholar]
- Collins, T.F. Precast Concrete Sandwich Panels for Tilt-Up Construction. J. Am. Concr. Inst. 1954, 50, 149–164. [Google Scholar] [CrossRef]
- Sorensen, T.J.; Dorafshan, S.; Thomas, R.J.; Maguire, M. Thermal Bridging in Concrete Sandwich Walls. Concr. Int. 2018, 40, 45–49. [Google Scholar]
- Balik, J.; Barney, G. Thermal Design of Precast Concrete Buildings. PCI J. 1985, 29, 48–98. [Google Scholar] [CrossRef]
- McCall, W.C. Thermal Properties of Sandwich Panels. Concr. Int. 1985, 7, 35–41. [Google Scholar]
- Lee, B.-J.; Pessiki, S. Analytical Investigation of Thermal Performance of Precast Concrete Three-Wythe Sandwich Wall Panels. PCI J. 2004, 49, 88–101. [Google Scholar] [CrossRef]
- Cox, B.; Syndergaard, P.; Al-Rubaye, S.; Pozo-Lora, F.F.; Tawadrous, R.; Maguire, M. Lumped GFRP Star Connector System for Partial Composite Action in Insulated Precast Concrete Sandwich Panels. Compos. Struct. 2019, 229, 111465. [Google Scholar] [CrossRef]
- Einea, A.; Salmon, D.C.; Tadros, M.K.; Culp, T. A New Structurally and Thermally Efficient Precast Sandwich Panel System. PCI J. 1994, 39, 90–101. [Google Scholar] [CrossRef]
- Salmon, D.C.; Einea, A.; Tadros, M.K.; Culp, T.D. Full-Scale Testing of Precast Concrete Sandwich Panels. Struct. J. 1997, 94, 354–362. [Google Scholar] [CrossRef]
- Maximos, H.N.; Pong, W.A.; Tadros, M.K.; Martin, L.D. Behavior and Design of Composite Precast Prestressed Concrete Sandwich Panels with NU-Tie; University of Nebraska: Lincoln, NE, USA, 2007. [Google Scholar]
- Losch, E.D.; Hynes, P.W.; Andrews, R., Jr.; Browning, R.; Cardone, P.; Devalapura, R.; Donahey, R.; Freedman, S.; Gleich, H.A.; Goettsche, G. State of the Art of Precast/Prestressed Concrete Sandwich Wall Panels. PCI J. 2011, 56, 131–176. [Google Scholar]
- Woltman, G.; Tomlinson, D.; Fam, A. Investigation of Various GFRP Shear Connectors for Insulated Precast Concrete Sandwich Wall Panels. J. Compos. Constr. 2013, 17, 711–721. [Google Scholar] [CrossRef]
- Gombeda, M.J.; Naito, C.J.; Quiel, S.E. Development and Performance of a Ductile Shear Tie for Precast Concrete Insulated Wall Panels. J. Build. Eng. 2020, 28, 101084. [Google Scholar] [CrossRef]
- He, Z.; Pan, P.; Ren, J.; Wang, H. Experimental and Numerical Investigation of Novel I-Shaped GFRP Connectors for Insulated Precast Concrete Sandwich Wall Panels. J. Compos. Constr. 2020, 24, 04020040. [Google Scholar] [CrossRef]
- Frankl, B.A.; Lucier, G.W.; Hassan, T.K.; Rizkalla, S.H. Behavior of Precast, Prestressed Concrete Sandwich Wall Panels Reinforced with CFRP Shear Grid. PCI J. 2011, 56, 42–54. [Google Scholar] [CrossRef]
- Pozo-Lora, F.; Maguire, M. Thermal Bowing of Concrete Sandwich Panels with Flexible Shear Connectors. J. Build. Eng. 2020, 29, 101124. [Google Scholar] [CrossRef]
- Arevalo, S.; Tomlinson, D. Experimental Thermal Bowing Response of Precast Concrete Insulated Wall Panels with Stiff Shear Connectors and Simple Supports. J. Build. Eng. 2020, 30, 101319. [Google Scholar] [CrossRef]
- Naito, C.; Hoemann, J.; Beacraft, M.; Bewick, B. Performance and Characterization of Shear Ties for Use in Insulated Precast Concrete Sandwich Wall Panels. J. Struct. Eng. 2012, 138, 52–61. [Google Scholar] [CrossRef]
- Choi, I.; Kim, J.; Kim, H.-R. Composite Behavior of Insulated Concrete Sandwich Wall Panels Subjected to Wind Pressure and Suction. Materials 2015, 8, 1264–1282. [Google Scholar] [CrossRef]
- Hodicky, K.; Sopal, G.; Rizkalla, S.; Hulin, T.; Stang, H. Experimental and Numerical Investigation of the FRP Shear Mechanism for Concrete Sandwich Panels. J. Compos. Constr. 2014, 19, 4014083. [Google Scholar] [CrossRef]
- Naito, C.J.; Hoemann, J.M.; Shull, J.S.; Saucier, A.; Salim, H.A.; Bewick, B.T.; Hammons, M.I. Precast/Prestressed Concrete Experiments Performance on Non-Load Bearing Sandwich Wall Panels; Black and Veatch: Overland Park, KS, USA, 2011. [Google Scholar]
- Trasborg, P.A. Analytical and Experimental Evaluation of Precast Sandwich Wall Panels Subjected to Blast, Breach, and Ballistic Demands; Lehigh University: Bethlehem, PA, USA, 2014. [Google Scholar]
- Pessiki, S.; Mlynarczyk, A. Experimental Evaluation of the Composite Behavior of Precast Concrete Sandwich Wall Panels. PCI J. 2003, 48, 54–71. [Google Scholar] [CrossRef]
- Benayoune, A.; Samad, A.A.A.; Trikha, D.N.; Ali, A.A.A.; Ellinna, S.H.M. Flexural Behaviour of Pre-Cast Concrete Sandwich Composite Panel—Experimental and Theoretical Investigations. Constr. Build. Mater. 2008, 22, 580–592. [Google Scholar] [CrossRef]
- Fernando, P.L.N.; Jayasinghe, M.T.R.; Jayasinghe, C. Structural Feasibility of Expanded Polystyrene (EPS) Based Lightweight Concrete Sandwich Wall Panels. Constr. Build. Mater. 2017, 139, 45–51. [Google Scholar] [CrossRef]
- Pantelides, C.P.; Surapaneni, R.; Reaveley, L.D. Structural Performance of Hybrid GFRP/Steel Concrete Sandwich Panels. J. Compos. Constr. 2008, 12, 570–576. [Google Scholar] [CrossRef]
- Choi, W.; Jang, S.-J.; Yun, H.-D. Design Properties of Insulated Precast Concrete Sandwich Panels with Composite Shear Connectors. Compos. B Eng. 2019, 157, 36–42. [Google Scholar] [CrossRef]
- Choi, I.; Kim, J.; You, Y.-C. Effect of Cyclic Loading on Composite Behavior of Insulated Concrete Sandwich Wall Panels with GFRP Shear Connectors. Compos. B Eng. 2016, 96, 7–19. [Google Scholar] [CrossRef]
- Pozo-Lora, F.F.; Maguire, M. Determination of the Mechanical Properties of Flexible Connectors for Use in Insulated Concrete Wall Panels. JoVE 2022, 188, e64292. [Google Scholar] [CrossRef]
- Newmark, N.M. Test and Analysis of Composite Beams with Incomplete Interaction. Proc. Soc. Exp. Stress Anal. 1951, 9, 75–92. [Google Scholar]
- Al-Rubaye, S.; Sorensen, T.; Olsen, J.; Maguire, M. Evaluating Elastic Behavior for Partially Composite Precast Concrete Sandwich Wall Panels. PCI J. 2018, 63, 71–88. [Google Scholar] [CrossRef]
- Maguire, M.; Al-Rubaye, S. Tilt-Up Partially Composite Insulated Wall Panels; University of Nebraska-Lincoln: Lincoln, NE, USA, 2022. [Google Scholar]
- Nowak, A.S.; Collins, K.R. Reliability of Structures; CRC Press: Boca Raton, FL, USA, 2012; ISBN 0415675758. [Google Scholar]
- ACI Committee 318. ACI 318-19 Building Code Requirements for Structural Concrete (ACI 318-19) and Commentary (ACI 318R-19); ACI: Singapore, 2019; ISBN 9781641950565. [Google Scholar]






| Insulation Thickness tins (mm) | Rwinter | Rsummer | ||
|---|---|---|---|---|
| (m2∙K/W) | (ft2∙°F∙h/Btu) | (m2∙K/W) | (ft2∙°F∙h/Btu) | |
| Solid Panel | 0.23 | 1.30 | 0.24 | 1.38 |
| 50 | 2.19 | 12.41 | 2.20 | 12.49 |
| 100 | 4.14 | 23.52 | 4.16 | 23.60 |
| 150 | 6.10 | 34.63 | 6.11 | 34.71 |
| 200 | 8.06 | 45.74 | 8.07 | 45.82 |
| 250 | 10.01 | 56.86 | 10.03 | 56.94 |
| Panel Designation | Wythe Thicknesses (mm) | Insulation Thickness (mm) | Length (mm) | Width (mm) | Longitudinal Rebar | Transverse Rebar | Intended Failure Mode by Design |
|---|---|---|---|---|---|---|---|
| FS50-1 | 50 | 50 | 6700 | 600 | 2 ϕ9.5 mm | ϕ9.5 mm @350mm | Flexure |
| FS50-2 | 50 | 50 | 6700 | 600 | 2 ϕ16 mm | ϕ9.5 mm @350mm | Horizontal Shear |
| FS200-1 | 75 | 200 | 6700 | 600 | 2 ϕ9.5 mm | ϕ9.5 mm @350mm | Flexure |
| FS200-2 | 75 | 200 | 6700 | 600 | 2 ϕ16 mm | ϕ9.5 mm @350mm | Horizontal Shear |
| FS250-1 | 75 | 250 | 6700 | 600 | 2 ϕ9.5 mm | ϕ9.5 mm @350mm | Flexural |
| FS250-2 | 75 | 250 | 6700 | 600 | 2 ϕ16 mm | ϕ9.5 mm @350mm | Horizontal Shear |
| Specimen Designation | Compressive Stress (MPa) | Modulus of Elasticity (MPa) | Tensile Strength (MPa) |
|---|---|---|---|
| Double Shear Specimens | |||
| F50-1 | 55.880 | - | - |
| F50-2 | 55.880 | - | - |
| F50-3 | 51.348 | - | - |
| F50-4 | 51.348 | - | - |
| F200-1 | 55.880 | - | - |
| F200-2 | 55.880 | - | - |
| F200-3 | 51.348 | - | - |
| F200-4 | 51.348 | - | - |
| F250-1 | 55.880 | - | - |
| F250-2 | 55.880 | - | - |
| F250-3 | 47.233 | - | - |
| F250-4 | 47.233 | - | - |
| Large–scale Panels | |||
| FS50-1 | 65.730 | 35,802 | 3.918 |
| FS50-2 | 46.809 | 31,944 | 2.894 |
| FS200-1 | 65.207 | 35,972 | 4.044 |
| FS200-2 | 46.809 | 31,944 | 2.894 |
| FS250-1 | 63.587 | 38,619 | 3.693 |
| FS250-2 | 46.809 | 31,944 | 2.894 |
| Designation | Elastic Load (kN) | Slip at Elastic Load (mm) | Elastic Stiffness KE0.4 (kN/mm) | Maximum Load (kN) | Slip at Maximum Load (mm) | Ultimate Stiffness KU0.4 (kN/mm) |
|---|---|---|---|---|---|---|
| F50-1 | 23.60 | 0.65 | 36.57 | 58.98 | 2.50 | 23.59 |
| F50-2 | 21.14 | 0.72 | 29.25 | 52.84 | 2.75 | 19.22 |
| F50-3 | 20.04 | 0.59 | 33.95 | 50.09 | 2.50 | 20.03 |
| F50-4 | 18.79 | 0.52 | 36.01 | 46.97 | 2.00 | 23.49 |
| Mean | 20.89 | 0.62 | 33.95 | 52.58 | 2.44 | 21.58 |
| COV (%) | 8% | 12% | 8% | 8% | 11% | 9% |
| F200-1 | 21.22 | 0.89 ** | 23.83 ** | 53.07 | 9.65 ** | 5.50 ** |
| F200-2 | 21.04 | 1.52 | 13.81 | 52.58 | 6.35 | 8.28 |
| F200-3 | 25.13 | 2.03 | 12.37 | 62.85 | 6.35 | 9.90 |
| F200-4 | 18.95 | 1.78 | 10.66 | 47.33 | 6.10 | 7.76 |
| Mean | 21.71 | 1.78 | 12.28 | 54.25 | 6.27 | 8.65 |
| COV (%) | 10% | 12% | 10% | 10% | 2% | 11% |
| F250-1 | 21.92 | 2.83 | 7.75 | 55.19 | 9.25 | 5.97 |
| F250-2 | 22.03 | 1.90 | 11.63 | 55.46 | 6.50 | 8.53 |
| F250-3 | 19.02 | 2.24 | 8.50 | 47.89 | 7.25 | 6.61 |
| F250-4 | 22.99 | 2.56 | 8.98 | 57.88 | 7.75 | 7.47 |
| Mean | 21.49 | 2.38 | 9.22 | 54.11 | 7.69 | 7.14 |
| COV (%) | 7% | 15% | 16% | 7% | 13% | 13% |
| Panel Designation | Applied Load at Failure | Applied Shear at Failure | Applied Moment at Failure | Failure Mode |
|---|---|---|---|---|
| kN | kN | kN·m | ||
| FS50-1 | 10.7 | 5.34 | 11.4 | flexural |
| FS50-2 | 10.9 | 5.47 | 11.7 | shear |
| FS200-1 | 25.6 | 12.8 | 27.3 | shear |
| FS200-2 | 25.3 | 12.6 | 26.9 | shear |
| FS250-1 | 25.0 | 12.5 | 26.7 | shear |
| FS250-2* | 25.1 | 12.6 | 26.8 | shear |
| * Values for F250-2 are for the post-cracking peak. | ||||
| Panel Designation | Experiments | Beam Spring Method | Holmberg and Plem | ISBT Method | ||||
|---|---|---|---|---|---|---|---|---|
| Observed Stiffness (kN/mm) | Measured Mc(kN-m) | Predicted ÷ Observed Stiffness | Predicted ÷ Observed Mcr | Predicted ÷ Observed Stiffness | Predicted ÷ Observed Mcr | Predicted ÷ Observed Stiffness | Predicted ÷ Observed Mcr | |
| FS50-1 | 0.51 | 4.98 | 0.83 | 1.10 | 0.83 | 1.14 | 0.83 | 1.17 |
| FS50-2 | 0.54 | 4.63 | 0.71 | 0.99 | 0.74 | 1.10 | 0.71 | 1.00 |
| FS200-1 | 1.35 | 12.22 | 1.06 | 1.10 | 1.06 | 1.18 | 1.05 | 1.15 |
| FS200-2 | 1.49 | 15.03 | 0.93 | 0.79 | 0.98 | 0.95 | 0.94 | 0.84 |
| FS250-2 | 1.52 | 14.86 | 1.03 | 0.90 | 1.18 | 0.99 | 1.08 | 0.94 |
| Panel Designation | Standard Shear Flow Procedure | |
|---|---|---|
| qu(kN/mm) | Measured/Predicted | |
| FS50-1 | 49.62 | - |
| FS50-2 | 50.98 | 0.99 |
| FS200-1 | 45.40 | 0.85 |
| FS200-2 | 44.54 | 0.83 |
| FS250-1 | 37.35 | 0.71 |
| FS250-2 | 38.64 | 0.73 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luebke, J.; Pozo-Lora, F.F.; Al-Rubaye, S.; Maguire, M. Out-of-Plane Flexural Behavior of Insulated Wall Panels Constructed with Large Insulation Thicknesses. Materials 2023, 16, 4160. https://doi.org/10.3390/ma16114160
Luebke J, Pozo-Lora FF, Al-Rubaye S, Maguire M. Out-of-Plane Flexural Behavior of Insulated Wall Panels Constructed with Large Insulation Thicknesses. Materials. 2023; 16(11):4160. https://doi.org/10.3390/ma16114160
Chicago/Turabian StyleLuebke, Jacob, Fray F. Pozo-Lora, Salam Al-Rubaye, and Marc Maguire. 2023. "Out-of-Plane Flexural Behavior of Insulated Wall Panels Constructed with Large Insulation Thicknesses" Materials 16, no. 11: 4160. https://doi.org/10.3390/ma16114160
APA StyleLuebke, J., Pozo-Lora, F. F., Al-Rubaye, S., & Maguire, M. (2023). Out-of-Plane Flexural Behavior of Insulated Wall Panels Constructed with Large Insulation Thicknesses. Materials, 16(11), 4160. https://doi.org/10.3390/ma16114160








