Effect of Varying Normal Stiffness on Soft Rock Joints under Cyclic Shear Loads
Abstract
:1. Introduction
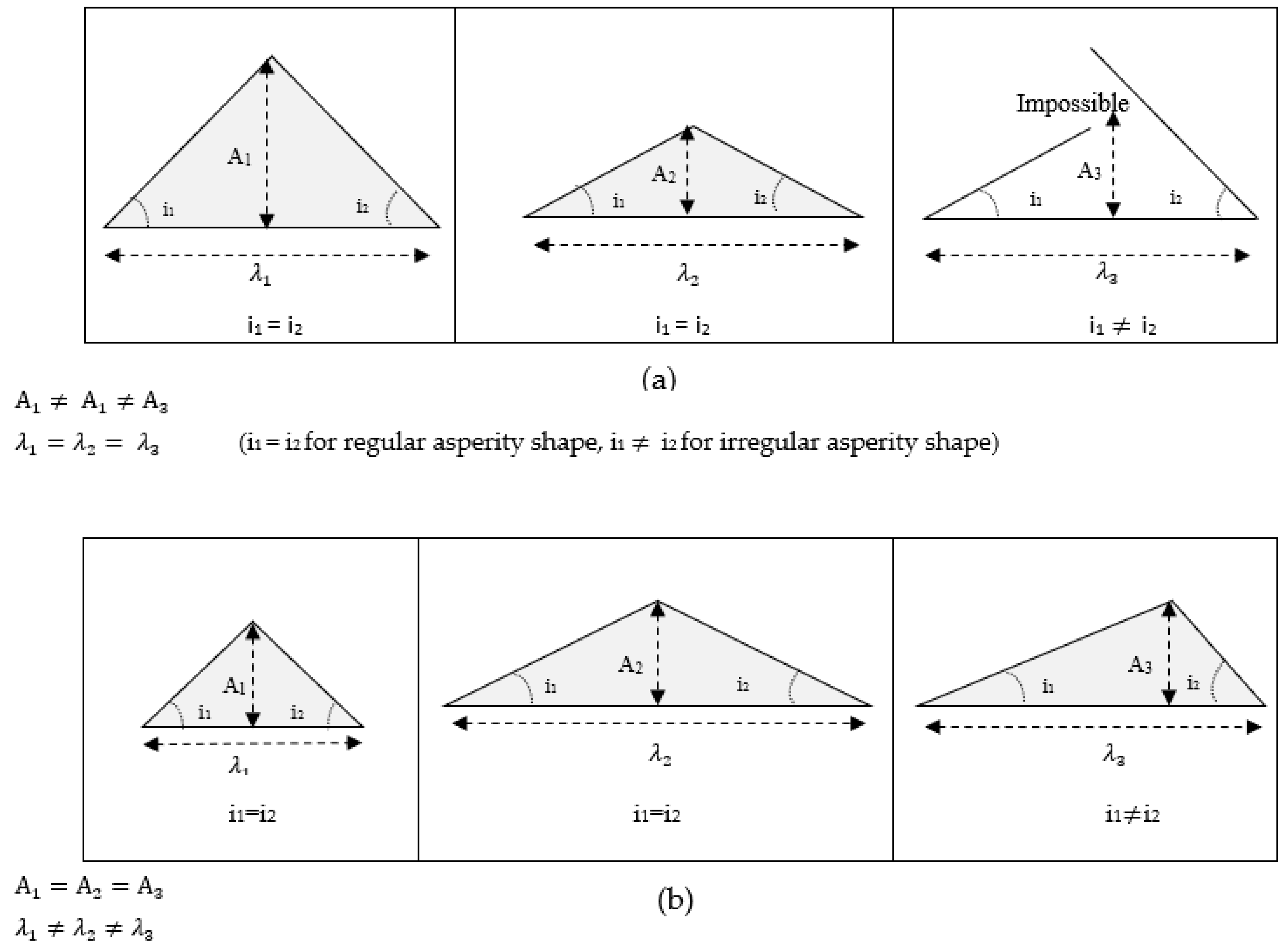
2. Approaches to the Simulation of Natural Rock Joint Asperities
3. Experimental Methodology
3.1. Experimental Material and Specimen Preparation
3.2. Automatic Shear Testing Machine

3.3. Testing Procedures
4. Results and Discussion
4.1. Joint with Regular Asperities (15°-15° and 30°-30°)
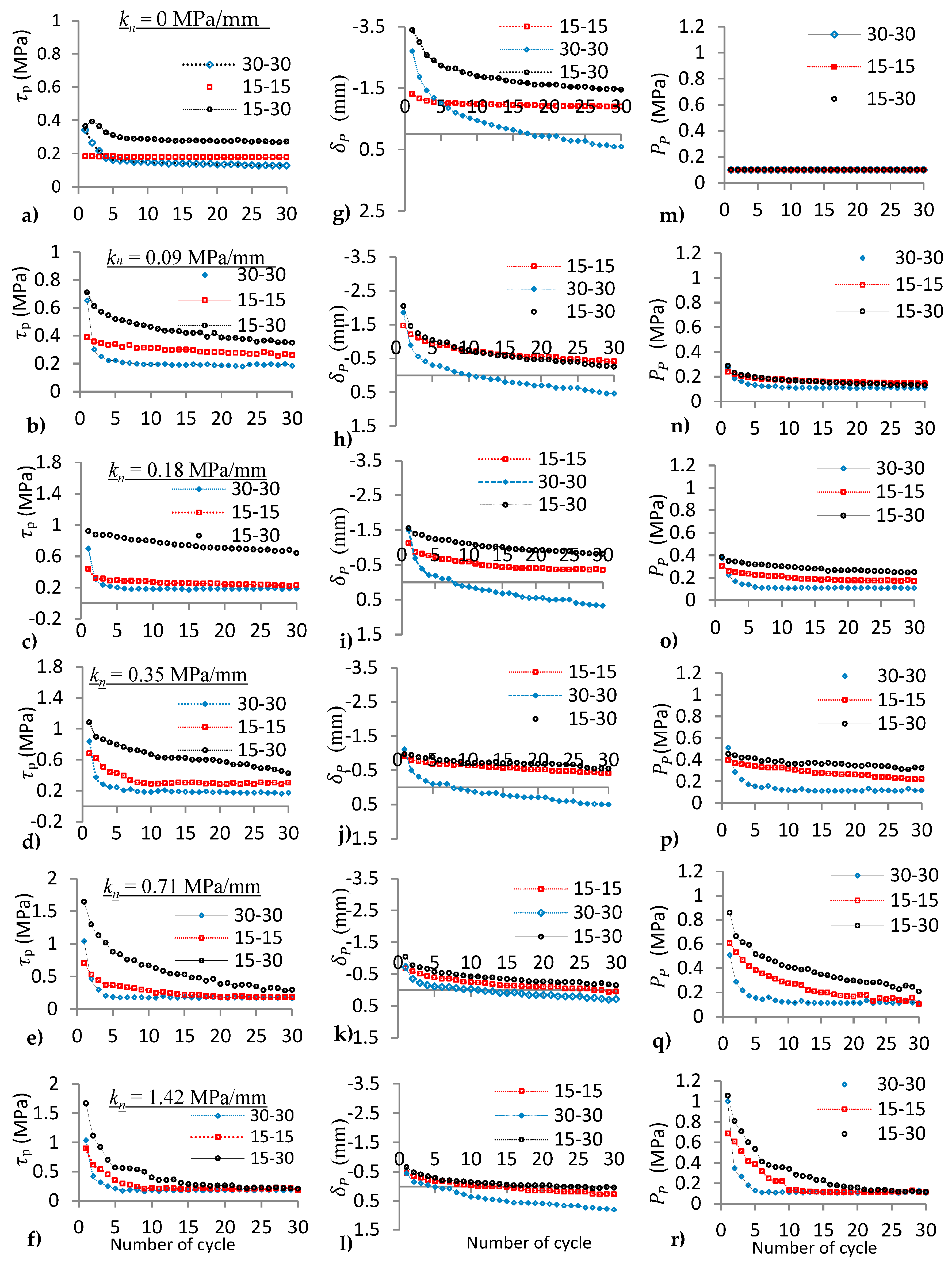
4.1.1. Shear Stress (τ) of the Joints under Varying kn
4.1.2. Normal Displacement (δ) of the Joints under Varying kn
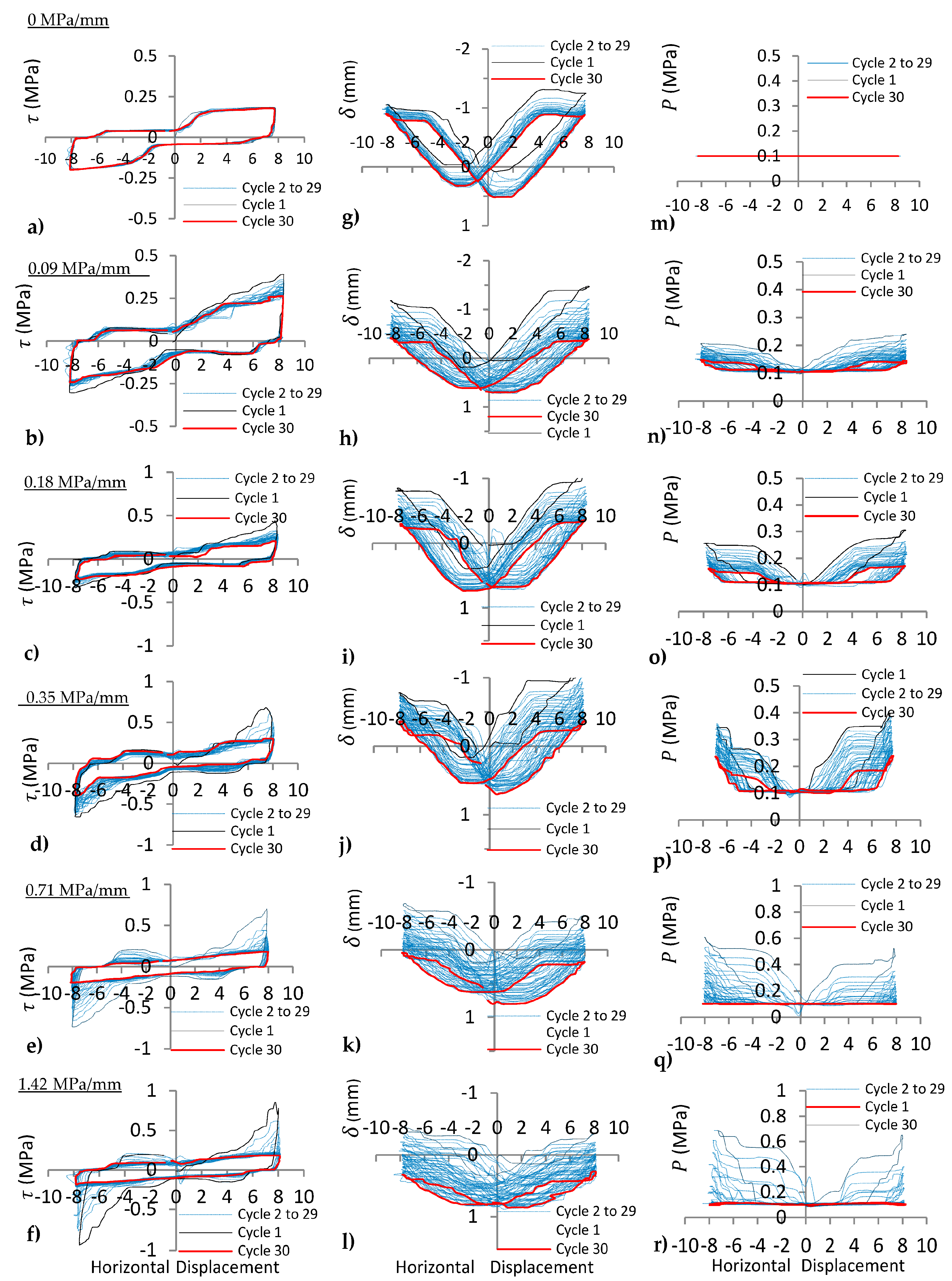

4.1.3. Normal Stress (P) of the Joints under Varying kn
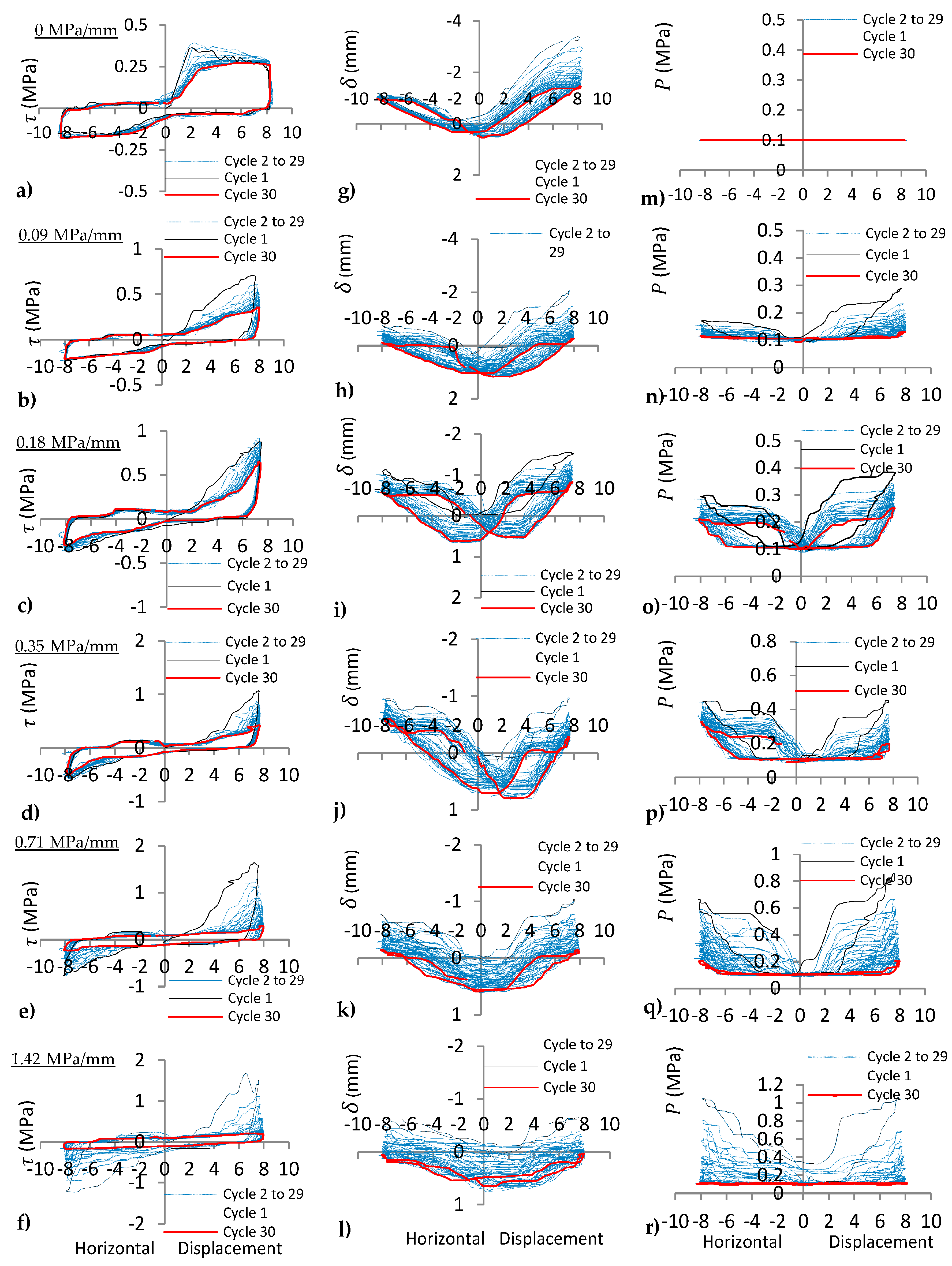
4.2. Joint with Irregular Asperity (15°-30°)
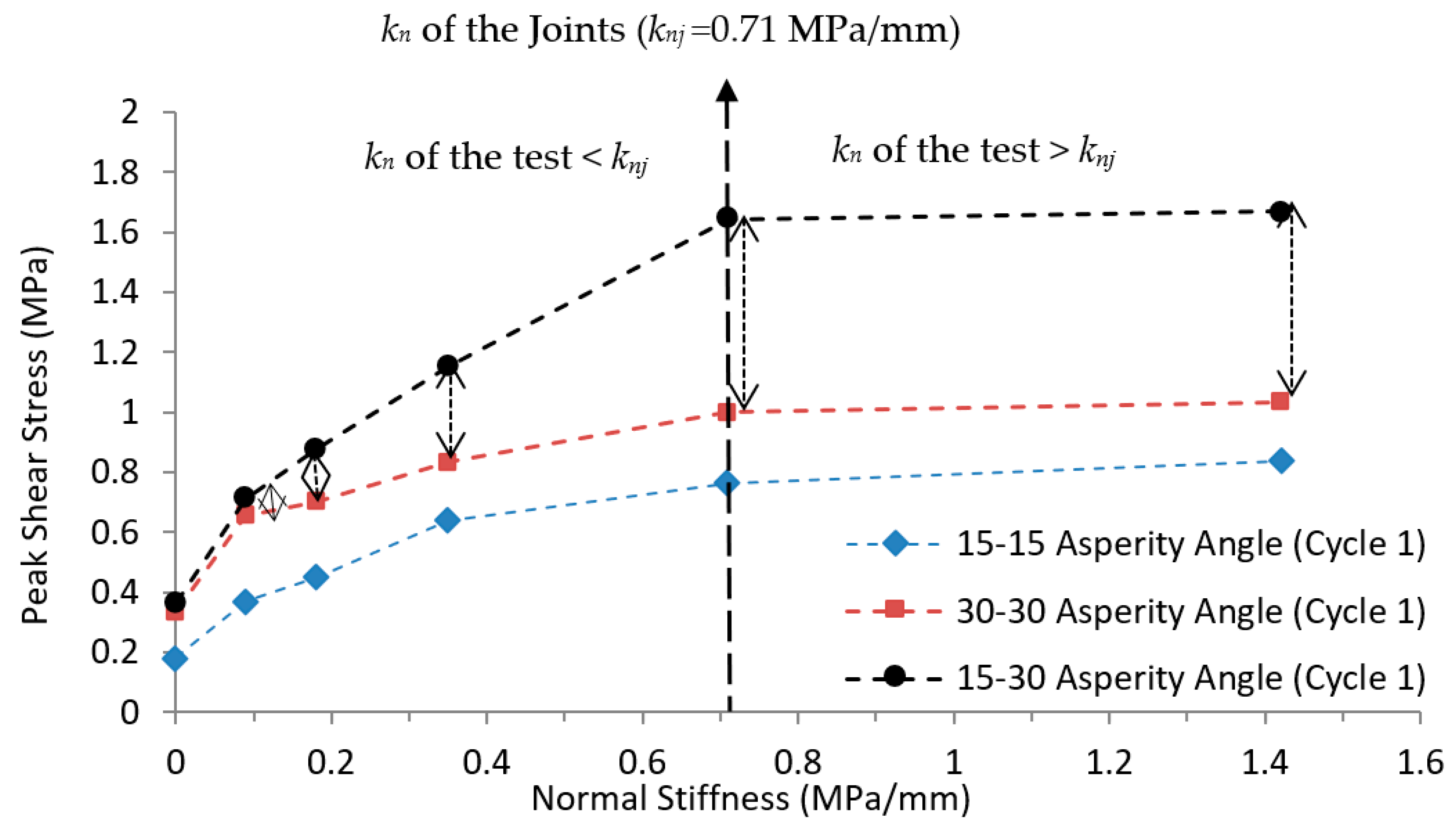
4.3. Comparison between the Joints under Varying kn
5. Prediction of Shear Strength under Cyclic Loads

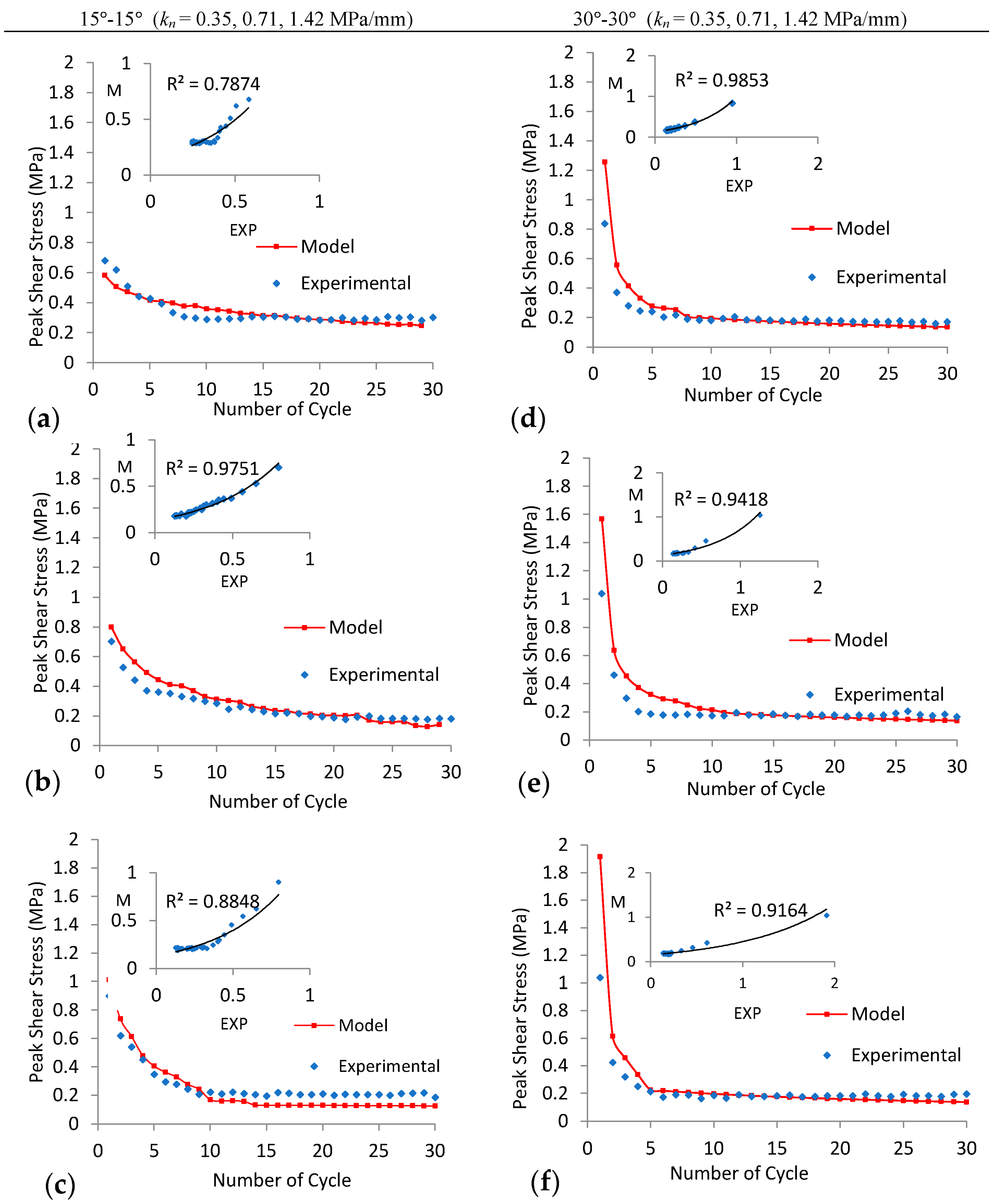
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jiang, X.-W.; Wan, L.; Wang, X.-S.; Liang, S.-H.; Hu, B.X. Estimation of fracture normal stiffness using a transmissivity-depth correlation. Int. J. Rock Mech. Min. Sci. 2009, 46, 51–58. [Google Scholar] [CrossRef]
- Patton, F.D. Multiple Modes of Shear Failure in Rock and Related Materials. Ph.D. Thesis, University of Illinois, Champaign, IL, USA, 1966. [Google Scholar]
- Ladany, B.; Archambault, G. Simulation of Shear Behavior of a Jointed Rock Mass. In Proceedings of the 11th US Symposium on Rock Mechanics, Berkeley, CA, USA, 16–19 June 1969; American Rock Mechanics Association (ARMA): New York, NY, USA, 1970; pp. 105–125. [Google Scholar]
- Jaeger, J.C. Friction of Rocks and Stability of Rock Slopes. Geotechnique 1971, 21, 97–134. [Google Scholar] [CrossRef]
- Barton, N. Review of a new shear-strength criterion for rock joints. Eng. Geol. 1973, 7, 287–332. [Google Scholar] [CrossRef]
- Barton, N.; Choubey, V. The shear strength of rock joints in theory and practice. Rock Mech. Rock Eng. 1977, 10, 1–54. [Google Scholar] [CrossRef]
- Amadei, B.; Saeb, S. Constitutive Models of Rock Joints. In Rock Joints: Proceedings of the International Symposium on Rock Joints, Loen, Norway, 4–6 June 1990; Barton, N., Stephansson, O., Eds.; Balkema: Rotterdam, The Netherlands; Brookfield, VT, USA, 1990; pp. 581–594. [Google Scholar]
- Kulatilake, P.; Shou, G.; Huang, T.; Morgan, R. New peak shear strength criteria for anisotropic rock joints. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 1995, 32, 673–697. [Google Scholar] [CrossRef]
- Seidel, J.P.; Haberfield, C.M. The application of energy principles to the determination of the sliding resistance of rock joints. Rock Mech. Rock Eng. 1995, 28, 211–226. [Google Scholar] [CrossRef]
- Grasselli, G.; Wirth, J.; Egger, P. Quantitative three-dimensional description of a rough surface and parameter evolution with shearing. Int. J. Rock Mech. Min. Sci. 2002, 39, 789–800. [Google Scholar] [CrossRef]
- Asadollahi, P.; Tonon, F. Constitutive model for rock fractures: Revisiting Barton’s empirical model. Eng. Geol. 2010, 113, 11–32. [Google Scholar] [CrossRef]
- Heuze, F.E. Dilatant Effects of Rock Joints. In Proceedings of the 4th ISRM Congress, Montreux, Switzerland, 2–8 September 1979; pp. 169–175. [Google Scholar]
- Johnston, I.W.; Lam, T.S.K. Shear Behavior of Regular Triangular Concrete/Rock Joints—Analysis. J. Geotech. Eng. 1989, 115, 711–727. [Google Scholar] [CrossRef]
- Saeb, S.; Amadei, B. Modelling rock joints under shear and normal loading. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 1992, 29, 267–278. [Google Scholar] [CrossRef]
- Skinas, C.A.; Bandis, S.C.; Demiris, C.A. Experimental Investigations and Modelling of Rock Joint Behaviour under Constant Stiffness. In Proceedings of the International Symposium on Rock Joints, Loen, Norway, 4–6 June 1990; Barton, N., Stephansson, O., Eds.; Balkema: Rotterdam, The Netherlands; Brookfield, VT, USA, 1990; pp. 301–308. [Google Scholar]
- Indraratna, B.; Haque, A.; Aziz, N. Laboratory Modelling of Shear Behaviour of Soft Joints under Constant Normal Stiffness Conditions. J. Geotech. Geol. Eng. 1998, 16, 17–44. [Google Scholar] [CrossRef]
- Haque, A. Shear Behaviour of Soft Rock Joints under Constant Normal Stiffness Condition. Ph.D. Thesis, University of Wollongong, Wollongong, Australia, 1999. [Google Scholar]
- Indraratna, B.; Haque, A. Shear Behaviour of Rock Joints; Balkema: Rotterdam, The Netherlands, 2021. [Google Scholar]
- Shrivastava, A.K.; Rao, K.S. Physical Modeling of Shear Behavior of Infilled Rock Joints Under CNL and CNS Boundary Conditions. Rock Mech. Rock Eng. 2018, 51, 101–118. [Google Scholar] [CrossRef]
- Hutson, R.; Dowding, C. Joint asperity degradation during cyclic shear. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 1990, 27, 109–119. [Google Scholar] [CrossRef]
- Huang, X.; Haimson, B.; Plesha, M.; Qiu, X. An investigation of the mechanics of rock joints—Part I. Laboratory investigation. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 1993, 30, 257–269. [Google Scholar] [CrossRef]
- Plesha, M.E. Constitutive models for rock discontinuities with dilatancy and surface degradation. Int. J. Numer. Anal. Methods Géoméch. 1987, 11, 345–362. [Google Scholar] [CrossRef]
- Qiu, X.; Plesha, M.; Huang, X.; Haimson, B. An investigation of the mechanics of rock joints—Part II. Analytical investigation. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 1993, 30, 271–287. [Google Scholar] [CrossRef]
- Jing, L.; Stephansson, O.; Nordlund, E. Study of rock joints under cyclic loading conditions. Rock Mech. Rock Eng. 1993, 26, 215–232. [Google Scholar] [CrossRef]
- Lee, H.S.; Park, Y.J.; Cho, T.F.; You, K.H. Influence of Asperity Degradation on the Mechanical Behavior of Rough Rock Joints under Cyclic Shear Loading. Int. J. Rock Mech. Min. Sci. 2001, 38, 967–980. [Google Scholar] [CrossRef]
- Jafari, M.; Hosseini, K.A.; Pellet, F.; Boulon, M.; Buzzi, O. Evaluation of shear strength of rock joints subjected to cyclic loading. Soil Dyn. Earthq. Eng. 2003, 23, 619–630. [Google Scholar] [CrossRef]
- Thongprapha, T.; Liapkrathok, P.; Chanpen, S.; Fuenkajorn, K. Frictional behavior of sandstone fractures under forward-backward pre-peak cyclic loading. J. Struct. Geol. 2020, 138, 104106. [Google Scholar] [CrossRef]
- Belem, T.; Souley, M.; Homand, F. Modeling surface roughness degradation of rock joint wall during monotonic and cyclic shearing. Acta Geotech. 2007, 2, 227–248. [Google Scholar] [CrossRef]
- Belem, T.; Souley, M.; Homand, F. Method for Quantification of Wear of Sheared Joint Walls Based on Surface Morphology. Rock Mech. Rock Eng. 2009, 42, 883–910. [Google Scholar] [CrossRef]
- Homand-Etienne, F.; Lefevre, F.; Belem, T.; Souley, M. Rock Joints Behaviour under Cyclic Direct Shear Tests. In Proceedings of the 37th US Symposium, Vail, CO, USA, 6–9 June 1999; pp. 399–406. [Google Scholar]
- Homand, F.; Belem, T.; Souley, M. Friction and degradation of rock joint surfaces under shear loads. Int. J. Numer. Anal. Methods Géoméch. 2001, 25, 973–999. [Google Scholar] [CrossRef]
- Jiang, Y.; Xiao, J.; Tanabashi, Y.; Mizokami, T. Development of an automated servo-controlled direct shear apparatus applying a constant normal stiffness condition. Int. J. Rock Mech. Min. Sci. 2004, 41, 275–286. [Google Scholar] [CrossRef]
- Mirzaghorbanali, A. Shear Behaviour of Rock Joints under Cyclic Loading and Constant Normal Stiffness Condition. Ph.D. Thesis, University of Wollongong, Wollongong, Australia, 2013. [Google Scholar]
- Mirzaghorbanali, A.; Nemcik, J.; Aziz, N. Effects of Shear Rate on Cyclic Loading Shear Behaviour of Rock Joints under Constant Normal Stiffness Conditions. Int. J. Rock Mech. Rock Eng. 2013, 47, 1931–1938. [Google Scholar] [CrossRef]
- Han, G.; Jing, H.; Jiang, Y.; Liu, R.; Wu, J. Effect of Cyclic Loading on the Shear Behaviours of Both Unfilled and Infilled Rough Rock Joints Under Constant Normal Stiffness Conditions. Rock Mech. Rock Eng. 2020, 53, 31–57. [Google Scholar] [CrossRef]
- Richards, L.R. Shear Strength of Joints in Weathered Rocks. Ph.D. Thesis, Imperial College of Science and Technology, London, UK, 1975. [Google Scholar]
- Dearman, W.R.; Baynes, F.J.; Irfan, T.Y. Engineering grading of weathered granite. Eng. Geol. 1978, 12, 345–374. [Google Scholar] [CrossRef]
- Özvan, A.; Dinçer, I.; Acar, A.; Özvan, B. The effects of discontinuity surface roughness on the shear strength of weathered granite joints. Bull. Eng. Geol. Environ. 2014, 73, 801–813. [Google Scholar] [CrossRef]
- Ram, B.K.; Basu, A. Shear Behavior of Unfilled-Planar Quartzitic Rock Joints with Reference to Weathering Grade of Joint Surfaces. Rock Mech. Rock Eng. 2019, 52, 4113–4121. [Google Scholar] [CrossRef]
- Zhang, Q.; Wu, C.; Fei, X.; Jang, B.A.; Liu, D. Time-Dependent Behavior of Rock Joints Considering Asperity Degradation. J. Struct. Geol. 2019, 121, 43–50. [Google Scholar] [CrossRef]
- Niktabar, S.M.M.; Rao, K.S.; Shrivastava, A.K. Automatic Static and Cyclic Shear Testing Machine under Constant Normal Stiffness Boundary Conditions. Geotech. Test. J. 2018, 41, 508–525. [Google Scholar] [CrossRef]
- Niktabar, S.M.; Rao, K.S.; Seshagiri, R.; Shrivastava, A.K. Effect of rock joint roughness on its cyclic shear behavior. J. Rock Mech. Geotech. Eng. 2017, 9, 1071–1084. [Google Scholar] [CrossRef]



| Joint Type | Asperity Angles i1,i2 [°] | Asperity Base Length [mm] | Asperity Amplitude A [mm] |
|---|---|---|---|
| Regular | - | 37.3 | 5 |
| Regular | - | 17.3 | 5 |
| Irregular | - | 27.3 | 5 |
| Parameters | Values |
|---|---|
| Normal stiffness, kn [MPa/mm] | 0, 0.09, 0.18, 0.35, 0.71, 1.42 |
| Initial normal stress, Pi [MPa] | 0.1 |
| Frequency [Hz] | 0.01 |
| Amplitude of shear load [mm] | ±8 |
| Number of cycles, N | 30 |
| kn = 0.09 MPa/mm | kn = 1.42 MPa/mm | |||||
|---|---|---|---|---|---|---|
| Joint Asperity i1,i2 [°] | First Peak Shear Stress [MPa] | Second Peak Shear Stress [MPa] | Difference (%) | First Peak Shear Stress [MPa] | Second Peak Shear Stress [MPa] | Difference (%) |
| - | 0.39 | 0.36 | 8 | 0.70 | 0.53 | 24 |
| - | 0.61 | 0.30 | 52 | 1.04 | 0.42 | 60 |
| - | 0.71 | 0.61 | 14 | 1.67 | 1.12 | 33 |
| kn [MPa/mm] | Pi [MPa] | Joint Asperity i1,i2 [°] | Peak Normal Stress Pp [MPa] | Increase in Pp with Respect to Pi [%] | Peak Shear Stress [MPa] | Increase in with Respect to CNL [%] |
|---|---|---|---|---|---|---|
| 0 (CNL) | 0.1 | 30-30 | 0.10 | 0 | 0.34 | 0 |
| 0.09 | 0.1 | 30-30 | 0.27 | 170 | 0.65 | 91 |
| 0.18 | 0.1 | 30-30 | 0.38 | 280 | 0.70 | 106 |
| 0.35 | 0.1 | 30-30 | 0.51 | 410 | 0.83 | 144 |
| 0.71 | 0.1 | 30-30 | 0.62 | 520 | 1.00 | 194 |
| 1.42 | 0.1 | 30-30 | 1.00 | 900 | 1.00 | 194 |
| 0 (CNL) | 0.1 | 15-15 | 0.10 | 0 | 0.18 | 0 |
| 0.09 | 0.1 | 15-15 | 0.24 | 140 | 0.39 | 117 |
| 0.18 | 0.1 | 15-15 | 0.3 | 200 | 0.45 | 150 |
| 0.35 | 0.1 | 15-15 | 0.40 | 300 | 0.65 | 261 |
| 0.71 | 0.1 | 15-15 | 0.59 | 490 | 0.76 | 322 |
| 1.42 | 0.1 | 15-15 | 0.67 | 570 | 0.84 | 367 |
| 0 (CNL) | 0.1 | 15-30 | 0.10 | 0 | 0.36 | 0 |
| 0.09 | 0.1 | 15-30 | 0.29 | 190 | 0.71 | 97 |
| 0.18 | 0.1 | 15-30 | 0.38 | 280 | 0.89 | 147 |
| 0.35 | 0.1 | 15-30 | 0.45 | 350 | 1.08 | 200 |
| 0.71 | 0.1 | 15-30 | 0.86 | 760 | 1.64 | 356 |
| 1.42 | 0.1 | 15-30 | 1.05 | 905 | 1.67 | 364 |
| N | 0.09 [MPa/mm] | 0.18 [MPa/mm] | 0.35 [MPa/mm] | 0.71 [MPa/mm] | 1.42 [MPa/mm] |
|---|---|---|---|---|---|
| 1 | 1.86 | 1.50 | 1.11 | 0.72 | 0.46 |
| 2 | 0.90 | 0.69 | 0.50 | 0.35 | 0.16 |
| 3 | 0.56 | 0.39 | 0.32 | 0.22 | 0.11 |
| 4 | 0.41 | 0.21 | 0.19 | 0.15 | 0.05 |
| 5 | 0.30 | 0.19 | 0.11 | 0.11 | 0.00 |
| 6 | 0.28 | 0.10 | 0.10 | 0.09 | 0.00 |
| 7 | 0.28 | 0.10 | 0.00 | 0.09 | 0.00 |
| 8 | 0.11 | 0.00 | 0.00 | 0.06 | 0.00 |
| 9 | 0.06 | 0.00 | 0.00 | 0.03 | 0.00 |
| 10 | 0.01 | 0.00 | 0.00 | 0.02 | 0.00 |
| 11 | 0.00 | 0.00 | 0.00 | 0.01 | 0.00 |
| 12 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 13 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 14 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 15 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 16 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 17 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 18 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 19 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 20 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 21 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 22 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 23 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 24 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 25 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 26 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 27 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 28 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 29 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 30 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| N | 0.09 [MPa/mm] | 0.18 [MPa/mm] | 0.35 [MPa/mm] | 0.71 [MPa/mm] | 1.42 [MPa/mm] |
|---|---|---|---|---|---|
| 1 | 1.38 | 1.12 | 0.91 | 0.68 | 0.45 |
| 2 | 1.18 | 0.87 | 0.80 | 0.59 | 0.35 |
| 3 | 1.12 | 0.82 | 0.77 | 0.51 | 0.29 |
| 4 | 1.02 | 0.77 | 0.74 | 0.44 | 0.21 |
| 5 | 0.94 | 0.72 | 0.69 | 0.39 | 0.17 |
| 6 | 0.89 | 0.67 | 0.69 | 0.36 | 0.19 |
| 7 | 0.89 | 0.67 | 0.69 | 0.36 | 0.19 |
| 8 | 0.81 | 0.62 | 0.65 | 0.32 | 0.09 |
| 9 | 0.76 | 0.60 | 0.69 | 0.26 | 0.07 |
| 10 | 0.73 | 0.60 | 0.64 | 0.24 | 0.02 |
| 11 | 0.71 | 0.54 | 0.64 | 0.23 | 0.00 |
| 12 | 0.69 | 0.49 | 0.63 | 0.22 | 0.02 |
| 13 | 0.73 | 0.48 | 0.59 | 0.18 | 0.01 |
| 14 | 0.62 | 0.47 | 0.59 | 0.23 | 0.00 |
| 15 | 0.60 | 0.44 | 0.56 | 0.14 | 0.00 |
| 16 | 0.58 | 0.43 | 0.58 | 0.14 | 0.00 |
| 17 | 0.57 | 0.41 | 0.56 | 0.12 | 0.00 |
| 18 | 0.56 | 0.41 | 0.54 | 0.11 | 0.00 |
| 19 | 0.56 | 0.41 | 0.52 | 0.10 | 0.00 |
| 20 | 0.56 | 0.41 | 0.52 | 0.10 | 0.00 |
| 21 | 0.56 | 0.41 | 0.52 | 0.10 | 0.00 |
| 22 | 0.55 | 0.39 | 0.49 | 0.11 | 0.00 |
| 23 | 0.47 | 0.37 | 0.47 | 0.04 | 0.00 |
| 24 | 0.47 | 0.37 | 0.47 | 0.04 | 0.00 |
| 25 | 0.47 | 0.37 | 0.47 | 0.04 | 0.00 |
| 26 | 0.45 | 0.38 | 0.45 | 0.05 | 0.00 |
| 27 | 0.42 | 0.38 | 0.44 | 0.00 | 0.00 |
| 28 | 0.45 | 0.36 | 0.45 | 0.00 | 0.00 |
| 29 | 0.41 | 0.38 | 0.43 | 0.00 | 0.00 |
| 30 | 0.41 | 0.36 | 0.41 | 0.00 | 0.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niktabar, S.M.M.; Rao, K.S.; Shrivastava, A.K.; Ščučka, J. Effect of Varying Normal Stiffness on Soft Rock Joints under Cyclic Shear Loads. Materials 2023, 16, 4272. https://doi.org/10.3390/ma16124272
Niktabar SMM, Rao KS, Shrivastava AK, Ščučka J. Effect of Varying Normal Stiffness on Soft Rock Joints under Cyclic Shear Loads. Materials. 2023; 16(12):4272. https://doi.org/10.3390/ma16124272
Chicago/Turabian StyleNiktabar, S. M. Mahdi, K. Seshagiri Rao, Amit Kumar Shrivastava, and Jiří Ščučka. 2023. "Effect of Varying Normal Stiffness on Soft Rock Joints under Cyclic Shear Loads" Materials 16, no. 12: 4272. https://doi.org/10.3390/ma16124272
APA StyleNiktabar, S. M. M., Rao, K. S., Shrivastava, A. K., & Ščučka, J. (2023). Effect of Varying Normal Stiffness on Soft Rock Joints under Cyclic Shear Loads. Materials, 16(12), 4272. https://doi.org/10.3390/ma16124272





