Investigations of Structural, Magnetic, and Electrochemical Properties of NiFe2O4 Nanoparticles as Electrode Materials for Supercapacitor Applications
Abstract
:1. Introduction
2. Experimental Details
3. Results and Discussion
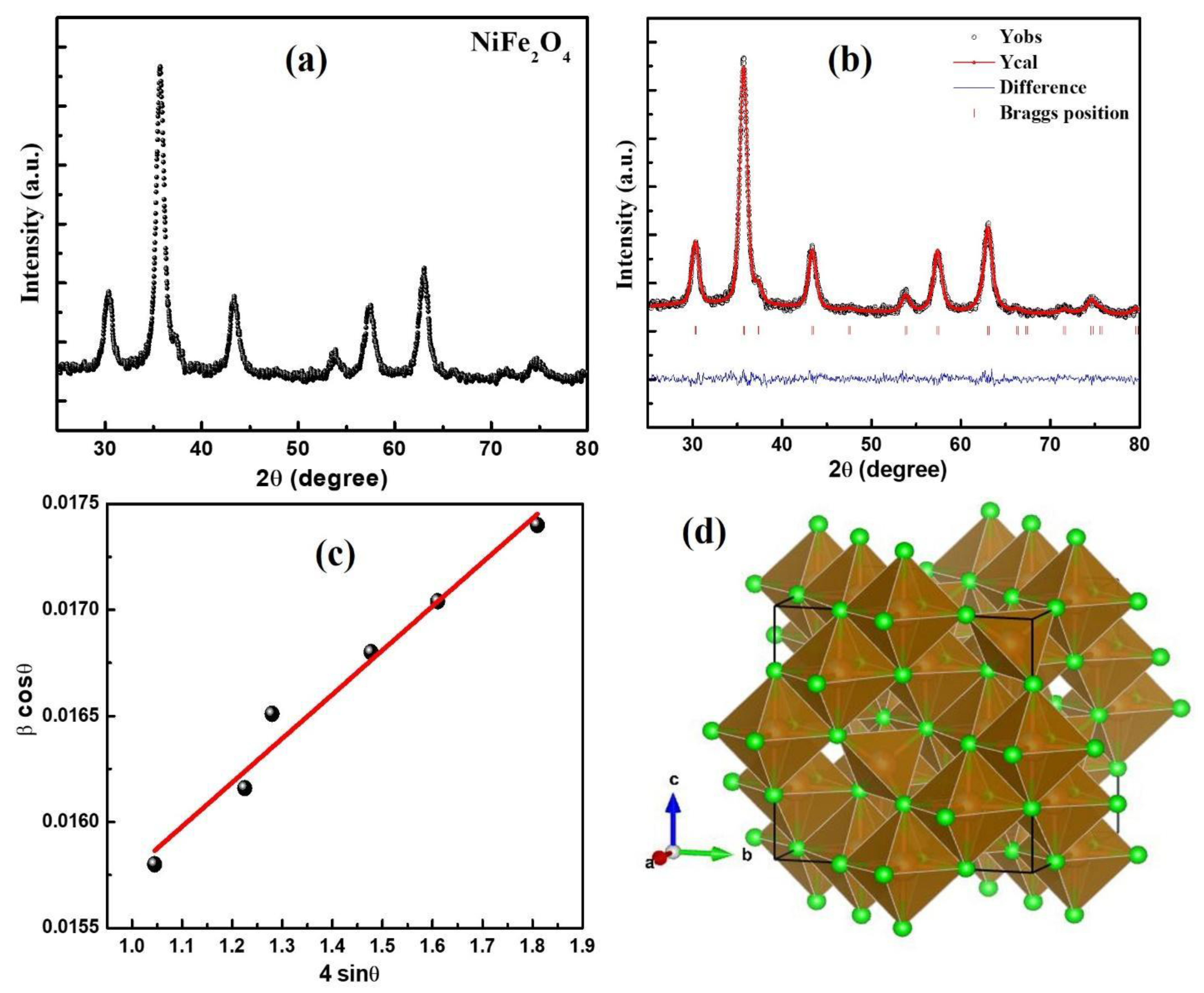
3.1. Structural Analysis
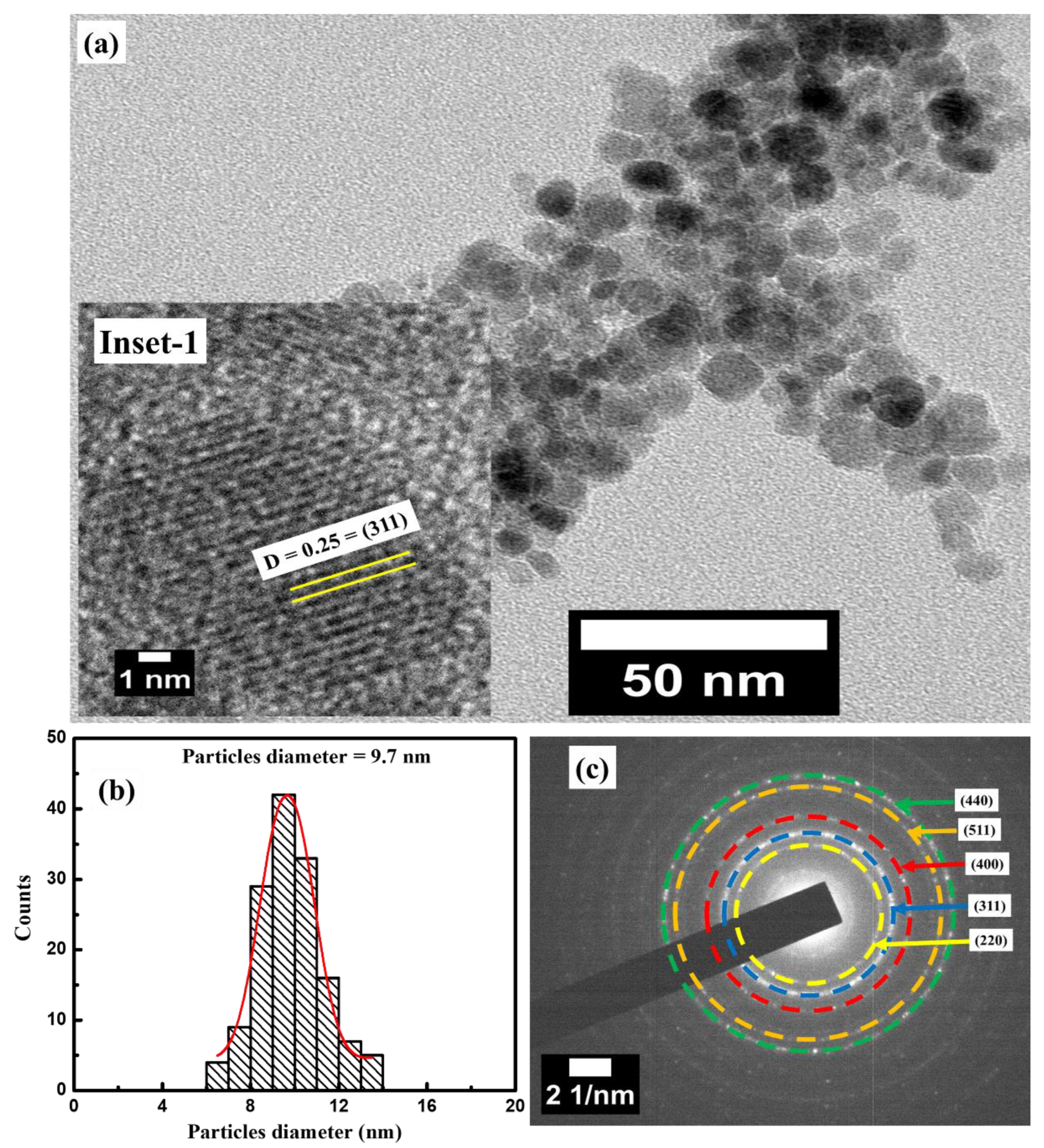
3.2. Morphological Analysis
3.3. Raman Spectroscopy
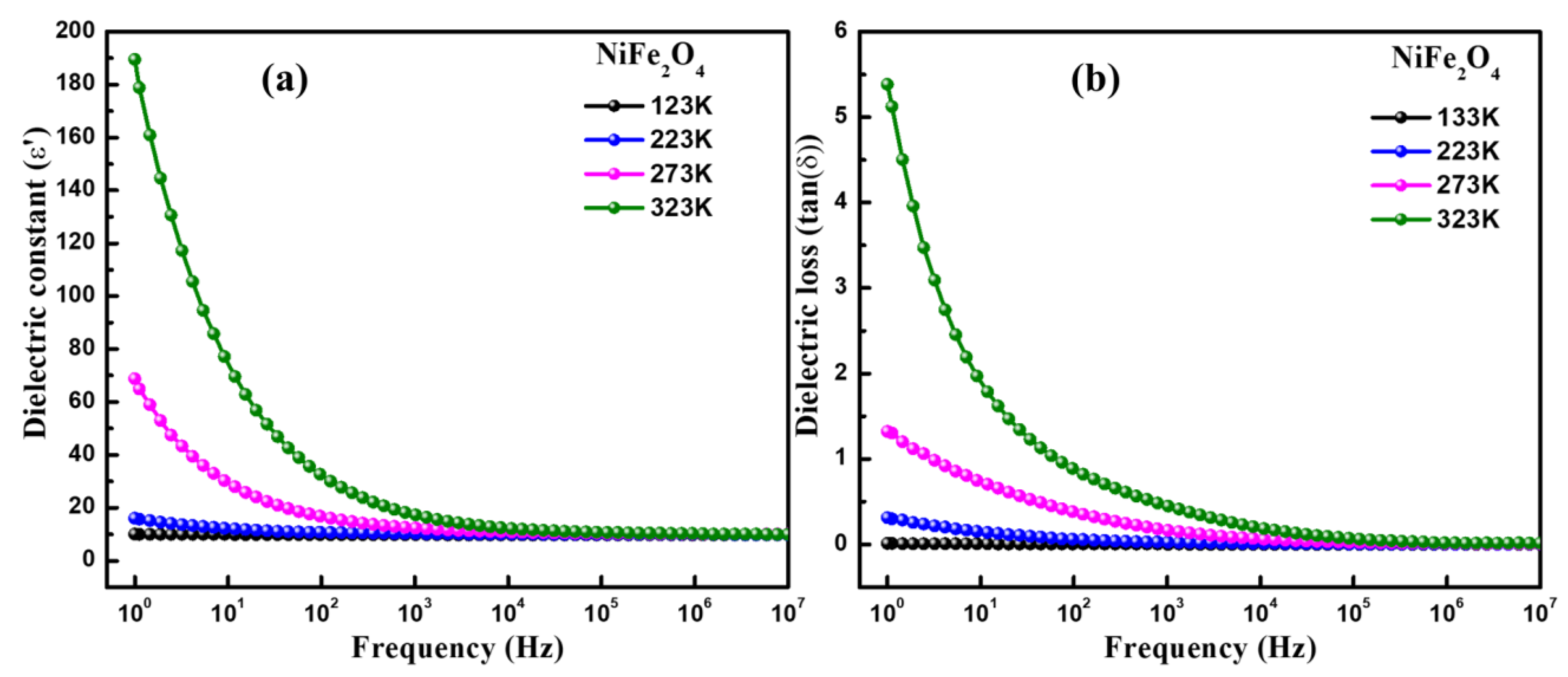
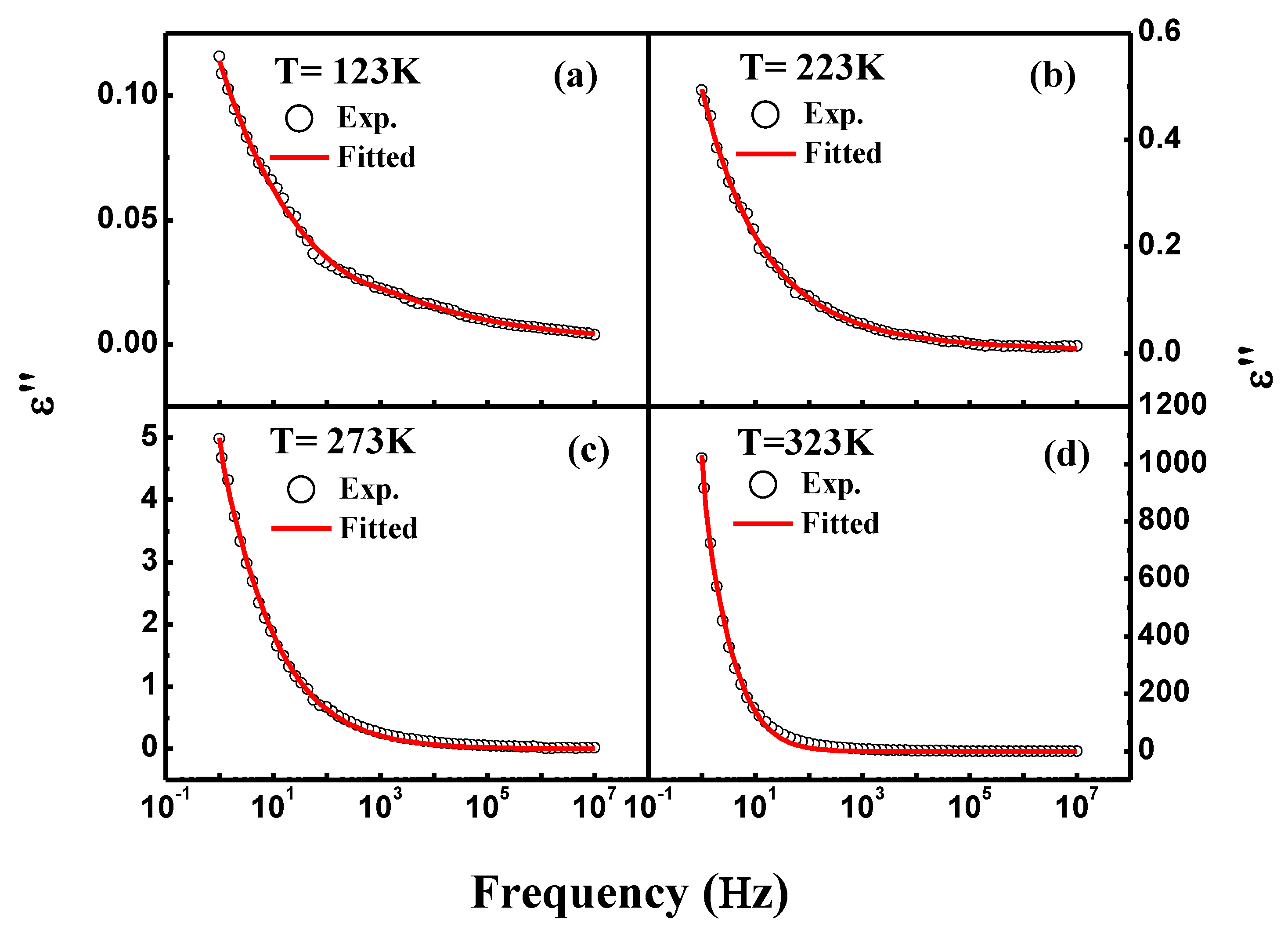
3.4. Dielectric Spectroscopy
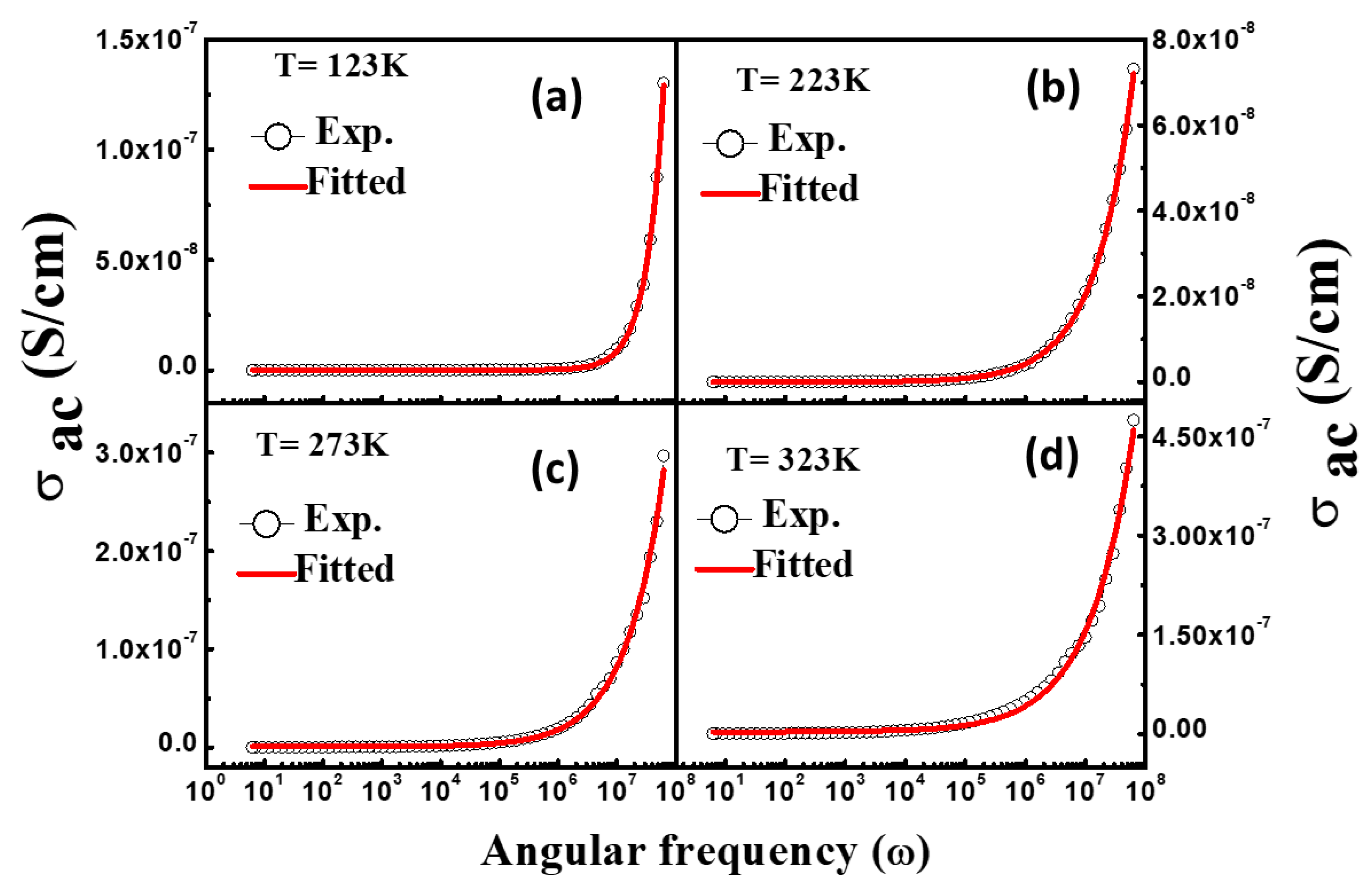
3.5. AC Conductivity
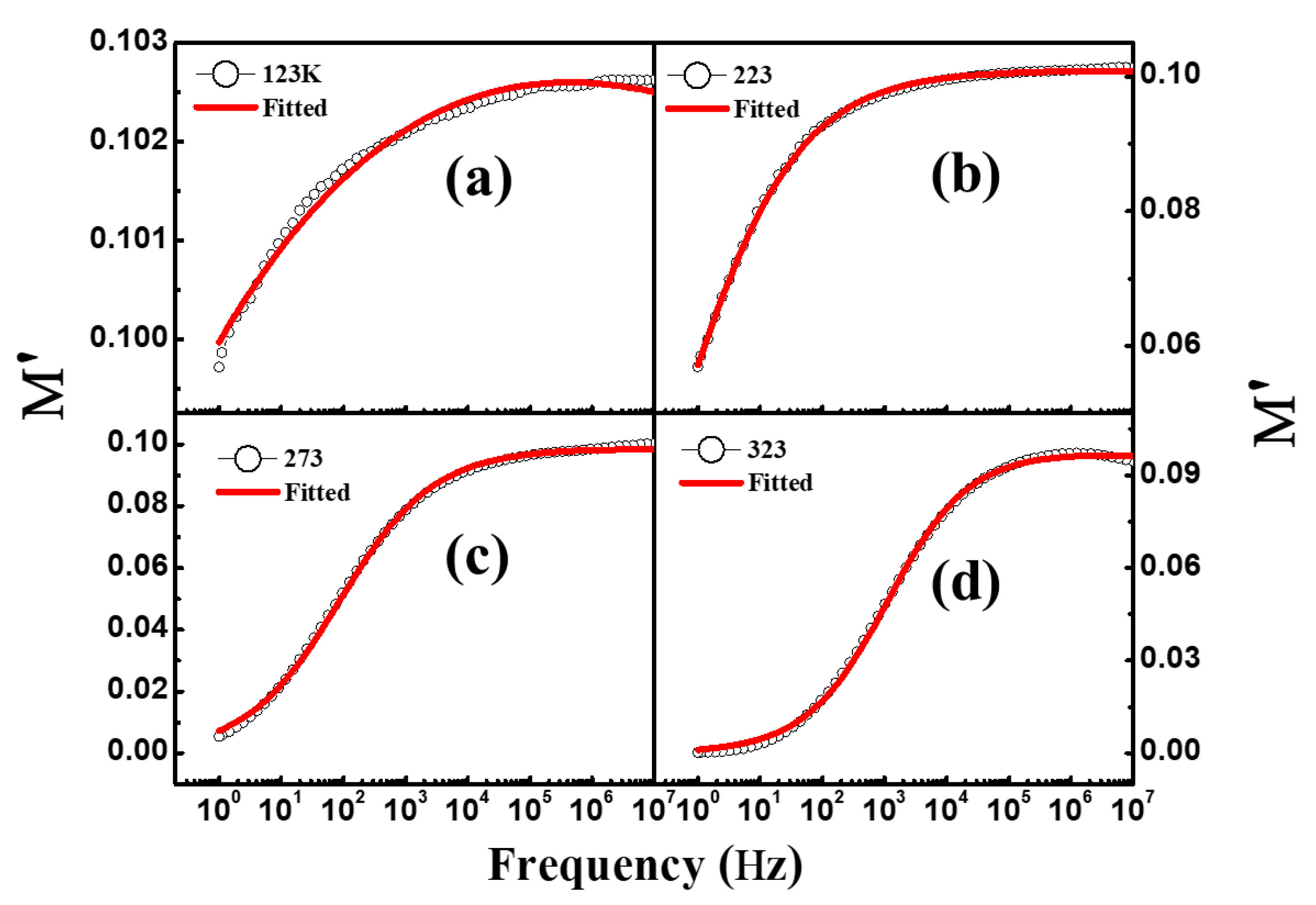
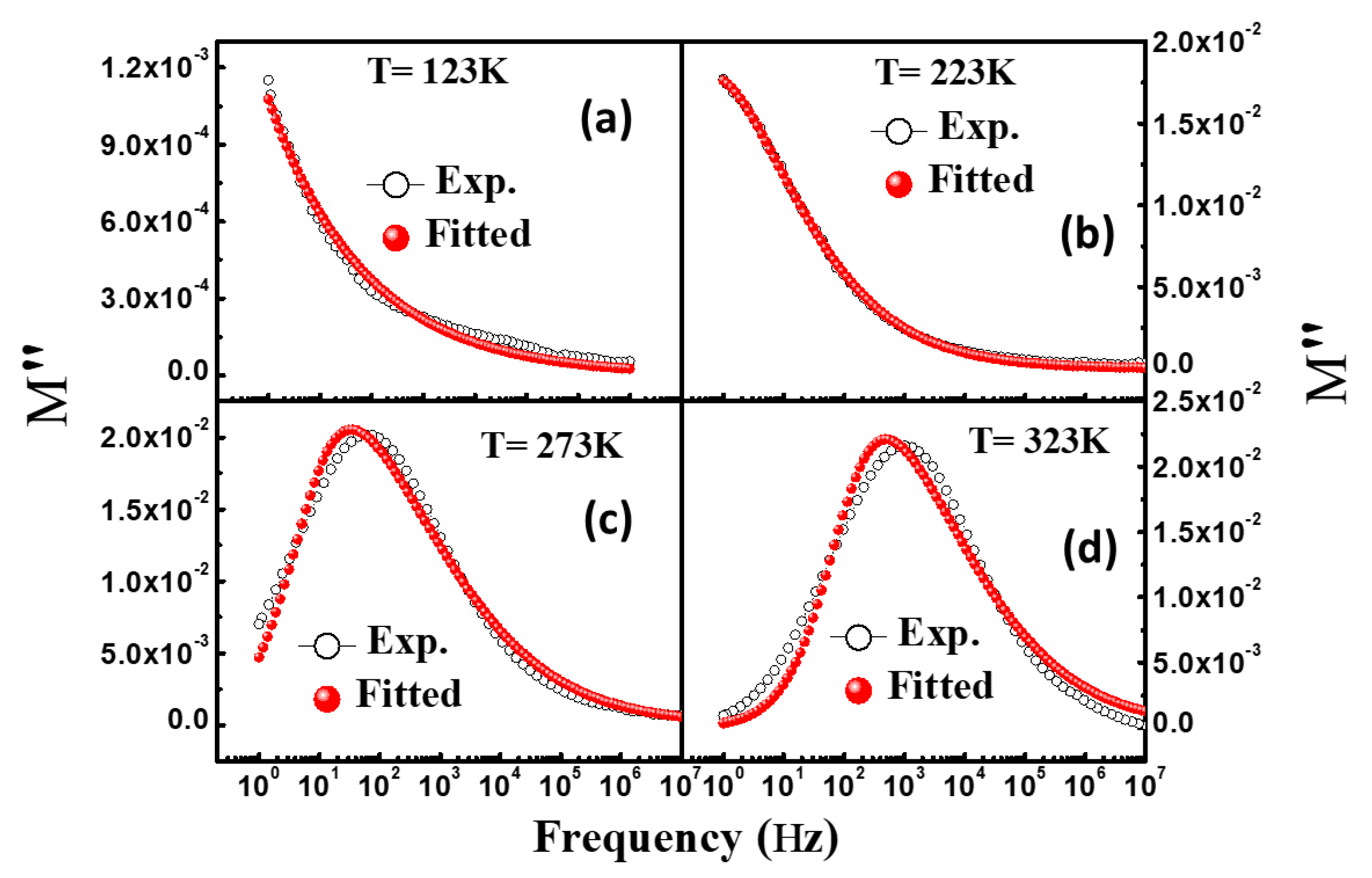
3.6. Modulus Spectroscopy
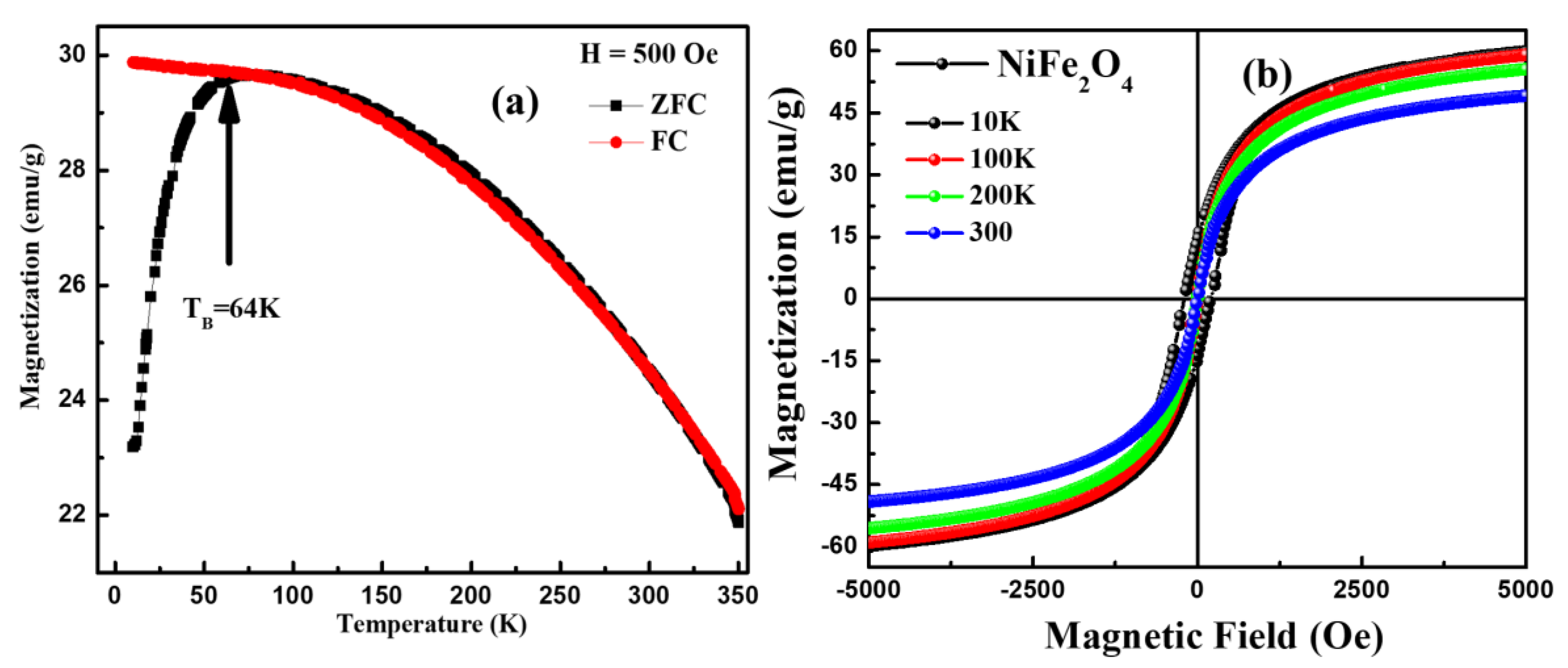
3.7. Magnetization Analysis
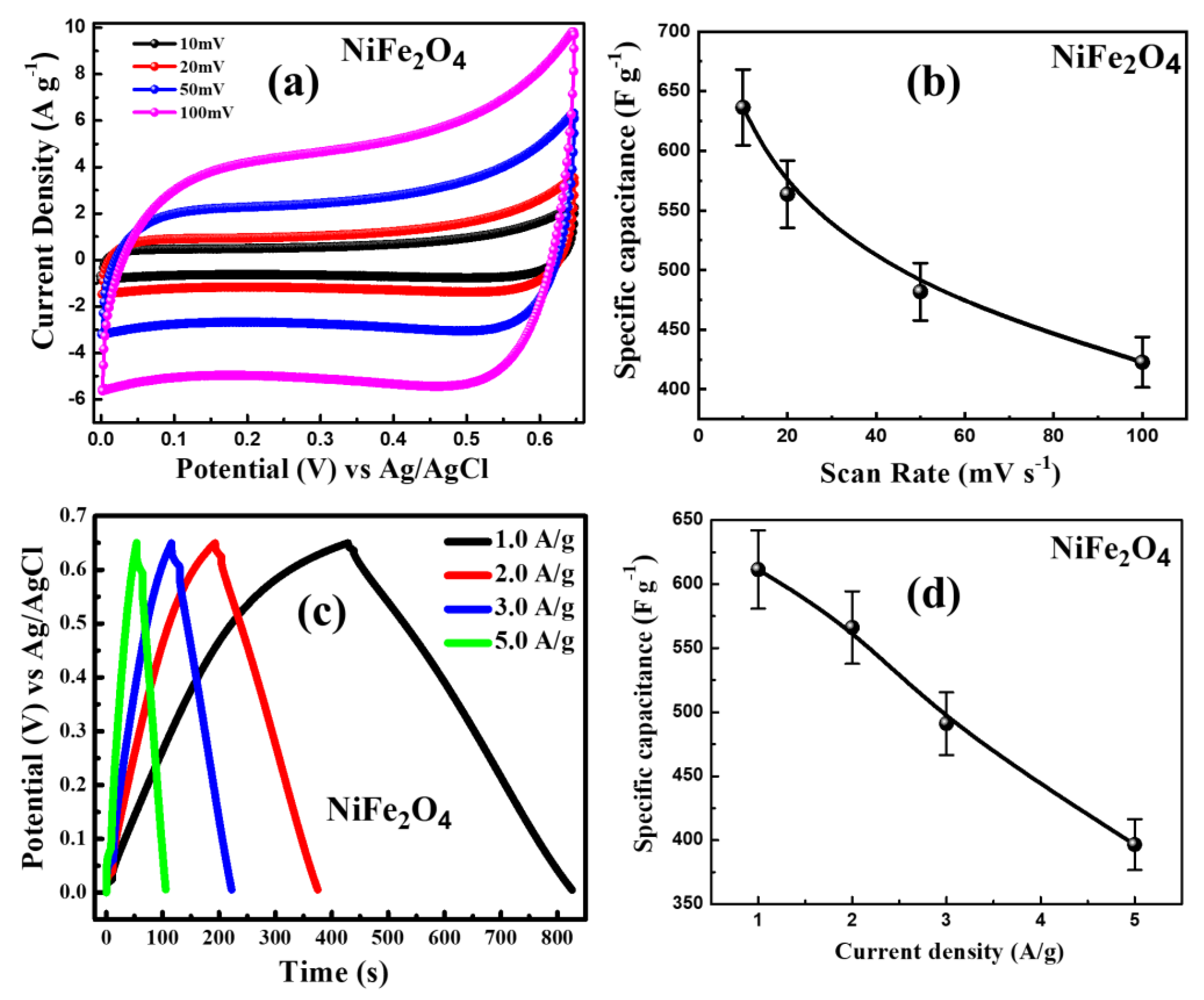
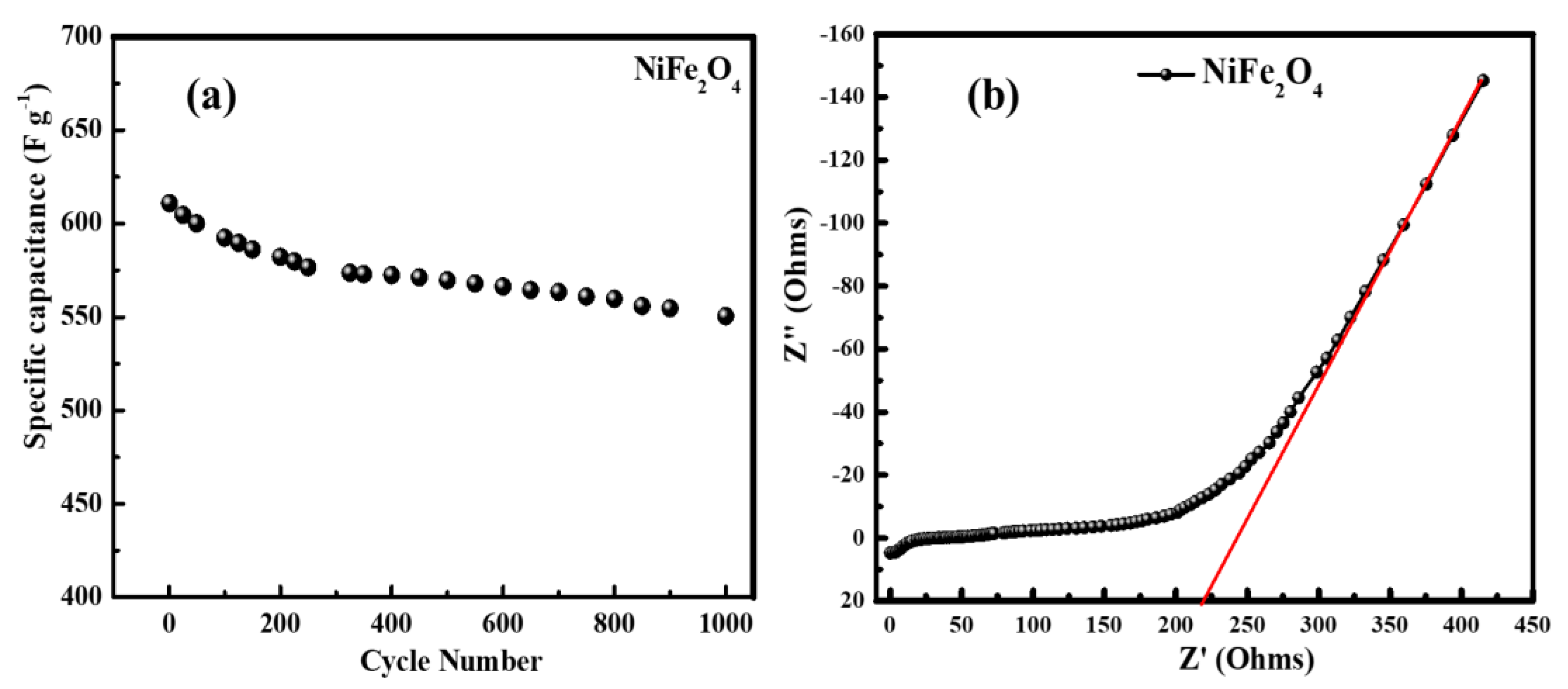
3.8. Electrochemical Performance
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tiwari, N.; Kadam, S.; Ingole, R.; Kulkarni, S. Facile hydrothermal synthesis of ZnFe2O4 nanostructures for high-performance supercapacitor application. Ceram. Int. 2022, 48, 29478–29483. [Google Scholar] [CrossRef]
- Bohra, M.; Alman, V.; Arras, R. Nanostructured ZnFe2O4: An Exotic Energy Material. Nanomaterials 2021, 11, 1286. [Google Scholar] [CrossRef]
- Kumar, P.; Mathpal, M.C.; Inwati, G.K.; Kumar, S.; Duvenhage, M.-M.; Roos, W.D.; Swart, H.C. Study of Defect-Induced Chemical Modifications in Spinel Zinc-Ferrites Nanostructures by In-Depth XPS Investigation. Magnetochemistry 2023, 9, 20. [Google Scholar] [CrossRef]
- Kumar, P.; Mathpal, M.C.; Inwati, G.K.; Duvenhage, M.-M.; Meyer, E.L.; Soler, M.; Swart, H.C. Chapter 32—Future of Smart Supercapacitors. In Smart Supercapacitors; Elsevier: Amsterdam, The Netherlands, 2023; pp. 851–866. [Google Scholar] [CrossRef]
- Inwati, G.K.; Mehetre, S.; Ameta, R.K.; Kumar, P.; Swart, H.C.; Yadav, V.K.; Makwana, B.A.; Kakodiya, S.D.; Gnanamoorthy, G. Chapter 8—Smart supercapacitors—A new perspective. In Smart Supercapacitors; Elsevier: Amsterdam, The Netherlands, 2023; pp. 159–176. [Google Scholar] [CrossRef]
- Chang, S.-K.; Zainal, Z.; Tan, K.-B.; Yusof, N.A.; Yusoff, W.M.D.W.; Prabaharan, S. Recent development in spinel cobaltites for supercapacitor application. Ceram. Int. 2015, 41, 11396–11401. [Google Scholar] [CrossRef]
- Venkatachalam, V.; Jayavel, R. Novel Synthesis of Ni-Ferrite (NiFe2O4) Electrode Material for Supercapacitor Applications. AIP Conf. Proc. 2015, 1665, 14001. [Google Scholar] [CrossRef]
- Choudhary, B.; Kumar, U.; Kumar, S.; Chander, S.; Kumar, S.; Dalela, S.; Dolia, S.; Alvi, P. Irreversible magnetic behavior with temperature variation of Ni0.5Co0.5Fe2O4 nanoparticles. J. Magn. Magn. Mater. 2020, 507, 166861. [Google Scholar] [CrossRef]
- Bandgar, S.B.; Vadiyar, M.M.; Jambhale, C.L.; Kim, J.-H.; Kolekar, S.S. Superfast ice crystal-assisted synthesis of NiFe2O4 and ZnFe2O4 nanostructures for flexible high-energy density asymmetric supercapacitors. J. Alloys Compd. 2021, 853, 157129. [Google Scholar] [CrossRef]
- Nithyayini, K.; Harish, M.; Nagashree, K. Electrochemical detection of nitrite at NiFe2O4 nanoparticles synthesised by solvent deficient method. Electrochim. Acta 2019, 317, 701–710. [Google Scholar] [CrossRef]
- Kasapoglu, N.; Birsöz, B.; Baykal, A.; Köseoglu, Y.; Toprak, M. Synthesis and magnetic properties of octahedral ferrite NiχCo1−χ Fe2O4 nanocrystals. Open Chem. 2007, 5, 570–580. [Google Scholar] [CrossRef]
- Jovalekic, C.; Nikolic, A.; Gruden-Pavlovic, M.; Pavlovic, M. Mechanochemical synthesis of stoichiometric nickel and nickel-zinc ferrite powders with Nicolson-Ross analysis of absorption coefficients. J. Serb. Chem. Soc. 2012, 77, 497–505. [Google Scholar] [CrossRef]
- Dantas, J.; Santos, J.R.D.; Cunha, R.B.L.; Kiminami, R.; Costa, A.C.F.M. Use of Ni-Zn ferrites doped with Cu as catalyst in the transesterification of soybean oil to methyl esters. Mater. Res. 2013, 16, 625–627. [Google Scholar] [CrossRef] [Green Version]
- Toghan, A.; Khairy, M.; Kamar, E.; Mousa, M. Effect of particle size and morphological structure on the physical properties of NiFe2O4 for supercapacitor application. J. Mater. Res. Technol. 2022, 19, 3521–3535. [Google Scholar] [CrossRef]
- Mordina, B.; Kumar, R.; Neeraj, N.S.; Srivastava, A.K.; Setua, D.K.; Sharma, A. Binder free high performance hybrid supercapacitor device based on nickel ferrite nanoparticles. J. Energy Storage 2020, 31, 101677. [Google Scholar] [CrossRef]
- Fu, M.; Chen, W.; Zhu, X.; Liu, Q. One-step preparation of one dimensional nickel ferrites/graphene composites for supercapacitor electrode with excellent cycling stability. J. Power Sources 2018, 396, 41–48. [Google Scholar] [CrossRef]
- Kumar, N.; Kumar, A.; Chandrasekaran, S.; Tseng, T.Y. Synthesis of Mesoporous NiFe2O4 Nanoparticles for Enhanced Supercapacitive Performance. J. Clean Energy Technol. 2018, 6, 51–55. [Google Scholar] [CrossRef] [Green Version]
- Kumar, R.; Kumar, R.; Sahoo, P.K.; Singh, M.; Soam, A. Synthesis of nickel ferrite for supercapacitor application. Mater. Today Proc. 2022, 67, 1001–1004. [Google Scholar] [CrossRef]
- Soam, A.; Kumar, R.; Sahoo, P.K.; Mahender, C.; Kumar, B.; Arya, N.; Singh, M.; Parida, S.; Dusane, R.O. Synthesis of Nickel Ferrite Nanoparticles Supported on Graphene Nanosheets as Composite Electrodes for High Performance Supercapacitor. Chemistryselect 2019, 4, 9952–9958. [Google Scholar] [CrossRef]
- Gao, X.; Wang, W.; Bi, J.; Chen, Y.; Hao, X.; Sun, X.; Zhang, J. Morphology-controllable preparation of NiFe2O4 as high performance electrode material for supercapacitor. Electrochim. Acta 2019, 296, 181–189. [Google Scholar] [CrossRef]
- Arun, T.; Kavinkumar, T.; Udayabhaskar, R.; Kiruthiga, R.; Morel, M.J.; Aepuru, R.; Dineshbabu, N.; Ravichandran, K.; Akbari-Fakhrabadi, A.; Mangalaraja, R. NiFe2O4 nanospheres with size-tunable magnetic and electrochemical properties for superior supercapacitor electrode performance. Electrochim. Acta 2021, 399, 139346. [Google Scholar] [CrossRef]
- Farea, A.; Kumar, S.; Batoo, K.M.; Yousef, A.; Lee, C.G. Alimuddin Influence of the doping of Ti4+ ions on electrical and magnetic properties of Mn1+xFe2−2xTixO4 ferrite. J. Alloys Compd. 2009, 469, 451–457. [Google Scholar] [CrossRef]
- Kumar, S.; Ahmed, F.; Shaalan, N.M.; Kumar, R.; Alshoaibi, A.; Arshi, N.; Dalela, S.; Sayeed, F.; Dwivedi, S.; Kumari, K. Structural, Magnetic, and Electrical Properties of CoFe2O4 Nanostructures Synthesized Using Microwave-Assisted Hydrothermal Method. Materials 2022, 15, 7955. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Alimuddin; Kumar, R.; Thakur, P.; Chae, K.H.; Angadi, B.; Choi, W.K. Electrical transport, magnetic, and electronic structure studies of Mg0.95Mn0.05Fe2−2xTi2xO4±δ(0 ≤ x ≤ 0.5) ferrites. J. Phys. Condens. Matter 2007, 19, 476210. [Google Scholar] [CrossRef]
- Sinha, A.; Dutta, A. Microstructure evolution, dielectric relaxation and scaling behavior of Dy-for-Fe substituted Ni-nanoferrites. RSC Adv. 2015, 5, 100330–100338. [Google Scholar] [CrossRef]
- He, Y.; Zhang, L.; Xiong, H.-W.; Kang, X. Evolution of lattice defects in nickel ferrite spinel: Oxygen vacancy and cation substitution. J. Alloys Compd. 2022, 917, 165494. [Google Scholar] [CrossRef]
- Ahlawat, A.; Sathe, V.G. Raman study of NiFe2 O4 nanoparticles, bulk and films: Effect of laser power. J. Raman Spectrosc. 2011, 42, 1087–1094. [Google Scholar] [CrossRef]
- Ahlawat, A.; Sathe, V.; Reddy, V.; Gupta, A. Mossbauer, Raman and X-ray diffraction studies of superparamagnetic NiFe2O4 nanoparticles prepared by sol–gel auto-combustion method. J. Magn. Magn. Mater. 2011, 323, 2049–2054. [Google Scholar] [CrossRef]
- Singh, A.K.; Goel, T.C.; Mendiratta, R.G.; Thakur, O.P.; Prakash, C. Dielectric properties of Mn-substituted Ni–Zn ferrites. J. Appl. Phys. 2002, 91, 6626. [Google Scholar] [CrossRef]
- Kumari, A.; Kumari, K.; Ahmed, F.; Alshoaibi, A.; Alvi, P.; Dalela, S.; Ahmad, M.M.; Aljawfi, R.N.; Dua, P.; Vij, A.; et al. Influence of Sm doping on structural, ferroelectric, electrical, optical and magnetic properties of BaTiO3. Vacuum 2021, 184, 109872. [Google Scholar] [CrossRef]
- Fawzi, A.S.; Sheikh, A.; Mathe, V. Structural, dielectric properties and AC conductivity of Ni(1−x)ZnxFe2O4 spinel ferrites. J. Alloys Compd. 2010, 502, 231–237. [Google Scholar] [CrossRef]
- Hashim, M.; Alimuddin; Kumar, S.; Shirsath, S.E.; Mohammed, E.; Chung, H.; Kumar, R. Studies on the activation energy from the ac conductivity measurements of rubber ferrite composites containing manganese zinc ferrite. Phys. B Condens. Matter 2012, 407, 4097–4103. [Google Scholar] [CrossRef]
- Khamzin, A. Trap-controlled fractal diffusion model of the Havriliak-Negami dielectric relaxation. J. Non-Cryst. Solids 2019, 524, 119636. [Google Scholar] [CrossRef]
- Dam, T.; Tripathy, S.N.; Paluch, M.; Jena, S.S.; Pradhan, D.K. Investigations of Relaxation Dynamics and Observation of Nearly Constant Loss Phenomena in PEO20-LiCF3SO3-ZrO2 Based Polymer Nano-Composite Electrolyte. Electrochim. Acta 2016, 202, 147–156. [Google Scholar] [CrossRef]
- Yadav, R.S.; Havlica, J.; Masilko, J.; Tkacz, J.; Kuřitka, I.; Vilcakova, J. Anneal-tuned structural, dielectric and electrical properties of ZnFe2O4 nanoparticles synthesized by starch-assisted sol–gel auto-combustion method. J. Mater. Sci. Mater. Electron. 2016, 27, 5992–6002. [Google Scholar] [CrossRef]
- Sinha, A.; Dutta, A. Structural Interpretation of Ion Transport and Small Polaron Hopping Conduction in Gd Substituted Nickel Nanoferrites. Phys. Status Solidi Appl. Mater. Sci. 2018, 215, 1700908. [Google Scholar] [CrossRef]
- Choudhury, S.; Sinha, M.; Dutta, H.; Mandal, M.; Pradhan, S.; Meikap, A. Activation behavior and dielectric relaxation of nanocrystalline zinc ferrite. Mater. Res. Bull. 2014, 60, 446–452. [Google Scholar] [CrossRef]
- Mannan, M.A.; Hossen, M.B. Dynamic electric, modulus and impedance study of Ni0.5Cu0.2Cd0.3Fe2-zAlzO4 nanoparticles with magnetization and Rietveld analysis. J. Mater. Sci. Mater. Electron. 2021, 32, 24524–24539. [Google Scholar] [CrossRef]
- Coşkun, M.; Polat, O.; Coşkun, F.M.; Durmuş, Z.; Çağlar, M.; Türüt, A. The electrical modulus and other dielectric properties by the impedance spectroscopy of LaCrO3 and LaCr0.90Ir0.10O3 perovskites. RSC Adv. 2018, 8, 4634–4648. [Google Scholar] [CrossRef] [Green Version]
- Kumar, L.; Kumar, P.; Kar, M. Cation distribution by Rietveld technique and magnetocrystalline anisotropy of Zn substituted nanocrystalline cobalt ferrite. J. Alloys Compd. 2013, 551, 72–81. [Google Scholar] [CrossRef]
- Rojas, P.C.R.; Tancredi, P.; Londoño-Calderón, C.L.; Londoño, O.M.; Socolovsky, L.M. Comparison of the anisotropy energy obtained from temperature dependent AC and DC magnetometry in iron oxide nanoparticles (IONPs) with controlled dipolar interactions. J. Magn. Magn. Mater. 2022, 547, 168790. [Google Scholar] [CrossRef]
- Sharma, S.; Vargas, J.; Pirota, K.; Kumar, S.; Lee, C.; Knobel, M. Synthesis and ageing effect in FeO nanoparticles: Transformation to core–shell FeO/Fe3O4 and their magnetic characterization. J. Alloys Compd. 2011, 509, 6414–6417. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, J.; Liu, A.; Yang, H.; Wang, L. Deposition of polyaniline on porous ZnFe2O4 as electrode for enhanced performance supercapacitor. J. Mater. Sci. Mater. Electron. 2018, 29, 16369–16377. [Google Scholar] [CrossRef]
- Kumar, S.; Ahmed, F.; Ahmad, N.; Shaalan, N.M.; Kumar, R.; Alshoaibi, A.; Arshi, N.; Dalela, S.; Albossed, M.; Chae, K.H.; et al. Role of Cr Doping on the Structure, Electronic Structure, and Electrochemical Properties of BiFeO3 Nanoparticles. Materials 2022, 15, 4118. [Google Scholar] [CrossRef] [PubMed]
- Moosavifard, S.E.; Najafi, F.; Izadi, M.; Gharibzadeh, Z.; Habibi, Z. Facile synthesis of nanoporous spinel nickel-manganese-cobalt ternary oxide hollow spheres as high-performance supercapacitor electrode material. Adv. Nanochem. 2020, 2, 7–10. [Google Scholar] [CrossRef]
- Mary, B.C.J.; Vijaya, J.J.; Saravanakumar, B.; Bououdina, M.; Kennedy, L.J. NiFe2O4 and 2D-rGO decorated with NiFe2O4 nanoparticles as highly efficient electrodes for supercapacitors. Synth. Met. 2022, 291, 117201. [Google Scholar] [CrossRef]
- Soam, A.; Kumar, R.; Thatoi, D.; Singh, M. Electrochemical Performance and Working Voltage Optimization of Nickel Ferrite/Graphene Composite based Supercapacitor. J. Inorg. Organomet. Polym. Mater. 2020, 30, 3325–3331. [Google Scholar] [CrossRef]
- Zate, M.K.; Shaikh, S.F.; Jadhav, V.V.; Waghmare, S.D.; Ahn, D.Y.; Mane, R.S.; Han, S.-H.; Joo, O.-S. Electrochemical Supercapacitive Properties of Sprayed Nickel Ferrite Nanostructured Thin Film Electrode. J. Nanoeng. Nanomanuf. 2014, 4, 93–97. [Google Scholar] [CrossRef]
- Bhojane, P.; Sharma, A.; Pusty, M.; Kumar, Y.; Sen, S.; Shirage, P. Synthesis of Ammonia-Assisted Porous Nickel Ferrite (NiFe2O4) Nanostructures as an Electrode Material for Supercapacitors. J. Nanosci. Nanotechnol. 2017, 17, 1387–1392. [Google Scholar] [CrossRef]
- Deyab, M.; Awadallah, A.E.; Ahmed, H.A.; Mohsen, Q. Progress study on nickel ferrite alloy-graphene nanosheets nanocomposites as supercapacitor electrodes. J. Energy Storage 2022, 46, 103926. [Google Scholar] [CrossRef]
- Soam, A.; Kavle, P.; Kumbhar, A.; Dusane, R.O. Performance enhancement of micro-supercapacitor by coating of graphene on silicon nanowires at room temperature. Curr. Appl. Phys. 2017, 17, 314–320. [Google Scholar] [CrossRef]
- Kumar, R.; Soam, A.; Dusane, R.O.; Bhargava, P. Sucrose derived carbon coated silicon nanowires for supercapacitor ap-plication. J. Mater. Sci. Mater. Electron. 2018, 29, 1947–1954. [Google Scholar] [CrossRef]
- Naderi, H.; Sobati, H.; Nasab, A.S.; Nasrabadi, M.R.; Arani, M.E.; Ganjali, M.R.; Ehrlich, H. Synthesis and Supercapacitor Application of Cerium Tungstate Nanostructure. Chem. Sel. 2019, 4, 2862–2867. [Google Scholar] [CrossRef]

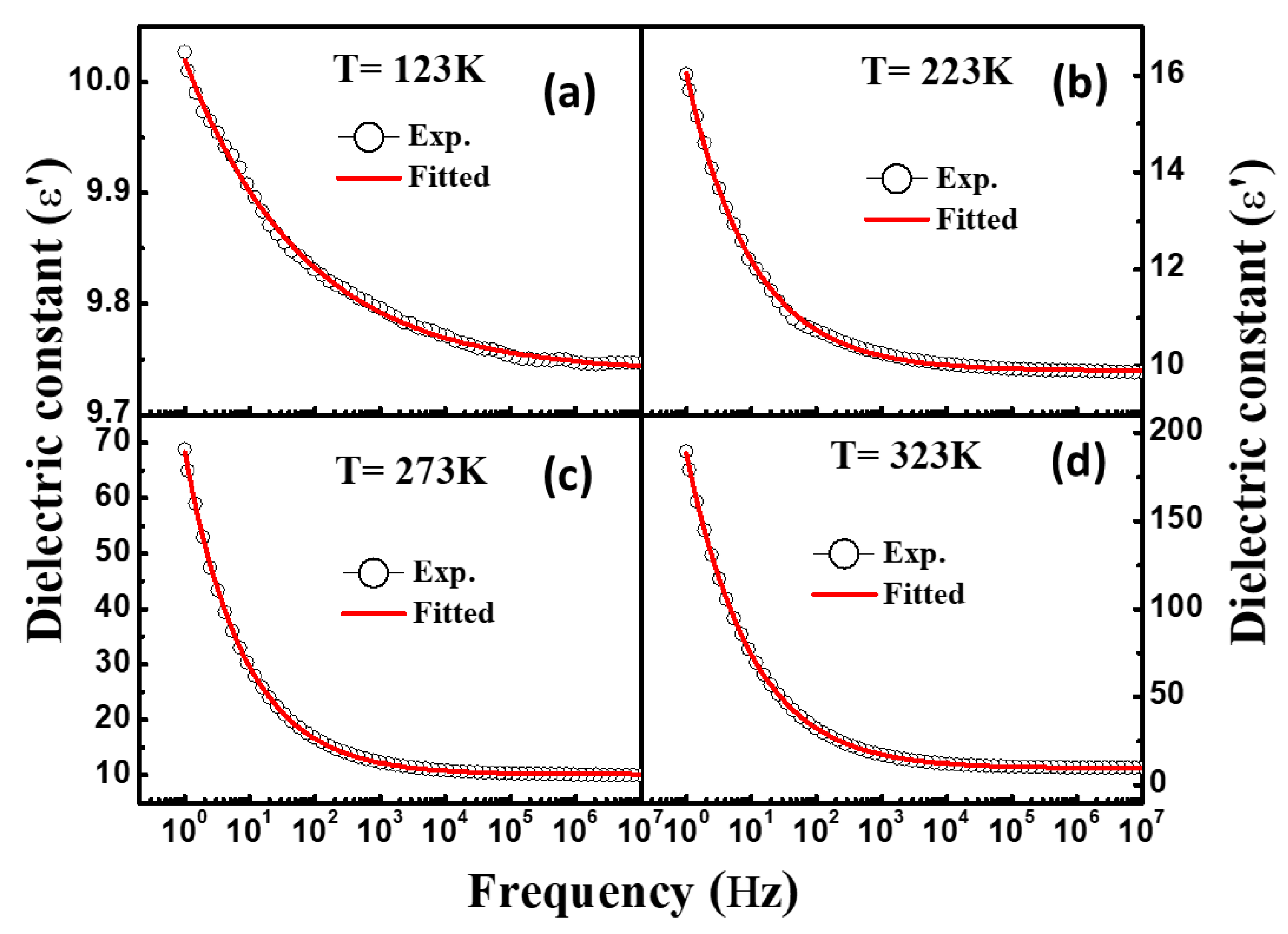

| Temperature (K) | Dielectric Strength (∆ε) | α | β | DC Conductivity (σdc) | Exponent (n) | Dielectric Constant at 1.0 kHz (ε′) | Loss Tangent at 1.0 kHz (tanδ) |
|---|---|---|---|---|---|---|---|
| 123 | 36.52 | 0.95 | 0.35 | 1.1 × 10−10 | 0.95 | 9.79 | 1.5 × 10−3 |
| 223 | 435.00 | 0.73 | 0.51 | 3.0 × 10−10 | 0.70 | 10.26 | 2.0 × 10−3 |
| 273 | 524.00 | 0.64 | 0.52 | 8.3 × 10−10 | 0.65 | 12.35 | 12.310−3 |
| 323 | 607.00 | 0.45 | 0.53 | 3.4 × 10−9 | 0.60 | 17.24 | 18,710−3 |
| Temperature (K) | MR (emu/g) × 10−2 | HC (Oe) | MS (emu/g) | Ms (emu/gm) from LAS |
|---|---|---|---|---|
| 10 | 1300 | 200 | 60.0 | 61.4 |
| 100 | 102 | 10 | 59.0 | 61.0 |
| 200 | 66 | 6.2 | 55.5 | 57.8 |
| 300 | 47 | 5.6 | 49.0 | 51.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, S.; Ahmed, F.; Shaalan, N.M.; Arshi, N.; Dalela, S.; Chae, K.H. Investigations of Structural, Magnetic, and Electrochemical Properties of NiFe2O4 Nanoparticles as Electrode Materials for Supercapacitor Applications. Materials 2023, 16, 4328. https://doi.org/10.3390/ma16124328
Kumar S, Ahmed F, Shaalan NM, Arshi N, Dalela S, Chae KH. Investigations of Structural, Magnetic, and Electrochemical Properties of NiFe2O4 Nanoparticles as Electrode Materials for Supercapacitor Applications. Materials. 2023; 16(12):4328. https://doi.org/10.3390/ma16124328
Chicago/Turabian StyleKumar, Shalendra, Faheem Ahmed, Nagih M. Shaalan, Nishat Arshi, Saurabh Dalela, and Keun Hwa Chae. 2023. "Investigations of Structural, Magnetic, and Electrochemical Properties of NiFe2O4 Nanoparticles as Electrode Materials for Supercapacitor Applications" Materials 16, no. 12: 4328. https://doi.org/10.3390/ma16124328









