Porous Talcum-Based Steatite Ceramics Fabricated by the Admixture of Organic Particles: Experimental Characterization and Effective Medium/Field Modeling of Thermo-Mechanical Properties
Abstract
:1. Introduction
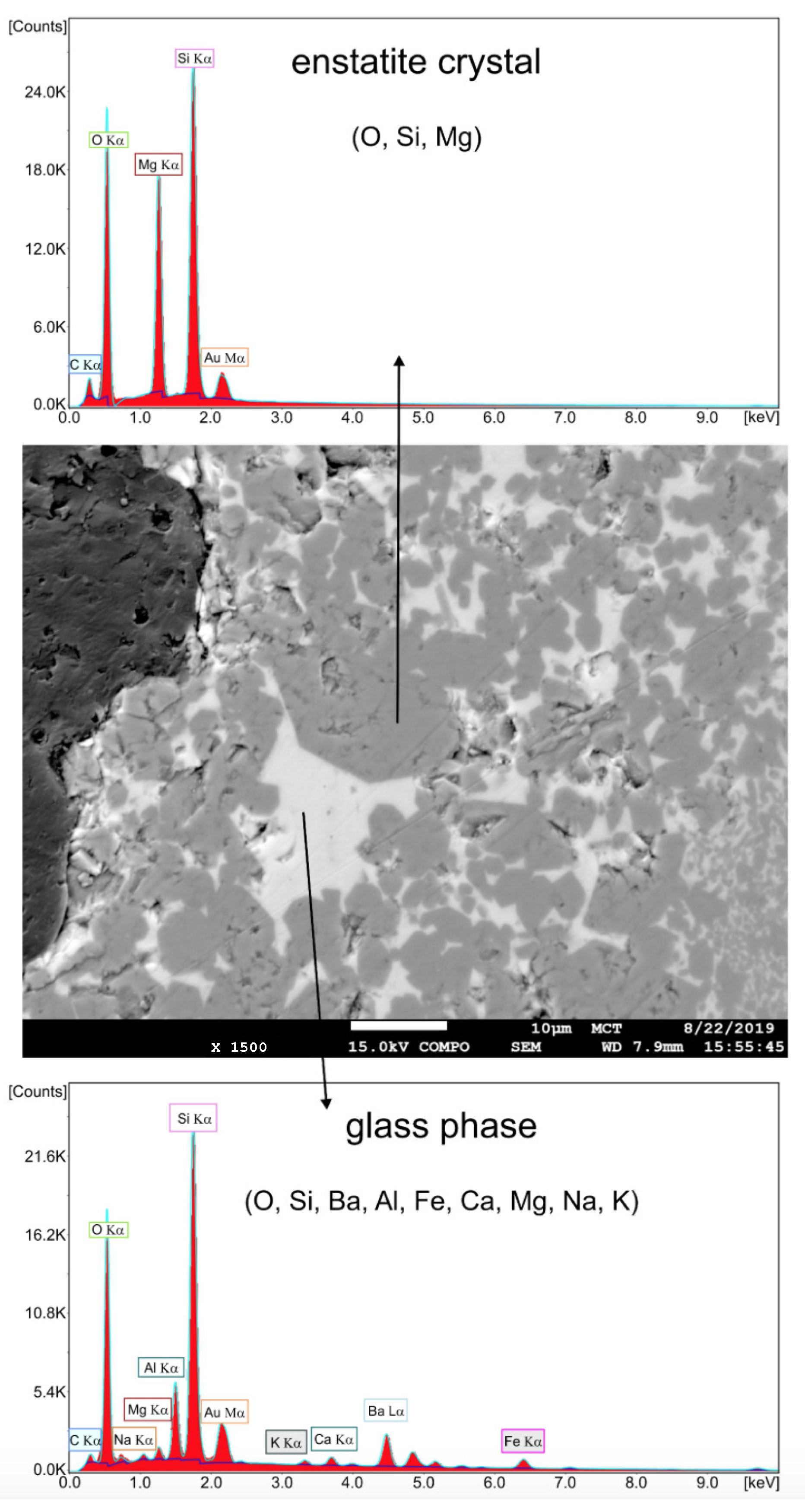
2. Material and Sample Preparation
3. Experimental Characterization
3.1. Thermal Properties
3.2. Mechanical Properties
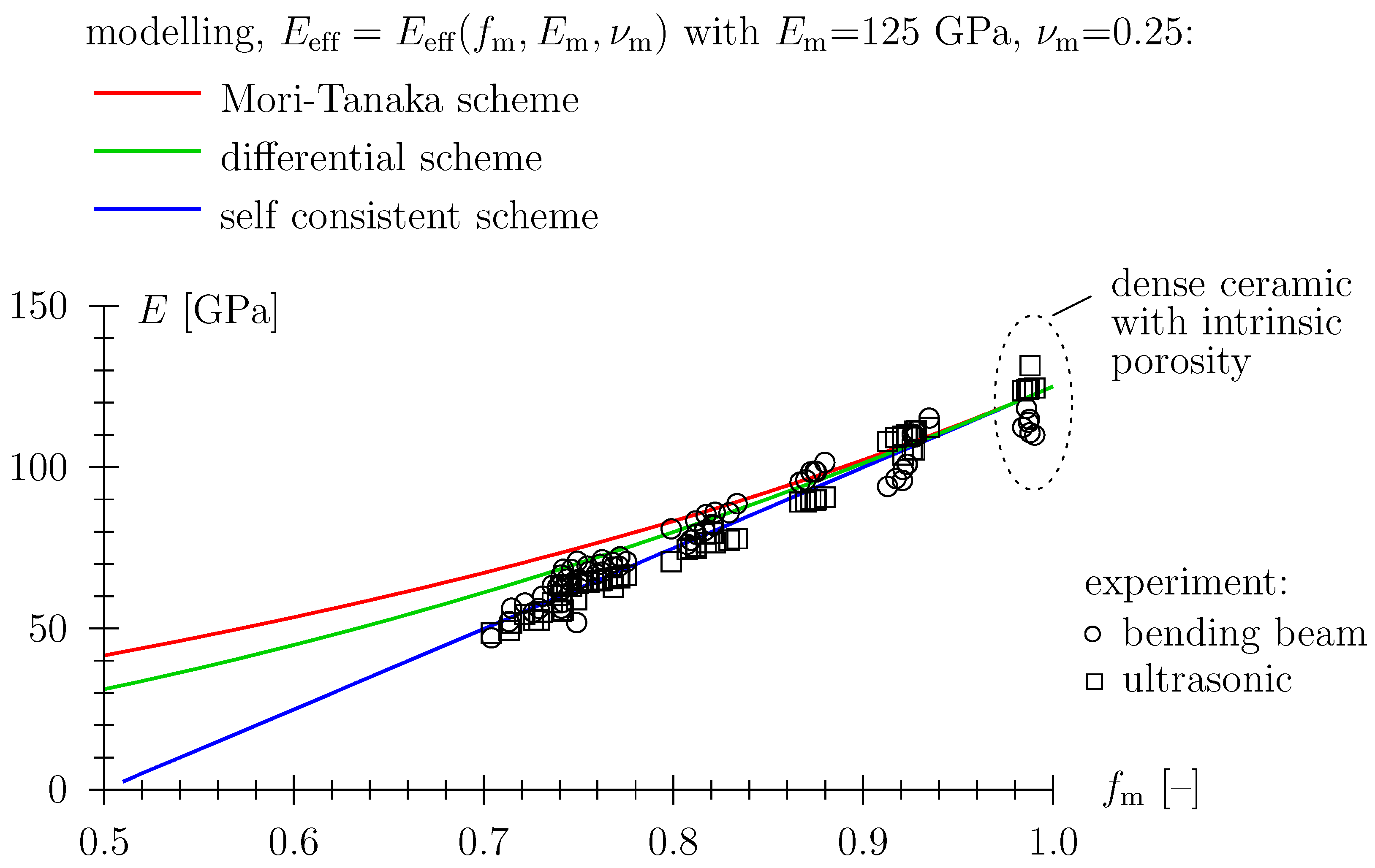
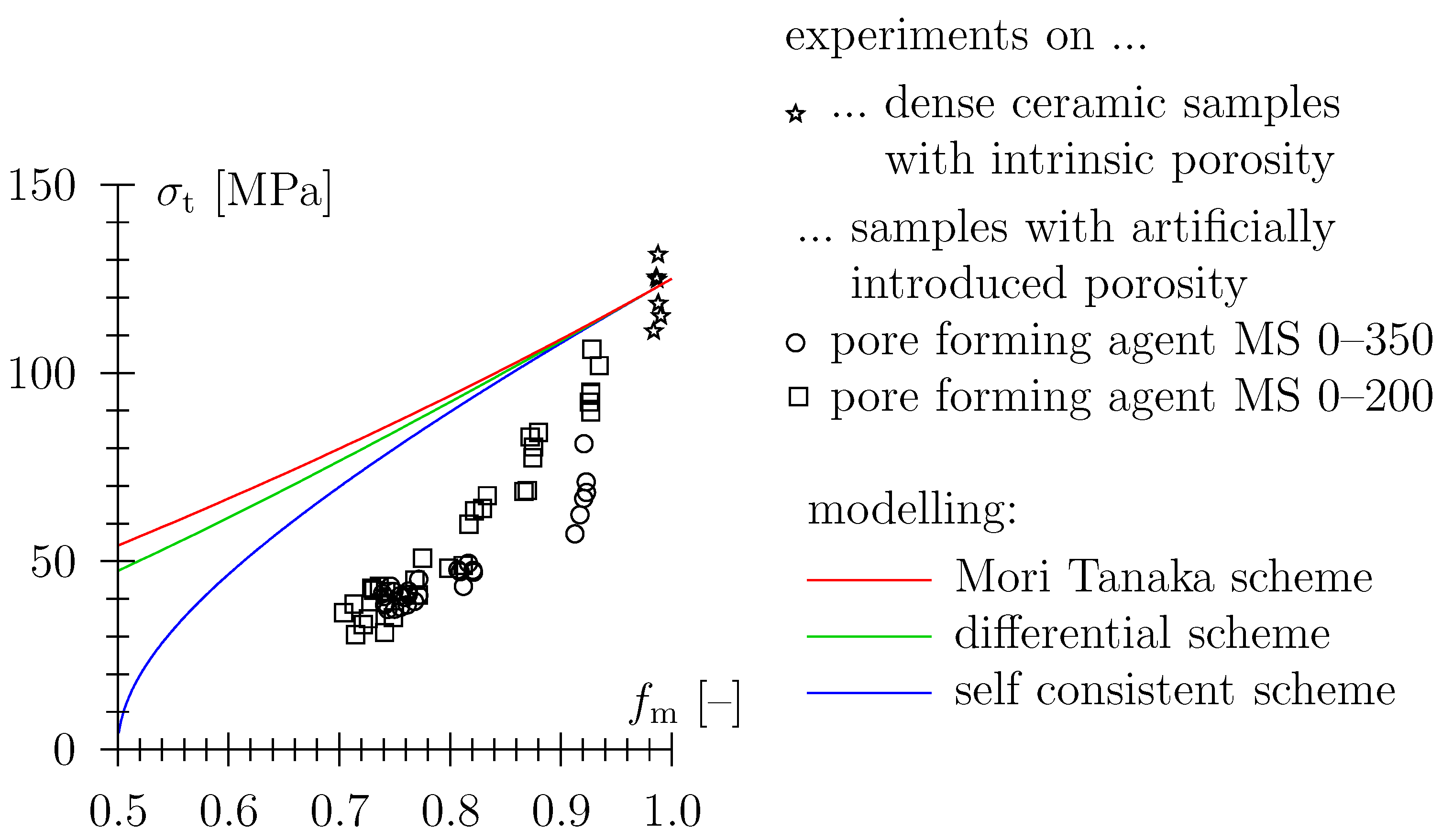
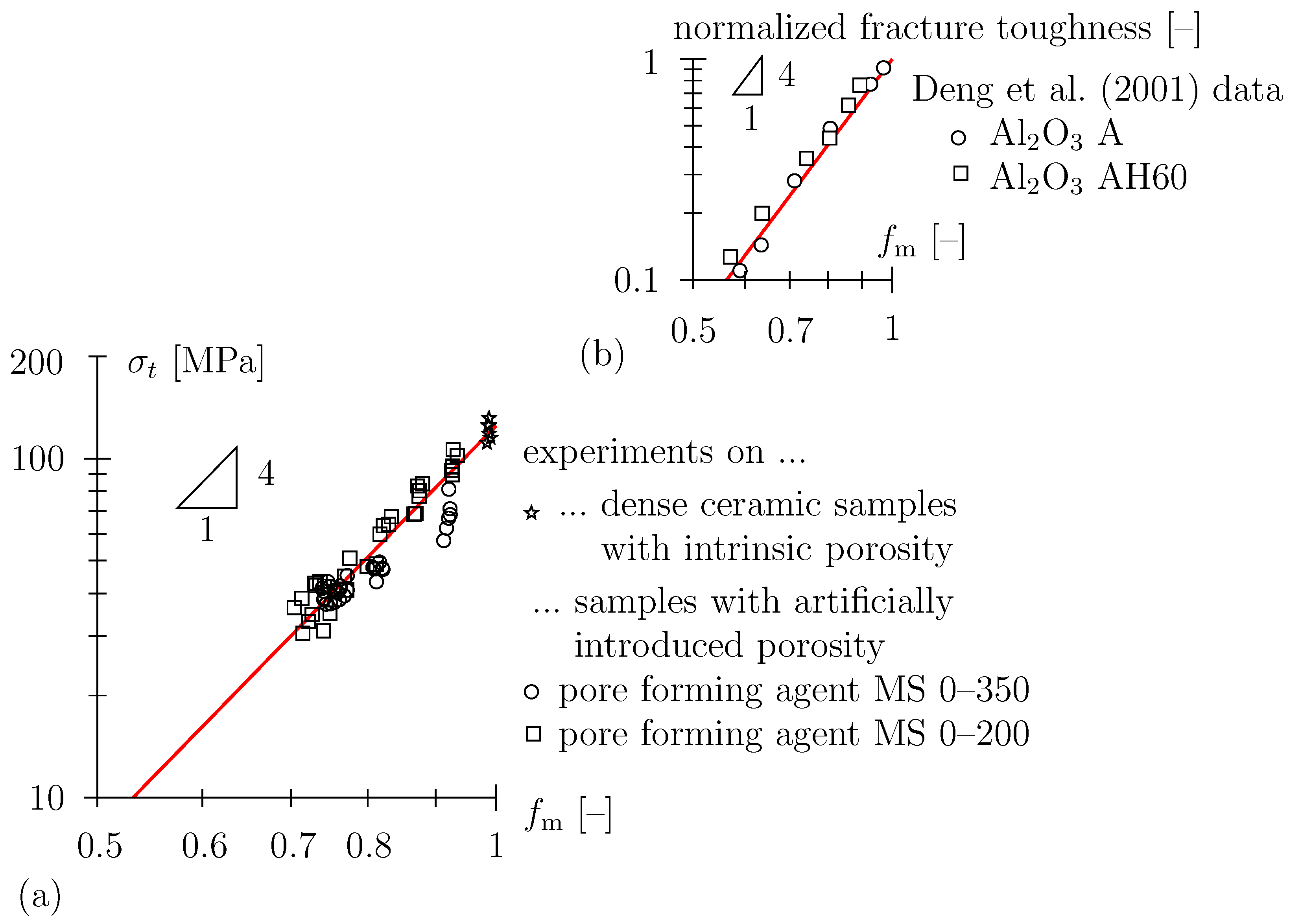
4. Discussion: Effective Medium/Field Modeling of Structure/Property-Relations
4.1. Thermal Conductivity
- Maxwell–Eucken expression [21], Kanaun–Levin method [22,23,24,25], or Hashin–Shtrikman upper bound [26] (in continuum micromechanics, the related homogenization method is referred to as the Mori–Tanaka scheme [27,28], see Appendix A):derived for a spatial configuration where the local temperature distortion in the vicinity of a pore does not affect the temperature field in the vicinity of neighboring pores [29,30]. The expression may be employed for moderate porosity values, e.g., for spherical pores for 0.2.
- The differential scheme (DS) [31,32,33] departs from this restriction, i.e., is suitable for materials with porosity in the medium range. This scheme follows from a recurring application of the dilute distribution estimation [34,35], the latter representing a spatial configuration where pores are diluted in the matrix material and, hence, their interaction can be neglected; starting with the homogeneous matrix material, pore volume is embedded in the matrix material in infinitesimal steps and the dilute distribution estimation is employed for the determination of effective behavior in each step, etc., finally giving:
- One may consider spheroidal pore shape for the Maxwell–Eucken expression, the Kanaun–Levin method, and the differential scheme, with the influence of oblate and prolate geometry on effective behavior derived in [20,36]. For an isotropic distribution of spheroidal pores, the differential scheme reads:(see Figure 5b) with shape factor a function of the aspect ratio of the spheroidal pores and corresponding to oblate, to prolate pore shape, respectively (see Appendix B). Figure 5a depicts the shape factor as a function of aspect ratio . Note that whereas a prolate shape only minorly influences the shape factor, oblate shape with significantly alters the effective thermal behavior (as compared to a composite with spherical pores), as gets excessively big. Even a small porosity may lead to a significant reduction of thermal conductivity.Further note that for non-spherical pore shape, the Kanaun–Levin method and the Maxwell–Euken scheme do not coincide (for spherical pores, they do), with:andrespectively (see Figure 5c,d).
4.2. Mechanical Properties
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Homogenization Schemes for Elastic and Transport Properties of Two-Phase Composite Material (Effective Medium Theory)
Specialization for Effective Thermal Conductivity of Porous Materials
Appendix B. Shape Factor for Spheroidal Pores
Appendix C. Stress Concentration Factors in the Vicinity of Spherical Pores
References
- Leonelli, C.; Kamseu, E.; Boccaccini, D.N.; Melo, U.C.; Rizzuti, A.; Billong, N.; Miselli, P. Volcanic ash as alternative raw materials for traditional vitrified ceramic products. Adv. Appl. Ceram. 2007, 106, 135–141. [Google Scholar] [CrossRef]
- Kamseu, E.; Boccaccini, D.N.; Sola, A.; Rizzuti, A.; Leonelli, C.; Melo, C.U.; Billong, N. Sintering behaviour, microstructure and mechanical properties of low quartz content vitrified ceramics using volcanic ash. Adv. Appl. Ceram. 2008, 107, 19–26. [Google Scholar] [CrossRef]
- Jin, S.; Choi, J.W.; Jeong, C.M.; Huh, J.B.; Lee, S.H.; Lee, H.; Yun, M.J. Evaluating the wear of resin teeth by different opposing restorative materials. Materials 2019, 12, 3684. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vu, V.A.; Cloutier, A.; Bissonnette, B.; Blanchet, P.; Dagenais, C. Steatite powder additives in wood-cement drywall particleboards. Materials 2020, 13, 4813. [Google Scholar] [CrossRef]
- Kannaiyan, S.; Huang, S.J.; Rathnaraj, D.; Srinivasan, S.A. Effect of ball-milled steatite powder on the latent heat energy storage properties and heat charging—Discharging periods of paraffin wax as phase change material. Micromachines 2022, 13, 1456. [Google Scholar] [CrossRef]
- Ashurov, M.K.; Nuritdinov, I.; Saidakhmedov, K.K.; Ismailov, S.K. Nature of the luminescence of SNC steatite ceramic. At. Energy 2021, 130, 259–299. [Google Scholar] [CrossRef]
- Lorenzoni, F.C.; Bonfante, E.A.; Valverde, G.B.; Coelho, P.G.; Bonfante, G.; Thompson, V.; Silva, N.R. Effect of indenter material on reliability of all-ceramic crowns. J. Mech. Behav. Biomed. Mater. 2020, 108, 103831. [Google Scholar] [CrossRef]
- Nawafleh, N.; Bibars, A.R.; Al Twal, E.; Öchsner, A. Influence of antagonist material on fatigue and fracture resistance of zirconia crowns. Eur. J. Dent. 2020, 14, 200–205. [Google Scholar] [CrossRef] [Green Version]
- Perfler, L.; Peyker, L.; Hörtnagel, M.; Weinberger, N.; Pichler, C.; Traxl, R.; Lackner, R. Pore space of steatite ceramics triggered by the allowance of natural fibers: High-resolution X-ray microscopy analysis and related thermo-mechanical properties. Mater. Des. 2022, 218, 110704. [Google Scholar] [CrossRef]
- Pichler, C.; Lackner, R. Sesqui-power scaling of elasticity of closed-cell foams. Mater. Lett. 2012, 73, 212–215. [Google Scholar] [CrossRef]
- Pichler, C.; Lackner, R. Sesqui-power scaling of plateau strength of closed-cell foams. Mater. Sci. Eng. A 2013, 580, 313–321. [Google Scholar] [CrossRef]
- Pichler, C.; Traxl, R.; Lackner, R. Power-law scaling of thermal conductivity of highly porous ceramics. J. Eur. Ceram. Soc. 2015, 35, 1933–1941. [Google Scholar] [CrossRef]
- Traxl, R.; Pichler, C.; Lackner, R. Thin-Shell Model for Effective Thermal and Electrical Conductivity of Highly Porous Closed-Cell Metal Foams. Transp. Porous Media 2016, 113, 629–638. [Google Scholar] [CrossRef] [Green Version]
- Parker, W.J.; Jenkins, R.J.; Butler, C.P.; Abbott, G.L. Flash Method of Determining Thermal Diffusivity, Heat Capacity, and Thermal Conductivity. J. Appl. Phys. 1961, 32, 1679–1684. [Google Scholar] [CrossRef]
- Cowan, R.D. Pulse Method of Measuring Thermal Diffusivity at High Temperatures. J. Appl. Phys. 1963, 34, 926–927. [Google Scholar] [CrossRef]
- Cape, J.A.; Lehman, G.W. Temperature and Finite Pulse-Time Effects in the Flash Method for Measuring Thermal Diffusivity. J. Appl. Phys. 1963, 34, 1909–1913. [Google Scholar] [CrossRef]
- Love, A.E.H. A Treatise of the Mathematical Theory of Elasticity, 4th ed.; Cambridge University Press: Cambridge, UK, 1959. [Google Scholar]
- Kohlhauser, C.; Hellmich, C. Ultrasonic contact pulse transmission for elastic wave velocity and stiffness determination: Influence of specimen geometry and porosity. Eng. Struct. 2013, 47, 115–133. [Google Scholar] [CrossRef] [Green Version]
- Kolsky, H. Stress Waves in Solids; Oxford University Press: London, UK, 1953. [Google Scholar]
- Sevostianov, I.; Kachanov, M. Non-interaction approximation in the problem of effective properties. In Effective Properties of Heterogeneous Materials; Kachanov, M., Sevostianov, I., Eds.; Springer: Dordrecht, The Netherlands, 2013. [Google Scholar]
- Maxwell, J.C. Treatise on Electricity and Magnetism, 3rd ed.; Oxford University Press: London, UK, 1904; Volume 1. [Google Scholar]
- Kanaun, S.K.; Levin, V.M. Effective field method in mechanics of matrix composite materials. In Recent Advances in Mathematical Modelling of Composite Materials; Markov, K.Z., Ed.; World Scientific: Singapore, 1994; pp. 1–58. [Google Scholar]
- Kanaun, S.K. Dielectric properties of matrix composite materials with high volume concentrations of inclusions (effective field approach). Int. J. Eng. Sci. 2003, 41, 1287–1312. [Google Scholar] [CrossRef]
- Markov, K.Z. Justification of an effective field method in elasto-statics of heterogenous solids. J. Mech. Phys. Solids 2001, 49, 2621–2634. [Google Scholar] [CrossRef]
- Kanaun, S.; Levin, V. Effective field method in the theory of heterogeneous media. In Effective Properties of Heterogeneous Materials; Kachanov, M., Sevostianov, I., Eds.; Springer: Dordrecht, The Netherlands, 2013. [Google Scholar]
- Hashin, Z.; Shtrikman, S. A variational approach to the theory of the effective magnetic permeability of multiphase materials. J. Appl. Phys. 1962, 33, 3125–3131. [Google Scholar] [CrossRef]
- Tanaka, K.; Mori, T. Note on volume integrals of the elastic field around an ellipsoidal inclusion. J. Elast. 1972, 2, 199–200. [Google Scholar] [CrossRef]
- Mori, T.; Tanaka, K. Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Zaoui, A. Structural morphology and constitutive behaviour of microheterogeneous materials. In Continuum Micromechanics, CISM Courses and Lectures No. 377; Suquet, P., Ed.; Springer: Vienna, Austria, 1997. [Google Scholar]
- Zaoui, A. Continuum micromechanics: Survey. J. Eng. Mech. (ASCE) 2002, 128, 808–816. [Google Scholar] [CrossRef] [Green Version]
- Bruggeman, D.A.G. Berechnung verschiedener physikalischer Konstanten von heterogenen Stoffen. I. Dielektrizitätskonstanten und Leitfähigkeiten [Determination of various physical constants of heterogenous media. I. Dielectric constants and conductivities]. Ann. Der Phys. Leipz. 1935, 24, 636–679. (In Germany) [Google Scholar] [CrossRef]
- McLaughlin, R. A study of the differential scheme for composite materials. Int. J. Eng. Sci. 1977, 15, 237–244. [Google Scholar] [CrossRef]
- Norris, A.N. A differential scheme for the effective moduli of composites. Mech. Mater. 1985, 4, 1–16. [Google Scholar] [CrossRef]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. Lond. A 1957, 241, 376–396. [Google Scholar]
- Eshelby, J.D. Elastic inclusions and inhomogeneities. In Progress in Solid Mechanics 2; Sneddon, I.N., Hill, R., Eds.; North-Holland Publishing Company: Amsterdam, The Netherlands, 1962; pp. 89–140. [Google Scholar]
- Sevostianov, I.; Kovacik, J.; Simancik, F. Elastic and electric properties of closed-cell aluminum foams: Cross-property connection. Mater. Sci. Eng. A 2006, 420, 87–99. [Google Scholar] [CrossRef]
- Hershey, A.V. The elasticity of an isotropic aggregate of anisotropic cubic crystals. J. Appl. Mech. (ASME) 1954, 21, 236–240. [Google Scholar] [CrossRef]
- Kroener, E. Berechnung der elastischen Konstanten des Vielkristalls aus den Konstanten des Einkristalls [Computation of the elastic constants of a polycrystal based on the constants of the single crystal]. Z. F. Phys. 1958, 151, 504–518. (In Germany) [Google Scholar] [CrossRef]
- Dormieux, L.; Kondo, D.; Ulm, F.J. Microporomechanics; Wiley: Chichester, UK, 2006. [Google Scholar]
- Traxl, R.; Lackner, R. Multi-level homogenization of strength properties of hierarchical-organized matrix-inclusion materials. Mech. Mater. 2015, 89, 98–118. [Google Scholar] [CrossRef]
- Deng, Z.Y.; Fukasawa, T.; Ando, M.; Zhang, G.J.; Ohji, T. Microstructure and mechanical properties of porous alumina ceramics fabricated by the decomposition of aluminum hydroxide. J. Am. Ceram. Soc. 2001, 84, 2638–2644. [Google Scholar] [CrossRef]
- Jelitto, H.; Schneider, G. A geometric model for the fracture toughness of porous materials. Acta Mater. 2018, 151, 443–453. [Google Scholar] [CrossRef]
- Jelitto, H.; Schneider, G.A. Fracture toughness of porous materials—Experimental methods and data. Data Brief 2019, 23, 103709. [Google Scholar] [CrossRef]
- Goodier, J.N. Concentration of stress around spherical and cylindrical inclusions and flaws. J. Appl. Mech. (ASME) 1933, 1, 39–44. [Google Scholar] [CrossRef]
- Boccaccini, A.R.; Ondracek, G.; Mombello, E. Determination of stress concentration factors in porous materials. J. Mater. Sci. Lett. 1995, 14, 534–536. [Google Scholar] [CrossRef]
- Ondracek, G. The quantitative microstructure field property correlation of multiphase and porous materials. Rev. Powder Metall. Phys. Ceram. 1987, 3, 205–232. [Google Scholar]
- Buchner, T.; Kiefer, T.; Königsberger, M.; Jäger, A.; Füssl, J. Continuum micromechanics model for fired clay bricks: Upscaling of experimentally identified microstructural features to macroscopic elastic stiffness and thermal conductivity. Mater. Des. 2021, 212, 110212. [Google Scholar] [CrossRef]
- Buchner, T.; Königsberger, M.; Jäger, A.; Füssl, J. A validated multiscale model linking microstructural features of fired clay brick to its macroscopic multiaxial strength. Mech. Mater. 2022, 170, 104334. [Google Scholar] [CrossRef]
- Timothy, J.J.; Meschke, G. Micromechanics model for tortuosity and homogenized diffusion properties of porous materials with distributed micro-cracks. PAMM 2011, 11, 555–556. [Google Scholar] [CrossRef]
- Timothy, J.J.; Meschke, G. Cascade continuum micromechanics model for the effective diffusivity of porous materials: Exponential hierarchy across cascade levels. PAMM 2015, 15, 471–472. [Google Scholar] [CrossRef]
- Timothy, J.J.; Meschke, G. A cascade continuum micromechanics model for the effective elastic properties of porous materials. Int. J. Solids Struct. 2016, 83, 1–12. [Google Scholar] [CrossRef]
- Timothy, J.J.; Meschke, G. Effective diffusivity of porous materials with microcracks: Self-similar mean-field homogenization and pixel finite element simulations. Transp. Porous Media 2018, 125, 413–434. [Google Scholar] [CrossRef]

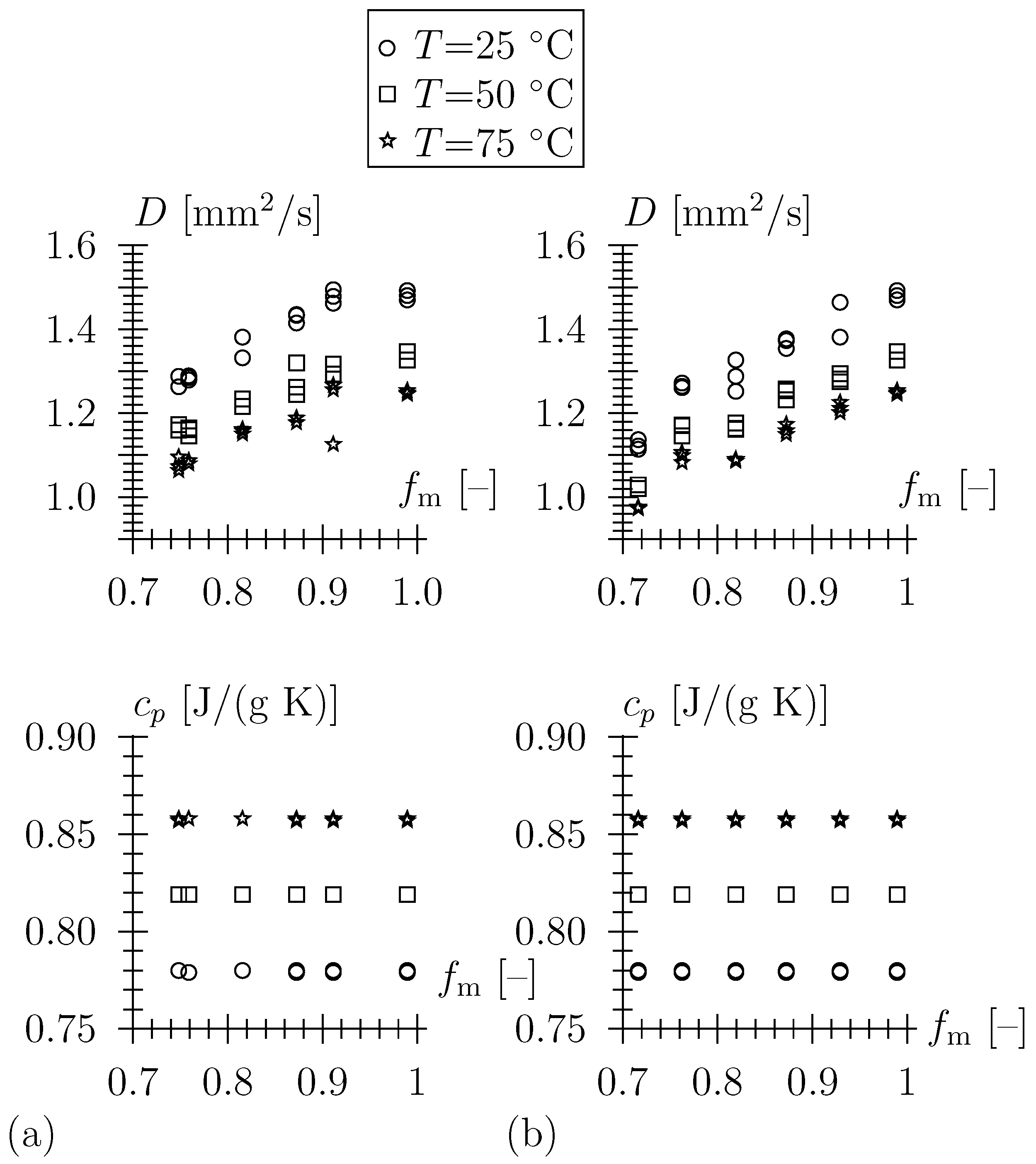
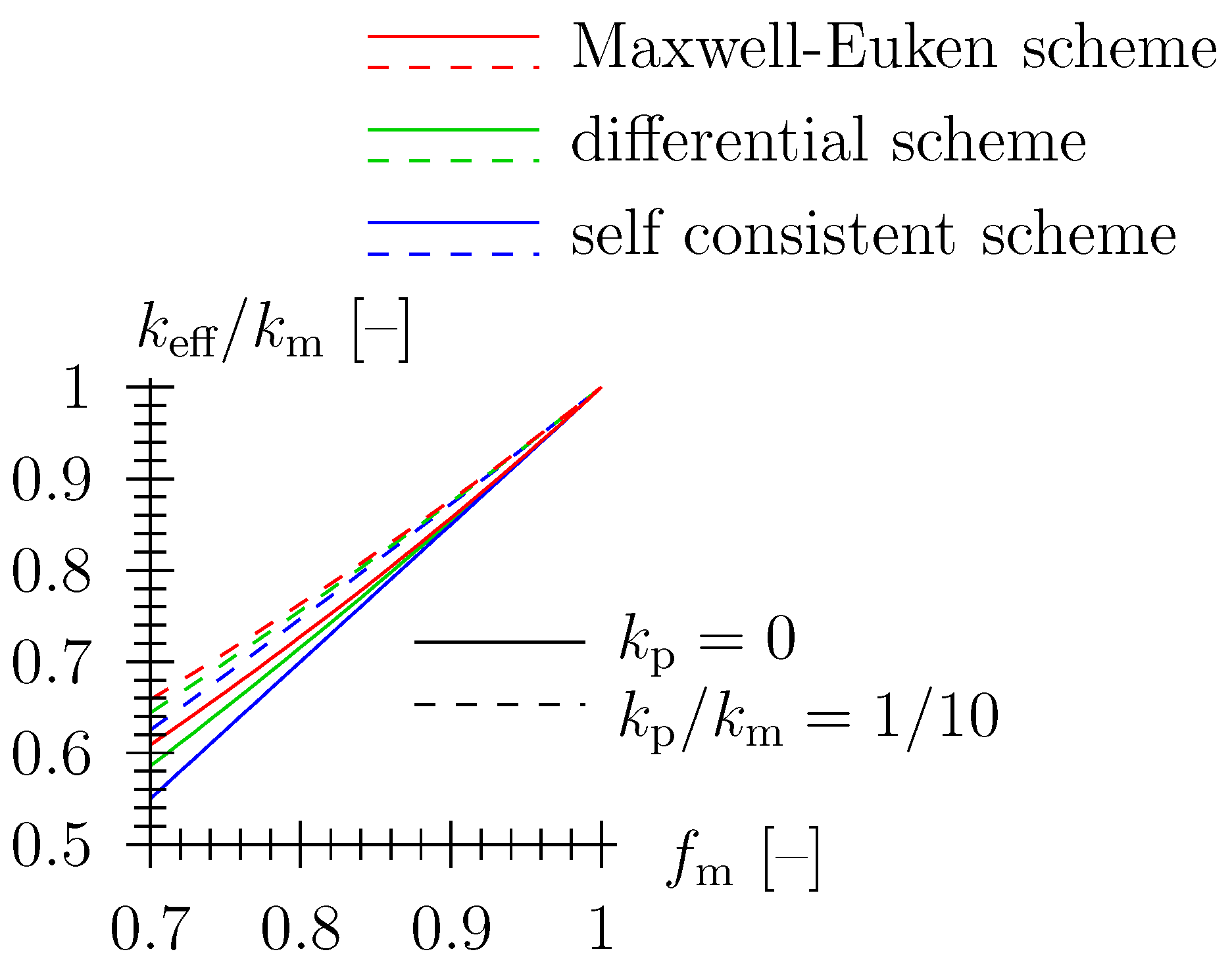

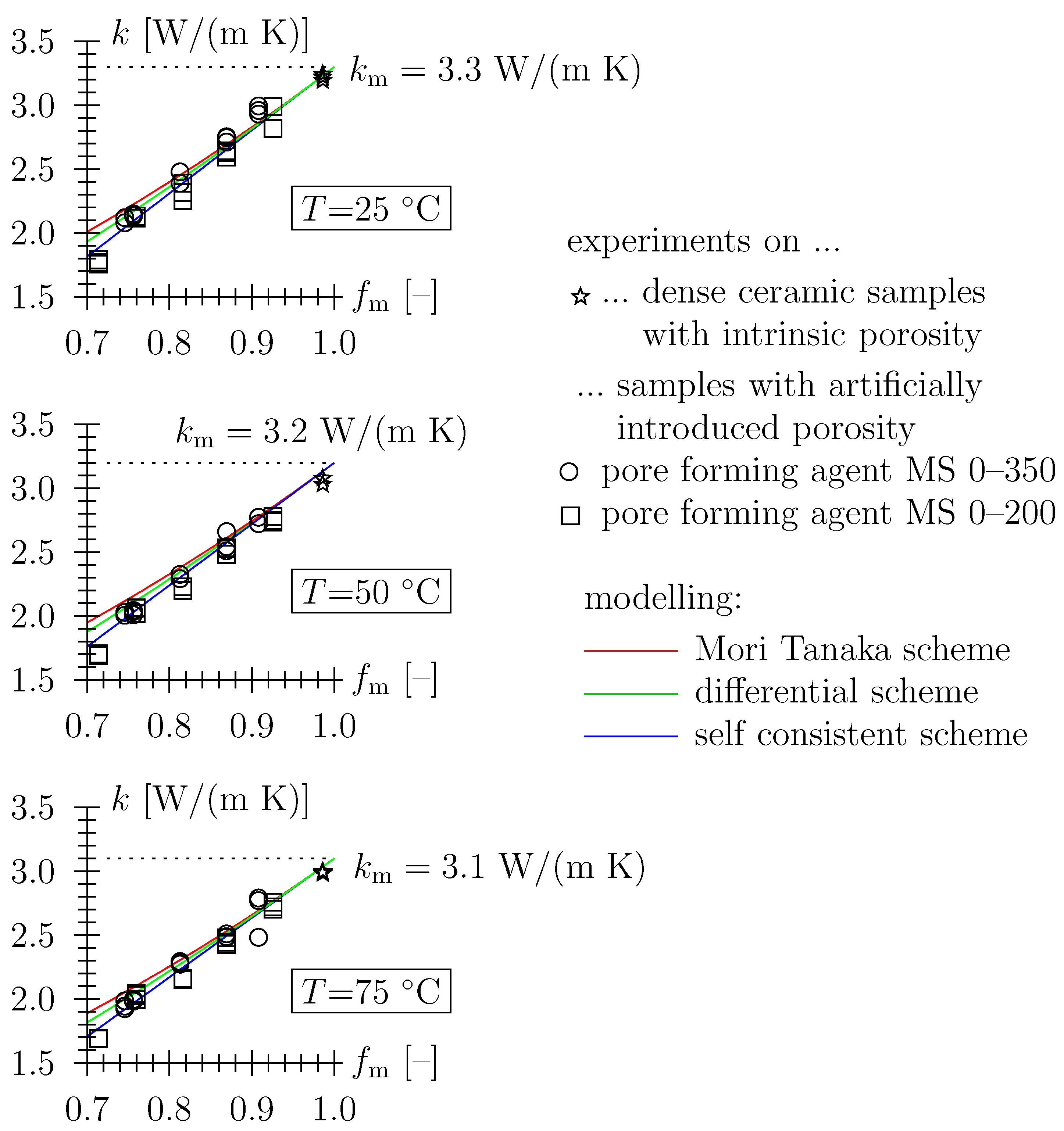
| Sample Notation | Organic Material Added Prior to Compaction and Sintering | Organic Content [m-%] | Sample Compaction Force [kN] |
|---|---|---|---|
| SC-0 | none, dense sample | 0 | 50 |
| with intrinsic | |||
| porosity | |||
| SC-350-02 | Rehofix MS 0–350 m | 2 | 65 |
| SC-350-04 | Rehofix MS 0–350 m | 4 | 69 |
| SC-350-06 | Rehofix MS 0–350 m | 6 | 71 |
| SC-350-08 | Rehofix MS 0–350 m | 8 | 88 |
| SC-350-10 | Rehofix MS 0–350 m | 10 | 95 |
| SC-200-02 | Rehofix MS 0–200 m | 2 | 73 |
| SC-200-04 | Rehofix MS 0–200 m | 4 | 82 |
| SC-200-06 | Rehofix MS 0–200 m | 6 | 88 |
| SC-200-08 | Rehofix MS 0–200 m | 8 | 95 |
| SC-200-10 | Rehofix MS 0–200 m | 10 | 106 |
| protoenstatite | 75.38 |
| clinoenstatite | 22.85 |
| cristobalite | 1.77 |
| 100.00 |
| Sample | Length | Width | Height | Mass | |
|---|---|---|---|---|---|
| (mm) | (mm) | (mm) | (mm) | (kg/m) | |
| SC-0 | 119.55 | 9.78 | 9.99 | 32.53 | 2790 |
| SC-350-02 | 119.54 | 10.00 | 10.04 | 30.86 | 2570 |
| SC-350-04 | 119.70 | 10.02 | 10.14 | 29.88 | 2460 |
| SC-350-06 | 119.60 | 10.01 | 10.13 | 27.85 | 2300 |
| SC-350-08 | 120.26 | 10.07 | 9.99 | 26.05 | 2150 |
| SC-350-10 | 120.43 | 10.09 | 10.03 | 25.65 | 2110 |
| SC-200-02 | 120.04 | 10.03 | 9.82 | 30.94 | 2620 |
| SC-200-04 | 120.17 | 10.04 | 9.93 | 29.51 | 2460 |
| SC-200-06 | 120.17 | 10.05 | 9.97 | 27.79 | 2310 |
| SC-200-08 | 120.62 | 10.08 | 10.12 | 26.48 | 2150 |
| SC-200-10 | 120.91 | 10.10 | 10.23 | 25.18 | 2020 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pichler, C.; Perfler, L.; Traxl, R.; Lackner, R. Porous Talcum-Based Steatite Ceramics Fabricated by the Admixture of Organic Particles: Experimental Characterization and Effective Medium/Field Modeling of Thermo-Mechanical Properties. Materials 2023, 16, 4420. https://doi.org/10.3390/ma16124420
Pichler C, Perfler L, Traxl R, Lackner R. Porous Talcum-Based Steatite Ceramics Fabricated by the Admixture of Organic Particles: Experimental Characterization and Effective Medium/Field Modeling of Thermo-Mechanical Properties. Materials. 2023; 16(12):4420. https://doi.org/10.3390/ma16124420
Chicago/Turabian StylePichler, Christian, Lukas Perfler, Roland Traxl, and Roman Lackner. 2023. "Porous Talcum-Based Steatite Ceramics Fabricated by the Admixture of Organic Particles: Experimental Characterization and Effective Medium/Field Modeling of Thermo-Mechanical Properties" Materials 16, no. 12: 4420. https://doi.org/10.3390/ma16124420
APA StylePichler, C., Perfler, L., Traxl, R., & Lackner, R. (2023). Porous Talcum-Based Steatite Ceramics Fabricated by the Admixture of Organic Particles: Experimental Characterization and Effective Medium/Field Modeling of Thermo-Mechanical Properties. Materials, 16(12), 4420. https://doi.org/10.3390/ma16124420






