Meta-Structure Hull Design with Periodic Layered Phononic Crystals Theory for Wide-Band Low-Frequency Sound Insolation
Abstract
:1. Introduction
2. Theoretical Derivations
2.1. Transfer Metrics of Acoustic–Phononic Lattices
2.2. Transfer Matrix Model of Phononic Lattice Meta-Structure
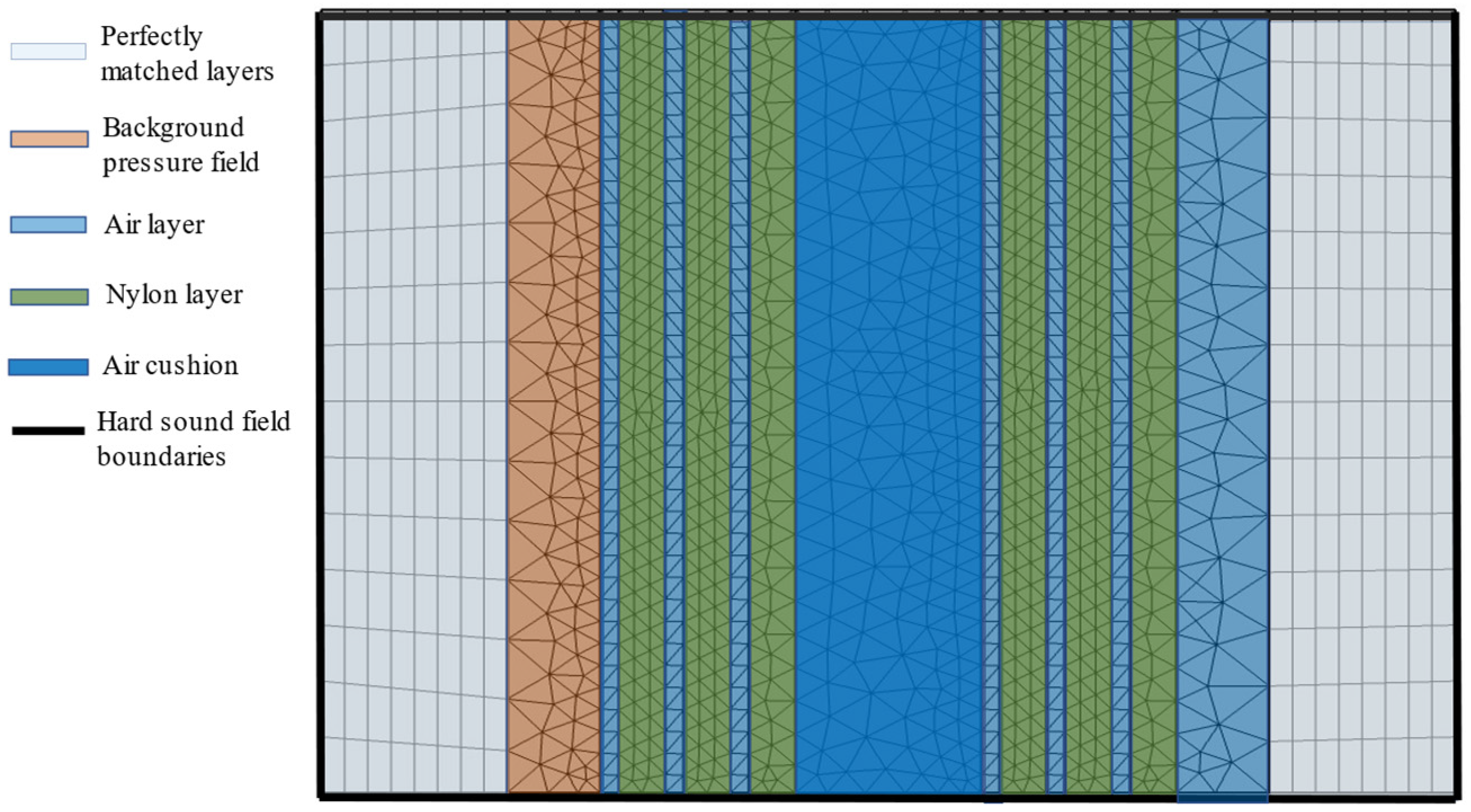
2.3. Finite-Element Analysis Setup
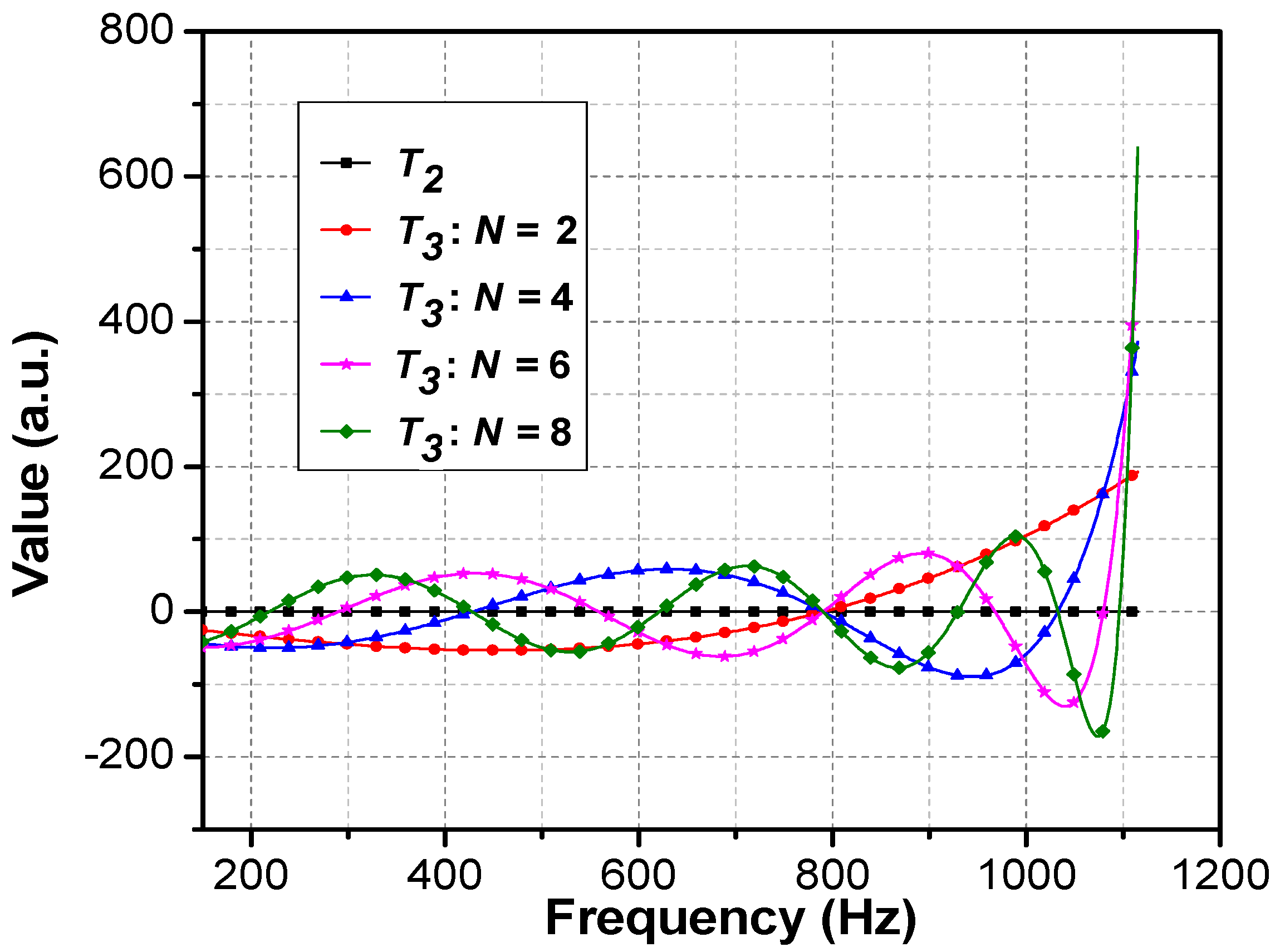
3. Theoretical Results
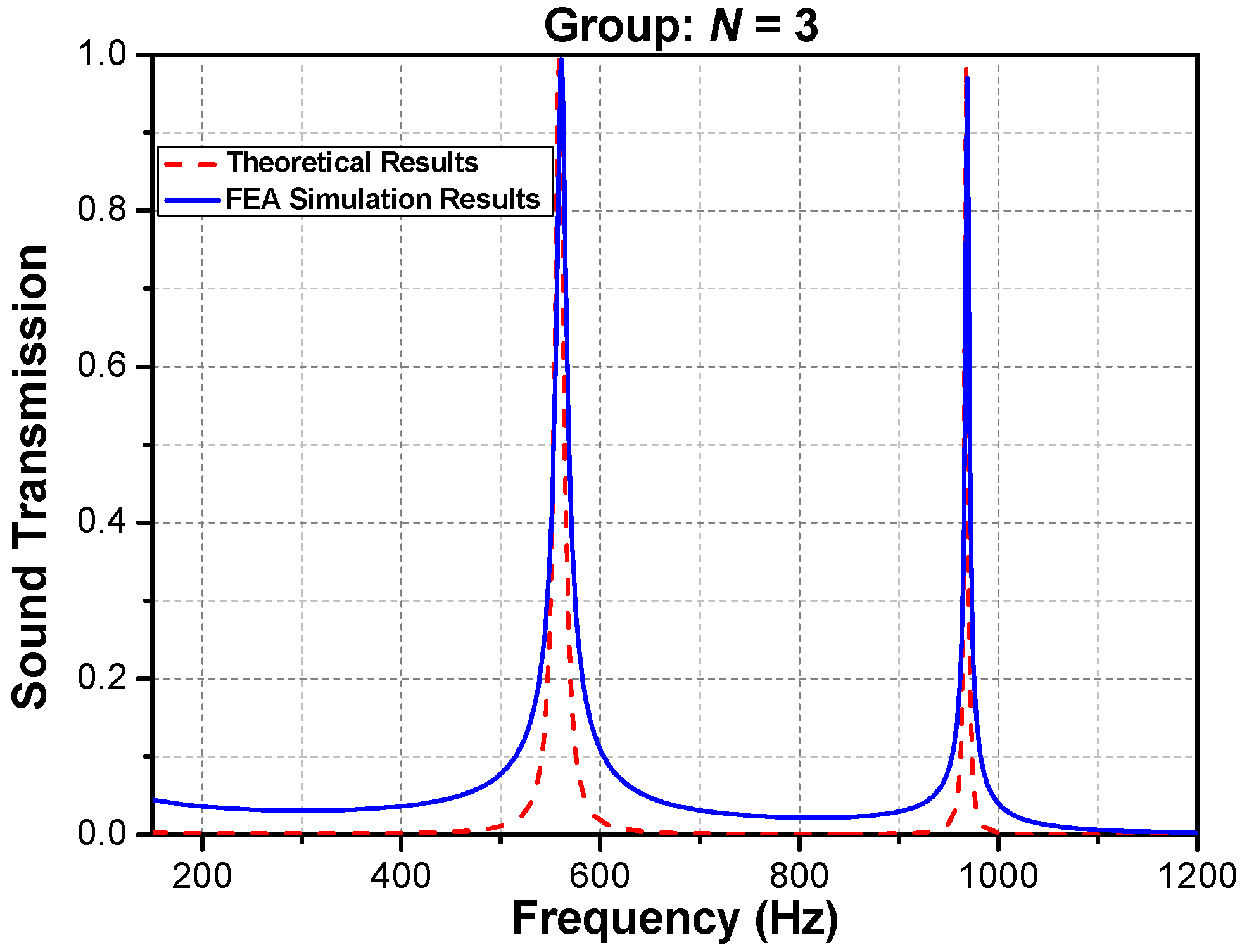
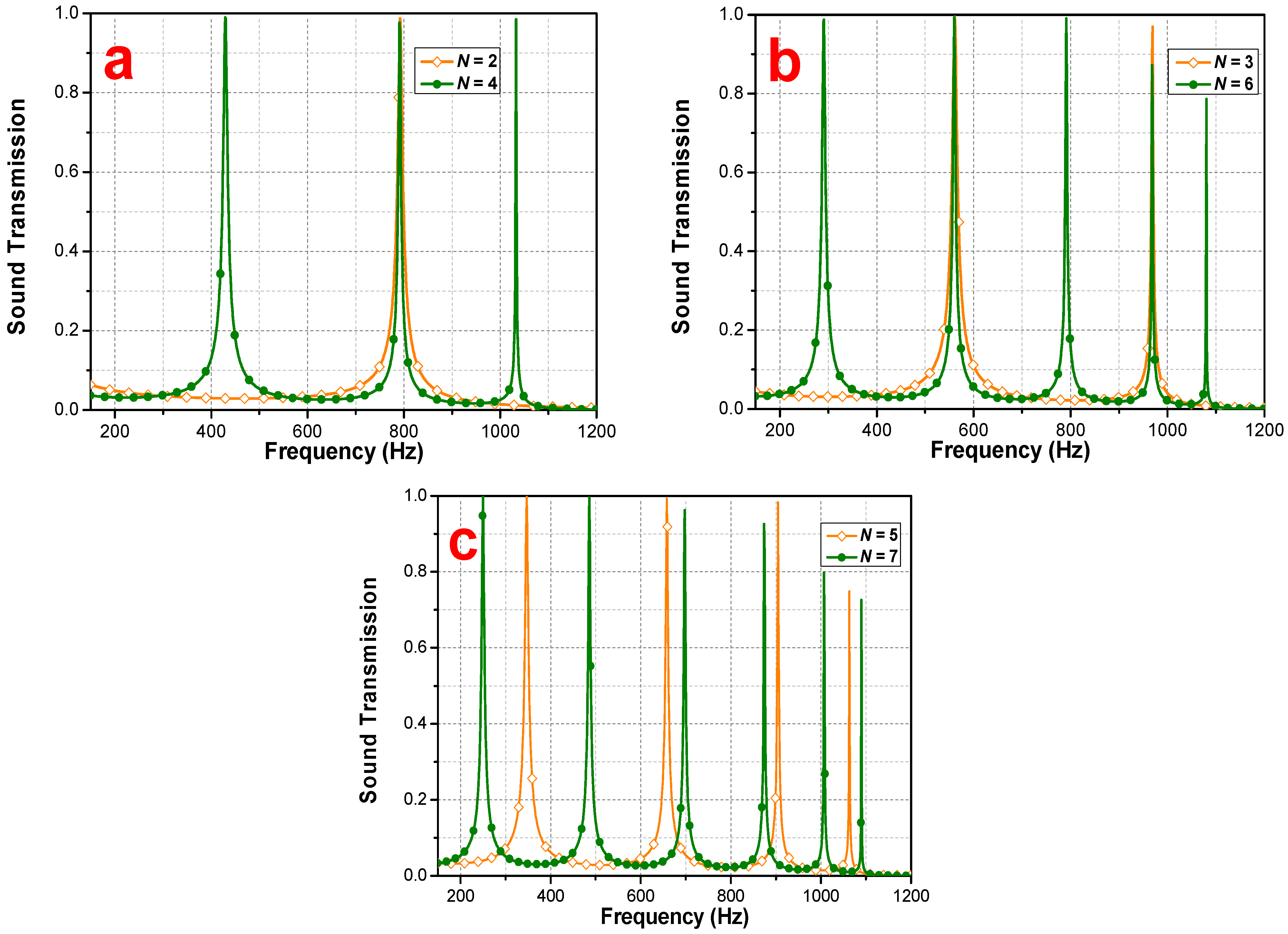
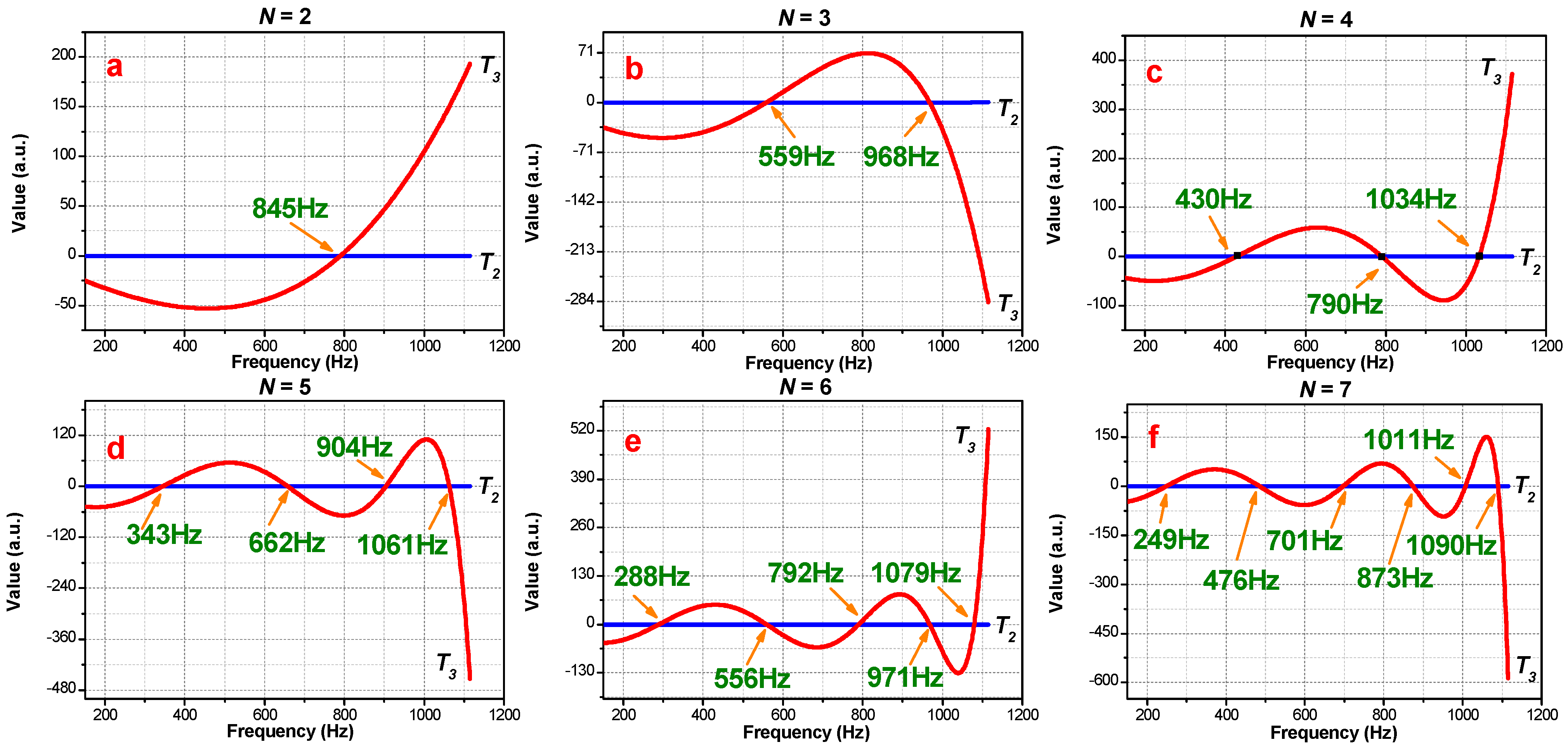
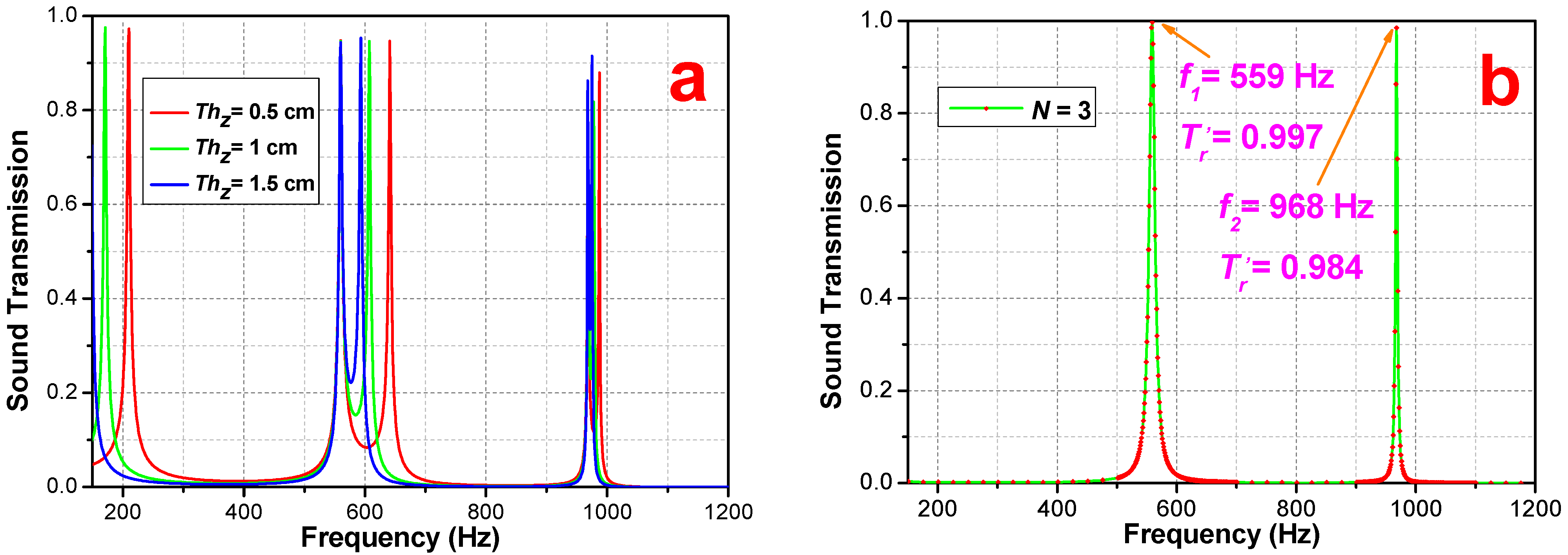
3.1. Periodic Phononic Lattices without an Air Layer
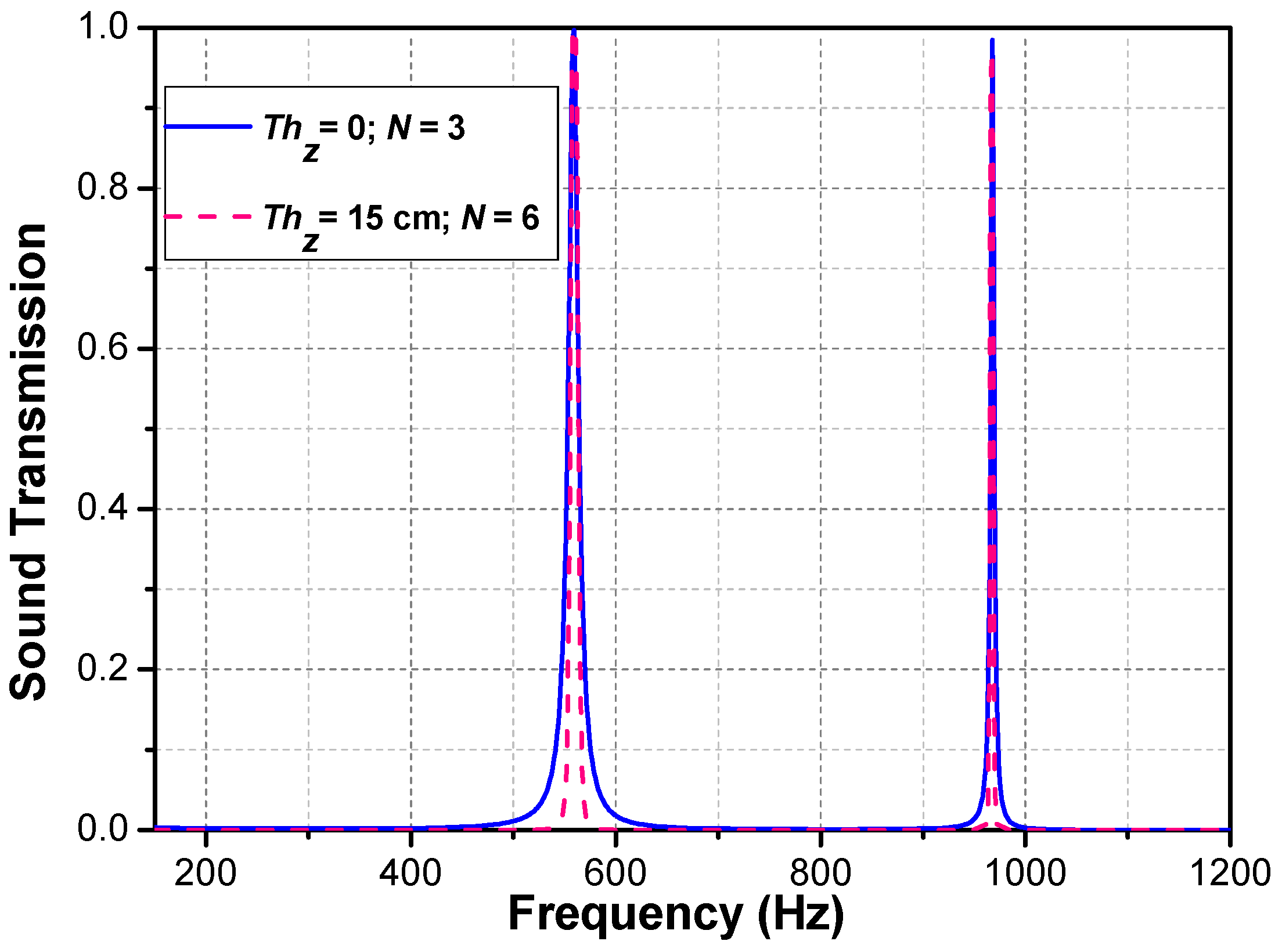
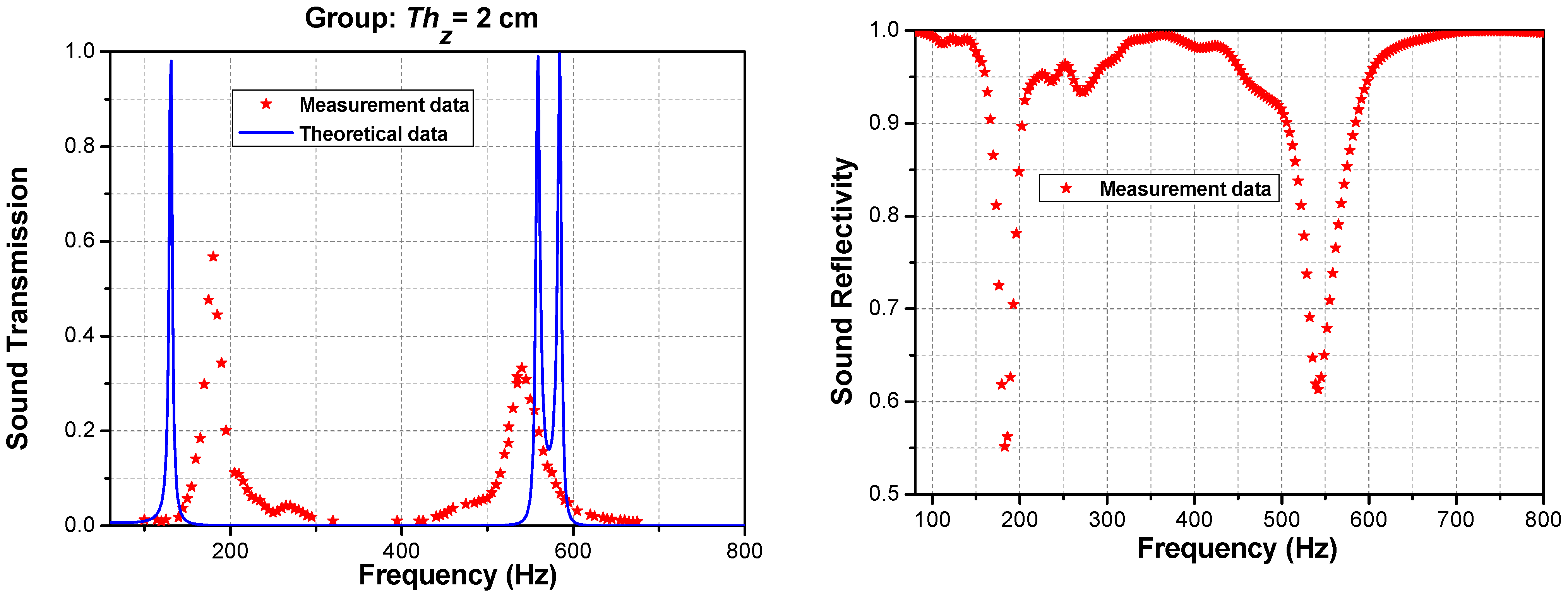
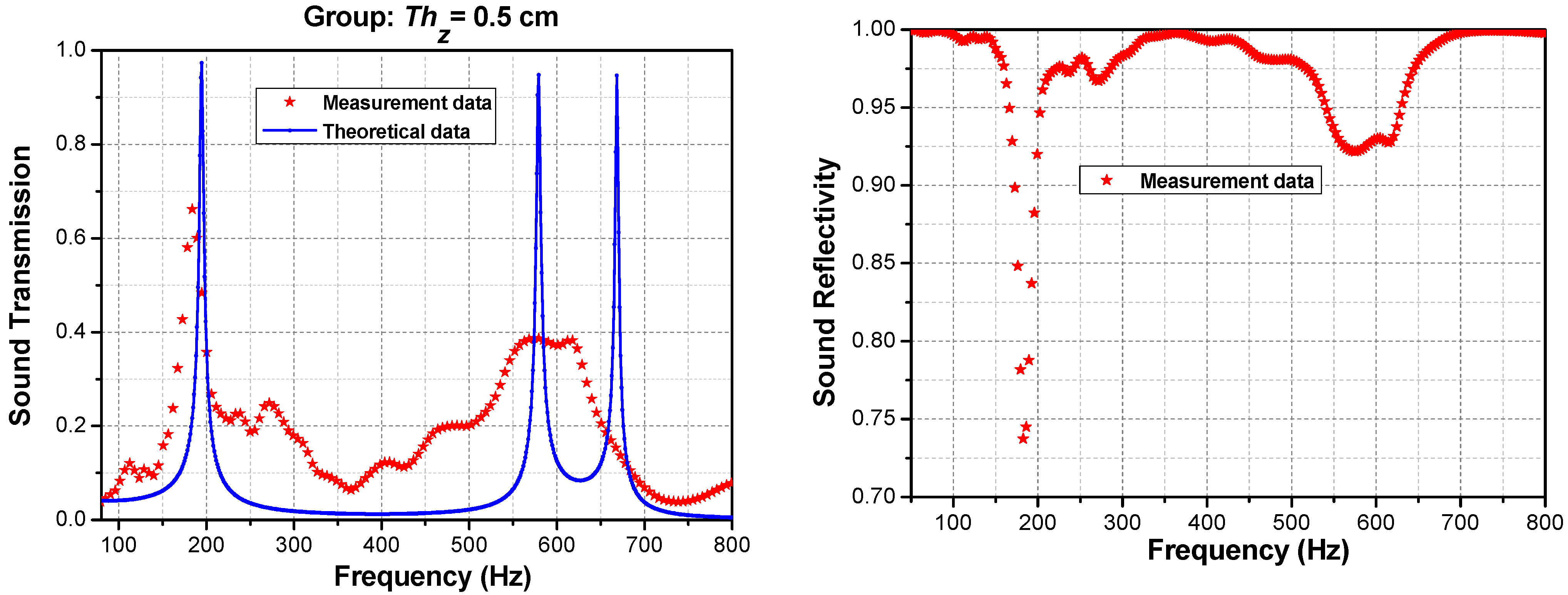
3.2. Periodic Phononic Lattices with an Air Cushion
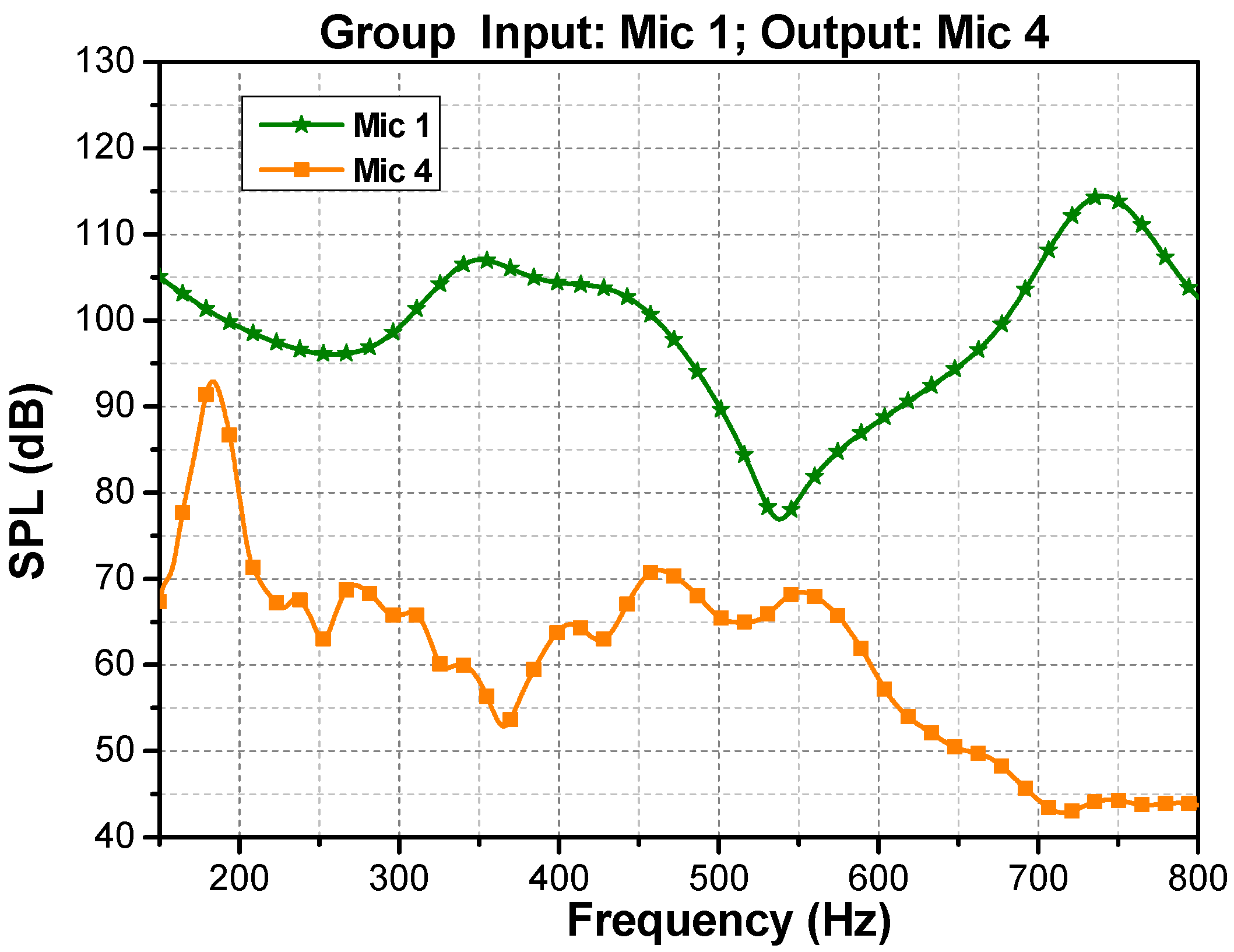
4. Experiment and Results
4.1. Experiment
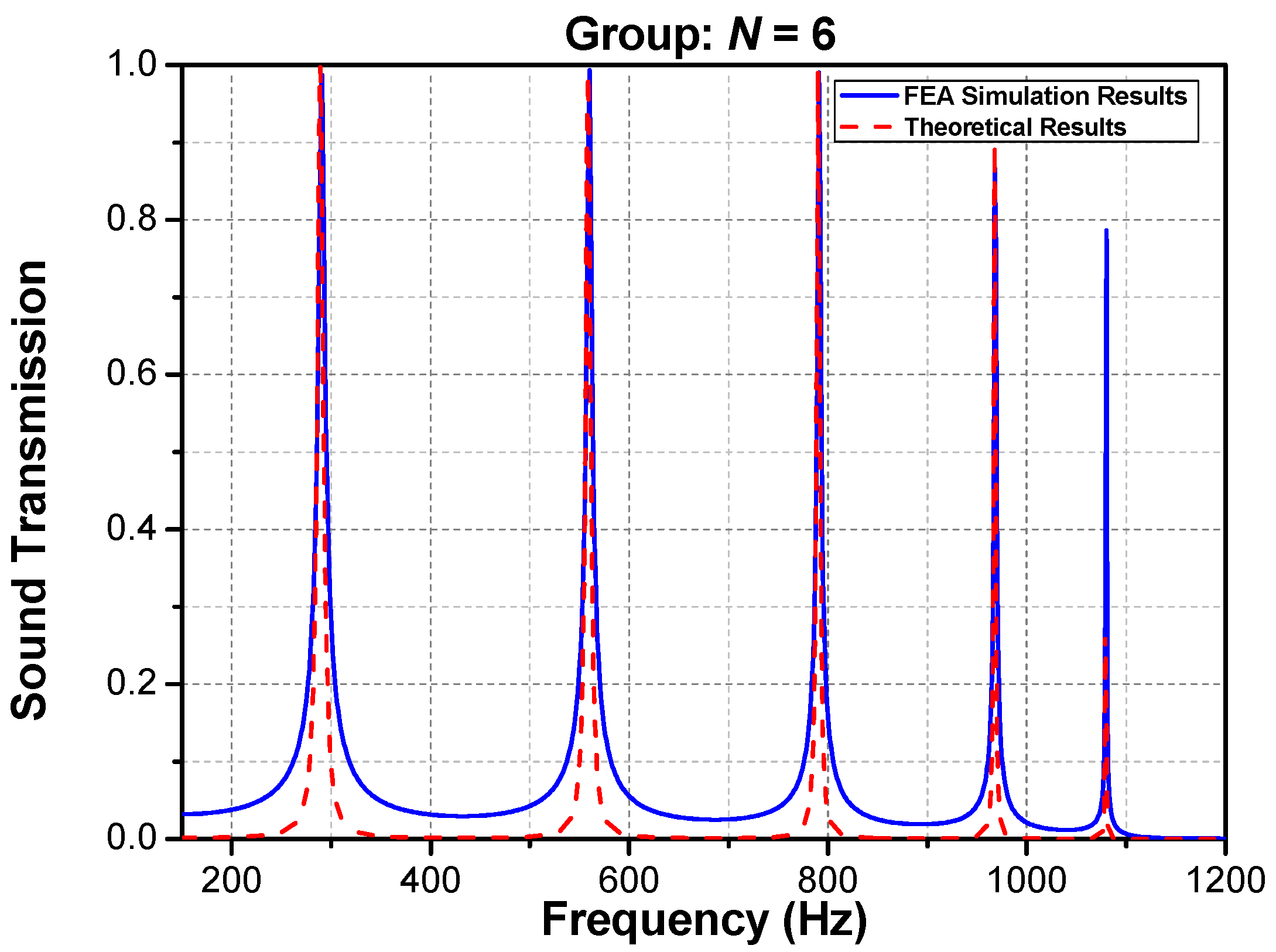
4.2. Measurement and Calculation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Junger, M.C. Dynamic behavior of reinforced cylindrical shells in a vacuum and in a fluid. J. Appl. Mech. 1954, 21, 35–41. [Google Scholar] [CrossRef]
- Bleich, H.H.; Baron, M.L. Free and forced vibrations of an infinitely long cylindrical shell in an infinite acoustic medium. J. Appl. Mech. 1954, 21, 167–177. [Google Scholar] [CrossRef]
- Maidanik, G. Response of ribbed panels to reverberant acoustic fields. J. Acoust. Soc. Am. 1962, 34, 809–826. [Google Scholar] [CrossRef] [Green Version]
- Mace, B.R. Sound radiation from a plate reinforced by two sets of parallel stiffeners. J. Sound Vib. 1980, 71, 435–441. [Google Scholar] [CrossRef]
- Yoshikawa, S.; Williams, E.G.; Washburn, K.B. Vibration of two concentric submerged cylindrical shells coupled by the entrained fluid. J. Acoust. Soc. Am. 1994, 95, 3273–3286. [Google Scholar] [CrossRef]
- Li, Y.; Yan, G. Vibration characteristics of innovative reentrant-chiral elastic metamaterials. Eur. J. Mech. A/Solids 2021, 90, 104350. [Google Scholar] [CrossRef]
- Guo, L.; Yang, C.; Liu, J.; Cao, Y.; Pan, G.; Song, B. Vibration analysis of the rudder drive system of an underwater glider. Int. J. Hydromechatron. 2022, 5, 191–204. [Google Scholar] [CrossRef]
- Liu, J.; Wang, L.; Shi, Z. Dynamic modelling of the defect extension and appearance in a cylindrical roller bearing. Mech. Syst. Signal Process. 2022, 173, 109040. [Google Scholar] [CrossRef]
- Chen, D.; Zi, H.; Li, Y.; Li, X. Low frequency ship vibration isolation using the band gap concept of sandwich plate-type elastic metastructures. Ocean Eng. 2021, 235, 109460. [Google Scholar] [CrossRef]
- Pilon, A.; Lyrintzis, A. An improved Kirchhoff method for jet aeroacoustics. In Proceedings of the Aeroacoustics Conference, State College, PA, USA, 6–8 May 1996; p. 1709. [Google Scholar]
- Harari, A.; Sandman, B.E. Radiation and vibrational properties of submerged stiffened cylindrical shells. J. Acoust. Soc. Am. 1990, 88, 1817–1830. [Google Scholar] [CrossRef]
- Zhu, Z.; Hu, N.; Wu, J.; Li, W.; Zhao, J.; Wang, M.; Zeng, F.; Dai, H.; Zheng, Y. A review of underwater acoustic metamaterials for underwater acoustic equipment. Front. Phys. 2022, 10, 1296. [Google Scholar] [CrossRef]
- Yin, J.; Cai, L.; Fang, X.; Xiao, Y.; Yang, H.; Zhang, H.; Wen, J. Review on research progress of mechanical metamaterials and their applications on vibration and noise control. Adv. Mech. 2022, 52, 508–586. [Google Scholar]
- Heaney, K.D.; Campbell, R.L.; Murray, J.J. Comparison of hybrid three-dimensional modeling with measurements on the continental shelf. J. Acoust. Soc. Am. 2012, 131, 1680–1688. [Google Scholar] [CrossRef] [PubMed]
- Fleury, R.; Alù, A. Extraordinary sound transmission through density-near-zero ultranarrow channels. Phys. Rev. Lett. 2013, 111, 055501. [Google Scholar] [CrossRef] [Green Version]
- Lee, I.K.; Kim, Y.J.; Oh, J.H.; Kim, Y.Y. One-dimensional broadband phononic crystal filter with unit cells made of two non-uniform impedance-mirrored elements. AIP Adv. 2013, 3, 022105. [Google Scholar] [CrossRef] [Green Version]
- Lee, I.K.; Seung, H.M.; Kim, Y.Y. Realization of high-performance bandpass filter by impedance-mirroring. J. Sound Vib. 2015, 355, 86–92. [Google Scholar] [CrossRef]
- Van Driel, H.M.; Vos, W.L. Multiple Bragg wave coupling in photonic band-gap crystals. Phys. Rev. B 2000, 62, 9872. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.Y.; Yang, Z.; Chan, C.T.; Sheng, P. Locally resonant sonic materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef]
- Xie, S.; Li, Z.; Yan, H.; Yang, S. Ultra-broadband sound absorption performance of a multi-cavity composite structure filled with polyurethane. Appl. Acoust. 2022, 189, 108612. [Google Scholar] [CrossRef]
- Zhao, P.; Zhang, K.; Qi, L.; Deng, Z. 3D chiral mechanical metamaterial for tailored band gap and manipulation of vibration isolation. Mech. Syst. Signal Process. 2022, 180, 109430. [Google Scholar] [CrossRef]
- Almeida, V.F.; Lima, V.D.; Arruda, J.R.F. Applying the phononic crystal concept to the intake muffler of a refrigeration compressor. Appl. Acoust. 2022, 194, 108800. [Google Scholar] [CrossRef]
- Xie, S.; Yang, S.; Yang, C.; Wang, D. Sound absorption performance of a filled honeycomb composite structure. Appl. Acoust. 2020, 162, 107202. [Google Scholar] [CrossRef]
- Feng, Y.; Zong, D.; Hou, Y.; Yin, X.; Zhang, S.; Duan, L.; Si, Y.; Jia, Y.; Ding, B. Gradient structured micro/nanofibrous sponges with superior compressibility and stretchability for broadband sound absorption. J. Colloid Interface Sci. 2021, 593, 59–66. [Google Scholar] [CrossRef] [PubMed]
- Opiela, K.C.; Zieliński, T.G.; Dvorák, T.; Kúdela, S., Jr. Perforated closed-cell aluminium foam for acoustic absorption. Appl. Acoust. 2021, 174, 107706. [Google Scholar] [CrossRef]
- Fouladi, M.H.; Ayub, M.; Nor, M.J.M. Analysis of coir fiber acoustical characteristics. Appl. Acoust. 2011, 72, 35–42. [Google Scholar] [CrossRef]
- Wang, W.; Zhou, Y.; Li, Y.; Hao, T. Aerogels-filled Helmholtz resonators for enhanced low-frequency sound absorption. J. Supercrit. Fluids 2019, 150, 103–111. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, Y.; Yu, D.; Yang, H.; Zhong, J.; Wu, F.; Wen, J. A double porosity material for low frequency sound absorption. Compos. Struct. 2020, 239, 111978. [Google Scholar] [CrossRef]
- Gao, N.; Tang, L.; Deng, J.; Lu, K.; Hou, H.; Chen, K. Design, fabrication and sound absorption test of composite porous metamaterial with embedding I-plates into porous polyurethane sponge. Appl. Acoust. 2021, 175, 107845. [Google Scholar] [CrossRef]
- Bravo, T.; Maury, C. Sound attenuation and absorption by micro-perforated panels backed by anisotropic fibrous materials: Theoretical and experimental study. J. Sound Vib. 2018, 425, 189–207. [Google Scholar] [CrossRef]
- Abbad, A.; Atalla, N.; Ouisse, M.; Doutres, O. Numerical and experimental investigations on the acoustic performances of membraned Helmholtz resonators embedded in a porous matrix. J. Sound Vib. 2019, 459, 114873. [Google Scholar] [CrossRef]
- Dong, E.; Cao, P.; Zhang, J.; Zhang, S.; Fang, N.X.; Zhang, Y. Underwater acoustic metamaterials. Natl. Sci. Rev. 2023, 10, nwac246. [Google Scholar] [CrossRef] [PubMed]
- Shen, M.; Cao, W. Acoustic band-gap engineering using finite-size layered structures of multiple periodicity. Appl. Phys. Lett. 1999, 75, 3713–3715. [Google Scholar] [CrossRef] [Green Version]
- Mizuno, S.; Tamura, S.I. Theory of acoustic-phonon transmission in finite-size superlattice systems. Phys. Rev. B 1992, 45, 734. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mizuno, S.; Tamura, S.I. Impurity levels and resonant transmission of acoustic phonons in a double-barrier system. Phys. Rev. B 1992, 45, 13423. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Červenka, M.; Bednařík, M. Calculation of an axial temperature distribution using the reflection coefficient of an acoustic wave. J. Acoust. Soc. Am. 2015, 138, EL359–EL364. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, H.J.; Lee, J.K.; Kim, Y.Y. Elastic metamaterial-based impedance-varying phononic bandgap structures for bandpass filters. J. Sound Vib. 2015, 353, 58–74. [Google Scholar] [CrossRef]
- Ilinskii, Y.A.; Lipkens, B.; Lucas, T.S.; Van Doren, T.W.; Zabolotskaya, E.A. Nonlinear standing waves in an acoustical resonator. J. Acoust. Soc. Am. 1998, 104, 2664–2674. [Google Scholar] [CrossRef] [Green Version]
- Cervenka, M.; Bednarik, M. On the optimization of an acoustic resonator shape with respect to acoustic pressure amplitude. Acta Acust. United Acust. 2013, 99, 183–191. [Google Scholar] [CrossRef]
- Červenka, M.; Bednařík, M. Acoustic bandpass filters employing shaped resonators. J. Sound Vib. 2016, 383, 76–88. [Google Scholar] [CrossRef]
- Chen, Y.; Meng, F.; Sun, G.; Li, G.; Huang, X. Topological design of phononic crystals for unidirectional acoustic transmission. J. Sound Vib. 2017, 410, 103–123. [Google Scholar] [CrossRef]
- Zhang, X.; Xing, J.; Liu, P.; Luo, Y.; Kang, Z. Realization of full and directional band gap design by non-gradient topology optimization in acoustic metamaterials. Extrem. Mech. Lett. 2021, 42, 101126. [Google Scholar] [CrossRef]
- Zhang, Z.; Yu, D.; Liu, J.; Hu, B.; Wen, J. Transmission and bandgap characteristics of a duct mounted with multiple hybrid Helmholtz resonators. Appl. Acoust. 2021, 183, 108266. [Google Scholar] [CrossRef]
- Liu, Y.; Du, J. Bandgap characteristics of a duct embedded with multiple membrane-cavity resonators in the presence of mean flow. Int. J. Mech. Sci. 2020, 169, 105330. [Google Scholar] [CrossRef]
- Shi, X.; Mak, C.M. Sound attenuation of a periodic array of micro-perforated tube mufflers. Appl. Acoust. 2017, 115, 15–22. [Google Scholar] [CrossRef]
- Joannopoulos, J.D.; Johnson, S.G.; Winn, J.N.; Meade, R.D. Photonic Crystals; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar] [CrossRef] [Green Version]
- Sigalas, M.M. Elastic and acoustic wave band structure. J. Sound Vib. 1992, 158, 377–382. [Google Scholar] [CrossRef]
- ASTM E2611-17; Standard Test Method for Measurement of Normal Incidence Sound Transmission of Acoustical Materials Based on the Transfer Matrix Method. American Society for Testing and Materials International: New York, NY, USA, 2017. [CrossRef]
- Zvoníček, T.; Vašina, M.; Pata, V.; Smolka, P. Three-Dimensional Printing Process for Musical Instruments: Sound Reflection Properties of Polymeric Materials for Enhanced Acoustical Performance. Polymers 2023, 15, 2025. [Google Scholar] [CrossRef]
- Monkova, K.; Vasina, M.; Monka, P.P.; Vanca, J.; Kozak, D. Effect of 3D-printed PLA structure on sound reflection properties. Polymers 2022, 14, 413. [Google Scholar] [CrossRef]
- Sun, X.; Jiang, F.; Wang, J. Acoustic properties of 316L stainless steel lattice structures fabricated via selective laser melting. Metals 2020, 10, 111. [Google Scholar] [CrossRef] [Green Version]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Sun, X.; Tao, W.; Wang, S.; Flowers, G.T.; Hu, Q.; Gaidai, O. Meta-Structure Hull Design with Periodic Layered Phononic Crystals Theory for Wide-Band Low-Frequency Sound Insolation. Materials 2023, 16, 4429. https://doi.org/10.3390/ma16124429
Zhang F, Sun X, Tao W, Wang S, Flowers GT, Hu Q, Gaidai O. Meta-Structure Hull Design with Periodic Layered Phononic Crystals Theory for Wide-Band Low-Frequency Sound Insolation. Materials. 2023; 16(12):4429. https://doi.org/10.3390/ma16124429
Chicago/Turabian StyleZhang, Fuxi, Xinyi Sun, Wei Tao, Shiming Wang, George T. Flowers, Qingsong Hu, and Oleg Gaidai. 2023. "Meta-Structure Hull Design with Periodic Layered Phononic Crystals Theory for Wide-Band Low-Frequency Sound Insolation" Materials 16, no. 12: 4429. https://doi.org/10.3390/ma16124429




