Formation of Twin Boundaries in Rapidly Solidified Metals through Deformation Twinning
Abstract
:1. Introduction
2. Materials and Methods
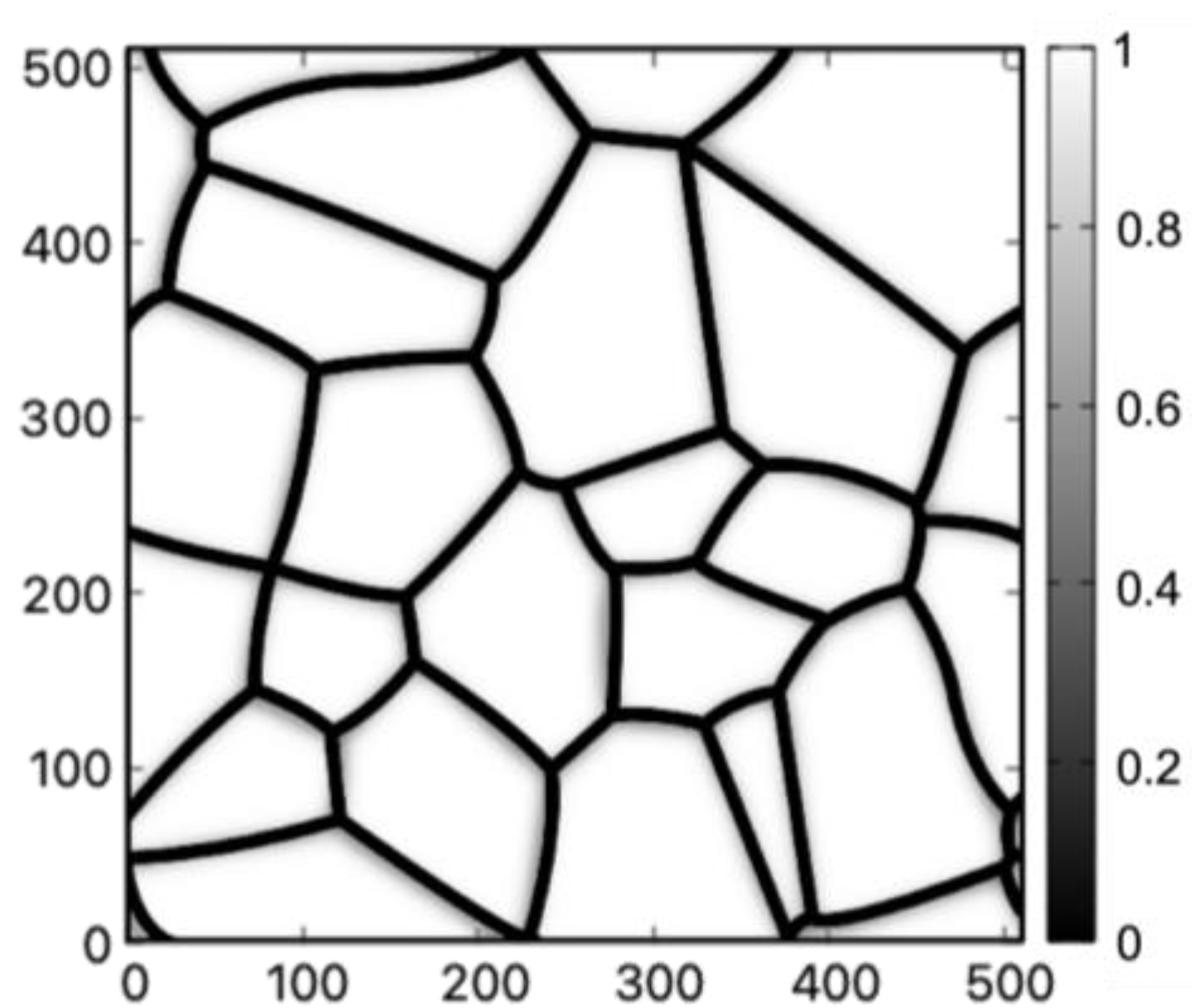
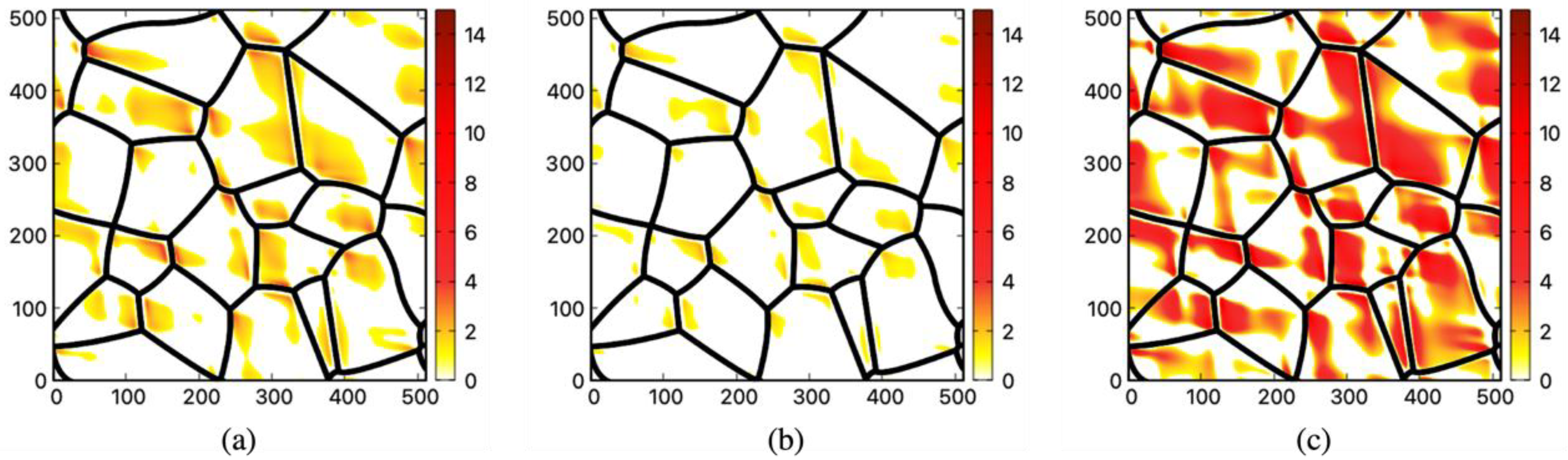
2.1. Thermal Strain Inhomogeneity in Polycrystalline Structures
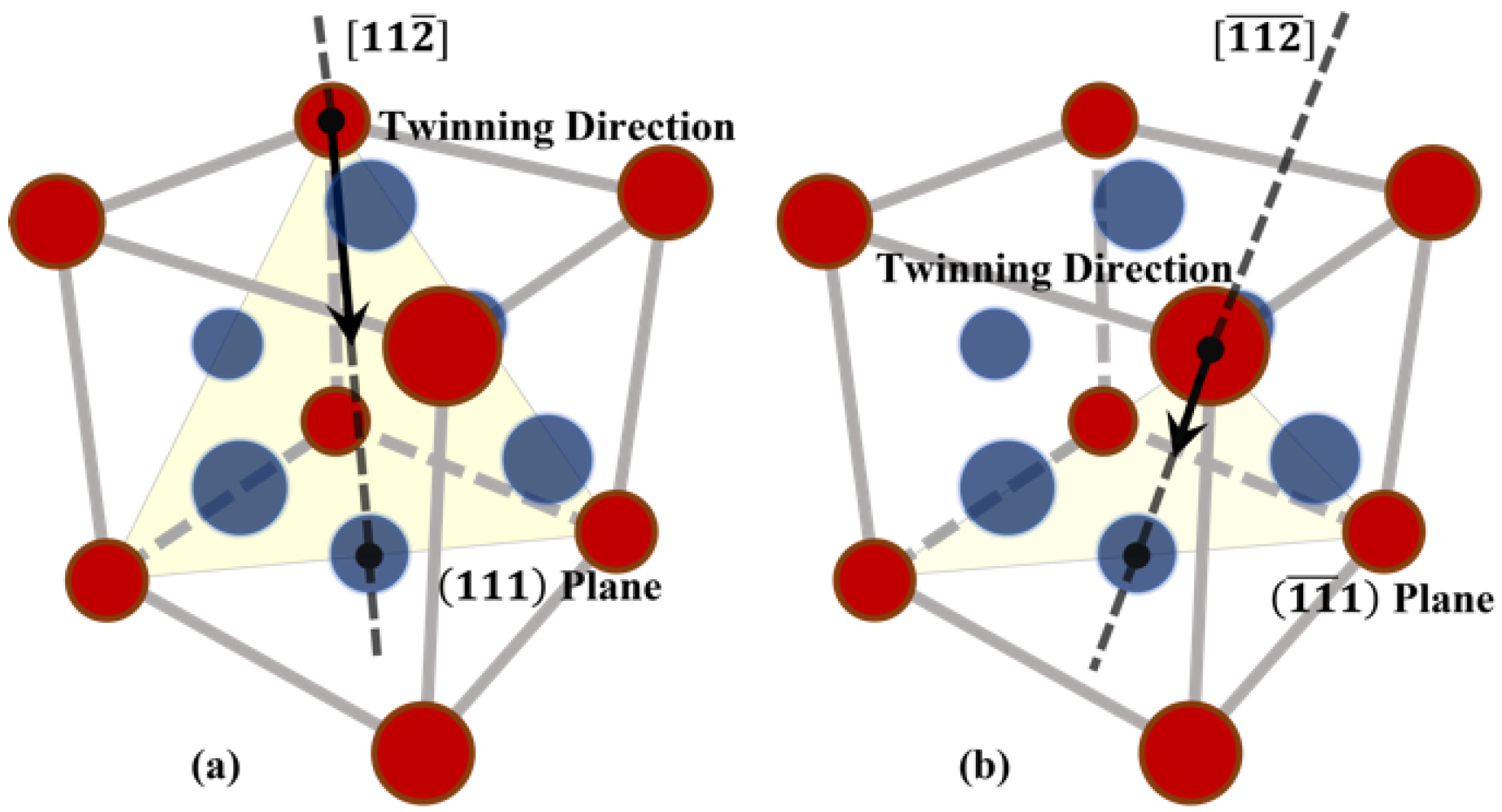
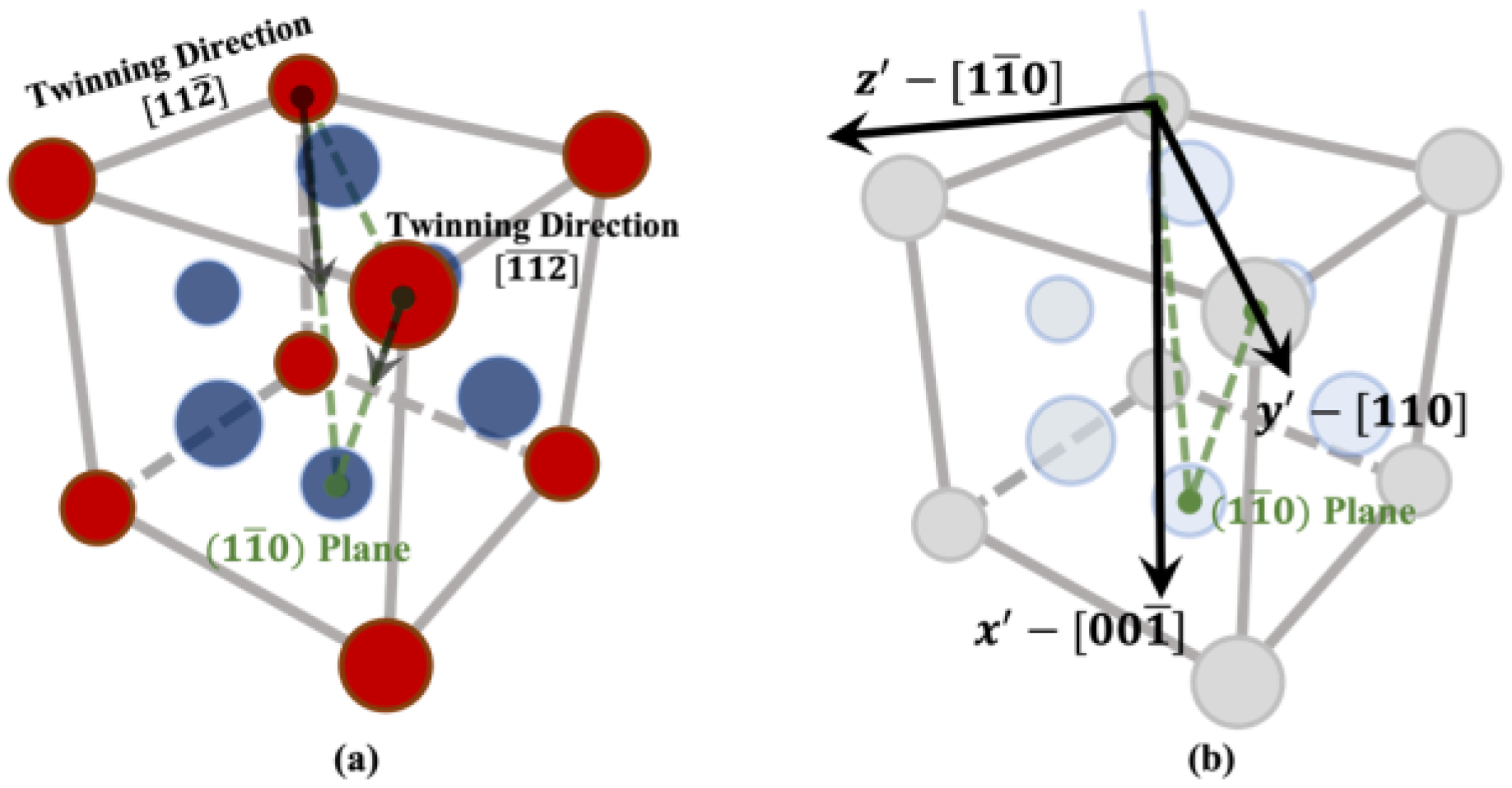
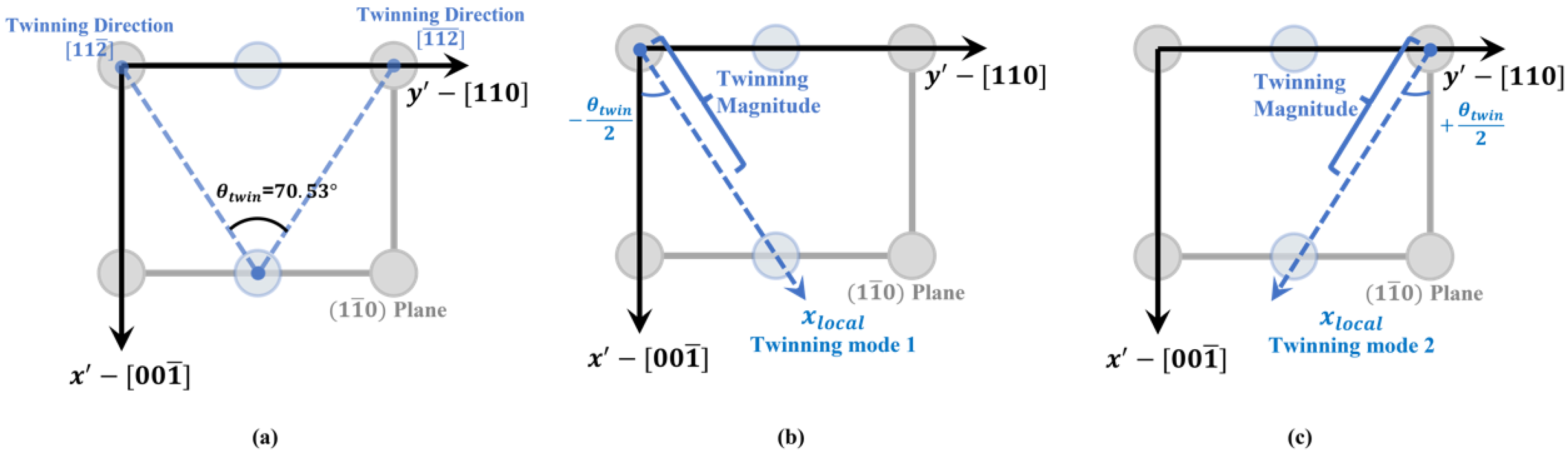
2.2. Phase-Field Model of Deformation Twinning
2.2.1. Energy Landscape
2.2.2. Interfacial Energy
2.2.3. Elastic Energy
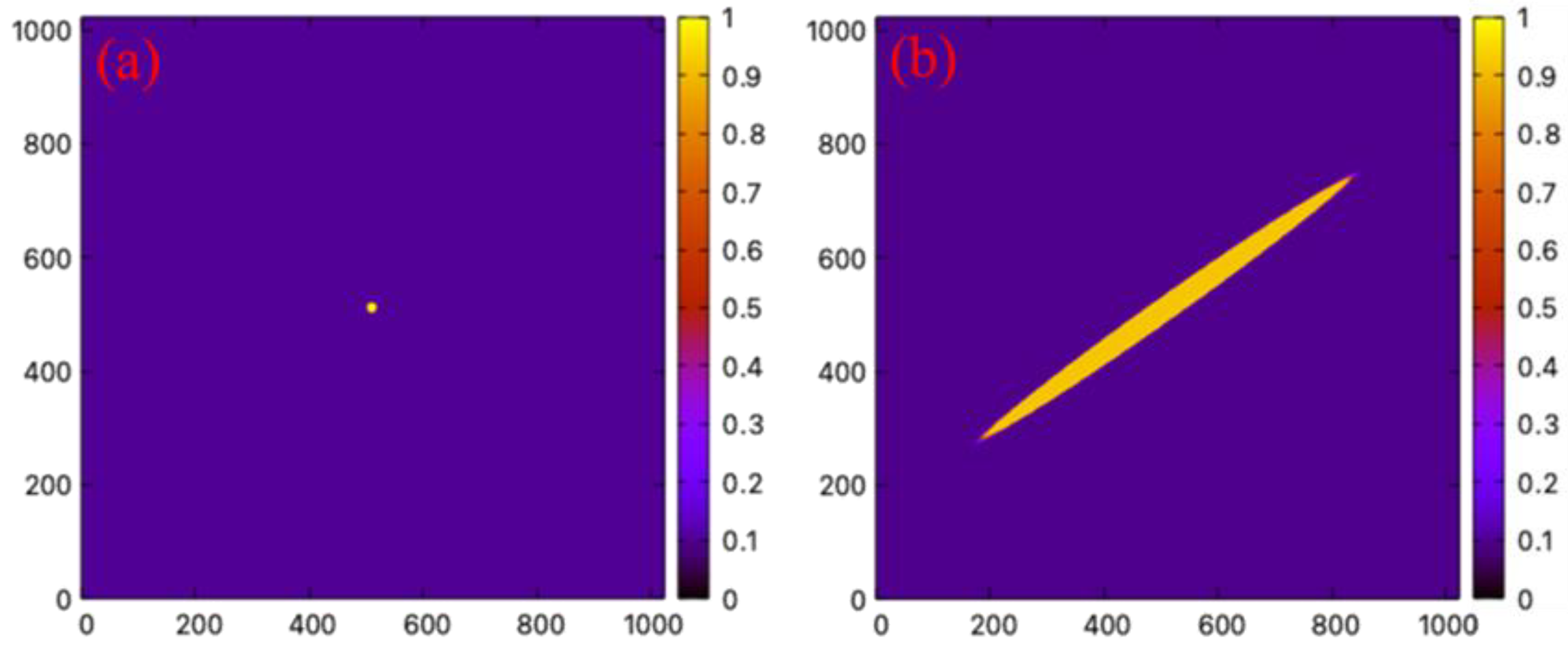
2.2.4. Order Parameters Evolution
3. Results and Discussion
4. Conclusions
- For Ni, the calculated critical shear strain for deformation twinning is about 0.4% which is similar to the experimentally observed residual strain.
- The formation of deformation twins is strongly affected by the shear modulus of the GBs.
- When the GB shear resistance is significantly reduced, the shear strains in grain interiors become large enough to trigger the deformation twinning.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Meyers, M.A.; Mishra, A.; Benson, D.J. Mechanical properties of nanocrystalline materials. Prog. Mater. Sci. 2006, 51, 427–556. [Google Scholar] [CrossRef]
- Zhang, Y.; Yuan, G.; Wang, Y.; Fang, F.; Zhang, W.; Zhang, X.; Wang, G. The evolution of Σ3 grain boundaries in the strip-cast Hi-B grain orientated Fe-6.5% Si alloy. Scr. Mater. 2021, 196, 113768. [Google Scholar] [CrossRef]
- Xu, X.L.; Liu, F. Recrystallization and twinning in rapidly solidified nickel based alloys without man-made plastic deformation. J. Alloy. Compd. 2014, 615, 156–162. [Google Scholar] [CrossRef]
- Pham, M.S.; Dovgyy, B.; Hooper, P.A. Twinning induced plasticity in austenitic stainless steel 316 L made by additive manufacturing. Mater. Sci. Eng. A 2017, 704, 102–111. [Google Scholar] [CrossRef]
- Wang, H.; An, Y.; Xu, X.; Guo, X.; Hu, Y. Rapid solidification microstructure evolution and grain refinement of deeply undercooled nickel alloys. Mater. Charact. 2020, 170, 110703. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Heo, T.W.; Chang, K.; Chen, L.Q. A spectral iterative method for the computation of effective properties of elastically inhomogeneous polycrystals. Commun. Comput. Phys. 2012, 11, 726–738. [Google Scholar] [CrossRef]
- Heo, T.W.; Wang, Y.; Bhattacharya, S.; Sun, X.; Hu, S.; Chen, L.Q. A phase-field model for deformation twinning. Philos. Mag. Lett. 2011, 91, 110–121. [Google Scholar] [CrossRef]
- Nieman, G.W.; Weertman, J.R.; Siegel, R.W. Mechanical Behavior of Nanocrystalline Metals; No. CONF-9010292-4; Argonne National Lab: Lemont, IL, USA, 1990. [Google Scholar]
- Bush, M.B. Modelling of nanophase materials. Mater. Sci. Eng. A 1993, 161, 127–134. [Google Scholar] [CrossRef]
- Kim, T.Y.; Dolbow, J.E.; Fried, E. Numerical study of the grain-size dependent Young’s modulus and Poisson’s ratio of bulk nanocrystalline materials. Int. J. Solids Struct. 2012, 49, 3942–3952. [Google Scholar] [CrossRef] [Green Version]
- Fecht, H.J. Thermodynamic properties and stability of grain boundaries in metals based on the universal equation of state at negative pressure. Acta Metall. Mater. 1990, 38, 1927–1932. [Google Scholar] [CrossRef]
- Tingdong, X.; Lei, Z. The elastic modulus in the grain-boundary region of polycrystalline materials. Philos. Mag. Lett. 2004, 84, 225–233. [Google Scholar] [CrossRef]
- Rappaz, M.; Jacot, A.; Boettinger, W.J. Last-stage solidification of alloys: Theoretical model of dendrite-arm and grain coalescence. Metall. Mater. Trans. A 2003, 34, 467–479. [Google Scholar] [CrossRef]
- Fensin, S.J.; Olmsted, D.; Buta, D.; Asta, M.; Karma, A.; Hoyt, J.J. Structural disjoining potential for grain-boundary premelting and grain coalescence from molecular-dynamics simulations. Phys. Rev. E 2010, 81, 031601. [Google Scholar] [CrossRef] [Green Version]
- Lobkovsky, A.E.; Warren, J.A. Phase field model of premelting of grain boundaries. Physica D Nonlinear Phenom. 2002, 164, 202–212. [Google Scholar] [CrossRef] [Green Version]
- Mishin, Y.; Boettinger, W.J.; Warren, J.A.; McFadden, G.B. Thermodynamics of grain boundary premelting in alloys. I. Phase-Field Model. Acta Mater. 2009, 57, 3771–3785. [Google Scholar]
- Berry, J.; Elder, K.R.; Grant, M. Melting at dislocations and grain boundaries: A phase field crystal study. Phys. Rev. B 2008, 77, 224114. [Google Scholar] [CrossRef] [Green Version]
- Wang, N.; Spatschek, R.; Karma, A. Multi-phase-field analysis of short-range forces between diffuse interfaces. Phys. Rev. E 2010, 81, 051601. [Google Scholar] [CrossRef] [Green Version]
- Broughton, J.Q.; Gilmer, G.H. Grain-boundary shearing as a test for interface melting. Model. Simul. Mater. Sci. Eng. 1998, 6, 87. [Google Scholar] [CrossRef]
- Chen, L.Q.; Yang, W. Computer simulation of the domain dynamics of a quenched system with a large number of nonconserved order parameters: The grain-growth kinetics. Phys. Rev. B 1994, 50, 15752. [Google Scholar] [CrossRef]
- Hu, S.Y.; Chen, L.Q. A phase-field model for evolving microstructures with strong elastic inhomogeneity. Acta Mater. 2001, 49, 1879–1890. [Google Scholar] [CrossRef]
- Yu, P.; Hu, S.Y.; Chen, L.Q.; Du, Q. An iterative-perturbation scheme for treating inhomogeneous elasticity in phase-field models. J. Comput. Phys. 2005, 208, 34–50. [Google Scholar] [CrossRef]
- Christian, J.W. The Theory of Transformations in Metals and Alloys; Elsevier: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Mahajan, S.; Williams, D.F. Deformation twinning in metals and alloys. Int. Metall. Rev. 1973, 18, 43–61. [Google Scholar] [CrossRef]
- Cottrell, A.H.; Bilby, B.A., LX. A mechanism for the growth of deformation twins in crystals. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1951, 42, 573–581. [Google Scholar] [CrossRef]
- Sleeswyk, A.W. ½< 111> screw dislocations and the nucleation of {112}<111> twins in the bcc lattice. Philos. Mag. 1963, 8, 1467–1486. [Google Scholar]
- Venables, J.A. On dislocation pole models for twinning. Philos. Mag. 1974, 30, 1165–1169. [Google Scholar] [CrossRef]
- Ogawa, K. Edge dislocations dissociated in {112} planes and twinning mechanism of bcc metals. Philos. Mag. 1965, 11, 217–233. [Google Scholar] [CrossRef]
- Leslie, W.C. Microstructural effects of high strain rate deformation. In Metallurgical Effects at High Strain Rates; Springer: Boston, MA, USA, 1973; pp. 571–586. [Google Scholar]
- Qin, B.; Bhadeshia, H.K.D.H. Plastic strain due to twinning in austenitic TWIP steels. Mater. Sci. Technol. 2008, 24, 969–973. [Google Scholar] [CrossRef]
- Kibey, S.; Liu, J.B.; Johnson, D.D.; Sehitoglu, H. Energy pathways and directionality in deformation twinning. Appl. Phys. Lett. 2007, 91, 181916. [Google Scholar] [CrossRef]
- Williams, D.F. A Discussion of Schmid Factors for Twinning in BCC Crystals. Met. Sci. J. 1967, 1, 94–96. [Google Scholar] [CrossRef]
- Ikeda, S.; Takeuchi, T. Stress and delay time for the appearance of twinning deformation in iron single crystals. J. Phys. Soc. Jpn. 1965, 20, 2152–2160. [Google Scholar] [CrossRef]
- Hull, D. Effect of grain size and temperature on slip, twinning and fracture in 3% silicon iron. Acta Metall. 1961, 9, 191–204. [Google Scholar] [CrossRef]
- Yang, P.; Xie, Q.; Meng, L.; Ding, H.; Tang, Z. Dependence of deformation twinning on grain orientation in a high manganese steel. Scr. Mater. 2006, 55, 629–631. [Google Scholar] [CrossRef]
- Yamakov, V.; Wolf, D.; Phillpot, S.R.; Gleiter, H. Deformation twinning in nanocrystalline Al by molecular-dynamics simulation. Acta Mater. 2002, 50, 5005–5020. [Google Scholar] [CrossRef]
- An, X.; Ni, S.; Song, M.; Liao, X. Deformation twinning and detwinning in face-centered cubic metallic materials. Adv. Eng. Mater. 2020, 22, 1900479. [Google Scholar] [CrossRef]
- Clayton, J.D.; Knap, J. A phase field model of deformation twinning: Nonlinear theory and numerical simulations. Physica D Nonlinear Phenom. 2011, 240, 841–858. [Google Scholar] [CrossRef] [Green Version]
- Hu, S.; Henager, C.H., Jr.; Chen, L. Simulations of stress-induced twinning and de-twinning: A phase field model. Acta Mater. 2010, 58, 6554–6564. [Google Scholar] [CrossRef]
- Kibey, S.; Liu, J.B.; Johnson, D.D.; Sehitoglu, H. Predicting twinning stress in fcc metals: Linking twin-energy pathways to twin nucleation. Acta Mater. 2007, 55, 6843–6851. [Google Scholar] [CrossRef]
- Chen, L.Q.; Shen, J. Applications of semi-implicit Fourier-spectral method to phase field equations. Comput. Phys. Commun. 1998, 108, 147–158. [Google Scholar] [CrossRef]
- Wilson, A.J.C. The thermal expansion of aluminium from 0 to 650 °C. Proc. Phys. Soc. 1941, 53, 235. [Google Scholar] [CrossRef]
- Hahn, T.A. Thermal expansion of copper from 20 to 800 K—Standard reference material 736. J. Appl. Phys. 1970, 41, 5096–5101. [Google Scholar] [CrossRef]
- Chen, M.; Ma, E.; Hemker, K.J.; Sheng, H.; Wang, Y.; Cheng, X. Deformation twinning in nanocrystalline aluminum. Science 2003, 300, 1275–1277. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, X.L.; Zhu, Y.T. Inverse grain-size effect on twinning in nanocrystalline Ni. Phys. Rev. Lett. 2008, 101, 025503. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kollie, T.G. Measurement of the thermal-expansion coefficient of nickel from 300 to 1000 K and determination of the power-law constants near the Curie temperature. Phys. Rev. B 1977, 16, 4872. [Google Scholar] [CrossRef]
- Lu, G.; Kioussis, N.; Bulatov, V.V.; Kaxiras, E. Generalized-stacking-fault energy surface and dislocation properties of aluminum. Phys. Rev. B 2000, 62, 3099. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.L.; Ma, E. Deformation twinning mechanisms in nanocrystalline Ni. Appl. Phys. Lett. 2006, 88, 061905. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Qian, D.; Xue, J.; Wan, J.; Zhang, A.; Tamura, N.; Chen, K. A synchrotron study of defect and strain inhomogeneity in laser-assisted three-dimensionally-printed Ni-based superalloy. Appl. Phys. Lett. 2015, 107, 181902. [Google Scholar] [CrossRef] [Green Version]
- Bufford, D.; Liu, Y.; Zhu, Y.; Bi, Z.; Jia, Q.X.; Wang, H.; Zhang, X. Formation mechanisms of high-density growth twins in aluminum with high stacking-fault energy. Mater. Res. Lett. 2013, 1, 51–60. [Google Scholar] [CrossRef]
- Guan, Q.F.; Pan, L.; Zou, H.; Wu, A.M.; Hao, S.Z.; Zhang, Q.Y.; Zou, G.T. Stacking fault tetrahedra in aluminum. J. Mater. Sci. 2004, 39, 6349–6351. [Google Scholar] [CrossRef]
- Zhang, X.; Misra, A.; Wang, H.; Nastasi, M.; Embury, J.D.; Mitchell, T.E.; Hoagland, R.G.; Hirth, J.P. Nanoscale-twinning-induced strengthening in austenitic stainless steel thin films. Appl. Phys. Lett. 2004, 84, 1096–1098. [Google Scholar] [CrossRef]
- Rappaz, M.; Dantzig, J.A. Solidification; EPFL Press: Lausanne, Switzerland, 2016. [Google Scholar]
- Asta, M.; Beckermann CKarma, A.; Kurz, W.; Napolitano, R.; Plapp, M.; Purdy, G.; Rappaz, M.; Trivedi, R. Solidification microstructures and solid-state parallels: Recent developments, future directions. Acta Mater. 2009, 57, 941. [Google Scholar] [CrossRef] [Green Version]
- Zhu, M.; Zhang, L.; Zhao, H.; Stefanescu, D.M. Modeling of microstructural evolution during divorced eutectic solidification of spheroidal graphite irons. Acta Mater. 2015, 84, 413–425. [Google Scholar] [CrossRef]
- Wang, N.; Smith, N.; Provatas, N. Investigating gas-phase defect formation in late-stage solidification using a novel phase-field crystal alloy model. Phys. Rev. Mater. 2017, 1, 043405. [Google Scholar] [CrossRef]
- Wang, N.; Kocher, G.; Provatas, N. A phase-field-crystal alloy model for late-stage solidification studies involving the interaction of solid, liquid and gas phases. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2018, 376, 20170212. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Karma, A.; Rappel, W.J. Quantitative phase-field modeling of dendritic growth in two and three dimensions. Phys. Rev. E 1998, 57, 4323. [Google Scholar] [CrossRef] [Green Version]

| Material | |||||
|---|---|---|---|---|---|
| Al | 114 | 62 | 32 | 215 | 113 |
| Ni | 261 | 151 | 132 | 324 | 110 |
| Cu | 225 | 153 | 115 | 200 | 40 |
| Material | |||||
|---|---|---|---|---|---|
| Al | 114 | 62 | 32 | 112 | 0.09 |
| Ni | 121.96 | 70.56 | 61.68 | 49.6 | 0.09 |
| Cu | 140 | 95.625 | 71.875 | 8.77 | 0.09 |
| Material | Critical Shear | |
|---|---|---|
| Al | 0.016 | 0.0113 |
| Ni | 0.006 | 0.0042 |
| Cu | 0.029 | 0.0205 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, B.; Yang, J.; Luo, Z.; Wang, Y.; Wang, N. Formation of Twin Boundaries in Rapidly Solidified Metals through Deformation Twinning. Materials 2023, 16, 4503. https://doi.org/10.3390/ma16134503
Huang B, Yang J, Luo Z, Wang Y, Wang N. Formation of Twin Boundaries in Rapidly Solidified Metals through Deformation Twinning. Materials. 2023; 16(13):4503. https://doi.org/10.3390/ma16134503
Chicago/Turabian StyleHuang, Binting, Jishi Yang, Zhiheng Luo, Yang Wang, and Nan Wang. 2023. "Formation of Twin Boundaries in Rapidly Solidified Metals through Deformation Twinning" Materials 16, no. 13: 4503. https://doi.org/10.3390/ma16134503
APA StyleHuang, B., Yang, J., Luo, Z., Wang, Y., & Wang, N. (2023). Formation of Twin Boundaries in Rapidly Solidified Metals through Deformation Twinning. Materials, 16(13), 4503. https://doi.org/10.3390/ma16134503






