Synthesis, Structure, and Physicochemical Characteristics of Zn1−xRexCr2Se4 Single Crystals
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
2.2.1. Chemical Vapour Transport (CVT)
2.2.2. Physicochemical Characteristic
3. Results and Discussion
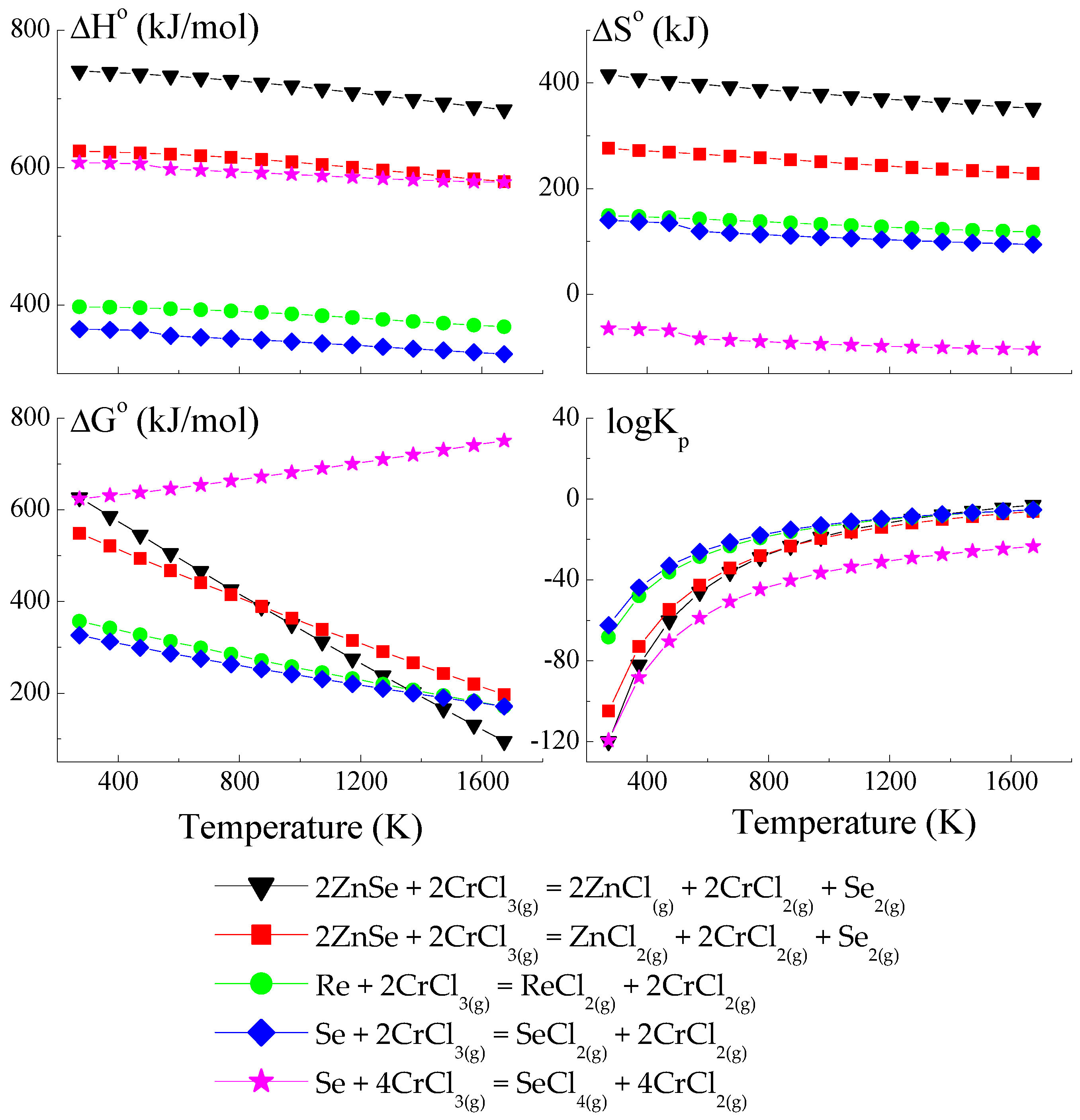
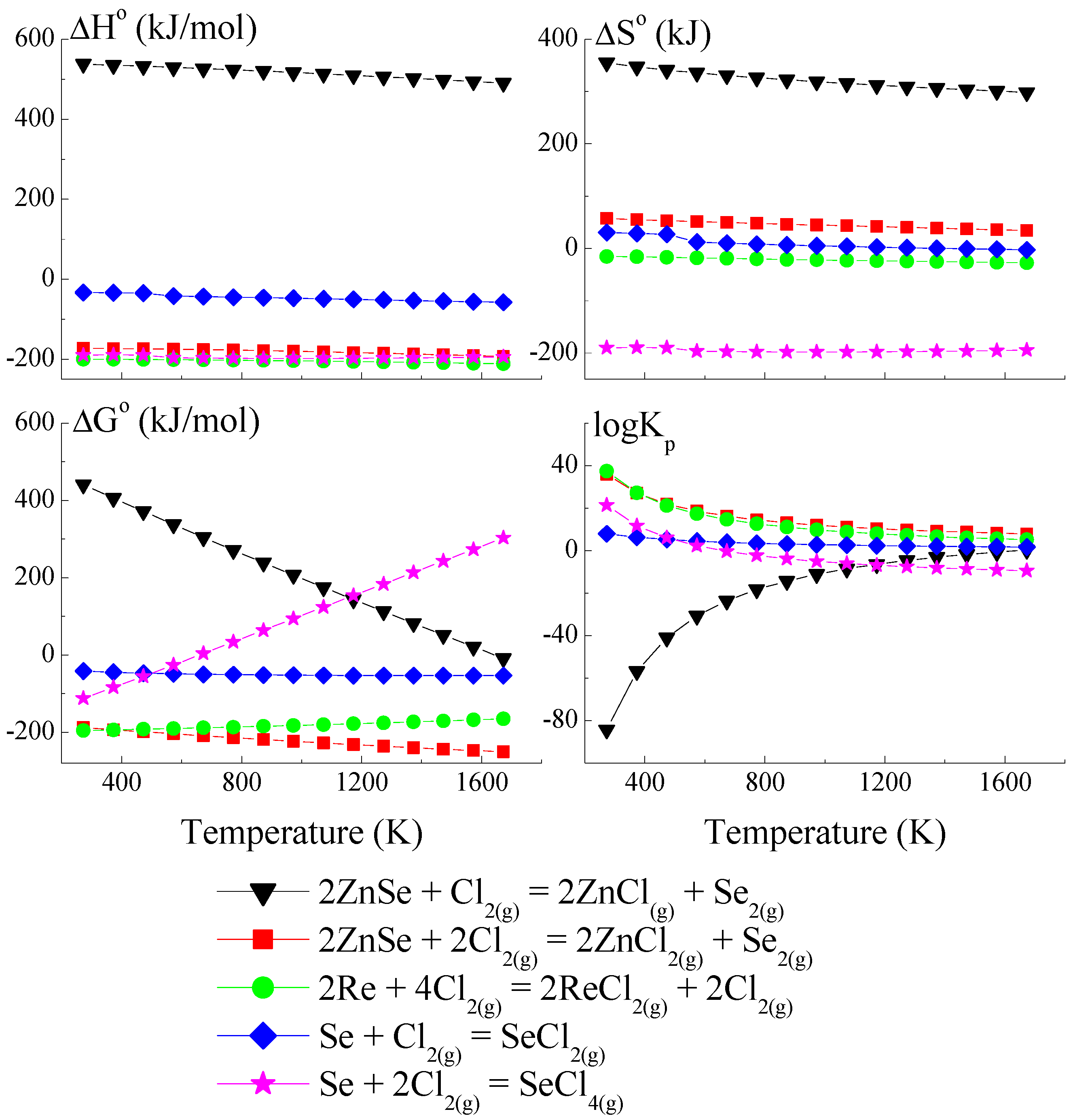
3.1. Thermodynamic Model of Chemical Vapour Transport in the ZnSe-Re-Se-CrCl3 System
3.2. Growth of ZnCr2Se4 Single Crystals Doped with Rhenium
for x = 0.1–0.4.
3.3. Chemical Composition
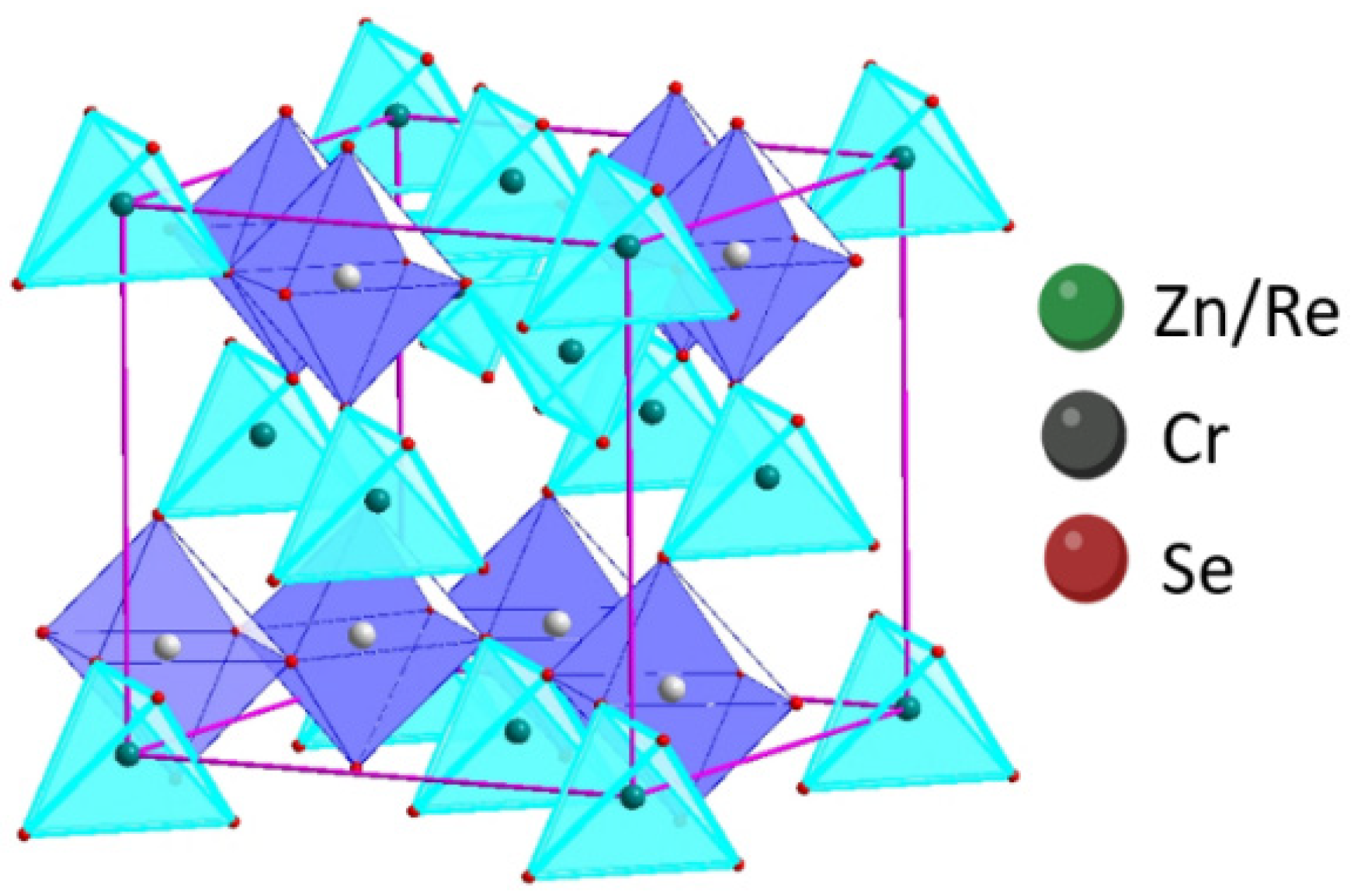
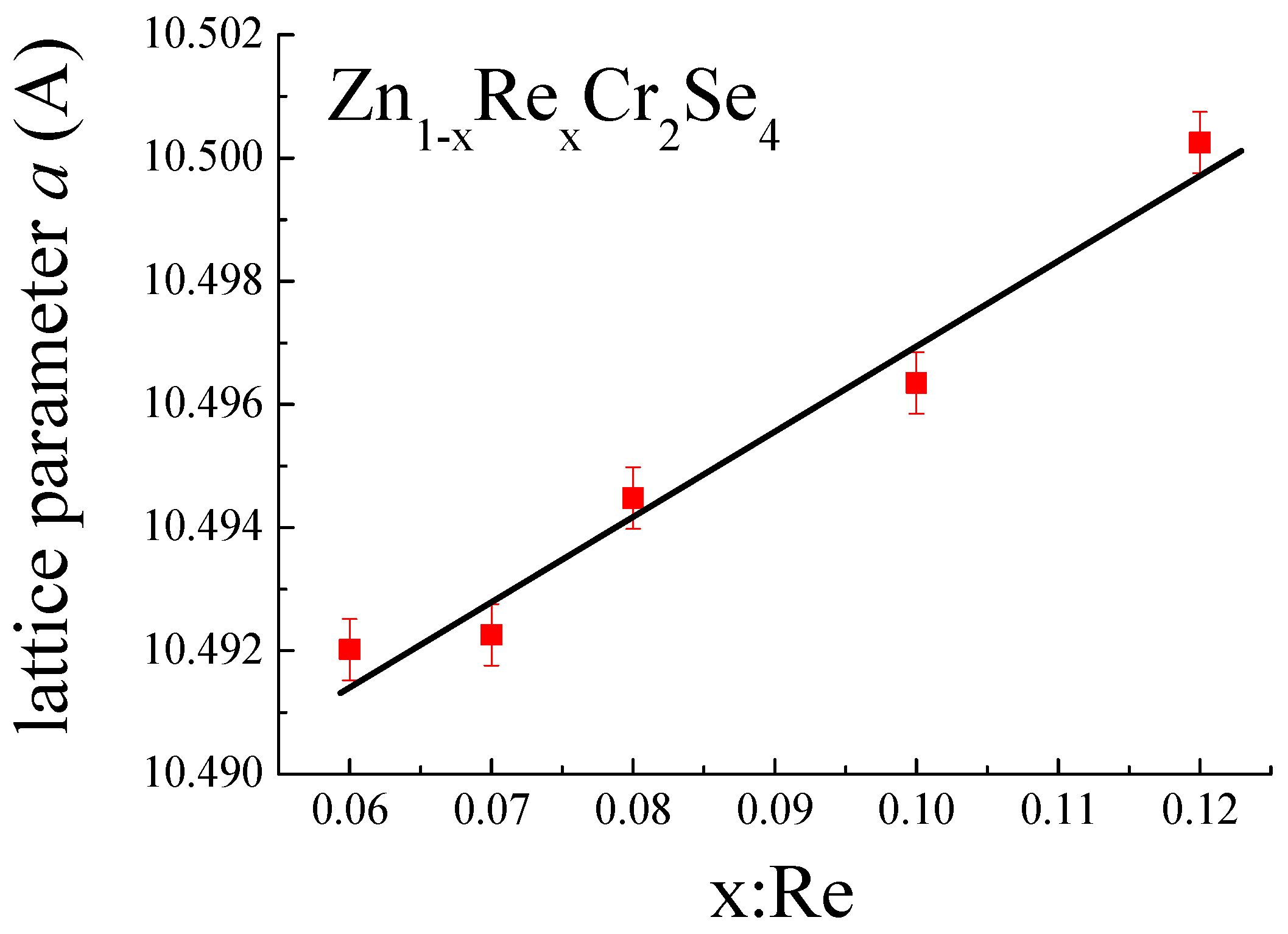
3.4. Structural Study
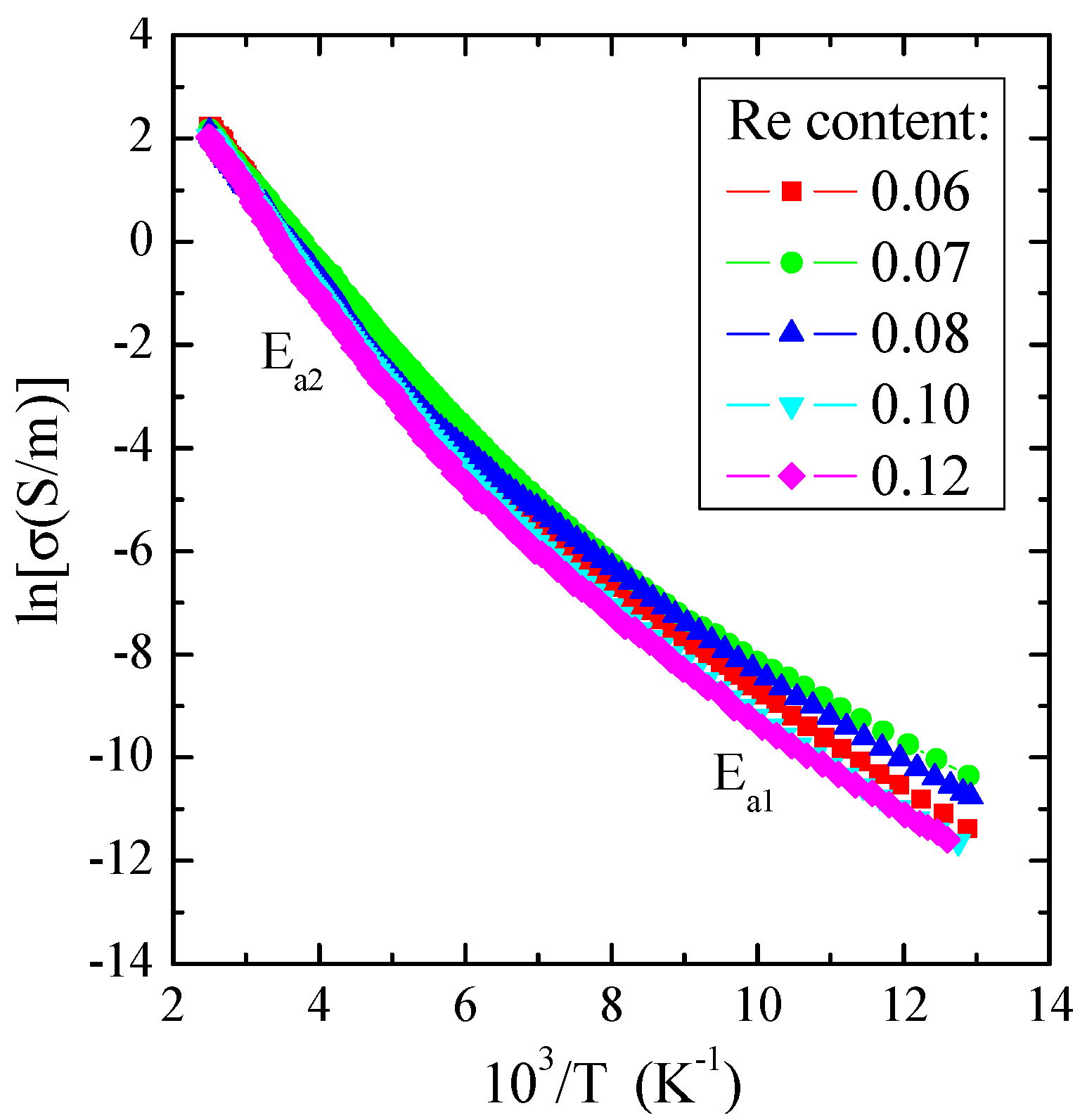
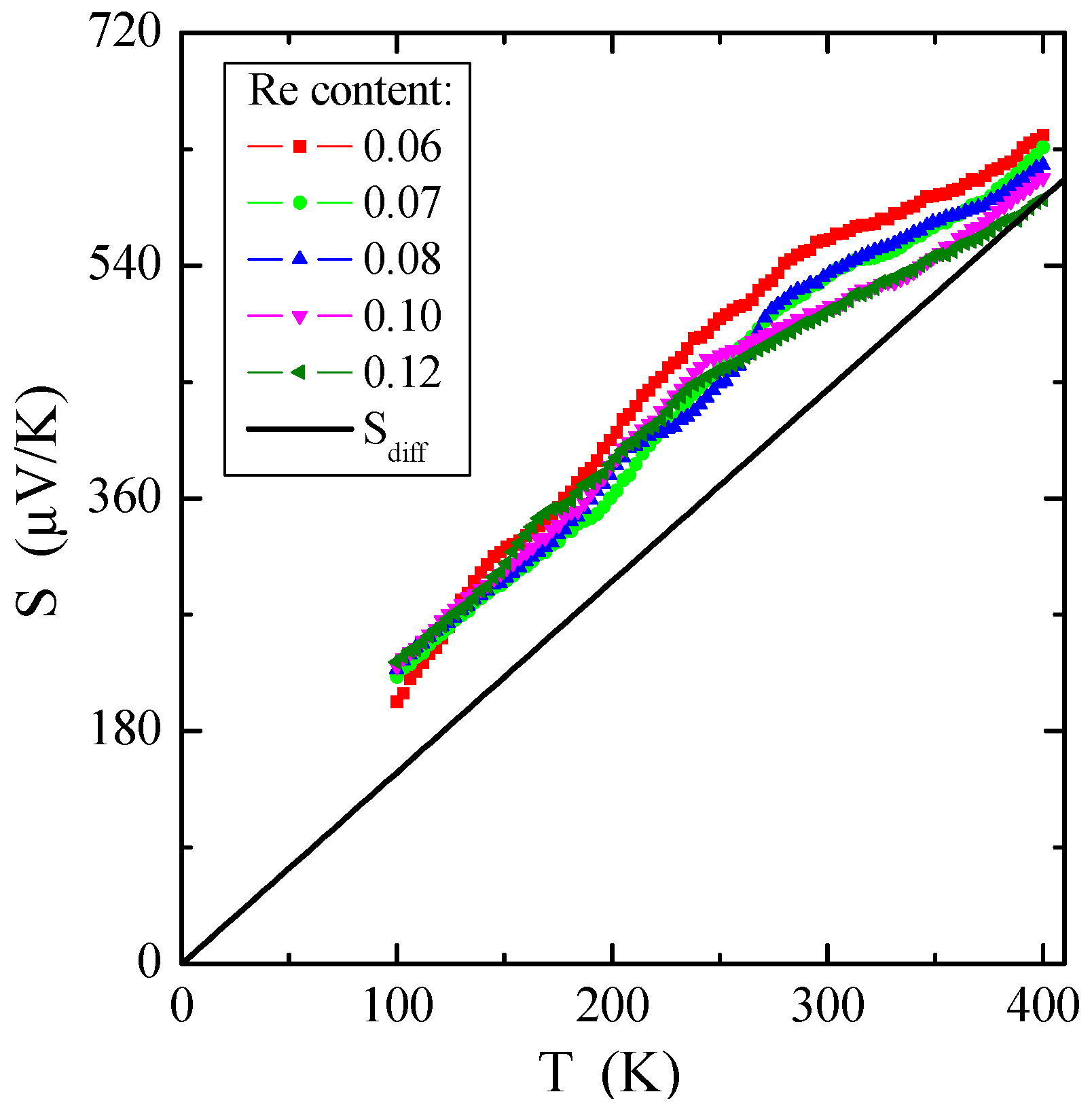
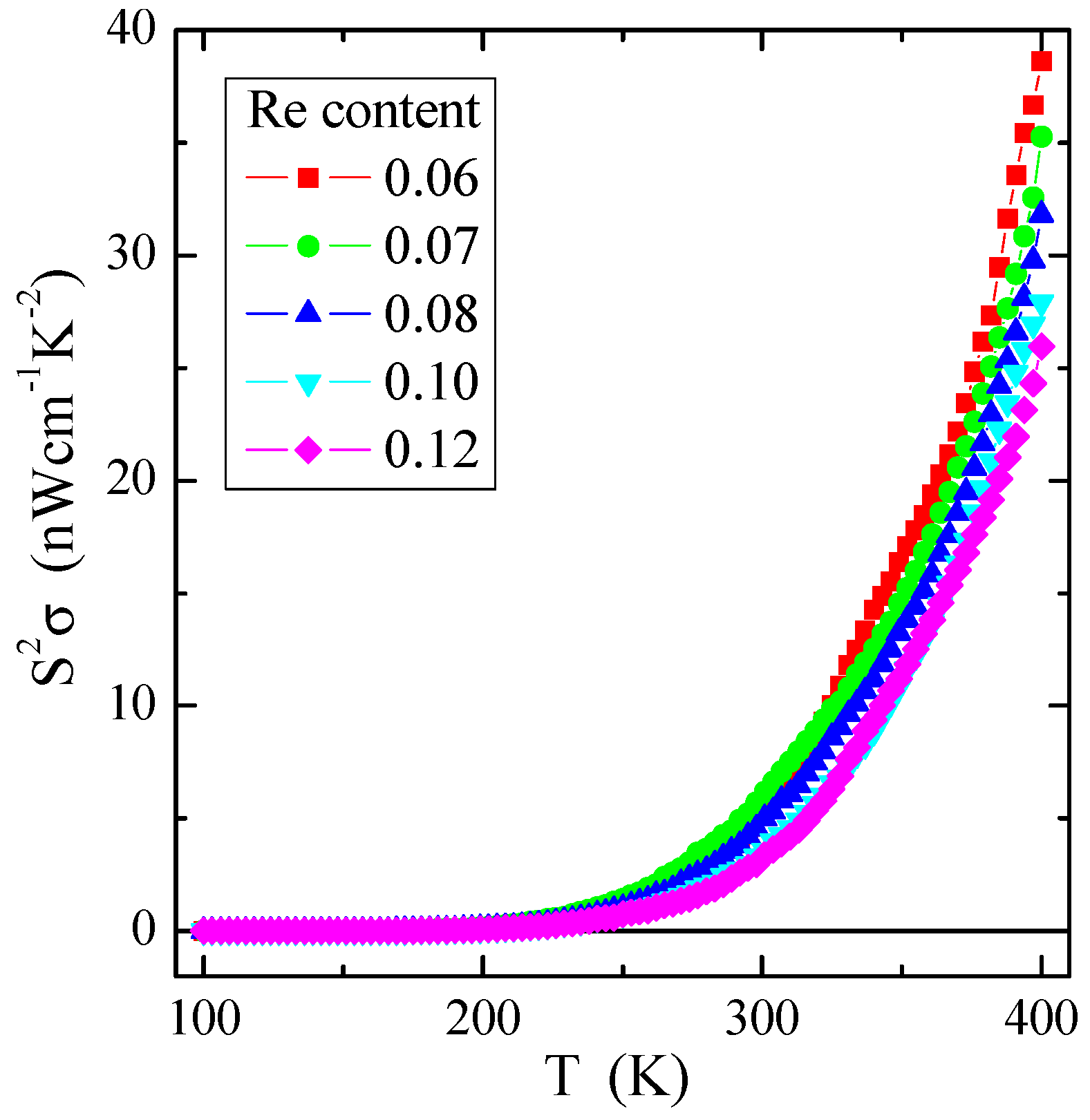
3.5. Electrical Studies
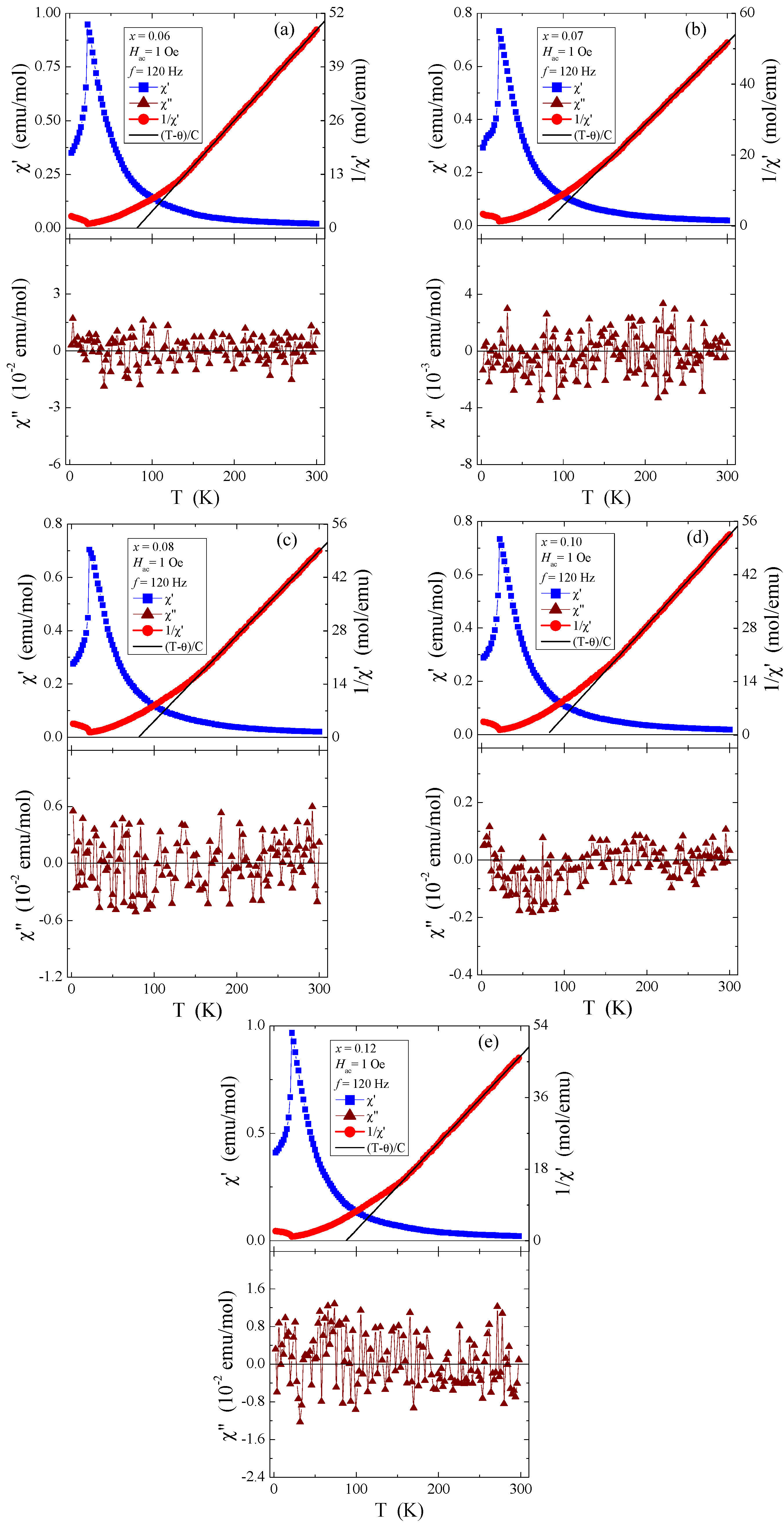
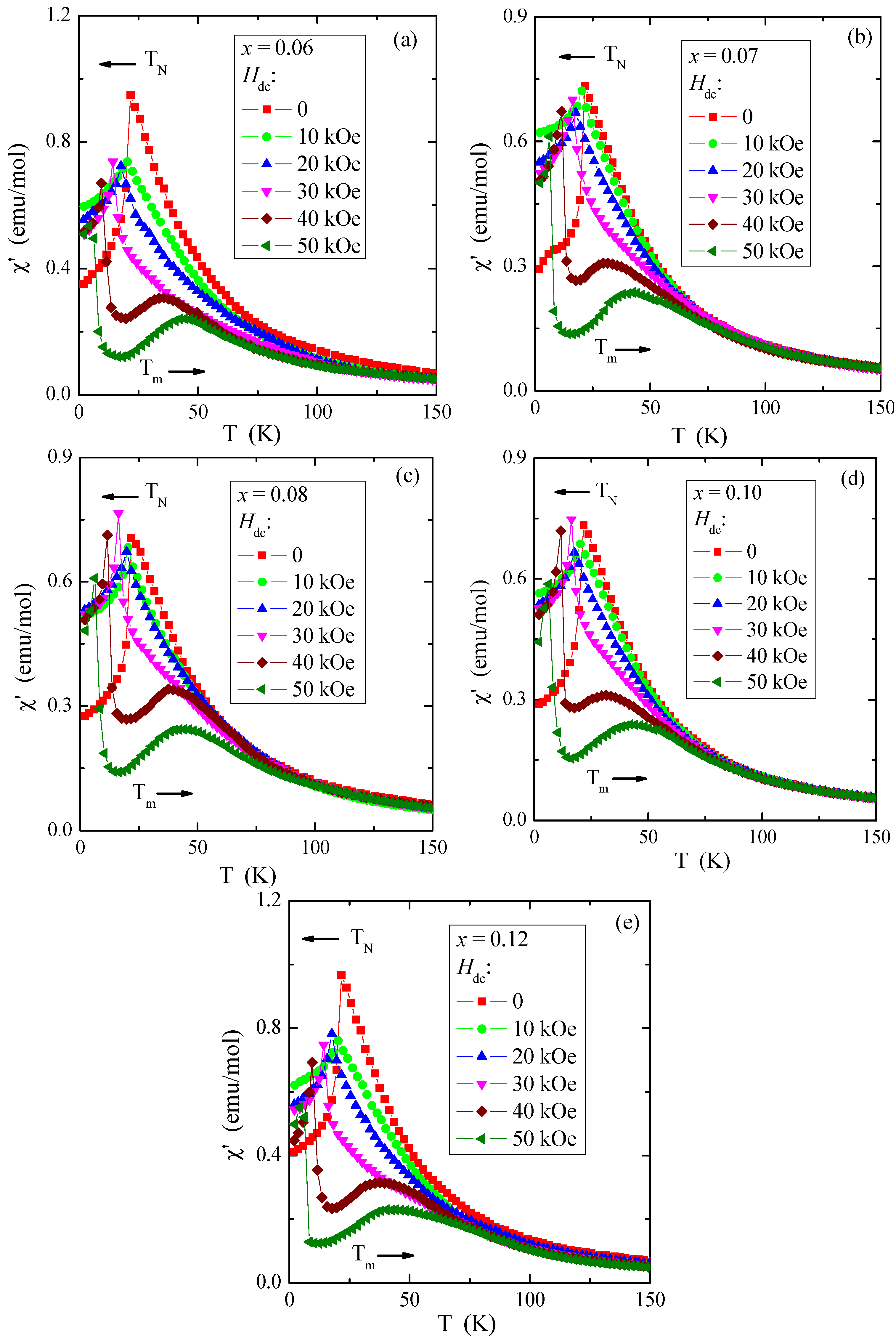
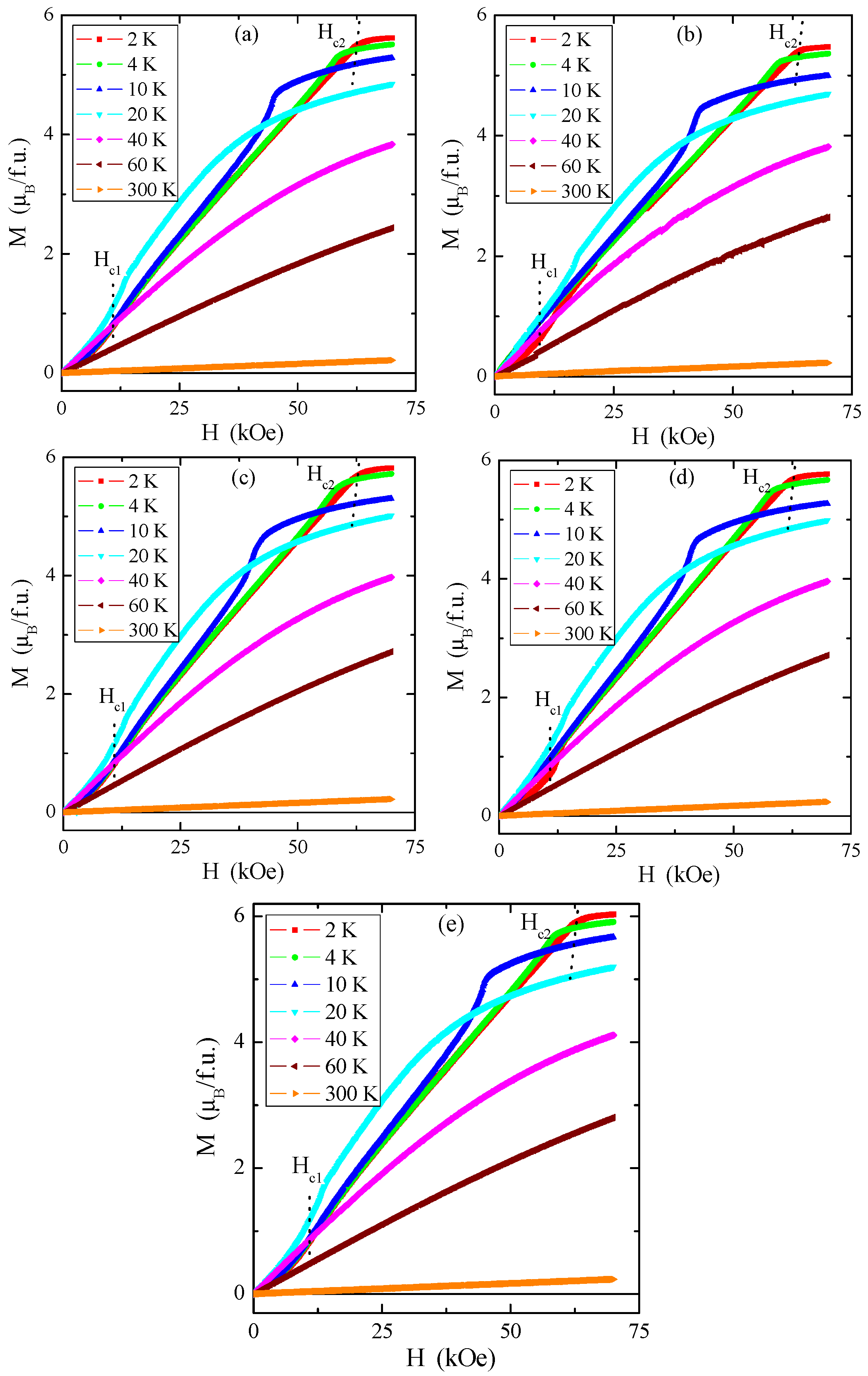
3.6. Magnetic Properties
3.7. Specific Heat Measurements
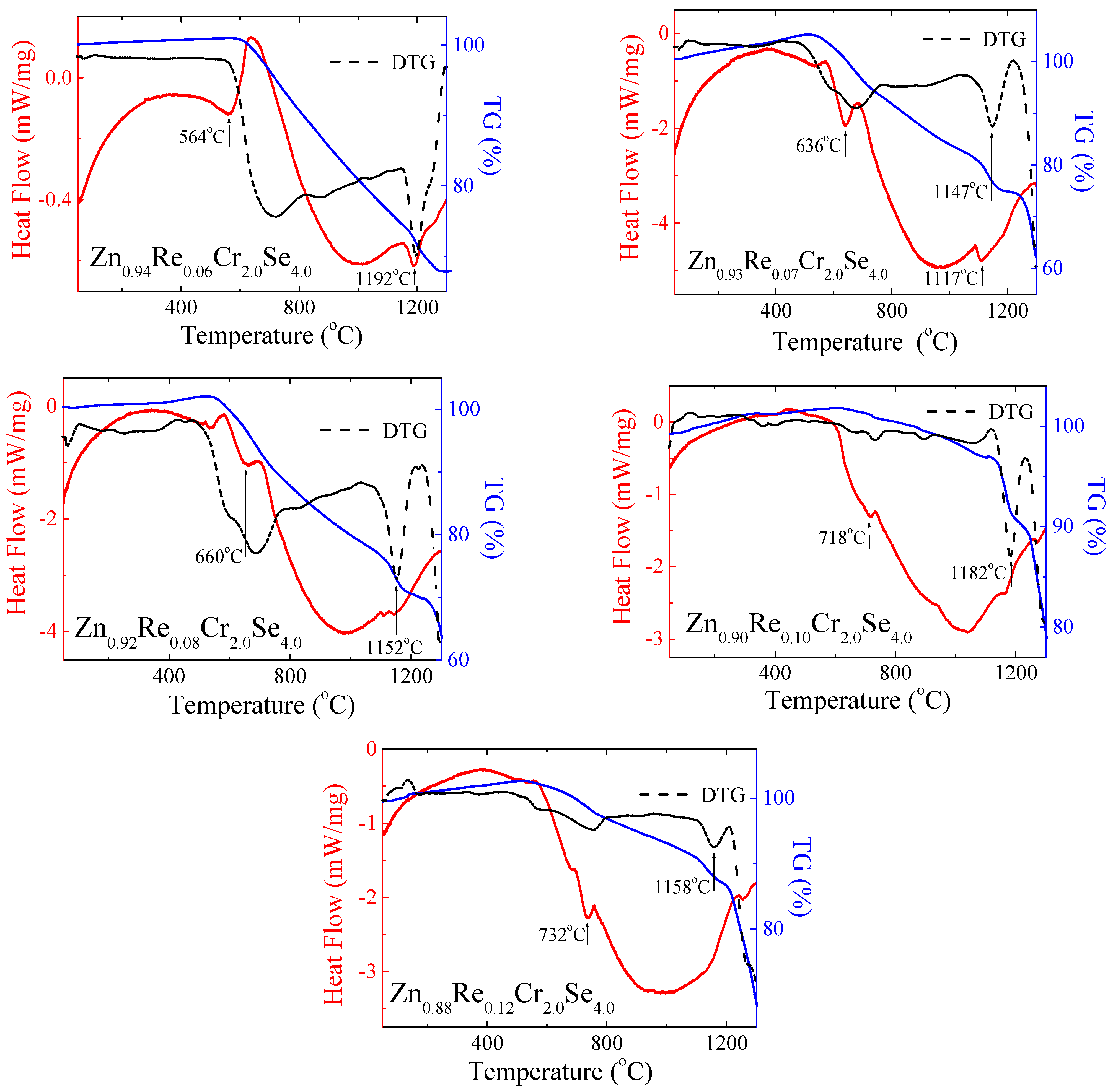
3.8. Thermal Study
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Snyder, G.J.; Caillat, T.; Fleurial, J.P. Thermoelectric properties of Chalcogenides with Spinel Structure. Mat. Res. Innov. 2001, 5, 67. [Google Scholar] [CrossRef]
- Korenskii, V.I.; Ignateva, I.S.; Kolenko, I.P.; Potiev, A.A.; Surat, L.L. Osobennosti Elektronnogo Stroeniya i Svoistva Twerdofaznych Soedinenii Titana i Vanadya; UNTS AN SSSR: Sverdlovsk, Russia, 1982. [Google Scholar]
- Armand, N.B. Materials for Advances Batteries; Minphy, M.W., Broadhead, J., Steele, B.C.H., Eds.; New York Plenum Press: New York, NY, USA, 1980. [Google Scholar]
- Thakeray, M.M.; David, W.I.F.; Goodenough, J.B. High-temperature lithiation of α-Fe2O3: A mechanistic study. J. Solid State Chem. 1984, 55, 280–286. [Google Scholar] [CrossRef]
- Lotgering, F.K. Ferromagnetic interactions in sulphides, selenides and tellurides with spinel structure. In Proceedings of the International Conference on Magnetism, Nottingham, UK, 7–11 September 1964; Institute of Physics and the Physical Society: London, UK, 1965; pp. 533–538. [Google Scholar]
- Plumier, R. Étude par diffraction de neutrons de l’antiferromagnétisme hélicoïdal du spinelle ZnCr2Se4 en présence d’un champ magnétique. J. Phys. 1966, 27, 213–219. [Google Scholar] [CrossRef]
- Greenwood, N.N. Ionenkristalle, Gitterdefekte und Nichtstöchiometrische Verbindungen; Verlag Chemie: Weinheim, Germany, 1973. [Google Scholar]
- Park, S.; Kwon, S.; Lee, S.; Khim, S.; Bhoi, D.; Park, C.B.; Kim, K.H. Interactions in the bond-frustrated helimagnet ZnCr2Se4 investigated by NMR. Sci. Rep. 2019, 9, 16627. [Google Scholar] [CrossRef] [PubMed]
- Hemberger, J.; von Nidda, H.-A.K.; Tsurkan, V.; Loidl, A. Large Magnetostriction and Negative Thermal Expansion in the Frustrated Antiferromagnet ZnCr2Se4. Phys. Rev. Lett. 2007, 98, 147203. [Google Scholar] [CrossRef]
- Yaresko, A.N. Electronic band structure and exchange coupling constants in ACr2X4 spinels (A=Zn, Cd, Hg; X=O, S, Se). Phys. Rev. 2008, 77, 115106. [Google Scholar] [CrossRef]
- Malicka, E.; Groń, T.; Pacyna, A.W.; Maciążek, E.; Duda, H.; Pawełczyk, M.; Zawisza, B.; Sitko, R. Influence of temperature on the critical fields in ZnCr2−xAlxSe4 antiferromagnets. J. Alloys Compd. 2009, 480, 67–69. [Google Scholar] [CrossRef]
- Groń, T.; Malicka, E.; Duda, H.; Pacyna, A.W.; Mydlarz, T.; Sitko, R.; Pawełczyk, M. Spin-glass-like behavior in ZnxCryAlzSe4. J. Phys. Chem. Solids 2009, 70, 1175–1180. [Google Scholar] [CrossRef]
- Okońska-Kozłowska, I.; Lutz, H.D.; Groń, T.; Krok, J.; Mydlarz, T. Darstellung, elektrische und magnetische Eingenschaften von-Zn1−xGa0.667xCr2Se4-Spinell-Einkristallen. Mater. Res. Bull. 1984, 19, 1–5. [Google Scholar] [CrossRef]
- Groń, T.; Duda, H.; Warczewski, J. Transport phenomena in the antiferromagnetic spinels Zn1−xGa2x/3Cr2Se4 (where 0.0 < × < 0.5). J. Mag. Mag. Mater. 1990, 83, 487–489. [Google Scholar]
- Groń, T.; Kopyczok, J.; Okońska-Kozłowska, I.; Warczewski, J. Seebeck effect in the antiferromagnetic single crystals of ZnCr2−xInxSe4 (0.0 < × < 0.15). J. Mag. Mag. Mater. 1992, 111, 53–55. [Google Scholar]
- Jendrzejewska, I.; Groń, T.; Kusz, J.; Żelechower, M.; Maciążek, E.; Ślebarski, A.; Fijałkowski, M. Spin-glass-like behaviour in tin doped ZnCr2Se4 single crystals. J. Alloys Compd. 2015, 635, 238–244. [Google Scholar] [CrossRef]
- Jendrzejewska, I.; Mroziński, J.; Groń, T.; Duda, H.; Zajdel, P.; Pacyna, A.W.; Maciążek, E.; Hanc, A. Effect of cation substitution on Fermi level of n-type ZnxSnyCrzSe4 spinels. J. Alloys Compd. 2009, 480, 63–66. [Google Scholar] [CrossRef]
- Jendrzejewska, I.; Groń, T.; Kusz, J.; Stokłosa, Z.; Pietrasik, E.; Goryczka, T.; Sawicki, B.; Goraus, J.; Jampilek, J.; Duda, H.; et al. The Zn1−xPbxCr2Se4-single crystals obtained by chemical vapour transport—structure and magnetic, electrical, and thermal properties. Materials 2022, 15, 5289. [Google Scholar] [CrossRef] [PubMed]
- Groń, T.; Wolff, J.; Hehenkamp, T.; Bärner, K.; Okońska-Kozłowska, I.; Jendrzejewska, I.; Malicka, E. Positron annihilation studies in single and polycrystals of Zn1−xCuxCr2Se4 spinel series. Radiat. Eff. Defects Solids 1996, 139, 97–107. [Google Scholar] [CrossRef]
- Groń, T.; Jendrzejewska, I.; Gołąbek, S.; Duda, H.; Krajewski, A.; Bärner, K. The thermoelectric power of ferromagnetically ordered ZnxCuyCrzSe4 single crystals. Phys. B Condens. Matter. 2003, 327, 88–95. [Google Scholar] [CrossRef]
- Mazur, S.; Groń, T.; Jendrzejewska, I. Influence of spin arrangement on thermopower in ZnxCuyCrzSe4 spinels. J. Alloys Compd. 2009, 480, 19–22. [Google Scholar] [CrossRef]
- Jendrzejewska, I.; Waśkowska, A.; Mydlarz, T. Influence of nickel substitution on the cation distribution and magnetic properties of ZnCr2Se4. J. Alloys Compd. 2001, 327, 73–77. [Google Scholar] [CrossRef]
- Jendrzejewska, I.; Zajdel, P.; Goryczka, T.; Goraus, J.; Kita, A.; Mydlarz, T. Influence of covalency and anion polarisation on magnetic and electronic properties of ZnCr2−xNixSe4. J. Alloys Compd. 2012, 520, 153–157. [Google Scholar] [CrossRef]
- Jendrzejewska, I.; Groń, T.; Goraus, J.; Pilch, M.; Pietrasik, E.; Barsova, Z.; Czerniewski, J.; Goryczka, T.; Witkowska-Kita, B.; Bienko, A.; et al. Synthesis and structural, magnetic, thermal and electronic properties of Mn-doped ZnCr2Se4. Mater. Chem. Phys. 2019, 238, 121901. [Google Scholar] [CrossRef]
- Jendrzejewska, I.; Zajdel, P.; Heimann, J.; Krok-Kowalski, J.; Mydlarz, T.; Mrzigod, J. Influence of manganese on magnetic and electronic properties of ZnCr2Se4 single Crystals. Mater. Res. Bull. 2012, 47, 1881–1886. [Google Scholar] [CrossRef]
- Jendrzejewska, I.; Groń, T.; Kwapuliński, P.; Kusz, J.; Pietrasik, E.; Goryczka, T.; Sawicki, B.; Ślebarski, A.; Fijałkowski, M.; Jampilek, J.; et al. Study of the structure, magnetic, thermal and electrical characterisation of ZnCr2Se4:Ta single crystals obtained by chemical vapour transport. Materials 2021, 14, 2749. [Google Scholar] [CrossRef] [PubMed]
- Jendrzejewska, I.; Groń, T.; Knizek, K.; Pilch, M.; Ślebarski, A.; Goraus, J.; Zajdel, P.; Stokłosa, Z.; Pietrasik, E.; Goryczka, T.; et al. Preparation, structure and magnetic, electronic and thermal properties of Dy3+-doped ZnCr2Se4 with unique geometric type spin-glass. J. Solid State Chem. 2021, 298, 122114. [Google Scholar] [CrossRef]
- Jendrzejewska, I.; Groń, T.; Maciążek, E.; Duda, H.; Kubisztal, M.; Ślebarski, A.; Pietrasik, E.; Fijałkowski, M. Specific heat and magnetic properties of single-crystalline ZnxDyyCrzSe4 spinels. J. Magn. Magn. Mater. 2016, 407, 122–128. [Google Scholar] [CrossRef]
- Maciążek, E.; Karolus, M.; Kubisztal, M.; Jendrzejewska, I.; Sitko, R.; Groń, T.; Ślebarski, A.; Fijałkowski, M. Magnetic and specific heat properties of a new Gd-doped ZnCr2Se4. Mater. Chem. Phys. 2015, 168, 187–192. [Google Scholar] [CrossRef]
- Jendrzejewska, I.; Groń, T.; Kusz, J.; Goraus, J.; Barsova, Z.; Pietrasik, E.; Czerniewski, J.; Goryczka, T.; Kubisztal, M. Growth, structure and physico-chemical properties of monocrystalline ZnCr2Se4:Ho prepared by chemical vapour transport. J. Solid State Chem. 2020, 281, 121024. [Google Scholar] [CrossRef]
- Jendrzejewska, I.; Groń, T.; Kusz, J.; Barsova, Z.; Pietrasik, E.; Goryczka, T.; Sawicki, B.; Ślebarski, A.; Fijałkowski, M.; Jampilek, J.; et al. Synthesis, crystal structure and characterisation of monocrystalline ZnCr2Se4 doped with neodymium. J. Solid State Chem. 2020, 292, 121661. [Google Scholar] [CrossRef]
- Piekarczyk, J. Thermodynamic model of chemical vapour transport and its application to some ternary compounds: I. The model. J. Cryst. Growth 1987, 82, 367–376. [Google Scholar] [CrossRef]
- Piekarczyk, J. Thermodynamic model of chemical vapour transport and its application to some ternary compounds: II. Application of the model to the complex oxides: ZnCr2O4, Y3Fe5O12 and Fe2TiO5. J. Cryst. Growth 1988, 89, 267–286. [Google Scholar] [CrossRef]
- Schmidt, P.M.; Binnewies, M.; Glaum, R.M.; Schmidt, M. Chemical Vapor Transport Reactions—Methods, Materials, Modeling. In Advanced Topics on Crystal Growth; IntechOpen: London, UK, 2013; Chapter 9; pp. 227–305. [Google Scholar]
- Jendrzejewska, I.; Żelechower, M.; Szamocka, K.; Mydlarz, T.; Waśkowska, A.; Okońska-Kozłowska, I. Growth of the CdxNiyCrzSe4 single crystals and their magnetic properties. J. Cryst. Growth 2004, 270, 30–37. [Google Scholar] [CrossRef]
- HSC Chemistry, version 6.01; Metso Outotec Corporation: Helsinki, Finland, 2009.
- Jurczyk, J.; Sitko, R.; Jendrzejewska, I. Thin sample in the XRF analysis. A new method of preparing microsamples of mono- and polycrystals, and silicate rocks. Chem. Anal. 1999, 44, 167–185. [Google Scholar]
- Groń, T.; Krok-Kowalski, J.; Duda, H.; Mydlarz, T.; Gilewski, A.; Walczak, J.; Filipek, E.; Bärner, K. Metamagnetism in Cr2V4−xMoxO13+0.5x. Phys. Rev. B 1995, 51, 16021–16024. [Google Scholar] [CrossRef]
- Krok-Kowalski, J.; Groń, T.; Warczewski, J.; Mydlarz, T.; Okońska-Kozłowska, I. Ferrimagnetism and metamagnetism in Cd1−xCuxCr2S4, spinels. J. Magn. Magn. Mater. 1997, 168, 129–138. [Google Scholar] [CrossRef]
- Morrish, A.H. Physical Principles of Magnetism; John Wiley & Sons, Inc.: New York, NY, USA, 1965. [Google Scholar]
- Particle Data Group; Workman, R.L.; Burkert, V.D.; Crede, V.; Klempt, E.; Thoma, U.; Tiator, L.; Agashe, K.; Aielli, G.; Allanach, B.C.; et al. The Review of Particle Physics. Prog. Theor. Exp. Phys. 2022, 2022, 083C01. [Google Scholar]
- Holland, W.E.; Brown, H.A. Application of the Weiss molecular field theory to the B-site spinel. Phys. Status Solidi 1972, 10, 249–253. [Google Scholar] [CrossRef]
- Clark, R.C.; Reid, J.S. The analytical calculation of absorption in multifaceted crystals. Acta Crystallogr. 1995, 51, 887–897. [Google Scholar] [CrossRef]
- Sheldrick, G.M. A short history of SHELX. Acta Crystallogr. 2008, 64, 112–122. [Google Scholar] [CrossRef]
- Plies, V. Massenspektrometrische Untersuchungen der Gasphase über CrCl3 und CrCl3/Cl2. Z. Anorg. Allg. Chem. 1988, 556, 120–125. [Google Scholar] [CrossRef]
- Von Oppermann, H. Das Reaktionsgleichgewicht 2CrCl3,f, g + Cl2,g = 2 CrCl4,g. Z. Anorg. Allg. Chem. 1968, 359, 51–57. [Google Scholar] [CrossRef]
- Shannon, R.D. Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides. Acta Cryst. 1976, A32, 751–767. [Google Scholar] [CrossRef]
- Dzięgielewski, J. Inorganic Chemistry—Script for Students; University of Silesia: Katowice, Poland, 1987. [Google Scholar]
- Busch, G.; Magyar, B.; Wachter, P. Optical absorption of some ferro- and antiferromagnetic spinels, containing Cr3+-ions. Phys. Lett. 1966, 23, 438–440. [Google Scholar] [CrossRef]
- Barnard, R.D. Thermoelectricity in Metals and Alloys; Taylor & Francis: London, UK, 1972. [Google Scholar]
- Trodahl, H.J. Thermopower of the superconducting cuprates. Phys. Rev. B 1995, 51, 5178–6175. [Google Scholar] [CrossRef] [PubMed]
- Kittel, C. Introduction to Solid State Physics; John Wiley & Sons, Inc.: New York, NY, USA, 1971; p. 641. [Google Scholar]
- Groń, T.; Bärner, K.; Kleeberg, C.; Okońska-Kozłowska, I. The thermoelectric power of ferromagnetically ordered Cu1−xGaxCr2Se4 spinels. Phys. B Condens. Matter 1996, 225, 191–196. [Google Scholar] [CrossRef]
- Sawicki, B.; Karolewicz, M.; Tomaszewicz, E.; Oboz, M.; Groń, T.; Kukuła, Z.; Pawlus, S.; Nowok, A.; Duda, H. Effect of Gd3+ substitution on thermoelectric power factor of paramagnetic Co2+-doped calcium molybdato-tungstates. Materials 2021, 14, 3692. [Google Scholar] [CrossRef]
- Sawicki, B.; Tomaszewicz, E.; Guzik, M.; Groń, T.; Oboz, M.; Duda, H.; Pawlus, S.; Urbanowicz, P. Effect of Ca2+ site substitution on structural, optical, electrical and magnetic properties in Nd3+ and Mn2+-co-doped calcium molybdato-tungstates. Ceram. Int. 2023, 49, 944–955. [Google Scholar] [CrossRef]
- Malicka, E.; Groń, T.; Ślebarski, A.; Pacyna, A.W.; Goraus, J.; Fijałkowski, M.; Heimann, J. Specific heat and magnetic susceptibility of single-crystalline ZnCr2−xAlxSe4 (x = 0.15, 0.23). J. Phys. Chem. Solids 2011, 72, 974–979. [Google Scholar] [CrossRef]
- Malicka, E.; Groń, T.; Ślebarski, A.; Gągor, A.; Pacyna, A.W.; Sitko, R.; Goraus, J.; Mydlarz, T.; Heimann, J. Specific heat and magnetic susceptibility of single-crystalline ZnCr2Se4 spinels doped with Ga, In and Ce. Mater. Chem. Phys. 2011, 131, 142–150. [Google Scholar] [CrossRef]



| N° | Amounts of Substrates (mmol) | Td (K) | Tc (K) | ΔT (K) | % Weight | Chemical Formula | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| nZnSe | n*ReSe | Zn | Re | Cr | Se | |||||
| (1) | 14.4 | 1.6 | 1173 | 1143 | 30 | 12.29 ± 0.19 | 2.02 ± 0.21 | 19.68 ± 0.36 | 66.01 ± 0.24 | Zn0.94Re0.06Cr2.0Se4.0 |
| (2) | 12.8 | 3.2 | 1143 | 1103 | 40 | 12.07 ± 0.21 | 2.59 ± 0.36 | 19.79 ± 0.34 | 65.55 ± 0.28 | Zn0.93Re0.07Cr2.0Se4.0 |
| (3) | 11.2 | 4.8 | 1203 | 1163 | 40 | 12.20 ± 0.23 | 3.12 ± 0.29 | 20.77 ± 0.35 | 63.91 ± 0.23 | Zn0.92Re0.08Cr2.0Se4.0 |
| (4) | 9.6 | 6.4 | 1203 | 1173 | 30 | 11.57 ± 0.18 | 3.78 ± 0.24 | 20.99 ± 0.39 | 63.65 ± 0.21 | Zn0.90Re0.10Cr2.0Se4.0 |
| (5) | 9.6 | 6.4 | 1193 | 1153 | 40 | 11.37 ± 0.18 | 4.21 ± 0.24 | 21.03 ± 0.39 | 63.39 ± 0.21 | Zn0.88Re0.12Cr2.0Se4.0 |
| x | Lattice Parameter (Å) | Volume (Å3) | Density Calc. (Mg/m3) | Absorption Coeff. (mm−1) | Goodness of Fit on F2 | R Parameters | |
|---|---|---|---|---|---|---|---|
| R1 | wR2 | ||||||
| 0.06 | 10.49212(16) | 1155.02 (5) | 5.664 | 33.879 | 1.176 | 0.0236 | 0.071 |
| 0.07 | 10.49206(19) | 1155.00 (6) | 5.678 | 34.048 | 1.720 | 0.0245 | 0.0760 |
| 0.08 | 10.49448(14) | 1155.80 (1) | 5.688 | 34.192 | 1.182 | 0.0266 | 0.0882 |
| 0.10 | 10.49635(14) | 1156.42 (2) | 5.713 | 34.509 | 1.212 | 0.0326 | 0.1077 |
| 0.12 | 10.50025(15) | 1157.71 (1) | 5.734 | 34.806 | 1.2690 | 0.0413 | 0.1259 |
| Chemical Formula | a (µV/K2) | EF (eV) | TF (K) | Ea1 (eV) | Ea2 (eV) |
|---|---|---|---|---|---|
| Zn0.94Re0.06Cr2Se4 | 1.60 | 0.045 | 531 | 0.173 | 0.084 |
| Zn0.93Re0.07Cr2Se4 | 1.58 | 0.046 | 534 | 0.146 | 0.072 |
| Zn0.92Re0.08Cr2Se4 | 1.55 | 0.047 | 545 | 0.162 | 0.078 |
| Zn0.90Re0.10Cr2Se4 | 1.52 | 0.048 | 557 | 0.172 | 0.083 |
| Zn0.88Re0.12Cr2Se4 | 1.48 | 0.050 | 580 | 0.176 | 0.082 |
| x | C (emu·K/mol) | TN (K) | θ (K) | µeff (µB/f.u.) | peff | Ms(2K) (µB/f.u.) | J1 (K) | J2 (K) | Hc1 (kOe) | Hc2 (kOe) | Ea (eV) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 4.082 | 21 | 90 | 5.714 | 5.477 | 6.0 | −1.65 | 1.28 | 10.0 | 65.0 | 0.135 |
| 0.06 | 4.554 | 21.7 | 81.5 | 6.035 | 5.666 | 5.62 | −1.90 | 1.22 | 11.4 | 61.2 | - |
| 0.07 | 4.365 | 21.7 | 74.7 | 5.901 | 5.697 | 5.48 | −2.01 | 1.17 | 12.3 | 62.5 | - |
| 0.08 | 4.478 | 21.7 | 80.8 | 5.985 | 5.727 | 5.82 | −1.91 | 1.22 | 11.1 | 61.0 | - |
| 0.10 | 4.212 | 21.7 | 79.2 | 5.804 | 5.788 | 5.77 | −1.94 | 1.20 | 12.9 | 60.0 | - |
| 0.12 | 4.565 | 21.7 | 87.7 | 6.042 | 5.849 | 6.03 | −1.79 | 1.27 | 12.4 | 61.8 | - |
| Re Content | Weight Loss (%) | Onset (o) | Endset (o) | Peak Minimum (o) | Peak Height (mW) | Peak Area (J) | Enthalpy (J/g) |
|---|---|---|---|---|---|---|---|
| 0.0 * | 35 | 735 | 771 | 755 | 6.47 | 1.09 | 236 |
| 0.6 | 32 | 359 1164 | 629 1219 | 564 1192 | 5.22 7.54 | 3.84 1.71 | 48.8 21.7 |
| 0.07 | 50 | 591 1091 | 669 1219 | 636 1117 | 6.64 3.96 | 1.94 2.39 | 235 291 |
| 0.08 | 46 | 582 | 697 | 660 | 4.11 | 1.04 | 92.0 |
| 0.10 | 32 | 695 | 732 | 718 | 2.32 | 0.25 | 11.8 |
| 0.12 | 58 | 712 | 754 | 732 | 5.34 | 0.65 | 37.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jendrzejewska, I.; Groń, T.; Kusz, J.; Stokłosa, Z.; Pietrasik, E.; Goryczka, T.; Sawicki, B.; Goraus, J.; Jampilek, J.; Witkowska-Kita, B. Synthesis, Structure, and Physicochemical Characteristics of Zn1−xRexCr2Se4 Single Crystals. Materials 2023, 16, 4565. https://doi.org/10.3390/ma16134565
Jendrzejewska I, Groń T, Kusz J, Stokłosa Z, Pietrasik E, Goryczka T, Sawicki B, Goraus J, Jampilek J, Witkowska-Kita B. Synthesis, Structure, and Physicochemical Characteristics of Zn1−xRexCr2Se4 Single Crystals. Materials. 2023; 16(13):4565. https://doi.org/10.3390/ma16134565
Chicago/Turabian StyleJendrzejewska, Izabela, Tadeusz Groń, Joachim Kusz, Zbigniew Stokłosa, Ewa Pietrasik, Tomasz Goryczka, Bogdan Sawicki, Jerzy Goraus, Josef Jampilek, and Beata Witkowska-Kita. 2023. "Synthesis, Structure, and Physicochemical Characteristics of Zn1−xRexCr2Se4 Single Crystals" Materials 16, no. 13: 4565. https://doi.org/10.3390/ma16134565
APA StyleJendrzejewska, I., Groń, T., Kusz, J., Stokłosa, Z., Pietrasik, E., Goryczka, T., Sawicki, B., Goraus, J., Jampilek, J., & Witkowska-Kita, B. (2023). Synthesis, Structure, and Physicochemical Characteristics of Zn1−xRexCr2Se4 Single Crystals. Materials, 16(13), 4565. https://doi.org/10.3390/ma16134565










