Shear Behaviour and Calculation Methods of Bearing-Shear Connectors for Prefabricated Steel–Concrete Composite Beams
Abstract
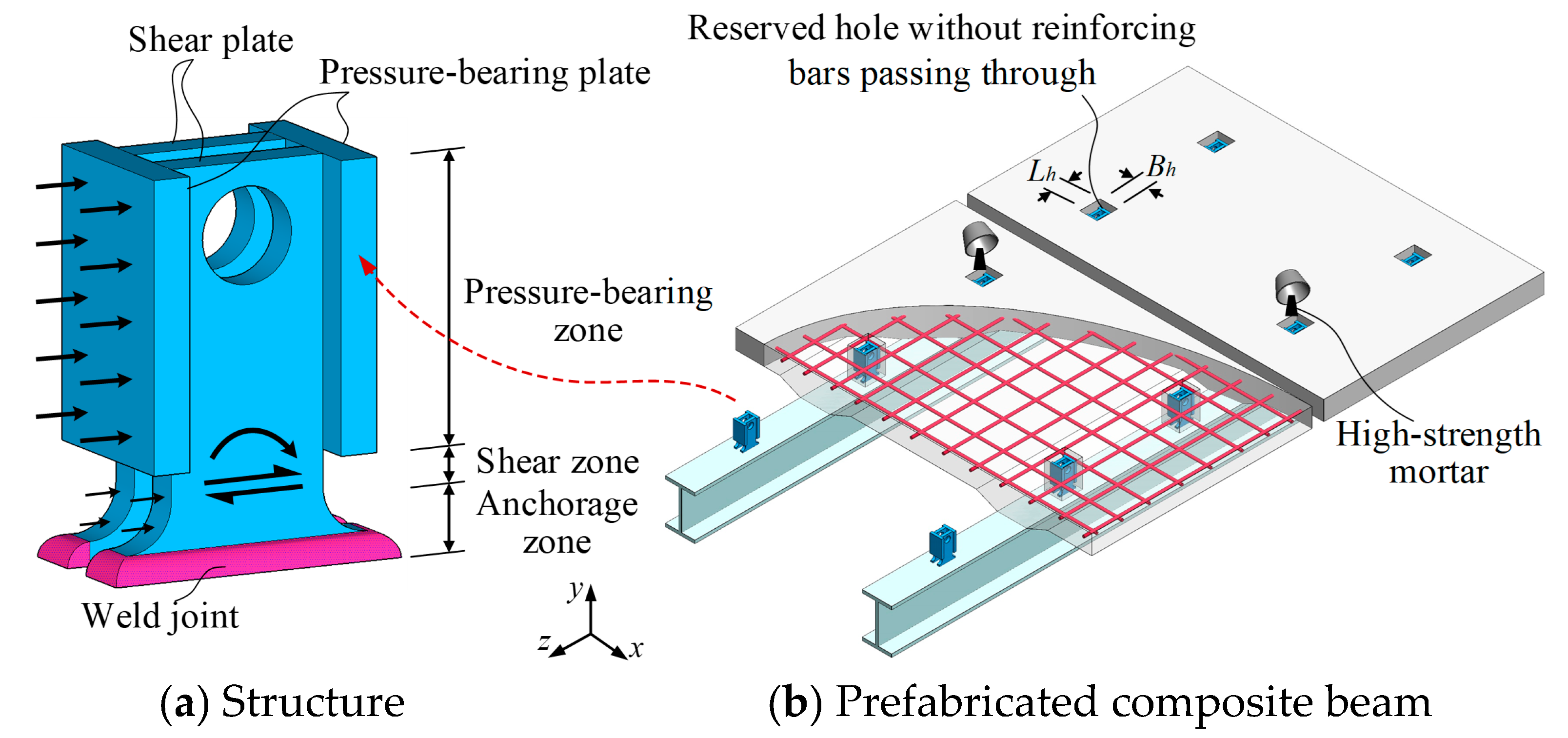
:1. Introduction
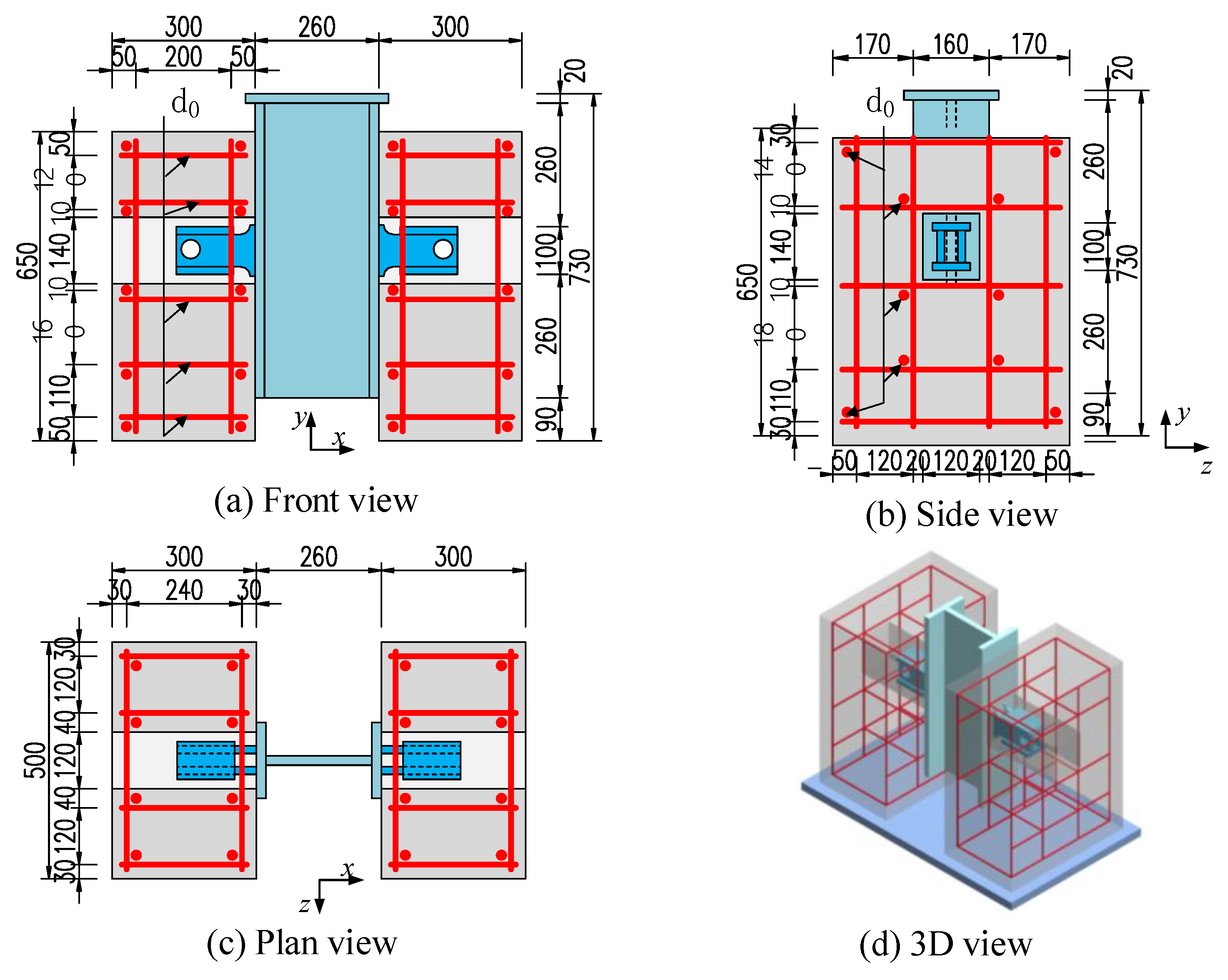
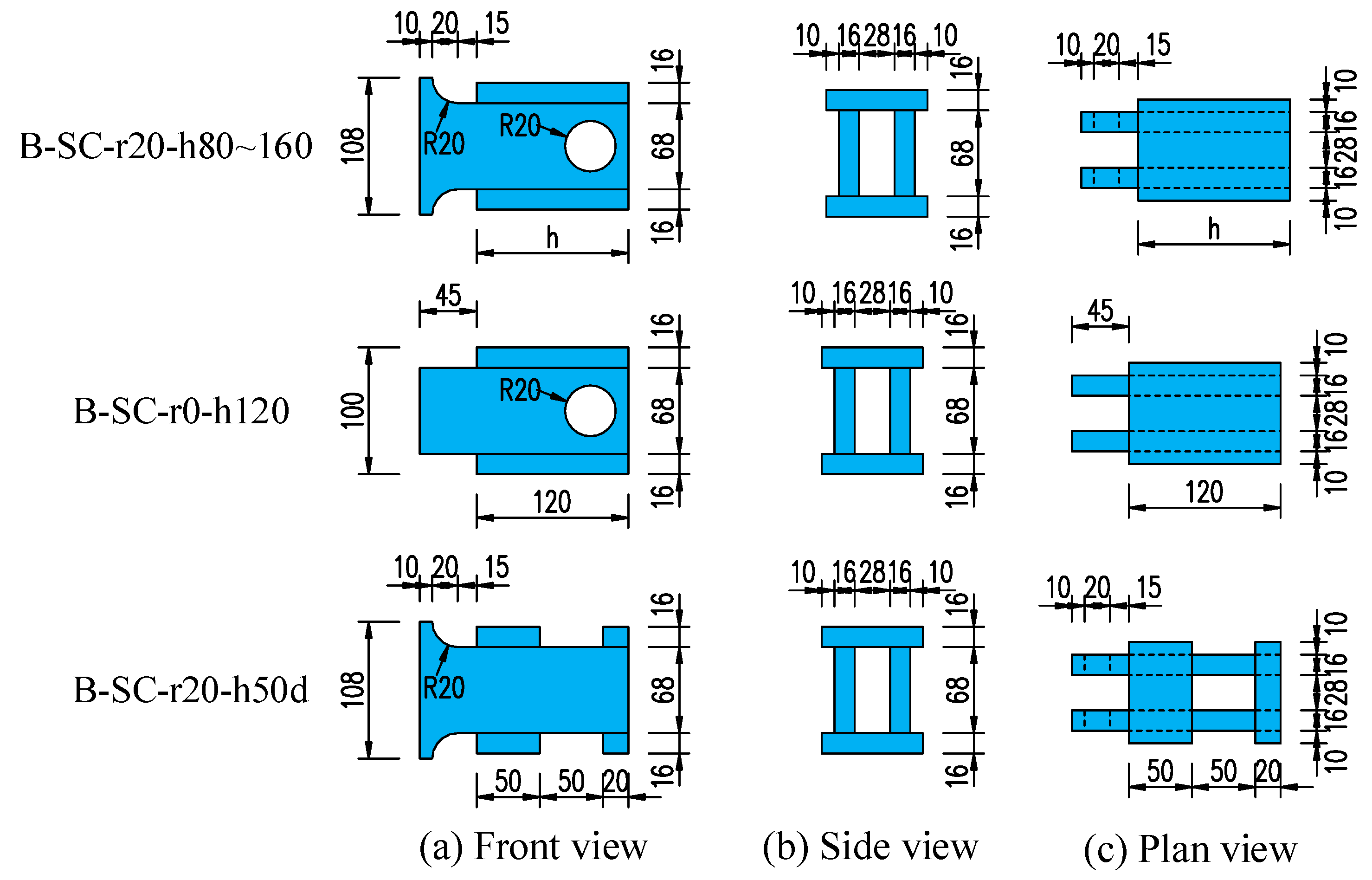
2. Summary of Push-Out Tests
3. Finite-Element Modelling
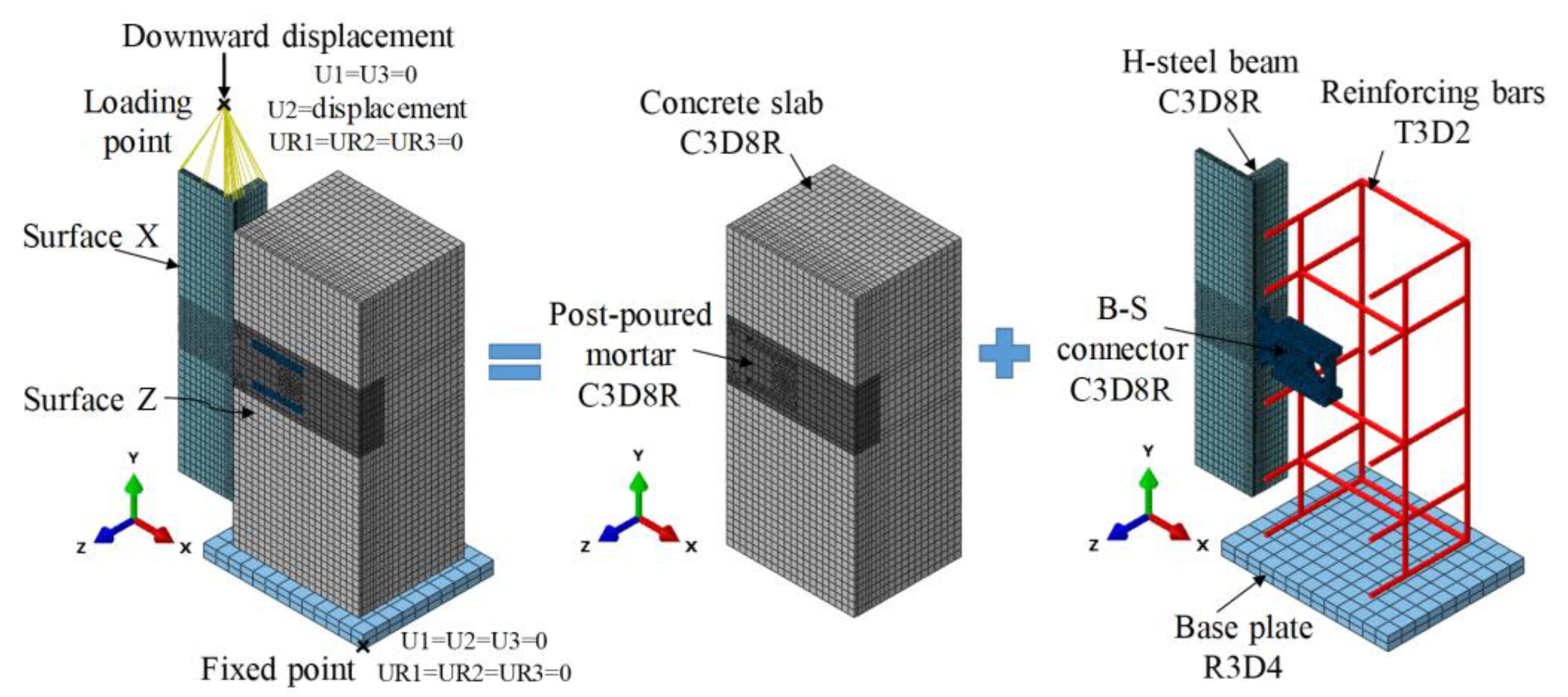
3.1. Geometry Model and Mesh
3.2. Boundary Conditions and Loading Protocol
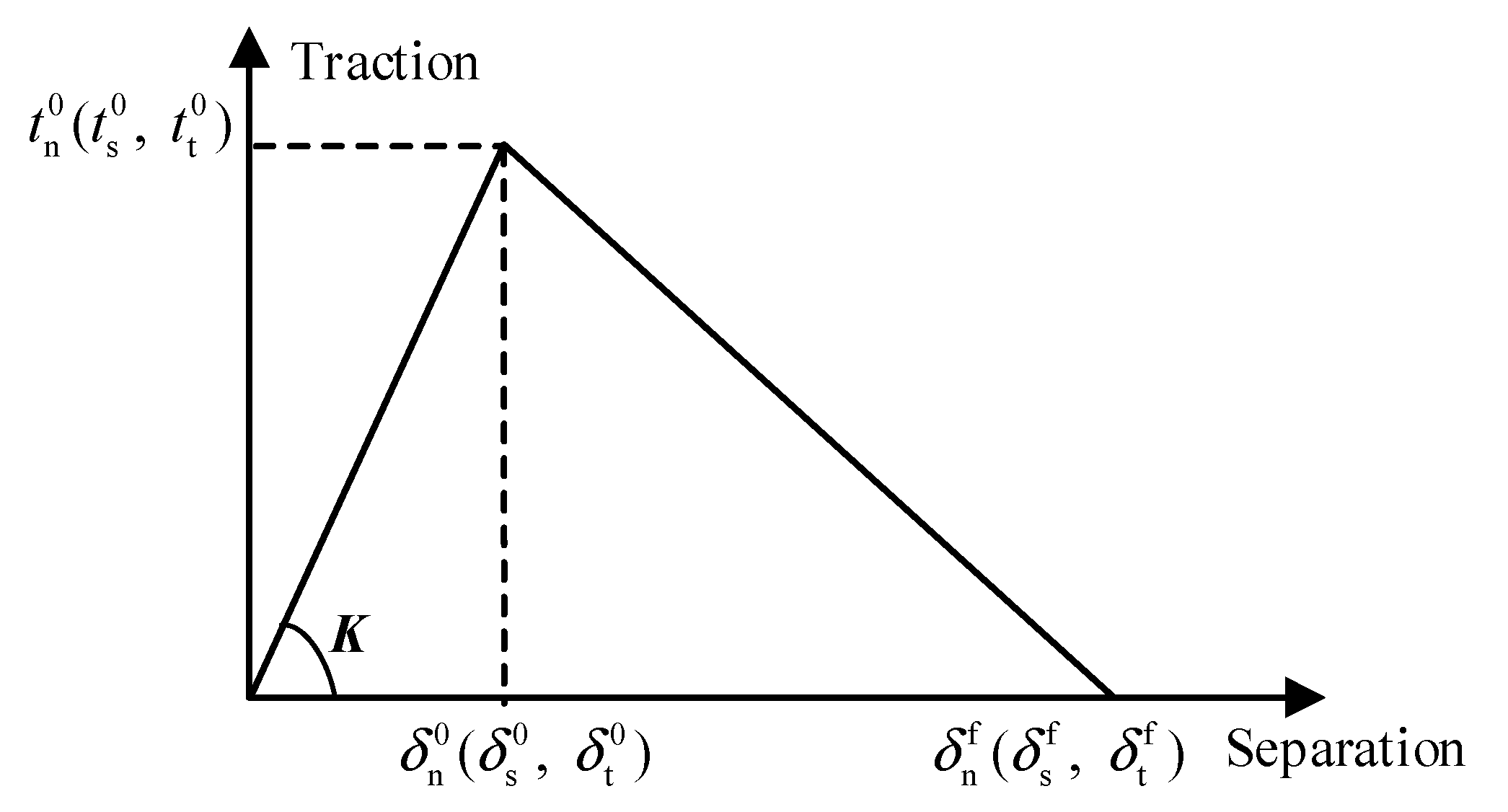
3.3. Contact Modelling
3.4. Material Models
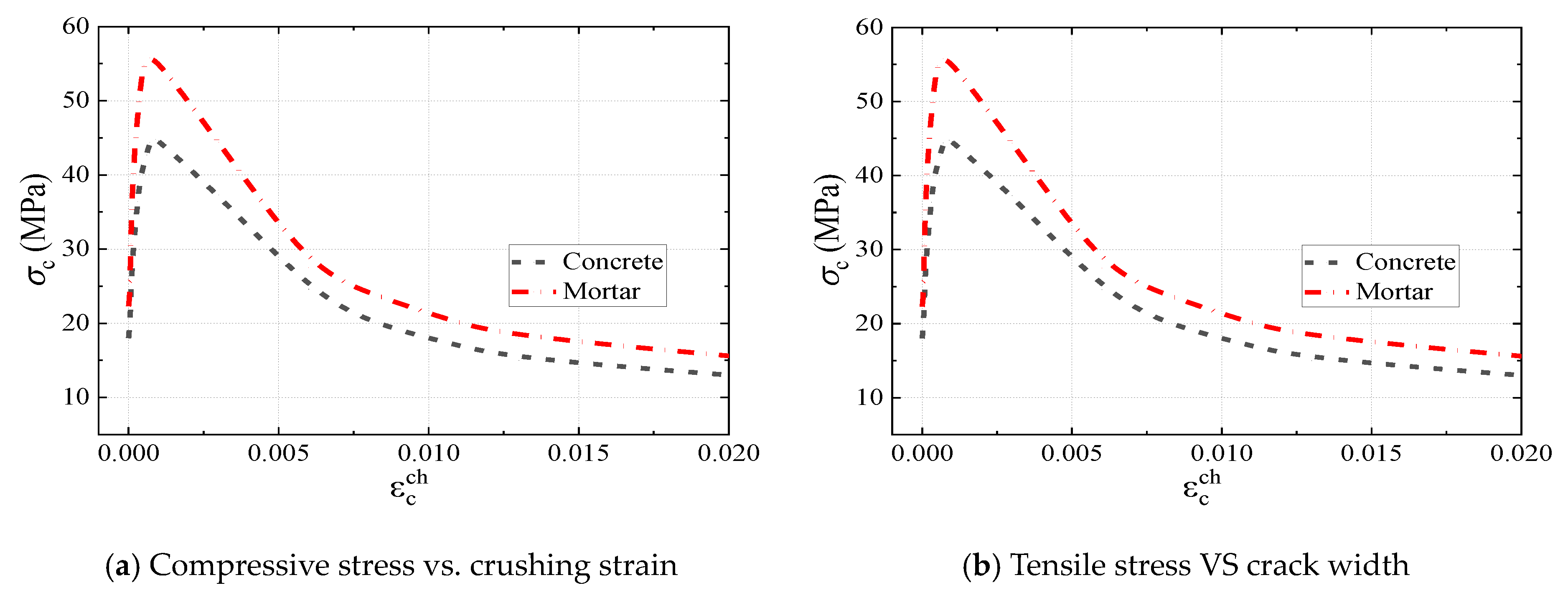
3.4.1. Concrete
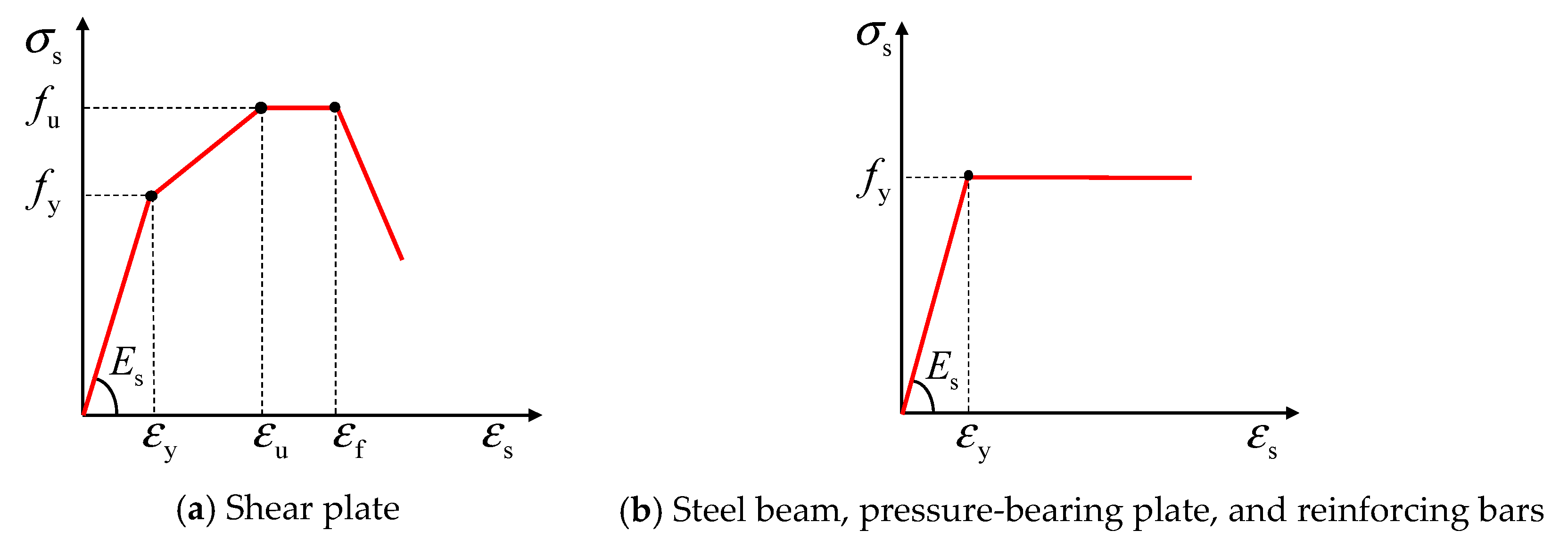
3.4.2. Steel Materials
4. Verification of the Numerical Model
4.1. Comparison of Shear Resistance and Slip Modulus
4.2. Comparison of Load-Slip Curves
4.3. Comparison of Failure Modes
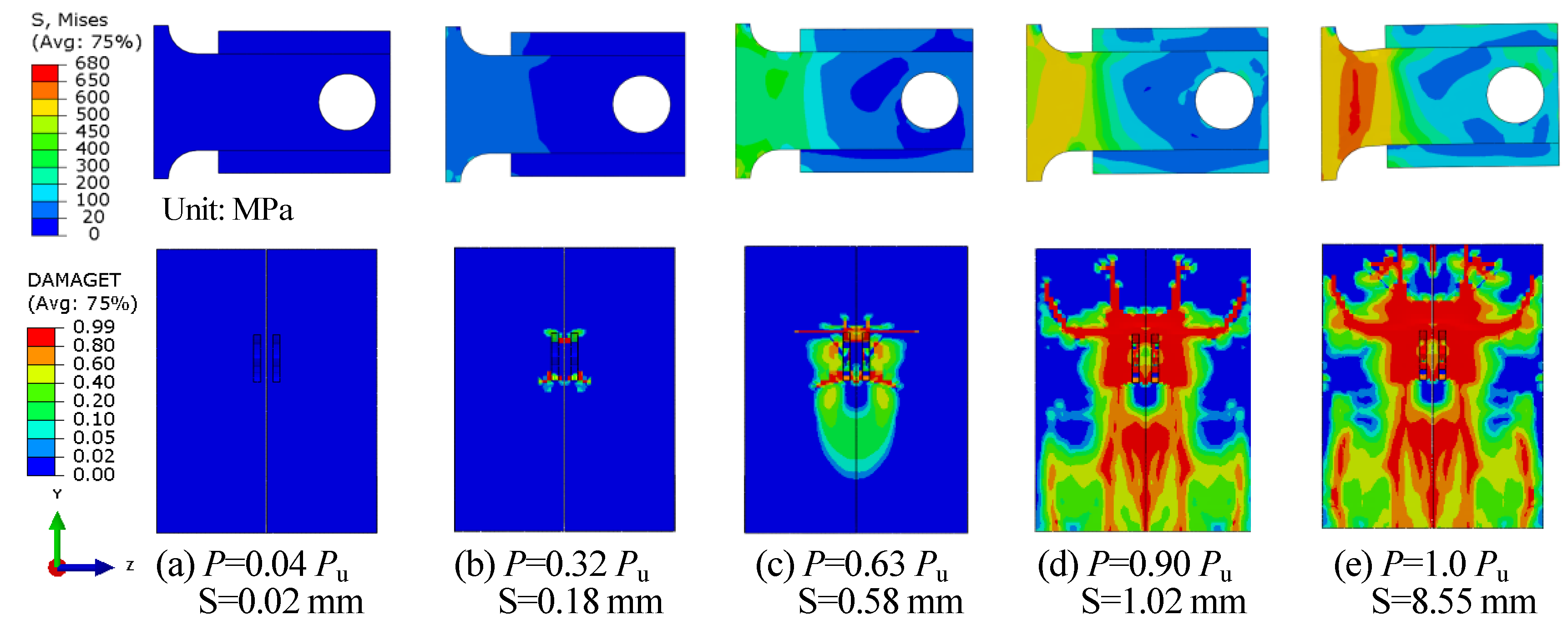
4.4. Failure Process of B-SCs
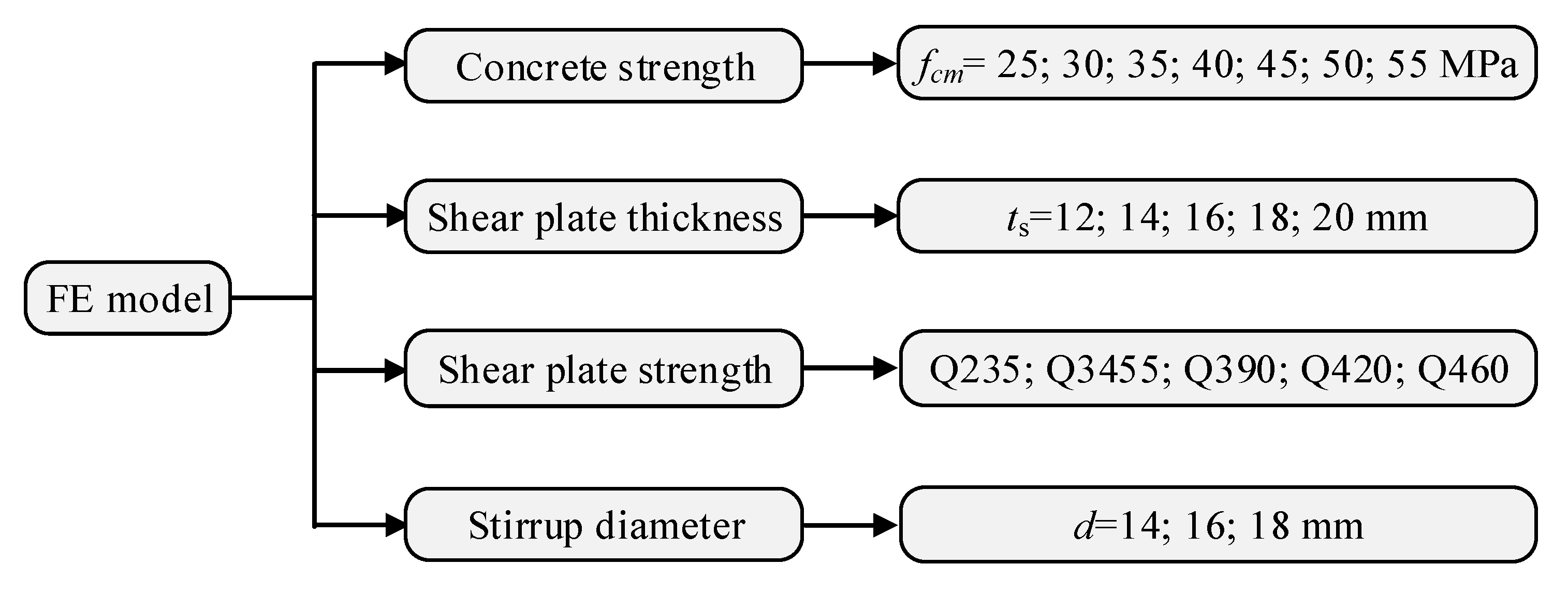
5. Parametric Study
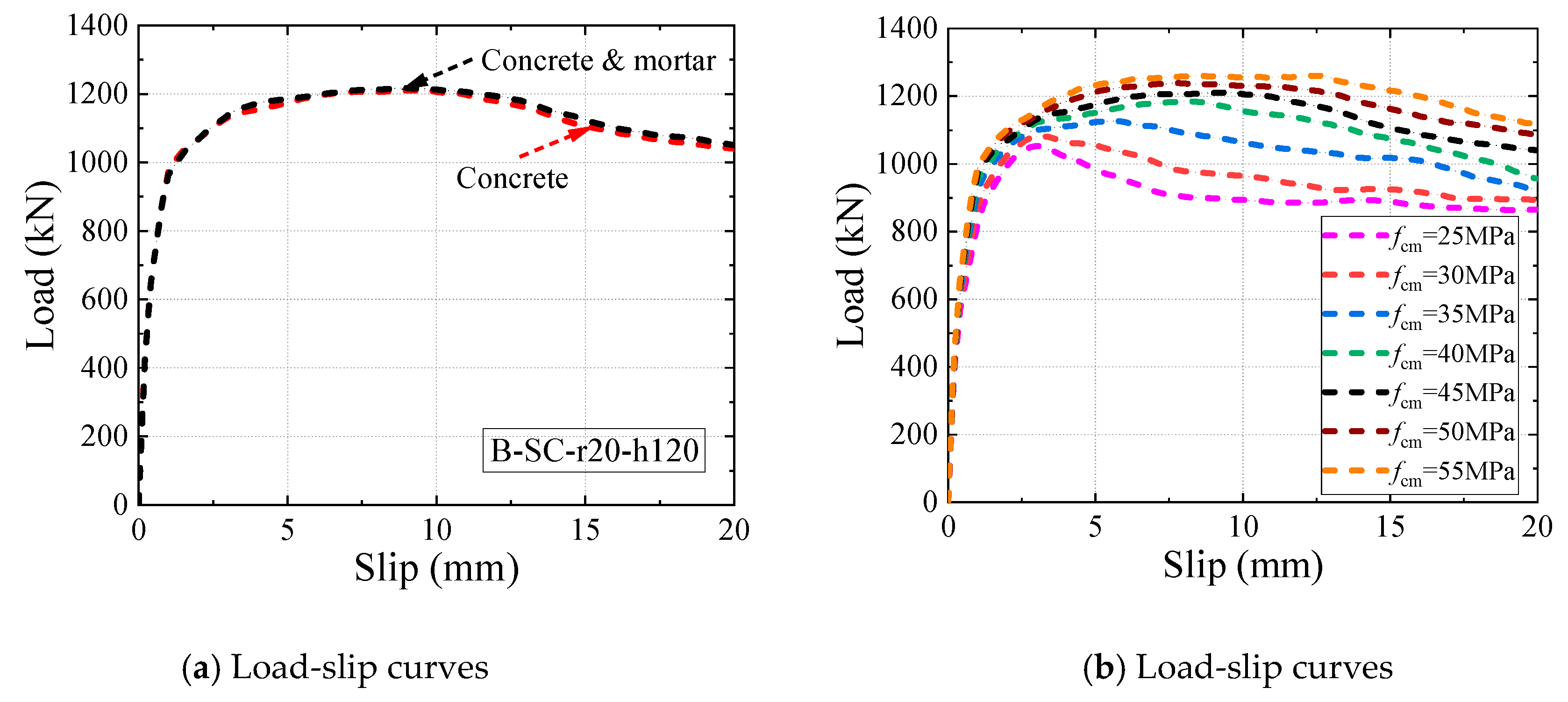
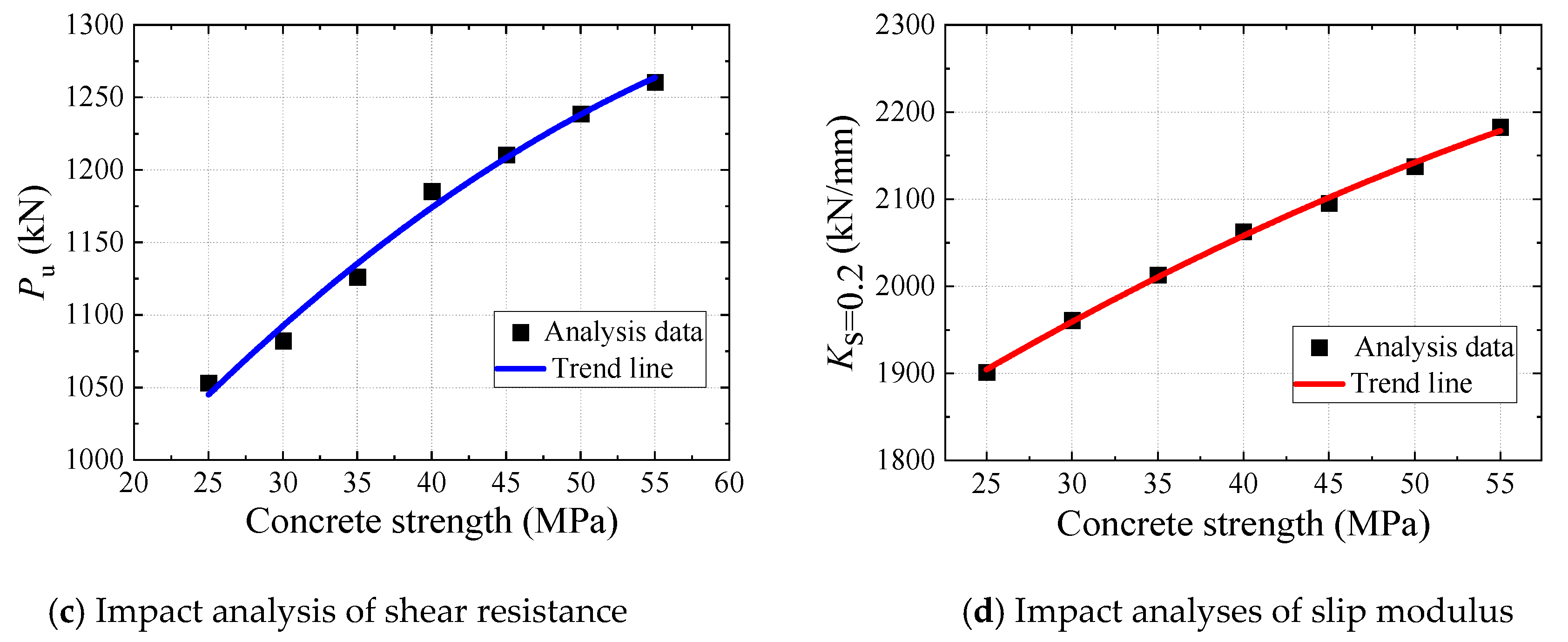
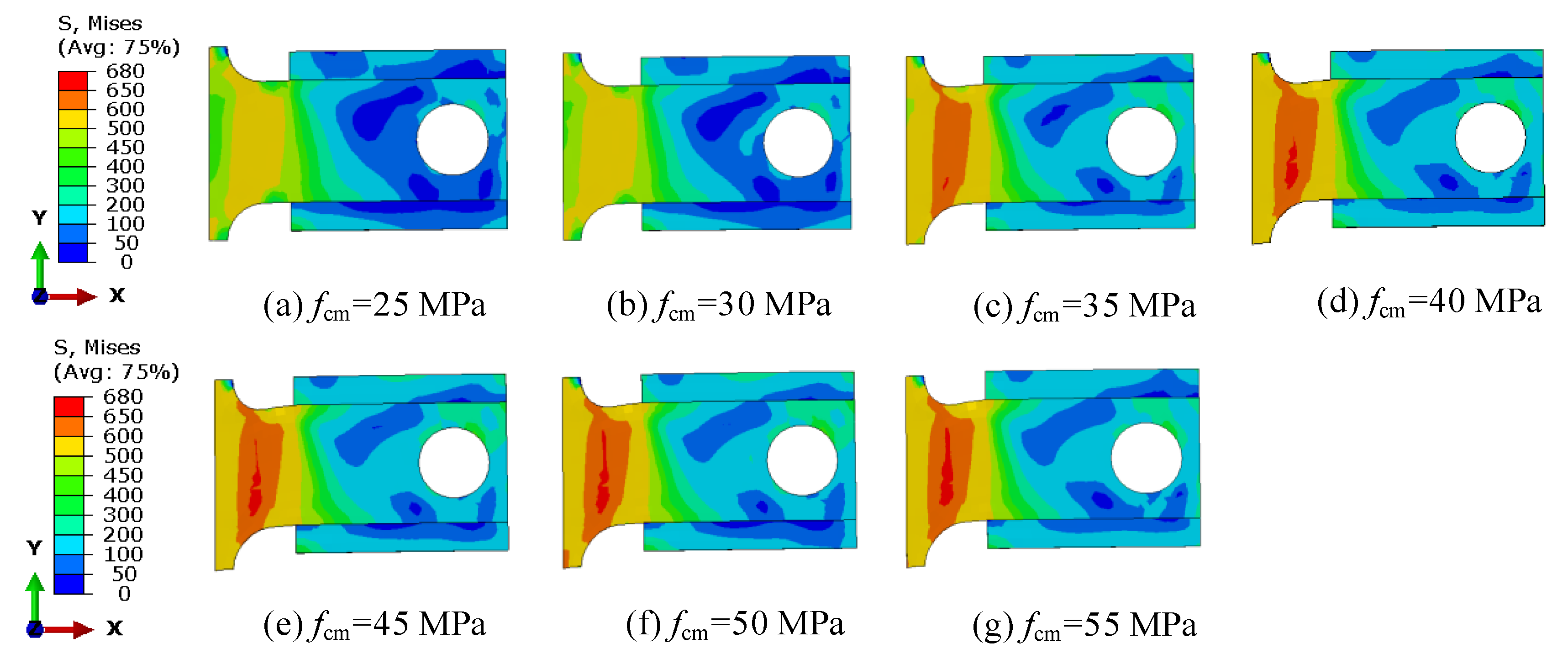
5.1. Effect of Concrete Strength
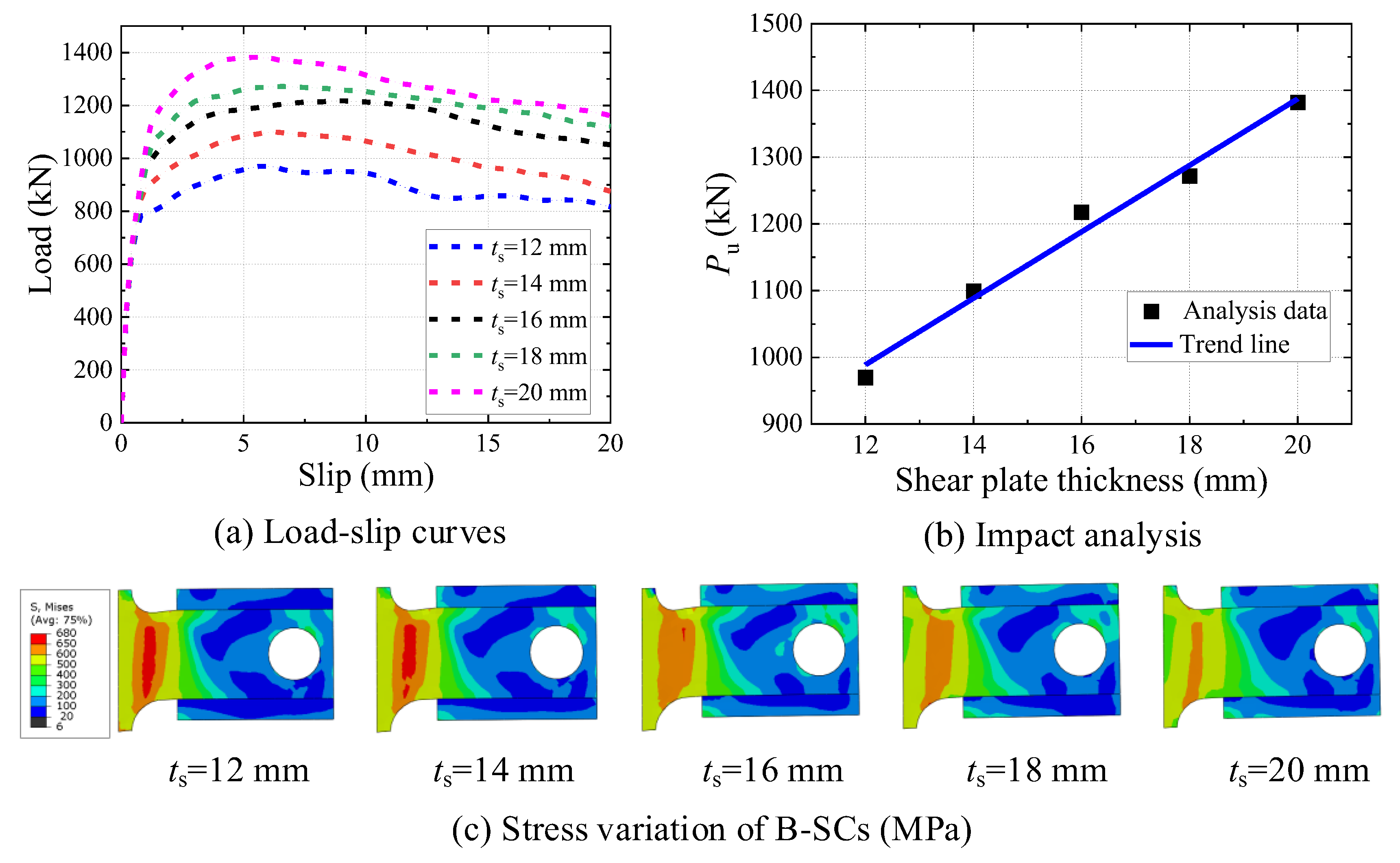
5.2. Effect of Shear-Plate Thickness
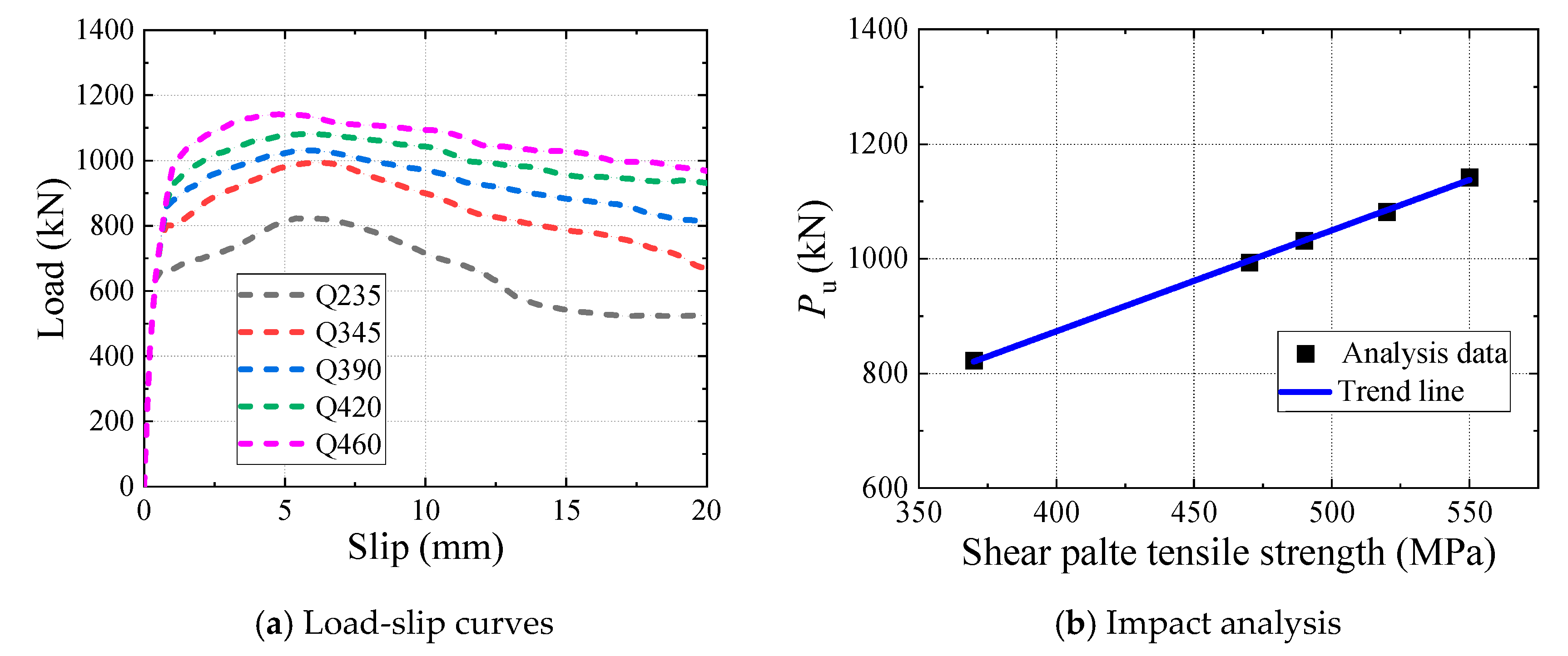
5.3. Effect of Shear-Plate Tensile Strength
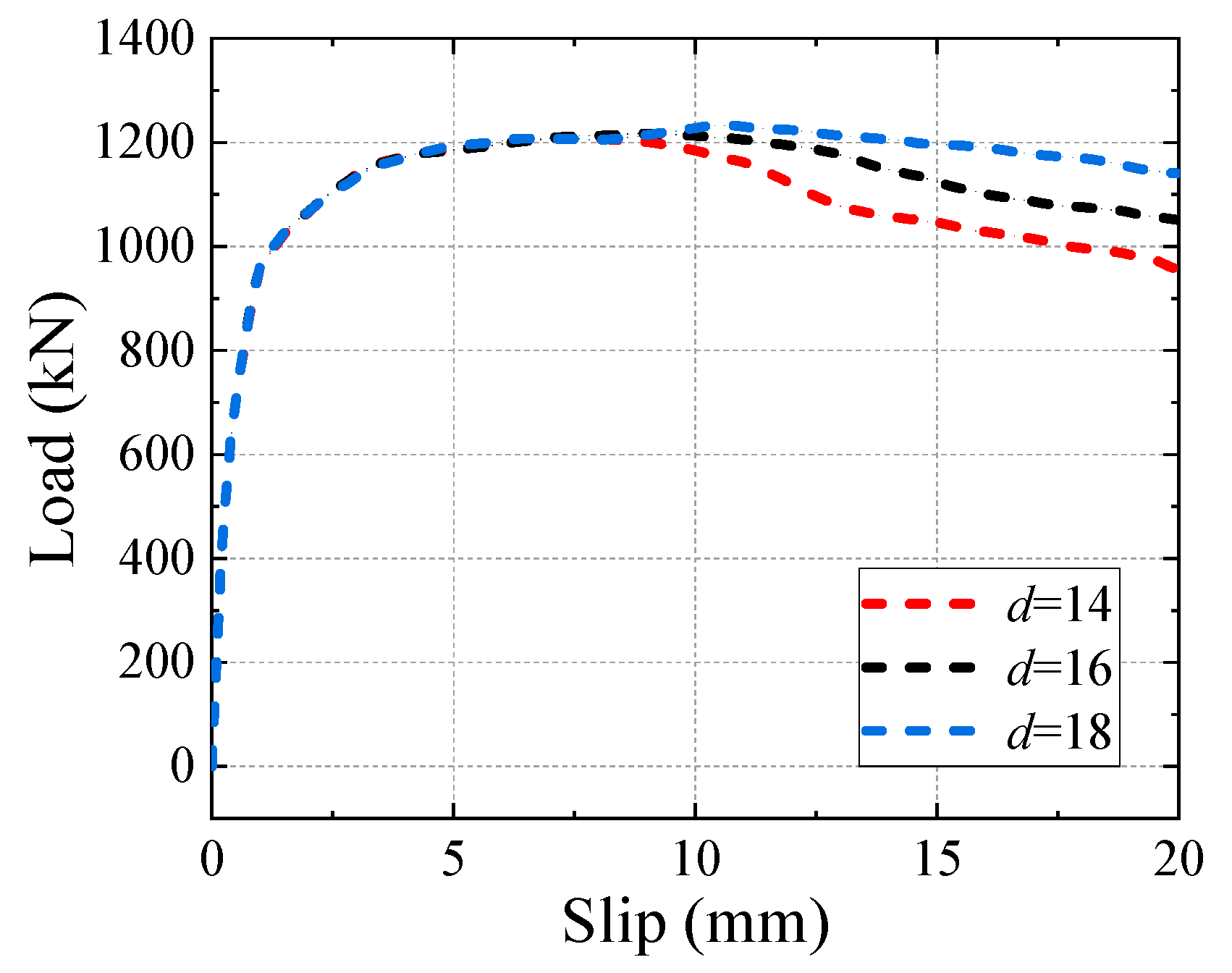
5.4. Effect of Stirrup Diameter
6. Proposed Shear-Calculation Formulae and Validation
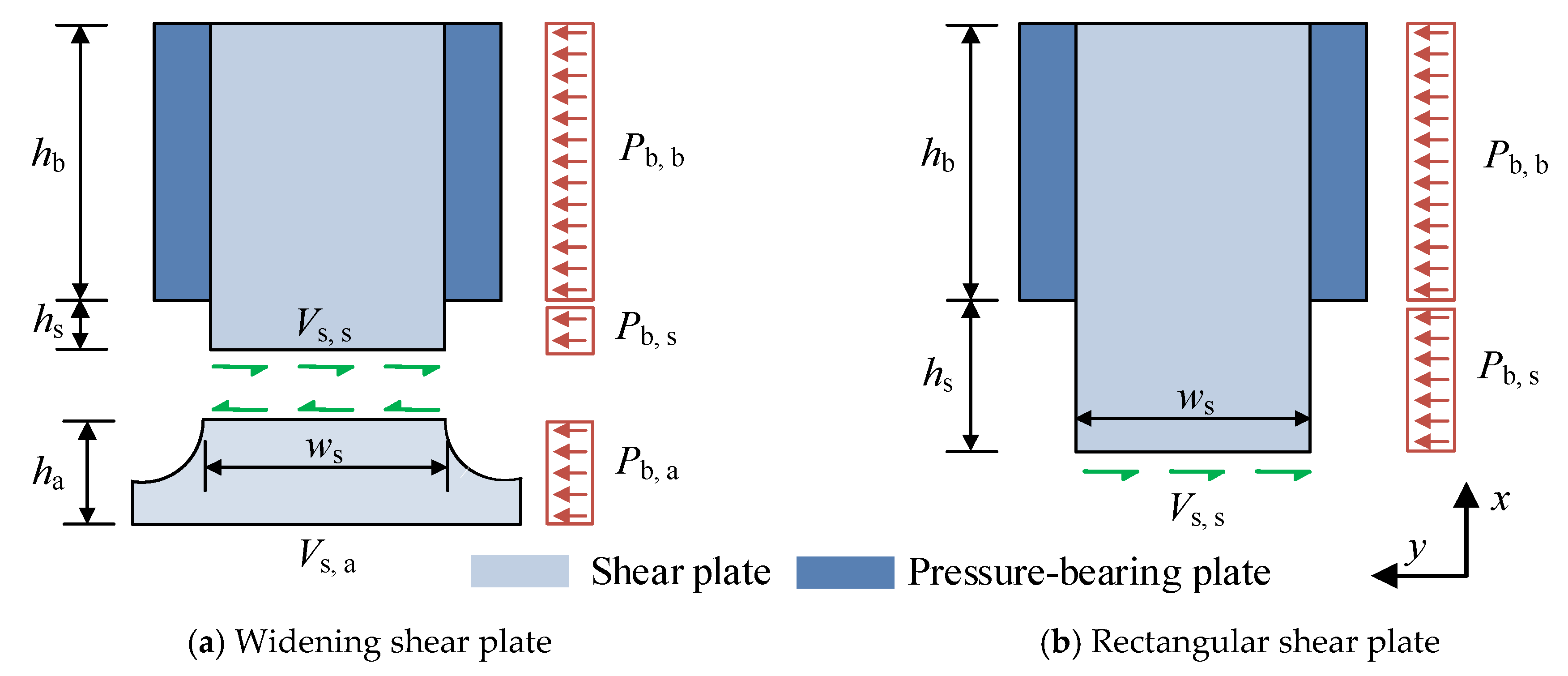
6.1. Proposed Formula for Predicating Ultimate Shear Resistance
6.2. Proposed Formula for Predicating Slip Modulus
7. Conclusions
- The numerical model matched well with the push-out tests in terms of the ultimate shear resistance, slip modulus, load-slip curves, and failure modes, indicating the accurate evaluation of the shear behaviour of B-SCs in prefabricated composite structures using the numerical model;
- All push-out specimens with B-SCs exhibited mixed failure modes composed of splitting and shear failures of the concrete slab and shear plate, respectively. The higher strength concrete enables concrete to support greater shear deformation of the shear plate, which increases the contribution of the shear plate to the shear resistance of B-SCs, thus improving the ultimate shear resistance of B-SCs;
- The ultimate shear resistance of B-SCs increased approximately linearly with the increase in the thickness and the tensile strength of the shear plate because the shear resistance of B-SCs was mainly determined by the shear resistance of the shear plate. However, these two parameters had a minor influence on the slip modulus of B-SCs;
- New calculation formulae for the ultimate shear resistance and slip modulus of the B-SCs were proposed. Both formulae, which accounted for the effect of concrete strength on the shear deformation of the shear plate, agreed well with the results of the push-out tests and numerical analysis.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Maximum separation of cohesive-contact property | |
| Crushing strain of concrete | |
| Tensile cracking strain of concrete | |
| Ab,a | Local bearing area of the anchorage zone |
| As,s | Cross-sectional area of the shear zone |
| b | ratio in Equation (6) |
| c1 and c2 | Coefficients in Equation (7) |
| d | Stirrup diameter |
| dc | Concrete compression-damage variable |
| ds | Stud diameter in Equation (16) |
| dt | Concrete tensile-damage variable |
| E0 | Undamaged elastic modulus of concrete |
| Ecm | Elastic modulus of concrete |
| Es | Elastic modulus of steel |
| fc | Concrete strength in Equations (16)–(18) |
| fcm | Cylinder compressive strength of concrete |
| ftm | Tensile strength of concrete |
| fu | Ultimate tensile strength of steel |
| fy | Yield strength of steel |
| Gch | Crushing energy per unit area of concrete |
| Gcm | Shear modulus of concrete |
| Gf | Crushing energy per unit area of concrete |
| hb/hs/ha | Height of the pressure-bearing zone/shear zone/anchorage zone |
| K | Second stress invariant ratio |
| K0.2 | Slip modulus (secant slope of the load-slip curves at a slip of 0.2 mm.) |
| K0.2,FE | Slip modulus obtained from finite element |
| K0.2,pre | Predicted slip modulus |
| K0.2,test | Slip modulus obtained from test |
| Knn, Kss, Ktt | Elastic stiffness of cohesive contact property |
| ks | Slip modulus of stud shear connector in Equation (16) |
| lck | Characteristic element length |
| Nomenclature | |
| P | Shear load |
| Pb,a | Compressive capacity of concrete in the anchorage zone |
| Pb,b | Compressive capacity of concrete in the pressure-bearing zone |
| Pb,s | Compressive capacity of concrete in the shear zone |
| Pmax | Ultimate shear resistance of stud shear connector in Equation (16) |
| Pu | Ultimate shear resistance |
| Pu,FE | Ultimate shear resistance obtained from finite element |
| Pu,pre | Predicted ultimate shear resistance |
| Pu,test | Ultimate shear resistance obtained from test |
| S | Relative ship |
| tn, ts, tt | Tractions of the cohesive contact property |
| ts, ws | Thickness and width of the shear plate in the shear zone |
| Vs,a | Shear capacity of the anchorage zone |
| Vss | Shear capacity of the shear zone |
| w | Cracking width of concrete |
| wc | Cracking width corresponding to the zero tensile stress |
| αc/αt/bc/bt | Dimensionless coefficients in Equations (8)–(11) |
| αE | Constant factor about concrete aggregates |
| ε | Flow potential eccentricity |
| εc | Compressive strain of concrete |
| εtm | Tensile peak strain of concrete |
| λb | Constant coefficient in Equation (14) |
| λs, α and β | Constant coefficient in Equation (13) |
| μ | Viscosity parameter |
| σbo/σco | Ratio of biaxial to uniaxial compressive strength |
| σc | Compressive stress of concrete |
| σt | Tensile stress of concrete |
| ψ | Dilatancy angle |
References
- Shim, C.-S.; Lee, P.-G.; Chang, S.-P. Design of shear connection in composite steel and concrete bridges with precast decks. J. Constr. Steel Res. 2001, 57, 203–219. [Google Scholar] [CrossRef]
- Shim, C.S.; Kim, J.H.; Chang, S.P.; Chung, C.H. The behaviour of shear connections in a composite beam with a full-depth precast slab. Struct. Build. 2000, 140, 101–110. [Google Scholar] [CrossRef]
- Song, S.-S.; Xu, F.; Chen, J.; Qin, F.; Huang, Y.; Yan, X. Feasibility and performance of novel tapered iron bolt shear connectors in demountable composite beams. J. Build. Eng. 2022, 53, 104528. [Google Scholar] [CrossRef]
- Wang, H.; Liu, X.-G.; Yue, Q.-R.; Zheng, M.-Z. Shear resistance of a novel wet connection for prefabricated composite beams under shear-bending coupling loading. J. Build. Eng. 2021, 45, 103636. [Google Scholar] [CrossRef]
- Johnson, R.P. Composite Structures of Steel and Concrete: Beams, Slabs, Columns, and Frames for Buildings, 3rd ed.; Blackwell Publishing: Hoboken, NJ, USA, 2008. [Google Scholar]
- Wang, Y.-H.; Yu, J.; Liu, J.-P.; Chen, Y.F. Shear behavior of shear stud groups in precast concrete decks. Eng. Struct. 2019, 187, 73–84. [Google Scholar] [CrossRef]
- Fang, Z.; Fang, H.; Huang, J.; Jiang, H.; Chen, G. Static behavior of grouped stud shear connectors in steel–precast UHPC composite structures containing thin full-depth slabs. Eng. Struct. 2022, 252, 113484. [Google Scholar] [CrossRef]
- Ding, J.; Zhu, J.; Kang, J.; Wang, X. Experimental study on grouped stud shear connectors in precast steel- UHPC composite bridge. Eng. Struct. 2021, 242, 112479. [Google Scholar] [CrossRef]
- Shim, C.-S.; Lee, P.-G.; Yoon, T.-Y. Static behavior of large stud shear connectors. Eng. Struct. 2004, 26, 1853–1860. [Google Scholar] [CrossRef]
- Badie, S.S.; Tadros, M.K.; Kakish, H.F.; Splittgerber, D.L.; Baishya, M.C. Large Shear Studs for Composite Action in Steel Bridge Girders. J. Bridg. Eng. 2002, 7, 195–203. [Google Scholar] [CrossRef]
- Wang, J.; Qi, J.; Tong, T.; Xu, Q.; Xiu, H. Static behavior of large stud shear connectors in steel-UHPC composite structures. Eng. Struct. 2018, 178, 534–542. [Google Scholar] [CrossRef]
- Wang, J.; Xu, Q.; Yao, Y.; Qi, J.; Xiu, H. Static behavior of grouped large headed stud-UHPC shear connectors in composite structures. Compos. Struct. 2018, 206, 202–214. [Google Scholar] [CrossRef]
- Pavlović, M.; Marković, Z.; Veljković, M.; Buđevac, D. Bolted shear connectors vs. headed studs behaviour in push-out tests. J. Constr. Steel Res. 2013, 88, 134–149. [Google Scholar] [CrossRef]
- Tan, E.L.; Varsani, H.; Liao, F. Experimental study on demountable steel-concrete connectors subjected to combined shear and tension. Eng. Struct. 2019, 183, 110–123. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, B.; Liu, A.; Pi, Y.-L.; Zhang, J.; Wang, Y.; Zhong, L. Experimental study on shear behavior of high strength bolt connection in prefabricated steel-concrete composite beam. Compos. Part B Eng. 2019, 159, 481–489. [Google Scholar] [CrossRef]
- Fang, Z.; Fang, H.; Li, P.; Jiang, H.; Chen, G. Interfacial shear and flexural performances of steel–precast UHPC composite beams: Full-depth slabs with studs vs. demountable slabs with bolts. Eng. Struct. 2022, 260, 114230. [Google Scholar] [CrossRef]
- Shariati, M.; Sulong, N.R.; Khanouki, M.A. Experimental assessment of channel shear connectors under monotonic and fully reversed cyclic loading in high strength concrete. Mater. Des. 2012, 34, 325–331. [Google Scholar] [CrossRef]
- Baran, E.; Topkaya, C. Behavior of steel–concrete partially composite beams with channel type shear connectors. J. Constr. Steel Res. 2014, 97, 69–78. [Google Scholar] [CrossRef]
- Shariati, M.; Sulong, N.R.; Shariati, A.; Kueh, A. Comparative performance of channel and angle shear connectors in high strength concrete composites: An experimental study. Constr. Build. Mater. 2016, 120, 382–392. [Google Scholar] [CrossRef]
- Shariati, A.; Sulong, N.R.; Suhatril, M. Investigation of channel shear connectors for composite concrete and steel T-beam. Int. J. Phys. Sci. 2012, 28, 1828–1831. [Google Scholar] [CrossRef]
- Shariati, M.; Sulong, N.R.; Suhatril, M.; Shariati, A.; Khanouki, M.A.; Sinaei, H. Behaviour of C-shaped angle shear connectors under monotonic and fully reversed cyclic loading: An experimental study. Mater. Des. 2012, 41, 67–73. [Google Scholar] [CrossRef]
- Shariati, M.; Shariati, A.; Sulong, N.R.; Suhatril, M.; Khanouki, M.A. Fatigue energy dissipation and failure analysis of angle shear connectors embedded in high strength concrete. Eng. Fail. Anal. 2014, 41, 124–134. [Google Scholar] [CrossRef]
- Qiu, S.-Y.; Guo, Y.-T.; Nie, X.; Fan, J.-S.; Tao, M.-X. Experimental study on shaped steel shear connectors used in large-scale composite structures. J. Constr. Steel Res. 2020, 172, 106201. [Google Scholar] [CrossRef]
- Vianna, J.; Costa-Neves, L.; Vellasco, P.; de Andrade, S. Structural behaviour of T-Perfobond shear connectors in composite girders: An experimental approach. Eng. Struct. 2008, 30, 2381–2391. [Google Scholar] [CrossRef] [Green Version]
- Zou, Y.; Qin, F.; Zhou, J.; Zheng, Z.; Huang, Z.; Zhang, Z. Shear behavior of a novel bearing-shear connector for prefabricated concrete decks. Constr. Build. Mater. 2020, 268, 121090. [Google Scholar] [CrossRef]
- Guo, J.; Zhou, Z.; Zou, Y.; Zhang, Z.; Jiang, J.; Wang, X. Static behavior of novel shear connectors with post-poured UHPC for prefabricated composite bridge. Structures 2022, 43, 1114–1133. [Google Scholar] [CrossRef]
- Cui, C.; Song, L.; Liu, R.; Liu, H.; Yu, Z.; Jiang, L. Shear behavior of stud connectors in steel bridge deck and ballastless track structural systems of high-speed railways. Constr. Build. Mater. 2022, 341, 127744. [Google Scholar] [CrossRef]
- Wang, S.; Fang, Z.; Ma, Y.; Jiang, H.; Zhao, G. Parametric investigations on shear behavior of perforated transverse angle connectors in steel–concrete composite bridges. Structures 2022, 38, 416–434. [Google Scholar] [CrossRef]
- Ataei, A.; Zeynalian, M. A study on structural performance of deconstructable bolted shear connectors in composite beams. Structures 2020, 29, 519–533. [Google Scholar] [CrossRef]
- Lima, J.M.; Bezerra, L.M.; Bonilla, J.; Barbosa, W.C. Study of the behavior and resistance of right-angle truss shear connector for composite steel concrete beams. Eng. Struct. 2022, 253, 113778. [Google Scholar] [CrossRef]
- EN1992-1-4; Design of Composite Steel and Concrete Structures. Part 1.1: General Rules and Rules for Buildings. European Committee for Standardization (CEN): Brussels, Belgium, 2004.
- GB 50017-2017; Standard for Design of Steel Structures. China Architecture & Building Press: Beijing, China, 2017. (In Chinese)
- ABAQUS Software, Version 6.14-5; Dassault Systèmes Simulia Corp: Providence, RI, USA, 2014. Available online: https://www.3ds.com/products-services/simulia/products/abaqus (accessed on 23 May 2023).
- Nguyen, H.T.; Kim, S.E. Finite element modeling of push-out tests for large stud shear connectors. J. Constr. Steel Res. 2009, 65, 1909–1920. [Google Scholar] [CrossRef]
- ABAQUS, Theory Manual, Version 6.14-5; Dassault Systèmes Simulia Corp: Providence, RI, USA, 2014. Available online: http://wufengyun.com:888/v6.14/books/usb/default.htm (accessed on 23 May 2023).
- CEB-FIP. Model Code 2010; Thomas Telford: London, UK, 2010. [Google Scholar]
- Birtel, V.; Mark, P. Parameterised finite element modelling of RC beam shear failure. In Proceedings of the 2006 ABAQUS Users’ Conference, Providence, RI, USA, 16 November 2006; Available online: https://www.researchgate.net/publication/266411260_Parameterised_Finite_Element_Modelling_of_RC_Beam_Shear_Failure (accessed on 23 May 2023).
- Alfarah, B.; López-Almansa, F.; Oller, S. New methodology for calculating damage variables evolution in Plastic Damage Model for RC structures. Eng. Struct. 2017, 132, 70–86. [Google Scholar] [CrossRef] [Green Version]
- Hillenborg, A.; Modéer, M.; Petersson, P.E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. In Selected Landmark Papers in Concrete Materials; American Concrete Institute: Farmington Hills, MI, USA, 2008; Available online: https://trid.trb.org/view/868768 (accessed on 23 May 2023).
- Vonk, R.A. A micromechanical investigation of softening of concrete loaded in compression. Heron 1993, 38. [Google Scholar]
- Hordijk, D.A. Tensile and tensile fatigue behaviour of concrete; experiments, modelling and analyses. Heron 1992, 37. Available online: https://trid.trb.org/view/366922 (accessed on 23 May 2023).
- Zou, Y.; Di, J.; Zhou, J.; Zhang, Z.; Li, X.; Zhang, H.; Qin, F. Shear behavior of perfobond connectors in the steel-concrete joints of hybrid bridges. J. Constr. Steel Res. 2020, 172, 106217. [Google Scholar] [CrossRef]
- Yu, J. Study on Mechanical Behavior of Assembled Steel Concrete Composite Beams with Group Stud and Steel Block Connections; Chongqing University: Chongqing, China, 2020; Available online: http://cdmd.cnki.com.cn/Article/CDMD-10611-1021541431.htm (accessed on 23 May 2023). (In Chinese)
- Oehlers, D.; Coughlan, C. The shear stiffness of stud shear connections in composite beams. J. Constr. Steel Res. 1986, 6, 273–284. [Google Scholar] [CrossRef]
- Suwaed, A.S.H.; Karavasilis, T.L. Novel Demountable Shear Connector for Accelerated Disassembly, Repair, or Replacement of Precast Steel-Concrete Composite Bridges. J. Bridg. Eng. 2017, 22, 04017052. [Google Scholar] [CrossRef] [Green Version]
- Xu, H.; Zhang, S.; Rong, B. Investigation on shear behavior of studs and PBL shear connectors in steel-concrete hybrid bridge girder. Structures 2022, 43, 1422–1435. [Google Scholar] [CrossRef]
- Langarudi, P.A.; Ebrahimnejad, M. Numerical study of the behavior of bolted shear connectors in composite slabs with steel deck. Structures 2020, 26, 501–515. [Google Scholar] [CrossRef]
- Xu, X.; Liu, Y.; He, J. Study on mechanical behavior of rubber-sleeved studs for steel and concrete composite structures. Constr. Build. Mater. 2014, 53, 533–546. [Google Scholar] [CrossRef]
- Zheng, S.; Liu, Y.; Yoda, T.; Lin, W. Parametric study on shear capacity of circular-hole and long-hole perfobond shear connector. J. Constr. Steel Res. 2016, 117, 64–80. [Google Scholar] [CrossRef]
- Hu, Y.; Qiu, M.; Chen, L.; Zhong, R.; Wang, J. Experimental and analytical study of the shear strength and stiffness of studs embedded in high strength concrete. Eng. Struct. 2021, 236, 111792. [Google Scholar] [CrossRef]
- JTG/T D64-01-2015; Specifications for Design and Construction of Highway Steel-concrete Composite Bridge. Ministry of Transport of the People’s Republic of China, China Communications Publishing & Media Management Co., Ltd.: Beijing, China, 2015. (In Chinese)




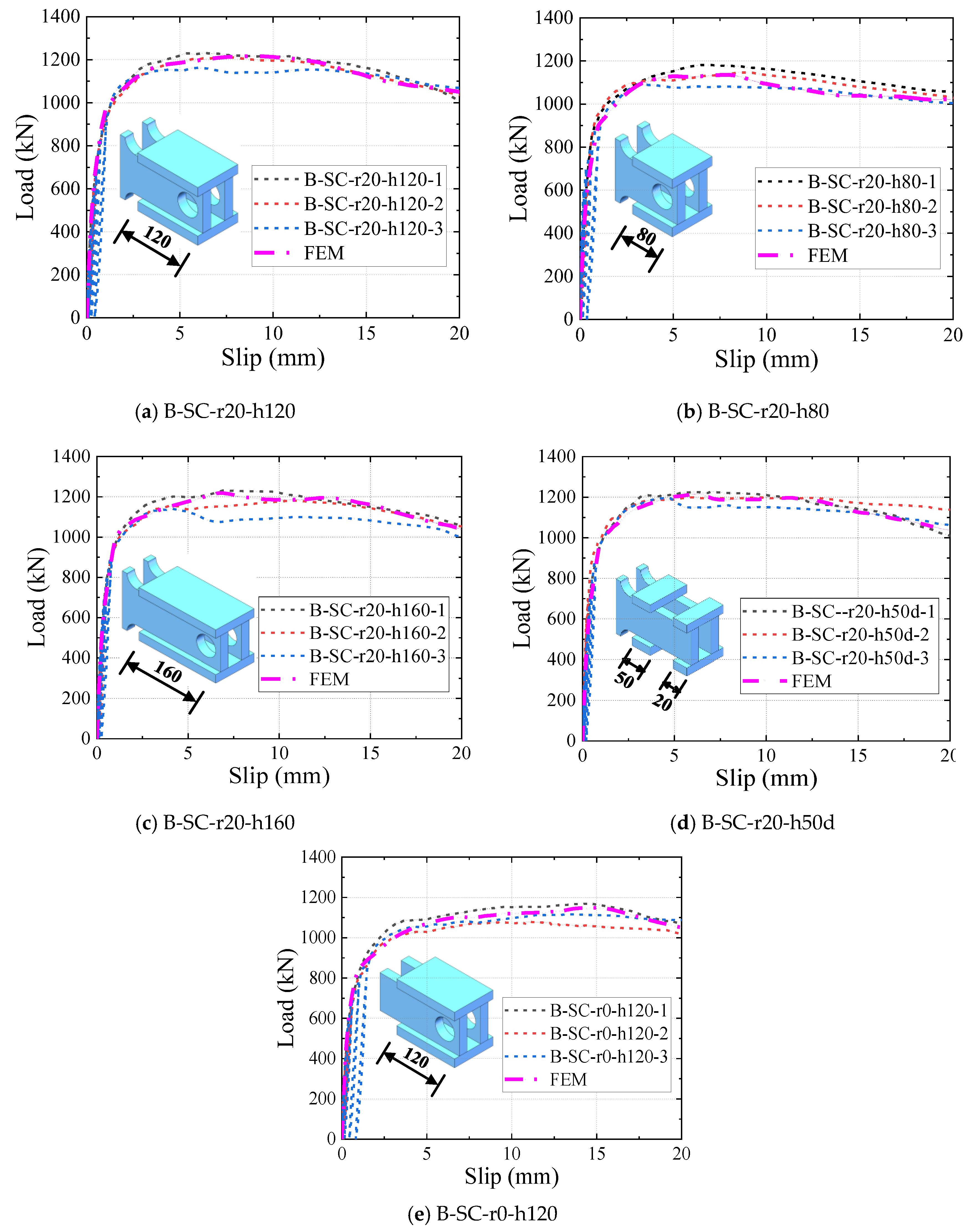


| Specimens | Pu,test | Pu,FE | K0.2,test | K0.2,FE | ||
|---|---|---|---|---|---|---|
| (kN) | (kN) | (kN/mm) | (kN/mm) | |||
| B-SC-r20-h120-1 | 1230.0 | 1217.4 | 2076.2 | 2073.7 | 1.01 | 1.00 |
| B-SC-r20-h120-2 | 1210.5 | 2013.7 | 0.99 | 0.97 | ||
| B-SC-r20-h120-3 | 1162.2 | 1997.6 | 0.95 | 0.96 | ||
| B-SC-r20-h80-1 | 1180.9 | 1135.8 | 1987.3 | 2008.2 | 1.04 | 0.99 |
| B-SC-r20-h80-2 | 1146.2 | 2056.6 | 1.01 | 1.02 | ||
| B-SC-r20-h80-3 | 1089.6 | 2051 | 0.96 | 1.02 | ||
| B-SC-r20-h160-1 | 1231.5 | 1219.0 | 2051.2 | 2060.7 | 1.01 | 1.00 |
| B-SC-r20-h160-2 | 1180.1 | 1984.7 | 0.97 | 0.96 | ||
| B-SC-r20-h160-3 | 1140.9 | 1927.9 | 0.94 | 0.94 | ||
| B-SC-r20-h50d-1 | 1228.1 | 1216.7 | 2142.3 | 2075.7 | 1.02 | 1.03 |
| B-SC-r20-h50d-2 | 1198 | 2165.0 | 0.94 | 1.04 | ||
| B-SC-r20-h50d-3 | 1197.6 | 2125.1 | 0.97 | 1.02 | ||
| B-SC-r0-h120-1 | 1168.8 | 1149.2 | 1975.4 | 1940.0 | 1.01 | 1.02 |
| B-SC-r0-h120-2 | 1079.2 | 1928.7 | 0.98 | 0.99 | ||
| B-SC-r0-h120-3 | 1116.1 | 1951.6 | 0.98 | 1.01 | ||
| Mean | 0.99 | 1.00 | ||||
| Standard deviation | 0.03 | 0.03 | ||||
| Specimens | Es (GPa) | fy (MPa) | fu (MPa) | Shear-Plate Thickness (mm) | Pu,FEM (kN) | K0.2,FEM (kN/mm) |
|---|---|---|---|---|---|---|
| B-SC-shear-12 | 201.5 | 449.6 | 600.2 | 12 | 969.9 | 2041.2 |
| B-SC-shear-14 | 14 | 1099.5 | 2058.6 | |||
| B-SC-shear-16 | 16 | 1217.4 | 2073.4 | |||
| B-SC-shear-18 | 18 | 1271.7 | 2077.6 | |||
| B-SC-shear-20 | 20 | 1381.9 | 2086.7 | |||
| B-SC-Q235 | 210 | 235 | 370 | 16 | 822.9 | 2073.4 |
| B-SC-Q345 | 210 | 345 | 470 | 993.5 | 2073.4 | |
| B-SC-Q390 | 210 | 390 | 490 | 1030.6 | 2073.4 | |
| B-SC-Q420 | 210 | 420 | 520 | 1081.8 | 2073.4 | |
| B-SC-Q460 | 210 | 460 | 550 | 1142.2 | 2073.4 |
| Specimen | d | Pu | K0.2 |
|---|---|---|---|
| mm | (kN) | (kN/mm) | |
| B-SC-stirrup-14 | 14 | 1212.3 | 2070.3 |
| B-SC-stirrup-16 | 16 | 1217.4 | 2070.3 |
| B-SC-stirrup-18 | 18 | 1232.9 | 2070.3 |
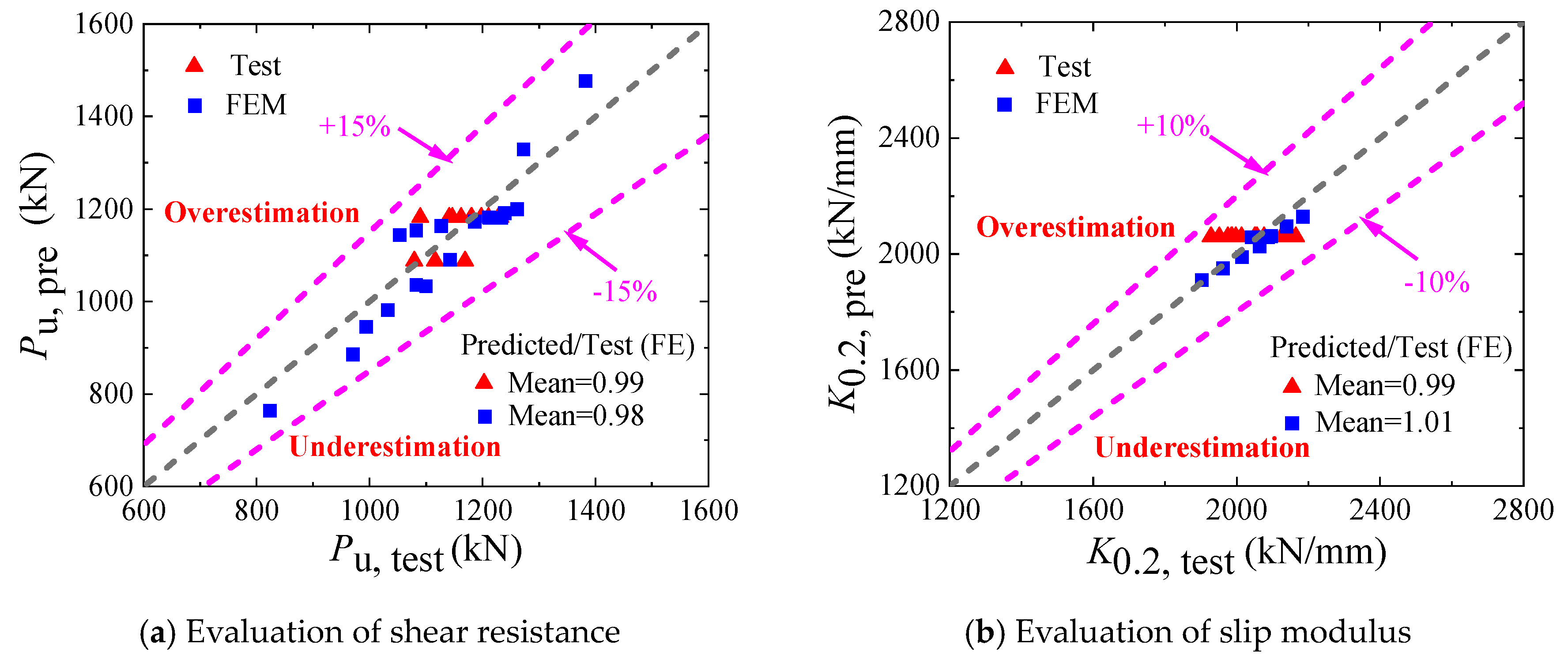
| Tests Specimens | Pu,test | Pu,pre | K0.2,test | K0.2,pre | ||
|---|---|---|---|---|---|---|
| (kN) | (kN) | (kN/mm) | (kN/mm) | |||
| B-SC-r20-h120-1 | 1230.0 | 1182.0 | 2076.2 | 2059.2 | 0.96 | 1.01 |
| B-SC-r20-h120-2 | 1210.5 | 1182.0 | 2013.7 | 2059.2 | 0.98 | 0.98 |
| B-SC-r20-h120-3 | 1162.2 | 1182.0 | 1997.6 | 2059.2 | 1.02 | 0.97 |
| B-SC-r20-h80-1 | 1180.9 | 1182.0 | 1987.3 | 2059.2 | 1.00 | 0.97 |
| B-SC-r20-h80-2 | 1146.2 | 1182.0 | 2056.6 | 2059.2 | 1.03 | 1.00 |
| B-SC-r20-h80-3 | 1089.6 | 1182.0 | 2051 | 2059.2 | 1.08 | 1.00 |
| B-SC-r20-h160-1 | 1231.5 | 1182.0 | 2051.2 | 2059.2 | 0.96 | 1.00 |
| B-SC-r20-h160-2 | 1180.1 | 1182.0 | 1984.7 | 2059.2 | 1.00 | 0.96 |
| B-SC-r20-h160-3 | 1140.9 | 1182.0 | 1927.9 | 2059.2 | 1.04 | 0.94 |
| B-SC-r20-h50d-1 | 1228.1 | 1182.0 | 2142.3 | 2059.2 | 0.96 | 1.04 |
| B-SC-r20-h50d-2 | 1198 | 1182.0 | 2165.0 | 2059.2 | 0.99 | 1.05 |
| B-SC-r20-h50d-3 | 1197.6 | 1182.0 | 2125.1 | 2059.2 | 0.99 | 1.03 |
| B-SC-r0-h120-1 | 1168.8 | 1088.0 | 1975.4 | 2059.2 | 0.93 | 0.96 |
| B-SC-r0-h120-2 | 1079.2 | 1088.0 | 1928.7 | 2059.2 | 1.01 | 0.94 |
| B-SC-r0-h120-3 | 1116.1 | 1088.0 | 1951.6 | 2059.2 | 0.97 | 0.95 |
| Mean | 0.99 | 0.99 | ||||
| Standard deviation | 0.037 | 0.035 | ||||
| Parametric Study | Specimens | Pu,FE | Pu,pre | K0.2,test | K0.2,pre | ||
|---|---|---|---|---|---|---|---|
| (kN) | (kN) | (kN/mm) | (kN/mm) | ||||
| Concrete strength | B-SC-fcm-25 | 1053.0 | 1144.3 | 1901.7 | 1911.1 | 1.09 | 1.00 |
| B-SC-fcm-30 | 1082.2 | 1154.6 | 1961.2 | 1951.9 | 1.07 | 1.00 | |
| B-SC-fcm-35 | 1126.3 | 1164.3 | 2013.4 | 1990.5 | 1.03 | 1.01 | |
| B-SC-fcm-40 | 1185.3 | 1173.7 | 2062.8 | 2027.4 | 0.99 | 1.02 | |
| B-SC-fcm-45 | 1210.6 | 1182.9 | 2095.3 | 2062.7 | 0.98 | 1.02 | |
| B-SC-fcm-50 | 1238.8 | 1191.7 | 2137.9 | 2096.7 | 0.96 | 1.02 | |
| B-SC-fcm-55 | 1260.7 | 1200.3 | 2183.0 | 2129.6 | 0.95 | 1.03 | |
| Shear-plate thickness | B-SC-shear-12 | 969.9 | 886.5 | 2041.2 | 2059.2 | 0.91 | 0.99 |
| B-SC-shear-14 | 1099.5 | 1034.2 | 2058.6 | 2059.2 | 0.94 | 1.00 | |
| B-SC-shear-16 | 1217.4 | 1182.0 | 2073.4 | 2059.2 | 0.97 | 1.01 | |
| B-SC-shear-18 | 1271.8 | 1329.7 | 2077.6 | 2059.2 | 1.05 | 1.01 | |
| B-SC-shear-20 | 1382.0 | 1477.4 | 2086.7 | 2059.2 | 1.07 | 1.01 | |
| Shear-plate tensile strength | B-SC-Q235 | 823.0 | 764.9 | 2070.3 | 2059.2 | 0.93 | 1.01 |
| B-SC-Q345 | 993.5 | 946.2 | 2070.3 | 2059.2 | 0.95 | 1.01 | |
| B-SC-Q390 | 1031.6 | 982.5 | 2070.3 | 2059.2 | 0.95 | 1.01 | |
| B-SC-Q420 | 1081.8 | 1036.9 | 2070.3 | 2059.2 | 0.96 | 1.01 | |
| B-SC-Q460 | 1142.2 | 1091.3 | 2070.3 | 2059.2 | 0.96 | 1.01 | |
| Stirrup diameter | B-SC-stirrup-14 | 1212.3 | 1182.0 | 2070.3 | 2059.2 | 0.97 | 1.01 |
| B-SC-stirrup-16 | 1217.4 | 1182.0 | 2070.3 | 2059.2 | 0.97 | 1.01 | |
| B-SC-stirrup-18 | 1232.9 | 1182.0 | 2070.3 | 2059.2 | 0.96 | 1.01 | |
| Mean | 0.98 | 1.01 | |||||
| Standard deviation | 0.048 | 0.008 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Z.; Zou, Y.; Chou, Y.; Qin, F.; Chen, F.; Di, J.; Zhang, Z. Shear Behaviour and Calculation Methods of Bearing-Shear Connectors for Prefabricated Steel–Concrete Composite Beams. Materials 2023, 16, 4616. https://doi.org/10.3390/ma16134616
Zheng Z, Zou Y, Chou Y, Qin F, Chen F, Di J, Zhang Z. Shear Behaviour and Calculation Methods of Bearing-Shear Connectors for Prefabricated Steel–Concrete Composite Beams. Materials. 2023; 16(13):4616. https://doi.org/10.3390/ma16134616
Chicago/Turabian StyleZheng, Zhichao, Yang Zou, Yaling Chou, Fengjiang Qin, Fengmin Chen, Jin Di, and Zhigang Zhang. 2023. "Shear Behaviour and Calculation Methods of Bearing-Shear Connectors for Prefabricated Steel–Concrete Composite Beams" Materials 16, no. 13: 4616. https://doi.org/10.3390/ma16134616
APA StyleZheng, Z., Zou, Y., Chou, Y., Qin, F., Chen, F., Di, J., & Zhang, Z. (2023). Shear Behaviour and Calculation Methods of Bearing-Shear Connectors for Prefabricated Steel–Concrete Composite Beams. Materials, 16(13), 4616. https://doi.org/10.3390/ma16134616









