One- and Two-Particle Correlation Functions in the Cluster Perturbation Theory for Cuprates
Abstract
:1. Introduction
2. Model and Methods
2.1. Model
2.2. Methods
2.2.1. CPT
2.2.2. CPT-RPA
2.2.3. Explicit Calculation of the Two-Particle Correlation Function (Spin-CPT and Charge-CPT)
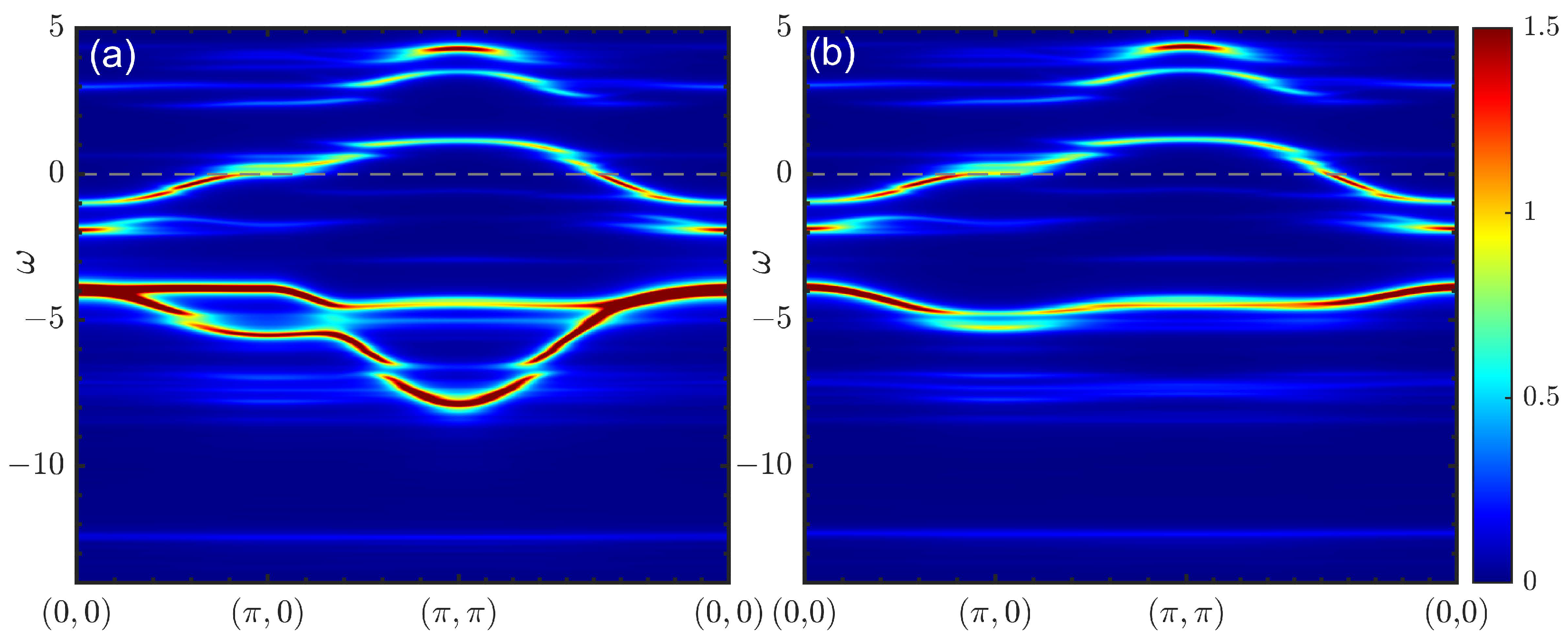
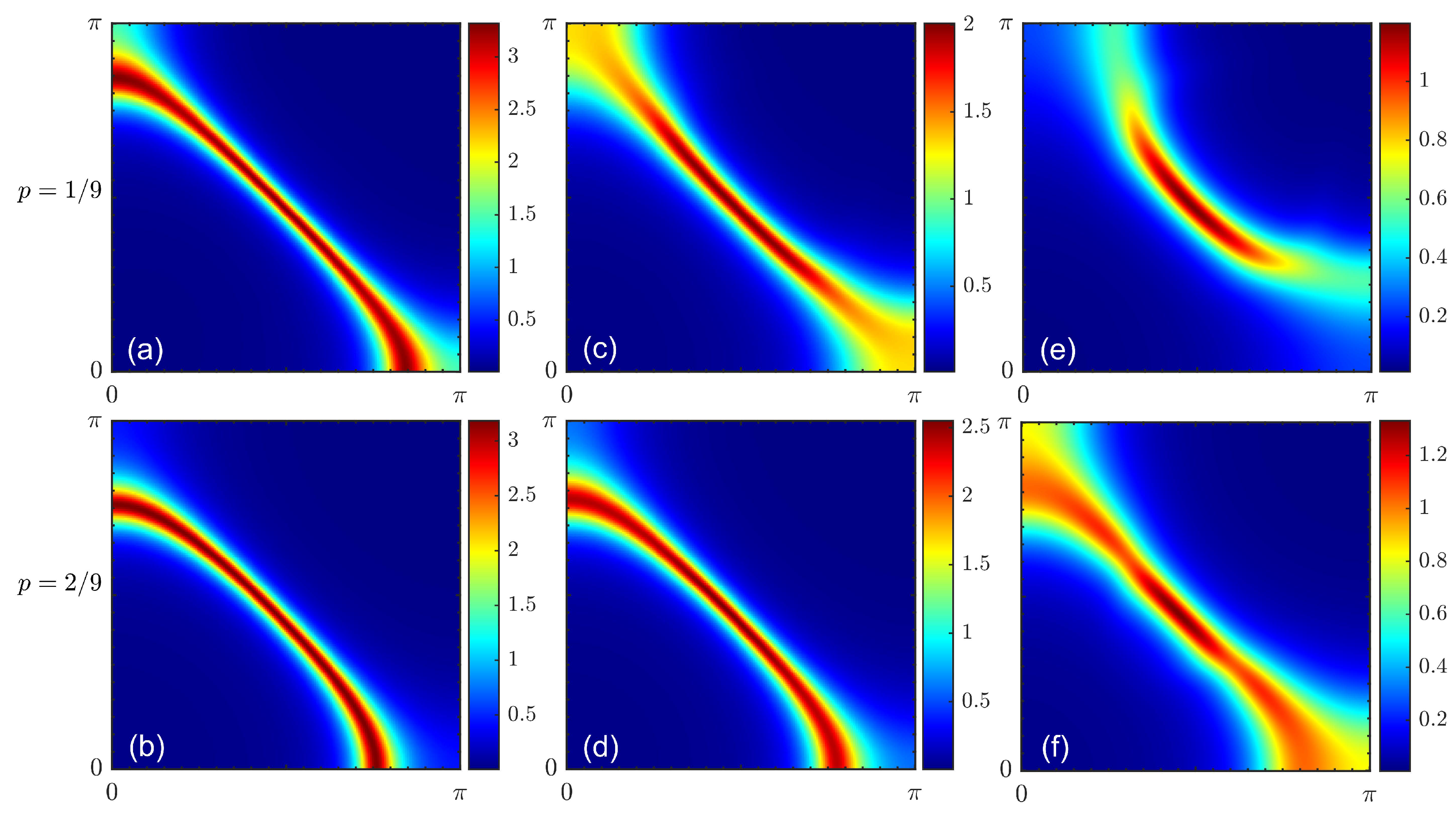
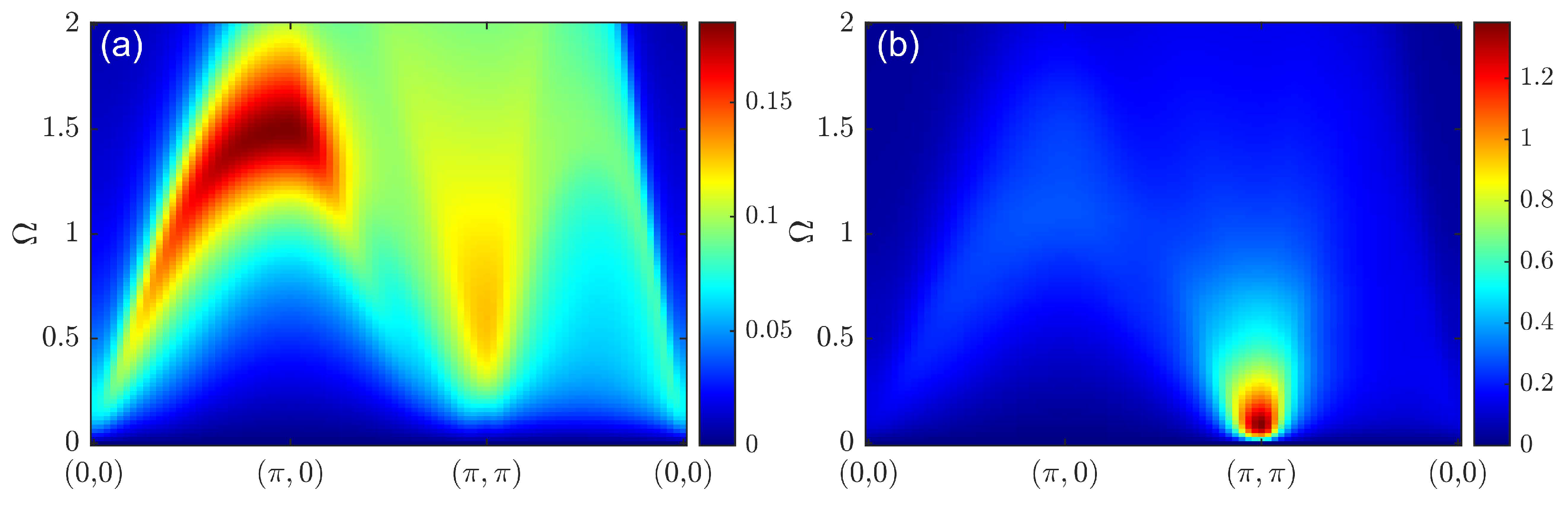
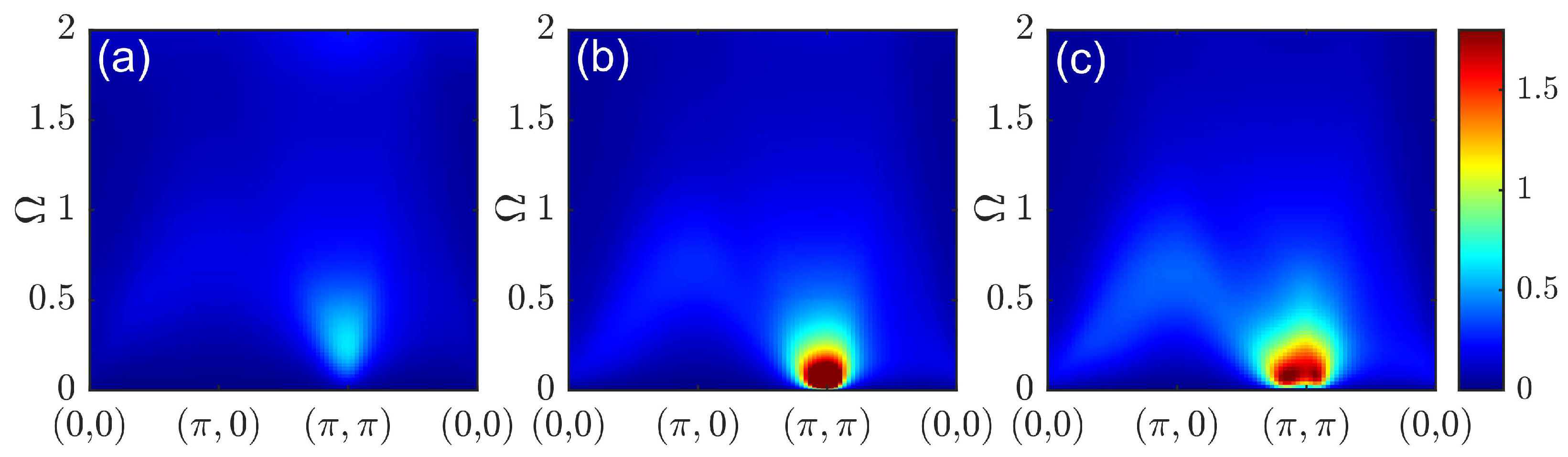
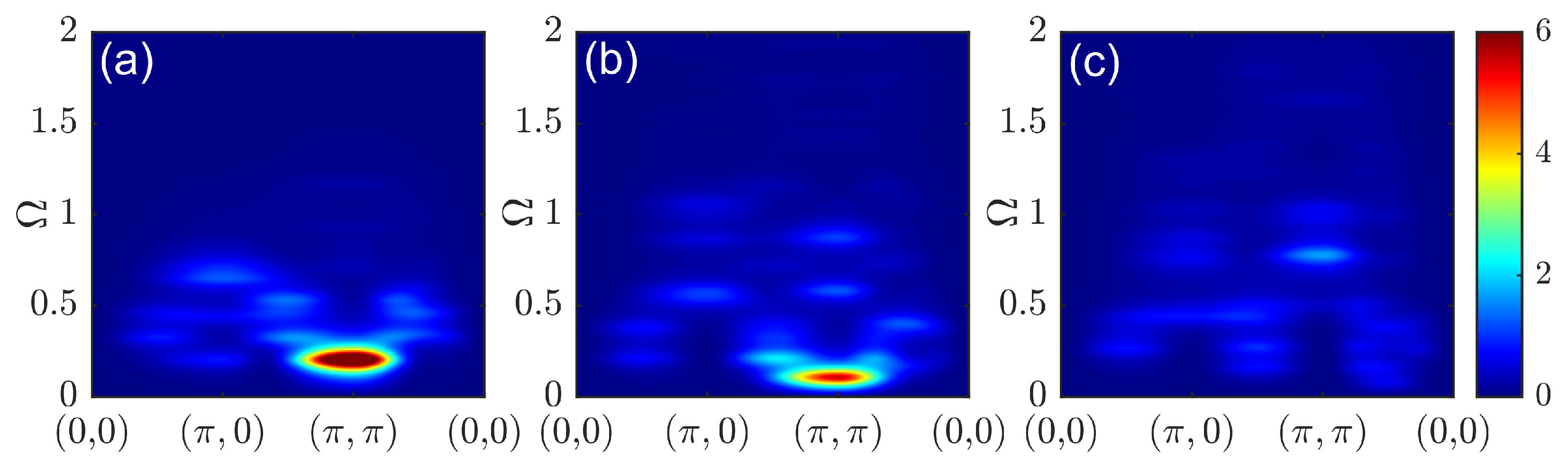
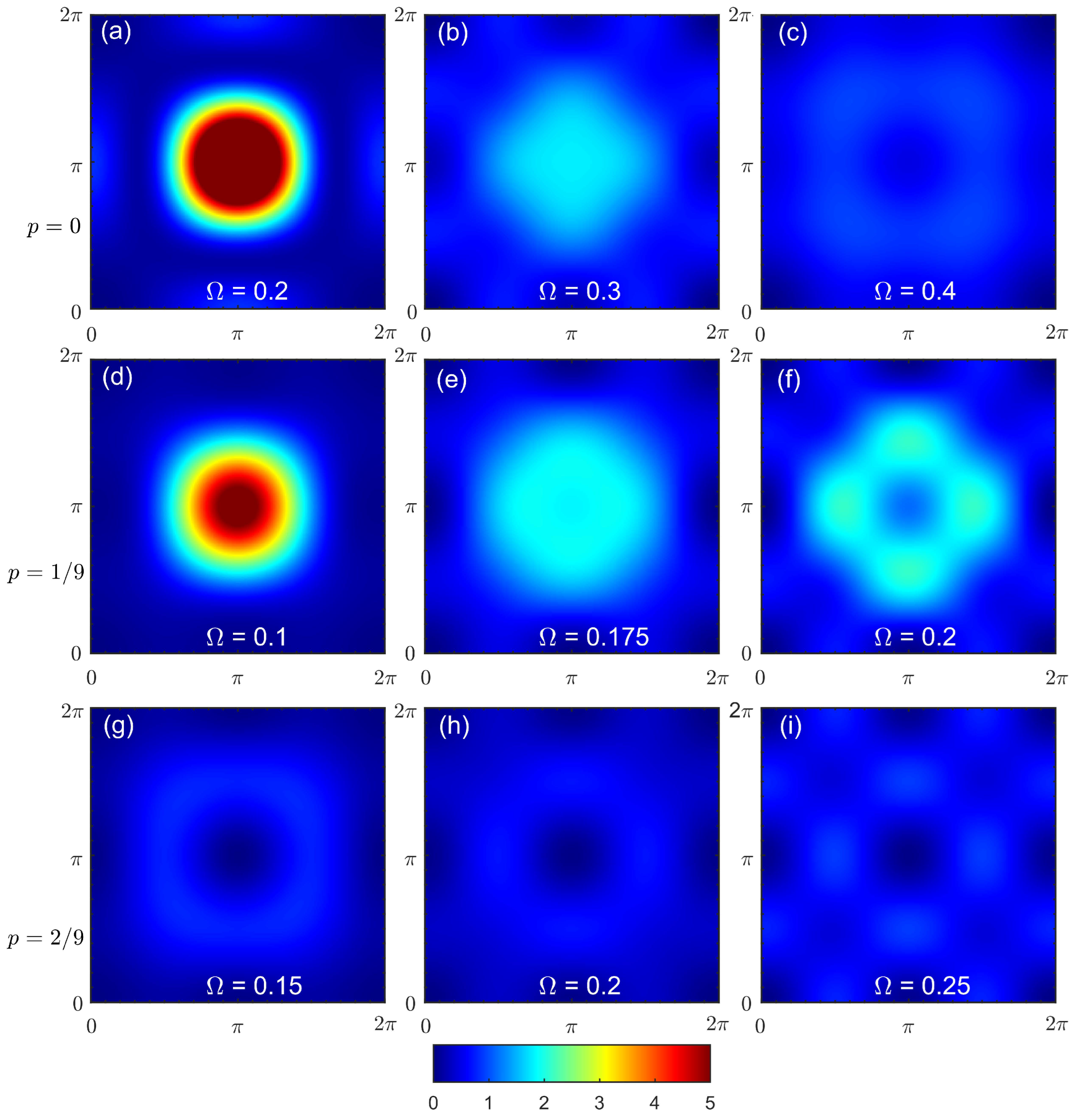
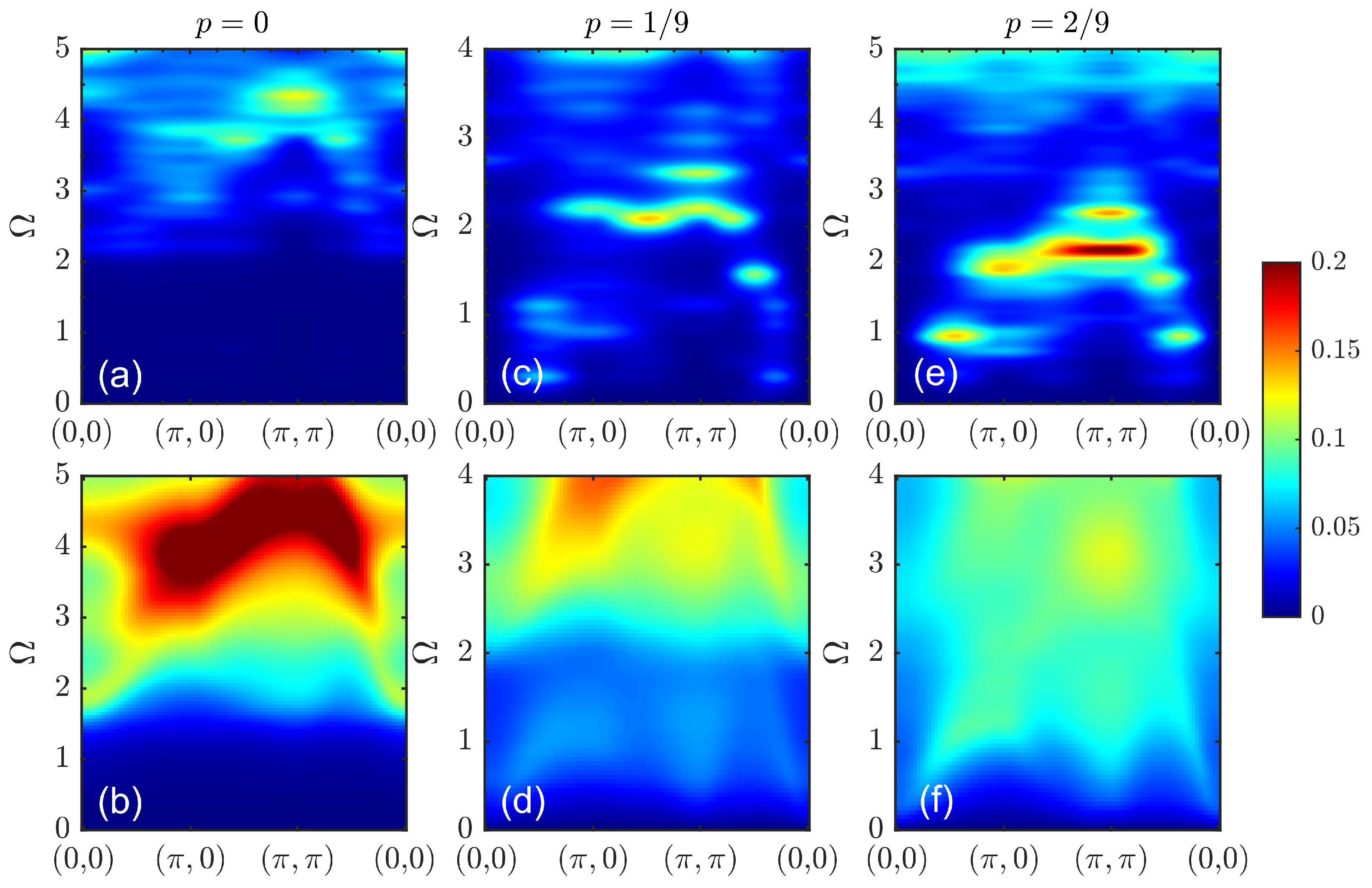
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Le Tacon, M.; Ghiringhelli, G.; Chaloupka, J.; Sala, M.M.; Hinkov, V.; Haverkort, M.; Minola, M.; Bakr, M.; Zhou, K.; Blanco-Canosa, S.; et al. Intense paramagnon excitations in a large family of high-temperature superconductors. Nat. Phys. 2011, 7, 725–730. [Google Scholar] [CrossRef]
- Le Tacon, M.; Minola, M.; Peets, D.C.; Moretti Sala, M.; Blanco-Canosa, S.; Hinkov, V.; Liang, R.; Bonn, D.A.; Hardy, W.N.; Lin, C.T.; et al. Dispersive spin excitations in highly overdoped cuprates revealed by resonant inelastic X-ray scattering. Phys. Rev. B 2013, 88, 020501. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; He, G.; Yang, Z.; Garcia-Fernandez, M.; Nag, A.; Zhou, K.; Minola, M.; Tacon, M.L.; Keimer, B.; Peng, Y.; et al. Paramagnons and high-temperature superconductivity in a model family of cuprates. Nat. Commun. 2022, 13, 3163. [Google Scholar] [CrossRef] [PubMed]
- Robarts, H.C.; Barthélemy, M.; Kummer, K.; García-Fernández, M.; Li, J.; Nag, A.; Walters, A.C.; Zhou, K.J.; Hayden, S.M. Anisotropic damping and wave vector dependent susceptibility of the spin fluctuations in La2−xSrxCuO4 studied by resonant inelastic X-ray scattering. Phys. Rev. B 2019, 100, 214510. [Google Scholar] [CrossRef] [Green Version]
- Ishii, K.; Tohyama, T.; Asano, S.; Sato, K.; Fujita, M.; Wakimoto, S.; Tustsui, K.; Sota, S.; Miyawaki, J.; Niwa, H.; et al. Observation of momentum-dependent charge excitations in hole-doped cuprates using resonant inelastic X-ray scattering at the oxygen K edge. Phys. Rev. B 2017, 96, 115148. [Google Scholar] [CrossRef] [Green Version]
- Damascelli, A.; Hussain, Z.; Shen, Z.X. Angle-resolved photoemission studies of the cuprate superconductors. Rev. Mod. Phys. 2003, 75, 473–541. [Google Scholar] [CrossRef] [Green Version]
- Sobota, J.A.; He, Y.; Shen, Z.X. Angle-resolved photoemission studies of quantum materials. Rev. Mod. Phys. 2021, 93, 025006. [Google Scholar] [CrossRef]
- Tranquada, J.M.; Xu, G.; Zaliznyak, I.A. Superconductivity, antiferromagnetism, and neutron scattering. J. Magn. Magn. Mater. 2014, 350, 148–160. [Google Scholar] [CrossRef] [Green Version]
- Fujita, M.; Hiraka, H.; Matsuda, M.; Matsuura, M.; M. Tranquada, J.; Wakimoto, S.; Xu, G.; Yamada, K. Progress in Neutron Scattering Studies of Spin Excitations in High-Tc Cuprates. J. Phys. Soc. Jpn. 2012, 81, 011007. [Google Scholar] [CrossRef] [Green Version]
- Sato, K.; Ikeuchi, K.; Kajimoto, R.; Wakimoto, S.; Arai, M.; Fujita, M. Coexistence of Two Components in Magnetic Excitations of La2−xSrxCuO4 (x = 0.10 and 0.16). J. Phys. Soc. Jpn. 2020, 89, 114703. [Google Scholar] [CrossRef]
- Lipscombe, O.J.; Vignolle, B.; Perring, T.G.; Frost, C.D.; Hayden, S.M. Emergence of Coherent Magnetic Excitations in the High Temperature Underdoped La2−xSrxCuO4 Superconductor at Low Temperatures. Phys. Rev. Lett. 2009, 102, 167002. [Google Scholar] [CrossRef] [Green Version]
- Hinkov, V.; Bourges, P.; Pailhes, S.; Sidis, Y.; Ivanov, A.; Frost, C.; Perring, T.; Lin, C.; Chen, D.; Keimer, B. Spin dynamics in the pseudogap state of a high-temperature superconductor. Nat. Phys. 2007, 3, 780–785. [Google Scholar] [CrossRef]
- Chan, M.; Dorow, C.; Mangin-Thro, L.; Tang, Y.; Ge, Y.; Veit, M.; Yu, G.; Zhao, X.; Christianson, A.; Park, J.; et al. Commensurate antiferromagnetic excitations as a signature of the pseudogap in the tetragonal high-Tc cuprate HgBa2CuO4+δ. Nat. Commun. 2016, 7, 10819. [Google Scholar] [CrossRef] [Green Version]
- Chan, M.K.; Tang, Y.; Dorow, C.J.; Jeong, J.; Mangin-Thro, L.; Veit, M.J.; Ge, Y.; Abernathy, D.L.; Sidis, Y.; Bourges, P.; et al. Hourglass Dispersion and Resonance of Magnetic Excitations in the Superconducting State of the Single-Layer Cuprate HgBa2CuO4+δ Near Optimal Doping. Phys. Rev. Lett. 2016, 117, 277002. [Google Scholar] [CrossRef] [Green Version]
- Emery, V.J. Theory of high-Tc superconductivity in oxides. Phys. Rev. Lett. 1987, 58, 2794–2797. [Google Scholar] [CrossRef] [Green Version]
- Maier, T.; Jarrell, M.; Pruschke, T.; Hettler, M.H. Quantum cluster theories. Rev. Mod. Phys. 2005, 77, 1027–1080. [Google Scholar] [CrossRef] [Green Version]
- Kotliar, G.; Savrasov, S.Y.; Haule, K.; Oudovenko, V.S.; Parcollet, O.; Marianetti, C.A. Electronic structure calculations with dynamical mean-field theory. Rev. Mod. Phys. 2006, 78, 865–951. [Google Scholar] [CrossRef] [Green Version]
- Rohringer, G.; Hafermann, H.; Toschi, A.; Katanin, A.A.; Antipov, A.E.; Katsnelson, M.I.; Lichtenstein, A.I.; Rubtsov, A.N.; Held, K. Diagrammatic routes to nonlocal correlations beyond dynamical mean field theory. Rev. Mod. Phys. 2018, 90, 025003. [Google Scholar] [CrossRef] [Green Version]
- Prokof’ev, N.V.; Svistunov, B.V.; Tupitsyn, I.S. Exact quantum Monte Carlo process for the statistics of discrete systems. J. Exp. Theor. Phys. Lett. 1996, 64, 911–916. [Google Scholar] [CrossRef] [Green Version]
- Kashurnikov, V.A.; Krasavin, A.V. Effective quantum Monte Carlo algorithm for modeling strongly correlated systems. J. Exp. Theor. Phys. 2007, 105, 69–78. [Google Scholar] [CrossRef]
- Gull, E.; Millis, A.J.; Lichtenstein, A.I.; Rubtsov, A.N.; Troyer, M.; Werner, P. Continuous-time Monte Carlo methods for quantum impurity models. Rev. Mod. Phys. 2011, 83, 349–404. [Google Scholar] [CrossRef] [Green Version]
- Spałek, J.; Fidrysiak, M.; Zegrodnik, M.; Biborski, A. Superconductivity in high-Tc and related strongly correlated systems from variational perspective: Beyond mean field theory. Phys. Rep. 2022, 959, 1–117. [Google Scholar] [CrossRef]
- Sénéchal, D.; Perez, D.; Pioro-Ladrière, M. Spectral Weight of the Hubbard Model through Cluster Perturbation Theory. Phys. Rev. Lett. 2000, 84, 522–525. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sénéchal, D.; Perez, D.; Plouffe, D. Cluster perturbation theory for Hubbard models. Phys. Rev. B 2002, 66, 075129. [Google Scholar] [CrossRef] [Green Version]
- Brehm, S.; Arrigoni, E.; Aichhorn, M.; Hanke, W. Theory of two-particle excitations and the magnetic susceptibility in high-Tc cuprate superconductors. Europhys. Lett. 2010, 89, 27005. [Google Scholar] [CrossRef] [Green Version]
- Kung, Y.F.; Bazin, C.; Wohlfeld, K.; Wang, Y.; Chen, C.C.; Jia, C.J.; Johnston, S.; Moritz, B.; Mila, F.; Devereaux, T.P. Numerically exploring the 1D-2D dimensional crossover on spin dynamics in the doped Hubbard model. Phys. Rev. B 2017, 96, 195106. [Google Scholar] [CrossRef] [Green Version]
- Raum, P.T.; Alvarez, G.; Maier, T.; Scarola, V.W. Two-particle correlation functions in cluster perturbation theory: Hubbard spin susceptibilities. Phys. Rev. B 2020, 101, 075122. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.C.; van Veenendaal, M.; Devereaux, T.P.; Wohlfeld, K. Fractionalization, entanglement, and separation: Understanding the collective excitations in a spin-orbital chain. Phys. Rev. B 2015, 91, 165102. [Google Scholar] [CrossRef] [Green Version]
- Pärschke, E.M.; Wang, Y.; Moritz, B.; Devereaux, T.P.; Chen, C.C.; Wohlfeld, K. Numerical investigation of spin excitations in a doped spin chain. Phys. Rev. B 2019, 99, 205102. [Google Scholar] [CrossRef] [Green Version]
- Nikolaev, S.V.; Korshunov, M.M. Spin and Charge Susceptibilities of the Two-Orbital Model within the Cluster Perturbation Theory for Fe-Based Materials. J. Supercond. Nov. Magn. 2016, 29, 3093. [Google Scholar] [CrossRef] [Green Version]
- Korshunov, M.M.; Gavrichkov, V.A.; Ovchinnikov, S.G.; Nekrasov, I.A.; Pchelkina, Z.V.; Anisimov, V.I. Hybrid LDA and generalized tight-binding method for electronic structure calculations of strongly correlated electron systems. Phys. Rev. B 2005, 72, 165104. [Google Scholar] [CrossRef] [Green Version]
- Anisimov, V.I.; Kondakov, D.E.; Kozhevnikov, A.V.; Nekrasov, I.A.; Pchelkina, Z.V.; Allen, J.W.; Mo, S.K.; Kim, H.D.; Metcalf, P.; Suga, S.; et al. Full orbital calculation scheme for materials with strongly correlated electrons. Phys. Rev. B 2005, 71, 125119. [Google Scholar] [CrossRef] [Green Version]
- Hybertsen, M.S.; Schlüter, M.; Christensen, N.E. Calculation of Coulomb-interaction parameters for La2CuO4 using a constrained-density-functional approach. Phys. Rev. B 1989, 39, 9028–9041. [Google Scholar] [CrossRef]
- Shastry, B.S. t-J model and nuclear magnetic relaxation in high-Tc materials. Phys. Rev. Lett. 1989, 63, 1288–1291. [Google Scholar] [CrossRef]
- Lovtsov, S.; Yushankhai, V. Effective singlet-triplet model for CuO2 plane in oxide superconductors: The change fluctuation regime. Phys. C Supercond. 1991, 179, 159–166. [Google Scholar] [CrossRef]
- Jefferson, J.H.; Eskes, H.; Feiner, L.F. Derivation of a single-band model for CuO2 planes by a cell-perturbation method. Phys. Rev. B 1992, 45, 7959–7972. [Google Scholar] [CrossRef]
- Schüttler, H.B.; Fedro, A.J. Copper-oxygen charge excitations and the effective-single-band theory of cuprate superconductors. Phys. Rev. B 1992, 45, 7588–7591. [Google Scholar] [CrossRef]
- Feiner, L.F.; Jefferson, J.H.; Raimondi, R. Effective single-band models for the high-Tc cuprates. I. Coulomb interactions. Phys. Rev. B 1996, 53, 8751–8773. [Google Scholar] [CrossRef]
- Raimondi, R.; Jefferson, J.H.; Feiner, L.F. Effective single-band models for the high-Tc cuprates. II. Role of apical oxygen. Phys. Rev. B 1996, 53, 8774–8788. [Google Scholar] [CrossRef]
- Gavrichkov, V.A.; Ovchinnikov, S.G.; Borisov, A.A.; Goryachev, E.G. Evolution of the band structure of quasiparticles with doping in copper oxides on the basis of a generalized tight-binding method. J. Exp. Theor. Phys. 2000, 91, 369–383. [Google Scholar] [CrossRef]
- Makarov, I.A.; Shneyder, E.I.; Kozlov, P.A.; Ovchinnikov, S.G. Polaronic approach to strongly correlated electron systems with strong electron-phonon interaction. Phys. Rev. B 2015, 92, 155143. [Google Scholar] [CrossRef] [Green Version]
- Shneyder, E.I.; Nikolaev, S.V.; Zotova, M.V.; Kaldin, R.A.; Ovchinnikov, S.G. Polaron transformations in the realistic model of the strongly correlated electron system. Phys. Rev. B 2020, 101, 235114. [Google Scholar] [CrossRef]
- Kung, Y.F.; Chen, C.C.; Wang, Y.; Huang, E.W.; Nowadnick, E.A.; Moritz, B.; Scalettar, R.T.; Johnston, S.; Devereaux, T.P. Characterizing the three-orbital Hubbard model with determinant quantum Monte Carlo. Phys. Rev. B 2016, 93, 155166. [Google Scholar] [CrossRef] [Green Version]
- Huang, E.W.; Ding, S.; Liu, J.; Wang, Y. Determinantal quantum Monte Carlo solver for cluster perturbation theory. Phys. Rev. Res. 2022, 4, L042015. [Google Scholar] [CrossRef]
- Graser, S.; Maier, T.A.; Hirschfeld, P.J.; Scalapino, D.J. Near-degeneracy of several pairing channels in multiorbital models for the Fe pnictides. New J. Phys. 2009, 11, 025016. [Google Scholar] [CrossRef]
- Korshunov, M.M. Itinerant spin fluctuations in iron-based superconductors. In Perturbation Theory: Advances in Research and Applications; Pirogov, Z., Ed.; Nova Science Publishers Inc.: New York, NY, USA, 2018; Chapter 2; pp. 61–138. [Google Scholar]
- Nikolaev, S.V.; Ovchinnikov, S.G. Cluster perturbation theory in Hubbard model exactly taking into account the short-range magnetic order in 2 × 2 cluster. JETP 2010, 111, 635–644. [Google Scholar] [CrossRef]
- Nikolaev, S.V.; Ovchinnikov, S.G. Effect of hole doping on the electronic structure and the Fermi surface in the Hubbard model within norm-conserving cluster pertubation theory. J. Exp. Theor. Phys. 2012, 114, 118–131. [Google Scholar] [CrossRef]
- Kuz’min, V.I.; Nikolaev, S.V.; Ovchinnikov, S.G. Comparison of the electronic structure of the Hubbard and t − J models within the cluster perturbation theory. Phys. Rev. B 2014, 90, 245104. [Google Scholar] [CrossRef]
- Kuz’min, V.I.; Visotin, M.A.; Nikolaev, S.V.; Ovchinnikov, S.G. Doping and temperature evolution of pseudogap and spin-spin correlations in the two-dimensional Hubbard model. Phys. Rev. B 2020, 101, 115141. [Google Scholar] [CrossRef] [Green Version]
- Rosenberg, P.; Sénéchal, D.; Tremblay, A.M.S.; Charlebois, M. Fermi arcs from dynamical variational Monte Carlo. Phys. Rev. B 2022, 106, 245132. [Google Scholar] [CrossRef]
- Korshunov, M.M.; Ovchinnikov, S.G. Doping-dependent evolution of low-energy excitations and quantum phase transitions within an effective model for high-Tc copper oxides. Eur. Phys. J. B 2007, 57, 271–278. [Google Scholar] [CrossRef] [Green Version]
- Ovchinnikov, S.G.; Shneyder, E.I.; Korshunov, M.M. From underdoped to overdoped cuprates: Two quantum phase transitions. J. Physics Condens. Matter. 2011, 23, 045701. [Google Scholar] [CrossRef] [Green Version]
- Mai, P.; Nichols, N.S.; Karakuzu, S.; Bao, F.; Del Maestro, A.; Maier, T.A.; Johnston, S. Robust charge-density wave correlations in the electron-doped single-band Hubbard model. arXiv 2022, arXiv:2210.14930. [Google Scholar] [CrossRef]
- Gröber, C.; Eder, R.; Hanke, W. Anomalous low-doping phase of the Hubbard model. Phys. Rev. B 2000, 62, 4336–4352. [Google Scholar] [CrossRef] [Green Version]
- Dong, X.; Chen, X.; Gull, E. Dynamical charge susceptibility in the Hubbard model. Phys. Rev. B 2019, 100, 235107. [Google Scholar] [CrossRef] [Green Version]
- Coldea, R.; Hayden, S.M.; Aeppli, G.; Perring, T.G.; Frost, C.D.; Mason, T.E.; Cheong, S.W.; Fisk, Z. Spin Waves and Electronic Interactions in La2CuO4. Phys. Rev. Lett. 2001, 86, 5377–5380. [Google Scholar] [CrossRef] [Green Version]
- Wakimoto, S.; Yamada, K.; Tranquada, J.M.; Frost, C.D.; Birgeneau, R.J.; Zhang, H. Disappearance of Antiferromagnetic Spin Excitations in Overdoped La2−xSrxCuO4. Phys. Rev. Lett. 2007, 98, 247003. [Google Scholar] [CrossRef] [Green Version]
- Lipscombe, O.J.; Hayden, S.M.; Vignolle, B.; McMorrow, D.F.; Perring, T.G. Persistence of High-Frequency Spin Fluctuations in Overdoped Superconducting La2−xSrxCuO4 (x = 0.22). Phys. Rev. Lett. 2007, 99, 067002. [Google Scholar] [CrossRef] [Green Version]
- Eremin, M.V.; Aleev, A.A.; Eremin, I.M. On interlay between the magnetic susceptibilities of localized and itinerant electrons in hole-doped HTSCs. JETP Lett. 2006, 84, 167–170. [Google Scholar] [CrossRef]
- Eremin, M.V.; Aleev, A.A.; Eremin, I.M. Dynamic spin susceptibility of hole-doped high-temperature superconductors in a singlet-correlated conduction band model. J. Exp. Theor. Phys. 2008, 106, 752–764. [Google Scholar] [CrossRef]
- Eremin, M.V.; Shigapov, I.M.; Eremin, I.M. Dual features of magnetic susceptibility in superconducting cuprates: A comparison to inelastic neutron scattering. Eur. Phys. J. B 2012, 85, 131. [Google Scholar] [CrossRef]
- Eremin, M.V.; Shigapov, I.M.; Thuy, H.T.D. Collective spin excitations in the singlet-correlated band model: A comparison with resonant inelastic X-ray scattering. J. Phys. Condens. Matter. 2013, 25, 345701. [Google Scholar] [CrossRef] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuz’min, V.I.; Nikolaev, S.V.; Korshunov, M.M.; Ovchinnikov, S.G. One- and Two-Particle Correlation Functions in the Cluster Perturbation Theory for Cuprates. Materials 2023, 16, 4640. https://doi.org/10.3390/ma16134640
Kuz’min VI, Nikolaev SV, Korshunov MM, Ovchinnikov SG. One- and Two-Particle Correlation Functions in the Cluster Perturbation Theory for Cuprates. Materials. 2023; 16(13):4640. https://doi.org/10.3390/ma16134640
Chicago/Turabian StyleKuz’min, Valerii I., Sergey V. Nikolaev, Maxim M. Korshunov, and Sergey G. Ovchinnikov. 2023. "One- and Two-Particle Correlation Functions in the Cluster Perturbation Theory for Cuprates" Materials 16, no. 13: 4640. https://doi.org/10.3390/ma16134640
APA StyleKuz’min, V. I., Nikolaev, S. V., Korshunov, M. M., & Ovchinnikov, S. G. (2023). One- and Two-Particle Correlation Functions in the Cluster Perturbation Theory for Cuprates. Materials, 16(13), 4640. https://doi.org/10.3390/ma16134640







