Study on the Mechanical Properties of Continuous Composite Beams under Coupled Slip and Creep
Abstract
:1. Introduction
2. Establishing Control Differential Equations
2.1. Basic Assumptions
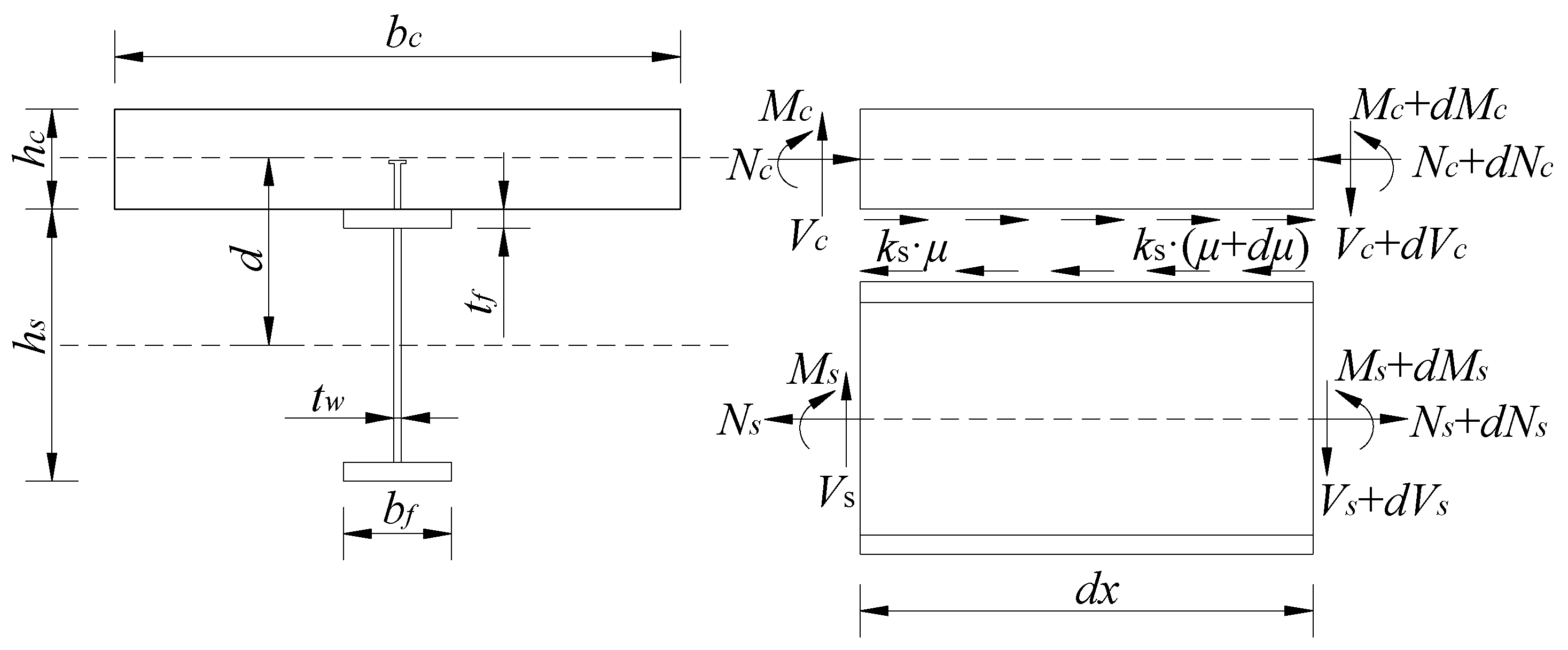
- Without considering the influence of transverse shear deformation in the composite beam, the curvatures of the steel beam and the concrete flange plate are completely consistent, and the vertical lifting phenomenon at the interface of the steel–concrete composite beam is ignored.
- The cross-sections of the concrete slab and the steel beam meet the plane section assumption, respectively, and the stud connector conforms to the elastic sandwich setting.
- The stress–strain relationship between the steel beam and the concrete is linear throughout the stressing phase, and the concrete is not cracked or spalled.
- The shear connectors are evenly distributed along the length direction of the composite beam, and the shear force of each shear connector is linearly related to the slip.
2.2. Coupling Analysis Considering the Effects of Slip and Creep
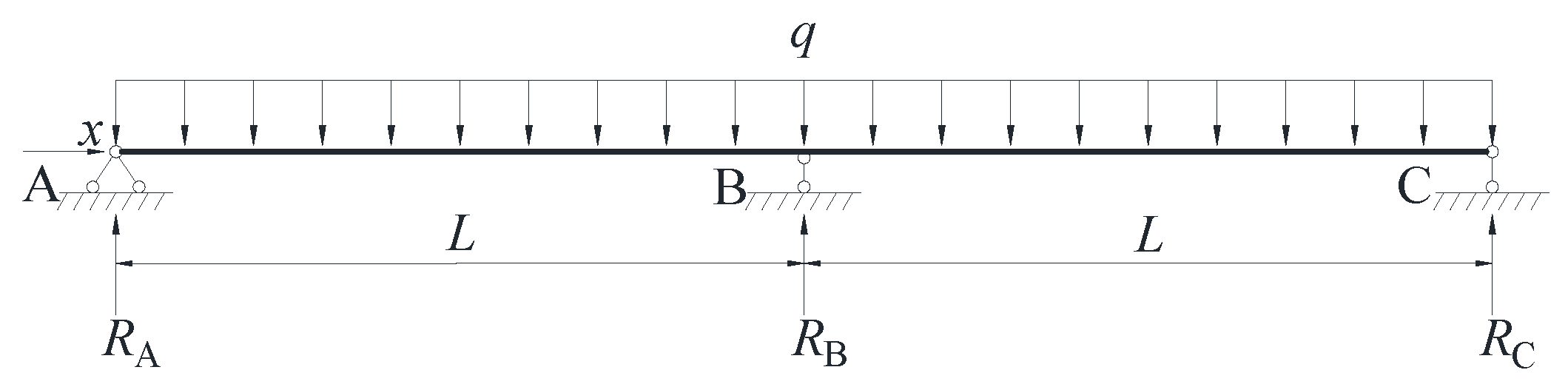
3. Analytical Solution of Continuous Composite Beams under a Uniform Load
3.1. Analytical Solution of Axial Force
3.2. Analytical Solution of Slip
3.3. Analytical Solution of Deflection
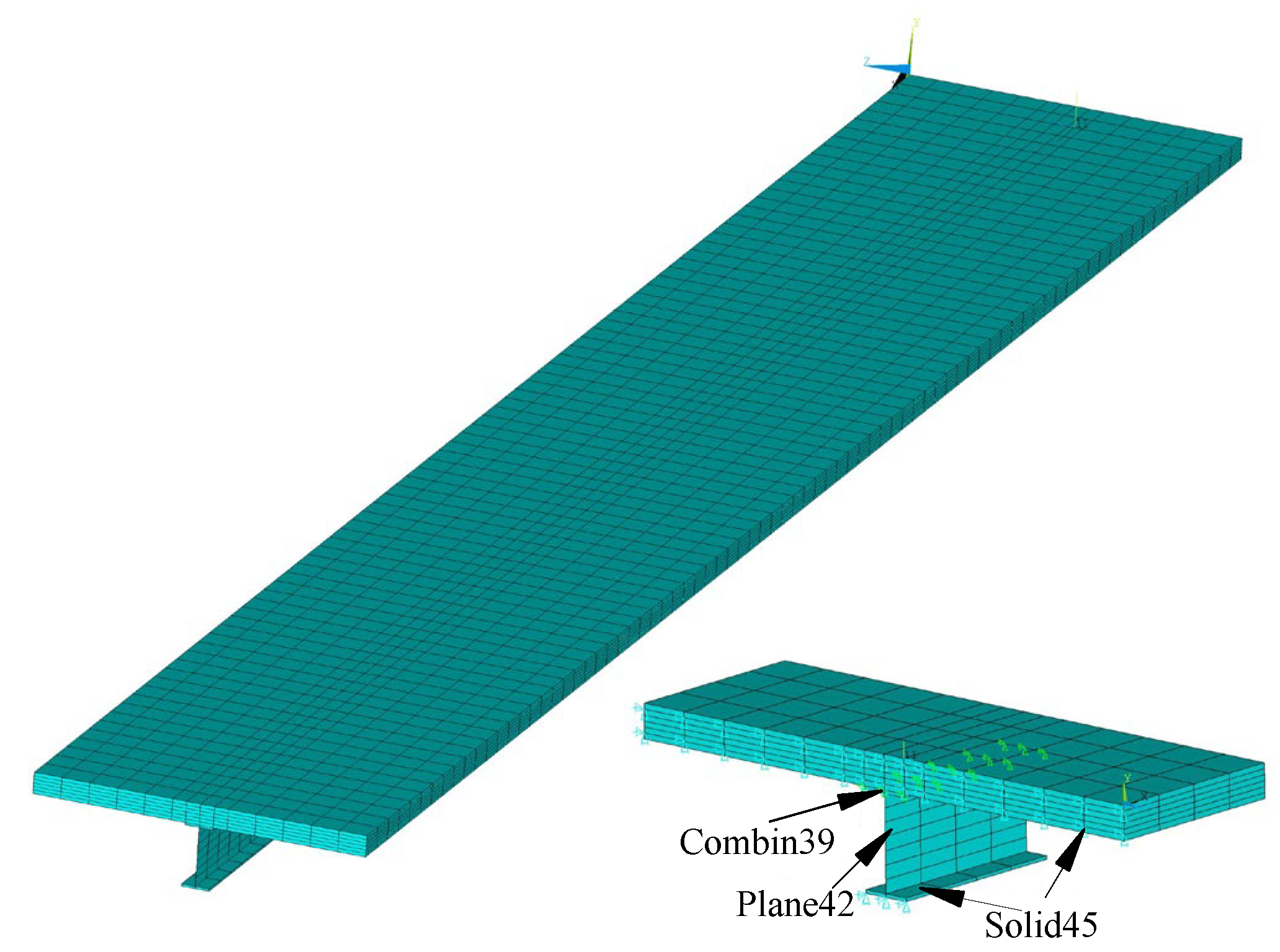
4. ANSYS Finite Element Analysis of Continuous Composite Beam
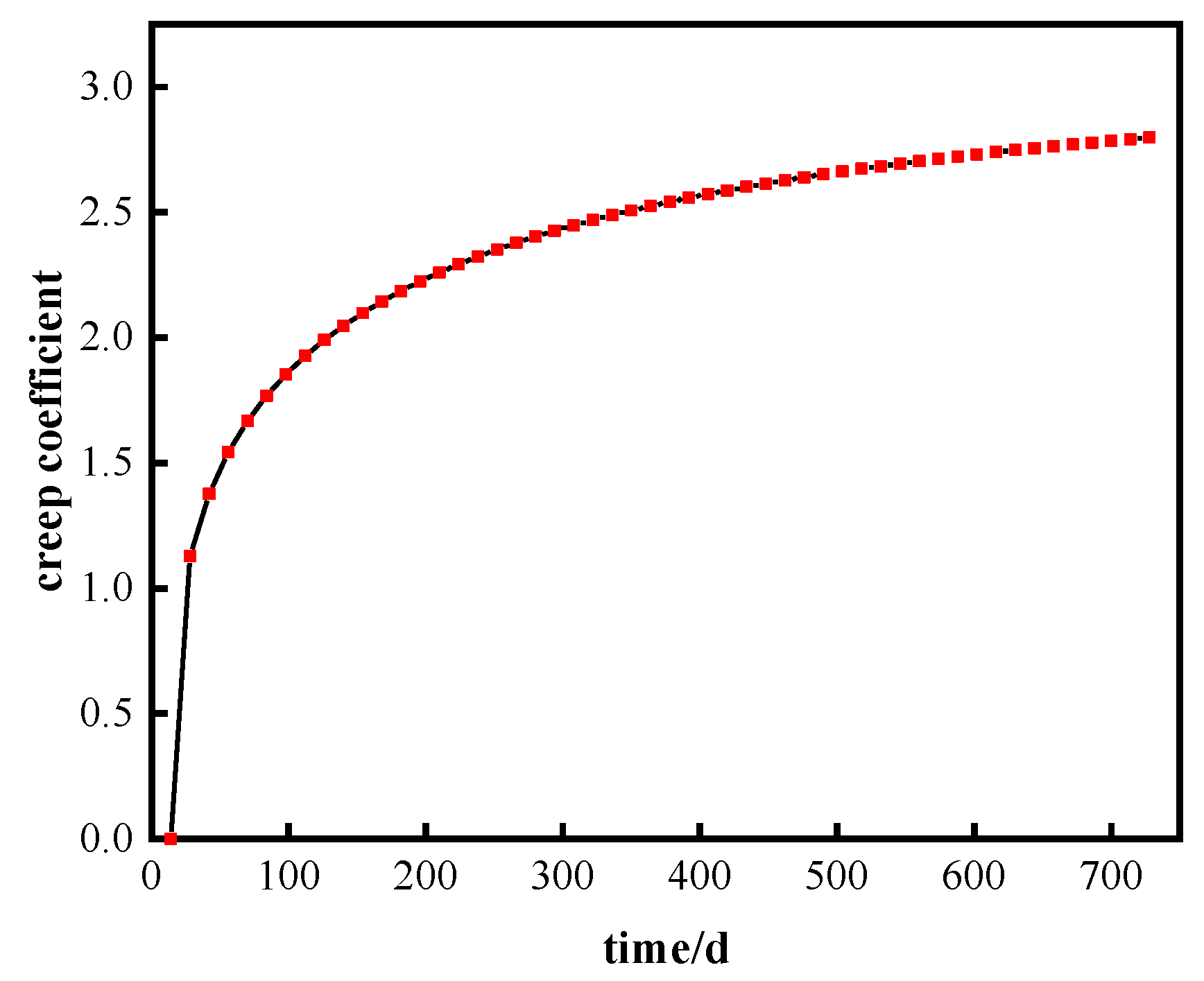
4.1. ANSYS Creep Calculation Method
4.2. Continuous Composite Beam Example Verification
4.3. Example Analysis of Continuous Composite Beam
5. Conclusions
- In this paper, the energy variational method is used to establish the control differential equation, considering the combined actions of slip and creep. The theoretical analytical solutions for the slip, deflection and axial forces of continuous composite beams under uniform loads are derived. The correctness of the analytical solution is verified by establishing a finite element composite beam model.
- For a composite beam under a long-term load, creep will increase the deflection of the composite beam and the steel beam bending moment, reducing the concrete bending moment. The deflection of the composite beam increases by 14% under the influence of creep, the bending moment of the steel beam increases by 12% and the bending moment of the concrete decreases by 49%. Creep has little effect on the slip and axial force of a composite beam, increasing by about 2%.
- The analytical solution obtained in this paper is suitable for the calculation and analysis of any equal-span continuous composite beam under a uniform load and can calculate any shear stiffness, which can quickly and intuitively reflect changes in the deflection, slip and axial force under a long-term load. The increase in the shear stiffnesses of shear connectors will increase the axial forces of composite beams and reduce slip, deflection and bending moments. The increase in shear stiffness will reduce the influence of creep on the axial forces and slip of composite beams and increase the influence of creep on deflection.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nie, J. Experiment Theory and Application of Steel-Concrete Composite Beams; Science Press: Beijing, China, 2005. (In Chinese) [Google Scholar]
- Wang, L. Theory and Calculation of Steel-Concrete Composite Structure; Science Press: Beijing, China, 2005. (In Chinese) [Google Scholar]
- Zeng, X.; Zhou, D. Calculation and analysis of interface slip of composite beams. J. Eng. Mech. 2013, 30, 162–174. (In Chinese) [Google Scholar]
- Jiang, L. Theoretical analysis of slip and deformation of steel-concrete composite beam under uniformly distributed load. J. Eng. Mech. 2003, 20, 133–137. (In Chinese) [Google Scholar]
- Huang, G. Creep and Shrinkage of Concrete; China Electric Power Press: Beijing, China, 2012. (In Chinese) [Google Scholar]
- Wang, C. Study on the influence of shrinkage and creep on the mechanical properties of composite beams. J. Highw. Transp. Res. Dev. (Appl. Technol. Ed.) 2015, 11, 254–256. (In Chinese) [Google Scholar]
- Dezi, L.; Tarantino, A.M. Creep in Composite Continuous Beams. I: Theoretical Treatment. J. Struct. Eng. 1993, 119, 2095–2111. [Google Scholar] [CrossRef]
- Dezi, L.; Tarantino, A.M. Creep in Composite Continuous Beams. II: Parametric Study. J. Struct. Eng. 1993, 119, 2112–2133. [Google Scholar] [CrossRef]
- Zhou, L. Analysis of composite beams of steel and concrete with slip and shear deformation. J. Eng. Mech. 2005, 22, 104–109. (In Chinese) [Google Scholar]
- Gara, F. Time Analysis of Composite Beams with Partial Interaction Using Available Modelling Techniques: A Comparative Study. J. Constr. Steel Res. 2006, 62, 917–930. [Google Scholar] [CrossRef]
- Zhou, D. Precise and Approximate Methods to Calculate Shrinkage and Creep Effects of Simply-Supported Composite Bean. J. Southwest Jiaotong Univ. 2015, 50, 1018–1024. (In Chinese) [Google Scholar]
- Wang, L. Analysis Method of Creep on Interface Slip and Axial Force of Curved Steel-concrete Composite Beams. J. Shenyang Jianzhu Univ. (Nat. Sci.) 2022, 38, 1–9. (In Chinese) [Google Scholar]
- Xiang, Y. Calculation of long-term slippage forexternally prestressing steel-concrete composite beam. J. Zhejiang Univ. (Eng. Sci.) 2022, 38, 1–9. (In Chinese) [Google Scholar]
- Ranzi, G.; Bradford, M.A. Analytical Solutions for the Time-Dependent Behaviour of Composite Beams with Partial Interaction. Int. J. Solids Struct. 2006, 43, 3770–3793. [Google Scholar] [CrossRef] [Green Version]
- Ban, H.; Uy, B.; Pathirana, S.W.; Henderson, I.; Mirza, O.; Zhu, X. Time-Dependent Behaviour of Composite Beams with Blind Bolts under Sustained Loads. J. Constr. Steel Res. 2015, 112, 196–207. [Google Scholar] [CrossRef]
- Nguyen, Q.-H.; Hjiaj, M. Nonlinear Time-Dependent Behavior of Composite Steel-Concrete Beams. J. Struct. Eng. 2016, 142, 04015175. [Google Scholar] [CrossRef]
- Ji, W. Calculation and Analysis of Deflection for Steel-concrete Composite Girder under Long-term Loads. J. Hunan Univ. (Nat. Sci.) 2021, 48, 51–60. (In Chinese) [Google Scholar]
- Wang, G.-M.; Zhu, L.; Ji, X.-L.; Ji, W.-Y. Finite Beam Element for Curved Steel–Concrete Composite Box Beams Considering Time-Dependent Effect. Materials 2020, 13, 3253. [Google Scholar] [CrossRef]
- Wu, W.; Dai, J.; Chen, L.; Liu, D.; Zhou, X. Experiment Analysis on Crack Resistance in Negative Moment Zone of Steel–Concrete Composite Continuous Girder Improved by Interfacial Slip. Materials 2022, 15, 8319. [Google Scholar] [CrossRef]
- Vasdravellis, G.; Valente, M.; Castiglioni, C.A. Dynamic Response of Composite Frames with Different Shear Connection Degree. J. Constr. Steel Res. 2009, 65, 2050–2061. [Google Scholar] [CrossRef]
- Taghipoor, H.; Sadeghian, A. Experimental Investigation of Single and Hybrid-Fiber Reinforced Concrete under Drop Weight Test. Structures 2022, 43, 1073–1083. [Google Scholar] [CrossRef]
- Sadeghian, A.; Moradi Shaghaghi, T.; Mohammadi, Y.; Taghipoor, H. Performance Assessment of Hybrid Fibre-Reinforced Concrete (FRC) under Low-Speed Impact: Experimental Analysis and Optimized Mixture. Shock. Vib. 2023, 2023, 7110987. [Google Scholar] [CrossRef]
- Lü, C. Effects of shrinkage and creep strains on bending behavior of steel-concrete composite beams. J. Build. Struct. 2010, 31, 32–39. (In Chinese) [Google Scholar]
- Huang, Q. Analytical method of steel-concrete composite beam based on interface slip and shear deformation. J. Nanjing Univ. Aeronaut. Astronaut. 2018, 50, 131–137. (In Chinese) [Google Scholar]
- Zhou, D. Method for Calculation of stress of composite beams with elastic shear connections. J. Eng. Mech. 2011, 28, 157–162. (In Chinese) [Google Scholar]
- Bazant, Z.P. Prediction of Concrete Creep Effects Using Age-Adjusted Effective Modulus Method. ACI J. 1972, 69, 212–217. [Google Scholar] [CrossRef] [Green Version]
- Amadio, C.; Fragiacomo, M. Simplified approach to evaluate creep and shrinkage effects in steel-concrete composite beams. J. Struct. Eng. 1997, 123, 1153–1162. [Google Scholar] [CrossRef]
- Torst, H. Auswirkungen Des Superpositionsprinzips Auf Kriech-Und Relaxationsprobleme Bei Beton Und Spannbeton. Beton-Und Stahlbetonbau 1967, 10, 230–238, 261–269. [Google Scholar]
- Wang, X. The value problem of aging coefficient x in age-adjusted effective modulus method. J. China Railw. Sci. 1996, 17, 12–23. (In Chinese) [Google Scholar]
- GB 50917-2013; Code for Design of Steel and Concrete Composite Bridges. China Planning Press: Beijing, China, 2014. (In Chinese)
- Zhou, L. Shrinkage Creep; China Railway Publishing House: Beijing, China, 1994. (In Chinese) [Google Scholar]
- JTG D62-2004; Code for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts. Ministry of Transport of the People’s Republic of China: Beijing, China, 2004. (In Chinese)



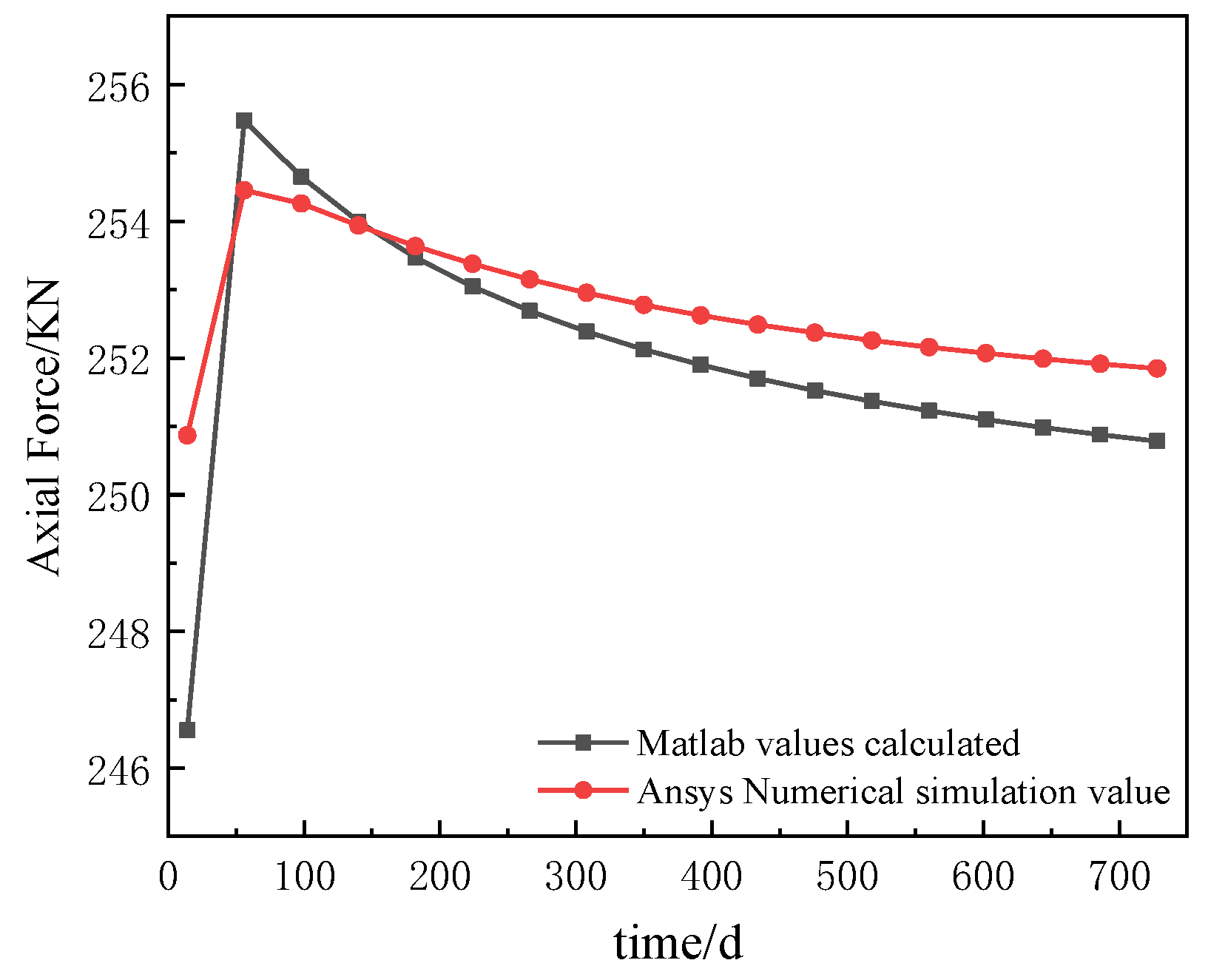
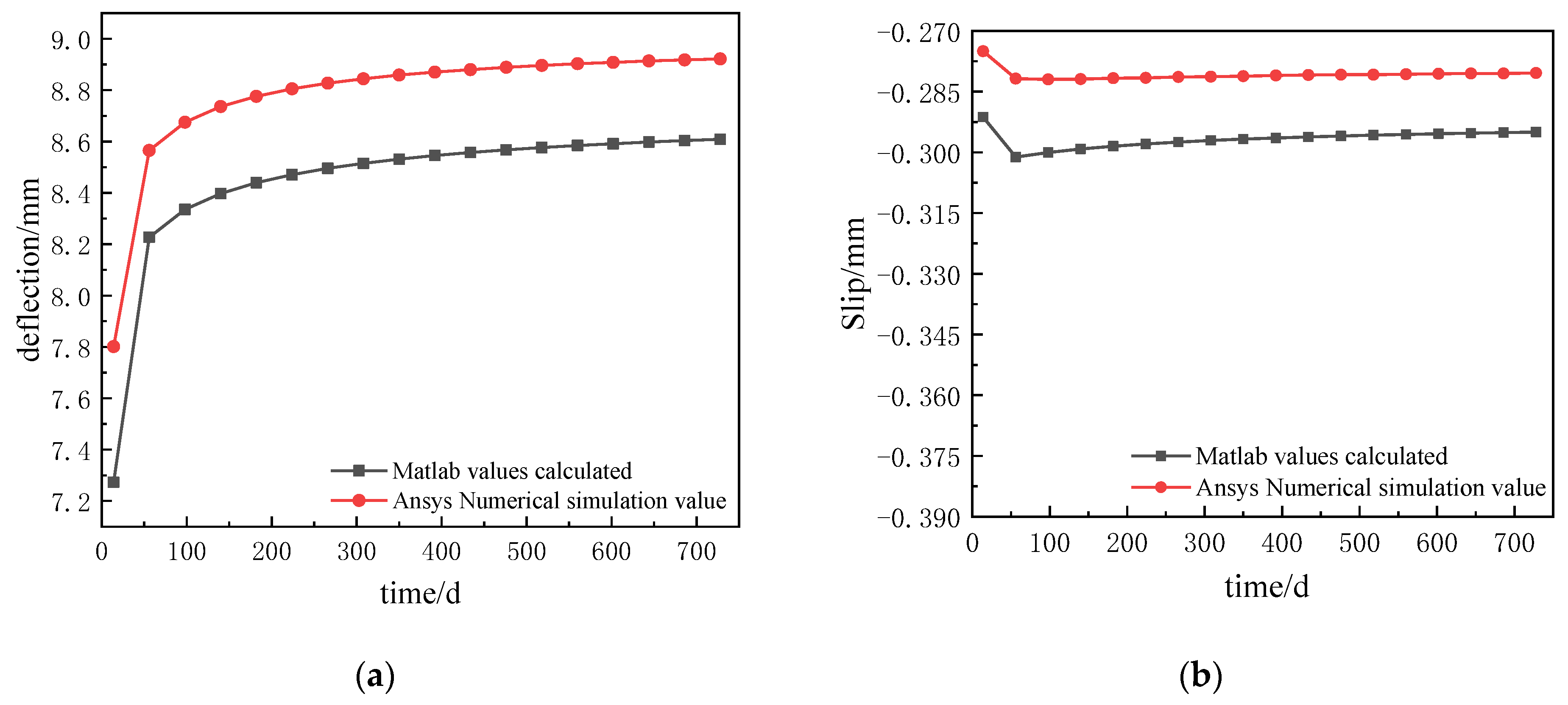



| Time/d | Error | ||
|---|---|---|---|
| 14 | 246.55 | 250.87 | 1.75% |
| 728 | 250.78 | 251.84 | 0.42% |
| Simulated Calculation Value | ANSYS Values Calculation | Error | ||||
|---|---|---|---|---|---|---|
| Time/d | Error 1 | Error 2 | ||||
| 14 | 7.27 | −0.2913 | 7.80 | −0.275 | 7.29% | 5.60% |
| 728 | 8.61 | −0.2950 | 8.92 | −0.2804 | 3.6% | 4.95% |
| Axial Force/KN | |||
|---|---|---|---|
| Time/d | |||
| 14 | 199.20 | 284.10 | 348.25 |
| 728 | 208.02 | 285.98 | 340.77 |
| Change rate | 4.43% | 0.67% | −2.15% |
| Slip/mm | Deflection/mm | |||||
|---|---|---|---|---|---|---|
| Time/d | ||||||
| 14 | 0.844 | −0.634 | −0.446 | −9.27 | −8.0 | −6.96 |
| 728 | −0.905 | −0.650 | −0.439 | −10.51 | −9.16 | −8.11 |
| Change rate | 7.23% | 2.52% | −1.57% | 13.38% | 14.50% | 16.52% |
| Concrete Bending Moment/KN/m | Steel Beam Bending Moment/KN/m | |||||
|---|---|---|---|---|---|---|
| Time/d | ||||||
| 14 | 70 | 62.64 | 55.92 | 275.20 | 252.0 | 231.0 |
| 728 | 35.38 | 31.88 | 28.98 | 307.40 | 282.0 | 260.60 |
| Change rate | −49.46% | −49.11% | −48.18% | 11.70% | 11.90% | 12.81% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nan, H.; Wang, P.; Zhang, Q.; Meng, D.; Lei, Q. Study on the Mechanical Properties of Continuous Composite Beams under Coupled Slip and Creep. Materials 2023, 16, 4741. https://doi.org/10.3390/ma16134741
Nan H, Wang P, Zhang Q, Meng D, Lei Q. Study on the Mechanical Properties of Continuous Composite Beams under Coupled Slip and Creep. Materials. 2023; 16(13):4741. https://doi.org/10.3390/ma16134741
Chicago/Turabian StyleNan, Hongliang, Peng Wang, Qinmin Zhang, Dayao Meng, and Qinan Lei. 2023. "Study on the Mechanical Properties of Continuous Composite Beams under Coupled Slip and Creep" Materials 16, no. 13: 4741. https://doi.org/10.3390/ma16134741






