Machinability Measurements in Milling and Recurrence Analysis of Thin-Walled Elements Made of Polymer Composites
Abstract
:1. Introduction
2. Materials and Methods
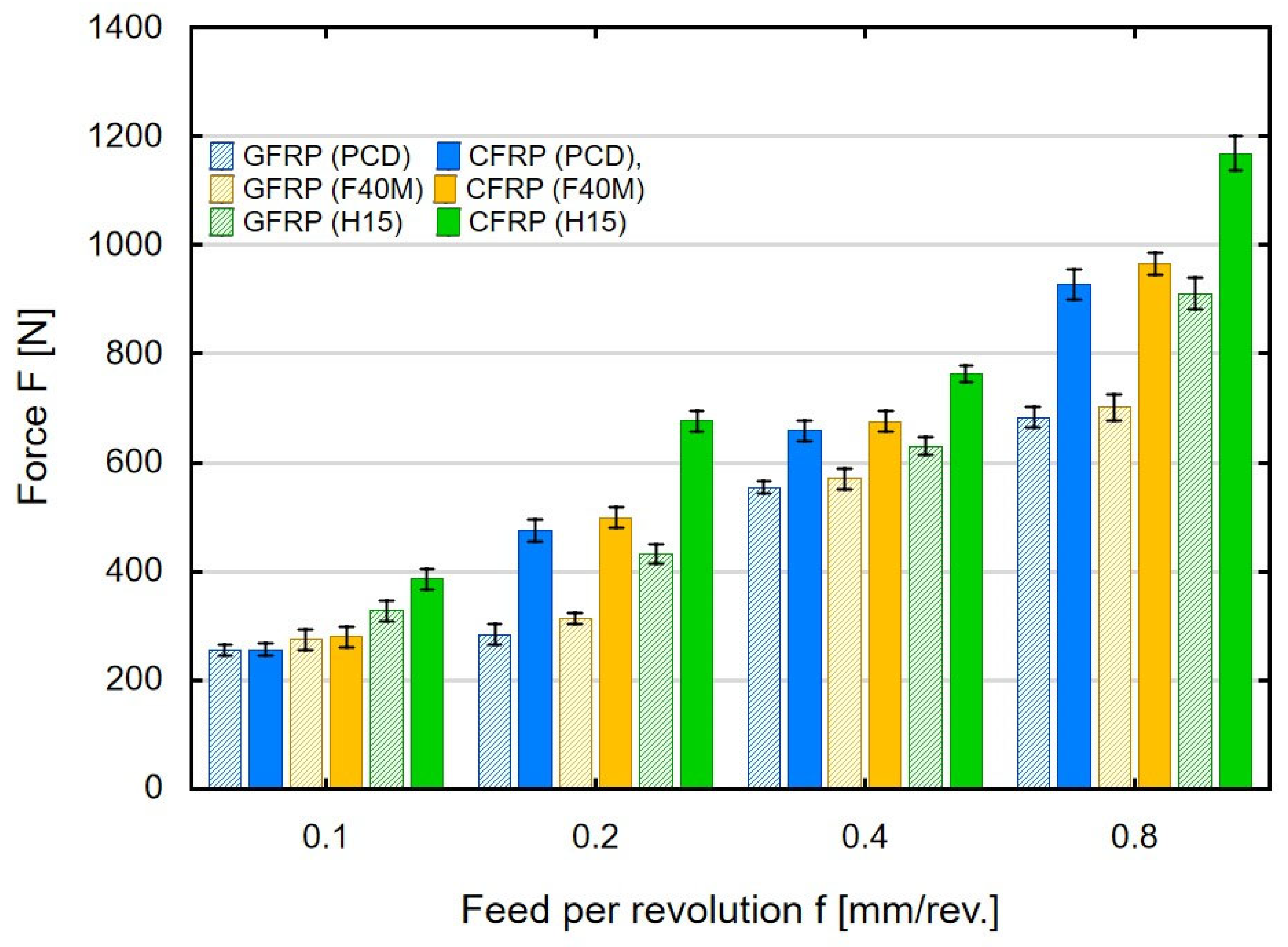
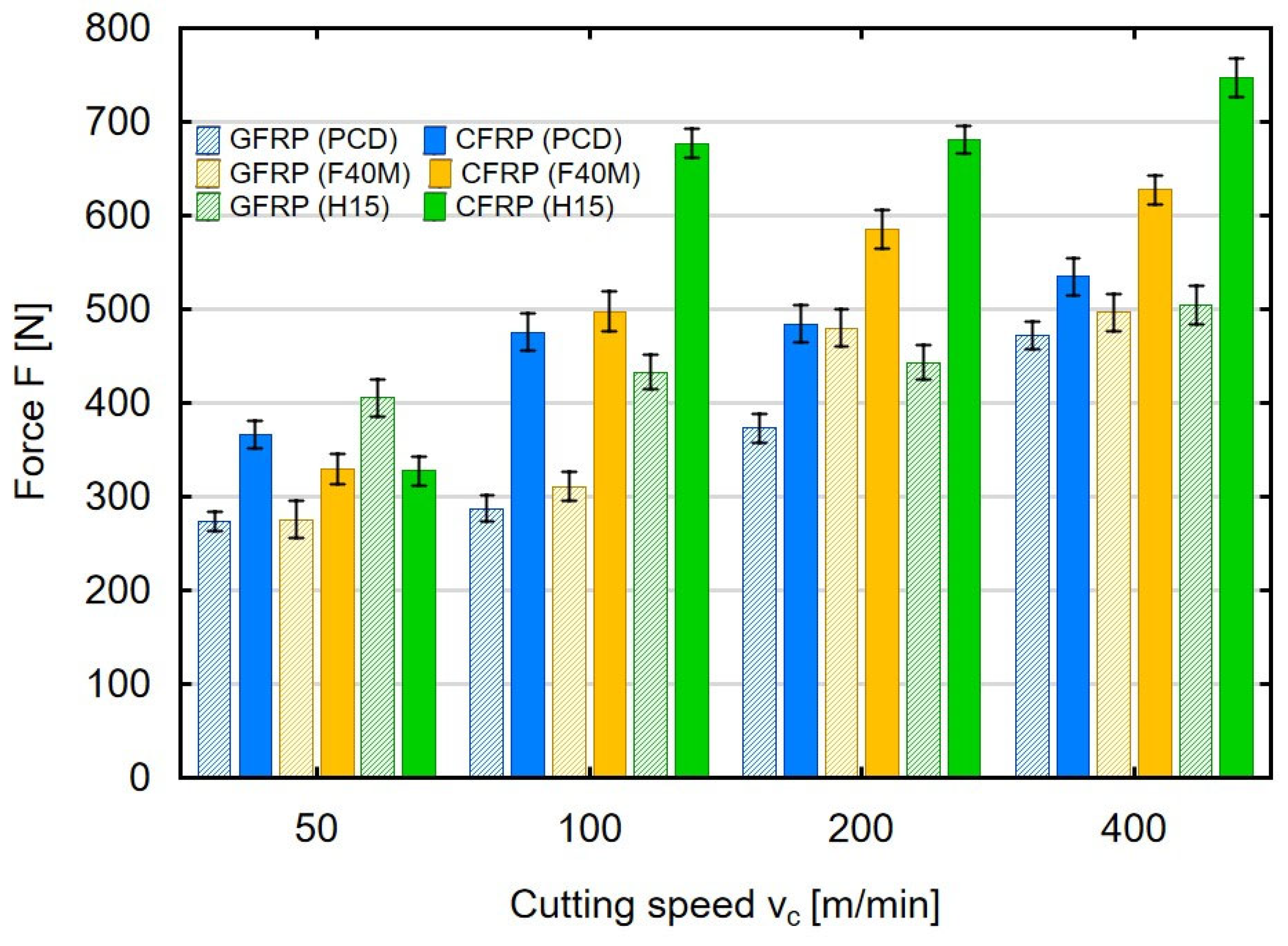
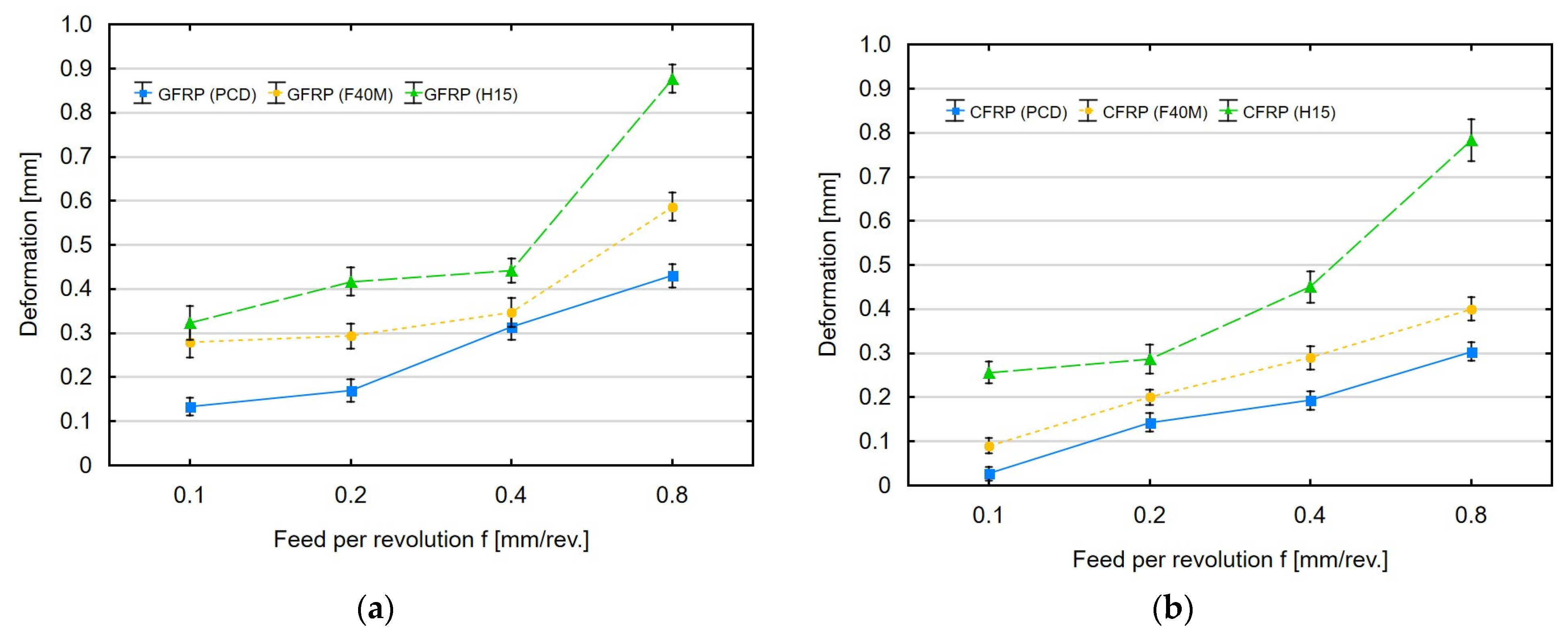
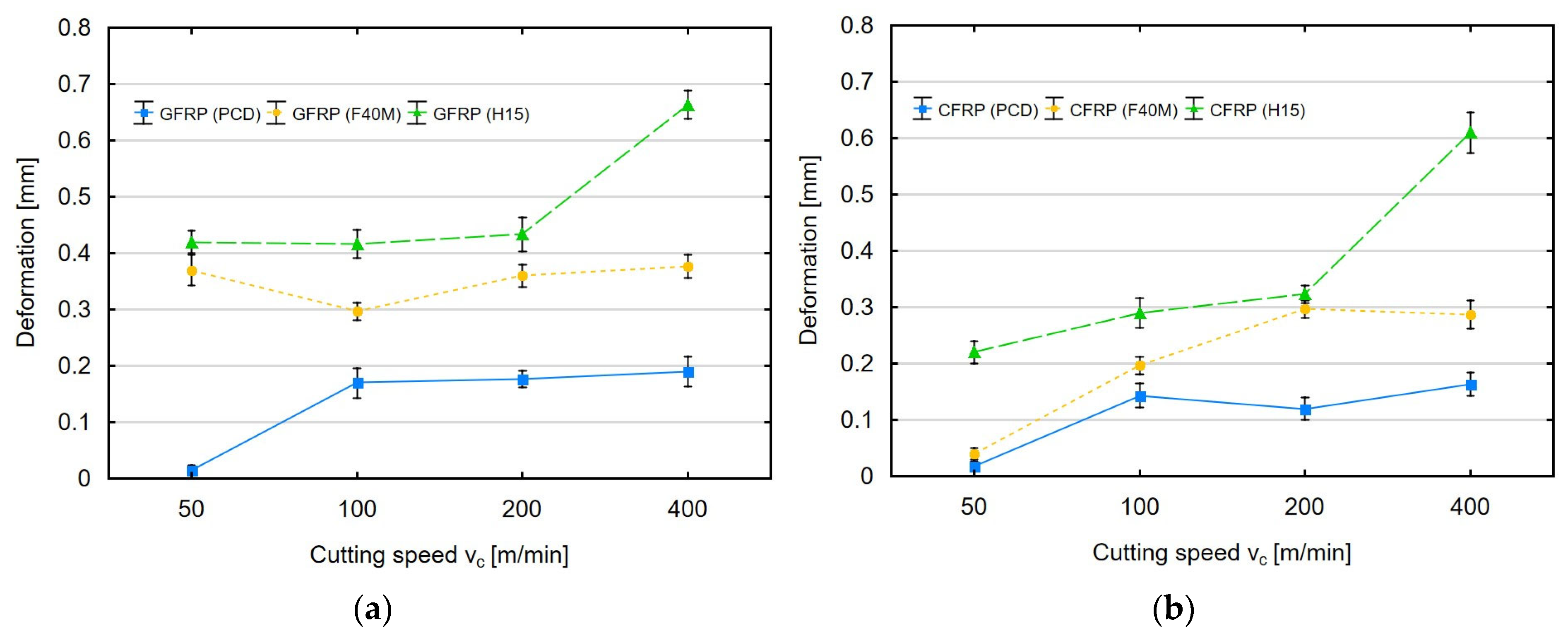
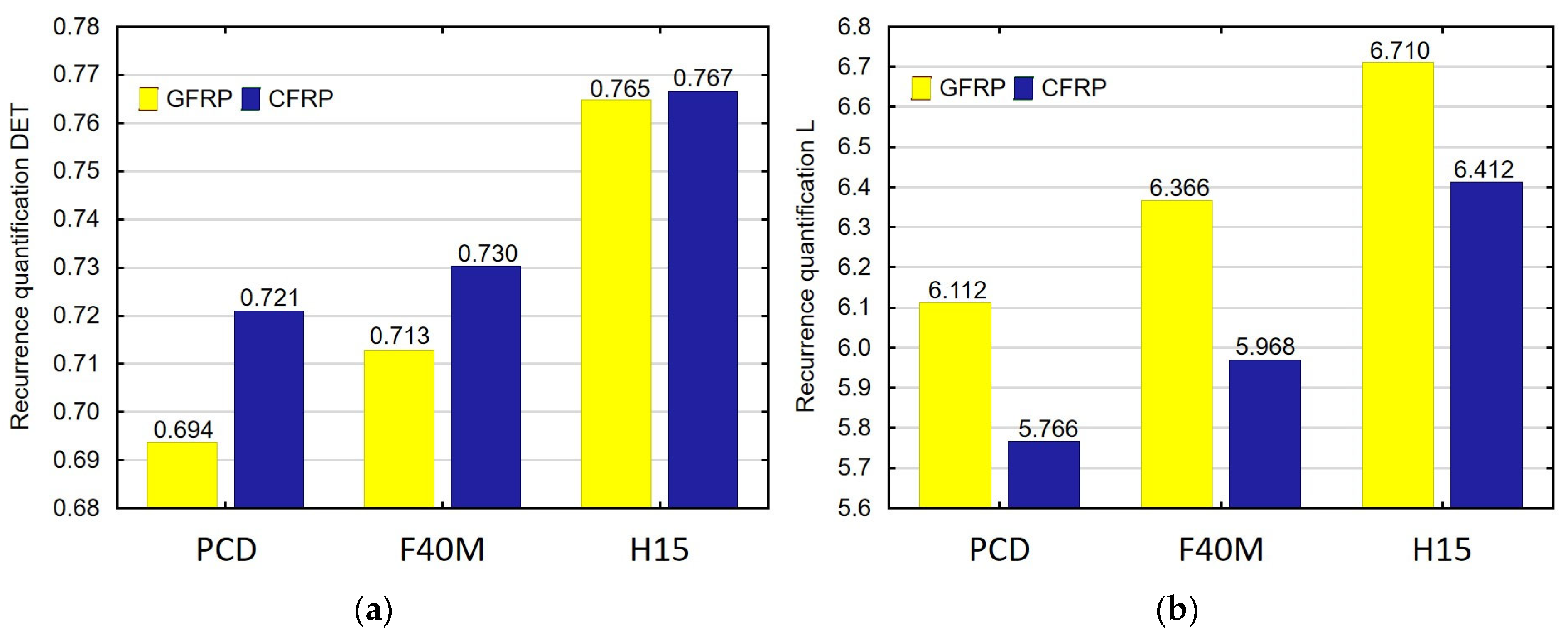
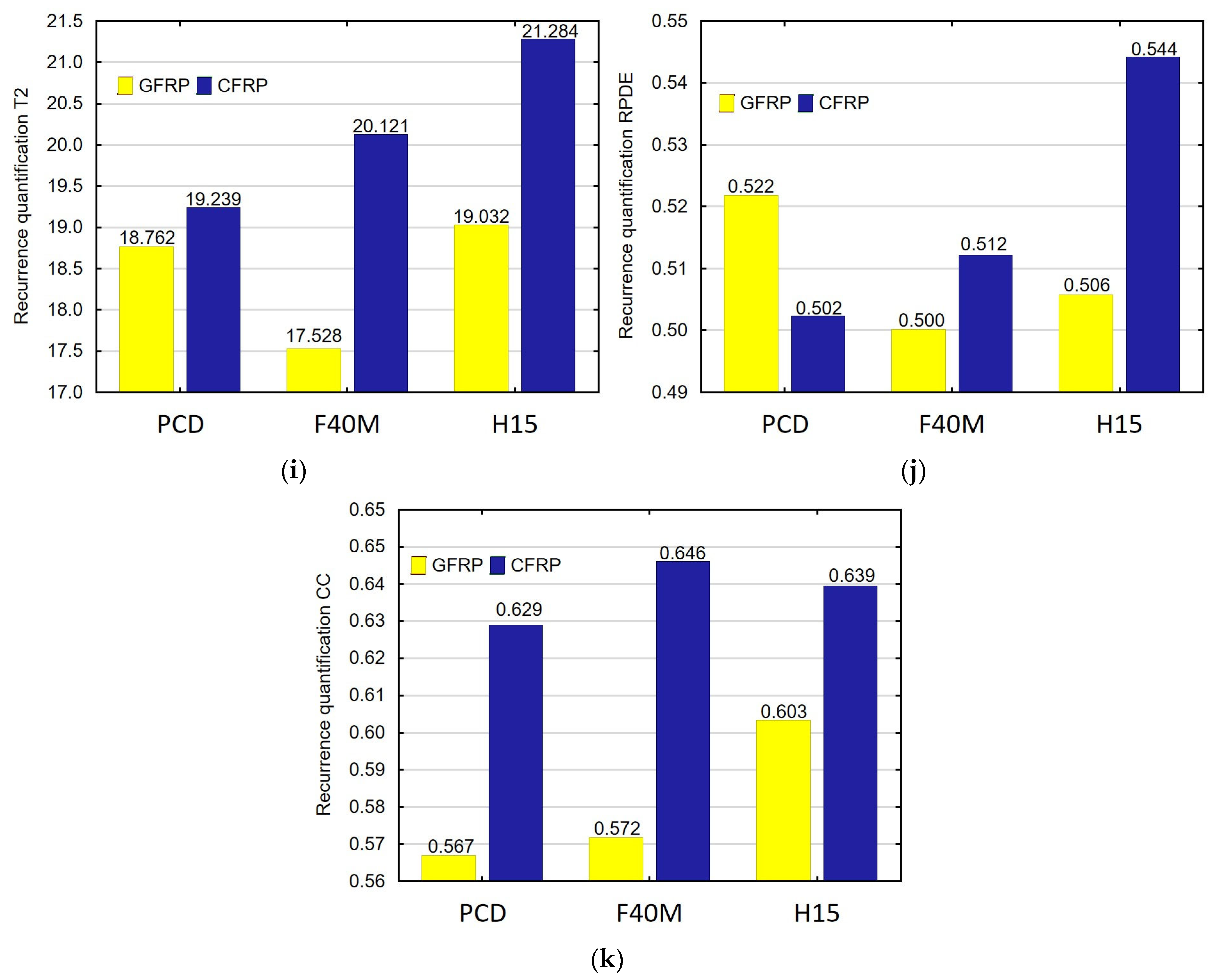
3. Results and Discussion
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Teti, R. Machining of Composite Materials. CIRP Ann. 2002, 51, 611–634. [Google Scholar] [CrossRef]
- Matuszak, J. Effect of Ceramic Brush Treatment on the Surface Quality and Edge Condition of Aluminium Alloy after Abrasive Waterjet Machining. Adv. Sci. Technol. Res. J. 2021, 15, 254–263. [Google Scholar] [CrossRef]
- Kuczmaszewski, J.; Zaleski, K.; Matuszak, J.; Mądry, J. Testing Geometric Precision and Surface Roughness of Titanium Alloy Thin-Walled Elements Processed with Milling. In Advances in Manufacturing II; Diering, M., Wieczorowski, M., Brown, C.A., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 95–106. ISBN 978-3-030-18681-4. [Google Scholar]
- Papakonstantinou, C.G.; Balaguru, P.; Lyon, R.E. Comparative Study of High Temperature Composites. Compos. Part B Eng. 2001, 32, 637–649. [Google Scholar] [CrossRef]
- Azmi, A.I.; Lin, R.J.T.; Bhattacharyya, D. Machinability Study of Glass Fibre-Reinforced Polymer Composites during end Milling. Int. J. Adv. Manuf. Technol. 2013, 64, 247–261. [Google Scholar] [CrossRef]
- Hintze, W.; Hartmann, D. Modeling of Delamination During Milling of Unidirectional CFRP. Procedia CIRP 2013, 8, 444–449. [Google Scholar] [CrossRef] [Green Version]
- Ghidossi, P.; El Mansori, M.; Pierron, F. Edge Machining Effects on the Failure of Polymer Matrix Composite Coupons. Compos. Part A Appl. Sci. Manuf. 2004, 35, 989–999. [Google Scholar] [CrossRef]
- Hosokawa, A.; Hirose, N.; Ueda, T.; Furumoto, T. High-Quality Machining of CFRP with High Helix end Mill. CIRP Ann. 2014, 63, 89–92. [Google Scholar] [CrossRef]
- Karpat, Y.; Polat, N. Mechanistic Force Modeling for Milling of Carbon Fiber Reinforced Polymers with Double Helix Tools. CIRP Ann. 2013, 62, 95–98. [Google Scholar] [CrossRef] [Green Version]
- Yuanyushkin, A.S.; Rychkov, D.A.; Lobanov, D.V. Surface Quality of the Fiberglass Composite Material after Milling. AMM 2014, 682, 183–187. [Google Scholar] [CrossRef]
- Teicher, U.; Rosenbaum, T.; Nestler, A.; Brosius, A. Characterization of the Surface Roughness of Milled Carbon Fiber Reinforced Plastic Structures. Procedia CIRP 2017, 66, 199–203. [Google Scholar] [CrossRef]
- Azmi, A.I.; Lin, R.J.T.; Bhattacharyya, D. Experimental Study of Machinability of GFRP Composites by end Milling. Mater. Manuf. Process. 2012, 27, 1045–1050. [Google Scholar] [CrossRef]
- Razfar, M.R.; Zadeh, M.R.Z. Optimum Damage and Surface Roughness Prediction in end Milling Glass Fibre-Reinforced Plastics, Using Neural Network and Genetic Algorithm. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2009, 223, 653–664. [Google Scholar] [CrossRef]
- Jenarthanan, M.P.; Karthikeyan, M.; Kumar, K.P. Experimental Investigation of Surface Roughness and Delamination Using Artificial Intelligence. Antofagasta, Chile. 2023, p. 020014. Available online: https://pubs.aip.org/aip/acp/article-abstract/2715/1/020014/2890547/Experimental-investigation-of-surface-roughness?redirectedFrom=fulltext (accessed on 4 June 2023).
- Davim, J.P.; Reis, P. Damage and Dimensional Precision on Milling Carbon Fiber-Reinforced Plastics Using Design Experiments. J. Mater. Process. Technol. 2005, 160, 160–167. [Google Scholar] [CrossRef]
- Kiliçkap, E.; Yardimeden, A.; Çelik, Y.H. Investigation of Experimental Study of End Milling of CFRP Composite. Sci. Eng. Compos. Mater. 2015, 22, 89–95. [Google Scholar] [CrossRef]
- Rusinek, R. Cutting Process of Composite Materials: An Experimental Study. Int. J. Non-Linear Mech. 2010, 45, 458–462. [Google Scholar] [CrossRef]
- Bayraktar, S.; Turgut, Y. Investigation of the Cutting Forces and Surface Roughness in Milling Carbon-Fiber-Reinforced Polymer Composite Material. Mater. Tehnol. 2016, 50, 591–600. [Google Scholar] [CrossRef]
- Chibane, H.; Serra, R.; Leroy, R. Optimal Milling Conditions of Aeronautical Composite Material under Temperature, Forces and Vibration Parameters. J. Compos. Mater. 2017, 51, 3453–3463. [Google Scholar] [CrossRef]
- Wei, Y.; An, Q.; Cai, X.; Chen, M.; Ming, W. Influence of Fiber Orientation on Single-Point Cutting Fracture Behavior of Carbon-Fiber/Epoxy Prepreg Sheets. Materials 2015, 8, 6738–6751. [Google Scholar] [CrossRef] [Green Version]
- Nurhaniza, M.; Ariffin, M.K.A.M.; Mustapha, F.; Baharudin, B.T.H.T. Analyzing the Effect of Machining Parameters Setting to the Surface Roughness during end Milling of CFRP-Aluminium Composite Laminates. Int. J. Manuf. Eng. 2016, 2016, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Saglam, H.; Unsacar, F.; Yaldiz, S. Investigation of the Effect of Rake Angle and Approaching Angle on Main Cutting Force and Tool Tip Temperature. Int. J. Mach. Tools Manuf. 2006, 46, 132–141. [Google Scholar] [CrossRef]
- Palanikumar, K.; Karunamoorthy, L.; Karthikeyan, R. Assessment of Factors Influencing Surface Roughness on the Machining of Glass Fiber-Reinforced Polymer Composites. Mater. Des. 2006, 27, 862–871. [Google Scholar] [CrossRef]
- Kurpiel, S.; Zagórski, K.; Cieślik, J.; Skrzypkowski, K. Investigation of Selected Surface Topography Parameters and Deformation during Milling of Vertical Thin-Walled Structures from Titanium Alloy Ti6Al4V. Materials 2023, 16, 3182. [Google Scholar] [CrossRef] [PubMed]
- Ciecieląg, K.; Zaleski, K. Milling of Three Types of Thin-Walled Elements Made of Polymer Composite and Titanium and Aluminum Alloys Used in the Aviation Industry. Materials 2022, 15, 5949. [Google Scholar] [CrossRef]
- Rai, J.K.; Xirouchakis, P. Finite Element Method Based Machining Simulation Environment for Analyzing Part Errors Induced during Milling of Thin-Walled Components. Int. J. Mach. Tools Manuf. 2008, 48, 629–643. [Google Scholar] [CrossRef]
- Rozylo, P.; Debski, H.; Wysmulski, P.; Falkowicz, K. Numerical and Experimental Failure Analysis of Thin-Walled Composite Columns with a Top-Hat Cross Section under Axial Compression. Compos. Struct. 2018, 204, 207–216. [Google Scholar] [CrossRef]
- Rozylo, P.; Falkowicz, K. Stability and Failure Analysis of Compressed Thin-Walled Composite Structures with Central Cut-out, Using Three Advanced Independent Damage Models. Compos. Struct. 2021, 273, 114298. [Google Scholar] [CrossRef]
- Ramanaiah, B.V.; Manikanta, B.; Ravi Sankar, M.; Malhotra, M.; Gajrani, K. Experimental Study of Deflection and Surface Roughness in Thin Wall Machining of Aluminum Alloy. Mater. Today Proc. 2018, 5, 3745–3754. [Google Scholar] [CrossRef]
- Borojevic, S.; Lukic, D.; Milosevic, M.; Vukman, J.; Kramar, D. Optimization of Process Parameters for Machining of Al 7075 Thin-Walled Structures. Adv Prod. Eng. Manag. 2018, 13, 125–135. [Google Scholar] [CrossRef]
- Bałon, P.; Rejman, E.; Świątoniowski, A.; Kiełbasa, B.; Smusz, R.; Szostak, J.; Cieślik, J.; Kowalski, Ł. Thin-Walled Integral Constructions in Aircraft Industry. Procedia Manuf. 2020, 47, 498–504. [Google Scholar] [CrossRef]
- Zawada-Michałowska, M.; Pieśko, P. Post-Machining Deformations of Thin-Walled Elements Made of EN AW-2024 T351 Aluminum Alloy as Regards the Mechanical Properties of the Applied, Rolled Semi-Finished Products. Materials 2021, 14, 7591. [Google Scholar] [CrossRef]
- Singh, A.; Agrawal, A. Investigation of Surface Residual Stress Distribution in Deformation Machining Process for Aluminum Alloy. J. Mater. Process. Technol. 2015, 225, 195–202. [Google Scholar] [CrossRef]
- Masoudi, S.; Amini, S.; Saeidi, E.; Eslami-Chalander, H. Effect of Machining-Induced Residual Stress on the Distortion of Thin-Walled Parts. Int J Adv Manuf Technol 2015, 76, 597–608. [Google Scholar] [CrossRef]
- Wiertel, M.; Zaleski, K.; Gorgol, M.; Skoczylas, A.; Zaleski, R. Impact of Impulse Shot Peening Parameters on Properties of Stainless Steel Surface. Acta Phys. Pol. A 2017, 132, 1611–1616. [Google Scholar] [CrossRef]
- Skoczylas, A.; Zaleski, K.; Zaleski, R.; Gorgol, M. Analysis of Surface Properties of Nickel Alloy Elements Exposed to Impulse Shot Peening with the Use of Positron Annihilation. Materials 2021, 14, 7328. [Google Scholar] [CrossRef] [PubMed]
- Eckmann, J.-P.; Kamphorst, S.O.; Ruelle, D. Recurrence Plots of Dynamical Systems. Europhys. Lett. 1987, 4, 973–977. [Google Scholar] [CrossRef] [Green Version]
- Fraser, A.M.; Swinney, H.L. Independent Coordinates for Strange Attractors from Mutual Information. Phys. Rev. A 1986, 33, 1134–1140. [Google Scholar] [CrossRef]
- Marwan, N.; Carmenromano, M.; Thiel, M.; Kurths, J. Recurrence Plots for the Analysis of Complex Systems. Phys. Rep. 2007, 438, 237–329. [Google Scholar] [CrossRef]
- Webber, C.L.; Zbilut, J.P. Dynamical Assessment of Physiological Systems and States Using Recurrence Plot Strategies. J. Appl. Physiol. 1994, 76, 965–973. [Google Scholar] [CrossRef]
- Zbilut, J.P.; Webber, C.L. Embeddings and Delays as Derived from Quantification of Recurrence Plots. Phys. Lett. A 1992, 171, 199–203. [Google Scholar] [CrossRef]
- Almeida-Ñauñay, A.F.; Benito, R.M.; Quemada, M.; Losada, J.C.; Tarquis, A.M. Recurrence Plots for Quantifying the Vegetation Indices Dynamics in a Semi-Arid Grassland. Geoderma 2022, 406, 115488. [Google Scholar] [CrossRef]
- Kecik, K.; Ciecielag, K.; Zaleski, K. Damage Detection by Recurrence and Entropy Methods on the Basis of Time Series Measured during Composite Milling. Int. J. Adv. Manuf. Technol. 2020, 111, 549–563. [Google Scholar] [CrossRef]
- Schinkel, S.; Dimigen, O.; Marwan, N. Selection of Recurrence Threshold for Signal Detection. Eur. Phys. J. Spec. Top. 2008, 164, 45–53. [Google Scholar] [CrossRef]
- Gao, J.; Cai, H. On the Structures and Quantification of Recurrence Plots. Phys. Lett. A 2000, 270, 75–87. [Google Scholar] [CrossRef]
- Marwan, N.; Wessel, N.; Meyerfeldt, U.; Schirdewan, A.; Kurths, J. Recurrence-Plot-Based Measures of Complexity and Their Application to Heart-Rate-Variability Data. Phys. Rev. E 2002, 66, 026702. [Google Scholar] [CrossRef] [Green Version]
- Thomasson, N.; Hoeppner, T.J.; Webber, C.L.; Zbilut, J.P. Recurrence Quantification in Epileptic EEGs. Phys. Lett. A 2001, 279, 94–101. [Google Scholar] [CrossRef]
- Iwaniec, J.; Iwaniec, M. Application of Recurrence-Based Methods to Heart Work Analysis. In Advances in Technical Diagnostics; Timofiejczuk, A., Łazarz, B.E., Chaari, F., Burdzik, R., Eds.; Springer International Publishing: Cham, Switzerland, 2018; Volume 10, pp. 343–352. ISBN 978-3-319-62041-1. [Google Scholar]
- Iwaniec, J.; Kurowski, P. Experimental Verification of Selected Methods Sensitivity to Damage Size and Location. J. Vib. Control 2017, 23, 1133–1151. [Google Scholar] [CrossRef]
- Iwaniec, J.; Uhl, T.; Staszewski, W.J.; Klepka, A. Detection of Changes in Cracked Aluminium Plate Determinism by Recurrence Analysis. Nonlinear Dyn 2012, 70, 125–140. [Google Scholar] [CrossRef]
- Litak, G.; Sawicki, J.T.; Kasperek, R. Cracked Rotor Detection by Recurrence Plots. Nondestruct. Test. Eval. 2009, 24, 347–351. [Google Scholar] [CrossRef] [Green Version]
- Ilie, C.O.; Alexa, O.; Lespezeanu, I.; Marinescu, M.; Grosu, D. Recurrence Plot Analysis to Study Parameters of a Gasoline Engine. Appl. Mech. Mater. 2016, 823, 323–328. [Google Scholar] [CrossRef]
- Mhalsekar, S.D.; Rao, S.S.; Gangadharan, K.V. Investigation on Feasibility of Recurrence Quantification Analysis for Detecting Flank Wear in Face Milling. Int. J. Eng. Sci. Tech 2010, 2, 23–38. [Google Scholar] [CrossRef]
- Kecik, K.; Ciecielag, K.; Zaleski, K. Damage Detection of Composite Milling Process by Recurrence Plots and Quantifications Analysis. Int J Adv Manuf Technol 2017, 89, 133–144. [Google Scholar] [CrossRef] [Green Version]
- Ciecieląg, K.; Kecik, K.; Zaleski, K. Defects Detection from Time Series of Cutting Force in Composite Milling Process by Recurrence Analysis. J. Reinf. Plast. Compos. 2020, 39, 890–901. [Google Scholar] [CrossRef]
- Ciecieląg, K.; Skoczylas, A.; Matuszak, J.; Zaleski, K.; Kęcik, K. Defect Detection and Localization in Polymer Composites Based on Drilling Force Signal by Recurrence Analysis. Measurement 2021, 186, 110126. [Google Scholar] [CrossRef]
- Rusinek, R.; Zaleski, K. Dynamics of Thin-Walled Element Milling Expressed by Recurrence Analysis. Meccanica 2016, 51, 1275–1286. [Google Scholar] [CrossRef] [Green Version]


| No. | Feed per Revolution [mm/rev] | Cutting Speed vc [m/min] | Depth of Cut ap [mm] |
|---|---|---|---|
| 1 | 0.1 | 100 | 2 |
| 2 | 0.2 | 100 | 2 |
| 3 | 0.4 | 100 | 2 |
| 4 | 0.8 | 100 | 2 |
| 5 | 0.2 | 50 | 2 |
| 6 | 0.2 | 100 | 2 |
| 7 | 0.2 | 200 | 2 |
| 8 | 0.2 | 400 | 2 |
| Description | XOEX060204FR PCD05 | XOEX060204FR-E03 F40M | XOEX060204FR-E03 H15 |
|---|---|---|---|
| Gradetype | PCD | Carbide PVD | Carbide Uncoated |
| Clearance angle major | 15° | 15° | 15° |
| Corner radius | 0.4 mm | 0.4 mm | 0.4 mm |
| Cutting edge effective length | 2.5 mm | 6.0 mm | 6.0 mm |
| Wiper edge length | 1.1 mm | 0.9 mm | 0.9 mm |
| Insert thickness | 2.45 mm | 2.45 mm | 2.45 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ciecieląg, K. Machinability Measurements in Milling and Recurrence Analysis of Thin-Walled Elements Made of Polymer Composites. Materials 2023, 16, 4825. https://doi.org/10.3390/ma16134825
Ciecieląg K. Machinability Measurements in Milling and Recurrence Analysis of Thin-Walled Elements Made of Polymer Composites. Materials. 2023; 16(13):4825. https://doi.org/10.3390/ma16134825
Chicago/Turabian StyleCiecieląg, Krzysztof. 2023. "Machinability Measurements in Milling and Recurrence Analysis of Thin-Walled Elements Made of Polymer Composites" Materials 16, no. 13: 4825. https://doi.org/10.3390/ma16134825
APA StyleCiecieląg, K. (2023). Machinability Measurements in Milling and Recurrence Analysis of Thin-Walled Elements Made of Polymer Composites. Materials, 16(13), 4825. https://doi.org/10.3390/ma16134825






