Constitutive Model for Grouted Rock Mass by Macro-Meso Damage
Abstract
1. Introduction
2. Establishment of a Constitutive Model for Grouted Rock Mass
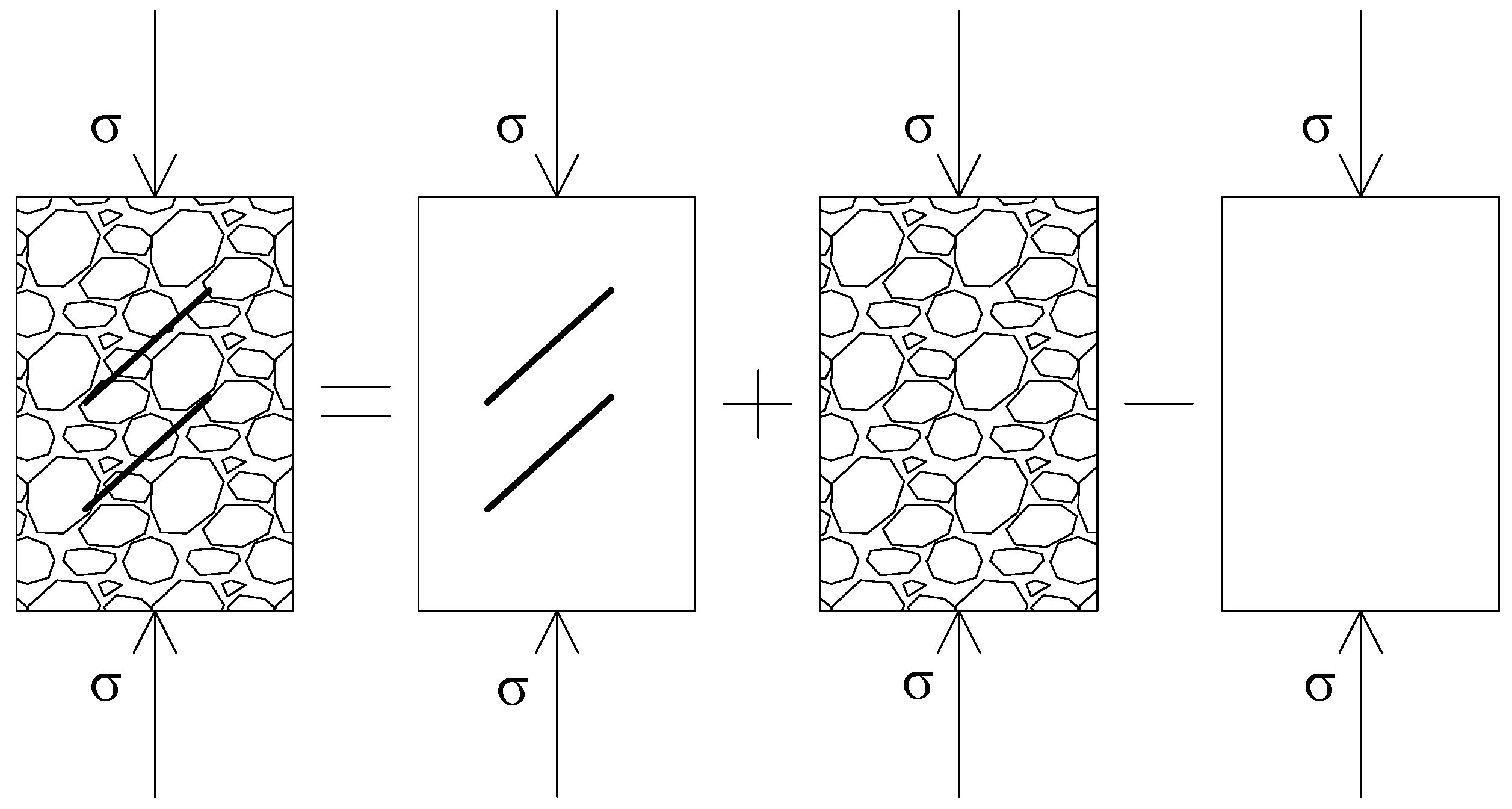
2.1. Damage Mechanism of the Fractured Rock Mass
- (1)
- The undamaged part of the rock mass during the test is always a linear elastic material.
- (2)
- Macroscopic fractures can be directly observed by using the naked eye, which can be the main feature used to distinguish macroscopic fractures and microscopic fractures. In addition, based on the distribution characteristics of macroscopic and microscopic fractures, macroscopic fractures are equated to anisotropic damage, while microscopic fractures are equated to isotropic damage in the study.
- (3)
- The microscopic damage and macroscopic damage are described by different methods, respectively. The microscopic damage can be defined as the damage caused by loading. The macroscopic damage is defined as the initial damage caused by the precast fractures to the rock, and the initial macroscopic damage does not change during the loading process.
2.2. Damage Constitutive Model of Grouted Rock Mass
2.2.1. Microscopic Damage Model of the Fractured Rock Mass
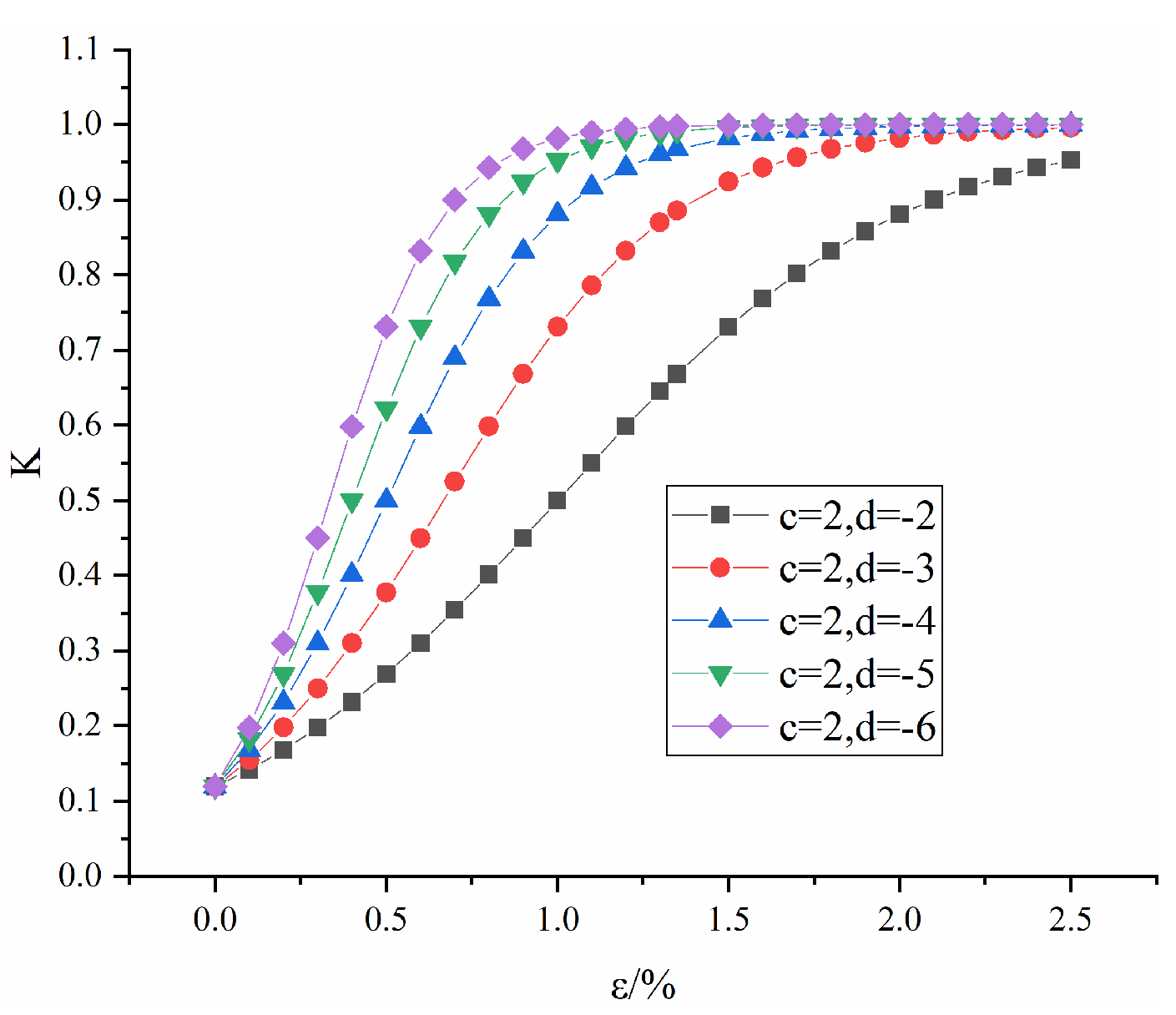
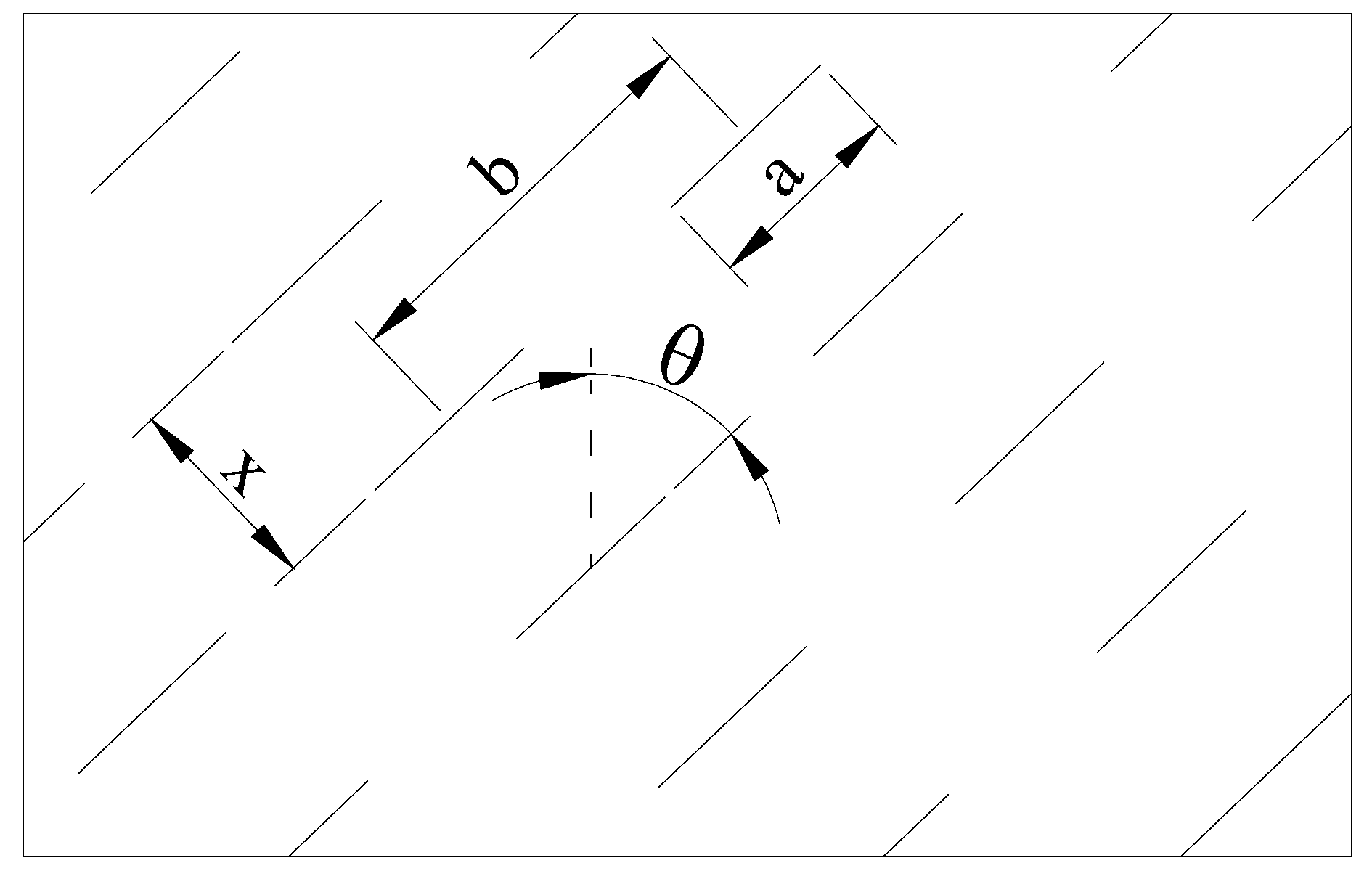
2.2.2. Macroscopic Damage Model of a Fractured Rock Mass
2.2.3. Effect of Grouting Reinforcement
3. Experiment and Model Validation
3.1. Test Equipment and Sample Preparation
- (1)
- A cubic specimen of intact red sandstone with a standard size, i.e., width × height of 50 mm × 100 mm, was produced. The cubic specimens were provided by Roke New Material Technology Co., Ltd., Chongqing, China, which independently developed automatic rock sample coring equipment and cooperates with many universities and scientific research institutions.
- (2)
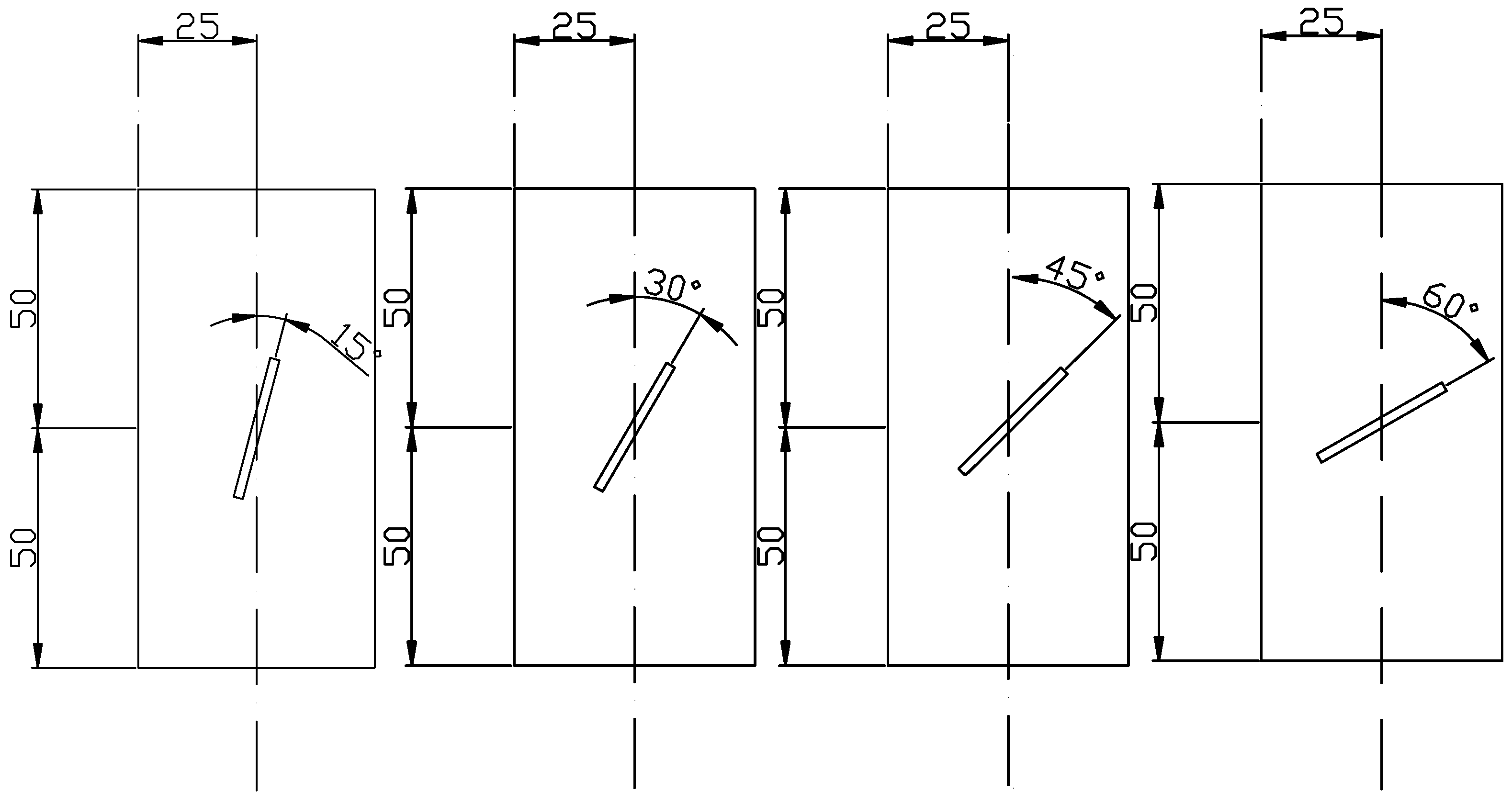
- The test specimens were divided into intact specimens and prefabricated fracture specimens. Non-through fractures were cut in the complete specimens by using a waterjet at fracture angles of 15°, 30°, 45° and 60°; a width of 2 mm; and a length of 30 mm, as shown in Figure 8.
- (3)
- PO42.5 concrete was used as the grouting material, which was purchased from China Zhucheng Yangchun Cement Co., Ltd., Weifang, China, whose products passed the ISO9001 quality management system certification. The concrete was injected into the precast fractures and allowed to stand for 48 h, and then the specimens were subjected to standard curing for 28 d before being removed for use. The experimental test was repeated 3 times for each kind of sample, and the average value was calculated as the test result.
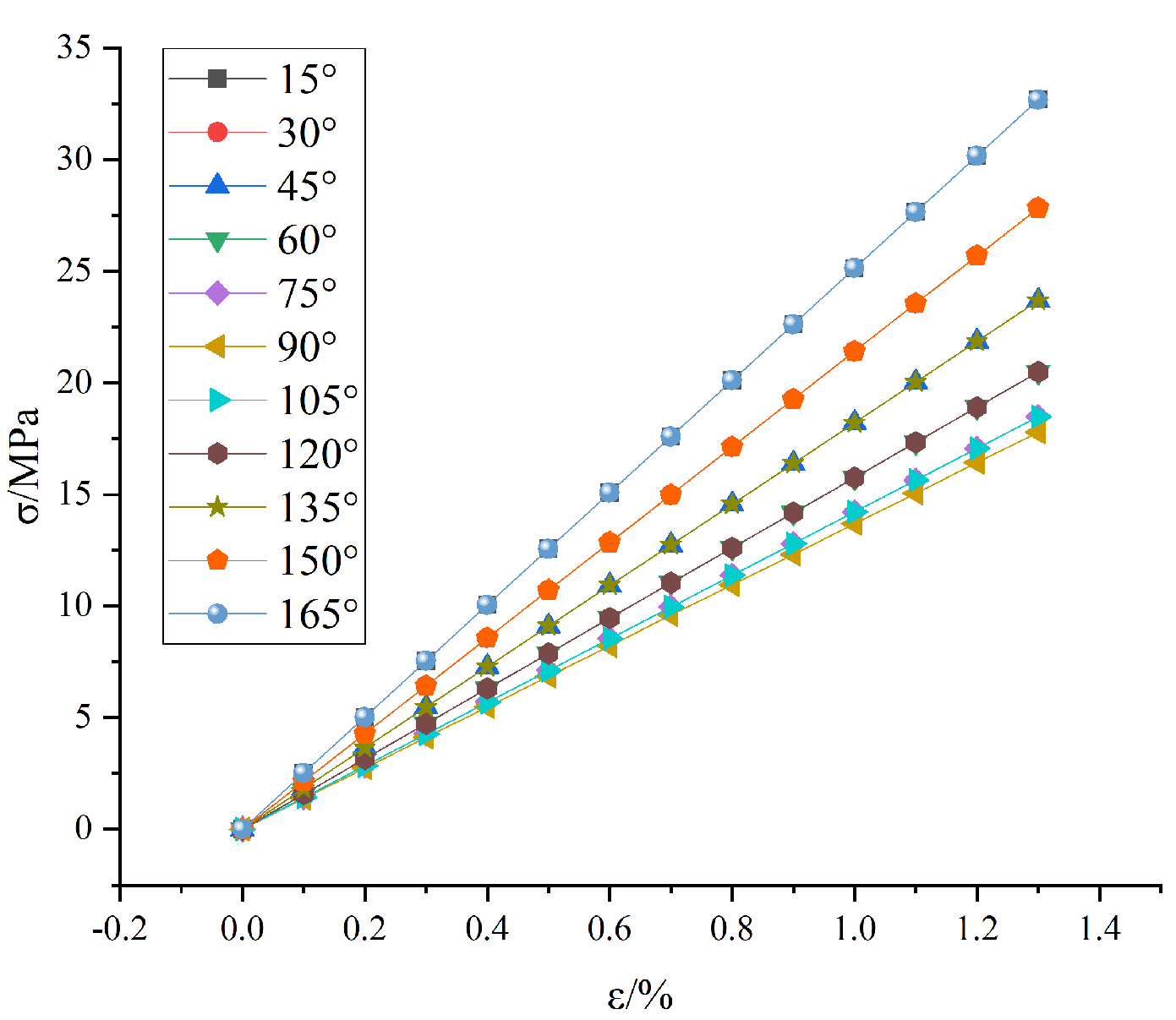
3.2. Test Results
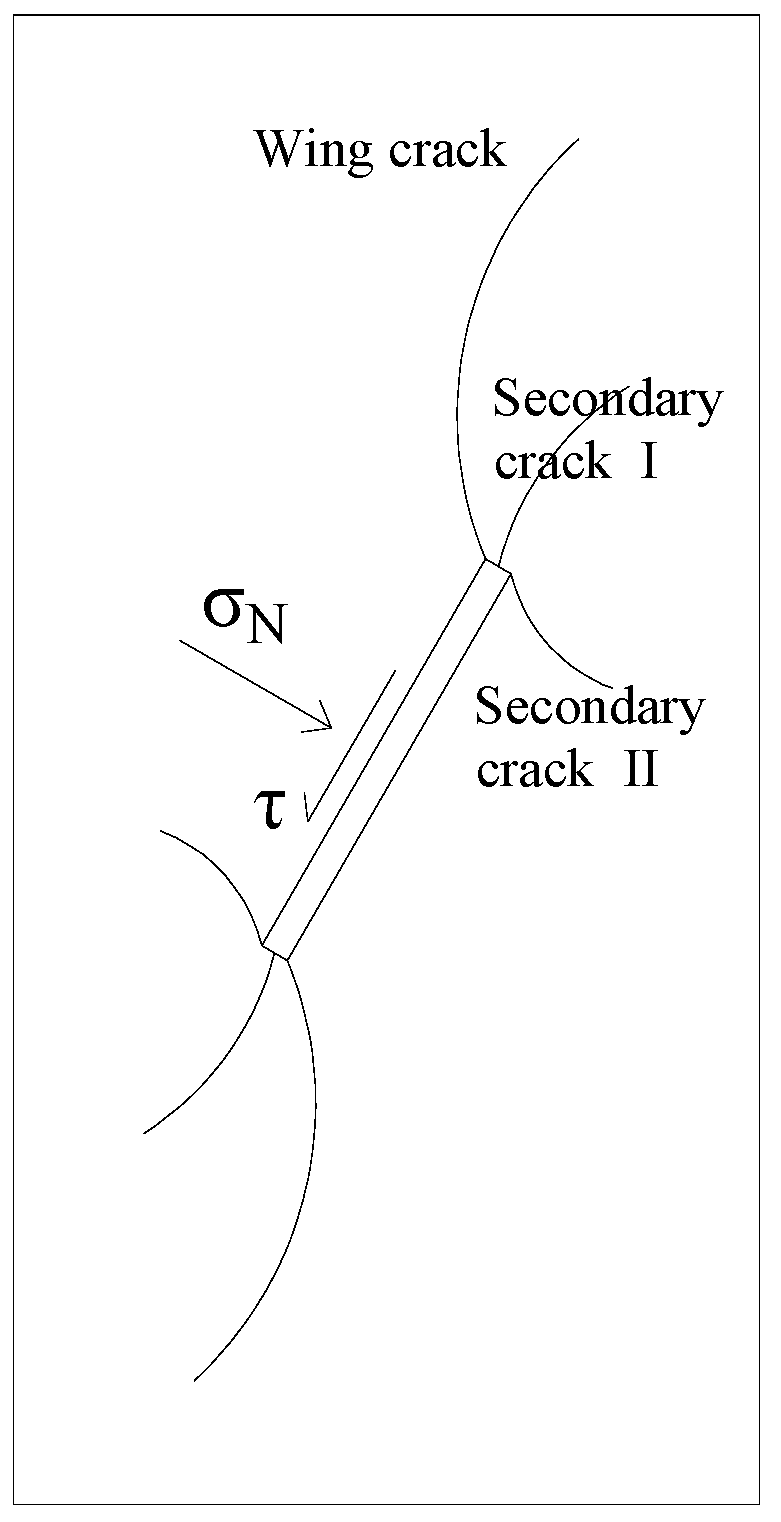
3.2.1. Rock Mass Crack Propagation
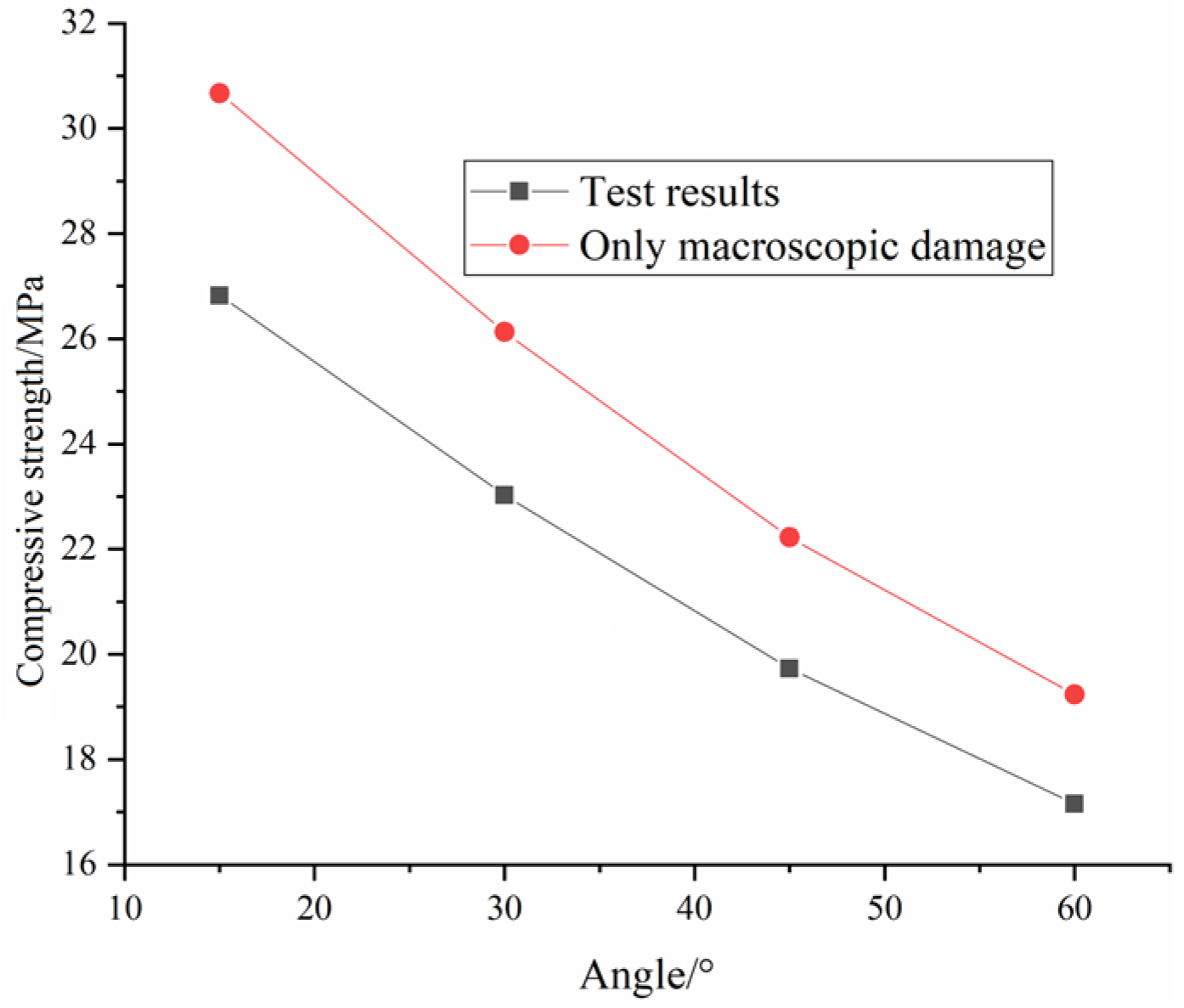
3.2.2. Test Results Analysis
3.3. Validation of the Constitutive Model
3.4. Validation of the Constitutive Model
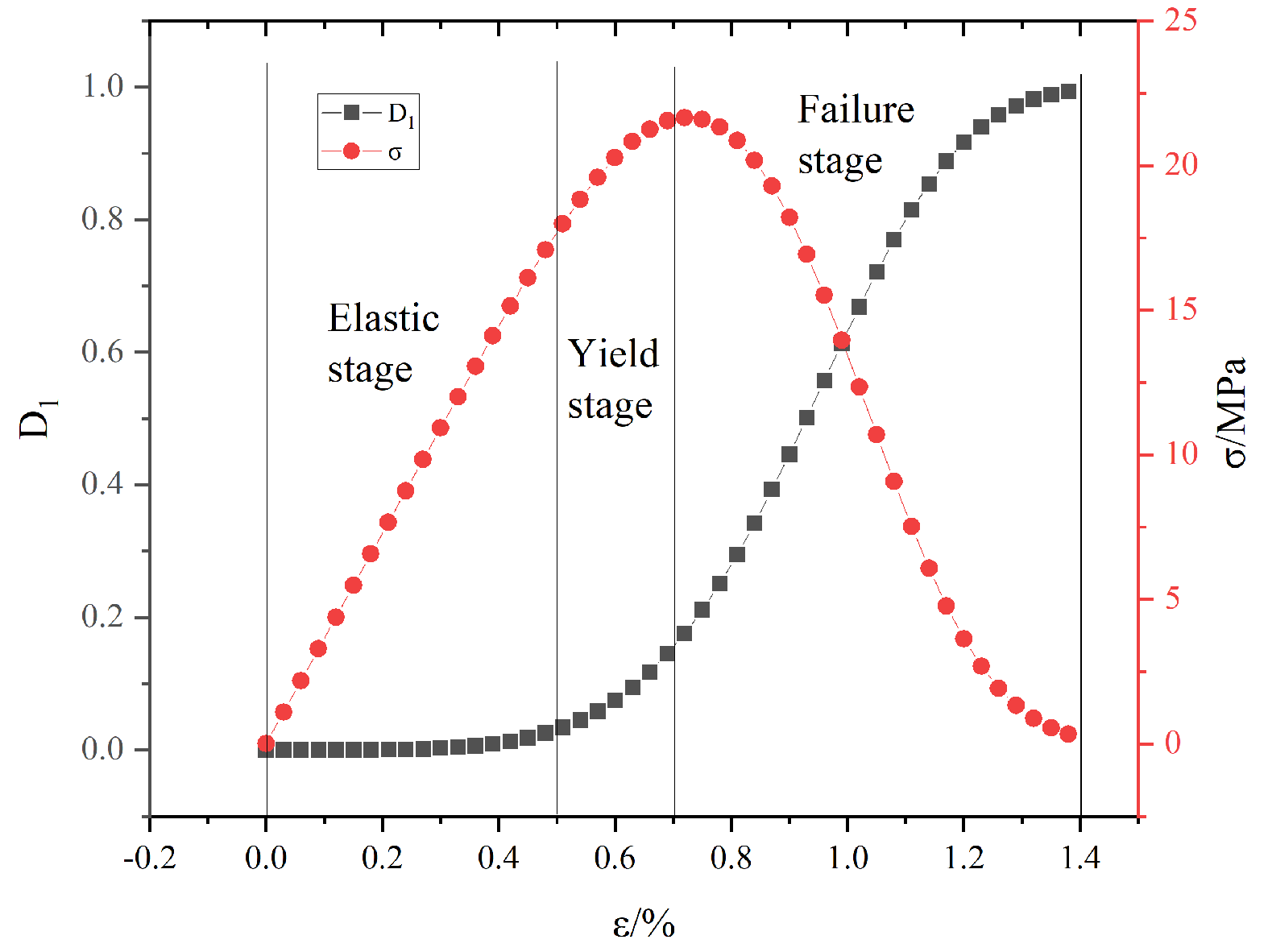
3.4.1. Evolution of Microscopic Damage
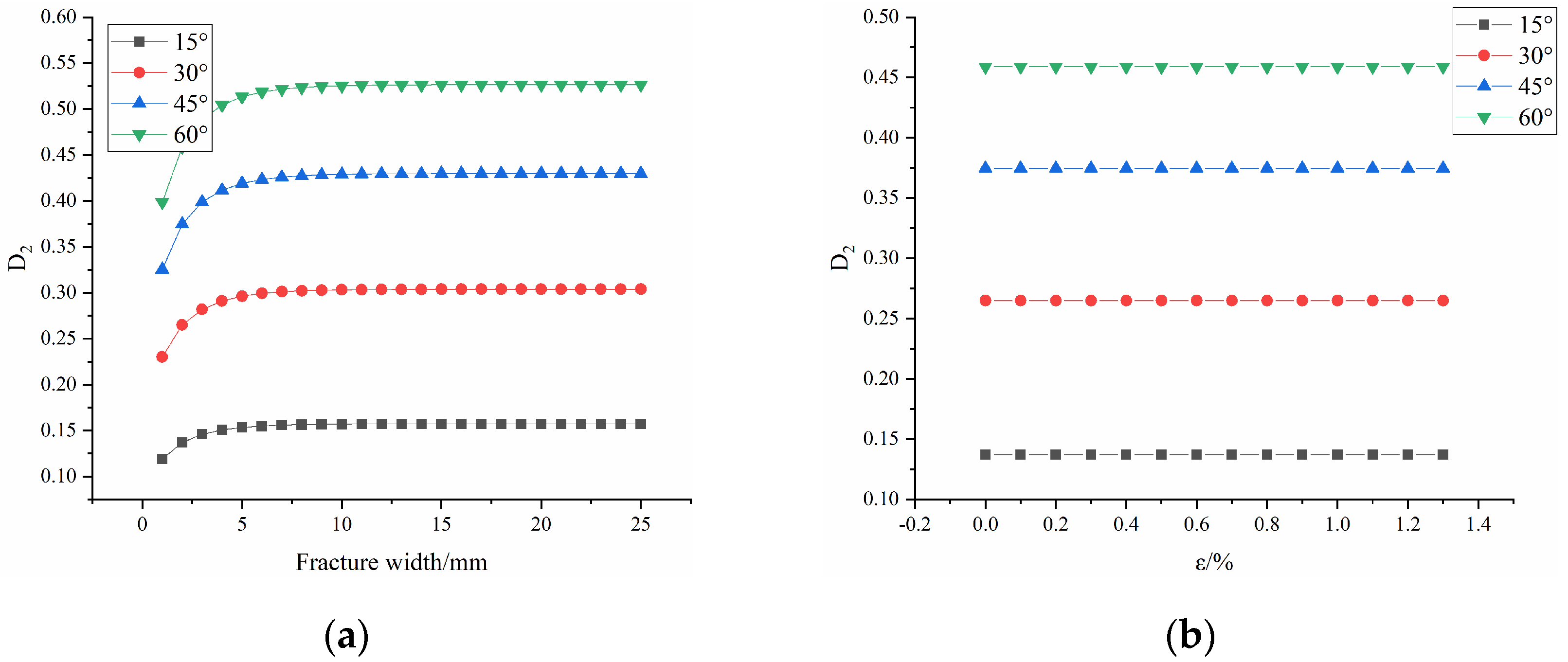
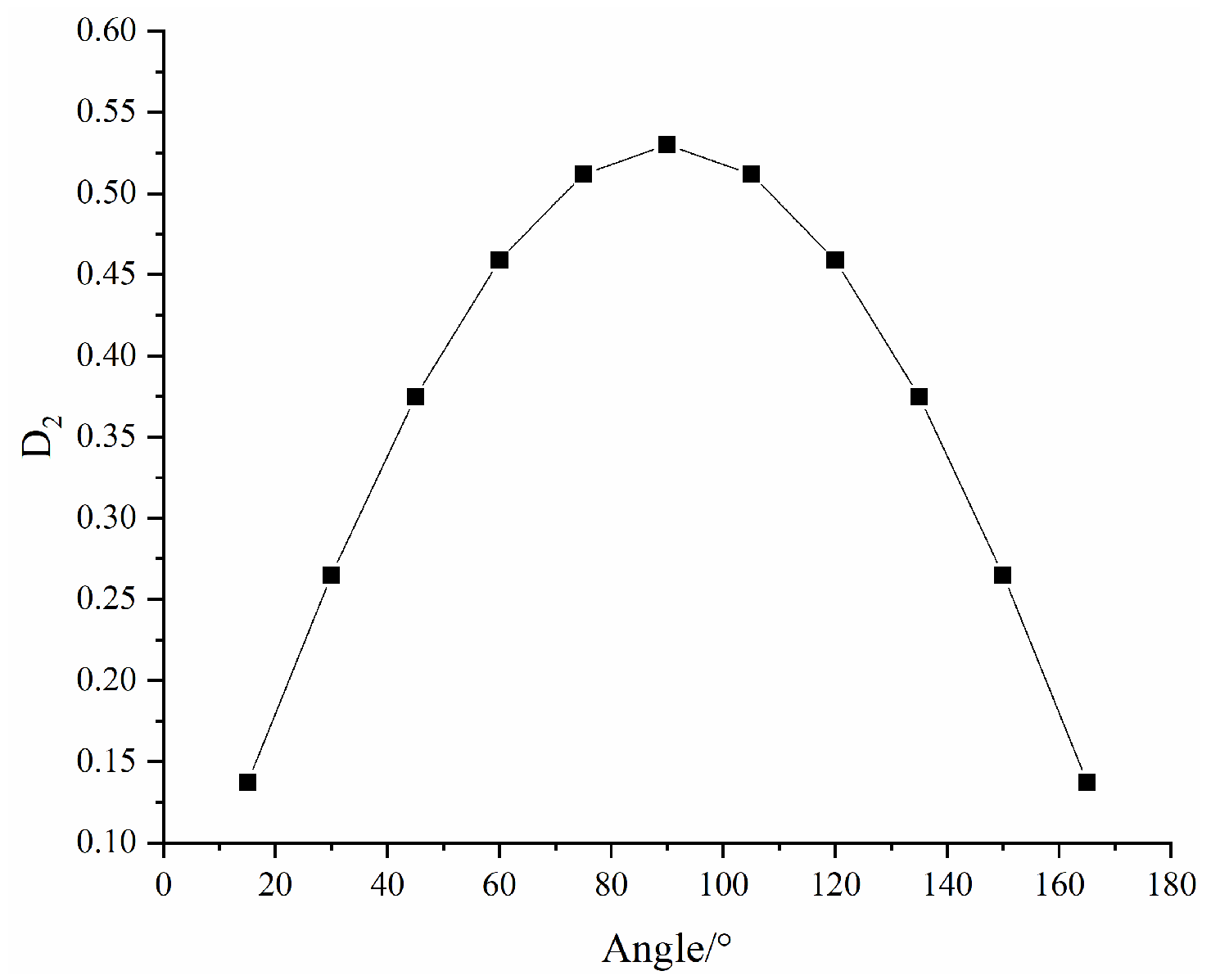
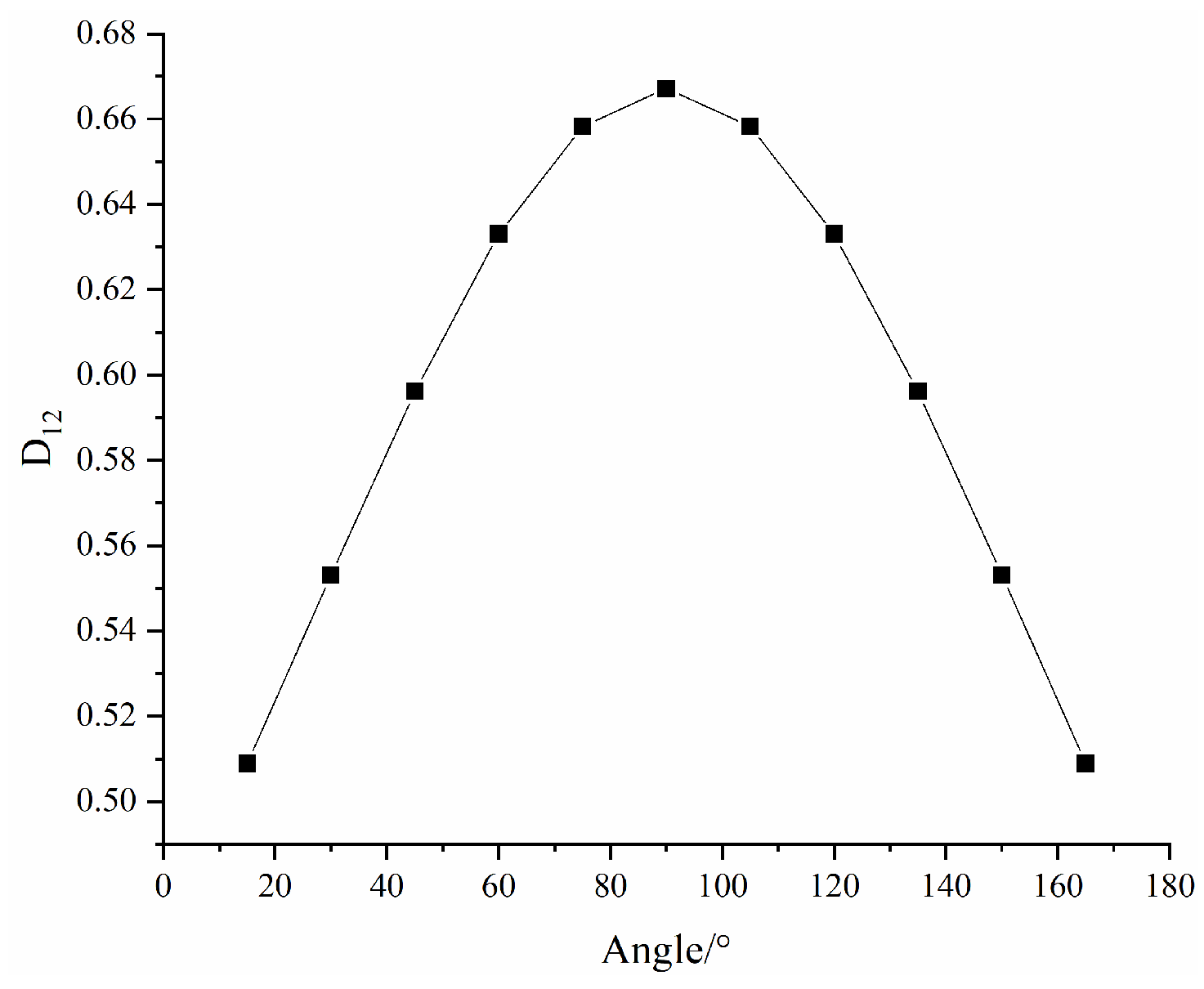
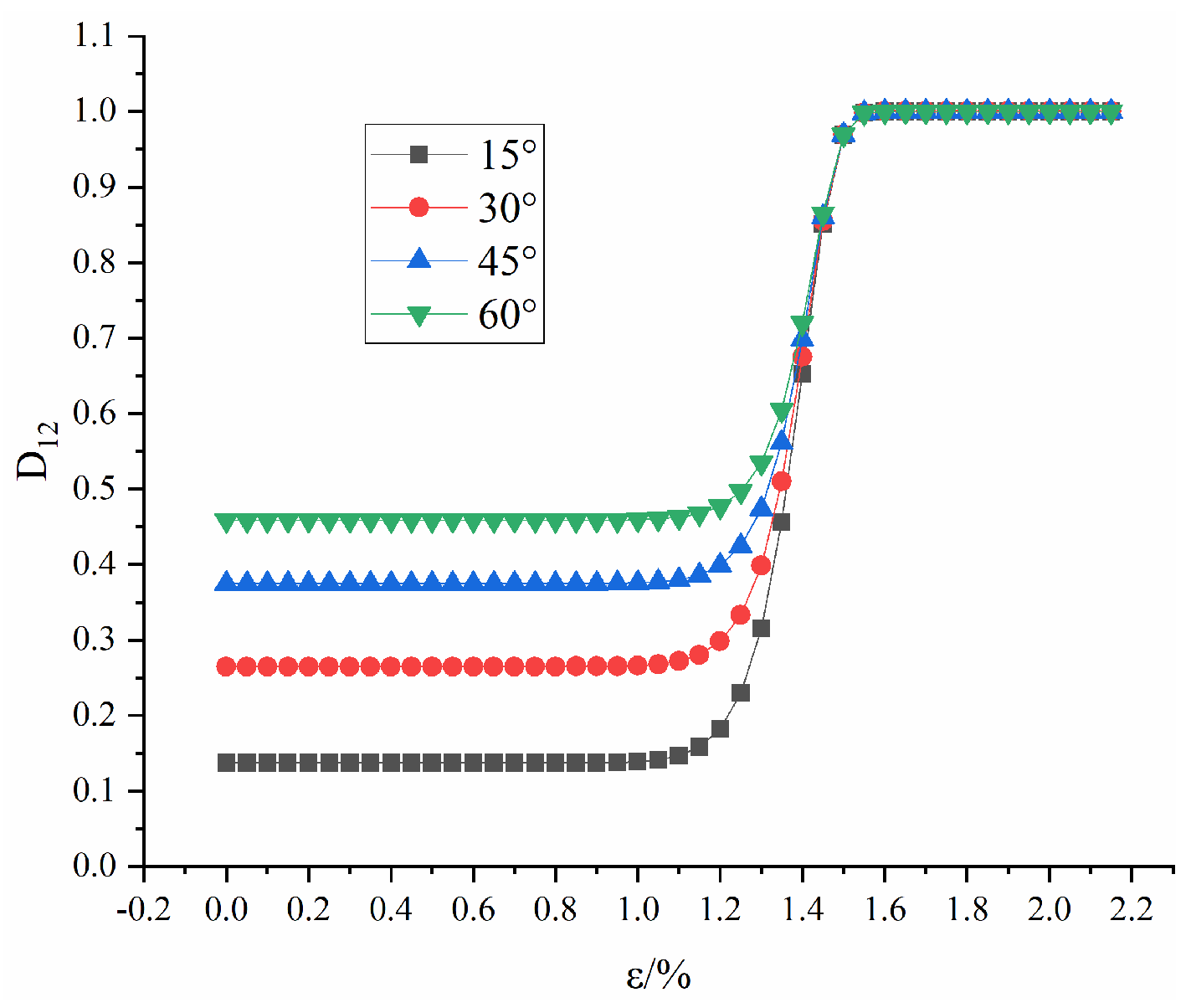
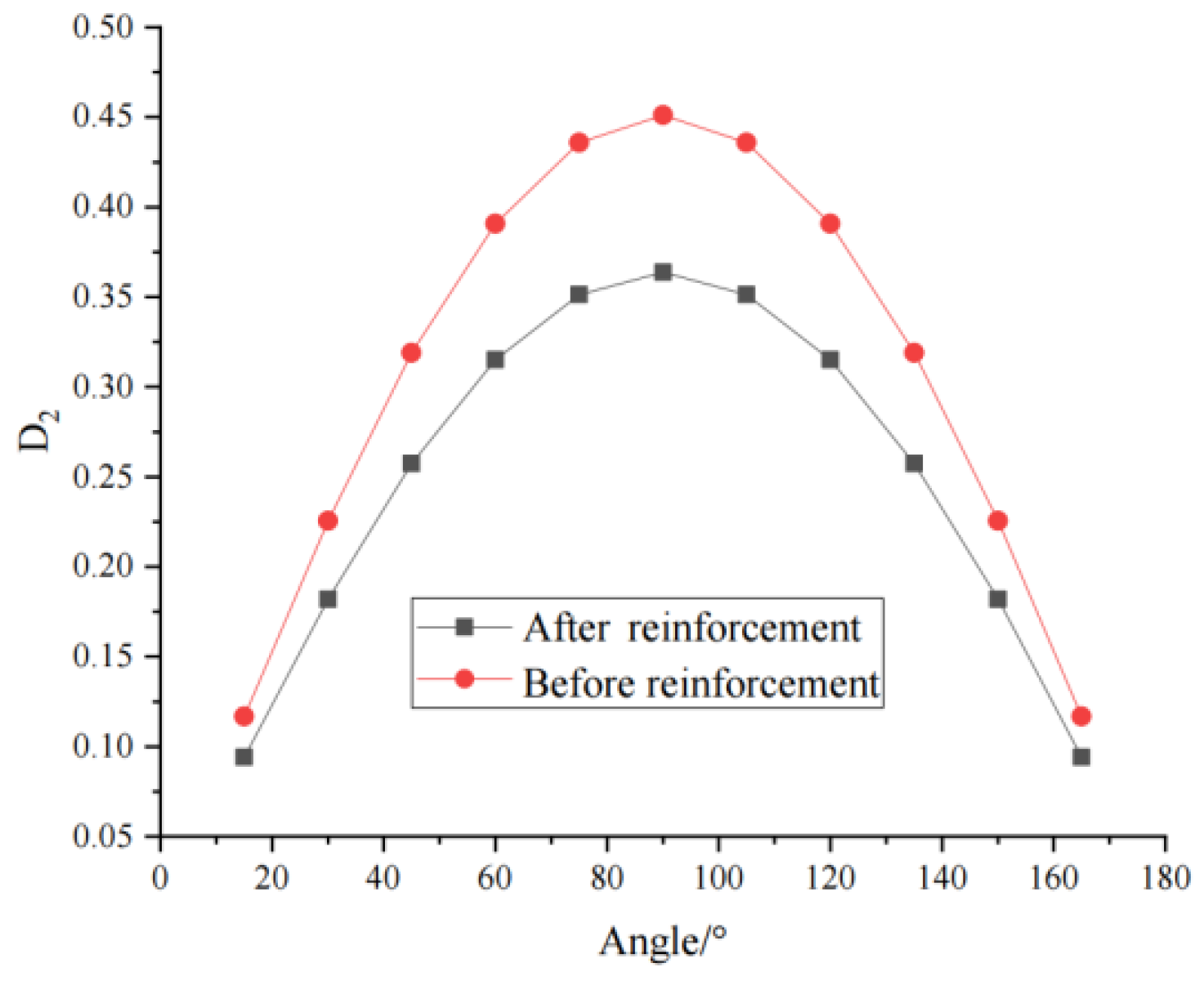
3.4.2. Evolution of Macroscopic Damage
3.4.3. Evolution of Coupled Damage
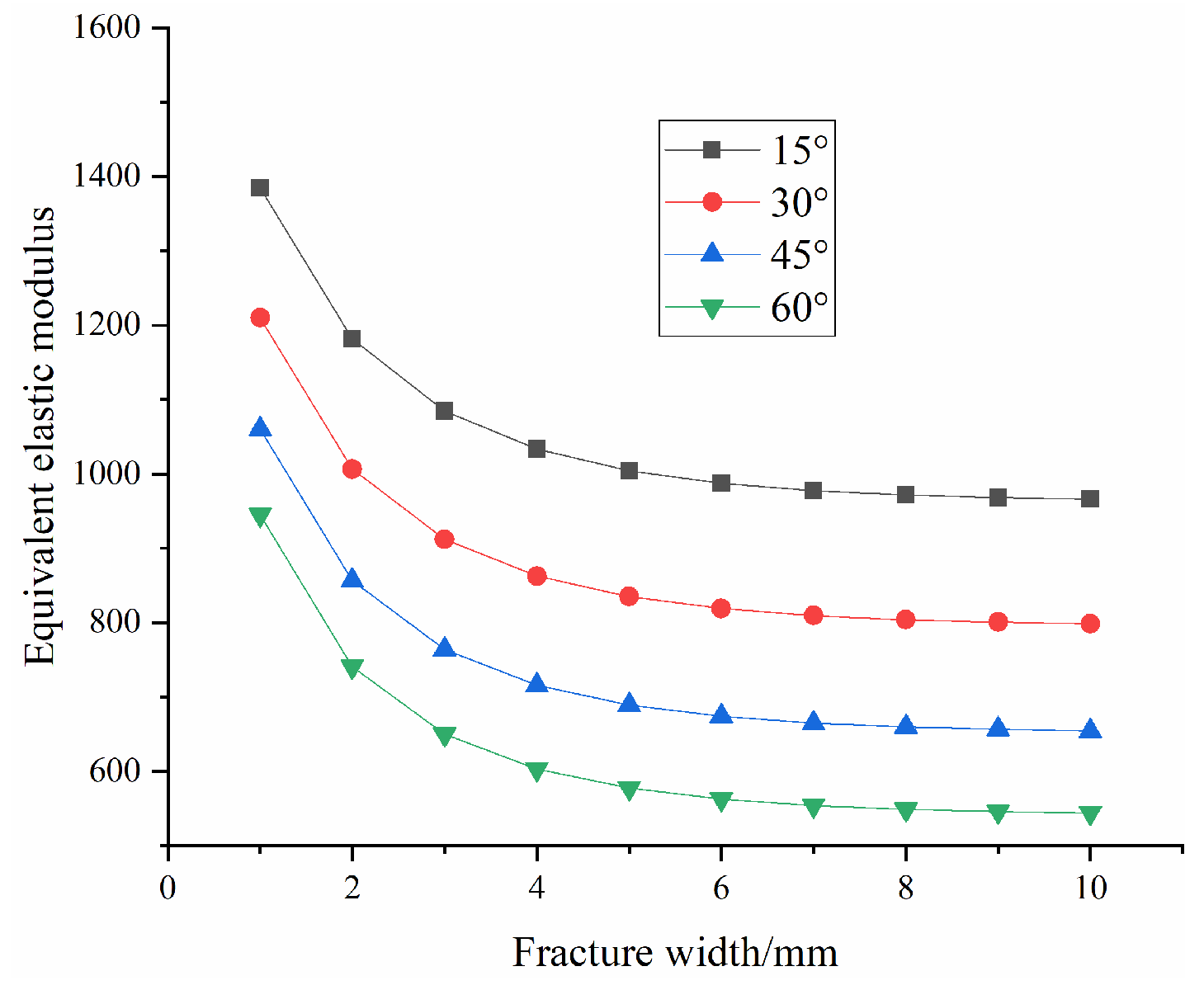
3.4.4. Evolution of the Grouting Reinforcement Effect
4. Conclusions
- (1)
- Based on the fact that the rock mass contains both macroscopic and microscopic damage, the original coupled damage model was improved by introducing fracture width, effective bearing area and Weibull model and by combining damage mechanics and fracture mechanics. The grouted rock mass was considered to be a composite material. The damage constitutive model of the grouting rock mass was derived by combining the elastic modulus mixing law of the composite material and the macroscopic damage tensor model. The new coupled damage model was proven to be reasonable in reflecting the deformation and strength of the grouted rock mass by experiment.
- (2)
- The macroscopic damage tensor model contains the main geometric characteristic parameters of the fracture and mechanical parameters, which can be used to comprehensively describe the macroscopic damage of the fractured rock mass. On this basis, the parameter of fracture width is introduced to describe the evolution law of macroscopic damage with fracture width, thereby improving the accuracy and applicability of the damage constitutive model for fractured rock masses.
- (3)
- The Weibull model can effectively describe the elastic stage and yield stage of the rock-deformation process. However, due to the limitations of the Weibull model itself, it is unable to accurately describe the compaction stage of the rock mass. Through the analysis of the uniaxial compression test results, the effective bearing area was introduced to optimize the Weibull model. The optimized Weibull model can accurately describe the law that holds that pores decrease and then increase with strain, which is consistent with the process of transition from the compression stage to the elastic stage, yield stage, and damage stage during the compression process of the rock mass, which is closer to reality.
- (4)
- The grouted rock mass is a standard composite material, which conforms to the “mixing law” of the elastic modulus. The original mixing model was improved by combining macroscopic damage tensor theory with the Reuss model, and the equivalent elastic modulus of the grouted rock mass was derived.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Babanouri, N.; Fattahi, H. Constitutive modeling of rock fractures by improved support vector regression. Environ. Earth Sci. 2018, 77, 243. [Google Scholar] [CrossRef]
- Chen, W.L.; Li, N. Damage model of the rock mass medium with intermittent cracks. Chin. J. Geotech. Eng. 2000, 22, 430–434. [Google Scholar]
- Chen, X.; Liao, Z.H.; Li, D.J. Experimental study of effects of joint inclination angle and connectivity rate on strength and deformation properties of rock masses under uniaxial compression. Chin. J. Rock Mech. Eng. 2011, 30, 781–789. [Google Scholar]
- Chen, Y.; Lin, H.; Xie, S.; Cao, R.; Sun, S.; Zha, W.; Hu, H. Fracture Closure Empirical Model and Theoretical Damage Model of Rock under Compression. Materials 2023, 16, 589. [Google Scholar] [CrossRef] [PubMed]
- Gour, S.; Kumar, D.; Yadav, V. Constitutive modeling for the tear fracture of rubber with filler particles. Sādhanā 2022, 47, 82. [Google Scholar] [CrossRef]
- Jaeger, J.; Cook, N. Fundamentals of Rock Mechanics; Chapman and Hall Ltd.: London, UK, 1969; pp. 100–105. [Google Scholar]
- Kawamoto, T.; Ichikawa, Y.; Kyoya, T. Deformation and fracturing behavior of discontinuous rock mass and damage mechanics theory. Int. J. Numer. Anal. Method Geomech. 1988, 12, 1–30. [Google Scholar] [CrossRef]
- Le, Q.; Barton, N. On the selection of joint constitutive models for geomechanics simulation of fractured rocks. Comput. Geotech. 2022, 145, 104707. [Google Scholar] [CrossRef]
- Liu, H.Y.; Huang, Y.S.; Lv, S.R. A compression damage constitutive model of jointed rock mass based on deformation components. J. Cent. South Univ. 2014, 45, 2014–2020. [Google Scholar]
- Liu, H.Y.; Lv, S.R.; Zhang, L.M. Dynamic damage constitutive model for persistent jointed rock mass based on combination model method. Chin. J. Geotech. Eng. 2014, 36, 1814–1821. [Google Scholar]
- Liu, H.Y.; Lv, S.R.; Zhang, L.M. A dynamic damage constitutive model for a rock mass with persistent joints. Int. J. Rock Mech. Min. Sci. 2015, 75, 132–139. [Google Scholar] [CrossRef]
- Liu, J.; Li, Y.; Zhang, H. Study on shale’s dynamic damage constitutive model based on statistical distribution. Shock Vib. 2015, 2015, 286097. [Google Scholar] [CrossRef]
- Ren, L.; Xie, H.P.; Xie, L.Z. Preliminary study on strength of cracked rock specimen based on fracture mechanics. Eng. Mech. 2013, 30, 156–162. [Google Scholar]
- Sun, W.J.; Zhou, W.Y. An elasto-plastic damage mechanics constitutive model for jointed rock mass. Chin. J. Rock Mech. Eng. 1990, 2, 108–119. [Google Scholar]
- Swoboda, G.; Shen, X.; Rosas, L. Damage model for jointed rock mass and its application to tunnelling. Comput. Geotech. 1998, 22, 183–203. [Google Scholar] [CrossRef]
- Zhu, R.; Gao, H.; Zhan, Y.; Wu, Z.X. Construction of Discrete Element Constitutive Relationship and Simulation of Fracture Performance of Quasi-Brittle Materials. Materials 2022, 15, 1964. [Google Scholar] [CrossRef]
- Zhu, W.S.; Zhang, Q.Y. Brittle elastic fracture damage constitutive model of jointed rock mass and its application to engineering. Chin. J. Rock Mech. Eng. 1999, 18, 245–249. [Google Scholar]
- Zhang, Z.; Ge, X. A new quasi-continuum constitutive model for crack growth in an isotropic solid. Eur. J. Mech.-A/Solids 2005, 24, 243–252. [Google Scholar] [CrossRef]
- Xiong, L.; Chen, H. Effects of high temperatures and loading rates on the splitting tensile strength of jointed rock mass. Geotech. Geol. Eng. 2020, 38, 1885–1898. [Google Scholar] [CrossRef]
- Meng, Q.X.; Wang, H.L.; Xu, W.Y.; Chen, Y.L. Numerical homogenization study on the effects of columnar jointed structure on the mechanical properties of rock mass. Int. J. Rock Mech. Min. Sci. 2019, 124, 104–127. [Google Scholar] [CrossRef]
- Wang, Y.C.; Chen, F.; Sui, W.H.; Meng, F.S.; Geng, F. Large-scale model test for studying the water inrush during tunnel excavation in fault. Bull. Eng. Geol. Environ. 2022, 81, 238. [Google Scholar] [CrossRef]
- Feng, P.; Liu, B.; Tang, R.; Wei, M.; Zhang, Y.; Li, H. Dynamic fracture behaviors and fragment characteristics of pre-compressed flawed sandstones. Int. J. Mech. Sci. 2022, 220, 107–162. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, L.; Sun, J.; Guo, Q.; Pan, J.; Gao, J. Strength characteristics and failure mechanism of granite with cross cracks at different angles based on dic method. Adv. Mater. Sci. Eng. 2022, 9144673. [Google Scholar] [CrossRef]
- Wang, J.; Shi, J.P. Calculation of stress intensity factor for crack in a finite plate. Chin. J. Rock Mech. Eng. 2005, 24, 963–968. [Google Scholar]
- Grady, D.E.; Kipp, M.E. The micromechanics of impact fracture of rock. Int. J. Rock Mech. Min. Sci. 1979, 16, 293–302. [Google Scholar] [CrossRef]
- Taylor, L.M.; Chen, E.P.; Kuszmaul, J.S. Microcrack-induced damage accumulation in brittle rock under dynamic loading. Comput. Methods Appl. Mech. Eng. 1986, 55, 301–320. [Google Scholar] [CrossRef]
- Dai, G.F.; Yin, G.Z.; Pi, W. Research on damage constitutive model and evolution equation of coal under uniaxial compression. Tongji Daxue Xuebao/J. Tongji Univ. 2004, 32, 986–989. [Google Scholar]
- Jia, W.B.; Li, X.; Chen, Z.; Zhao, K.; Fang, L. Viscoplastic constitutive model of a nickel-based superalloy under multiaxial loading conditions. J. Iron Steel Res. Int. 2021, 28, 1190–1202. [Google Scholar] [CrossRef]
- Xie, M.; Zheng, S.S.; Wang, B.; Li, L.; Wang, W. Stochastic Damage Constitutive Model for Concrete Subjected to Uniaxial tension Stress. In Key Engineering Materials; Trans Tech Publications Ltd.: Zurich, Switzerland, 2010; Volume 417, pp. 921–924. [Google Scholar]
- Yang, S.; Wang, W.; Lin, C.; Shen, W.; Li, Y. Improved constitutive model of the jellyroll for cylindrical lithium ion batteries considering microscopic damage. Energy 2019, 185, 202–212. [Google Scholar] [CrossRef]
- Chen, S.; Qiao, C.; Ye, Q.; Khan, M.U. Comparative study on three-dimensional statistical damage constitutive modified model of rock based on power function and Weibull distribution. Environ. Earth Sci. 2018, 77, 108. [Google Scholar] [CrossRef]
- Xie, M.; Hao, H. Stochastic Damage Constitutive Law of Concrete under Uniaxial Compression. In Proceedings of the 2017 3rd International Forum on Energy, Environment Science and Materials (IFEESM 2017), Shenzhen, China, 25–26 November 2017; Atlantis Press: Paris, France, 2018; pp. 603–606. [Google Scholar]
- Lee, S.; Ravichandran, G. Crack initiation in brittle solids under multiaxial compression. Eng. Fract. Mech. 2003, 70, 1645–1658. [Google Scholar] [CrossRef]
- Wang, Z.L.; Li, Y.C.; Wang, J.G. A damage-softening statistical constitutive model considering rock residual strength. Comput. Geosci. 2007, 33, 1–9. [Google Scholar] [CrossRef]
- Luo, Y. Isotropized voigt-reuss model for prediction of elastic properties of particulate composites. Mech. Adv. Mater. Struct. 2021, 29, 3934–3941. [Google Scholar] [CrossRef]
- Tian, W.; Qi, L.; Su, C.; Liang, J.; Zhou, J. Numerical evaluation on mechanical properties of short-fiber-reinforced metal matrix composites: Twostep mean-field homogenization procedure. Compos. Struct. 2016, 139, 96–103. [Google Scholar] [CrossRef]
- Gnäupel-Herold, T.; Creuziger, A.A.; Iadicola, M. A model for calculating diffraction elastic constants. J. Appl. Crystallogr. 2012, 45, 197–206. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, Y.C.; Geng, F.; Zhang, Z. Study on dust distribution in a highway tunnel during the full-face excavation with Drilling-Blasting method. Tunn. Undergr. Space Technol. 2023, 139, 105229. [Google Scholar] [CrossRef]
- Jiang, W.; Wang, Y.C.; Yang, J.G.; Zhang, Z. Surrounding rock quality evaluation and application development for highway tunnel based on engineering applicability. Bull. Eng. Geol. Environ. 2023, 82, 115. [Google Scholar] [CrossRef]
- Wang, G.; Wang, R.; Sun, F.; Liu, B.; Zhang, L.; Cao, T.; Li, B. Analysis of nonlinear energy evolution in fractured limestone under uniaxial compression. Theor. Appl. Fract. Mech. 2022, 120, 103387. [Google Scholar] [CrossRef]
- Chen, F.; Wang, Y.C.; Jiang, W.; Zheng, S.H. Numerical simulation of ground movement induced by water and sand gushing in subway through fault based on DEM-CFD. Comput. Geotech. 2021, 139, 104282. [Google Scholar] [CrossRef]
- Wang, Y.C.; Chen, F.; Li, X.Z.; Yin, X.; Geng, F.; Zheng, S.H. Experimental Investigation on Mass Loss Characteristics of Broken Rocks with Discontinuous Gradation. Int. J. Geomech. 2021, 21, 04021168. [Google Scholar] [CrossRef]
- Wang, Y.C.; Li, Z.Y.; Jing, H.W.; Li, Y.B.; Wang, M.T. Study on the seepage characteristics of deep buried tunnels under variable high-pressure water heads. Bull. Eng. Geol. Environ. 2021, 80, 1477–1487. [Google Scholar] [CrossRef]
- Hu, B.; Wang, Z.; Li, J.; Wei, E.; Ma, L.; Liu, J.; Xiaobo, Y. A new shear creep damage model for rock masses after considering initial damage. PLoS ONE 2023, 18, e0280793. [Google Scholar] [CrossRef] [PubMed]
- Hou, Z.; Li, X.; Zhang, Y.; Liang, H.; Guo, Y.; Cheng, H.; Gao, R. A Strain Rate Dependent Constitutive Model for the Lower Silurian Longmaxi Formation Shale in the Fuling Gas Field of the Sichuan Basin, China. Acta Geol. Sin.-Engl. Ed. 2019, 93, 972–981. [Google Scholar] [CrossRef]
- Du, B.; Bai, H. A damage constitutive model of red sandstone under coupling of wet-dry cycles and impact load. Shock Vib. 2019, 2019, 7692424. [Google Scholar] [CrossRef]
- Duarte, M.T.; Liu, H.Y.; Kou, S.Q.; Lindqvist, P.A.; Miskovsky, K. Microstructural modeling approach applied to rock material. J. Mater. Eng. Perform. 2005, 14, 104–111. [Google Scholar] [CrossRef]
- Kolo, I.; Abu Al-Rub, R.K.; Sousa, R.L. Computational modelling of fracture propagation in rocks using a coupled elastic-plasticity-damage model. Math. Probl. Eng. 2016, 2016, 3231092. [Google Scholar] [CrossRef]
- Deng, P.; Liu, Q.; Lu, H. FDEM numerical study on the mechanical characteristics and failure behavior of heterogeneous rock based on the Weibull distribution of mechanical parameters. Comput. Geotech. 2023, 154, 105–138. [Google Scholar] [CrossRef]
- Xie, S.; Han, Z.; Zhou, T. A semiempirical constitutive relationship for rocks under uniaxial compression considering the initial damage recovery. Fatigue Fract. Eng. Mater. Struct. 2023, 46, 1300–1313. [Google Scholar] [CrossRef]
- Budiansky, B.; O’connell, R.J. Elastic moduli of a cracked solid. Int. J. Solids Struct. 1976, 12, 81–97. [Google Scholar] [CrossRef]
- Nakamura, H.; Nanri, T.; Miura, T.; Roy, S. Experimental investigation of compressive strength and compressive fracture energy of longitudinally cracked concrete. Cem. Concr. Compos. 2018, 93, 1–18. [Google Scholar] [CrossRef]
- Xu, Y.C.; Li, K.Q.; Xie, X.F.; Liu, S.Q.; Lv, B. Grouting reinforcement of fractured rock mass based on damage mechanics. J. Xian Univ. Sci. Technol. 2017, 37, 26–31. [Google Scholar]



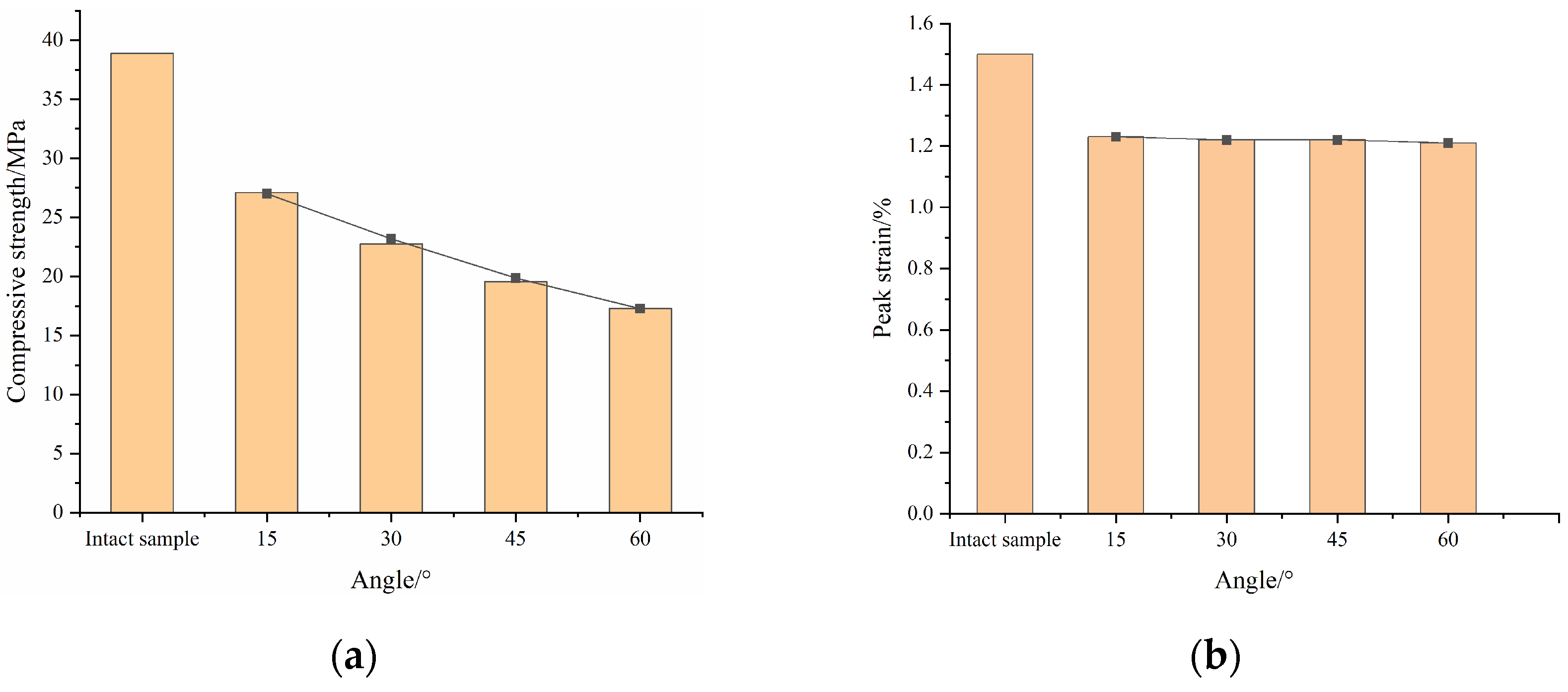
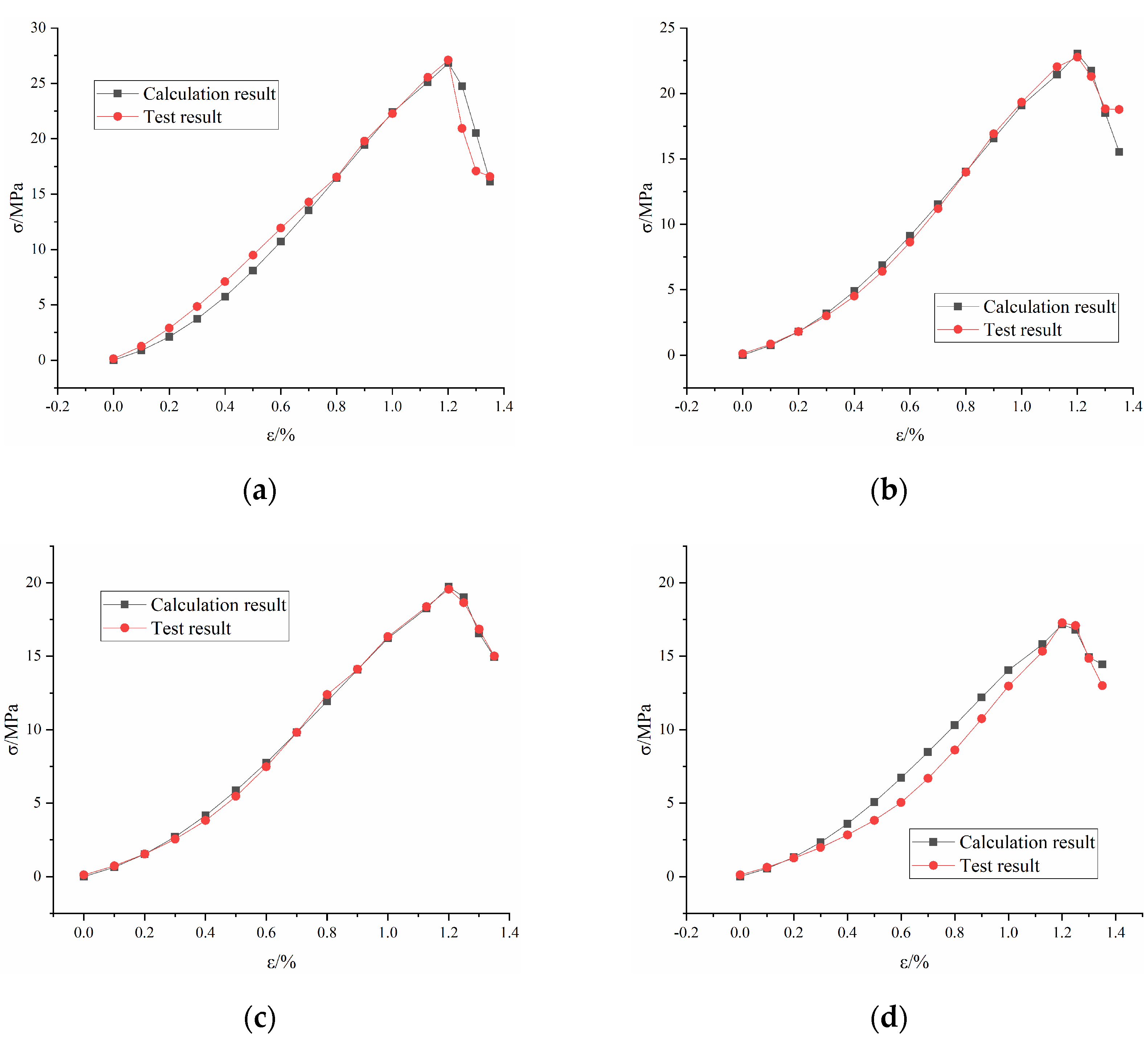

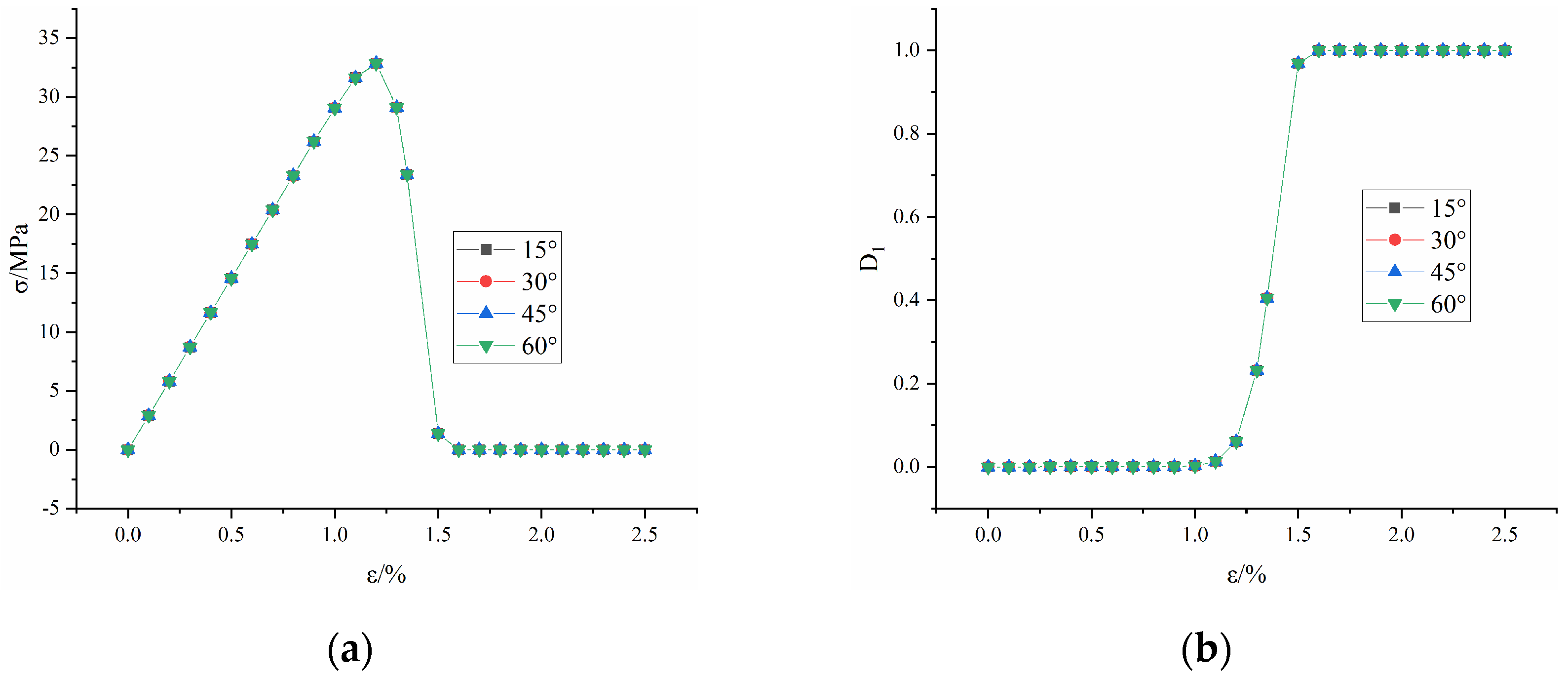
| Fracture Width | ||||
|---|---|---|---|---|
| 0 mm | 2 mm | 3 mm | 5 mm | |
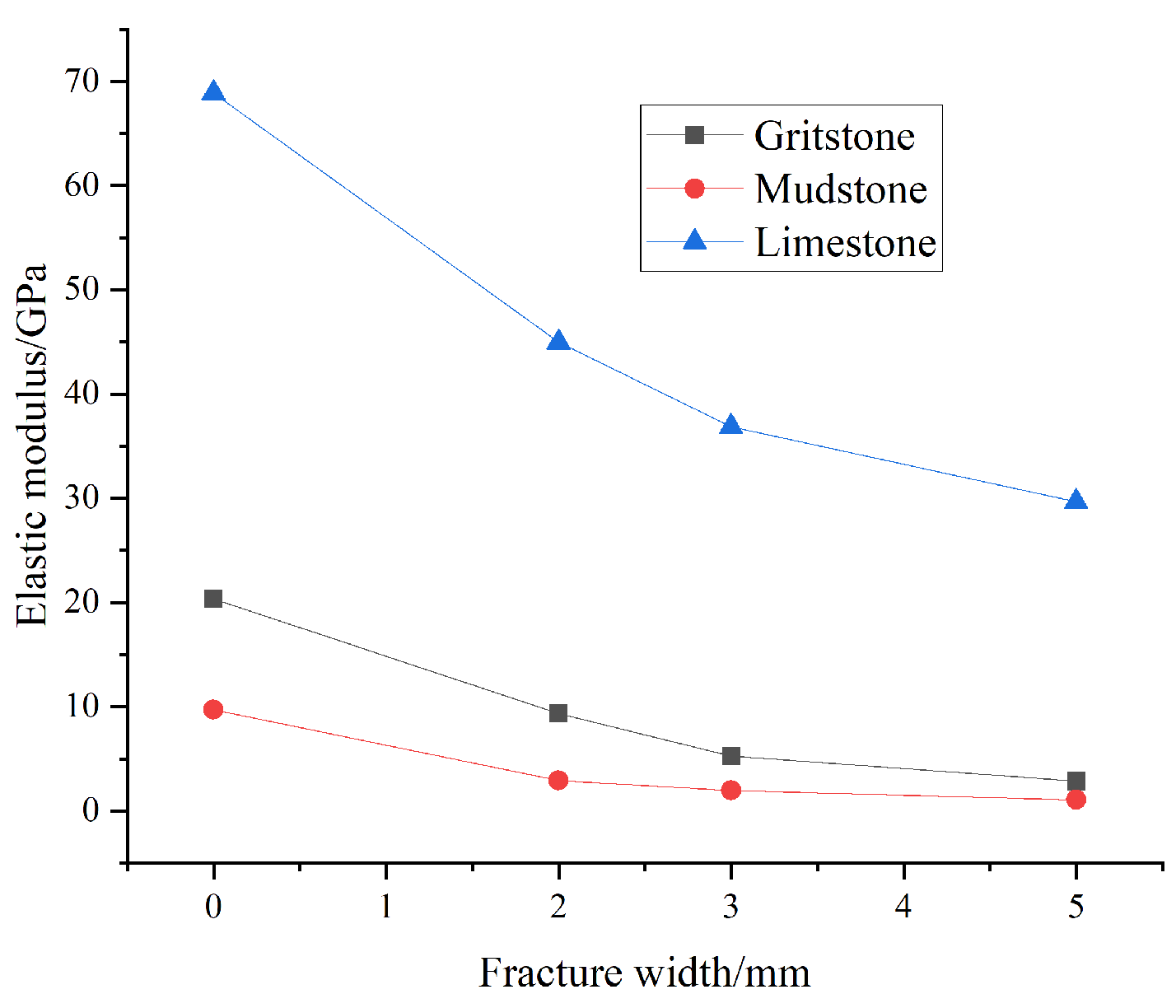
| Gritstone | 20.343 GPa | 9.36 GPa | 5.262 GPa | 2.847 GPa |
| Mudstone | 9.721 GPa | 2.927 GPa | 1.98 GPa | 1.064 GPa |
| Limestone | 68.882 GPa | 44.992 GPa | 36.888 GPa | 29.661 GPa |
| Compressive Strength | ||||
| Intact sample | 15° | 30° | 45° | 60° |
| 38.9 MPa | 27.1 MPa | 22.76 MPa | 19.57 MPa | 17.26 MPa |
| Peak Strain | ||||
| Intact sample | 15° | 30° | 45° | 60° |
| 1.52% | 1.23% | 1.22% | 1.21% | 1.21% |
| Elastic Modulus of Rock () | ε0 | ||
| 2910 MPa | 18 | 1.4% | −0.5 |
| ) | |||
| 1880 MPa | −3.055 | 0.937 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Wang, Y.; Zhong, Z.; Li, Q.; Zuo, Y. Constitutive Model for Grouted Rock Mass by Macro-Meso Damage. Materials 2023, 16, 4859. https://doi.org/10.3390/ma16134859
Liu Y, Wang Y, Zhong Z, Li Q, Zuo Y. Constitutive Model for Grouted Rock Mass by Macro-Meso Damage. Materials. 2023; 16(13):4859. https://doi.org/10.3390/ma16134859
Chicago/Turabian StyleLiu, Yang, Yingchao Wang, Zhibin Zhong, Qingli Li, and Yapeng Zuo. 2023. "Constitutive Model for Grouted Rock Mass by Macro-Meso Damage" Materials 16, no. 13: 4859. https://doi.org/10.3390/ma16134859
APA StyleLiu, Y., Wang, Y., Zhong, Z., Li, Q., & Zuo, Y. (2023). Constitutive Model for Grouted Rock Mass by Macro-Meso Damage. Materials, 16(13), 4859. https://doi.org/10.3390/ma16134859





