Numerical Modeling of Transient Flow Characteristics on the Top Surface of a Steel Slab Continuous Casting Strand Using a Large Eddy Simulation Combined with Volume of Fluid Model
Abstract
:1. Introduction
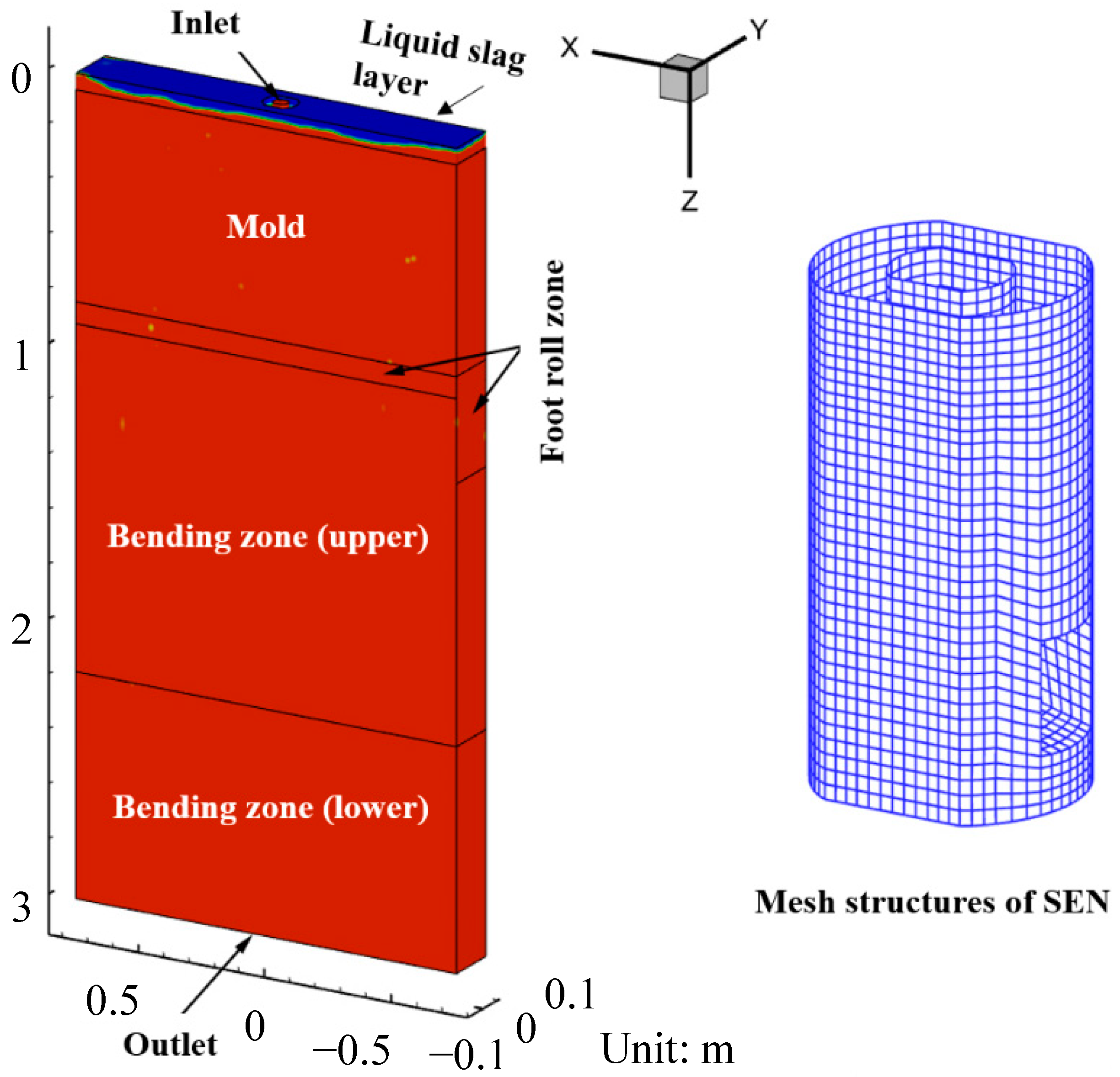
2. Computational Models
2.1. Assumptions
- The molten steel is treated as incompressible Newtonian fluids, and the process of solidification and heat transfer in the mold are ignored;
- The physical properties of molten steel and mold powder are set as constants;
- The computational domain extends from the mold to the bending zone, and its direction is simplified to vertical downward;
- The molten steel flow at the outlet of calculation domain is assumed to be fully developed turbulence.
2.2. Continuity Equations
2.3. LES Model
2.4. Volume of Fluid Model
2.5. Numerical Details
3. Nail Board Measurements
4. Results and Discussion
4.1. Numerical Simulation Validation
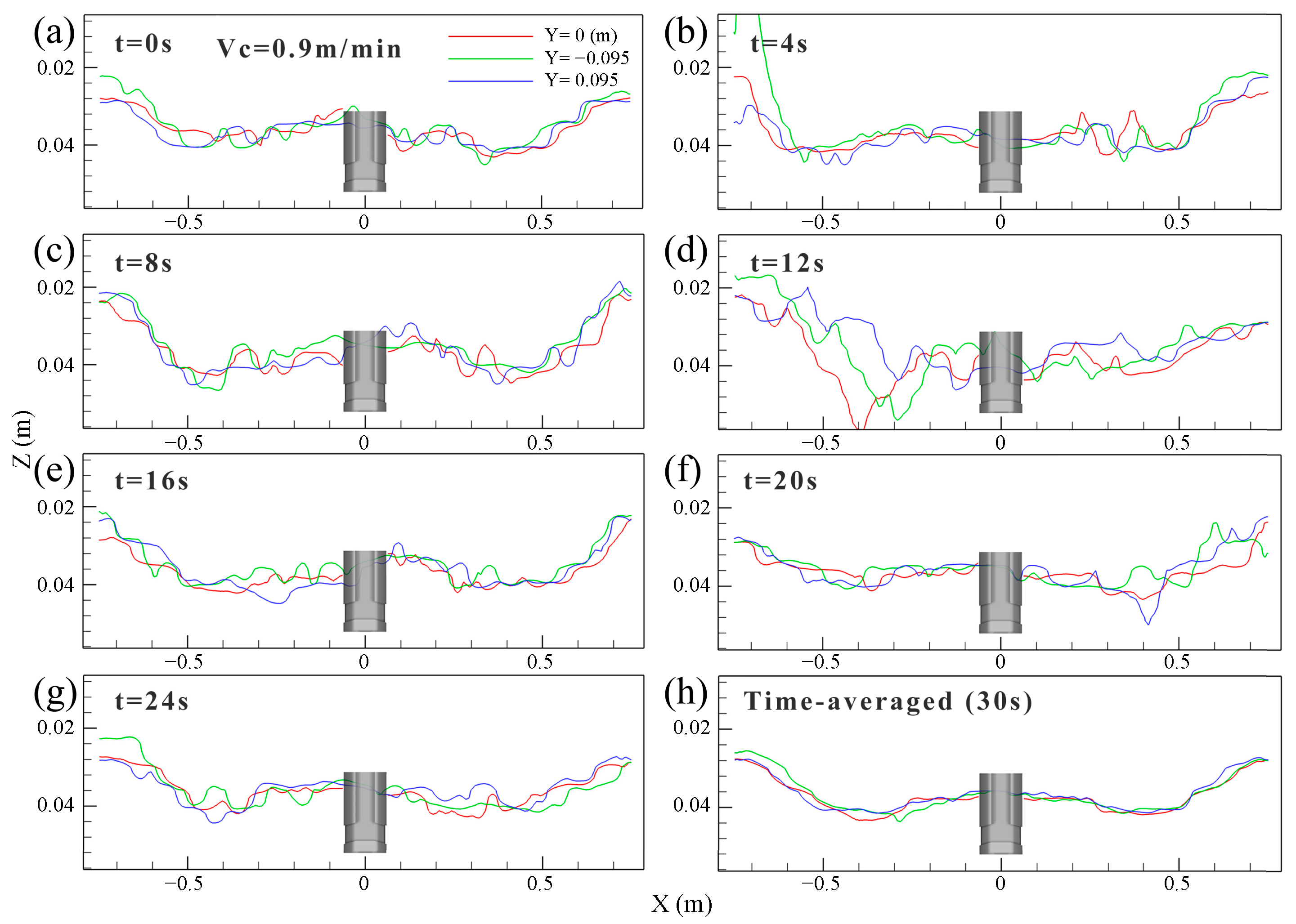
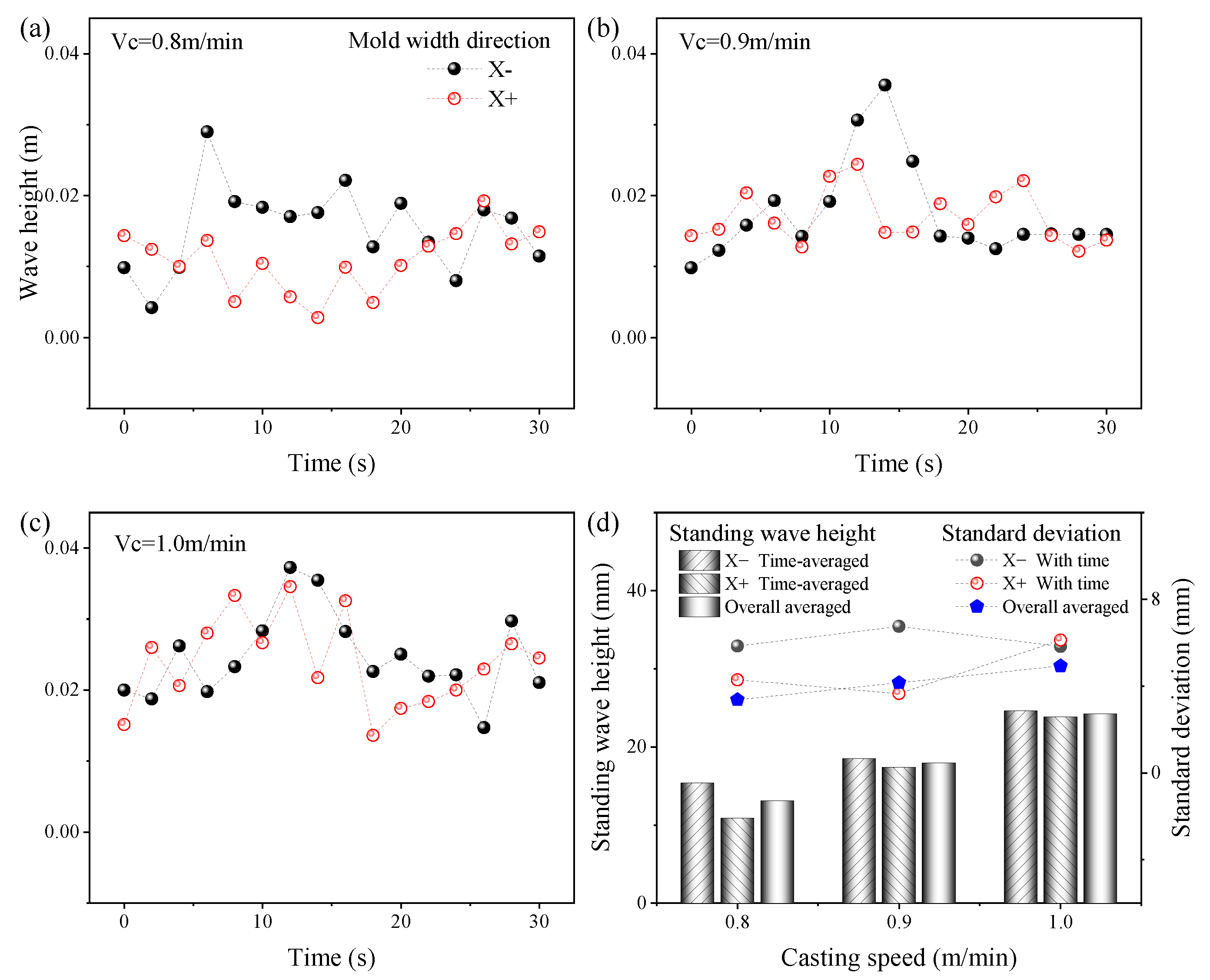
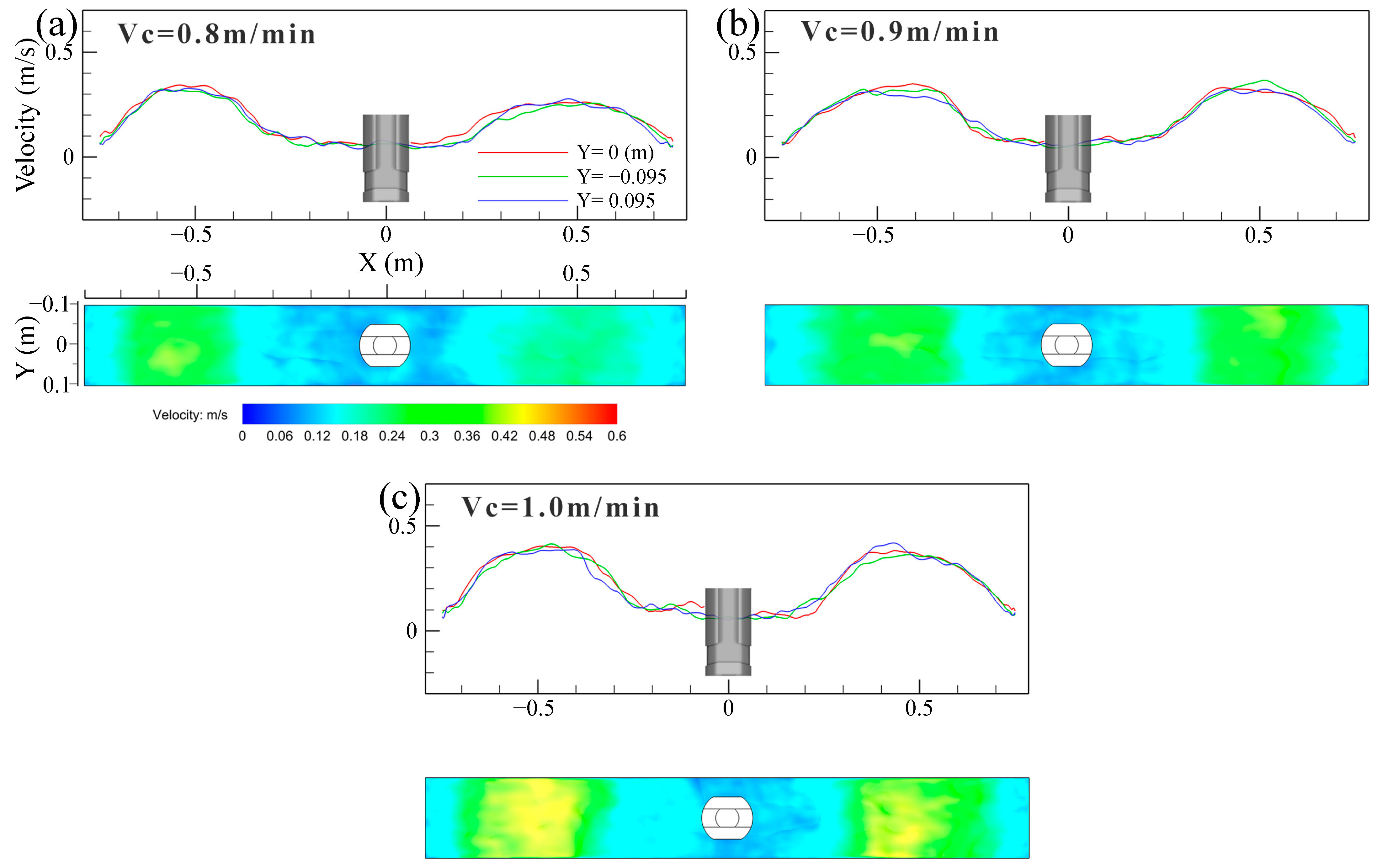
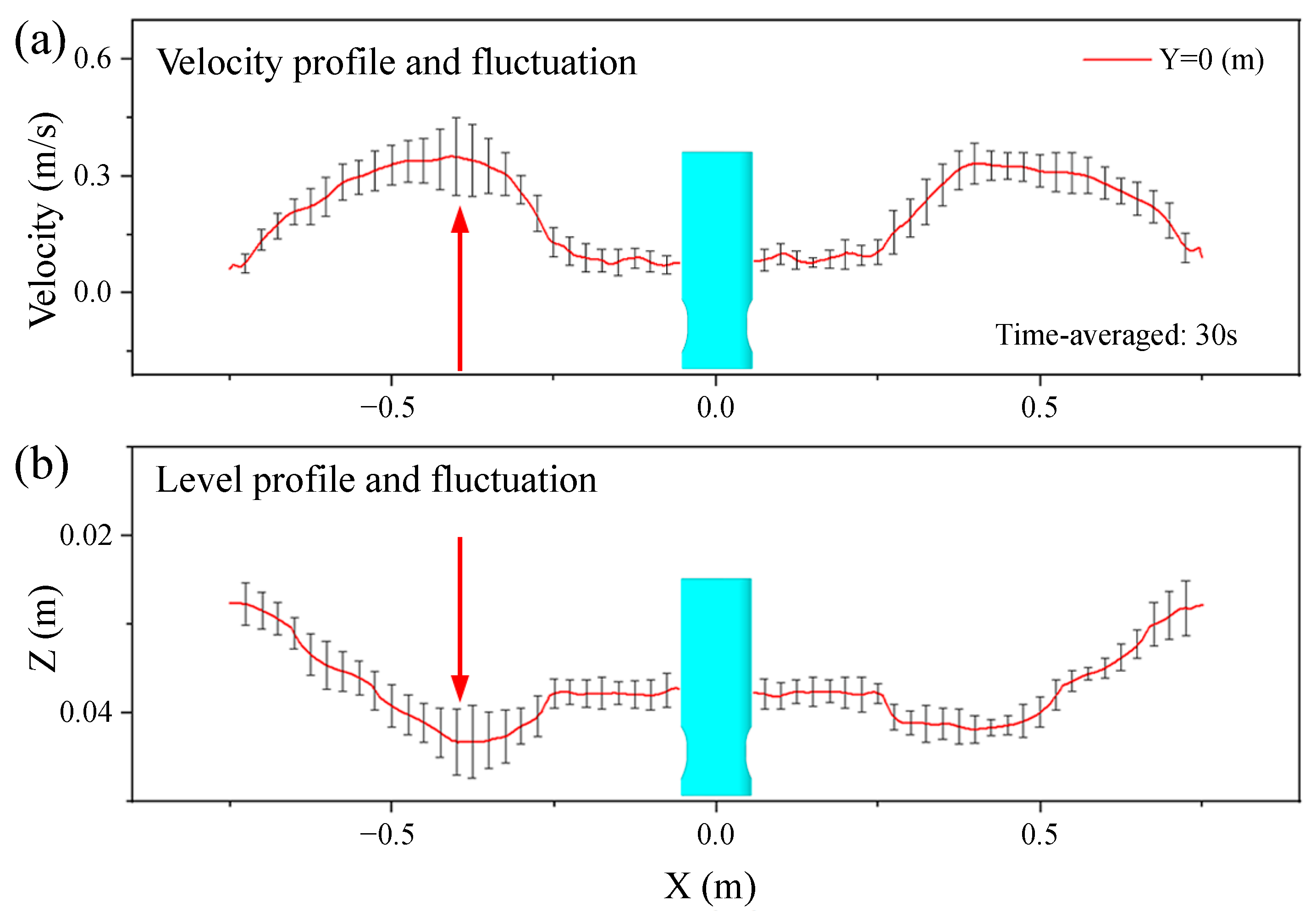
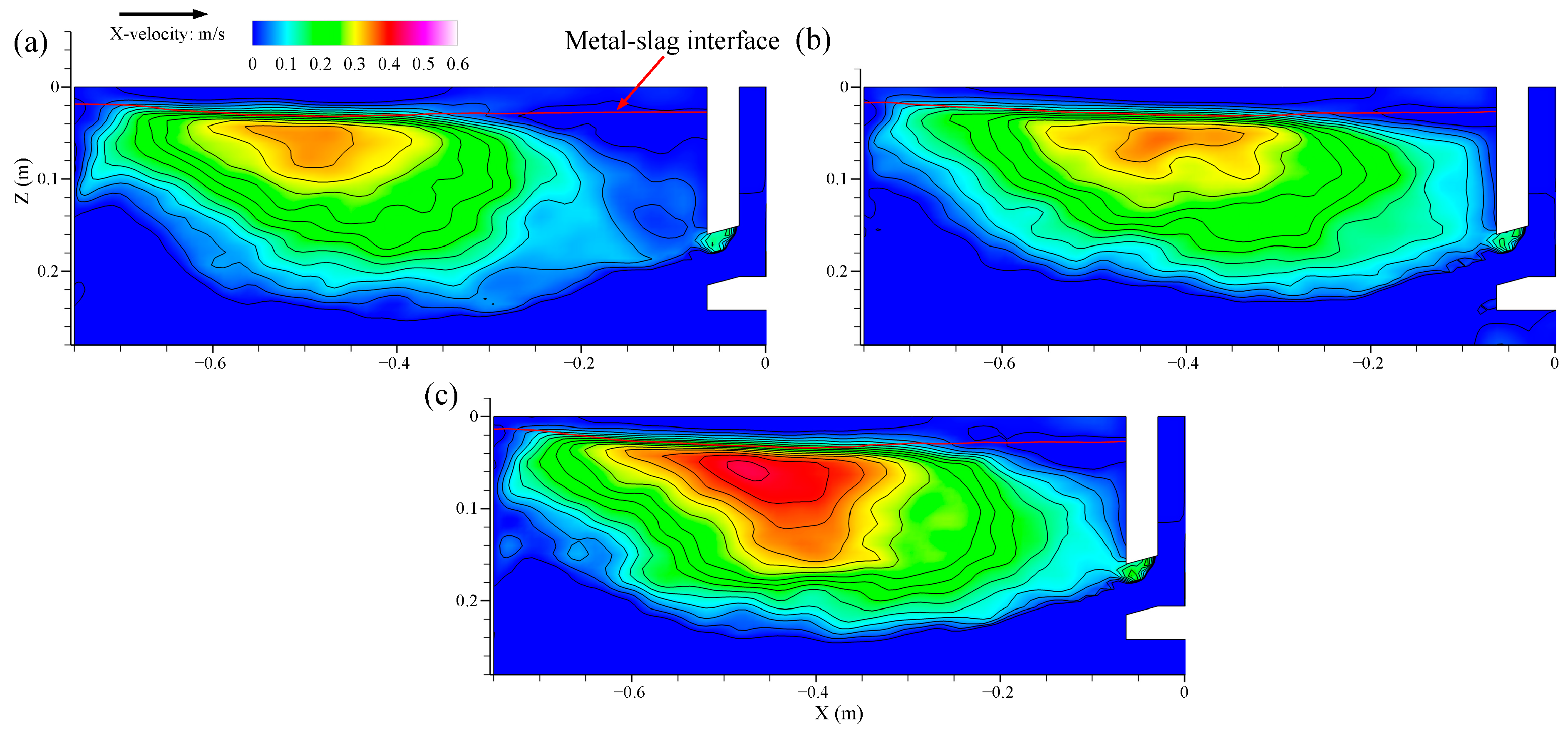
4.2. Effect of Casting Speed on Top Surface Level Profile
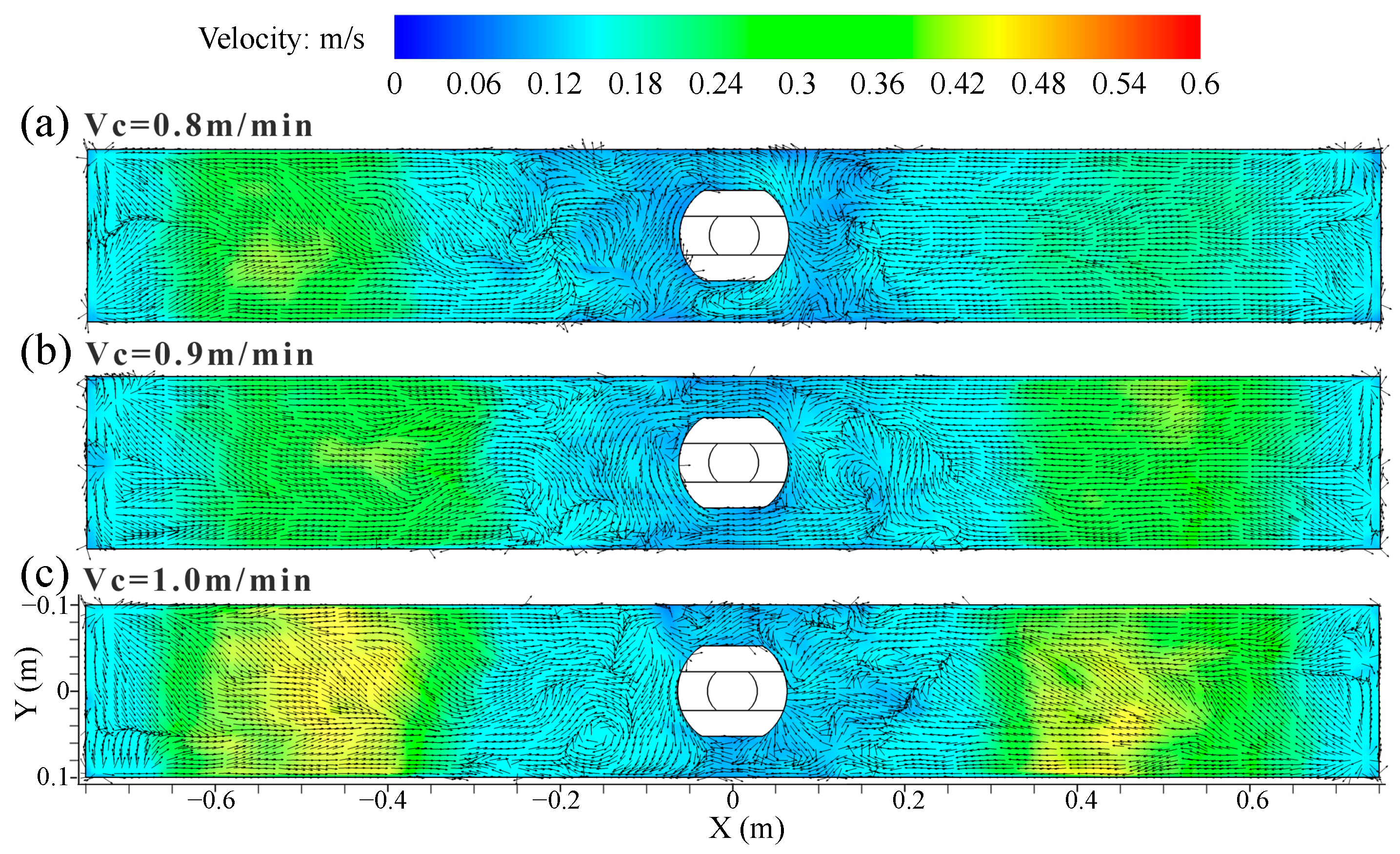
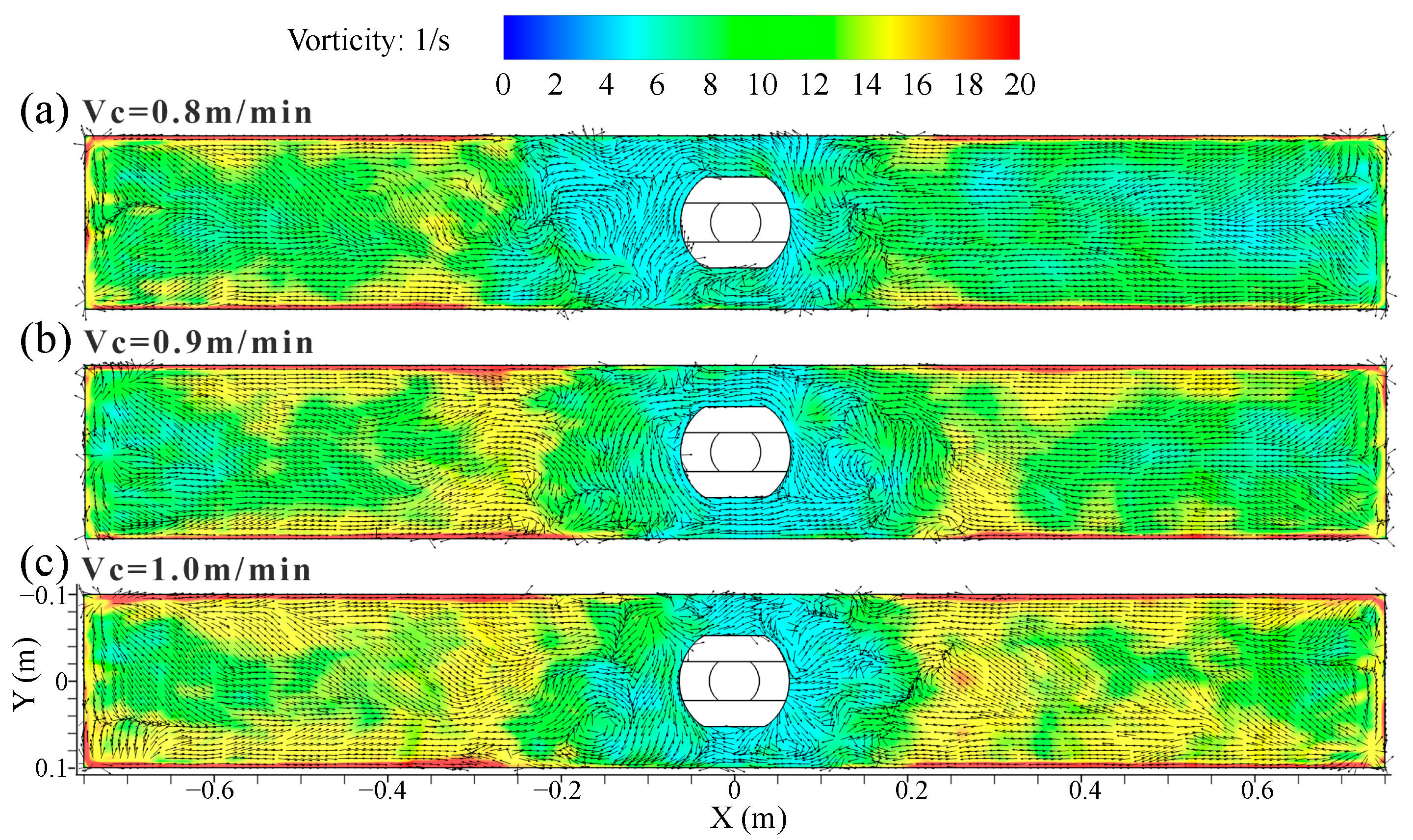
4.3. Effect of Casting Speed on Vortex Distribution
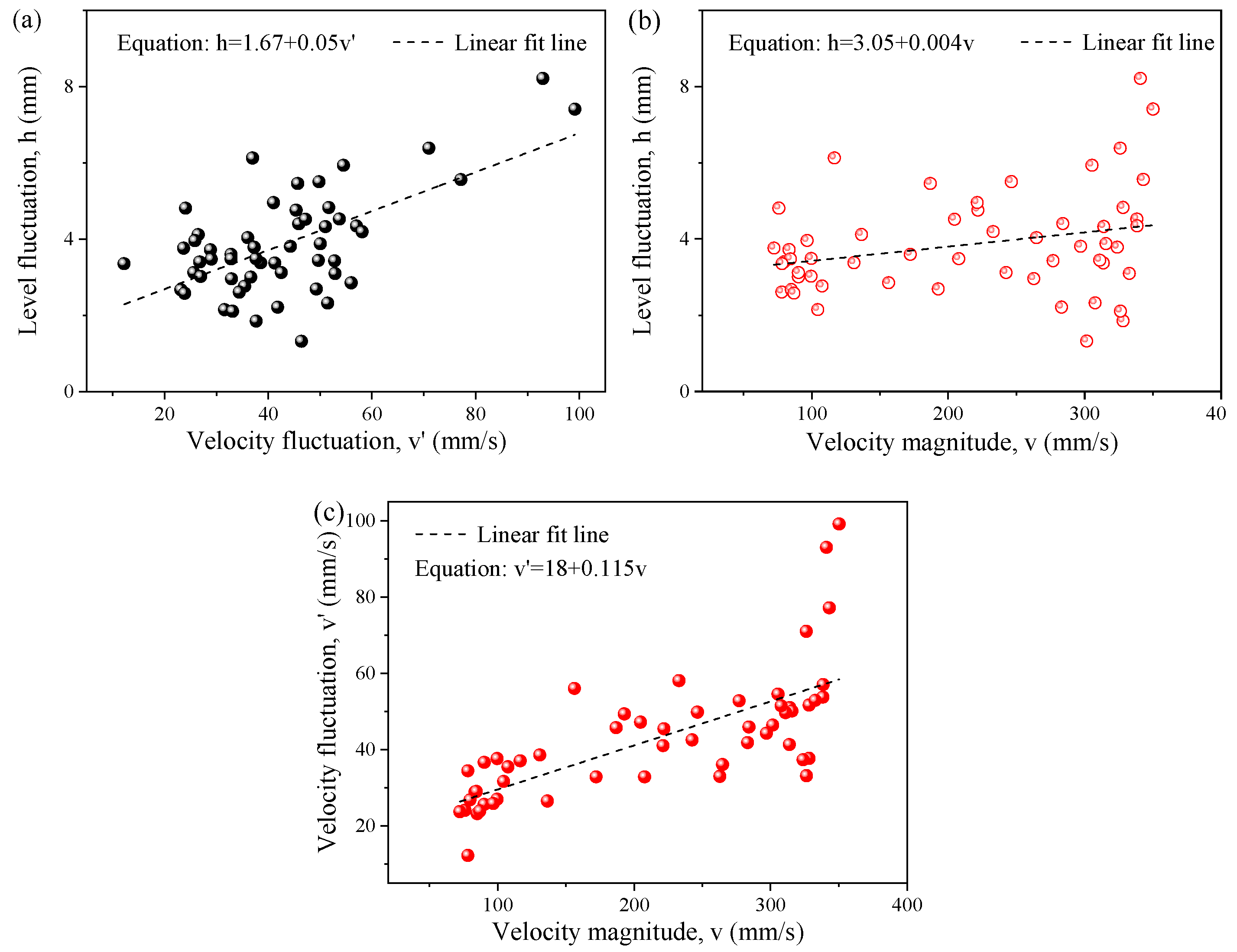
4.4. Effect of Surface Flow Velocity on Instantaneous Level Fluctuation
5. Conclusions
- The level variation profile migrated after a period of time, moving from one width side of the mold to the other side. Under the DRF pattern, with the increase in the casting speed, the SW height of the top surface increased, and the transient fluctuation degree of the wave height increased.
- The vortex on the top surface of the mold was easy to generate in the low-speed confluence area near the SEN. The velocity, vorticity, and relative pressure of the vortex center were small, while the velocity and vorticity of the edge were large. When the vorticity peak was concentrated on the outer edge of the low-speed confluence zone close to the SEN, it was beneficial to promote the formation of the vortex.
- The surface velocity fluctuation was larger at the 1/4 mold width, and it was smaller at the low-speed zone near the narrow face and the SEN. The level fluctuation increased with an increase in the velocity fluctuation, and the velocity fluctuation increased with the increase in velocity magnitude. The level fluctuation as a function of the surface velocity magnitude was predicted. The results of this study are expected to help us develop and preliminarily verify various ideas for suppress the slag entrainment.
6. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, L. Non-Metallic Inclusions in Steels: Industrial Practice; Metallurgical Industry Press: Beijing, China, 2019; pp. 63–70. (In Chinese) [Google Scholar]
- Kalter, R.; Tummers, M.; Kenjereš, S.; Righolt, B.; Kleijn, C. Oscillations of the fluid flow and the free surface in a cavity with a submerged bifurcated nozzle. Int. J. Heat Fluid Flow 2013, 44, 365–374. [Google Scholar] [CrossRef]
- Asad, A.; Kratzsch, C.; Schwarze, R. Numerical investigation of the free surface in a model mold. Steel Res. Int. 2016, 87, 181–190. [Google Scholar] [CrossRef]
- Teshima, T.; Kubota, J.; Suzuki, M.; Ozawa, K.; Masaoka, T.; Miyahara, S. Influence of casting conditions on molten steel flow in continuous casting mold at high speed casting of slabs. Tetsu-to-Hagane 1993, 79, 576–582. [Google Scholar] [CrossRef] [PubMed]
- Gupta, D.; Lahiri, A. Water-modeling study of the surface disturbances in continuous slab caster. Metall. Mater. Trans. B 1994, 25, 227–233. [Google Scholar] [CrossRef]
- Li, B.; Tsukihashi, F. Vortexing flow patterns in a water model of slab continuous casting mold. ISIJ Int. 2005, 45, 30–36. [Google Scholar] [CrossRef]
- Kasai, N.; Iguchi, M. Water-model experiment on melting powder trapping by vortex in the continuous casting mold. ISIJ Int. 2007, 47, 982–987. [Google Scholar] [CrossRef]
- Lee, J.; Han, S.; Cho, H.; Park, I. Numerical and experimental study of the meniscus vortex core in a water model of continuous casting mold. Metall. Mater. Trans. B 2021, 52, 178–189. [Google Scholar] [CrossRef]
- Zhang, K.; Liu, J.; Cui, H.; Xiao, C. Analysis of meniscus fluctuation in a continuous casting slab mold. Metall. Mater. Trans. B 2018, 49, 1174–1184. [Google Scholar] [CrossRef]
- Jiang, Z.; Su, Z.; Xu, C.; Chen, J.; He, J. Abnormal mold level fluctuation during slab casting of peritectic steels. J. Iron Steel Res. Int. 2020, 27, 160–168. [Google Scholar] [CrossRef]
- Cockcroft, S. Optimization of industrial casting processes. Metals 2020, 10, 360. [Google Scholar] [CrossRef]
- Panaras, G.; Theodorakakos, A.; Berggeles, G. Numerical investigation of the free surface in a continuous steel casting mold model. Metall. Mater. Trans. B 1998, 29, 1117–1126. [Google Scholar] [CrossRef]
- Smirnov, A.; Kuberskii, S.; Smirnov, E.; Verzilov, A.; Maksaev, E. Influence of meniscus fluctuations in the mold on crust formation in slab casting. Steel Transl. 2017, 47, 478–482. [Google Scholar] [CrossRef]
- Matsushita, A.; Isogami, K.; Temma, M.; Ninomiya, T.; Tsutsumi, K. Direct observation of molten steel meniscus in CC mold during casting. Trans. Iron Steel Inst. Jpn. 1988, 28, 531–534. [Google Scholar] [CrossRef]
- Zhang, T.; Yang, J.; Jiang, P. Measurement of molten steel velocity near the surface and modeling for transient fluid flow in the continuous casting mold. Metals 2019, 9, 36. [Google Scholar] [CrossRef]
- Huang, C.; Zhou, H.; Zhang, L.; Yang, W.; Zhang, J.; Ren, Y.; Chen, W. Effect of casting parameters on the flow pattern in a steel continuous casting slab mold: Numerical simulation and industrial trials. Steel Res. Int. 2022, 93, 2100350. [Google Scholar] [CrossRef]
- Cho, S.; Kim, S.; Thomas, B. Transient fluid flow during steady continuous casting of steel slabs: Part I. Measurements and modeling of two-phase flow. ISIJ Int. 2014, 54, 845–854. [Google Scholar] [CrossRef]
- Ren, L.; Zhang, L.; Wang, Q. Measurements of surface velocity and level fluctuation in an actual continuous wide slab casting mold. Metall. Res. Technol. 2018, 115, 102. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, X.; Lan, P.; Zhang, J. Control of mould level fluctuation through the modification of steel composition. Int. J. Min. Met. Mater. 2013, 20, 138–145. [Google Scholar] [CrossRef]
- Hibbeler, L.; Thomas, B. Mold slag entrainment mechanisms in continuous casting molds. Iron Steel Technol. 2013, 10, 121–136. [Google Scholar]
- Thomas, B.; Huang, X.; Sussman, R. Simulation of argon gas flow effects in a continuous slab caster. Metall. Mater. Trans. B 1994, 25, 527–547. [Google Scholar] [CrossRef]
- Codur, Y.; Guvot, V.; Martin, J. Control of steel level in a continuous casting mould: Relation with withdrawal of the slab. Rev. Metall. Cah. Inf. Tech. 1994, 91, 1055–1061. [Google Scholar]
- Yoon, U.-S.; Bang, I.-W.; Rhee, J.H.; Kim, S.-Y.; Lee, J.-D.; Oh, K.H. Analysis of mold level hunching by unsteady bulging during thin slab casting. ISIJ Int. 2002, 42, 1103–1111. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Y.; Zuo, X. Flow transport and inclusion motion in steel continuous-casting mold under submerged entry nozzle clogging condition. Metall. Mater. Trans. B 2008, 39, 534–550. [Google Scholar] [CrossRef]
- Liu, R.; Thomas, B.; Sengupta, J.; Chung, S.; Trinh, M. Measurements of molten steel surface velocity and effect of stopper-rod movement on transient multiphase fluid flow in continuous casting. ISIJ Int. 2014, 54, 2314–2323. [Google Scholar] [CrossRef]
- Zhao, P.; Li, Q.; Kuang, S.; Zou, Z. LBM-LES simulation of the transient asymmetric flow and free surface fluctuations under steady operating conditions of slab continuous casting process. Metall. Mater. Trans. B 2017, 48, 456–470. [Google Scholar] [CrossRef]
- Zhu, X.; Li, D.; Wu, C.; Oleksandr, T.; Wang, Q. Influence of large-scale vortex movement in lower recirculation zone on instable flow field in the mold. ISIJ Int. 2018, 58, 1687–1694. [Google Scholar] [CrossRef]
- Cho, S.; Thomas, B.; Kim, S. Effect of nozzle port angle on transient flow and surface slag behavior during continuous steel-slab casting. Metall. Mater. Trans. B 2019, 50, 52–76. [Google Scholar] [CrossRef]
- Chen, W.; Ren, Y.; Zhang, L.; Scheller, P. Numerical simulation of steel and argon gas two-phase flow in continuous casting using LES + VOF + DPM model. JOM 2019, 71, 1158–1168. [Google Scholar] [CrossRef]
- Lei, H.; Liu, J.; Tang, G.; Zhang, H.; Jiang, Z.; Lv, P. Deep insight into mold level fluctuation during casting different steel grades. JOM 2023, 75, 914–919. [Google Scholar] [CrossRef]
- Brackbill, J.; Kothe, D.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Smagorinsky, J. General circulation experiments with the primitive equations: I. The basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Hirt, C.; Nichols, B. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Mcdavid, R.; Thomas, B. Flow and thermal behavior of the top surface flux/powder layers in continuous casting molds. Metall. Mater. Trans. B 1996, 27, 672–685. [Google Scholar] [CrossRef]
- Rietow, B.; Thomas, B. Using nail board experiments to quantify surface velocity in the CC mold. In Proceedings of the AISTech 2008 Steelmaking Conference, Pittsburgh, PA, USA, 5–8 May 2008. [Google Scholar]
- Zhou, H.; Zhang, L.; Chen, W.; Ren, Y.; Yang, W.; Jiang, R. Determination of transient flow pattern in steel continuous casting molds using nail board measurement and onsite top flux observation. Metall. Mater. Trans. B 2021, 52, 1106–1117. [Google Scholar] [CrossRef]
- Liu, Z.; Qi, F.; Li, B.; Jiang, M. Vortex flow pattern in a slab continuous casting mold with argon gas injection. J. Iron Steel Res. Int. 2014, 21, 1081–1089. [Google Scholar] [CrossRef]
- Thomas, B.; Yuan, Q.; Sivaramakrishnan, S.; Shi, T.; Vanka, S.; Assar, M. Comparison of four methods to evaluate fluid velocities in a continuous slab casting mold. ISIJ Int. 2001, 41, 1262–1271. [Google Scholar] [CrossRef]
- Chaudhary, R.; Lee, G.; Thomas, B.; Cho, S.; Kim, S.; Kwon, O. Effect of stopper-rod misalignment on fluid flow in continuous casting of steel. Metall. Mater. Trans. B 2011, 42, 300–315. [Google Scholar] [CrossRef]







| Year | Authors | Causes of Level Fluctuation on Top Surface | Ref. |
|---|---|---|---|
| 1988 | Teshima et al. | Impact of molten steel flow on the top surface of the mold | [4] |
| 1991 | Herbertson et al. | Bias flow of molten steel in the mold | [20] |
| 1994 | Thomas et al. | Disturbance of argon blowing on top surface of the mold | [21] |
| 1994 | Codur et al. | Nozzle blockage, stopper rod erosion, and static pressure change in molten steel in the tundish; transient variations in casting speed and slab bulging | [22] |
| 2002 | Yoon et al. | Influence of slab bulging under unsteady casting conditions | [23] |
| 2008 | Zhang et al. | Serious SEN clogging causing severe level fluctuation of the top surface | [24] |
| 2013 | Li et al. | Slab bulging as the root cause of periodic fluctuation of the top surface | [19] |
| 2014 | Liu et al. | Disturbance of the stopper rod | [25] |
| 2017 | Zhao et al. | Up and down fluctuation of the molten steel jet causing the asymmetric distribution of the flow field and generation of vortices | [26] |
| 2018 | Zhu et al. | Large-scale vortex structure in the lower recirculation zone of the mold | [27] |
| 2019 | Cho et al. | When the flow field of the mold was a single roll flow pattern, the drastic change in the jet led to a large fluctuation on the top surface. | [28] |
| 2019 | Chen et al. | Up and down swing of the molten steel stream from the SEN | [29] |
| 2020 | Jiang et al. | Abnormal mold level fluctuation was mainly induced by the shell bulging while moving through the rollers. | [10] |
| 2023 | Lei et al. | Abnormal mold level fluctuation of HP steel came from the resonance phenomenon. | [30] |
| Parameter | Value |
|---|---|
| Mold width × thickness | 1500 mm × 200 mm |
| Mold height | 900 mm |
| Length of calculation domain | 3000 mm |
| Mold work level | 800 mm |
| Inner diameter of SEN | 58 mm |
| Length of SEN | 890 mm |
| SEN outport angle | 15° down |
| Height of SEN port | 55 mm |
| Width of SEN port | 45 mm |
| Submergence depth of SEN | 130 mm |
| Casting speed | 0.8 to 1.0 m/min |
| Thickness of liquid slag | 30 mm |
| C | Si | Mn | P | S | N | Als | Fe |
|---|---|---|---|---|---|---|---|
| 0.16 | 0.31 | 1.35 | 0.016 | 0.005 | 0.003 | 0.030 | 98.126 |
| SiO2 | CaO | Al2O3 | Fe2O3 | MgO | Na2O | K2O | MnO2 | LiO2 | C |
|---|---|---|---|---|---|---|---|---|---|
| 39.94 | 34.87 | 7.60 | 2.14 | 3.84 | 1.83 | 0.47 | 5.03 | 1.22 | 3.06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Y.; Zhou, H.; Wang, G.; Xu, L.; Qiu, S.; Zhu, R. Numerical Modeling of Transient Flow Characteristics on the Top Surface of a Steel Slab Continuous Casting Strand Using a Large Eddy Simulation Combined with Volume of Fluid Model. Materials 2023, 16, 5665. https://doi.org/10.3390/ma16165665
Tian Y, Zhou H, Wang G, Xu L, Qiu S, Zhu R. Numerical Modeling of Transient Flow Characteristics on the Top Surface of a Steel Slab Continuous Casting Strand Using a Large Eddy Simulation Combined with Volume of Fluid Model. Materials. 2023; 16(16):5665. https://doi.org/10.3390/ma16165665
Chicago/Turabian StyleTian, Yushi, Haichen Zhou, Guobin Wang, Lijun Xu, Shengtao Qiu, and Rong Zhu. 2023. "Numerical Modeling of Transient Flow Characteristics on the Top Surface of a Steel Slab Continuous Casting Strand Using a Large Eddy Simulation Combined with Volume of Fluid Model" Materials 16, no. 16: 5665. https://doi.org/10.3390/ma16165665
APA StyleTian, Y., Zhou, H., Wang, G., Xu, L., Qiu, S., & Zhu, R. (2023). Numerical Modeling of Transient Flow Characteristics on the Top Surface of a Steel Slab Continuous Casting Strand Using a Large Eddy Simulation Combined with Volume of Fluid Model. Materials, 16(16), 5665. https://doi.org/10.3390/ma16165665





