Experimental vs. Theoretical Viscosity Determination of Aluminosilicate Glasses
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Analysis
3.1. Determination of Chemical Composition
3.2. Determination of Temperatures for Constant Viscosity Values by Experimental Methods
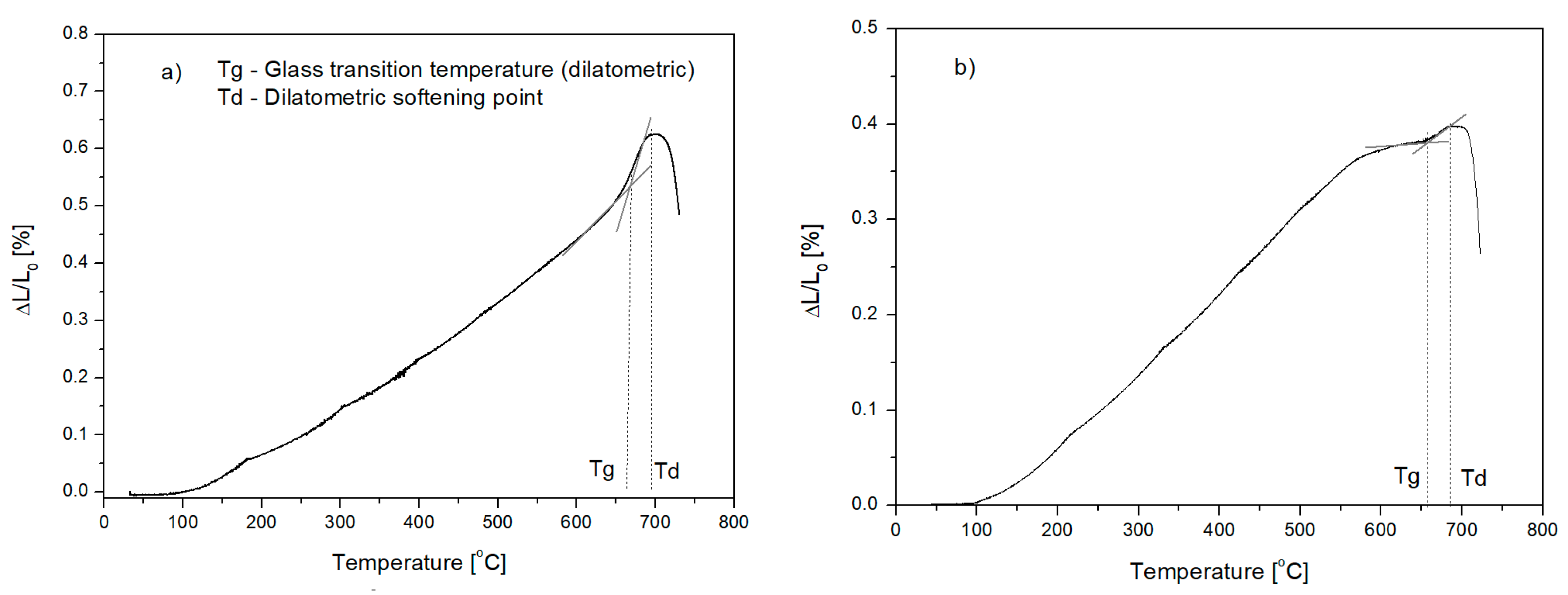
3.2.1. Dilatometric Test
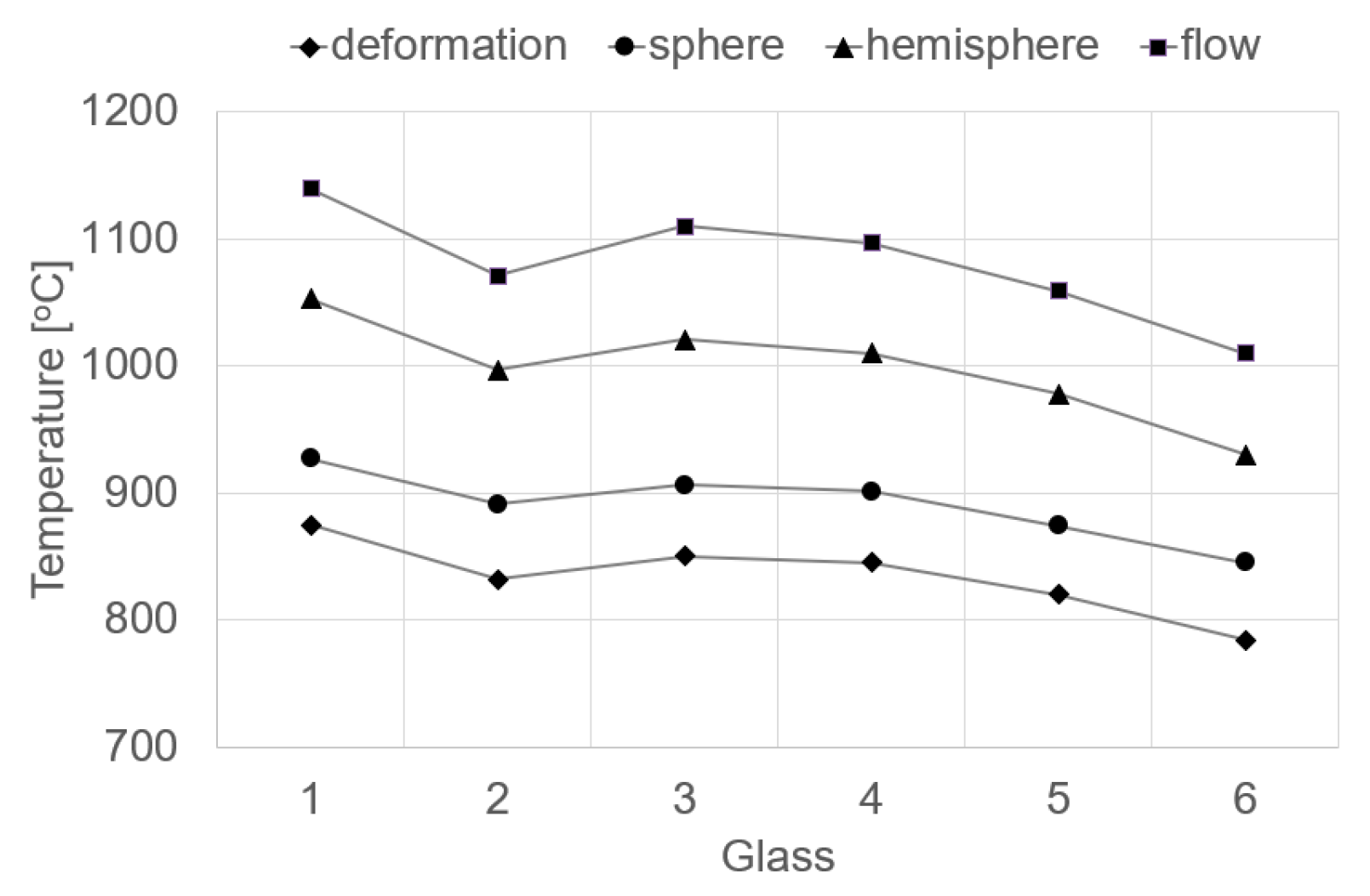
3.2.2. High Temperature Microscopy
3.3. Calculation Methods
3.3.1. Viscosity—Vogel–Fulcher–Tammann Method
3.3.2. Viscosity—M.W. Ochotin Method
- T—temperature [°C]
- x—percentage content of Na2O
- y—percentage content of the sum of CaO and MgO
- z—percentage content of Al2O3
| Viscosity [dPa·s] | Coefficients | |||
|---|---|---|---|---|
| A | B | C | D | |
| 1013 | −7.32 | 3.49 | 5.37 | 603.4 |
| 104 | −17.49 | −9.95 | 5.9 | 1381.4 |
| Viscosity [dPa·s] | Glass | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Temperature [°C] | ||||||
| 1013 | 677 | 683 | 686 | 689 | 669 | 650 |
| 104 | 1262 | 1134 | 1198 | 1175 | 1147 | 1118 |
3.3.3. Viscosity—Tuszynski Method
3.3.4. Viscosity Calculated from Polynomial for Aluminosilicate Glasses
3.4. Viscosity Curve Plotting Based on Specific Temperatures at Viscosities of 1013 and 104 [dPa·s]
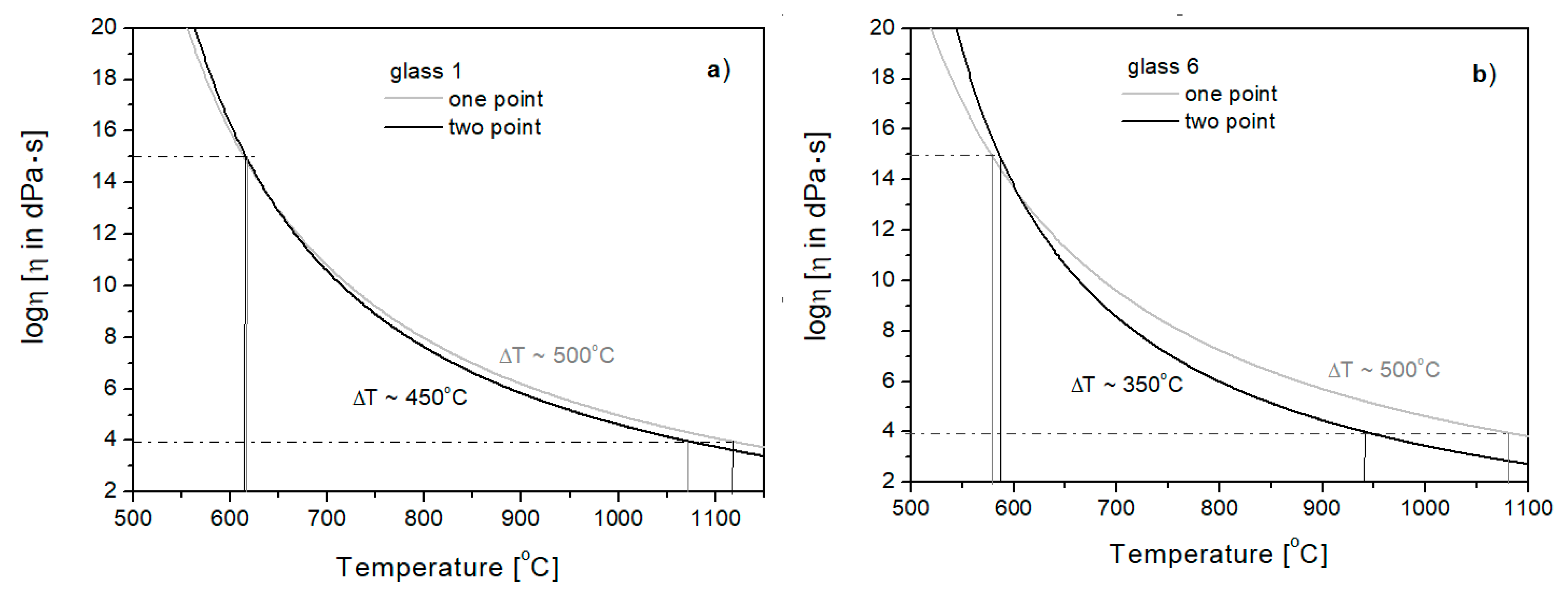
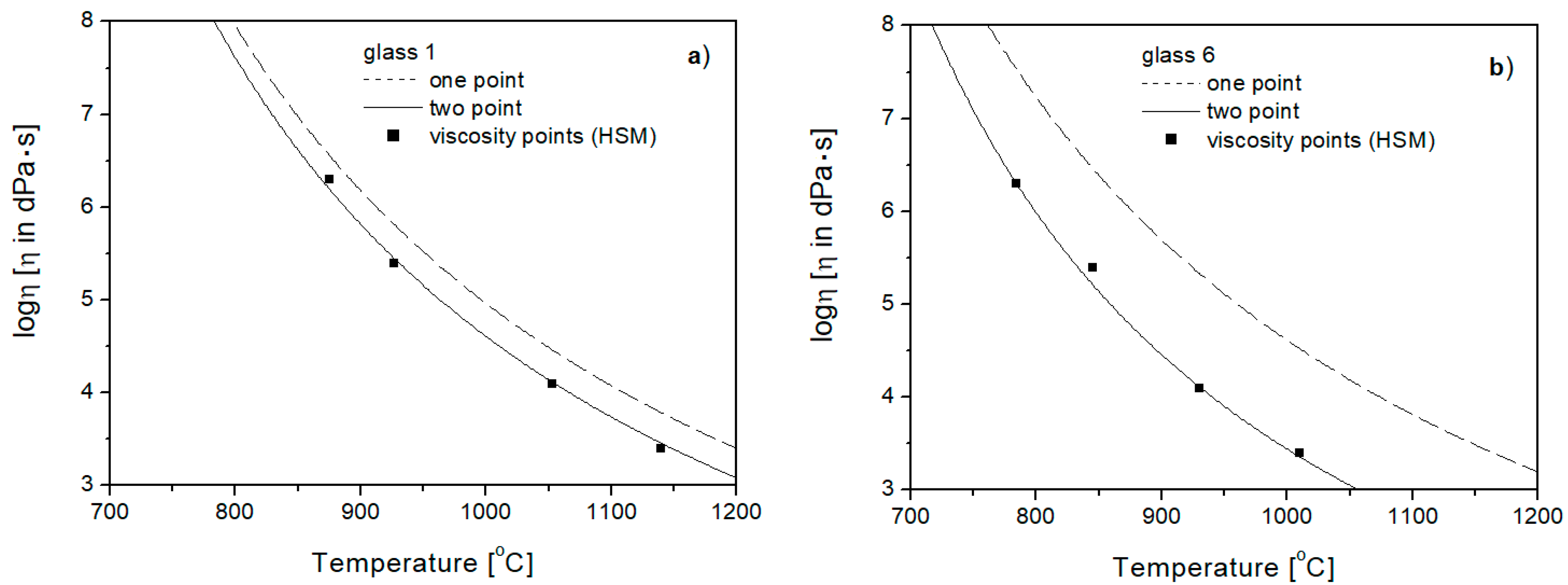
3.4.1. One-Point Method
- Tg—transition temperature at a viscosity of 1013 [dPa·s];
- T—temperature [°C];
- C1, C2—constant: C1—14.97; C2—278.

3.4.2. Two-Point Method
4. Conclusions
- Based on the analytical methods used to assess the viscosity of the glass mass in a wide temperature range, it was found that when selecting the appropriate calculation model, the basic chemical composition of the glass should always be taken into account, with particular emphasis on the share of amphoteric elements.
- It was justified that in order to plot the viscosity curve with the correct slope in the forming range, for aluminosilicate glasses it is appropriate to use the two-point method, based on fixed viscosity points for viscosities of 104 [dPa·s] (working point) and 1013 [dPa·s] (transition temperature).
- Amphoteric metal ions (e.g., Al3+, Fe3+ and Mg2+) have a significant impact on the viscosity of the glass mass, and thus on the quality of the manufactured products. The way they are embedded in the glass structure can cause a modifying effect (coordination number 6) or a binding effect (coordination number 4). An increase in the content of metal ions in coordination number 4 results in the incorporation of these ions into the glass network, and thus its strengthening, which in turn causes an increase in the viscosity of the melt.
- In the range of high temperatures, with at viscosity in the range of from η = 103 to 107 [dPa·s], the modifying effect of the addition of basalt and cullet was found, manifested by a decline in the viscosity of the glass mass, accompanied by a drop in the TE temperature in the working range.
- In the process of producing aluminosilicate glass, a thorough analysis of the temperature parameters characterizing the raw material sets is of great importance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Scholze, H. Glass: Nature, Structure, and Properties; Springer: New York, NY, USA, 1991. [Google Scholar] [CrossRef]
- Cantini, A.; Leoni, L.; Ferraro, S.; De Carlo, F.; Martini, C.; Martini, F.; Salvio, M. Technological Energy Efficiency Improvements in Glass-Production Industries and Their Future Perspectives in Italy. Processes 2022, 10, 2653. [Google Scholar] [CrossRef]
- Seo, K.; Edgar, T.F.; Baldea, M. Optimal demand response operation of electric boosting glass furnaces. Appl. Energy 2020, 269, 115077. [Google Scholar] [CrossRef]
- Galewicz, M.; Wasylak, J. Możliwości obniżenia temperatury topienia szkła opakowaniowego. Szkło i Ceramika 2008, 59, 11–15. [Google Scholar]
- Shao, Z.F.; Bao, Y.W.; Jia, Y.N.; Rao, C.D.; Sui, M.; Wang, Y.F.; Xiang, Z.K. Analysis of influence of high temperature homogenizing on UV transmittance of quartz glass. Key Eng. Mater. 2016, 680, 285–288. [Google Scholar] [CrossRef]
- Kim, Y.; Morita, K. Thermal conductivity of molten B2O3, B2O3-SiO2, Na2O-B2O3, and Na2O-SiO2 systems. J. Am. Ceram. Soc. 2015, 98, 1588–1595. [Google Scholar] [CrossRef]
- Liu, C.K.; Lee, R.Y.; Lin, K.F. Effects of lanthanum-to-calcium ratio on the thermal and crystalline properties of BaO-Al2O3-B2O3-SiO2 based glass sealants for solid oxide fuel cells. J. Ceram. Soc. Jpn. 2015, 123, 239–244. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, X.; Liu, W.; Lv, X.; Bai, C.; Wang, L. Relationship between structure and viscosity of CaO–SiO2–Al2O3–MgO–TiO2 slag. J. Non-Cryst. Solids 2014, 402, 214–222. [Google Scholar] [CrossRef]
- Brosh, E.; Pelton, A.D.; Decterov, S.A. A model to calculate the viscosity of silicate melts: Part IV: Alkali-free borosilicate melts. Int. J. Mater. Res. 2012, 103, 494–501. [Google Scholar] [CrossRef]
- Gan, L.; Xin, J.; Zhou, Y. Accurate Viscosity Calculation for Melts in SiO2–Al2O3–CaO–MgO Systems. ISIJ Int. 2017, 57, 1303–1312. [Google Scholar] [CrossRef]
- Gan, L.; Lai, C.A. General Viscosity Model for Molten Blast Furnace Slag. Metall. Mater. Trans. B 2014, 45, 875–888. [Google Scholar] [CrossRef]
- Shelby, J.E. Introduction to Glass Science and Technology, 2nd ed.; RSC: New York, NY, USA, 2005; pp. 120–122. [Google Scholar]
- Ciecińska, M.; Dorosz, D.; Greiner-Wrona, E.; Gruszka, B.; Kucharski, J.; Lisiecki, M.; Łączka, M. Technologia Szkła, Właściwości Fizykochemiczne, Część I; Polskie Towarzystwo Ceramiczne: Kraków, Poland, 2002. [Google Scholar]
- Ochotin, M.W. Calculation of Viscosity of Commercial Silicate Classes by the Use of Nomographs. Steklo i Keram 1954, 11, 7–11. [Google Scholar]
- Jebsten-Marwedel, H.; Bruckner, R. Glastechnische Fabrikationsfehler; Springer: New York, NY, USA, 1980. [Google Scholar]
- Mauro, J.C.; Yue, Y.; Ellison, A.J.; Guptac, P.K.; Allan, D.C. Viscosity of glass-forming liquids. Proc. Natl. Acad. Sci. USA 2009, 106, 19780–19784. [Google Scholar] [CrossRef] [PubMed]
- Han, C.; Chen, M.; Zhang, W.; Zhao, Z.; Evans, T.; Zhao, B. Evaluation of Existing Viscosity Data and Models and Developments of New Viscosity Model for Fully Liquid Slag in the SiO2-Al2O3-CaO-MgO System. Metall. Mater. Trans. B 2016, 47, 2861–2874. [Google Scholar] [CrossRef]
- Grundy, A.N.; Liu, H.; Jung, I.-H.; Decterov, S.A.; Pelton, A.D. A model to calculate the viscosity of silicate melts: Part I: Viscosity of binary SiO2–MeOx systems (Me = Na, K, Ca, Mg, Al). Int. J. Mater. Res. 2008, 99, 1185–1194. [Google Scholar] [CrossRef]
- Zawada, A.; Bieniarz, P.; Kolan, C.; Hessenkemper, H. Modelling Selected Properties of Glasses Based on Slag from a Waste. Inciner. Plant. Glass Tech. Eur. J. Glass Sci. Tech. Part A 2013, 54, 72–76. [Google Scholar]
- Zawada, A.; Lubasa, M.; Przerada, I. Mössbauer spectroscopy and FT-IR to describe coordination of amphoteric ions in structure of glasses from the SiO2–Na2O–MgO–CaO–Al2O3–Fe2O3 system. J. Mol. Struct. 2023, 1285, 135368. [Google Scholar] [CrossRef]
- Karlsson, S. Viscosity of alumina doped soda lime silicate glasses—Observation of anomaly in the linear increase as Al2O3 replaces SiO2. J. Non-Cryst. Solids 2021, 573, 121149. [Google Scholar] [CrossRef]
- Clarke, J.B.; Hastie, J.W.; Kihlborg, L.H.E.; Metselaar, R.; Thackeray, M.M. Definitions of terms relating to phase transitions of the solid state (IUPAC Recommendations 1994). Pure Appl. Chem. 1994, 66, 577–594. [Google Scholar] [CrossRef]
- Hutchinson, J.M. Determination of the glass transition temperature. J. Therm. Anal. Calorim. 2009, 98, 579. [Google Scholar] [CrossRef]
- Dietzel, A.; Brückner, R. Ein Fixpunkt der Zähigkeit im Verarbeitungsbereich der Gläser. Schnellbestimmung des Viskositäts-, Temperatur- Verlaufes. Glastech. Berichte 1957, 3, 73–79. [Google Scholar]
- Mazurin, O.V.; Gankin, Y.V. Glass transition temperature: Problems of measurements and analysis of the existing data. In Proceedings of the International Congress on Glass, Strasbourg, France, 1–6 July 2007. [Google Scholar]
- Le Bourhis, E. Glass—Mechanics and Technology; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2007. [Google Scholar]
- Zawada, A.; Lubasa, M.; Przerada, I.; Sitarz, M.; Adamczyk-Habrajska, M. The Effect of the Reducing Melting Atmosphere on Coordination Moieties in Aluminosilicate Glasses. J. Mol. Struct. 2020, 1218, 128474. [Google Scholar] [CrossRef]
- Yuan, F.; Zhao, Z.; Zhang, Y.; Wu, T. Effect of Al2O3 content on the viscosity and structure of CaO–SiO2–Cr2O3–Al2O3 slags. Int. J. Miner. Metall. Mater. 2022, 29, 1522–1531. [Google Scholar] [CrossRef]
- Lü, J.; Jin, Z.; Yang, H.; Tong, L.-L.; Chen, G.-B.; Xiao, F.-X. Effect of the CaO/SiO2 mass ratio and FeO content on the viscosity of CaO–SiO2–“FeO”–12wt%ZnO–3wt%Al2O3 slags. Int. J. Miner. Metall. Mater. 2017, 24, 756–767. [Google Scholar] [CrossRef]
- Richet, P. Encyclopedia of Glass Science, Technology, History, and Culture; Wiley: Hoboken, NJ, USA, 2021; pp. 538–539. [Google Scholar]
- Gao, Y.; Wang, S.; Hong, C. Effects of basicity and MgO content on the viscosity of the SiO2-CaO-MgO-9wt%Al2O3 slag system. Int. J. Miner. Metall. Mater. 2014, 21, 353–362. [Google Scholar] [CrossRef]
- Nowak, A.; Caban, A.; Lubas, M.; Iwaszko, J. Właściwości modyfikowanego szkła amfibolitowego. Mater. Ceram./Ceram. Mater. 2020, 72, 161–170. [Google Scholar]
- Pascual, M.J.; Pascual, L.; Durán, A. Determination of the viscosity temperature curve for glasses on the basis of fixed viscosity points determined by hot stage microscopy. Phys. Chem. Glasses 2001, 42, 61–66. [Google Scholar]
- Stábile, F.M.; Piccico, M.; Serra, M.F.; Rafti, M.; Súarez, G.; Rendtorff, N.M. Viscosity and Thermal Evolution of Density and Wetting Angle of a Commercial Glaze by Means of Hot Stage Microscopy. Procedia Mater. Sci. 2015, 9, 563–570. [Google Scholar] [CrossRef]
- Wasylak, J.; Czarnacki, K. Wpływ stłuczki szklanej z recyklingu na właściwości produkowanych opakowań szklanych w aspekcie nowych metod uszlachetniania powierzchni. Prace Instytutu Ceramiki i Materiałów Budowlanych 2012, 11, 9–19. [Google Scholar]
- Reben, M.; Wasylak, J.; Lisiecki, M.; Kuciński, G.; Kosmal, M. Surowce odpadowe jako nukleatory krystalizacji stłuczki kineskopowej. Mater. Ceram./Ceram. Mater. 2012, 64, 405–410. [Google Scholar]
- Teschner, R. Glasviskosität. In Glasfasern; Springer Vieweg: Berlin/Heidelberg, Germany, 2019. [Google Scholar] [CrossRef]
- Gao, Q.; Jian, Z. Fragility and Vogel-Fulcher-Tammann parameters near Glass transition temmperature. Mater. Chem. Phys. 2020, 252, 123252. [Google Scholar] [CrossRef]
- Zawada, A.; Przerada, I.; Lubas, M.; Sitarz, M.; Leśniak, M. Application of Statistical Methods in Predicting the Properties of Glass-Ceramic Materials Obtained from Inorganic Solid Waste. Materials 2021, 14, 2651. [Google Scholar] [CrossRef] [PubMed]


| Oxide | Amphibolite | Basalt | Dolomite | Float Cullet |
|---|---|---|---|---|
| SiO2 | 55.58 | 41.01 | 3.27 | 71.89 |
| Al2O3 | 15.23 | 14.22 | 1.37 | 0.59 |
| CaO | 6.27 | 11.01 | 59.34 | 9.28 |
| Fe2O3 | 10.62 | 13.71 | 0.83 | 0.08 |
| MgO | 4.93 | 10.20 | 36.93 | 3.94 |
| Na2O | 5.58 | 5.43 | 0.37 | 13.72 |
| TiO2 | 1.11 | 1.14 | 0.04 | 0.06 |
| K2O | 0.23 | 1.31 | 0.19 | 0.11 |
| P2O5 | 0.10 | 1.02 | 0.06 | <0.1 |
| MnO | 0.26 | 0.22 | 0.19 | 0.01 |
| ZrO2 | 0.10 | - | 0.26 | 0.02 |
| Raw Materials in Sets [wt%] | ||||
| Set | Amphibolite | Basalt | Dolomite | Float Cullet |
| 1 | 100 | - | - | - |
| 2 | 70 | - | 10 | 20 |
| 3 | 85 | - | 5 | 10 |
| 4 | 40 | 50 | - | 10 |
| 5 | 30 | 50 | - | 20 |
| 6 | 20 | 50 | - | 30 |
| Oxides | Glasses | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| SiO2 | 56.28 | 53.86 | 54.73 | 46.97 | 48.59 | 50.23 |
| Al2O3 | 14.53 | 11.20 | 13.25 | 13.21 | 11.84 | 10.47 |
| CaO | 6.27 | 11.92 | 9.01 | 9.31 | 9.30 | 9.30 |
| Fe2O3 | 9.62 | 7.39 | 8.85 | 9.29 | 8.32 | 7.34 |
| MgO | 5.93 | 7.75 | 6.76 | 8.15 | 7.70 | 7.25 |
| Na2O | 5.58 | 6.72 | 6.01 | 6.35 | 7.79 | 9.24 |
| TiO2 | 1.11 | 0.77 | 0.94 | 2.07 | 1.90 | 1.72 |
| K2O | 0.23 | 0.16 | 0.18 | 0.85 | 0.82 | 0.79 |
| P2O5 | 0.10 | 0.00 | 0.00 | 0.43 | 0.43 | 0.43 |
| MnO | 0.26 | 0.23 | 0.27 | 0.15 | 0.13 | 0.11 |
| ZrO2 | 0.10 | 0.00 | 0.00 | 3.21 | 3.17 | 3.13 |
| Oxides | SiO2 | Al2O3 | CaO | MgO | Fe2O3 | Na2O | K2O |
|---|---|---|---|---|---|---|---|
| wt% | 46–56 | 10–15 | 6–12 | 5–8 | 7–11 | 5–9 | 0–1 |
| Glass | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Tg | 661 | 600 | 639 | 657 |
| Td | 695 | 636 | 642 | 685 |
| Glass | Characteristic Temperatures [°C] | |||
|---|---|---|---|---|
| Deformation logη = 6.3 | Sphere logη = 5.4 | Hemisphere logη = 4.1 | Flow logη = 3.4 | |
| 1 | 875 | 927 | 1053 | 1140 |
| 2 | 832 | 891 | 997 | 1071 |
| 3 | 850 | 906 | 1021 | 1110 |
| 4 | 845 | 901 | 1010 | 1097 |
| 5 | 820 | 874 | 978 | 1059 |
| 6 | 784 | 845 | 930 | 1010 |
| Viscosity [dPa·s] | Glass | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Temperature [°C] | ||||||
| 1013 | 929 | 903 | 925 | 929 | 897 | 865 |
| 104 | 3149 | 3281 | 3269 | 3412 | 3259 | 3118 |
| Viscosity [dPa·s] | A1 | A2 | A3 | A4 | A5 |
|---|---|---|---|---|---|
| 103 | 16.73 | 23.2 | 0.63 | 9.6 | −6.14 |
| 104 | 13.63 | 19.5 | 3.68 | 9.7 | −3.86 |
| 105 | 11.79 | 16.8 | 5.54 | 10.5 | −3.58 |
| 106.5 | 9.70 | 14.3 | 7.51 | 11.0 | −2.49 |
| 107 | 9.03 | 13.4 | 7.85 | 10.5 | −1.33 |
| 108 | 8.12 | 12.4 | 8.59 | 10.0 | −0.59 |
| 109 | 6.57 | 10.2 | 8.87 | 8.9 | 4.52 |
| 1010 | 7.18 | 10.7 | 9.82 | 8.8 | −1.43 |
| 1011 | 6.75 | 10.1 | 10.90 | 8.1 | −1.24 |
| 1012 | 6.46 | 10.0 | 9.66 | 6.7 | −0.97 |
| 1013 | 6.10 | 9.9 | 9.25 | 5.3 | −0.04 |
| Viscosity [dPa·s] | Glass | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Temperature [°C] | ||||||
| 1013 | 554 | 591 | 584 | 544 | 538 | 532 |
| 104 | 1067 | 1046 | 1080 | 983 | 969 | 954 |
| Oxide | SiO2 | Al2O3 | CaO | MgO | Fe2O3 | R2O * |
|---|---|---|---|---|---|---|
| wt% | 45–60 | 8–20 | 10–25 | 3–15 | 2–10 | 4–6 |
| Viscosity [dPa·s] | Glass | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Temperature [°C] | ||||||
| 1013 | 641 | 630 | 637 | 645 | 625 | 605 |
| 104 | 1070 | 1012 | 1038 | 1026 | 994 | 943 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zawada, A.; Lubas, M.; Nowak, A. Experimental vs. Theoretical Viscosity Determination of Aluminosilicate Glasses. Materials 2023, 16, 5789. https://doi.org/10.3390/ma16175789
Zawada A, Lubas M, Nowak A. Experimental vs. Theoretical Viscosity Determination of Aluminosilicate Glasses. Materials. 2023; 16(17):5789. https://doi.org/10.3390/ma16175789
Chicago/Turabian StyleZawada, Anna, Malgorzata Lubas, and Adrian Nowak. 2023. "Experimental vs. Theoretical Viscosity Determination of Aluminosilicate Glasses" Materials 16, no. 17: 5789. https://doi.org/10.3390/ma16175789
APA StyleZawada, A., Lubas, M., & Nowak, A. (2023). Experimental vs. Theoretical Viscosity Determination of Aluminosilicate Glasses. Materials, 16(17), 5789. https://doi.org/10.3390/ma16175789






