Field Investigation of the Dynamic Response of Culvert–Embankment–Culvert Transitions in a High-Speed Railway
Abstract
:1. Introduction
2. Material Properties and Construction Process
2.1. Assignment of Construction Equipment
2.2. The Ratio of Graded Crushed Stone
2.3. Quality Inspection of Raw Filling Material
2.4. Grading of Gravel
2.5. Compaction Test and Unconfined Compressive Strength Test
2.6. Compaction or Rolling Effect
3. Field Test of the Transition Section
3.1. Brief Introduction of the Test Site
3.2. Basic Test Parameters and Test Instruments
4. Signal Processing
5. Dynamic Responses of the Transition Sections
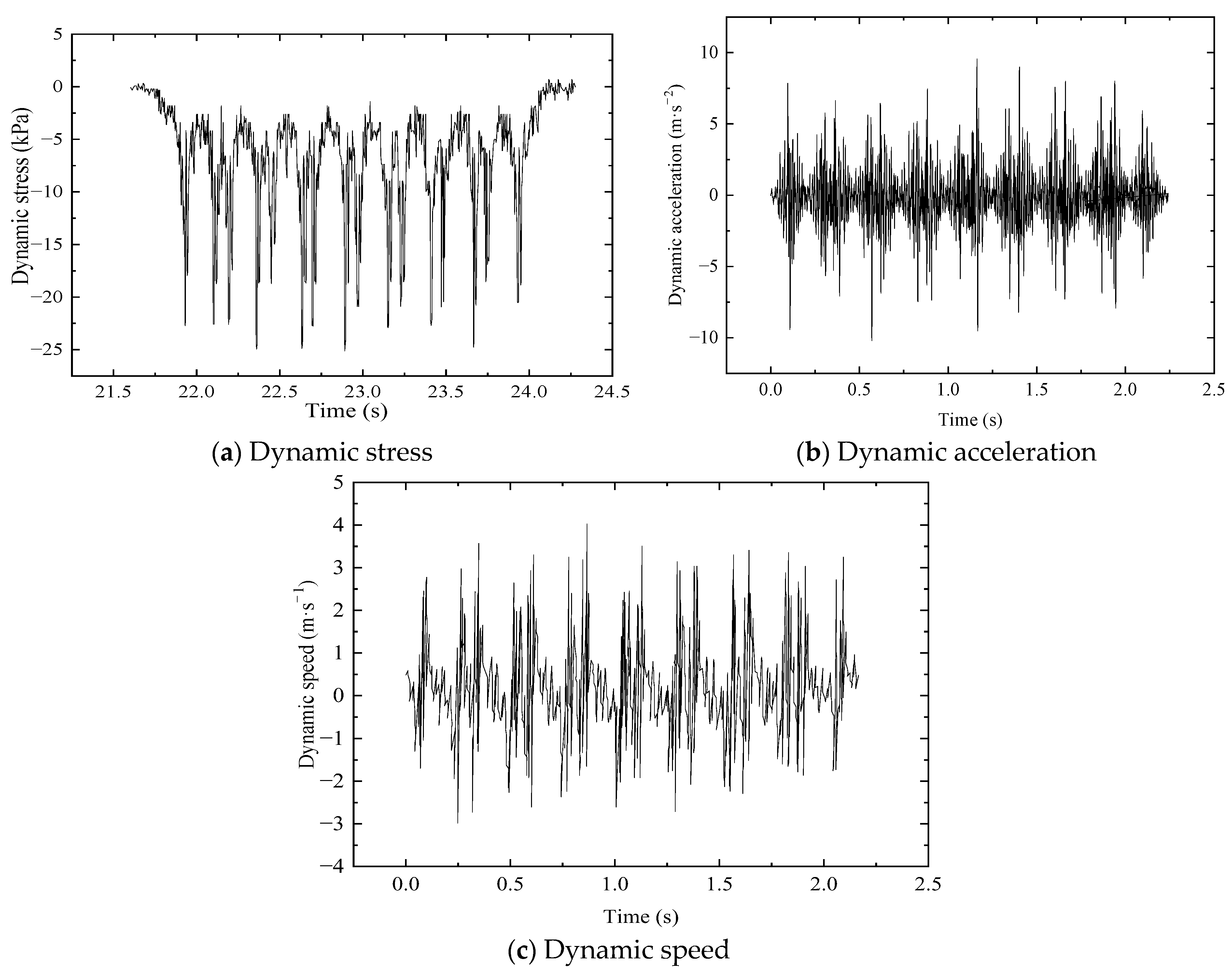
5.1. Time–History Domain Analysis
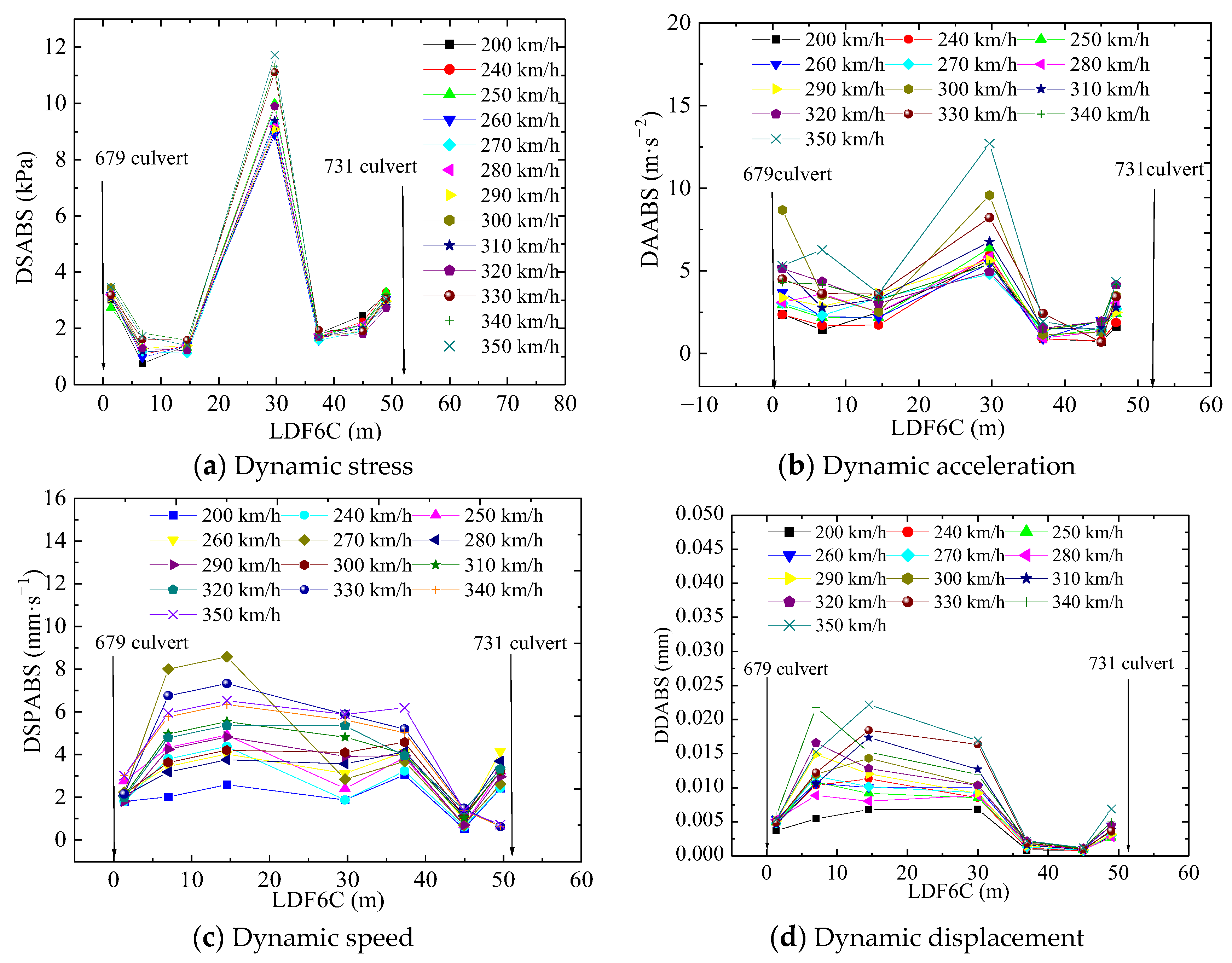
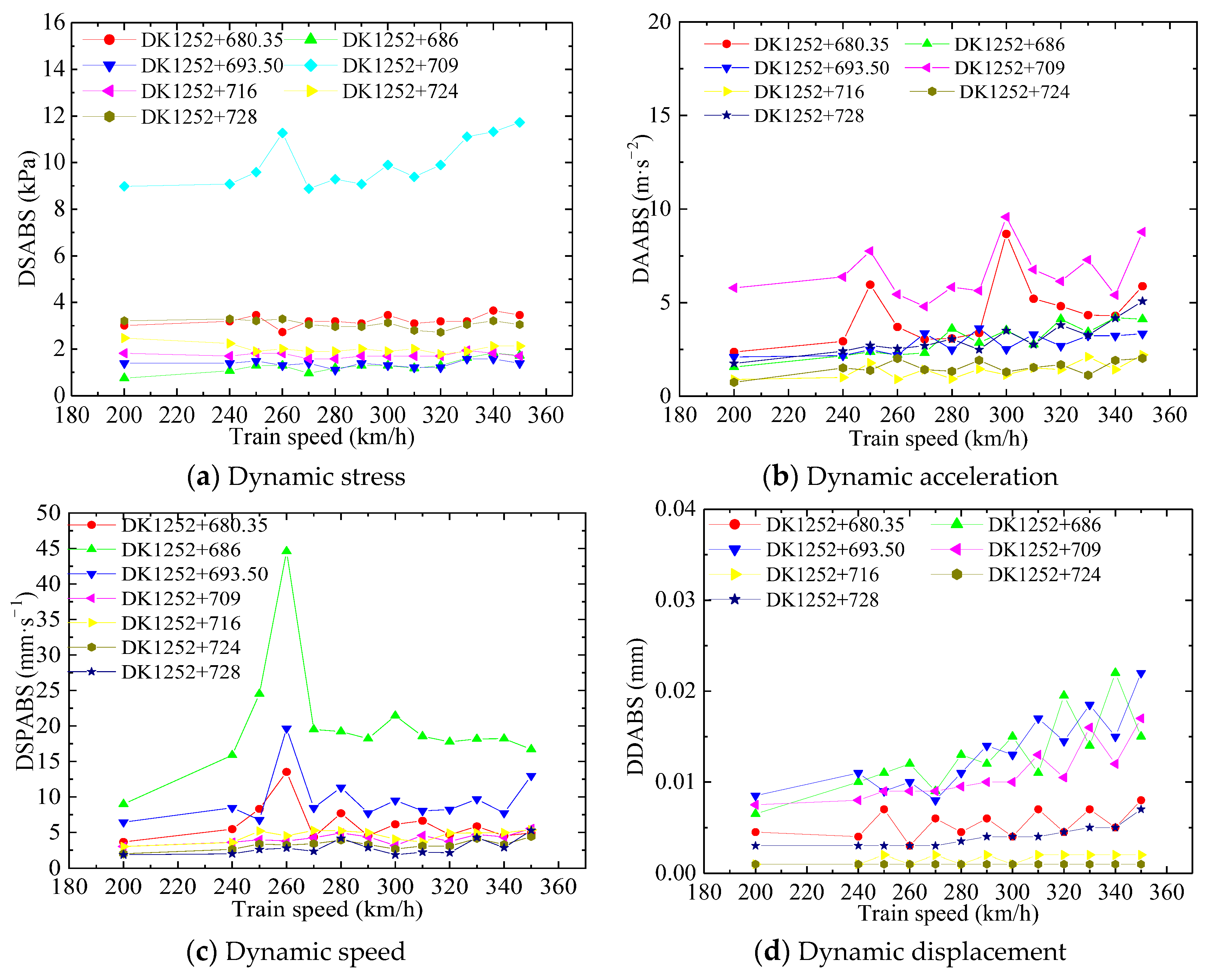
5.2. Responses along the Railway Line
5.3. Response along the Depth
5.4. Response to Train Running Speed
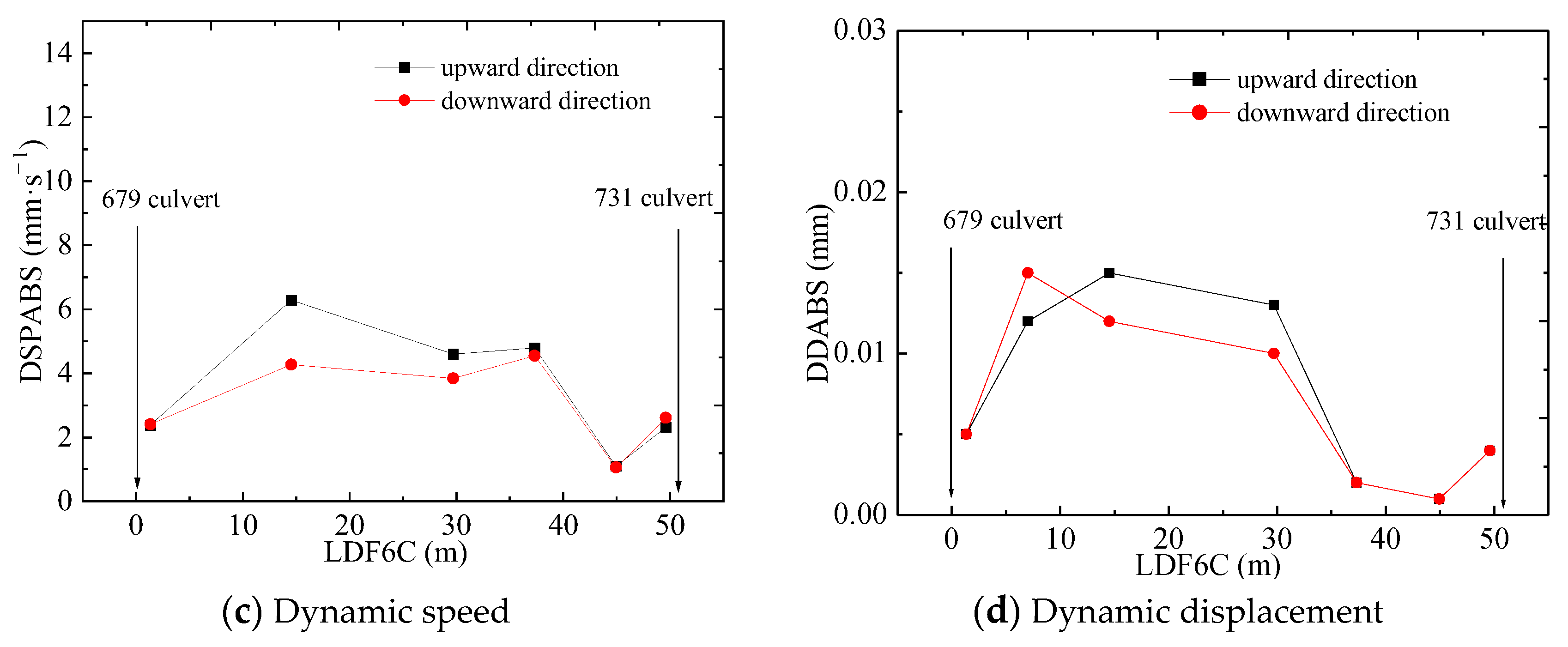
5.5. Response to Train’s Running Direction
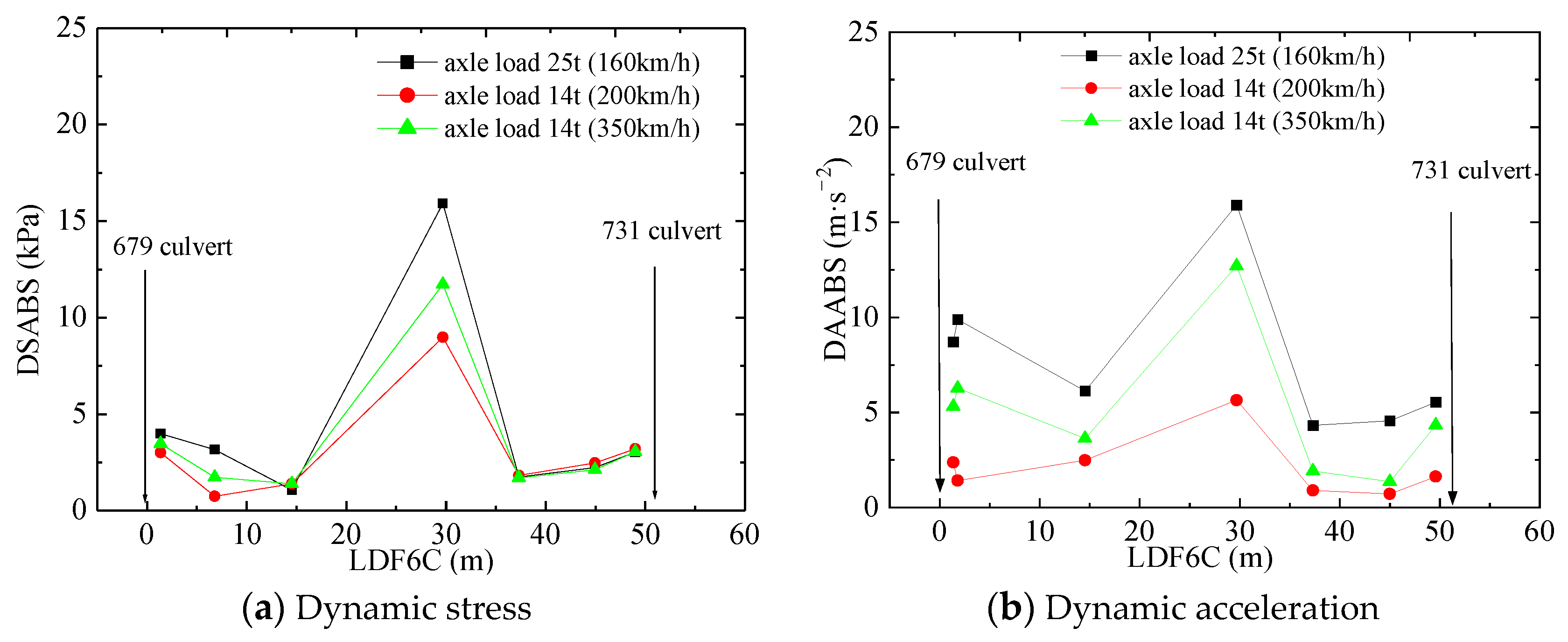
5.6. Response to Vehicle Axle Weight
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hu, N.; Dai, G.L.; Yan, B.; Liu, K. Recent development of design and construction of medium and long span high-speed railway bridges in China. Eng. Struct. 2014, 74, 233–241. [Google Scholar] [CrossRef]
- Moliner, E.; Martínez-Rodrigo, M.D.; Museros, P. Dynamic performance of existing double track railway bridges at resonance with the increase of the operational line speed. Eng. Struct. 2017, 132, 98–109. [Google Scholar] [CrossRef]
- Albalate, D.; Bel, G. The Economics and Politics of High-Speed Rail: Lessons from Experiences Abroad; Lexington Books: Plymouth, UK, 2012. [Google Scholar]
- Taniguchi, M. High-Speed Rail in Japan: A Review and Evaluation of the Shinkansen Train; Working Paper No. 103; University of California Transportation Center: Berkeley, CA, USA, 1992. [Google Scholar]
- Bouley, J. Short history of “high-speed” railway in France before the TGV. Jpn. Railw. Transp. Rev. 1994, 3, 49–51. [Google Scholar]
- European Commission. High-Speed Europe, a Sustainable Link between Citizens; Publications Office of the European Union: Luxembourg, 2010; p. 22.
- Gourvish, T. The High Speed Rail Revolution: History and Prospects; HS2 Ltd.: London, UK, 2010. [Google Scholar]
- Zuber, W. High speed rail in Europe-a three decade success story. Network 2011, 73, 8–11. (In Chinese) [Google Scholar]
- Harrison, J.; Dezarn, S.; Dobbins, A.; Issac, L. Short history of HSR in the USA. Network 2011, 73, 17–19. [Google Scholar]
- Amtrak. High-Speed Rail: A National Perspective, High-Speed Rail Experience in the United States; Cambridge Systematics: Austin, TX, USA, 2008. (In Chinese) [Google Scholar]
- Todorovich, P.; Schned, D.; Lane, R. High-Speed Rail International Lessons for U.S. Policy Makers; Lincoln Institute of Land Policy: Cambridge, MO, USA, 2011. [Google Scholar]
- Albalate, D.; Bel, G. High-speed rail: Lessons for policy makers from experiences abroad. Public Adm. Rev. 2012, 72, 336–349. [Google Scholar] [CrossRef]
- Li, D.; Otter, D.; Carr, G. Railway bridge approaches under heavy axle load traffic: Problems, causes, and remedies. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2010, 224, 383–390. [Google Scholar] [CrossRef]
- Shan, Y.; Shu, Y.; Zhou, S. Finite-infinite element coupled analysis on the influence of material parameters on the dynamic properties of transition zones. Constr. Build. Mater. 2017, 148, 548–558. [Google Scholar] [CrossRef]
- Mishra, D.; Tutumluer, E.; Stark, T.D.; Hyslip, J.P.; Chrismer, S.M.; Tomas, M. Investigation of differential movement at railroad bridge approaches through geotechnical instrumentation. J. Zhejiang Univ. Sci. A 2012, 13, 814–824. [Google Scholar] [CrossRef]
- Shan, Y.; Albers, B.; Savidis, S.A. Influence of different transition zones on the dynamic response of track-subgrade systems. Comput. Geotech. 2013, 48, 21–28. [Google Scholar] [CrossRef]
- Li, W.; Bian, X. Dynamic performance of pile-supported bridge-embankment transition zones under high-speed train moving loads. Procedia Eng. 2016, 143, 1059–1067. [Google Scholar] [CrossRef]
- European Rail Research Institute. D State of the Art Report. Embankment Structure Transition; Bridge Ends/European Rail Research Institute: Brussels, Belgium, 2016. [Google Scholar]
- Supertrack—Sustained Performance of Railway Tracks. 2002–2005. 2013. Available online: http://cordis.europa.eu/projects/rcn/63386_en.html (accessed on 28 July 2023).
- Ribeiro, C.A.; Calçada, R.; Delgado, R. Experimental assessment of the dynamic behaviour of the train-track system at a culvert transition zone. Eng. Struct. 2017, 138, 215–228. [Google Scholar] [CrossRef]
- Berggren, E. Railway Track Stiffness: Dynamic Measurements and Evaluation for Efficient Maintenance; Division of Rail Vehicles, Royal Institute of Technology (KTH): Stockholm, Sweden, 2009. [Google Scholar]
- Li, D.; Davis, D. Transition of railroad bridge approaches. J. Geotech. Geoenvironmental Eng. 2005, 131, 1392–1398. [Google Scholar] [CrossRef]
- Le, T.H.M.; Lee, S.H.; Park, D.W.; Lee, D.W. Evaluation on the full-scale testbed performance of lightweight foamed soil using railroad loading system. Constr. Build. Mater. 2022, 230, 127249. [Google Scholar]
- Bebianoa, R.; Calçadab, R.; Camotima, D.; Silvestre, N. Dynamic analysis of high-speed railway bridge decks using generalised beam theory. Thin-Walled Struct. 2017, 114, 22–31. [Google Scholar] [CrossRef]
- Sheng, X.; Zhon, T.; Li, Y. Vibration and sound radiation of slab high-speed railway tracks subject to a moving harmonic load. J. Sound Vib. 2017, 395, 160–186. [Google Scholar] [CrossRef]
- Sheng, X.; Xiao, X.; Zhang, S. The time domain moving Green function of a railway track and its application to wheel-rail interactions. J. Sound Vib. 2016, 377, 133–154. [Google Scholar] [CrossRef]
- Lu, L.; Lin, Y.L.; Guo, D.D.; Xing, H.; Zhang, Z.; Duan, J.Y. A modified Newmark block method for determining the seismic displacement of a slope reinforced by prestressed anchors. Comput. Geotech. 2023, 162, 105697. [Google Scholar] [CrossRef]
- Lin, Y.L.; Lu, L.; Li, Y.X.; Xue, Y.; Feng, Z.J.; Wang, Z.M.; Yang, G.L. On determining seismic anchor force of anchoring frame structure supporting three-stage slope. Geomech. Eng. 2020, 22, 265–275. [Google Scholar]
- Sajjad, M.B.; Indraratna, B.; Ngo, T.; Kelly, R.; Rujikiatkamjorn, C. A computational approach to smoothen the abrupt stiffness variation along railway transitions. J. Geotech. Geoenvironmental Eng. 2023, 149, 04023063. [Google Scholar] [CrossRef]
- Gallego, I.; Muñoz, J.; Rivas, A.; Sánchez-Cambronero, S. Vertical track stiffness as a new parameter involved in designing high-speed railway infrastructure. J. Transp. Eng. 2011, 137, 971–979. [Google Scholar] [CrossRef]
- Bian, X.; Jiang, H.; Chang, C.; Hu, J.; Chen, Y. Track and ground vibrations generated by high-speed train running on ballastless railway with excitation of vertical track irregularities. Soil Dyn. Earthq. Eng. 2015, 76, 29–43. [Google Scholar] [CrossRef]
- Giner, G.I.; Pita, A.L. Numerical simulation of embankment-structure transition design. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2009, 223, 331–343. [Google Scholar] [CrossRef]
- Lin, Y.L.; Jin, J.; Jiang, Z.H.; Liu, W.; Liu, H.D.; Li, R.F.; Liu, X. Seismic response of combined retaining structure with inclined rock slope. Struct. Eng. Mech. 2022, 84, 591–604. [Google Scholar]
- Lin, Y.L.; Li, Y.X.; Zhao, L.H.; Yang, T.Y. Investigation on the seismic response of a three-stage soil slope supported by the anchor frame structure. J. Cent. South Univ. 2020, 27, 1290–1305. [Google Scholar] [CrossRef]
- Lin, Y.L.; Lu, L.; Yang, G.L. Seismic behavior of a single-form lattice anchoring structure and a combined retaining structure supporting soil slope: A comparison. Environ. Earth Sci. 2020, 79, 78. [Google Scholar] [CrossRef]
- Lin, Y.L.; Zhao, L.H.; Yang, T.Y.; Yang, G.L.; Chen, X.B. Investigation on seismic behavior of combined retaining structure with different rock shapes. Struct. Eng. Mech. 2020, 73, 599–612. [Google Scholar]
- Lin, Y.L.; Cheng, X.M.; Yang, G.L. Shaking table test and numerical simulation on a combined retaining structure response to earthquake loading. Soil Dyn. Earthq. Eng. 2018, 108, 29–45. [Google Scholar] [CrossRef]
- Le Pen, L.; Watson, G.; Powrie, W.; Yeo, G.; Weston, P.; Roberts, C. The behaviour of railway level crossings: Insights through field monitoring. Transp. Geotech. 2014, 1, 201–213. [Google Scholar] [CrossRef]
- Paixo, A.; Fortunato, E.; Calcada, R. Transition zones to railway bridges: Track measurements and numerical modelling. Eng. Struct. 2014, 80, 435–443. [Google Scholar] [CrossRef]
- Zhai, W.; Wei, K.; Song, X.; Shao, M. Experimental investigation into ground vibrations induced by very high speed trains on a non-ballasted track. Soil Dyn. Earthq. Eng. 2015, 72, 24–36. [Google Scholar] [CrossRef]
- Paixão, A.; Fortunato, E.; Calçada, R. A contribution for integrated analysis of railway track performance at transition zones and other discontinuities. Constr. Build. Mater. 2016, 111, 699–709. [Google Scholar] [CrossRef]
- Connolly, D.P.; Kouroussis, G.; Woodward, P.K.; Alves Costa, P.; Verlinden, O.; Forde, M.C. Field testing and analysis of high speed rail vibrations. Soil Dyn. Earthq. Eng. 2014, 67, 102–118. [Google Scholar] [CrossRef]
- Connolly, D.P.; Alves Costa, P.; Kouroussis, G.; Galvin, P.; Woodward, P.K.; Laghrouche, O. Large scale international testing of railway ground vibrations across Europe. Soil Dyn. Earthq. Eng. 2015, 71, 1–12. [Google Scholar] [CrossRef]
- Kouroussis, G.; Connolly, D.P.; Olivier, B.; Laghrouche, O.; Costa, P.A. Railway cuttings and embankments: Experimental and numerical studies of ground vibration. Sci. Total Environ. 2016, 557, 110–122. [Google Scholar] [CrossRef] [PubMed]
- Olivier, B.; Connolly, D.P.; Alves Costa, P.; Kouroussis, G. The effect of embankment on high speed rail ground vibrations. Int. J. Rail Transp. 2016, 4, 229–246. [Google Scholar] [CrossRef]
- Feng, S.; Zhang, X.; Wang, L.; Zheng, Q.; Du, F.; Wang, Z. In situ experimental study on high speed train induced ground vibrations with the ballast-less track. Soil Dyn. Earthq. Eng. 2017, 102, 195–214. [Google Scholar] [CrossRef]
- TB10621-2014; Code for Design of High Speed Railway. National Railway Administration: Beijing, China, 2019.
- TB/T2328.14-2008; Test Method for Railway Ballast. China Railway Publishing House: Beijing, China, 2008.
- TB 10001-2016; Code for Design on Subgrade of Railway. China Railway Publishing House: Beijing, China, 2016.
- Hu, P.; Zhang, C.; Chen, S.; Wang, Y.; Wang, W.; Duan, W. Dynamic responses of bridge–embankment transitions in high speed railway: Field tests and data analyses. Eng. Struct. 2018, 175, 565–576. [Google Scholar] [CrossRef]
- Hu, P.; Zhang, C.; Guo, W.; Wang, Y. Dynamic response of a bridge-embankment transition with emphasis on the coupled train- track-subgrade system. Appl. Sci. 2020, 10, 5982. [Google Scholar] [CrossRef]

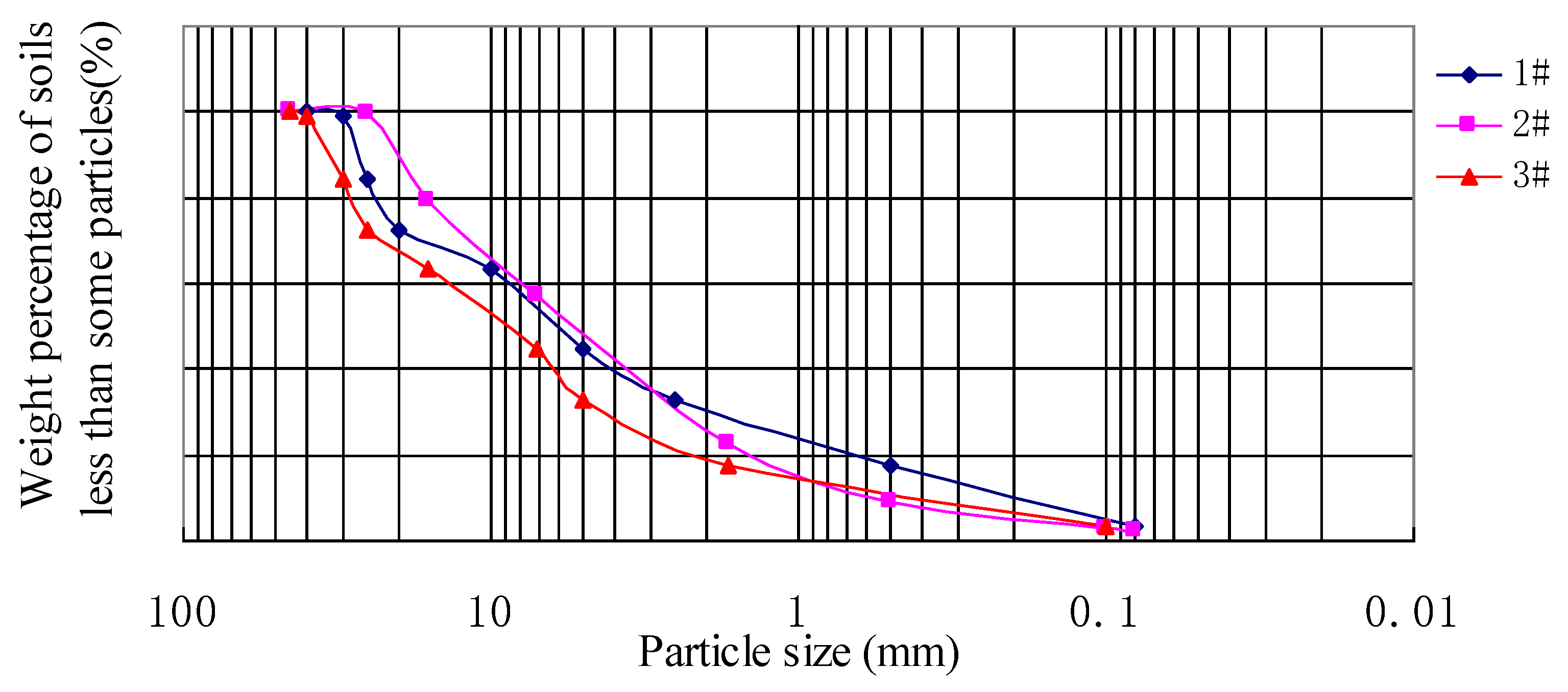


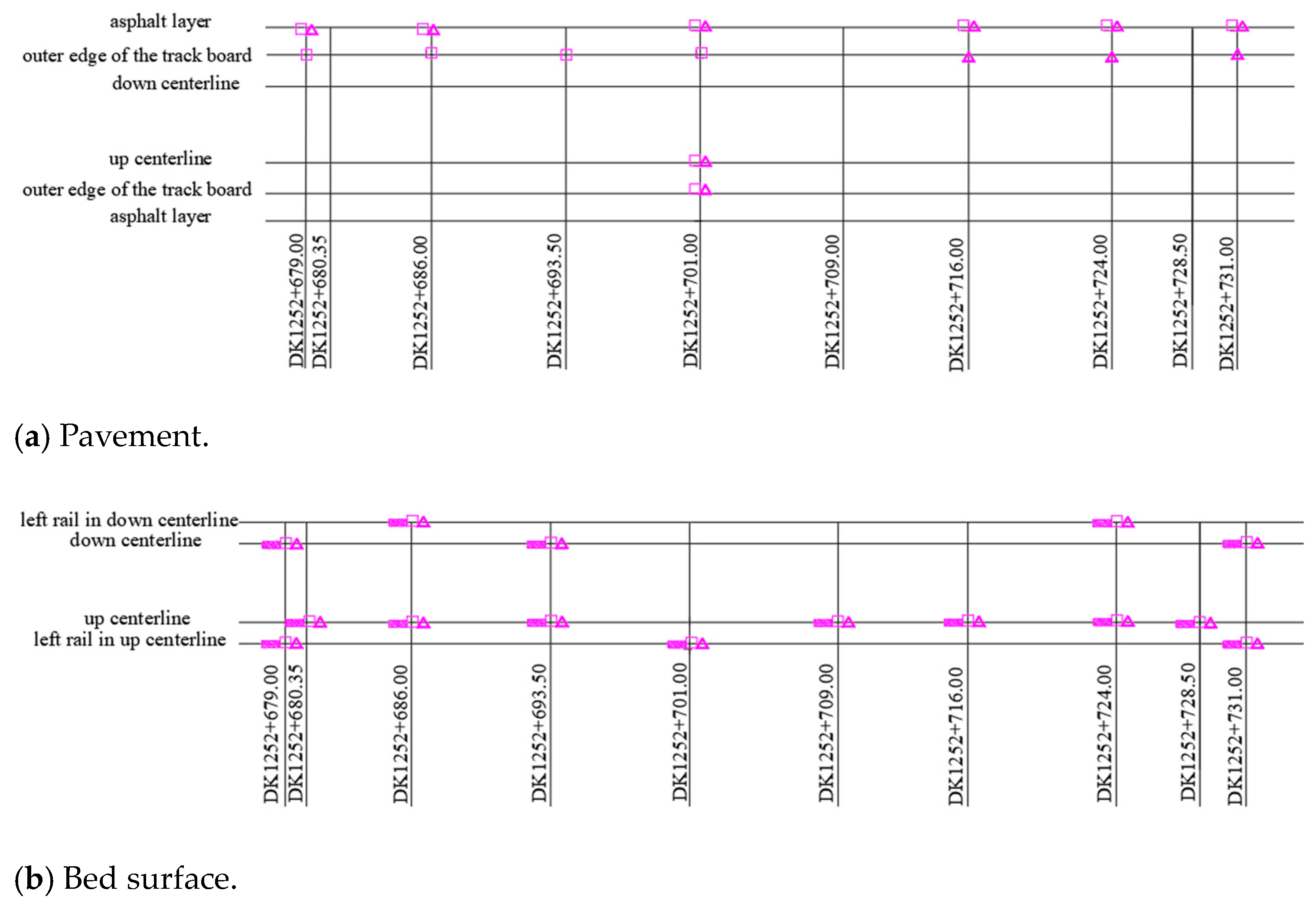
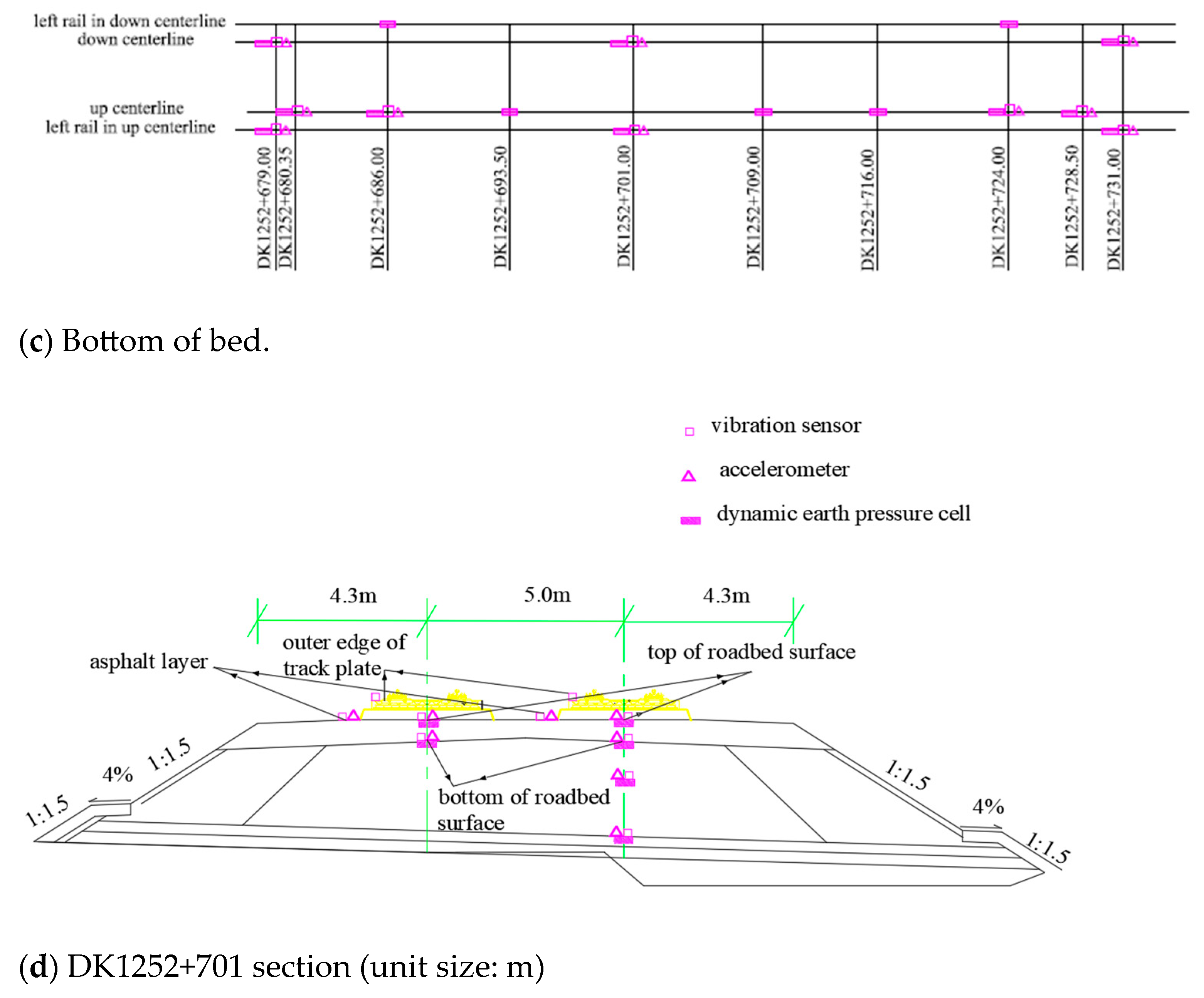


| Tested Items | Value |
|---|---|
| Particle size (>22.4 mm) content with crushed surface | 45.0% |
| Wear rate of particles (>1.7 mm) | 17.9% |
| Soaking loss rate of sodium sulfate solution of particles (>1.7 mm) | 1.0% |
| Liquid limit of fine particles (<0.5 mm) | 16.8% |
| Plasticity index of fine particles (<0.5 mm) | 3.3% |
| Content of clay and other impurities | 0.9% |
| Content of needle-shaped soil particles | 8.4% |
| Grading Parameters | 1# | 2# | 3# |
|---|---|---|---|
| Cu | 28.67 | 16 | 16 |
| Cc | 1.53 | 1.56 | 1.82 |
| Sample Number | Maximum Dry Density | Optimum Moisture Content | Unconfined Compressive Strength after 7 Days of Curing | Number of Sample Groups |
|---|---|---|---|---|
| 1# | 2.36 g/cm3 | 4.6% | 5.5 MPa | 5 |
| 2# | 2.32 g/cm3 | 4.2% | 3.1 MPa | 5 |
| 3# | 2.35 g/cm3 | 4.5% | 5.2 MPa | 5 |
| Virtual laying thickness | 1# | ||||
| K30 (MPa/m) | Ev2 (MPa) | Ev2/Ev1 | Evd (MPa) | Porosity n % | |
| 25 cm | 260 | 501.7 | 2.43 | 67.3 | 17.0 |
| 30 cm | 256 | 294.3 | 2.47 | 84.6 | 19.6 |
| Virtual laying thickness | 2# | ||||
| K30 (MPa/m) | Ev2 (MPa) | Ev2/Ev1 | Evd (MPa) | Porosity n % | |
| 25 cm | 185 | 365.3 | 3.76 | 66.5 | 21.5 |
| 30 cm | 173 | 286.4 | 4.67 | 52.5 | 27.2 |
| Dynamic Response | Depth from Top of Bed Surface (m) | Average Value | Percentage of Dynamic Response Decay (%) |
|---|---|---|---|
| Dynamic stress (kPa) | 0 | 1.78 | -- |
| 0.4 | 3.45 | −93.82 | |
| 1.4 | 15.57 | 859.15 | |
| 2.7 | 7.77 | −336.52 | |
| Dynamic acceleration (m/s2) | 0 | 3.21 | -- |
| 0.4 | 2.37 | 26.17 | |
| 1.4 | 1.34 | 40.40 | |
| 2.7 | 0.51 | 84.11 | |
| Dynamic speed (mm/s) | 0 | 5.92 | -- |
| 0.4 | 5.57 | 5.91 | |
| 1.4 | 4.08 | 64.84 | |
| 2.7 | 2.98 | 49.66 | |
| Dynamic displacement (mm) | 0 | 0.017 | -- |
| 0.4 | 0.014 | 17.65 | |
| 1.4 | 0.011 | 64.69 | |
| 2.7 | 0.009 | 47.06 |
| Response Type | Distance from 679 Culvert (m) | Upward Direction | Downward Direction | Percentage (%) |
|---|---|---|---|---|
| Dynamic stress(kPa) | 1.27 | 2.62 | 3.40 | 22.94 |
| 6.80 | 1.26 | 1.28 | 1.56 | |
| 14.54 | 1.41 | 1.50 | 6.00 | |
| 29.70 | 9.72 | 12.24 | 20.59 | |
| 37.33 | 1.76 | 1.93 | 8.81 | |
| 52 | 3.02 | 3.76 | 19.68 | |
| Dynamic acceleration (m/s2) | 1.27 | 4.331 | 4.312 | −0.44 |
| 6.80 | 3.201 | 2.836 | −12.87 | |
| 14.54 | 2.459 | 3.133 | 21.51 | |
| 29.70 | 6.356 | 6.743 | 5.74 | |
| 37.325 | 1.141 | 1.684 | 32.24 | |
| 45 | 1.524 | 1.404 | −8.55 | |
| 49.6 | 3.142 | 2.985 | −5.26 | |
| Dynamic speed (mm/s) | 1.27 | 2.243 | 2.250 | 0.31 |
| 14.54 | 6.28 | 4.27 | −47.07 | |
| 29.7 | 4.60 | 3.84 | −19.79 | |
| 37.325 | 4.894 | 4.779 | −2.41 | |
| 45 | 1.256 | 1.255 | −0.08 | |
| 49.6 | 2.32 | 2.61 | 11.11 | |
| Dynamic displacement (mm) | 1.27 | 0.005 | 0.005 | 0.00 |
| 6.80 | 0.012 | 0.015 | 20.00 | |
| 14.54 | 0.015 | 0.012 | −25.00 | |
| 29.7 | 0.013 | 0.010 | −30.00 | |
| 37.325 | 0.002 | 0.002 | 0.00 | |
| 45 | 0.001 | 0.001 | 0.00 | |
| 49.6 | 0.004 | 0.004 | 0.00 |
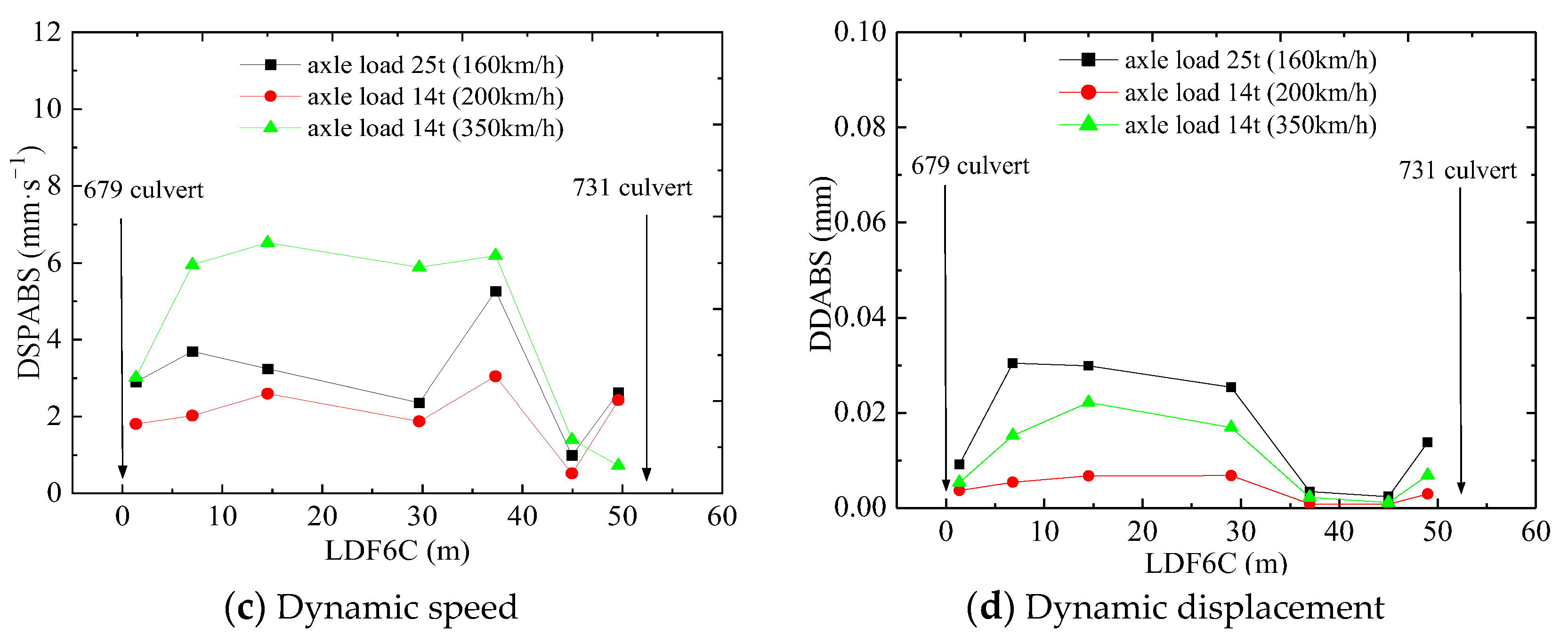
| Dynamic Responses | Section Away from 679 Culvert (m) | HST (Running Speed (km/h)) | Track Train (Running Speed (km/h) | Increased Percentage (%) |
|---|---|---|---|---|
| Dynamic stress (kPa) | 1.35 | 3.01 (200) | 3.99 (160) | 32.56 |
| 3.46 (350) | 15.32 | |||
| 29.7 | 8.98 (200) | 15.92 (160) | 77.28 | |
| 11.72 (350) | 35.84 | |||
| 49 | 3.04 (200) | 3.03 (160) | -0.33 | |
| 3.20 (350) | -5.31 | |||
| Dynamic acceleration (m/s2) | 1.35 | 2.38 (200) | 8.71 (160) | 265.97 |
| 5.31 (350) | 64.03 | |||
| 29.7 | 5.64 (200) | 15.90 (160) | 181.91 | |
| 12.70 (350) | 25.20 | |||
| 49 | 1.63 (200) | 5.54(160) | 239.88 | |
| 4.34 (350) | 27.65 | |||
| Dynamic speed (mm/s) | 1.35 | 1.81 (200) | 2.90 (160) | 60.22 |
| 3.01 (350) | 3.65 | |||
| 29.7 | 1.87 (200) | 2.36 (160) | 26.20 | |
| 5.88 (350) | −59.86 | |||
| 49 | 2.43 (200) | 2.63 (160) | 8.23 | |
| 0.72 (350) | 265.28 | |||
| Dynamic displacement (mm) | 1.35 | 0.004(200) | 0.009 (160) | 125.00 |
| 0.005 (350) | 80.00 | |||
| 29.7 | 0.007(200) | 0.025 (160) | 257.14 | |
| 0.017 (350) | 47.06 | |||
| 49 | 0.003(200) | 0.014 (160) | 366.67 | |
| 0.007 (350) | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, P.; Liu, H.; Tang, Y.-Z.; Lin, Y.-L. Field Investigation of the Dynamic Response of Culvert–Embankment–Culvert Transitions in a High-Speed Railway. Materials 2023, 16, 5832. https://doi.org/10.3390/ma16175832
Hu P, Liu H, Tang Y-Z, Lin Y-L. Field Investigation of the Dynamic Response of Culvert–Embankment–Culvert Transitions in a High-Speed Railway. Materials. 2023; 16(17):5832. https://doi.org/10.3390/ma16175832
Chicago/Turabian StyleHu, Ping, Huo Liu, Yi-Zhi Tang, and Yu-Liang Lin. 2023. "Field Investigation of the Dynamic Response of Culvert–Embankment–Culvert Transitions in a High-Speed Railway" Materials 16, no. 17: 5832. https://doi.org/10.3390/ma16175832






