CFD Modeling of Primary Breakup in an EIGA Atomizer for Titanium Alloy Powder Production
Abstract
:1. Introduction
2. Materials and Methods
2.1. EIGA Atomization Tower
2.2. Modeling the Discontinuous Droplets Primary Breakup Process
3. Results and Discussion
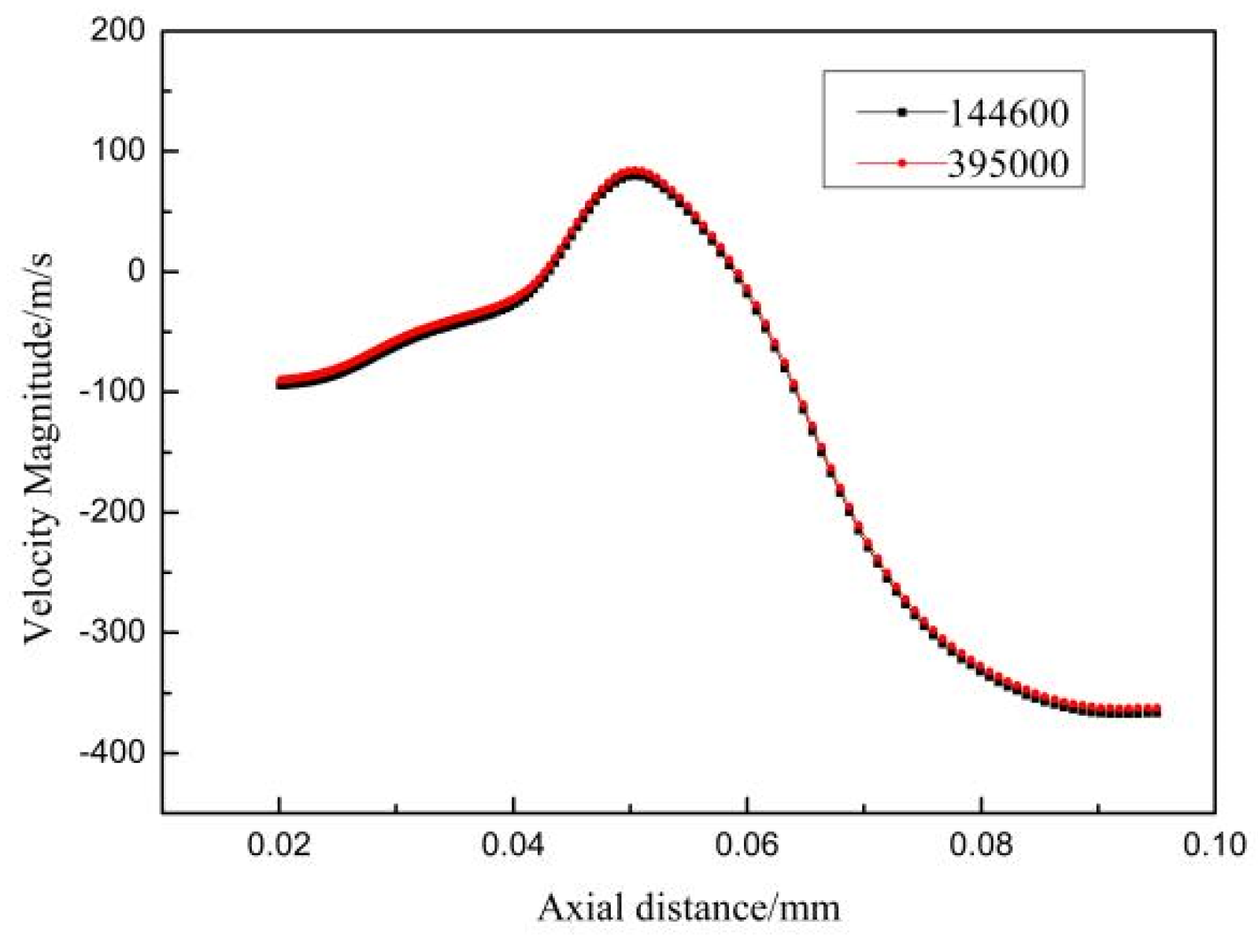
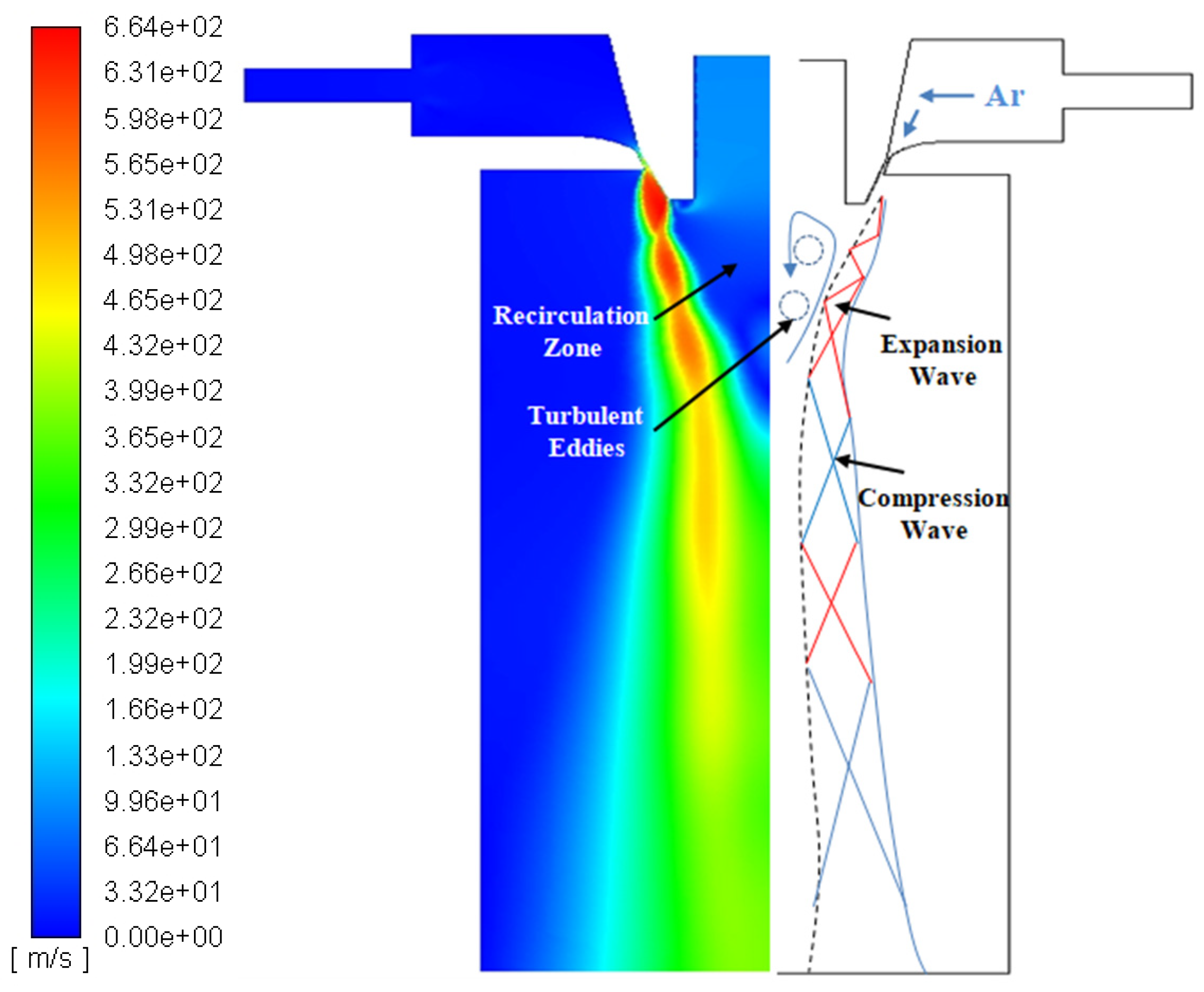
3.1. Single-phase Flow Field
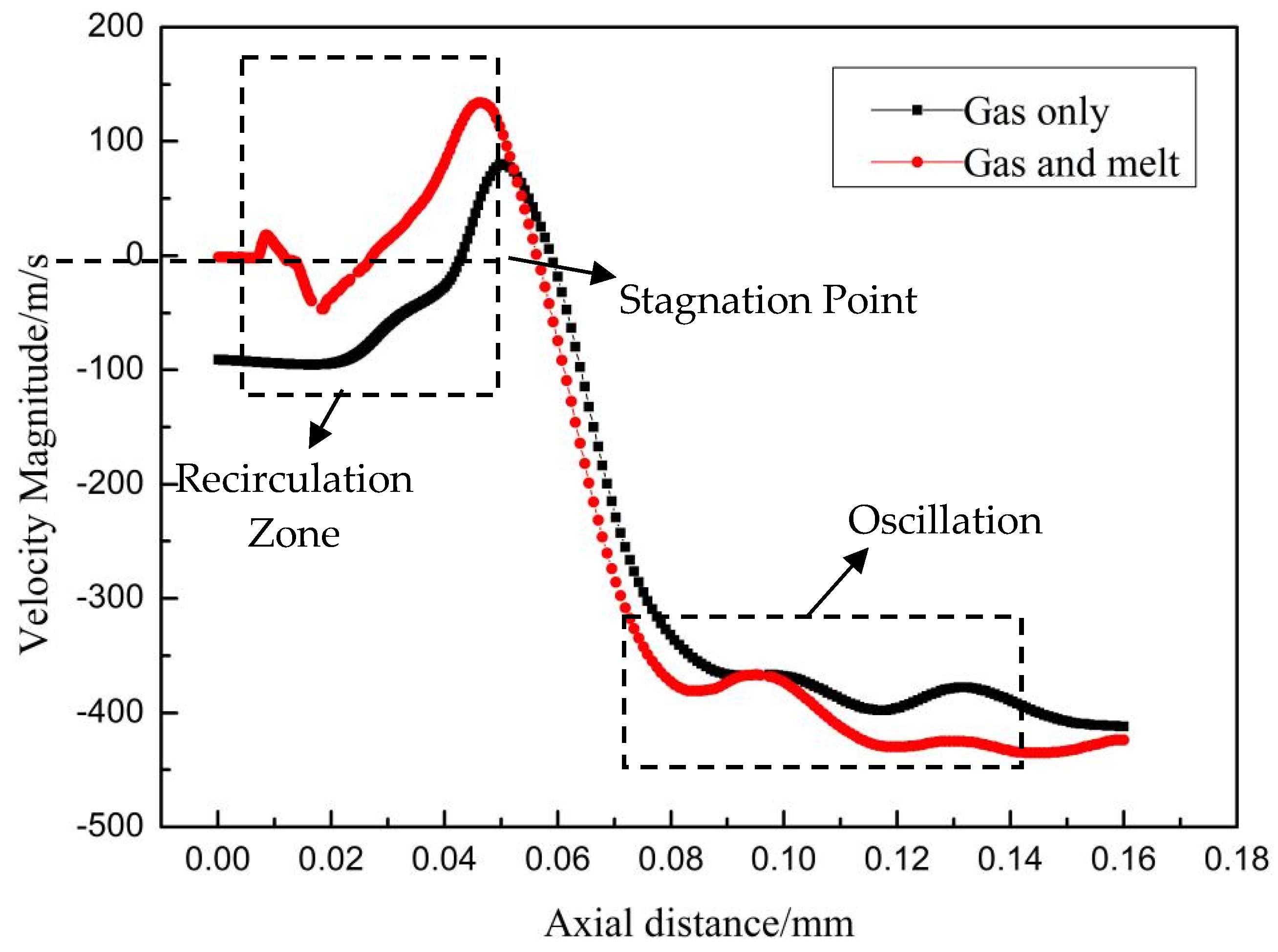
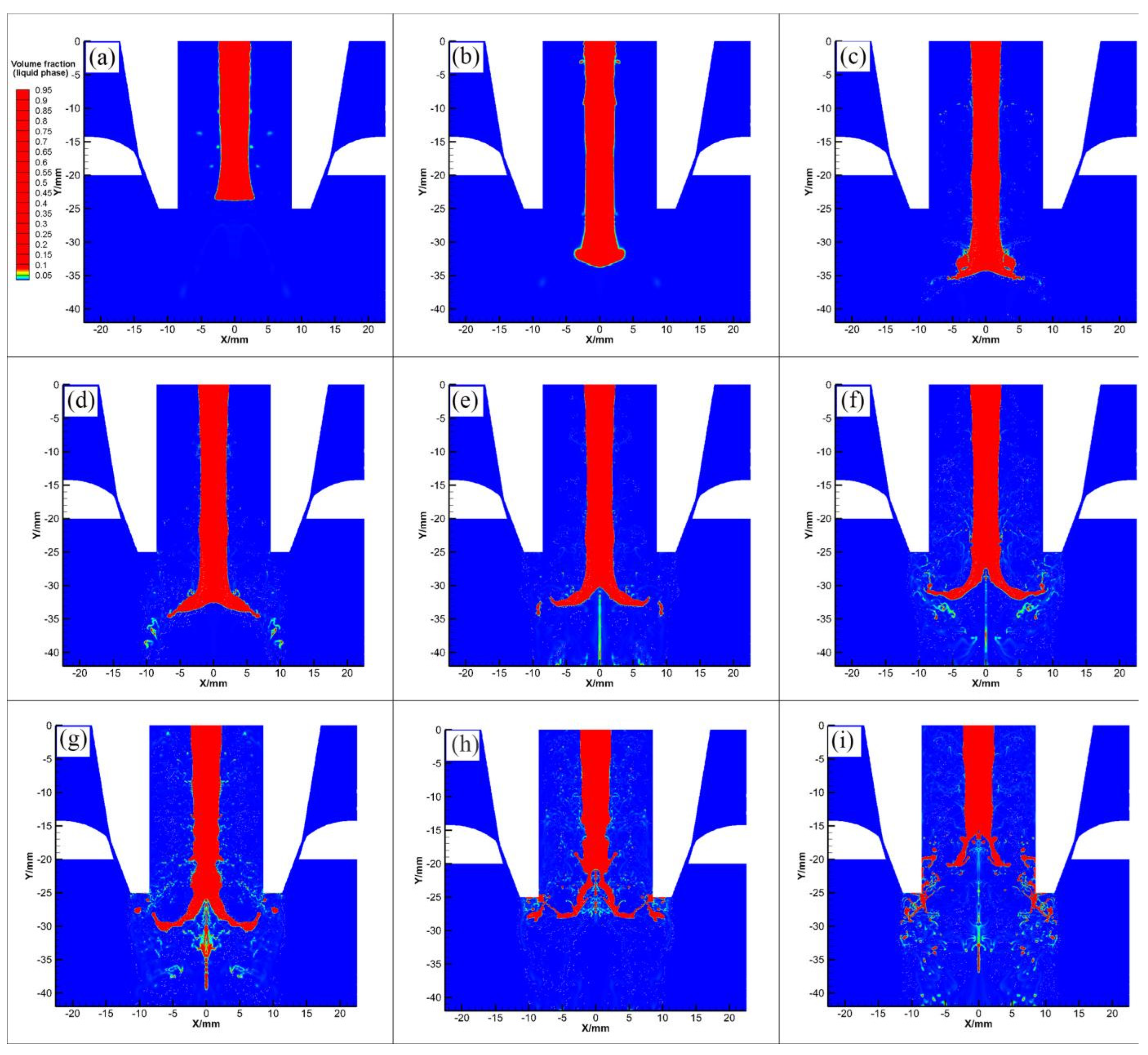
3.2. Gas−Liquid Two-Phase Flow Field
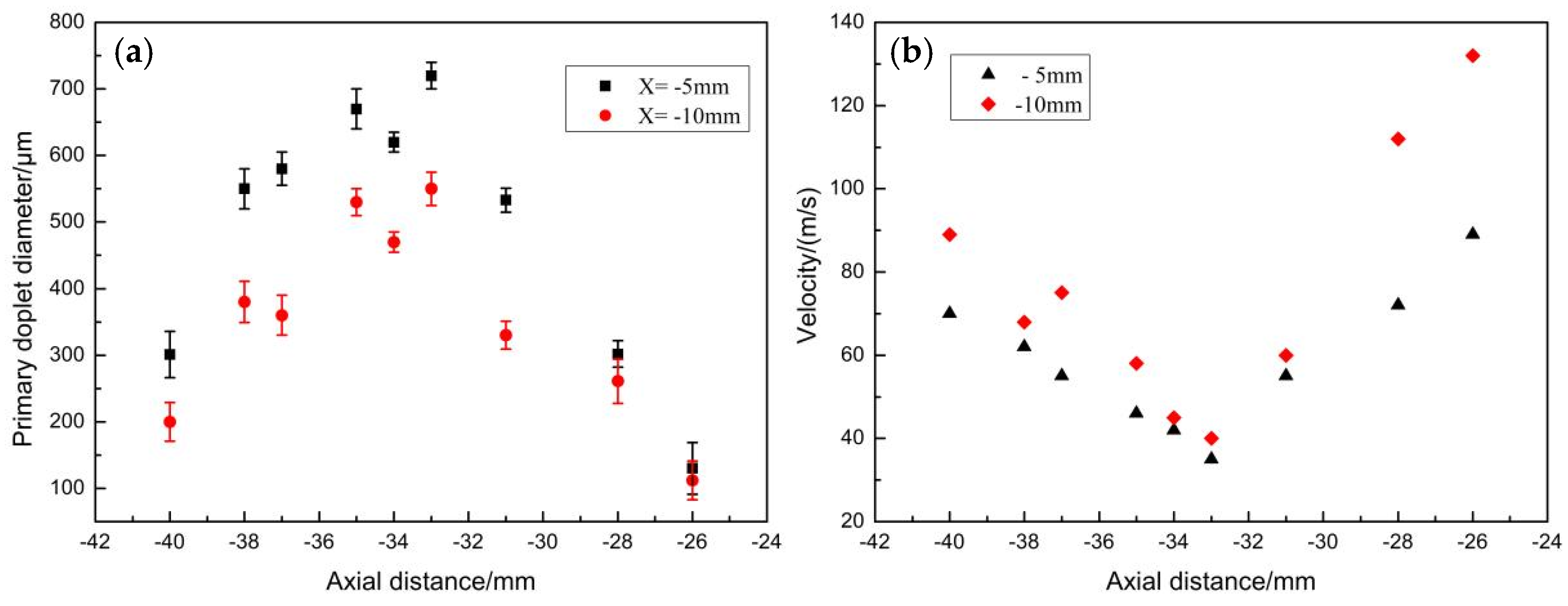
3.3. Mechanisms of Droplet Formation in Primary Atomization Process
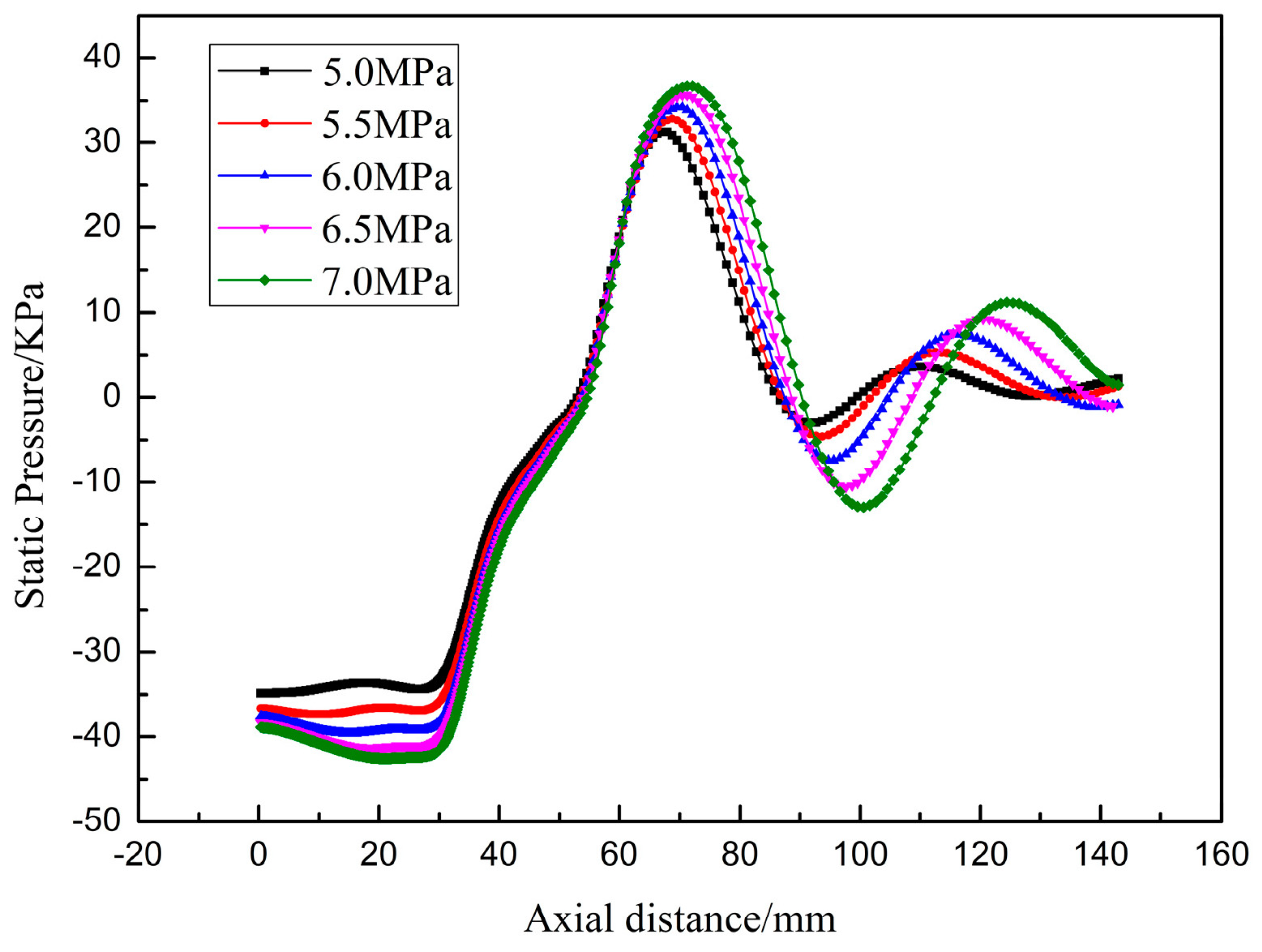
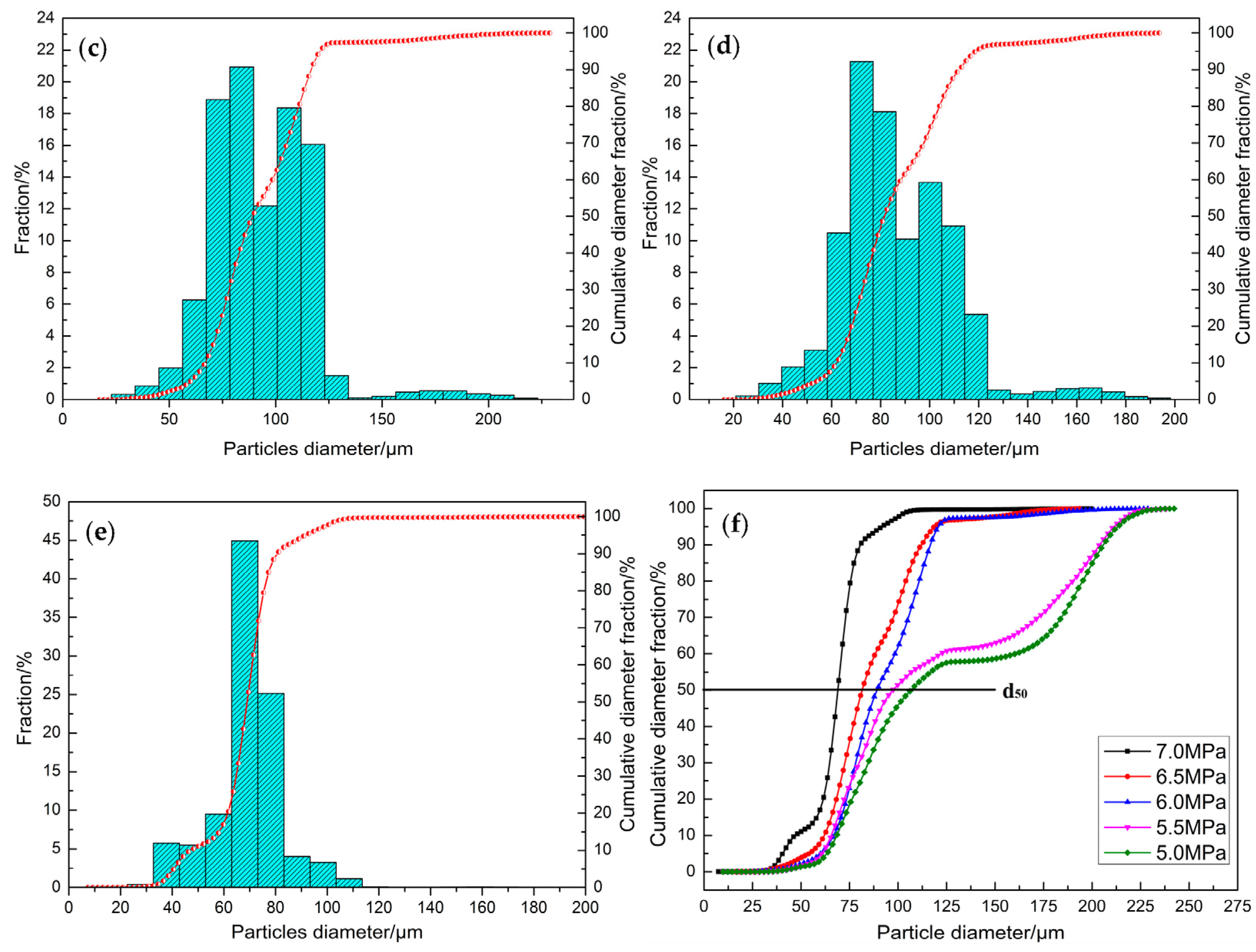
3.4. Effect of Gas Pressure on Powder Particle Size
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sibisi, P.N.; Popoola, A.P.I.; Arthur, N.K.K.; Pityana, S.L. Review on direct metal laser deposition manufacturing technology for the Ti-6Al-4V alloy. Int. J. Adv. Manuf. Technol. 2020, 107, 1163–1178. [Google Scholar] [CrossRef]
- Olakanmi, E.O.; Cochrane, R.F.; Dalgarno, K.W. A review on selective laser sintering/melting (SLS/SLM) of aluminium alloy powders: Processing, microstructure, and properties. Prog. Mater Sci. 2015, 74, 401–477. [Google Scholar] [CrossRef]
- Wei, M.; Chen, S.; Liang, J.; Liu, C. Effect of atomization pressure on the breakup of TA15 titanium alloy powder prepared by EIGA method for laser 3D printing. Vacuum 2017, 143, 185–194. [Google Scholar] [CrossRef]
- Liu, Z.; Zhao, Z.; Liu, J.; Wang, Q.; Guo, Z.; Zeng, Y.; Yang, G.; Gong, S. Effects of the crystallographic and spatial orientation of α lamellae on the anisotropic in-situ tensile behaviors of additive manufactured Ti–6Al–4V. J. Alloys Compd. 2021, 850, 156886. [Google Scholar] [CrossRef]
- Srivastava, M.; Rathee, S.; Patel, V.; Kumar, A.; Koppad, P.G. A review of various materials for additive manufacturing: Recent trends and processing issues. J. Mater. Res. Technol. 2022, 21, 2612–2641. [Google Scholar] [CrossRef]
- Leo, V.M.; Antony, R.G.R. Processes for Production of High-Purity Metal Powders. JOM 2003, 55, 14–18. [Google Scholar]
- Iver, E.; Anderson, R.L.T. Progress toward gas atomization processing with increased uniformity and control. Mater. Sci. Eng. A 2002, 326, 101–109. [Google Scholar]
- Dawes, J.; Bowerman, R.; Trepleton, R. Introduction to the Additive Manufacturing Powder Metallurgy Supply Chain. Johns. Matthey Technol. Rev. 2015, 59, 243–256. [Google Scholar] [CrossRef]
- Zeoli, N.; Gu, S. Numerical modelling of droplet break-up for gas atomisation. Comput. Mater. Sci. 2006, 38, 282–292. [Google Scholar] [CrossRef]
- Zeoli, N.; Tabbara, H.; Gu, S. CFD modeling of primary breakup during metal powder atomization. Chem. Eng. Sci. 2011, 66, 6498–6504. [Google Scholar] [CrossRef]
- Thompson, J.S.; Hassan, O.; Rolland, S.A.; Sienz, J. The identification of an accurate simulation approach to predict the effect of operational parameters on the particle size distribution (PSD) of powders produced by an industrial close-coupled gas atomiser. Powder Technol. 2016, 291, 75–85. [Google Scholar] [CrossRef]
- Li, X.-g.; Fritsching, U. Process modeling pressure-swirl-gas-atomization for metal powder production. J. Mater. Process. Technol. 2017, 239, 1–17. [Google Scholar] [CrossRef]
- Guo, K.-K.; Liu, C.-S.; Chen, S.-Y.; Dong, H.-H.; Wang, S.-Y. High pressure EIGA preparation and 3D printing capability of Ti—6Al—4V powder. Trans. Nonferrous Met. Soc. China 2020, 30, 147–159. [Google Scholar] [CrossRef]
- Feng, S.; Xia, M.; Ge, C.-C. Oxidation during the production of FGH4095 superalloy powders by electrode induction-melt inert gas atomization. Chin. Phys. B 2018, 27, 044701. [Google Scholar] [CrossRef]
- Lu, L.; Zhang, S.; Xu, J.; He, H.; Zhao, X. Numerical study of titanium melting by high frequency inductive heating. Int. J. Heat Mass Transf. 2017, 108, 2021–2028. [Google Scholar] [CrossRef]
- Bojarevics, V.; Dughiero, F.; Roy, A.; Pericleous, K. Numerical model of electrode induction melting for gas atomization. Compel-Int. J. Comp. Math. Electr. Electron. Eng. 2011, 30, 1455–1466. [Google Scholar] [CrossRef]
- Antipas, G.S.E. Modelling of the break up mechanism in gas atomization of liquid metals Part II. The gas flow model. Comput. Mater. Sci 2009, 46, 955–959. [Google Scholar] [CrossRef]
- Allimant, A.; Planche, M.P.; Bailly, Y.; Dembinski, L.; Coddet, C. Progress in gas atomization of liquid metals by means of a De Laval nozzle. Powder Technol. 2009, 190, 79–83. [Google Scholar] [CrossRef]
- Mi, J.; Figliola, R.S.; Anderson, I.E. A numerical simulation of gas flow field effects on high pressure gas atomization due to operating pressure variation. Mater. Sci. Eng. A 1996, 208, 20–29. [Google Scholar] [CrossRef]
- Wang, P.; Liu, J.; Dong, Y.; Zhu, Z.; Pang, J.; Zhang, J. Breakup process modeling and production of FeSiAl magnetic powders by close-coupled gas atomization. J. Mater. Res. Technol. 2023, 23, 730–743. [Google Scholar] [CrossRef]
- Wang, J.F.; Xia, M.; Wu, J.L.; Ge, C.C. Ladle Nozzle Clogging in Vacuum Induction Melting Gas Atomization: Influence of Delivery-Tube Geometry. Rare Met. Mater. Eng. 2022, 51, 3214–3222. [Google Scholar]
- Qaddah, B.; Chapelle, P.; Bellot, J.P.; Jourdan, J.; Rimbert, N.; Deborde, A.; Hammes, R.; Franceschini, A. Swirling supersonic gas flow in an EIGA atomizer for metal powder production: Numerical investigation and experimental validation. J. Mater. Process. Technol. 2023, 311, 117814. [Google Scholar] [CrossRef]
- Ling, Y.; Zaleski, S.; Scardovelli, R. Multiscale simulation of atomization with small droplets represented by a Lagrangian point-particle model. Int. J. Multiph. Flow 2015, 76, 122–143. [Google Scholar] [CrossRef]
- Xiao, F.; Wang, Z.G.; Sun, M.B.; Liang, J.H.; Liu, N. Large eddy simulation of liquid jet primary breakup in supersonic air crossflow. Int. J. Multiph. Flow 2016, 87, 229–240. [Google Scholar] [CrossRef]
- Wang, H.; Wang, Z.; Sun, M.; Qin, N. Combustion characteristics in a supersonic combustor with hydrogen injection upstream of cavity flameholder. Proc. Combust. Inst. 2013, 34, 2073–2082. [Google Scholar] [CrossRef]
- Ting, J.; Peretti, M.W.; Eisen, W.B. The effect of wake-closure phenomenon on gas atomization performance. Mater. Sci. Eng. A 2002, 326, 110–121. [Google Scholar] [CrossRef]
- Abarzhi, S.I. Review of theoretical modelling approaches of Rayleigh–Taylor instabilities and turbulent mixing. Philos. Trans. R. Soc. A-Math. Phys. Eng. Sci. 2010, 368, 1809–1828. [Google Scholar] [CrossRef] [PubMed]
- Dombrowski, N.; Johns, W.R. The aerodynamic instability and disintegration of viscous liquid sheets. Chem. Eng. Sci. 1963, 18, 203–214. [Google Scholar] [CrossRef]
- Matsumoto, T.; Fujii, H.; Ueda, T.; Kamai, M.; Nogi, K. Measurement of surface tension of molten copper using the free-fall oscillating drop method. Meas. Sci. Technol. 2005, 16, 432. [Google Scholar] [CrossRef]
- BorÉE, J.; Ishima, T.; Flour, I. The effect of mass loading and inter-particle collisions on the development of the polydispersed two-phase flow downstream of a confined bluff body. J. Fluid Mech. 2001, 443, 129–165. [Google Scholar] [CrossRef]






| Reported by | Process | Condition | Model | Atomizing Process |
|---|---|---|---|---|
| Thompson et al. [11] | close-coupled gas atomiser | Sim | Euler–Lagrange(DPM) | primary atomization secondary atomization |
| Xing et al. [12] | pressure-swirl-gas-atomization | Sim | VOF + k-ω SST | primary atomization secondary atomization |
| Zeoli et al. [10] | VIGA | Sim | VOF +RSM | - |
| Wang et al. [20] | close-coupled gas atomiser | Sim + Exp | VOF + k-ω SST | primary atomization secondary atomization |
| Wang et al. [21] | VIGA | Sim + Exp | VOF + LES | primary atomization |
| Baraa et al. [22] | EIGA | Sim | RANS + k-ω SST | - |
| Wei et al. [3] | EIGA | Sim + Exp | - | - |
| Zeoli et al. [9] | gas atomization | Sim | RSM | secondary atomization |
| Thermophysical Properties | Density kg m−3 | Condition | Surface Tension N m−1 | Specific Capacity J kg−1 K−1 | Thermal Conductivity Wm−1 K−1 |
|---|---|---|---|---|---|
| titanium | 4500 | 2.0 × 10− 5 | 1.588 | 812 | 25.8 |
| argon | Ideal-gas | 2.125 × 10− 5 | - | 520.64 | 0.0158 |
| Gas Pressure (MPa) | 5.0 | 5.5 | 6.0 | 6.5 | 7.0 |
| Static pressure (KPa) | −34.88 | −36.62 | −37.62 | −38.32 | −38.90 |
| suction pressure (KPa) | −134.88 | −136.62 | −137.62 | −138.90 | −138.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, K.; Liu, C.; Chen, W.; Luo, C.; Li, J. CFD Modeling of Primary Breakup in an EIGA Atomizer for Titanium Alloy Powder Production. Materials 2023, 16, 5900. https://doi.org/10.3390/ma16175900
Guo K, Liu C, Chen W, Luo C, Li J. CFD Modeling of Primary Breakup in an EIGA Atomizer for Titanium Alloy Powder Production. Materials. 2023; 16(17):5900. https://doi.org/10.3390/ma16175900
Chicago/Turabian StyleGuo, Kuaikuai, Changsheng Liu, Wei Chen, Chang Luo, and Jianzhong Li. 2023. "CFD Modeling of Primary Breakup in an EIGA Atomizer for Titanium Alloy Powder Production" Materials 16, no. 17: 5900. https://doi.org/10.3390/ma16175900
APA StyleGuo, K., Liu, C., Chen, W., Luo, C., & Li, J. (2023). CFD Modeling of Primary Breakup in an EIGA Atomizer for Titanium Alloy Powder Production. Materials, 16(17), 5900. https://doi.org/10.3390/ma16175900








