Quenched Residual Stress Reduction in Pentagon-Curved Aluminum Alloy Forgings Using the Bulging Process
Abstract
:1. Introduction
2. Models Description
2.1. Quenching Model
2.2. Bulging Model
3. Results and Discussion
3.1. Quenching Residual Stress
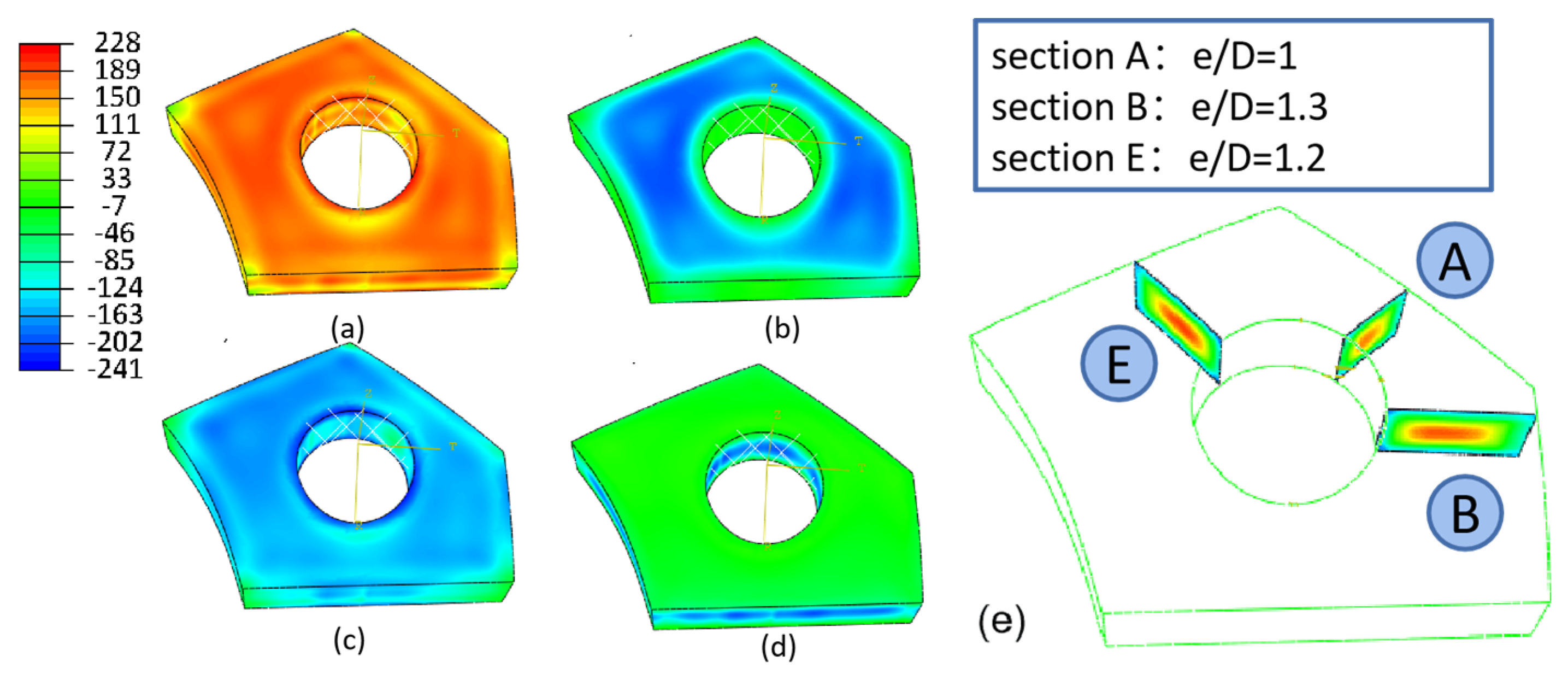
3.1.1. Overall Residual Stress Distribution
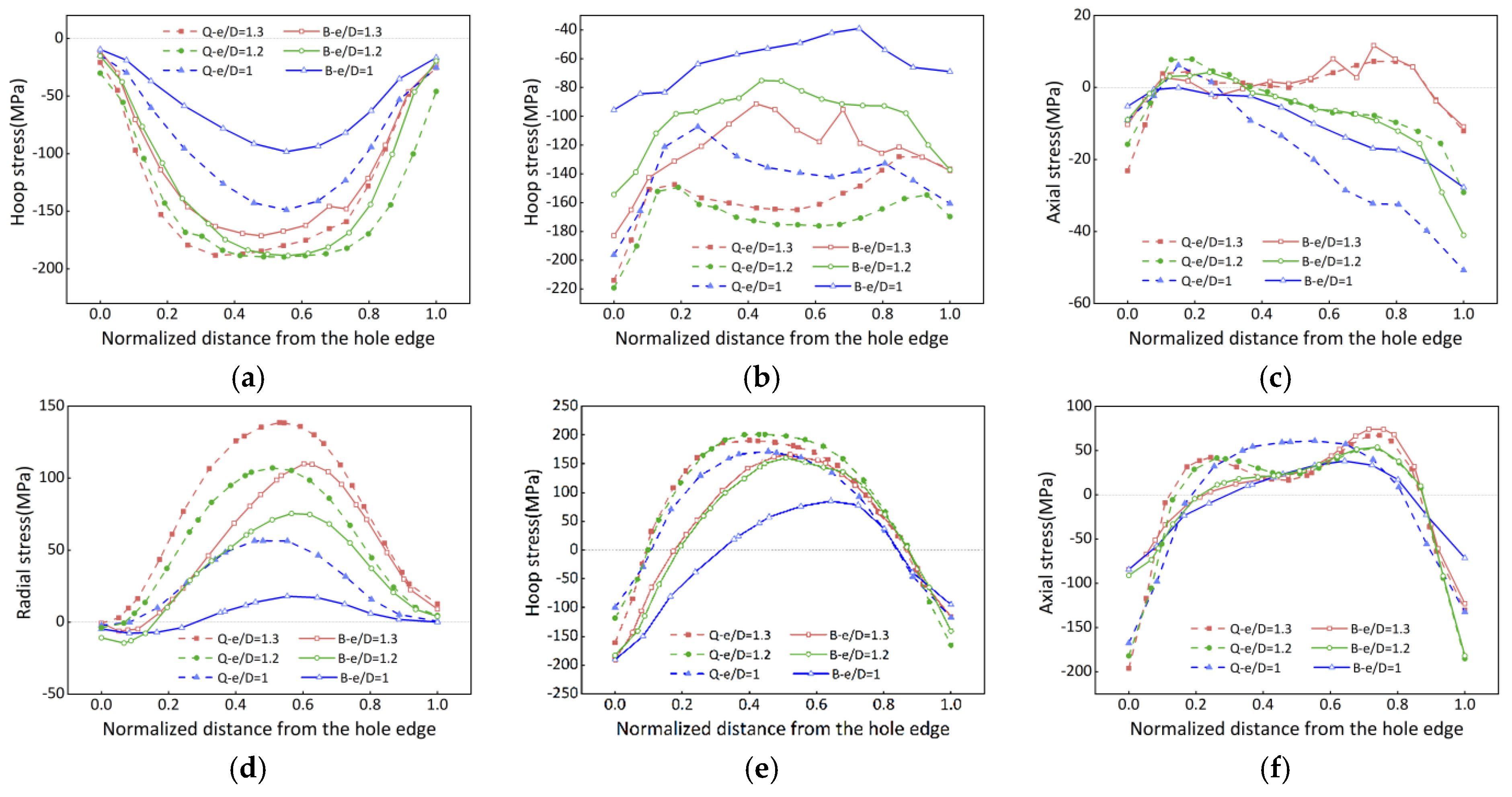
3.1.2. Surface Residual Stress
3.1.3. Internal Residual Stress
3.2. Bulging Residual Stress
3.2.1. Overall Residual Stress Distribution
3.2.2. Evolution of Stress after Bulging
3.3. Assessment of the Overall Stress Reduction
3.4. Experiment Validation
3.4.1. Experiments
3.4.2. X-ray Diffraction Residual Stress Measurement
3.4.3. The Contour Method Stress Measurement
3.4.4. Experiment Results
4. Conclusions
- (1)
- The geometric features of the PCG were characterized based on the edge distance ratio (e/D). Three types of sections were identified: e/D = 1, 1.2, and 1.3.
- (2)
- A thermo-mechanical FE model was developed to study the quenching process of the PCG. The analysis revealed that as the e/D ratio decreases, the stress amplitude increases. At e/D = 1.2, both hoop and radial component stresses reached peak values of approximately −200 MPa on the surface due to limitations in the quenching yield strength. Stresses at the hole edge and free edges are higher than those on the surface due to different heat transfer boundary conditions, with minimum values occurring at corners. Axial stresses on the upper and lower surfaces ranged from −50 MPa to 10 MPa, with maximum values concentrated in surfaces parallel to the axis orientation. Internally, the hoop stress reached its peak value at e/D = 1.2 (approximately 200 MPa), while the radial stress is relatively smaller, but increases with increasing e/D. When e/D exceeds 1, the axial stress distribution transitions from an inverted U-shaped curve to an M-shaped curve.
- (3)
- An FE model for the bulging process was established to simulate stress reduction. Average stress reduction (Ra) and peak stress reduction (Rp) were used to calculate surface stress reduction and internal stress reduction, respectively. The results demonstrate that stress reduction increases as the e/D ratio decreases. Stress reduction exhibits a pattern of initial increase followed by a decrease along the path from the hole edge to the free edge. Furthermore, the results indicate that the bulging process is more effective in reducing surface stress than internal stress.
- (4)
- Further simulations have been conducted to assess stress reduction under different bulging ratios (1%, 2%, 3%). An overall stress reduction evaluation was performed using a weight function based on different e/D ratios. The calculated results show that the overall stress reduction increases with the bulging ratio. Considering the contribution of stress reduction and the adverse factors of stress reversal, a bulging ratio of 2% is recommended as the most suitable for the PCG. The radial component stress reduction and hoop component stress reduction are determined to be 42.2% and 54.8%, respectively.
- (5)
- X-ray diffraction and the contour method were employed to determine the surface and internal stresses of the PCG with CE = 2%. Comparative analysis of the measurement results with those obtained from the simulation revealed an 8% deviation in surface stress and a 13.2% deviation in internal stress. This indicates that the FE model for stress reduction during the bulging process exhibits good predictive accuracy.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, J.-G.; Wang, S.-Q. Distortion caused by residual stresses in machining aeronautical aluminum alloy parts: Recent advances. Int. J. Adv. Manuf. Technol. 2017, 89, 997–1012. [Google Scholar] [CrossRef]
- Carvalho, A.; Renaudin, L.; Zara, A.; Martins, J. Microstructure analysis of 7050 aluminum alloy processed by multistage aging treatments. J. Alloys Compd. 2022, 907, 164400. [Google Scholar] [CrossRef]
- Wen, K.; Xiong, B.; Zhang, Y.; Li, Z.; Li, X.; Huang, S.; Yan, L.; Yan, H.; Liu, H. Over-aging influenced matrix precipitate characteristics improve fatigue crack propagation in a high Zn-containing Al-Zn-Mg-Cu alloy. Mater. Sci. Eng. A 2018, 716, 42–54. [Google Scholar] [CrossRef]
- Nguyen, T.T.V.; Phung, H.T.T.; Le, B.T.; Thi, H.P.N.; La, D.D. Nanostructured phases, mechanical properties, exfoliation and intergranular corrosion behaviours of 7075 Al–Zn–Mg–Cu alloy–Effect of one-stage and two-stage aging processes. Adv. Nat. Sci. Nanosci. Nanotechnol. 2020, 11, 045002. [Google Scholar] [CrossRef]
- Jiang, K.; Lan, Y.; Pan, Q.; Deng, Y. Effect of the Zn/Mg ratio on microstructures, mechanical properties and corrosion performances of Al-Zn-Mg alloys. Materials 2020, 13, 3299. [Google Scholar] [CrossRef] [PubMed]
- Tang, Z.T.; Yu, T.; Xu, L.Q.; Liu, Z.Q. Machining deformation prediction for frame components considering multifactor coupling effects. Int. J. Adv. Manuf. Technol. 2013, 68, 187–196. [Google Scholar] [CrossRef]
- Li, J.; Li, F.; Ma, X.; Li, J.; Liang, S. Effect of grain boundary characteristic on intergranular corrosion and mechanical properties of severely sheared Al-Zn-Mg-Cu alloy. Mater. Sci. Eng. A 2018, 732, 53–62. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, T.; Gong, H.; Wu, Y. Effect of Cold Pressing and Aging on Reduction and Evolution of Quenched Residual Stress for Al-Zn-Mg-Cu T-Type Rib. Appl. Sci. 2021, 11, 5439. [Google Scholar] [CrossRef]
- Tanner, D.; Robinson, J. Reducing residual stress in 2014 aluminum alloy die forgings. Mater. Des. 2008, 29, 1489–1496. [Google Scholar] [CrossRef]
- Sun, Y.; Jiang, F.; Zhang, H.; Su, J.; Yuan, W. Residual stress relief in Al–Zn–Mg–Cu alloy by a new multistage interrupted artificial aging treatment. Mater. Des. 2016, 92, 281–287. [Google Scholar] [CrossRef]
- Bouissa, Y.; Bohlooli, N.; Shahriari, D.; Champliaud, H.; Jahazi, M. FEM modeling and experimental validation of quench-induced distortions of large size steel forgings. J. Manuf. Process. 2020, 58, 592–605. [Google Scholar] [CrossRef]
- Koc, M.; Culp, J.; Altan, T. Prediction of residual stresses in quenched aluminum blocks and their reduction through cold working processes. J. Mater. Process. Technol. 2006, 174, 342–354. [Google Scholar] [CrossRef]
- Zhang, Y.; Yi, Y.; Huang, S.; He, H. Influence of Temperature-Dependent Properties of Aluminum Alloy on Evolution of Plastic Strain and Residual Stress during Quenching Process. Metals 2017, 7, 228. [Google Scholar] [CrossRef]
- Younger, M.S.; Eckelmeyer, K.H. Overcoming Residual Stresses and Machining Distortion in the Production of Aluminum Alloy Satellite Boxes; Sandia National Laboratories (SNL): Albuquerque, NM, USA; Livermore, CA, USA, 2007. [CrossRef]
- Younger, M.S.; Eckelmeyer, K.H. Aluminum Alloys for Satellite Boxes: Engineering Guidelines for Obtaining Adequate Strength While Minimizing Residual Stresses and Machining Distortion; Sandia National Laboratories (SNL): Albuquerque, NM, USA; Livermore, CA, USA, 2007. [CrossRef]
- Wang, Z.J.; Chen, W.Y.; Zhang, Y.D.; Chen, Z.T.; Liu, Q. Study on the machining distortion of thin walled part caused by redistribution of residual stress. Chin. J. Aeronaut. 2005, 18, 175–179. [Google Scholar] [CrossRef]
- Guo, H.; Zuo, D.W.; Wu, H.B.; Xu, F.; Tong, G.Q. Prediction on milling distortion for aero-multi-frame parts. Mater. Sci. Eng. A-Struct. Mater. Prop. Microstruct. Process. 2009, 499, 230–233. [Google Scholar] [CrossRef]
- Tanner, D.A.; Robinson, J.S. Modelling stress reduction techniques of cold compression and stretching in wrought aluminum alloy products. Finite Elem. Anal. Des. 2003, 39, 369–386. [Google Scholar] [CrossRef]
- Liu, X.; Robert, C.; Gong, H.; Liu, Y.; Chen, D.; Liu, Y.; Wu, Y.; Li, C. Residual Stress Determination in Quenched and Cold Compressed T-section 7050 Forging by Neutron Diffraction and Contour Method. Annu. Rep. China Inst. At. Energy 2018, 27, 6049–6057. [Google Scholar] [CrossRef]
- Ayatollahi, M.R.; Nik, M.A. Edge distance effects on residual stress distribution around a cold expanded hole in Al 2024 alloy. Comput. Mater. Sci. 2009, 45, 1134–1141. [Google Scholar] [CrossRef]
- Zhang, Y.; Fitzpatrick, M.; Edwards, L. Analysis of the residual stress around a cold-expanded fastener hole in a finite plate. Strain 2005, 41, 59–70. [Google Scholar] [CrossRef]
- Wei, Z.; Li, J.; Yang, Y. Effect of Bulging Process on Residual Stress and Its Distribution of TC4 Alloy Ring Forgings. Rare Met. Mater. Eng. 2019, 48, 7. [Google Scholar]
- Li, J.; Wu, Y.; Gong, H. Effect of bulging on quenching residual stress of 2219 aluminum alloy ring. Heat Treat. Met. 2021, 46, 7. [Google Scholar] [CrossRef]
- Prime, M.B.; Hill, M.R. Residual stress, stress relief, and inhomogeneity in aluminum plate. Scr. Mater. 2002, 46, 77–82. [Google Scholar] [CrossRef]
- Hu, S.; Zeng, S. The Theoretical Model of the Thermal Stress Evolution Mechanism during Quenching of no Phase Change Alloy. Rare Met. Mater. Eng. 2006, 4, 538–541. [Google Scholar] [CrossRef]
- Prime, M.B. Cross-sectional mapping of residual stresses by measuring the surface contour after a cut. J. Eng. Mater. Technol. 2001, 123, 162–168. [Google Scholar] [CrossRef]
- Thibault, D.; Bocher, P.; Thomas, M.; Gharghouri, M.; Cote, M. Residual stress characterization in low transformation temperature 13%Cr-4%Ni stainless steel weld by neutron diffraction and the contour method. Mater. Sci. Eng. 2010, 527, 6205–6210. [Google Scholar] [CrossRef]
- Pavan, M.; Furfari, D.; Ahmad, B.; Gharghouri, M.A.; Fitzpatrick, M.E. Fatigue crack growth in a laser shock peened residual stress field. Int. J. Fatigue 2019, 123, 157–167. [Google Scholar] [CrossRef]
- Woo, W.; An, G.B.; Em, V.T.; De Wald, A.T.; Hill, M.R. Through-thickness distributions of residual stresses in an 80 mm thick weld using neutron diffraction and contour method. J. Mater. Sci. 2015, 50, 784–793. [Google Scholar] [CrossRef]
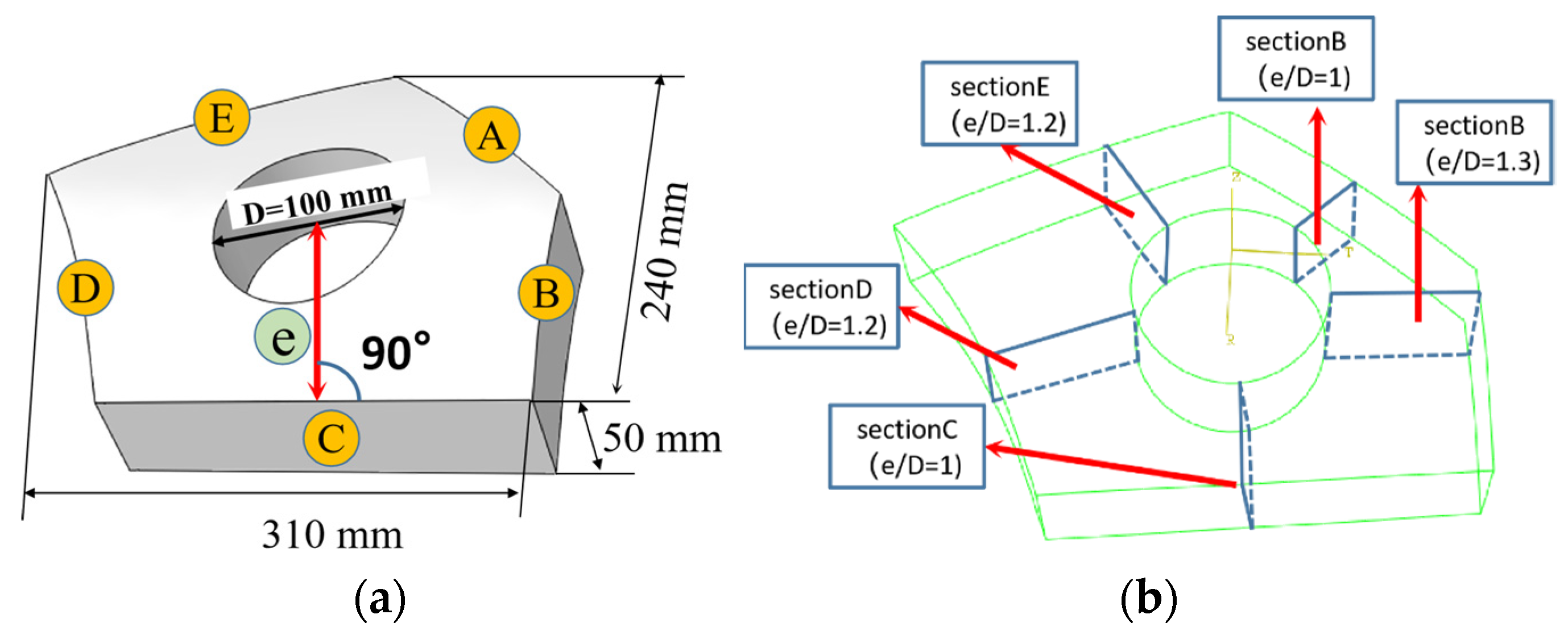
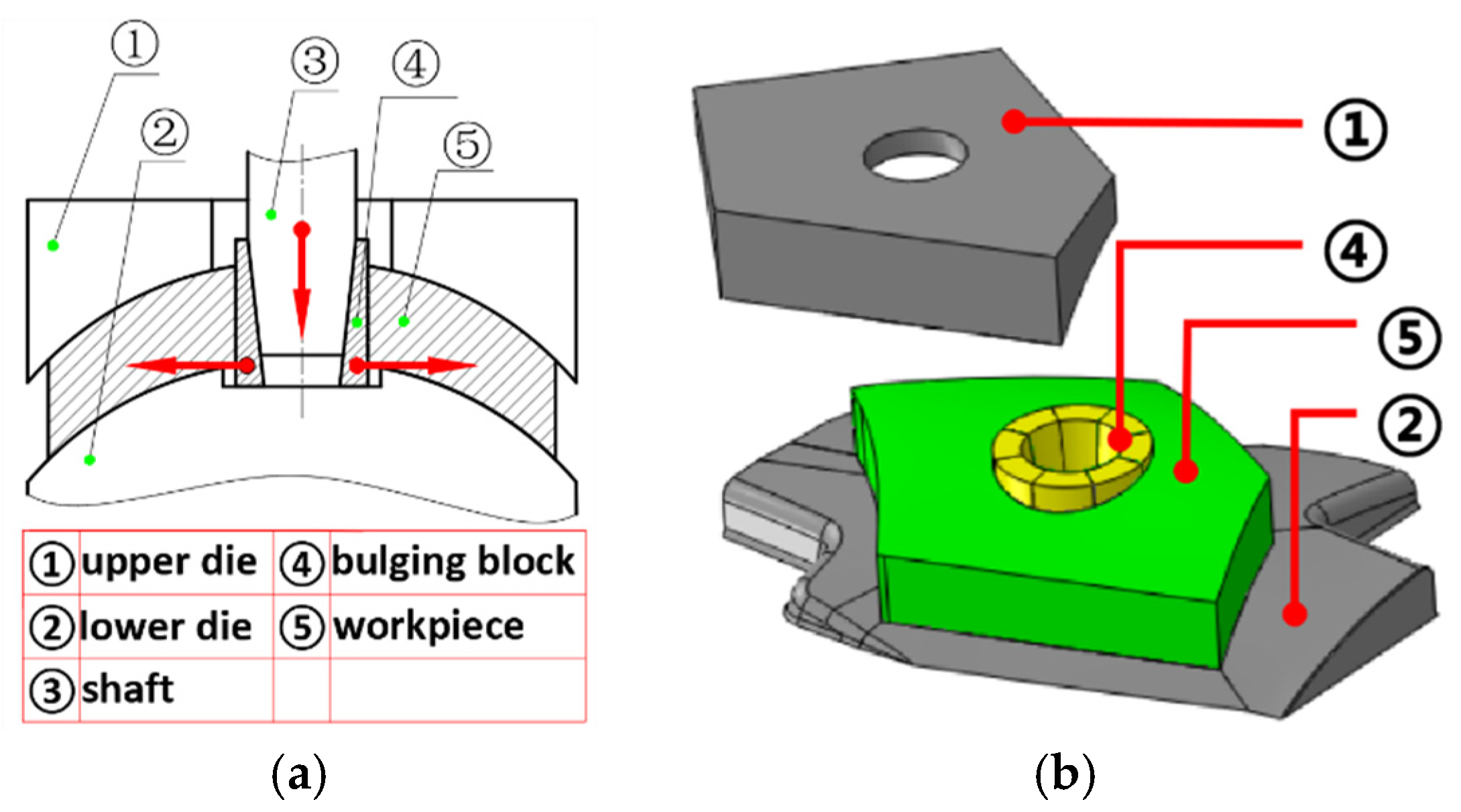







| Series | Distance | e/D |
|---|---|---|
| A | 98 mm | 0.98 |
| B | 130 mm | 1.3 |
| C | 97 mm | 0.97 |
| D | 121 mm | 1.21 |
| E | 119 mm | 1.19 |
| Temperature °C | Conductivity w/m·°C | Elastic Modulus MPa | Yield Stress MPa | Specific Heat Capacity J/kg·°C | Density Kg/m3 | Thermal Expansion m/°C |
|---|---|---|---|---|---|---|
| 25 | 112 | 71,500 | 286 | 788 | 2730 | 3.00 × 10−5 |
| 50 | 116 | 69,460 | 245 | 852 | 2730 | |
| 100 | 126 | 66,830 | 218 | 925 | 2720 | |
| 150 | 137 | 64,100 | 199 | 937 | 2710 | |
| 200 | 155 | 61,420 | 162 | 861 | 2700 | |
| 250 | 168 | 58,580 | 146 | 938 | 2680 | |
| 300 | 168 | 55,330 | 94 | 1013 | 2670 | |
| 350 | 163 | 51,620 | 49 | 1053 | 2660 | |
| 400 | 158 | 49,960 | 39 | 1105 | 2650 | |
| 450 | 153 | 28,930 | 24 | 1113 | 2640 |
| e/D | Radial Stress Reduction | Hoop Stress Reduction | Axial Stress Reduction | |
|---|---|---|---|---|
| Surface stress | 1 | 36% | 56% | 51% |
| 1.2 | 18% | 41% | −42% | |
| 1.3 | 15% | 20% | −138% | |
| Internal stress | 1 | 69% | 66% | 37% |
| 1.2 | 28% | 20% | 28% | |
| 1.3 | 20% | 12% | 20% |
| Component | CE 1% Stress Reduction | CE 2% Stress Reduction | CE 3% Stress Reduction | |||
|---|---|---|---|---|---|---|
| Radial Stress | Hoop Stress | Radial Stress | Hoop Stress | Radial Stress | Hoop Stress | |
| 36% | 56% | 77% | 34% | 86% | 25% | |
| 18% | 42% | 23% | 77% | 34% | 85% | |
| 15% | 22% | 33% | 46% | 46% | 61% | |
| 22.5% | 40.2% | 42.2% | 54.8% | 53.2% | 59.8% | |
| X-ray Diffraction Parameters | Values |
|---|---|
| X-ray diffractometer | XRD, STRESSTECH 3000 |
| Tube type | Cr |
| Supplied current during the experiment | 6.7 mA |
| Supplied voltage during the experiment | 30 kV |
| Exposure time for the calibration | 8 s |
| Exposure time for the measurement | 10 s |
| Collimator diameter | 2 mm |
| Collimator distance | 10.5 mm |
| Tilt angle | −45°~45° |
| Number of tilts | 5/5 |
| Angle of deviation | 139.7 |
| Crystal face of deviation | 313 |
| Stress resolution | ±10 MPa |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, C.; Li, C.; Zhang, X.; Wu, Y.; Zhang, T. Quenched Residual Stress Reduction in Pentagon-Curved Aluminum Alloy Forgings Using the Bulging Process. Materials 2023, 16, 5910. https://doi.org/10.3390/ma16175910
Luo C, Li C, Zhang X, Wu Y, Zhang T. Quenched Residual Stress Reduction in Pentagon-Curved Aluminum Alloy Forgings Using the Bulging Process. Materials. 2023; 16(17):5910. https://doi.org/10.3390/ma16175910
Chicago/Turabian StyleLuo, Chuanwei, Chen Li, Xinquan Zhang, Yunxin Wu, and Tao Zhang. 2023. "Quenched Residual Stress Reduction in Pentagon-Curved Aluminum Alloy Forgings Using the Bulging Process" Materials 16, no. 17: 5910. https://doi.org/10.3390/ma16175910
APA StyleLuo, C., Li, C., Zhang, X., Wu, Y., & Zhang, T. (2023). Quenched Residual Stress Reduction in Pentagon-Curved Aluminum Alloy Forgings Using the Bulging Process. Materials, 16(17), 5910. https://doi.org/10.3390/ma16175910





