Constitutive Damage Model of Foamed Lightweight Concrete Using Statistical Damage Theory
Abstract
:1. Introduction
2. Application of Foamed Lightweight Concrete
3. Damage Constitutive Model
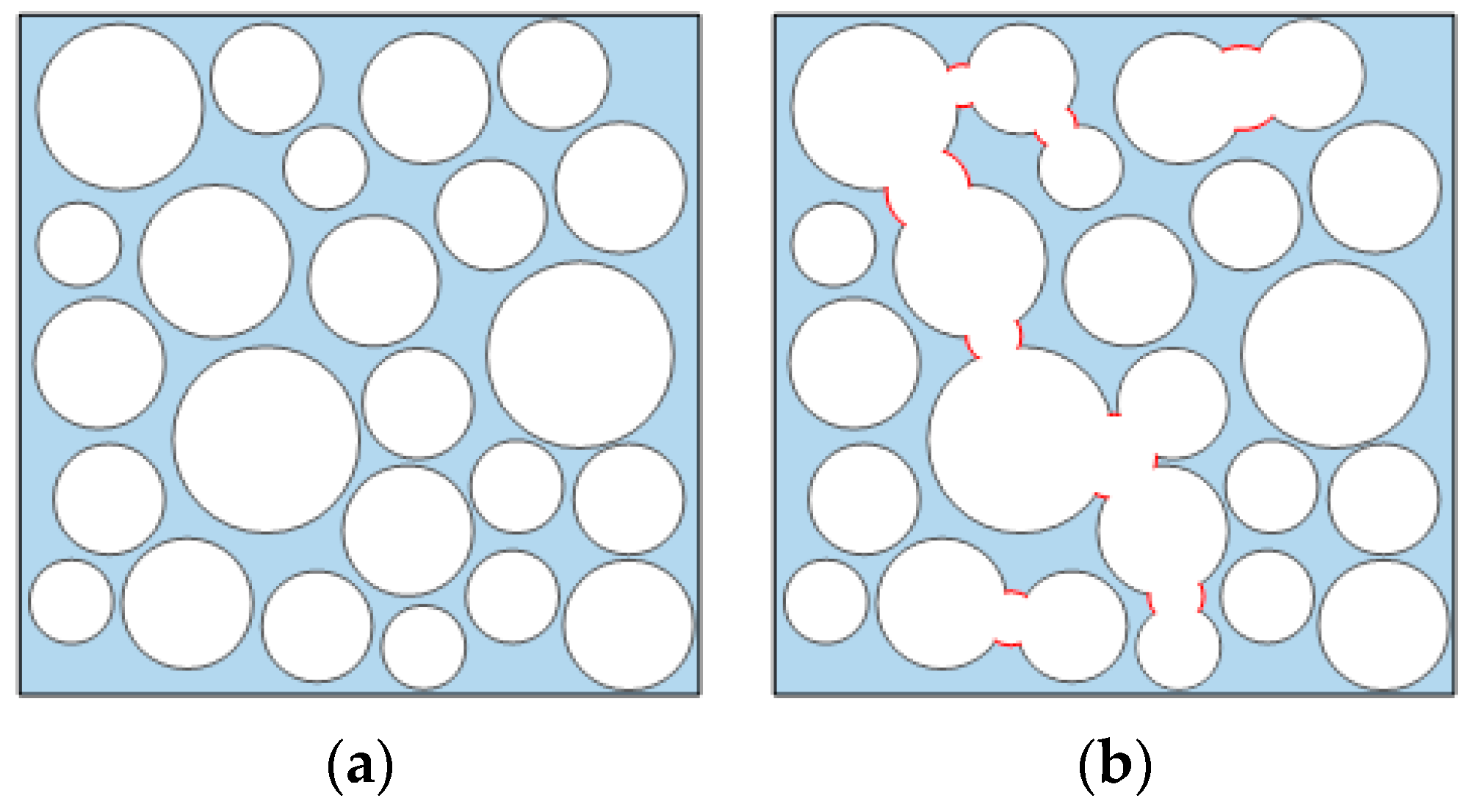
3.1. Statistical Damage Variable
3.2. Weibull Distribution Function
3.3. Derivation of Damage Constitutive Model
3.4. Determination of Damage Model Parameters
3.4.1. Weibull Parameters m and K
3.4.2. Parameters and
4. Model Validation
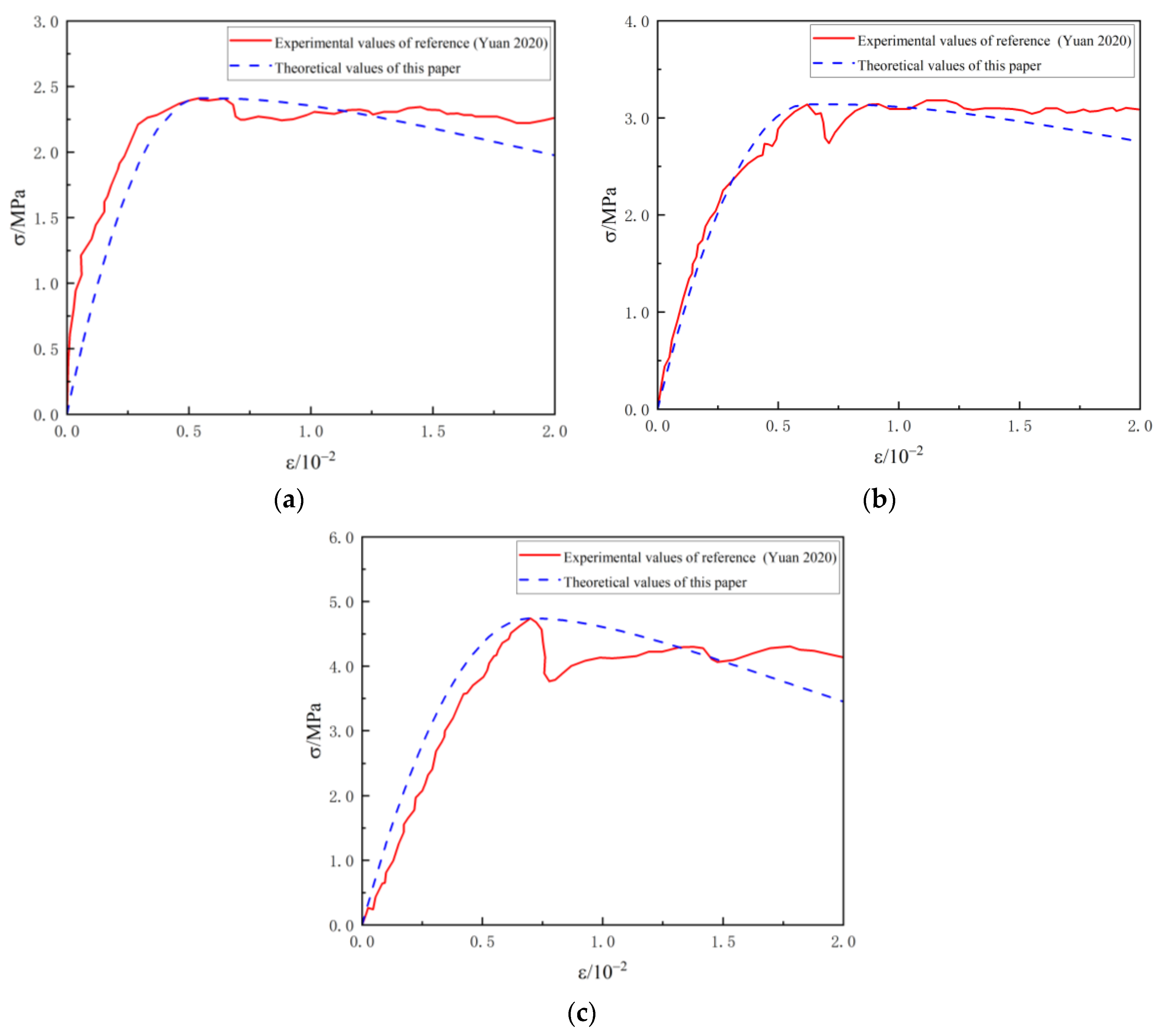
4.1. Comparison of Different Densities
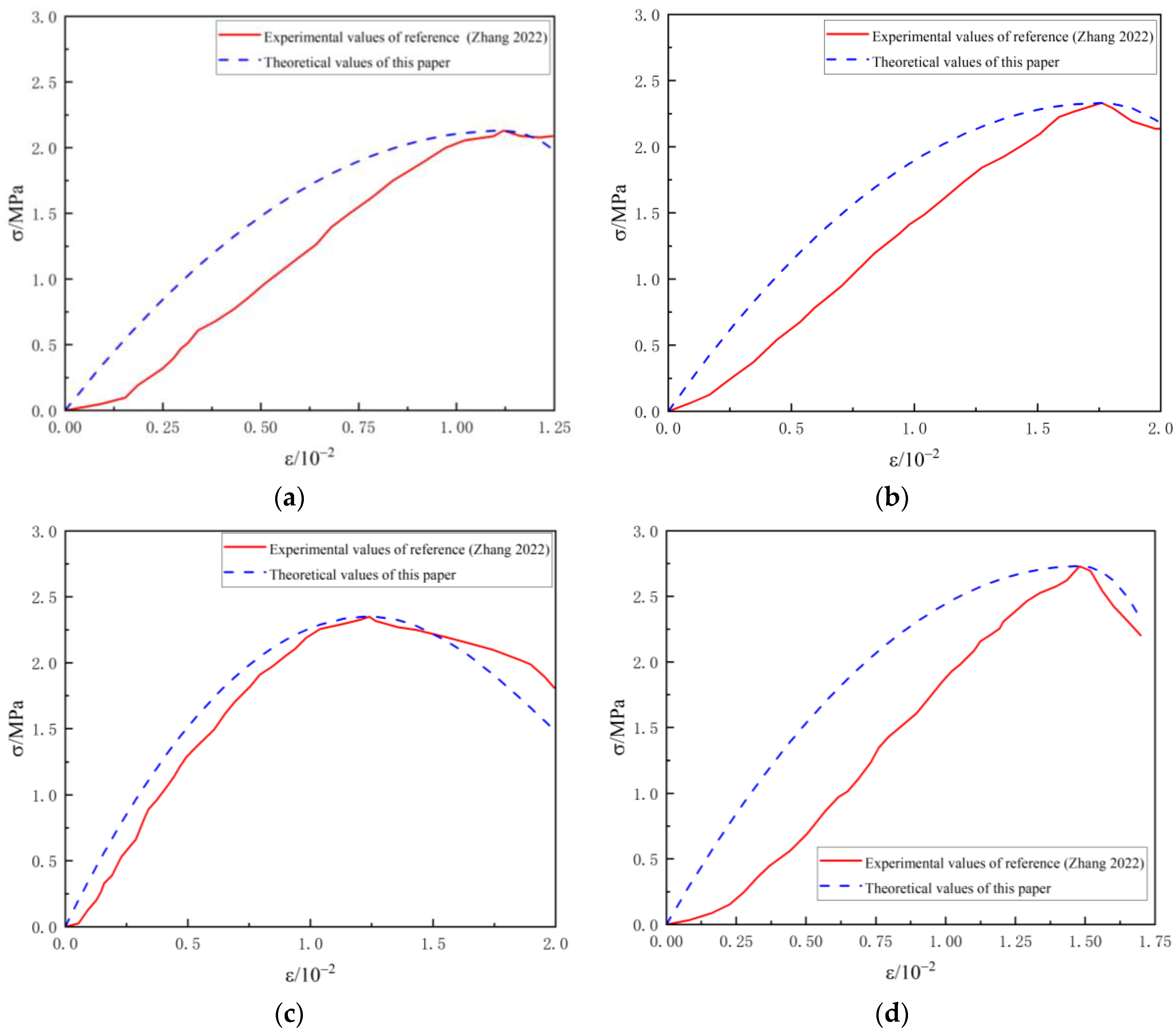
4.2. Comparison of Different Confining Pressures
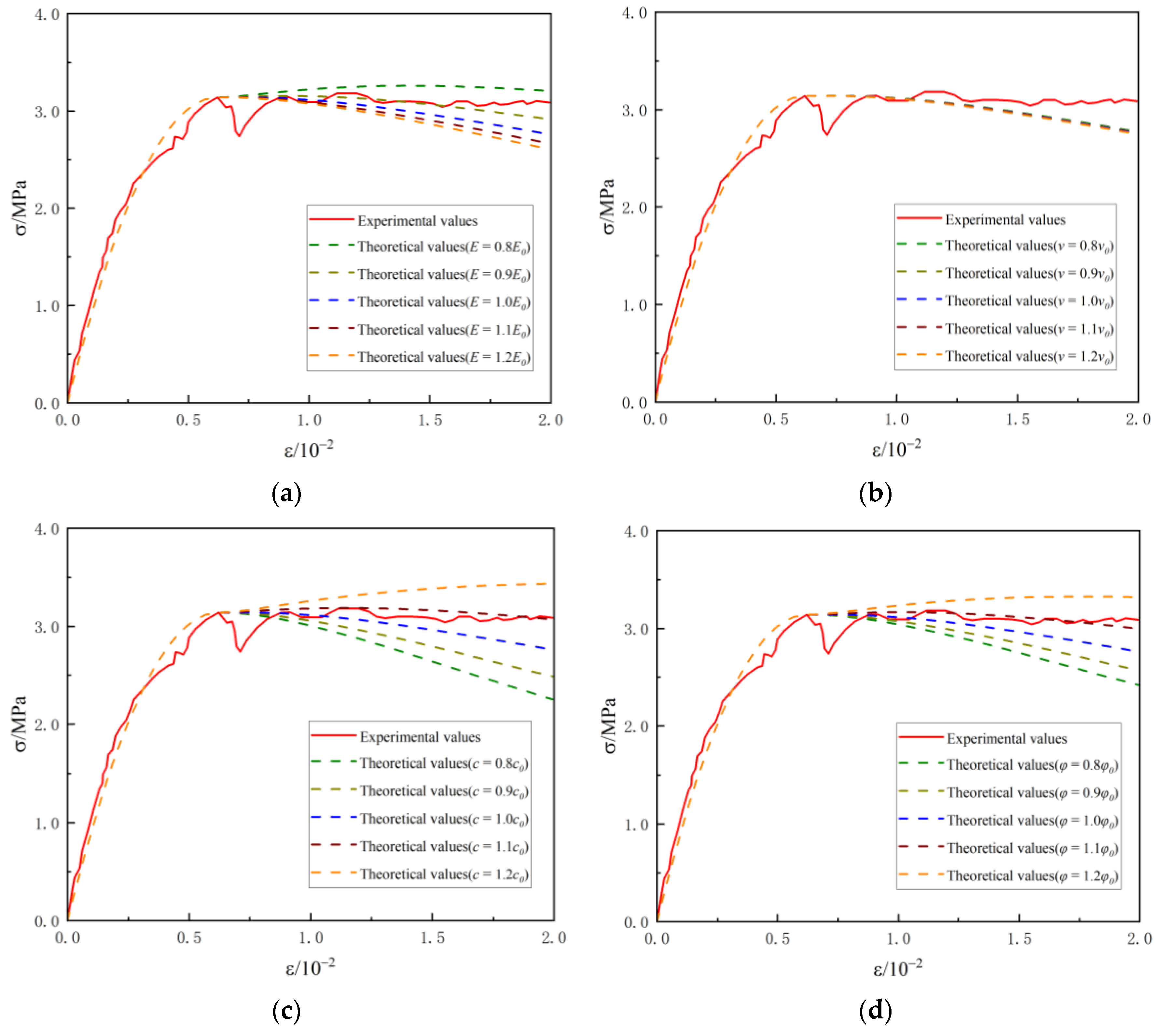
5. Parameter Sensitivity Analysis
6. Conclusions
- A damage constitutive model of foamed lightweight concrete on the basis of statistical damage theory is proposed, fully considering the strength heterogeneity caused by the micro-pore damage of foamed lightweight concrete under external load.
- The key parameters of the damage model were deduced by combining the Weibull function and the M-C criterion, and the rationality of the damage constitutive model was determined.
- The triaxial compression test data verify that the damage constitutive method can fit the stress–strain curve of the foamed lightweight concrete under external load well, and the best results are obtained when the confining pressure is 0.3 MPa and the density is 700 kg·m−3. The model is sensitive to the friction angle and cohesion, and the optimal correction coefficient is 1.1.
- Although the selected density and confining pressure are widely used in different types of structures and engineering, there will be more structural and load conditions in actual engineering. Therefore, future research can verify the accuracy and applicability of the model through data from more projects.
- Due to the equipment limitation, theoretical analysis is mainly used. It is a significant expansion direction to consider the fracture channel in combination with CT scanning technology.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fediuk, R.; Amran, M.; Vatin, N.; Vasilev, Y.; Lesovik, V.; Ozbakkaloglu, T. Acoustic properties of innovative concretes: A review. Materials 2021, 14, 398. [Google Scholar] [CrossRef] [PubMed]
- She, W.; Chen, Y.Q.; Zhang, Y.S.; Jones, M.R. Characterization and simulation of microstructure and thermal properties of foamed concrete. Constr. Build. Mater. 2013, 47, 1278–1291. [Google Scholar]
- Kurpińska, M.; Haustein, E. Experimental study of the resistance to influence of aggressive liquids on lightweight concrete. Materials 2021, 14, 4185. [Google Scholar] [CrossRef] [PubMed]
- Gong, C.J.; Wang, Y.Y.; Peng, Y.C.; Ding, W.Q.; Lei, M.F.; Da, Z.H.; Shi, C.H. Three-dimensional coupled hydromechanical analysis of localized joint leakage in segmental tunnel linings. Tunn. Undergr. Space Technol. 2022, 130, 104726. [Google Scholar] [CrossRef]
- Dara, A.; Bahubalendruni, M.V.A.R.; Mertens, A.J.; Balamurali, G.J. Numerical and experimental investigations of novel nature inspired open lattice cellular structures for enhanced stiffness and specific energy absorption. Mater. Today Commun. 2022, 31, 103286. [Google Scholar] [CrossRef]
- Ma, J.X.; Pei, H.F.; Zhu, H.H.; Shi, B.; Yin, J.H. A review of previous studies on the applications of fiber optic sensing technologies in geotechnical monitoring. Rock Mech. Bull. 2022, 2, 100021. [Google Scholar] [CrossRef]
- He, M. The Future of Rock Mechanics Lies with China: Inaugural editorial for Rock Mechanics Bulletin. Rock Mech. Bull. 2022, 1, 100010. [Google Scholar] [CrossRef]
- Amran, M.; Fediuk, R.; Vatin, N.; Lee, Y.H.; Murali, G.; Ozbakkaloglu, T.; Klyuev, S.; Alabduljabber, H. Fibre-reinforced foamed concretes: A review. Materials 2020, 13, 4323. [Google Scholar] [CrossRef]
- Su, B.Y.; Zhou, Z.W.; Li, Z.Q.; Wang, Z.H.; Shu, X.F. Experimental investigation on the mechanical behavior of foamed concrete under uniaxial and triaxial loading. Constr. Build. Mater. 2019, 209, 41–51. [Google Scholar] [CrossRef]
- Liu, W.; Xu, X.Y.; Mu, C.M. Development of Damage Type Viscoelastic Ontological Model for Soft and Hard Materials under High-Strain-Rate Conditions. Appl. Sci. 2022, 12, 8407. [Google Scholar] [CrossRef]
- Guo, H.; Guo, W.G.; Shi, Y.J. Computational modeling of the mechanical response of lightweight foamed concrete over a wide range of temperatures and strain rates. Constr. Build. Mater. 2015, 96, 622–631. [Google Scholar] [CrossRef]
- Luo, X.; Xu, J.Y.; Liu, Y. The static constitutive model of fiber reinforced cellular materials. Constr. Build. Mater. 2018, 187, 903–906. [Google Scholar] [CrossRef]
- Zhou, Z.; Hu, J.F.; Li, F.; Zhang, J.J.; Lei, M.F. Elastic modulus prediction model of foamed concrete based on the Walsh formula. Appl. Sci. 2022, 12, 5142. [Google Scholar] [CrossRef]
- Batool, F.; Bindiganavile, V. Air-void size distribution of cement based foam and its effect on thermal conductivity. Constr. Build. Mater. 2017, 149, 17–28. [Google Scholar] [CrossRef]
- Nguyen, T.; Kashani, A.; Ngo, T.; Bordas, S. Deep neural network with high-order neuron for the prediction of foamed concrete strength. Comput. Aided Civ. Infrastruct. Eng. 2019, 34, 316–332. [Google Scholar] [CrossRef]
- Falliano, D.; De Domenico, D.; Sciarrone, A.; Ricciardi, G.; Restuccia, L.; Tulliani, J.M.C.; Gugliandolo, E. Fracture behavior of lightweight foamed concrete: The crucial role of curing conditions. Theor. Appl. Fract. Mech. 2019, 103, 102297. [Google Scholar] [CrossRef]
- Yang, Y.Y.; Zhou, Q.; Deng, Y. The reinforcement attributes of multi-scale hybrid fiber throughout the uniaxial compression of ultra-low-weight foamed cement-based composites. Constr. Build. Mater. 2020, 242, 118184. [Google Scholar] [CrossRef]
- Su, B.Y. Mechanical Properties and Elastoplastic Damage Constitutive Model for Foamed Concrete. Ph.D. Thesis, Taiyuan University of Technology, Taiyuan, China, 2017. (In Chinese). [Google Scholar]
- Dara, A.; Mertens, A.J.; Bahubalendruni, M.V.A.R. Characterization of penetrate and interpenetrate tessellated cellular lattice structures for energy absorption. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2023, 237, 906–913. [Google Scholar] [CrossRef]
- Kavussi, A.; Motevalizadeh, S.M. Fracture failure evaluation of foam WMA mixes containing RAP by applying weibull probability distribution function. Int. J. Pavement Res. Technol. 2021, 15, 1277–1296. [Google Scholar] [CrossRef]
- Adamu, M.; Mohammed, B.S.; Liew, M.S.; Alaloul, W.S. Evaluating the impact resistance of roller compacted concrete containing crumb rubber and nanosilica using response surface methodology and Weibull distribution. World J. Eng. 2019, 16, 33–43. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, J.J.; Gong, C.J. Hybrid semantic segmentation for tunnel lining cracks based on Swin Transformer and convolutional neural network. Comput. Aided Civ. Infrastruct. Eng. 2023. [Google Scholar] [CrossRef]
- Tan, X.J.; Chen, W.Z.; Yang, D.Y.; Liu, H.Y.; Chan, A.H. Experimental and theoretical studies on effect of height-to-diameter ratios on failure forms and mechanical characteristics of foamed concrete. J. Mater. Civ. Eng. 2019, 31, 04018341. [Google Scholar] [CrossRef]
- Yuan, H.Q.; Zhu, D.Y.; Zhang, H.Q.; Wu, J.J.; Xu, X.X.; Sun, R.J. Compression characteristics of foamed lightweight soil under triaxial stress. Bull. Chin. Ceram. Soc. 2020, 39, 3379–3385. (In Chinese) [Google Scholar]
- Zhang, H.B.; Liu, M.M.; Sun, Y.H.; Yang, Q.; Song, X.G.; Li, X.L. Triaxial mechanical characteristic of the silt- based foamed concrete. J. Shandong Univ. (Eng. Sci.) 2022, 52, 39–46+57. (In Chinese) [Google Scholar]


| Notation | Meaning |
|---|---|
| Dc | Fracture damage variable |
| Ec | Elasticity modulus after fracture damage |
| E0 | Elasticity modulus before fracture is produced |
| P(f) | Probability density of Weibull distribution |
| m, K | Parameters of Weibull distribution |
| σ | Nominal stress |
| σp | Peak stress |
| ε | Strain produced by the nominal stress acting on the damaged material |
| ε′ | Strain produced by the effective stress acting on the undamaged material |
| εp | Peak strain |
| , | Parameters of the damage model |
| ρ/kg·m−3 | c/Mpa | φ/(°) | E/Mpa | σp/Mpa | εp | v | σ3/Mpa |
|---|---|---|---|---|---|---|---|
| 700 | 0.7 | 18 | 1011 | 2.41 | 0.0054 | 0.21 | 0.5 |
| 800 | 1.01 | 20 | 1217 | 3.14 | 0.0062 | 0.22 | 0.5 |
| 900 | 1.26 | 22 | 1460 | 4.74 | 0.0070 | 0.21 | 0.5 |
| ρ/kg·m−3 | m | K | ||
|---|---|---|---|---|
| 700 | 0.5164 | 1.4172 | −82,647.4623 | 892.5926 |
| 800 | 0.4988 | 1.8947 | −81,685.7440 | 1012.9032 |
| 900 | 0.6700 | 3.8099 | −96,734.6939 | 1354.2857 |
| ρ/kg·m−3 | c/MPa | φ/(°) | E/MPa | σp/MPa | εp | v | σ3/MPa |
|---|---|---|---|---|---|---|---|
| 700 | 0.65 | 23.9 | 208 | 2.13 | 0.0112 | 0.23 | 0.1 |
| 700 | 0.65 | 23.9 | 148 | 2.33 | 0.0176 | 0.23 | 0.2 |
| 700 | 0.65 | 23.9 | 255 | 2.35 | 0.0124 | 0.23 | 0.3 |
| 700 | 0.65 | 23.9 | 189 | 2.73 | 0.0148 | 0.23 | 0.4 |
| σ3/MPa | m | K | ||
|---|---|---|---|---|
| 0.1 | 8.1386 | 5.4866 | −16,980.2296 | 380.3571 |
| 0.2 | 6.0484 | 6.5911 | −7521.9525 | 264.7727 |
| 0.3 | 2.6132 | 9.0041 | −15,283.5588 | 379.0323 |
| 0.4 | 9.8381 | 6.8319 | −12,463.4770 | 368.9189 |
| i | Ei | vi | ci | φi |
|---|---|---|---|---|
| 0.8 | E1 = 0.8 E0 | v1 = 0.8 v0 | c1 = 0.8 c0 | φ1 = 0.8 φ0 |
| 0.9 | E2 = 0.9 E0 | v2 = 0.9 v0 | c2 = 0.9 c0 | φ2 = 0.9 φ0 |
| 1.0 | E3 = 1.0 E0 | v3 = 1.0 v0 | c3 = 1.0 c0 | φ3 = 1.0 φ0 |
| 1.1 | E4 = 1.1 E0 | v4 = 1.1 v0 | c4 = 1.1 c0 | φ4 = 1.1 φ0 |
| 1.2 | E5 = 1.2 E0 | v5 = 1.2 v0 | c5 = 1.2 c0 | φ5 = 1.2 φ0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z.; Zheng, Y.; Xie, G.; Li, F.; Ji, Z.; Gong, C. Constitutive Damage Model of Foamed Lightweight Concrete Using Statistical Damage Theory. Materials 2023, 16, 5946. https://doi.org/10.3390/ma16175946
Zhou Z, Zheng Y, Xie G, Li F, Ji Z, Gong C. Constitutive Damage Model of Foamed Lightweight Concrete Using Statistical Damage Theory. Materials. 2023; 16(17):5946. https://doi.org/10.3390/ma16175946
Chicago/Turabian StyleZhou, Zhong, Yidi Zheng, Guiqiu Xie, Fan Li, Zigang Ji, and Chenjie Gong. 2023. "Constitutive Damage Model of Foamed Lightweight Concrete Using Statistical Damage Theory" Materials 16, no. 17: 5946. https://doi.org/10.3390/ma16175946
APA StyleZhou, Z., Zheng, Y., Xie, G., Li, F., Ji, Z., & Gong, C. (2023). Constitutive Damage Model of Foamed Lightweight Concrete Using Statistical Damage Theory. Materials, 16(17), 5946. https://doi.org/10.3390/ma16175946







