First-Principles Study on Si Atom Diffusion Behavior in Ni-Based Superalloys
Abstract
:1. Introduction
2. Computational Details
3. Results and Discussion
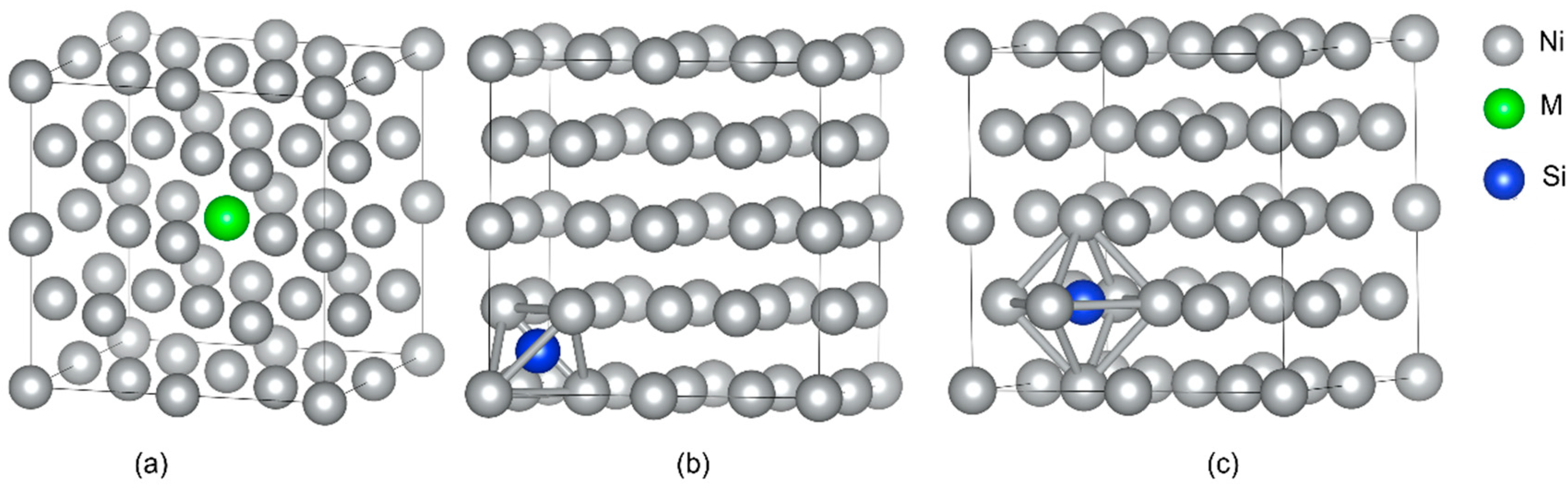
3.1. Structural Characteristics
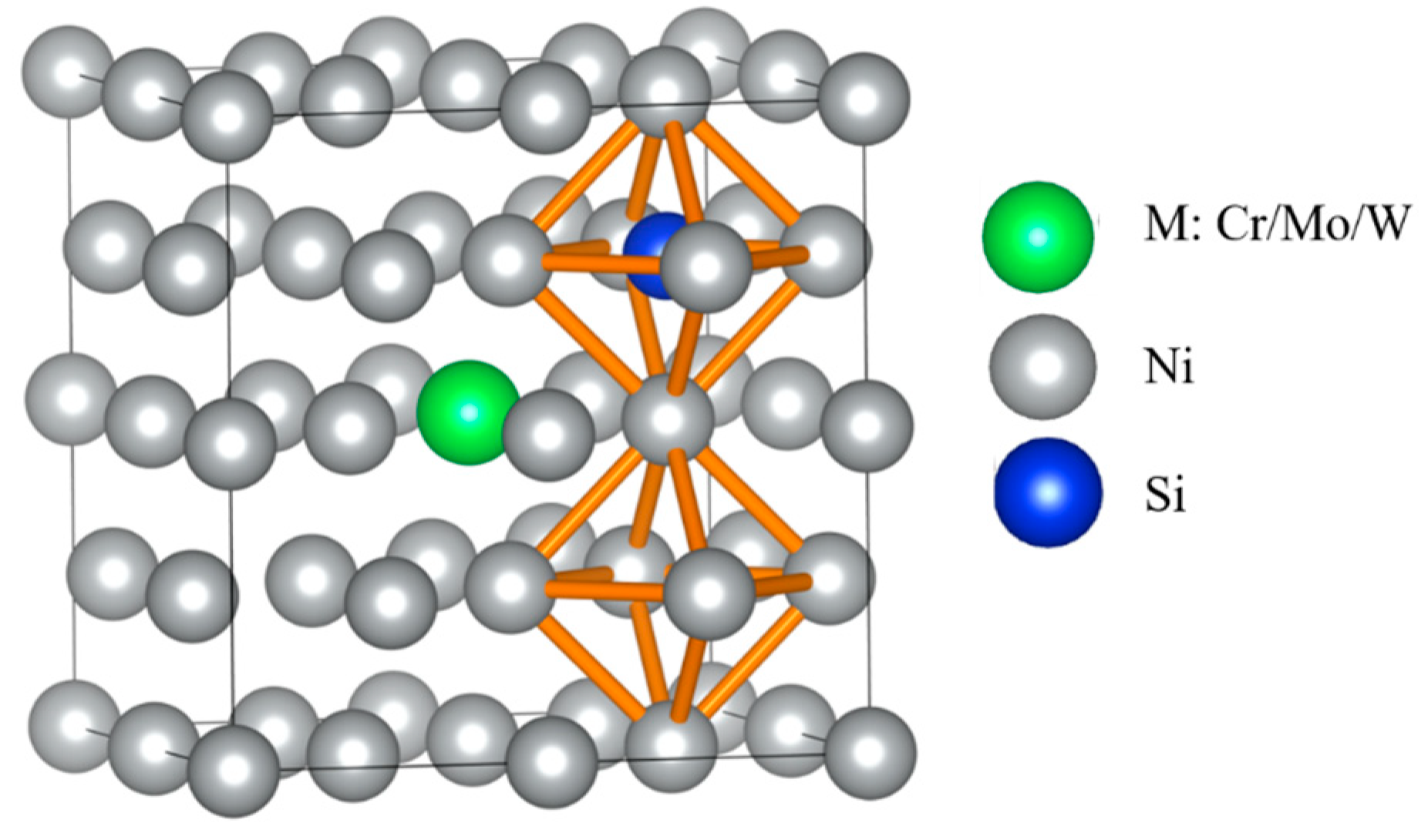
3.2. Occupying Tendency of Si Atoms as MPD Elements in γ-Ni and γ′-Ni3Fe
3.3. Si Atom Diffusion Behaviors in γ-Ni and γ′-Ni3Fe Supercells
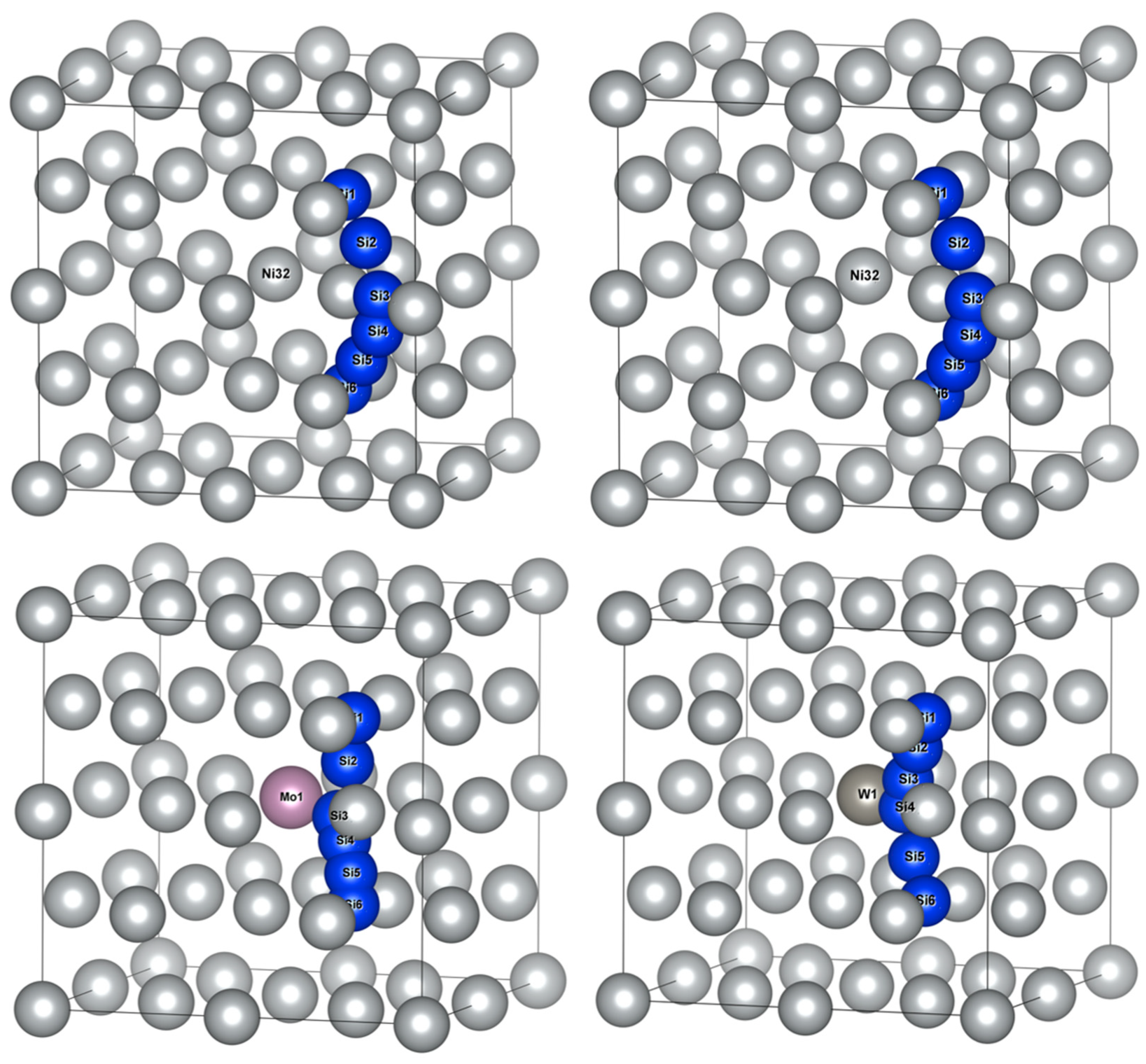
3.3.1. Si Atom Diffusion Behavior in γ-Ni Supercells
3.3.2. Si Atom Diffusion Behavior in the γ′-Ni3Fe Supercell
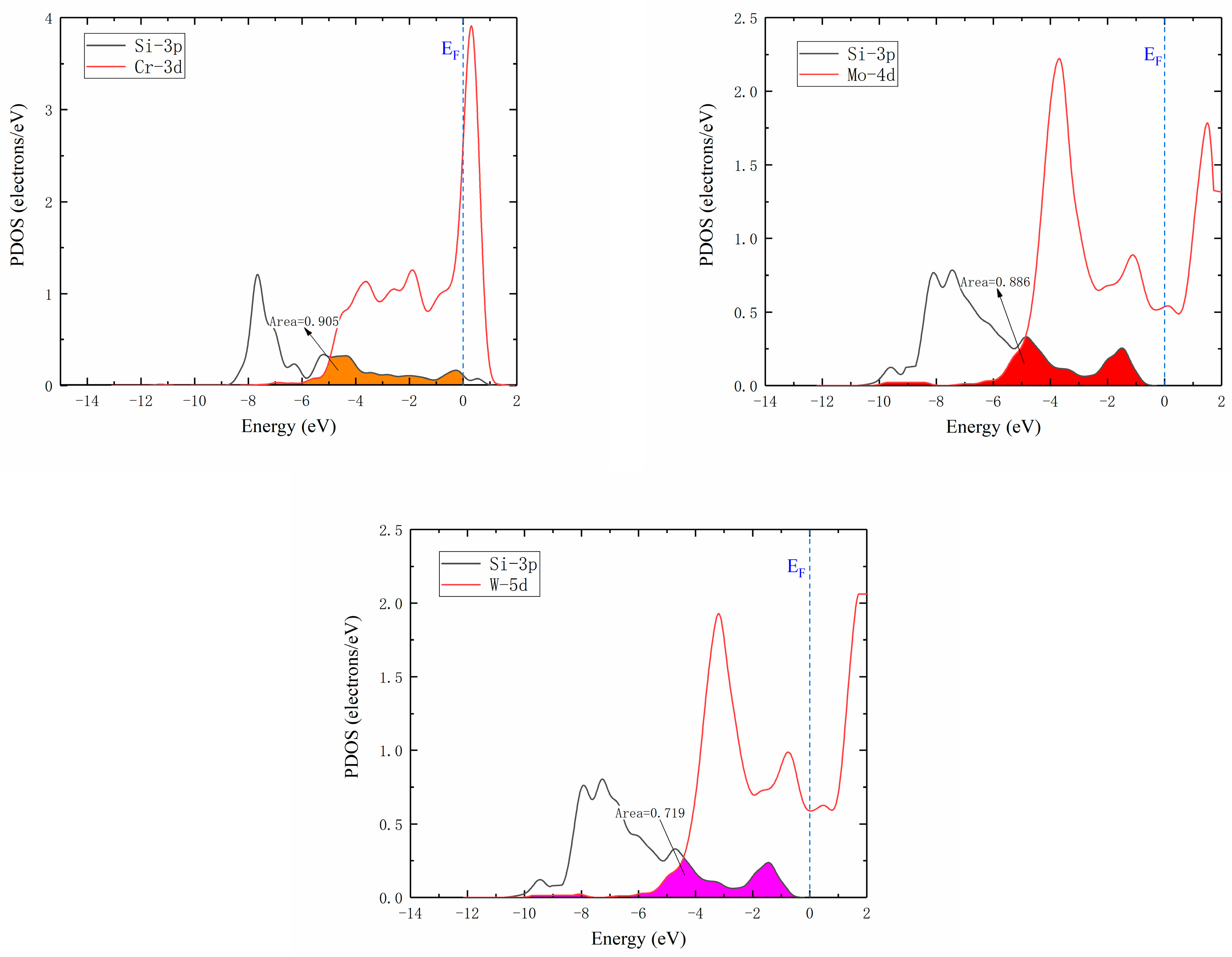
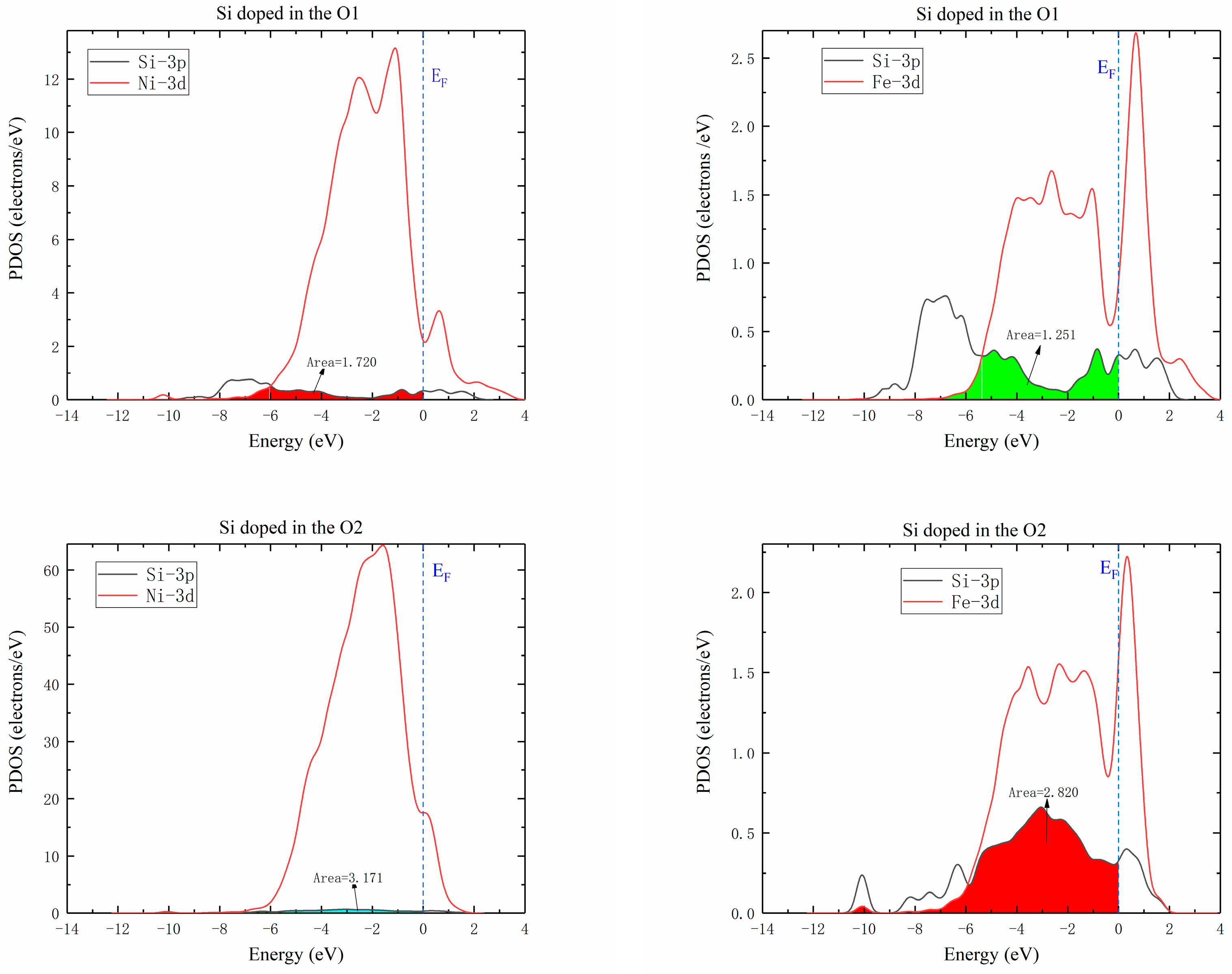
3.3.3. Relation between Si Diffusion Properties and Electronic Structure
3.3.4. Diffusion Coefficient
4. Conclusions
- (1)
- Doping of alloying elements M (Cr, Mo, W) in both γ-Ni and γ′-Ni3Fe supercells significantly decreased formation enthalpy with the increase of the radius of the doped atoms and Si atoms tended to occupy more octahedral interstitial sites in γ-Ni and γ′-Ni3Fe;
- (2)
- Two adjacent octahedral interstitials closest to M (Cr, Mo, W) atoms were adopted as the initial and final positions of Si diffusion in γ-Ni supercells. It was found that diffusion energy barrier was increased by increasing the atomic radius of alloying elements M, indicating that the doping of large-size atoms caused higher lattice distortions, resulting in higher diffusion energy barriers;
- (3)
- Si atoms occupied two types of octahedral interstitial sites (O1 and O2) in γ′-Ni3Fe. When diffusing with O1 as the isovalent site, single-peak energy barrier distributions were observed, while Si atom diffusing with O2 as the isovalent site presented an approximately double-peak energy barrier distribution. The energy barriers of the two diffusion paths were also increased with the increase of the radius of the doped M atom, but Si diffusion energy barrier around the shared Fe atoms (O2 diffusion path) between adjacent octahedral interstices was significantly lower than that around the shared Ni atoms (O1 diffusion path). This indicated that Si atoms tended to occupy O2 octahedral interstitial sites;
- (4)
- Increase of interaction strength between the doped M atom/Octahedron constituent atom and Si atom increased the diffusion of Si atom and decreased the diffusion energy barrier.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chaharlang, R.; Hajjari, E.; Baghal, S.M.L.; Siahpoosh, M. Premature damage of the second stage nozzle guide vanes of a gas turbine made of Inconel 738LC. Eng. Fail. Anal. 2019, 105, 803–816. [Google Scholar] [CrossRef]
- Kwon, H.-J.; Lee, D.; Lee, Y.-K. Failure analysis of blades and vanes of a compressor for a gas turbine engine. Eng. Fail. Anal. 2021, 124, 105386. [Google Scholar] [CrossRef]
- García-Martínez, M.; del Hoyo Gordillo, J.C.; González, P.V. Failure study of an aircraft engine high pressure turbine (HPT) first stage blade. Eng. Fail. Anal. 2023, 149, 107251. [Google Scholar] [CrossRef]
- Xiao, H.; Warren, M. Wide gap braze repair of gas turbine blades and vanes—A review. J. Eng. Gas Turbines Power 2012, 134, 010801. [Google Scholar]
- Fritsche, B.; Satir-Kolorz, A.; Baumann, R. Repair brazing of nickel-base turbine blades. Weld. Res. Counc. Prog. Rep. 2001, 47, 16–20. [Google Scholar]
- Heikinheimo, L.S.K.; Laukkanen, A.; Veivo, J. Joint Characterisation for Repair Brazing of Superalloys. Weld. World 2005, 49, 5–12. [Google Scholar] [CrossRef]
- Henhoeffer, T.; Huang, X.; Yand, S.; Au, P.; Nagy, D. Microstructure and high temperature tensile properties of wide gap brazed cobalt based superalloy X-40. Mater. Sci. Technol. 2010, 26, 431–439. [Google Scholar] [CrossRef]
- McGuire, D.; Huang, X.; Nagy, D.; Chen, W. Effect of Tungsten Addition on the Nucleation of Borides in Wide Gap Brazed Joint. J. Eng. Gas Turbines Power 2010, 132, 062101. [Google Scholar] [CrossRef]
- Ren, X.; Liu, W.; Ren, H.; Jing, Y.; Mao, W.; Xiong, H. Microstructures and joining characteristics of NbSS/Nb5Si3 composite joints by newly-developed Ti66-Ni22-Nb12 filler alloy. J. Mater. Sci. Technol. 2020, 58, 95–99. [Google Scholar] [CrossRef]
- Li, R.; Yu, Z.; Qi, K. Vacuum Brazing of GH2132 Superalloy Using BNi-2+BNi-5 Composite Filler. Adv. Mater. Res. 2012, 602–604, 2087–2091. [Google Scholar] [CrossRef]
- Collier, J.P.; Keefe, P.W.; Tien, J.K. The effects of replacing the refractory elements W, Nb, and Ta with Mo in nickel-base superalloys on microstructural, microchemistry, and mechanical properties. Metall. Trans. A 1986, 17, 651–661. [Google Scholar] [CrossRef]
- Ji, J.Y.; Zhang, Z.; Chen, J.; Zhang, H.; Zhang, Y.Z.; Lu, H. Effect of refractory elements M (=Re, W, Mo or Ta) on the diffusion properties of boron in nickel-based single crystal superalloys. Vacuum 2023, 211, 111923. [Google Scholar] [CrossRef]
- Chen, Y.; Yu, H.; Chen, Y.; Di, H.; Xu, W. The strengthening effects and mechanisms of alloying elements on interfaces for multiphase Ni-based superalloys: A first-principles study. J. Mater. Res. Technol. 2023, 23, 4802–4813. [Google Scholar] [CrossRef]
- Gong, W.; Zhao, W.; Miao, N.; Zhou, J.; Sun, Z.; Li, S.; Gong, S. Strengthening effects of alloying elements W and Re on Ni3Al: A first-principles study. Comput. Mater. Sci. 2018, 144, 23–31. [Google Scholar] [CrossRef]
- Chen, Z.; Okamoto, N.L.; Chikugo, K.; Inui, H. On the possibility of simultaneously achieving sufficient oxidation resistance and creep property at high temperatures exceeding 1000 °C in Co-based superalloys. J. Alloys Compd. 2021, 858, 157724. [Google Scholar] [CrossRef]
- Liu, X.-J.; He, Y.-Q.; Cao, G.-M.; Jia, T.; Wu, T.Z.; Liu, Z.Y. Effect of Si Content and Temperature on Oxidation Resistance of Fe-Si Alloys. J. Iron SteelRes. Int. 2015, 22, 238–244. [Google Scholar] [CrossRef]
- Bridges, D.; Nielsen, B.; Zhang, L.; Zhang, S.; Xu, R.; Hu, A. Wettability, Diffusion behaviors, and modeling of Ni nanoparticles and nanowires in brazing Inconel 718. Adv. Eng. Mater. 2021, 23, 2001053. [Google Scholar] [CrossRef]
- Zeng, Y.P.; Liu, Y.L.; Min, Q.H.; Wen, S.; Du, C.; Zheng, Z.; Liu, H.; Du, Y.; Premovic, M.; Wang, J. Diffusion coefficients and atomic mobilities in fcc Ni-Cu-Mo alloys: Experiment and modeling. Calphad-Comput. Coupling Phase Diagr. Thermochem. 2020, 71, 102209. [Google Scholar] [CrossRef]
- Chen, J.; Xiao, J.K.; Wang, C.Y.; Zhang, L. Diffusion behavior of fcc and L1(2) Ni-Al-Cr alloys. Vacuum 2021, 189, 110238. [Google Scholar] [CrossRef]
- Azeem, M.M.; Wang, Q.; Zhang, Y.; Liu, S.; Zubair, M. Effect of grain boundary on diffusion of P in alpha-Fe: A molecular dynamics study. Front. Phys. 2019, 7, 97. [Google Scholar] [CrossRef]
- Kresse, G. Ab initio molecular dynamics for liquid metals. Hafner J. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B—Condens. Matter Mater. Phys. 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Henkelman, G.; Uberuaga, B.P.; Jónsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 2000, 113, 9901–9904. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B—Condens. Matter Mater. Phys. 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Blochl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Chadi, D.J. Special points for Brillouin-zone integrations. Phys. Rev. B 1977, 16, 1746–1747. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA: A three-dimensional visualization system for electronic and structural analysis. J. Appl. Crystallogr. 2008, 41, 653–658. [Google Scholar] [CrossRef]
- Jiang, C.; Sordelet, D.J.; Gleeson, B. Site preference of ternary alloying elements in Ni3Al: A first-principles study. Acta Mater. 2006, 54, 1147–1154. [Google Scholar] [CrossRef]
- Li, Y.-J.; Hu, Q.M.; Xu, D.S.; Yang, R. Strengthening of γ-TiAl-Nb by short-range ordering of point defects. Intermetallics 2011, 19, 793–796. [Google Scholar] [CrossRef]
- Jinlong, Y.A.; Chuanyun, X.I.; Shangda, X.; Kelin, W. Site preference of alloying additions in intermetallic compounds. J. Phys. Condens. Matter 1993, 5, 6653–6662. [Google Scholar] [CrossRef]
- Wolf, W.; Podloucky, R.; Rogl, P.; Erschbaumer, H. Atomic modelling of Nb, V, Cr and Mn substitutions in γ-TiAl. 2: Electronic structure and site preference. Intermetallics 1996, 4, 201–209. [Google Scholar] [CrossRef]
- Wu, Q.; Li, S. Alloying element additions to Ni3Al: Site preferences and effects on elastic properties from first-principles calculations. Comput. Mater. Sci. 2012, 53, 436–443. [Google Scholar] [CrossRef]
- Wen, M.; Wang, C. Effect of alloying elements on the ideal strength and charge redistribution of γ′-Ni3Al: A first-principles study of tensile deformation. RSC Adv. 2016, 6, 77489. [Google Scholar] [CrossRef]
- Arrhenius, S. On the reaction rate of the inversion of non-refined sugar upon souring. Z. Phys. Chem. 1889, 4, 226. [Google Scholar] [CrossRef]
- Demorton, M.E. Measurement of nitrogen diffusion in chromium by anelastic methods. J. Appl. Phys. 1962, 33, 2768. [Google Scholar] [CrossRef]
- Gomer, R. Diffusion of adsorbates on metal surfaces. Rep. Prog. Phys. 1990, 53, 917. [Google Scholar] [CrossRef]
- Nowick, A.S.; Burton, J. Diffusion in Solids: Recent Developments; Academic Press: New York, NY, USA, 1975. [Google Scholar]
- Evangelakis, G.A.; Papanicolaou, N.I. Adatom self-diffusion processes on (001) copper surface by molecular dynamics. Surf. Sci. 1996, 347, 376. [Google Scholar] [CrossRef]
- Wert, C.; Zener, C. Interstitial atomic diffusion coefficients. Phys. Rev. B 1949, 76, 1169. [Google Scholar] [CrossRef]
- Wert, C. Diffusion coefficient of C in α-iron. Phys. Rev. B 1950, 79, 601. [Google Scholar] [CrossRef]
- Rao, J.P.; Ouyang, C.Y.; Lei, M.S.; Jiang, F.Y. First principles investigation of interaction between metal Nb and interstitial hydrogen atoms. Acta Phys. Sin. 2012, 61, 047105. (In Chinese) [Google Scholar]





| Unit Cell | Et (eV) | (eV) | Lattice Parameters (Å) | V (Å3) |
|---|---|---|---|---|
| Ni32 | −173.4105 | a = b = c = 7.0116 a = b = c = 7.108 [12] | 345.37 359.052 [12] | |
| Ni31Cr | −177.9648 | s | a = b = c = 7.0162 | 345.39 |
| Ni31Mo | −179.6984 | −0.0249 | a = b = c = 7.0469 | 349.94 |
| Ni31W | −181.9596 | −0.0346 | a = b = c = 7.0488 | 350.23 |
| Ni24Fe8 | −191.8737 | 0.0050 | a = b = c = 6.9859 | 340.94 |
| Ni24Al8 | a = b = c = 7.183 [12] | 370.735 [12] | ||
| Ni24Fe7Cr | −193.4393 | 0.0124 | a = b = c = 6.9950 | 342.27 |
| Ni24Al7Cr | a = b = c = 7.1426 [33] | |||
| Ni24Fe7Mo | −195.0244 | 0.0050 | a = b = c = 7.0270 | 346.99 |
| Ni24Al7Mo | a = b = c = 7.1688 [33] | |||
| Ni24Al7Mo | a = b = c = 7.146 [34] | |||
| Ni24Fe7W | −197.2241 | −0.0023 | a = b = c = 7.0294 | 347.33 |
| Ni24Al7W | a = b = c = 7.1702 [33] | |||
| Ni24Al7W | a = b = c = 7.146 [34] |
| Unit Cell | Et (eV) | (eV) | Lattice Parameters (Å) | V (Å3) |
|---|---|---|---|---|
| Ni32Si(O) | −177.9082 | 0.8325 | a = b = c = 7.0615 | 352.12 |
| Ni32Si(T) | −177.0116 | 1.7291 | a = b = c = 7.1576 | 366.69 |
| Ni24Fe8Si(O1) | −195.1897 | 2.1774 | a = b = c = 7.0747 | 354.1 |
| Ni24Fe8Si(O2) | −195.7070 | 1.6601 | a = b = c = 7.0747 | 354.1 |
| Ni24Fe8Si(T) | −194.5941 | 2.7038 | a = b = c = 7.0747 | 354.1 |
| Unit | Ni32Si (O) | Ni31CrSi (O) | Ni31MoSi (O) | Ni31Wsi (O) |
|---|---|---|---|---|
| Distance (Å) | 3.57128 | 3.84391 | 3.40285 | 3.50334 |
| Unit | Ni24Fe8Si (O1) | Ni24Fe7CrSi(O1) | Ni24Fe7MoSi (O1) | Ni24Fe7Wsi (O1) |
| Distance (Å) | 3.55823 | 3.56805 | 3.25186 | 3.27886 |
| Unit | Ni24Fe8Si (O2) | Ni24Fe7CrSi (O2) | Ni24Fe7CrSi (O2) | Ni24Fe7W (O2) |
| Distance (Å) | 3.54195 | 3.53302 | 3.15737 | 3.14115 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Wang, Z.; Du, M.; Du, Y.; Zhang, W. First-Principles Study on Si Atom Diffusion Behavior in Ni-Based Superalloys. Materials 2023, 16, 5989. https://doi.org/10.3390/ma16175989
Sun Y, Wang Z, Du M, Du Y, Zhang W. First-Principles Study on Si Atom Diffusion Behavior in Ni-Based Superalloys. Materials. 2023; 16(17):5989. https://doi.org/10.3390/ma16175989
Chicago/Turabian StyleSun, Yubo, Zhiping Wang, Mingrun Du, Yimeng Du, and Wang Zhang. 2023. "First-Principles Study on Si Atom Diffusion Behavior in Ni-Based Superalloys" Materials 16, no. 17: 5989. https://doi.org/10.3390/ma16175989




