Surface-Induced Electronic and Vibrational Level Shifting of [Fe(py)2bpym(NCS)2] on Al(100)
Abstract
:1. Introduction
2. Computational Details
3. Results and Discussion
3.1. Adsorption Configurations and Spin State Energetics
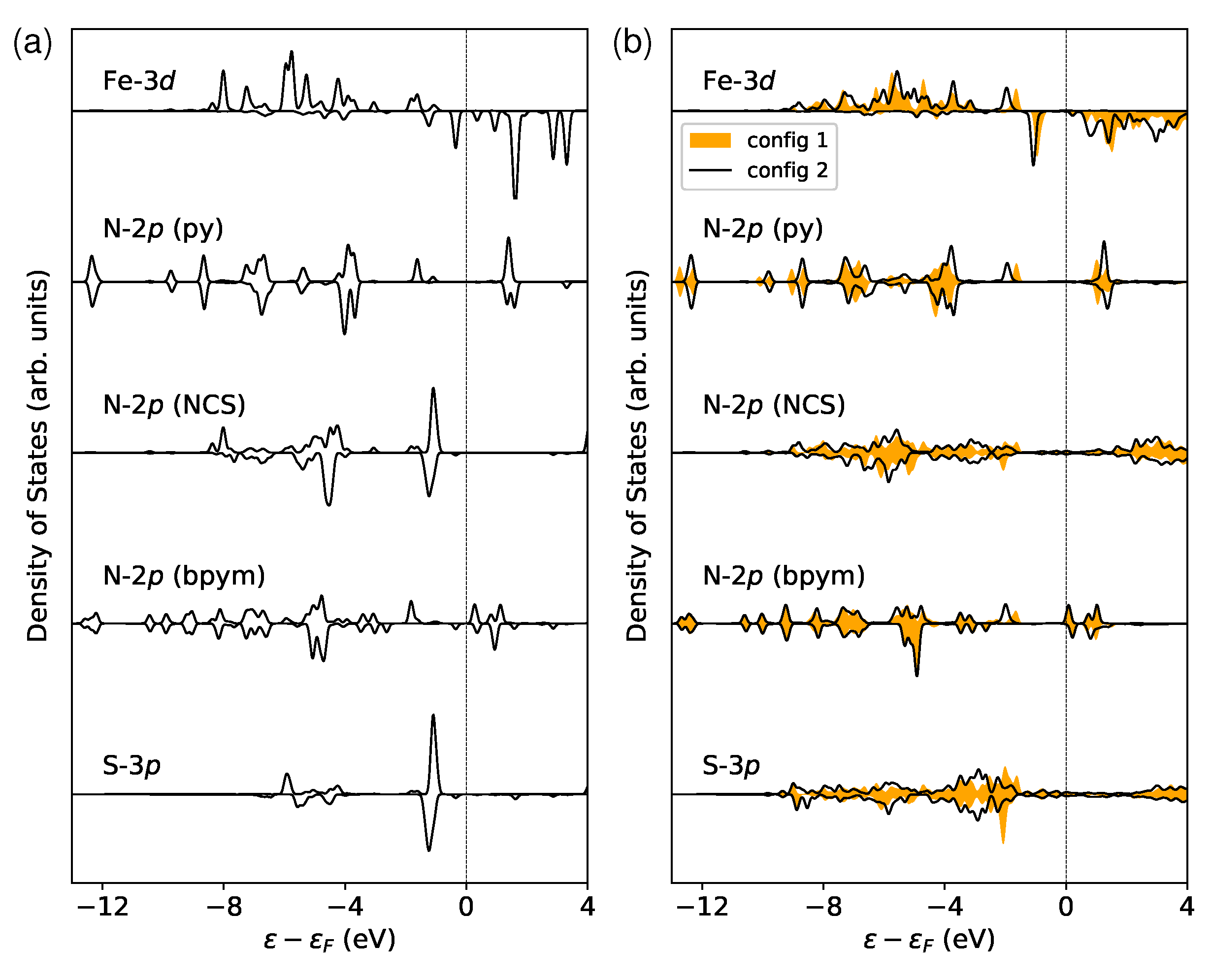
3.2. On-Site Coulomb Repulsion and Ligand Field
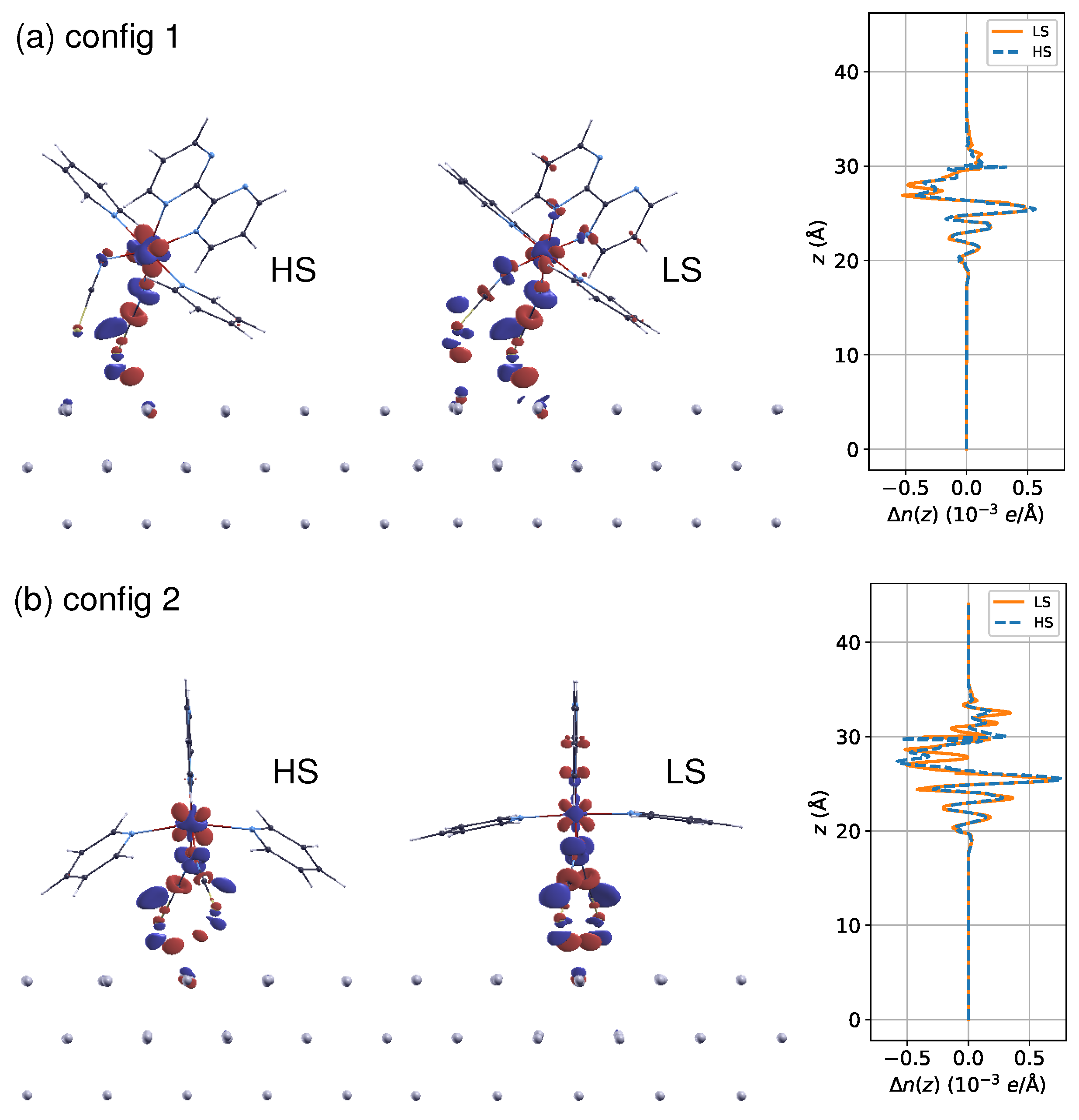
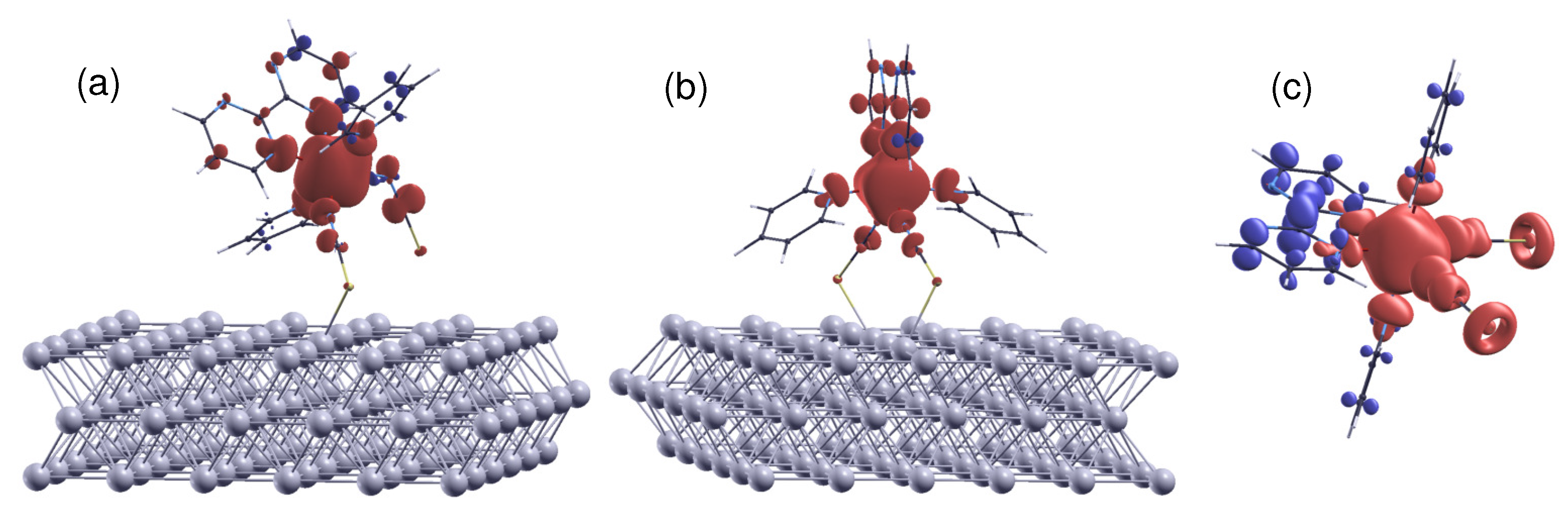
3.3. Spin Distribution and Charge Transfer
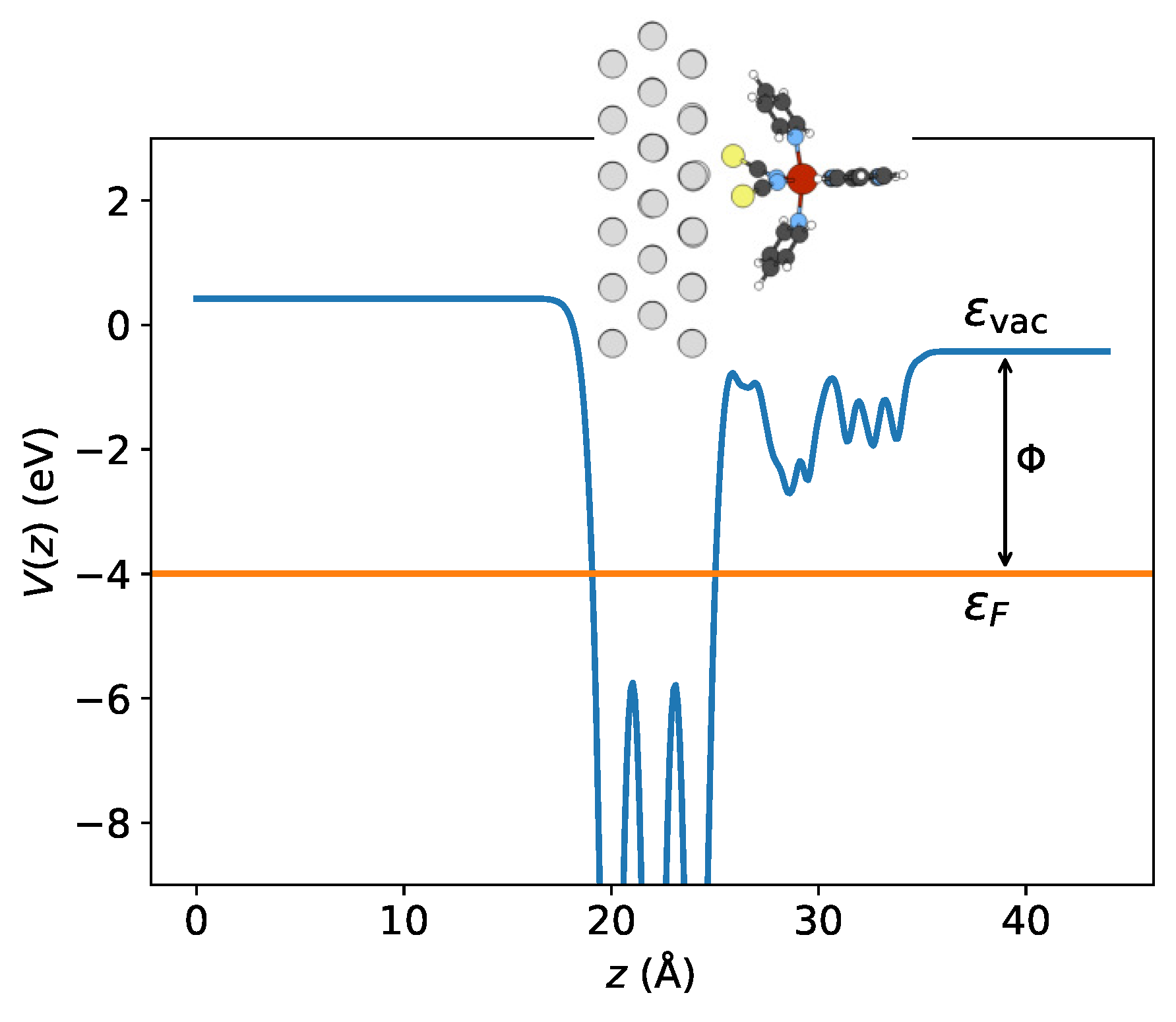
3.4. Work Function and Surface Dipole
3.5. Vibrational Contributions
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Molnár, G.; Rat, S.; Salmon, L.; Nicolazzi, W.; Bousseksou, A. Spin Crossover Nanomaterials: From Fundamental Concepts to Devices. Adv. Mater. 2018, 30, 1703862. [Google Scholar] [CrossRef] [PubMed]
- Kipgen, L.; Bernien, M.; Tuczek, F.; Kuch, W. Spin-Crossover Molecules on Surfaces: From Isolated Molecules to Ultrathin Films. Adv. Mater. 2021, 33, 2008141. [Google Scholar] [CrossRef] [PubMed]
- Kumar, K.S.; Ruben, M. Emerging trends in spin crossover (SCO) based functional materials and devices. Coord. Chem. Rev. 2017, 346, 176–205. [Google Scholar] [CrossRef]
- Ridier, K.; Bas, A.C.; Shalabaeva, V.; Nicolazzi, W.; Salmon, L.; Molnár, G.; Bousseksou, A.; Lorenc, M.; Bertoni, R.; Collet, E.; et al. Finite Size Effects on the Switching Dynamics of Spin-Crossover Thin Films Photoexcited by a Femtosecond Laser Pulse. Adv. Mater. 2019, 31, 1901361. [Google Scholar] [CrossRef] [PubMed]
- Konstantinov, N.; Tauzin, A.; Noumbé, U.N.; Dragoe, D.; Kundys, B.; Majjad, H.; Brosseau, A.; Lenertz, M.; Singh, A.; Berciaud, S.; et al. Electrical read-out of light-induced spin transition in thin film spin crossover/graphene heterostructures. J. Mater. Chem. C 2021, 9, 2712–2720. [Google Scholar] [CrossRef]
- van Geest, E.P.; Shakouri, K.; Fu, W.; Robert, V.; Tudor, V.; Bonnet, S.; Schneider, G.F. Contactless Spin Switch Sensing by Chemo-Electric Gating of Graphene. Adv. Mater. 2020, 32, 1903575. [Google Scholar] [CrossRef]
- Mahfoud, T.; Molnár, G.; Cobo, S.; Salmon, L.; Thibault, C.; Vieu, C.; Demont, P.; Bousseksou, A. Electrical Properties and Non-Volatile Memory Effect of the [Fe(HB(pz)3)2] Spin Crossover Complex Integrated in a Microelectrode Device. Appl. Phys. Lett. 2011, 99, 053307. [Google Scholar] [CrossRef]
- Ekanayaka, T.K.; Hao, G.; Mosey, A.; Dale, A.S.; Jiang, X.; Yost, A.J.; Sapkota, K.R.; Wang, G.T.; Zhang, J.; N’Diaye, A.T.; et al. Nonvolatile Voltage Controlled Molecular Spin-State Switching for Memory Applications. Magnetochemistry 2021, 7, 37. [Google Scholar] [CrossRef]
- Ossinger, S.; Kipgen, L.; Naggert, H.; Bernien, M.; Britton, A.J.; Nickel, F.; Arruda, L.M.; Kumberg, I.; Engesser, T.A.; Golias, E.; et al. Effect of ligand methylation on the spin-switching properties of surface-supported spin-crossover molecules. J. Phys. Condens. Matter 2020, 32, 114003. [Google Scholar] [CrossRef]
- Villalva, J.; Develioglu, A.; Montenegro-Pohlhammer, N.; Sánchez-de Armas, R.; Gamonal, A.; Rial, E.; García-Hernández, M.; Ruiz-Gonzalez, L.; Costa, J.S.; Calzado, C.J.; et al. Spin-state-dependent electrical conductivity in single-walled carbon nanotubes encapsulating spin-crossover molecules. Nat. Commun. 2021, 12, 1578. [Google Scholar] [CrossRef]
- Torres-Cavanillas, R.; Morant-Giner, M.; Escorcia-Ariza, G.; Dugay, J.; Canet-Ferrer, J.; Tatay, S.; Cardona-Serra, S.; Giménez-Marqués, M.; Galbiati, M.; Forment-Aliaga, A.; et al. Spin-crossover nanoparticles anchored on MoS2 layers for heterostructures with tunable strain driven by thermal or light-induced spin switching. Nat. Chem. 2021, 13, 1101. [Google Scholar] [CrossRef]
- Gentili, D.; Liscio, F.; Demitri, N.; Schäfer, B.; Borgatti, F.; Torelli, P.; Gobaut, B.; Panaccione, G.; Rossi, G.; Degli Esposti, A.; et al. Surface Induces Different Crystal Structures in a Room Temperature Switchable Spin Crossover Compound. Dalton Trans. 2016, 45, 134–143. [Google Scholar] [CrossRef]
- Rubio-Giménez, V.; Bartual-Murgui, C.; Galbiati, M.; Núñez-López, A.; Castells-Gil, J.; Quinard, B.; Seneor, P.; Otero, E.; Ohresser, P.; Cantarero, A.; et al. Effect of nanostructuration on the spin crossover transition in crystalline ultrathin films. Chem. Sci. 2019, 10, 4038–4047. [Google Scholar] [CrossRef]
- Sakaida, S.; Otsubo, K.; Otake, K.i.; Kawaguchi, S.; Maesato, M.; Kitagawa, S.; Kitagawa, H. Surface morphology-induced spin-crossover-inactive high-spin state in a coordination framework. Chem. Commun. 2021, 57, 1462–1465. [Google Scholar] [CrossRef] [PubMed]
- Yazdani, S.; Phillips, J.; Ekanayaka, T.K.; Cheng, R.; Dowben, P.A. The Influence of the Substrate on the Functionality of Spin Crossover Molecular Materials. Molecules 2023, 28, 3735. [Google Scholar] [CrossRef] [PubMed]
- Beniwal, S.; Zhang, X.; Mu, S.; Naim, A.; Rosa, P.; Chastanet, G.; Létard, J.F.; Liu, J.; Sterbinsky, G.E.; Arena, D.A.; et al. Surface-induced spin state locking of the [Fe(H2B(pz)2)2(bipy)] spin crossover complex. J. Phys. Condens. Matter 2016, 28, 206002. [Google Scholar] [CrossRef]
- Zhang, X.; Costa, P.S.; Hooper, J.; Miller, D.P.; N’Diaye, A.T.; Beniwal, S.; Jiang, X.; Yin, Y.; Rosa, P.; Routaboul, L.; et al. Locking and Unlocking the Molecular Spin Crossover Transition. Adv. Mater. 2017, 29, 1702257. [Google Scholar] [CrossRef]
- Gueddida, S.; Alouani, M. Spin Crossover in a Single Fe(phen)2(NCS)2 Molecule Adsorbed onto Metallic Substrates: An ab initio Calculation. Phys. Rev. B 2013, 87, 144413. [Google Scholar] [CrossRef]
- Zhang, Y. Surface effects on temperature-driven spin crossover in Fe(phen)2(NCS)2. J. Chem. Phys. 2020, 153, 134704. [Google Scholar] [CrossRef] [PubMed]
- Serra, A.M.; Dhingra, A.; Asensio, M.C.; Real, J.A.; Royo, J.F.S. Surface stabilisation of the high-spin state of Fe(ii) spin-crossover complexes. Phys. Chem. Chem. Phys. 2023, 25, 14736–14741. [Google Scholar] [CrossRef]
- Montenegro-Pohlhammer, N.; Palomino, C.M.; Calzado, C.J. Exploring the potential as molecular quantum-dot cellular automata of a mixed-valence Ru2 complex deposited on a Au(111) surface. Inorg. Chem. Front. 2023, 10, 2484–2492. [Google Scholar] [CrossRef]
- Ye, S.; Neese, F. Accurate Modeling of Spin-State Energetics in Spin-Crossover Systems with Modern Density Functional Theory. Inorg. Chem. 2010, 49, 772–774. [Google Scholar] [CrossRef]
- Janet, J.P.; Chan, L.; Kulik, H.J. Accelerating Chemical Discovery with Machine Learning: Simulated Evolution of Spin Crossover Complexes with an Artificial Neural Network. J. Phys. Chem. Lett. 2018, 9, 1064–1071. [Google Scholar] [CrossRef] [PubMed]
- Cirera, J.; Ruiz, E. Assessment of the SCAN Functional for Spin-State Energies in Spin-Crossover Systems. J. Phys. Chem. A 2020, 124, 5053–5058. [Google Scholar] [CrossRef] [PubMed]
- Paulsen, H.; Trautwein, A.X. Density Functional Theory Calculations for Spin Crossover Complexes. Top. Curr. Chem. 2004, 235, 197–219. [Google Scholar] [CrossRef]
- Gueddida, S.; Alouani, M. Calculated Impact of Ferromagnetic Substrate on the Spin Crossover in a Fe(1,10-phenanthroline)2(NCS)2 Molecule. Phys. Rev. B 2016, 93, 184433. [Google Scholar] [CrossRef]
- Zhang, Y. Fe(phen)2(NCS)2 on Al(100): Influence of AlN layer on spin crossover barrier. Phys. Chem. Chem. Phys. 2021, 23, 23758–23767. [Google Scholar] [CrossRef]
- Mejía-Rodríguez, D.; Albavera-Mata, A.; Fonseca, E.; Chen, D.T.; Cheng, H.P.; Hennig, R.G.; Trickey, S. Barriers to predictive high-throughput screening for spin-crossover. Comput. Mater. Sci. 2022, 206, 111161. [Google Scholar] [CrossRef]
- Lebègue, S.; Pillet, S.; Ángyán, J.G. Modeling Spin-Crossover Compounds by Periodic DFT + U Approach. Phys. Rev. B 2008, 78, 024433. [Google Scholar] [CrossRef]
- Hsu, H.; Umemoto, K.; Wu, Z.; Wentzcovitch, R.M. Spin-State Crossover of Iron in Lower-Mantle Minerals: Results of DFT + U Investigations. Rev. Mineral. Geochem. 2010, 71, 169–199. [Google Scholar] [CrossRef]
- Zhang, Y. Predicting Critical Temperatures of Iron(II) Spin Crossover Materials: Density Functional Theory plus U Approach. J. Chem. Phys. 2014, 141, 214703. [Google Scholar] [CrossRef] [PubMed]
- Lazaar, K.; Aouaini, F.; Gueddida, S. Binuclear spin-crossover [Fe(bt)(NCS)2]2(bpm) complex: A study using first principles calculations. J. Chem. Phys. 2023, 158. [Google Scholar] [CrossRef]
- Bučko, T.; Hafner, J.; Lebègue, S.; Ángyán, J.G. Spin Crossover Transition of Fe(phen)2(NCS)2: Periodic Dispersion-Corrected Density-Functional Study. Phys. Chem. Chem. Phys. 2012, 14, 5389–5396. [Google Scholar] [CrossRef] [PubMed]
- Kreutzburg, L.; Hübner, C.G.; Paulsen, H. Cooperativity of Spin Crossover Complexes: Combining Periodic Density Functional Calculations and Monte Carlo Simulation. Materials 2017, 10, 172. [Google Scholar] [CrossRef] [PubMed]
- Vela, S.; Novoa, J.J.; Ribas-Arino, J. Insights into the crystal-packing effects on the spin crossover of [FeII(1-bpp)]2+-based materials. Phys. Chem. Chem. Phys. 2014, 16, 27012–27024. [Google Scholar] [CrossRef] [PubMed]
- Vela, S.; Fumanal, M.; Ribas-Arino, J.; Robert, V. Towards an accurate and computationally-efficient modelling of Fe(ii)-based spin crossover materials. Phys. Chem. Chem. Phys. 2015, 17, 16306–16314. [Google Scholar] [CrossRef]
- Jiang, H. First-Principles Approaches for Strongly Correlated Materials: A Theoretical Chemistry Perspective. Int. J. Quantum Chem. 2015, 115, 722–730. [Google Scholar] [CrossRef]
- Zhang, Y. Calculating spin crossover temperatures by a first-principles LDA + U scheme with parameter U evaluated from GW. J. Chem. Phys. 2019, 151, 134701. [Google Scholar] [CrossRef]
- D’Avino, G.; Painelli, A.; Boukheddaden, K. Vibronic model for spin crossover complexes. Phys. Rev. B 2011, 84, 104119. [Google Scholar] [CrossRef]
- Fahs, A.; Nicolazzi, W.; Molnár, G.; Bousseksou, A. Role of Surface Effects in the Vibrational Density of States and the Vibrational Entropy in Spin Crossover Nanomaterials: A Molecular Dynamics Investigation. Magnetochemistry 2021, 7, 27. [Google Scholar] [CrossRef]
- Ronayne, K.L.; Paulsen, H.; Höfer, A.; Dennis, A.C.; Wolny, J.A.; Chumakov, A.I.; Schünemann, V.; Winkler, H.; Spiering, H.; Bousseksou, A.; et al. Vibrational spectrum of the spin crossover complex [Fe(phen)2(NCS)2] studied by IR and Raman spectroscopy, nuclear inelastic scattering and DFT calculations. Phys. Chem. Chem. Phys. 2006, 8, 4685–4693. [Google Scholar] [CrossRef]
- Wu, J.; Sousa, C.; de Graaf, C. The Role of Vibrational Anharmonicity in the Computational Study of Thermal Spin Crossover. Magnetochemistry 2019, 5, 49. [Google Scholar] [CrossRef]
- Claude, R.; Real, J.A.; Zarembowitch, J.; Kahn, O.; Ouahab, L.; Grandjean, D.; Boukheddaden, K.; Varret, F.; Dworkin, A. Spin transition in iron Fe(py)2L(NCS)2 complexes where py = pyridine and L = 2,2′-bipyrimidine (bpym) and 1,10-phenanthroline (phen): Magnetic, calorimetric, and Moessbauer-effect investigation. Crystal structure of [Fe(py)2bpym(NCS)2].0.25py. Inorg. Chem. 1990, 29, 4442–4448. [Google Scholar] [CrossRef]
- Enkovaara, J.; Rostgaard, C.; Mortensen, J.J.; Chen, J.; Dułak, M.; Ferrighi, L.; Gavnholt, J.; Glinsvad, C.; Haikola, V.; Hansen, H.A.; et al. Electronic Structure Calculations with GPAW: A Real-Space Implementation of the Projector Augmented-Wave Method. J. Phys. Condens. Matter 2010, 22, 253202. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector Augmented-Wave Method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef]
- Larsen, A.H.; Mortensen, J.J.; Blomqvist, J.; Castelli, I.E.; Christensen, R.; Dułak, M.; Friis, J.; Groves, M.N.; Hammer, B.; Hargus, C.; et al. The atomic simulation environment—A Python library for working with atoms. J. Phys. Condens. Matter 2017, 29, 273002. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization, 2nd ed.; Springer: New York, NY, USA, 2006. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and Simple Analytic Representation of the Electron-Gas Correlation Energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef]
- Anisimov, V.I.; Zaanen, J.; Andersen, O.K. Band Theory and Mott Insulators: Hubbard U Instead of Stoner I. Phys. Rev. B 1991, 44, 943–954. [Google Scholar] [CrossRef]
- Himmetoglu, B.; Floris, A.; de Gironcoli, S.; Cococcioni, M. Hubbard-Corrected DFT Energy Functionals: The LDA + U Description of Correlated Systems. Int. J. Quantum Chem. 2014, 114, 14–49. [Google Scholar] [CrossRef]
- Cococcioni, M.; de Gironcoli, S. Linear Response Approach to the Calculation of the Effective Interaction Parameters in the LDA + U Method. Phys. Rev. B 2005, 71, 035105. [Google Scholar] [CrossRef]
- Dudarev, S.L.; Botton, G.A.; Savrasov, S.Y.; Humphreys, C.J.; Sutton, A.P. Electron-Energy-Loss Spectra and the Structural Stability of Nickel Oxide: An LSDA + U Study. Phys. Rev. B 1998, 57, 1505–1509. [Google Scholar] [CrossRef]
- Bengtsson, L. Dipole Correction for Surface Supercell Calculations. Phys. Rev. B 1999, 59, 12301–12304. [Google Scholar] [CrossRef]
- Frederiksen, T.; Paulsson, M.; Brandbyge, M.; Jauho, A.P. Inelastic transport theory from first principles: Methodology and application to nanoscale devices. Phys. Rev. B 2007, 75, 205413. [Google Scholar] [CrossRef]
- Palomino, C.M.; Sánchez-de Armas, R.; Calzado, C.J. Theoretical inspection of the spin-crossover [Fe(tzpy)2(NCS)2] complex on Au(100) surface. J. Chem. Phys. 2021, 154, 034701. [Google Scholar] [CrossRef]
- Tersoff, J.; Hamann, D.R. Theory of the scanning tunneling microscope. Phys. Rev. B 1985, 31, 805–813. [Google Scholar] [CrossRef] [PubMed]
- Miyamachi, T.; Gruber, M.; Davesne, V.; Bowen, M.; Boukari, S.; Joly, L.; Scheurer, F.; Rogez, G.; Yamada, T.K.; Ohresser, P.; et al. Robust Spin Crossover and Memristance across a Single Molecule. Nat. Commun. 2012, 3, 938. [Google Scholar] [CrossRef]
- Beniwal, S.; Sarkar, S.; Baier, F.; Weber, B.; Dowben, P.; Enders, A. Site selective adsorption of the spin crossover complex Fe(phen)2(NCS)2 on Au(111). J. Phys. Condens. Matter 2020, 32, 324003. [Google Scholar] [CrossRef]
- Gruber, M.; Berndt, R. Spin-Crossover Complexes in Direct Contact with Surfaces. Magnetochemistry 2020, 6, 35. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate ab initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Zhang, Y. Driving spin transition at interface: Role of adsorption configurations. J. Chem. Phys. 2018, 148, 044706. [Google Scholar] [CrossRef]
- Vela, S.; Fumanal, M.; Cirera, J.; Ribas-Arino, J. Thermal spin crossover in Fe(ii) and Fe(iii). Accurate spin state energetics at the solid state. Phys. Chem. Chem. Phys. 2020, 22, 4938–4945. [Google Scholar] [CrossRef] [PubMed]
- Gruber, M.; Miyamachi, T.; Davesne, V.; Bowen, M.; Boukari, S.; Wulfhekel, W.; Alouani, M.; Beaurepaire, E. Spin Crossover in Fe(phen)2(NCS)2 Complexes on Metallic Surfaces. J. Chem. Phys. 2017, 146, 092312. [Google Scholar] [CrossRef]
- Kumar, K.S.; Studniarek, M.; Heinrich, B.; Arabski, J.; Schmerber, G.; Bowen, M.; Boukari, S.; Beaurepaire, E.; Dreiser, J.; Ruben, M. Engineering On-Surface Spin Crossover: Spin-State Switching in a Self-Assembled Film of Vacuum-Sublimable Functional Molecule. Adv. Mater. 2018, 30, 1705416. [Google Scholar] [CrossRef] [PubMed]
- Rohlf, S.; Grunwald, J.; Jasper-Toennies, T.; Johannsen, S.; Diekmann, F.; Studniarek, M.; Berndt, R.; Tuczek, F.; Rossnagel, K.; Gruber, M. Influence of Substrate Electronic Properties on the Integrity and Functionality of an Adsorbed Fe(II) Spin-Crossover Compound. J. Phys. Chem. C 2019, 123, 17774–17780. [Google Scholar] [CrossRef]
- Jiang, X.; Hao, G.; Wang, X.; Mosey, A.; Zhang, X.; Yu, L.; Yost, A.J.; Zhang, X.; DiChiara, A.D.; N’Diaye, A.T.; et al. Tunable spin-state bistability in a spin crossover molecular complex. J. Phys. Condens. Matter 2019, 31, 315401. [Google Scholar] [CrossRef]
- Gruber, M.; Davesne, V.; Bowen, M.; Boukari, S.; Beaurepaire, E.; Wulfhekel, W.; Miyamachi, T. Spin State of Spin-Crossover Complexes: From Single Molecules to Ultrathin Films. Phys. Rev. B 2014, 89, 195415. [Google Scholar] [CrossRef]
- Sánchez-de Armas, R.; Calzado, C.J. Spin-crossover Fe(ii) complexes on a surface: A mixture of low-spin and high-spin molecules at low temperature from quantum-chemistry calculations. Inorg. Chem. Front. 2022, 9, 753–760. [Google Scholar] [CrossRef]
- Kulik, H.J. Perspective: Treating Electron Over-Delocalization with the DFT+U Method. J. Chem. Phys. 2015, 142, 240901. [Google Scholar] [CrossRef]
- Zhang, X.; N’Diaye, A.T.; Jiang, X.; Zhang, X.; Yin, Y.; Chen, X.; Hong, X.; Xu, X.; Dowben, P.A. Indications of magnetic coupling effects in spin cross-over molecular thin films. Chem. Commun. 2018, 54, 944–947. [Google Scholar] [CrossRef]
- Mugarza, A.; Robles, R.; Krull, C.; Korytár, R.; Lorente, N.; Gambardella, P. Electronic and Magnetic Properties of Molecule-Metal Interfaces: Transition-Metal Phthalocyanines Adsorbed on Ag(100). Phys. Rev. B 2012, 85, 155437. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Clarendon (Oxford University Press): New York, NY, USA, 1990. [Google Scholar]
- Tang, W.; Sanville, E.; Henkelman, G. A grid-based Bader analysis algorithm without lattice bias. J. Phys. Condens. Matter 2009, 21, 084204. [Google Scholar] [CrossRef] [PubMed]
- Postnikov, A.V.; Kortus, J.; Pederson, M.R. Density Functional Studies of Molecular Magnets. Phys. Stat. Sol. B 2006, 243, 2533–2572. [Google Scholar] [CrossRef]
- Wolny, J.A.; Paulsen, H.; Trautwein, A.X.; Schünemann, V. Density Functional Theory Calculations and Vibrational Spectroscopy on Iron Spin-Crossover Compounds. Coord. Chem. Rev. 2009, 253, 2423–2431. [Google Scholar] [CrossRef]
- Rudavskyi, A.; Sousa, C.; de Graaf, C.; Havenith, R.W.A.; Broer, R. Computational Approach to the Study of Thermal Spin Crossover Phenomena. J. Chem. Phys. 2014, 140, 184318. [Google Scholar] [CrossRef]
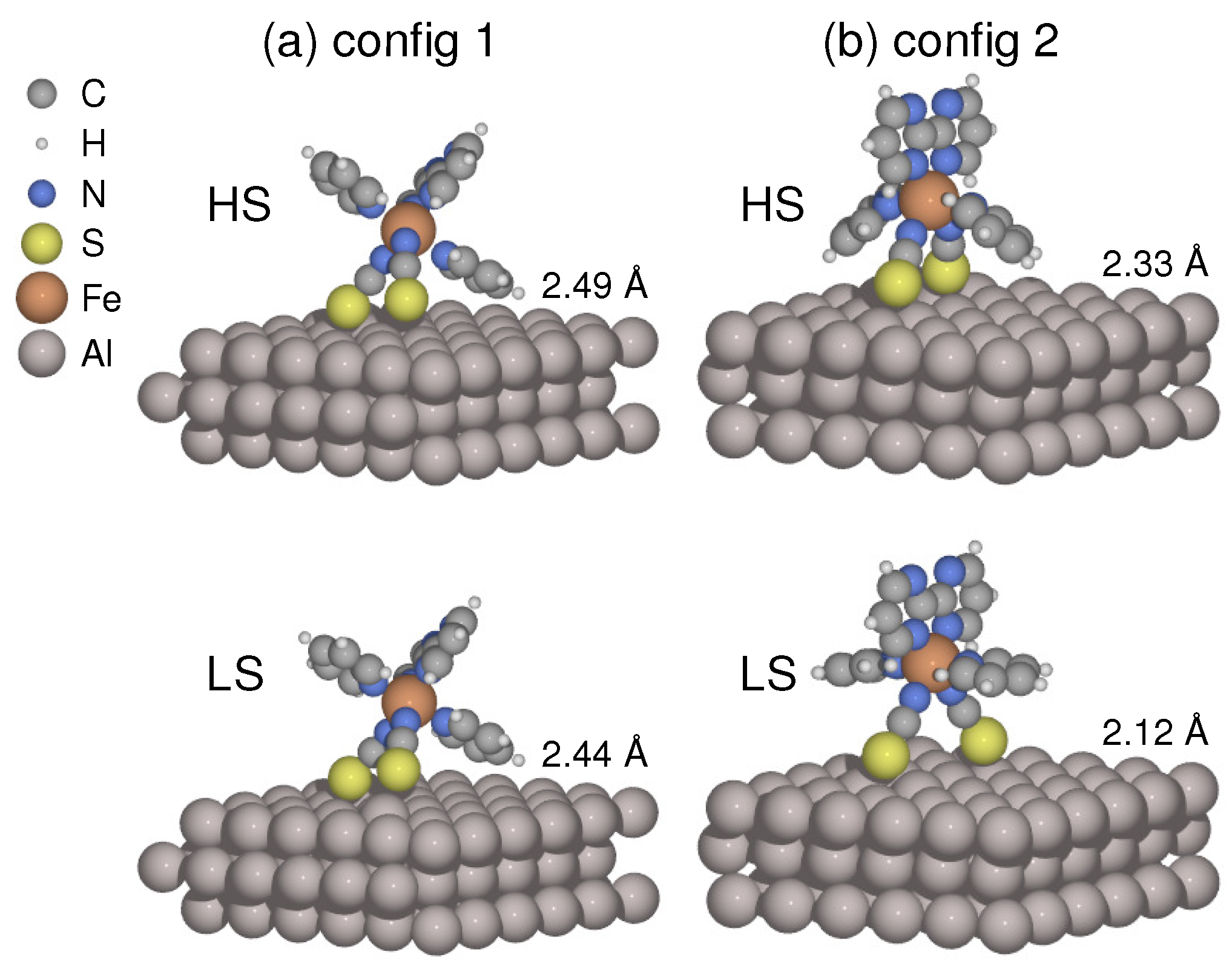
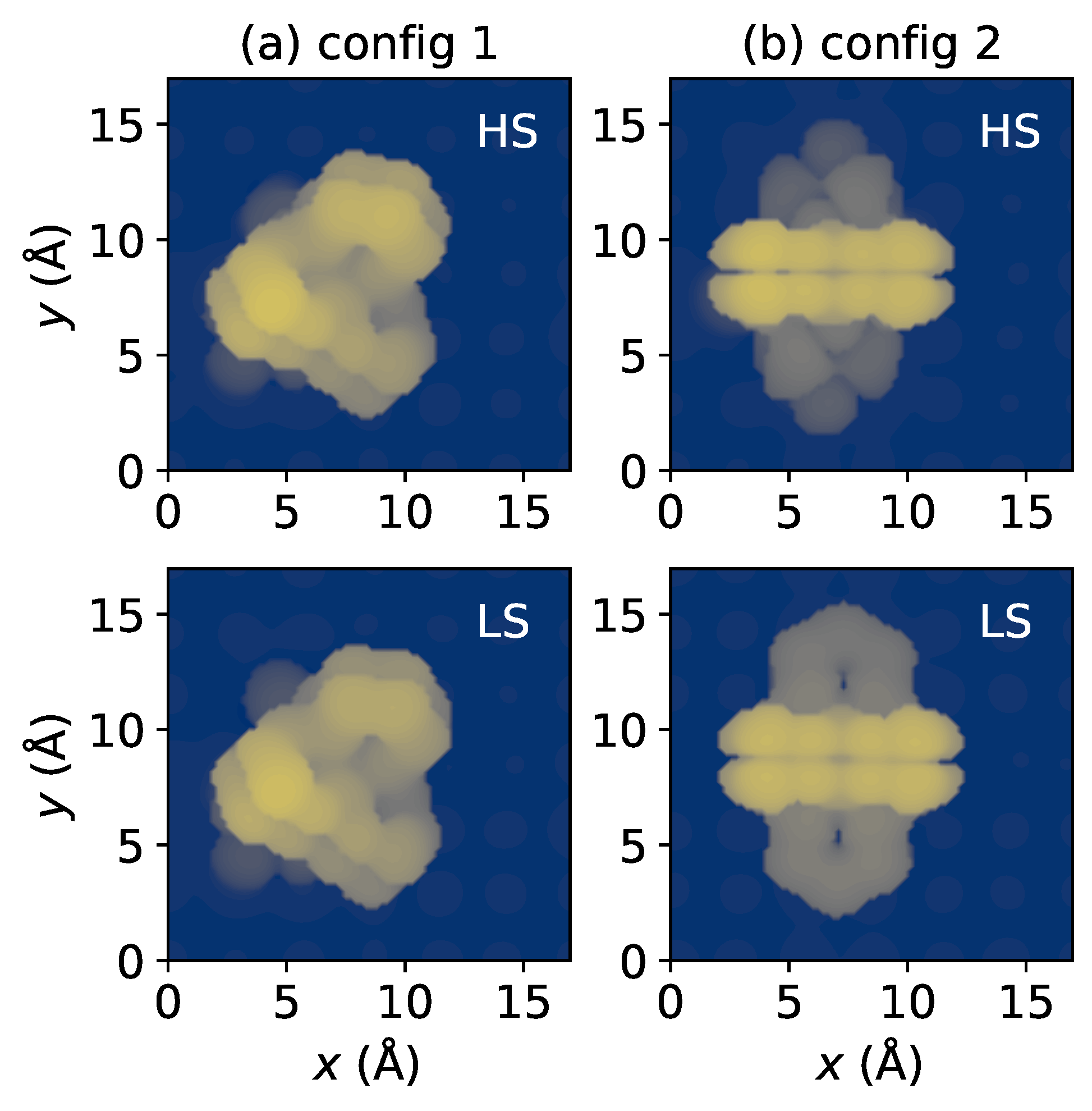
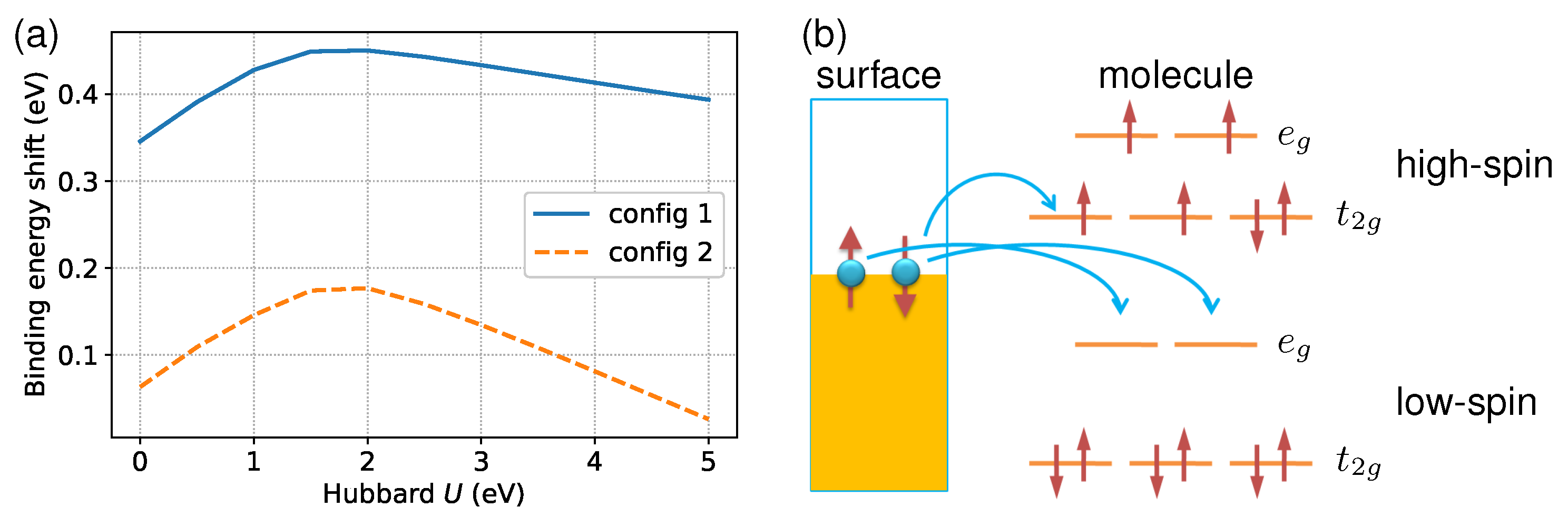
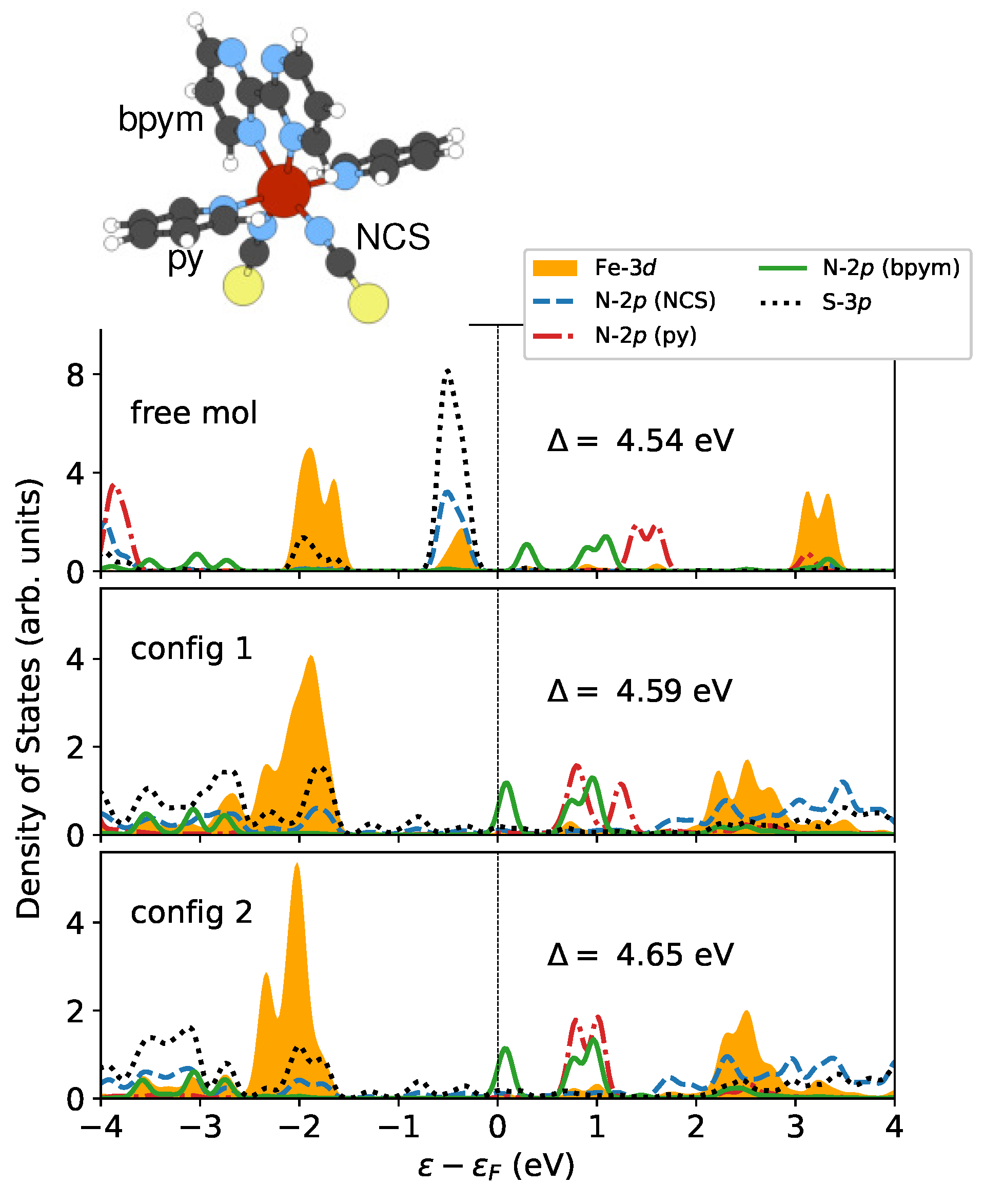
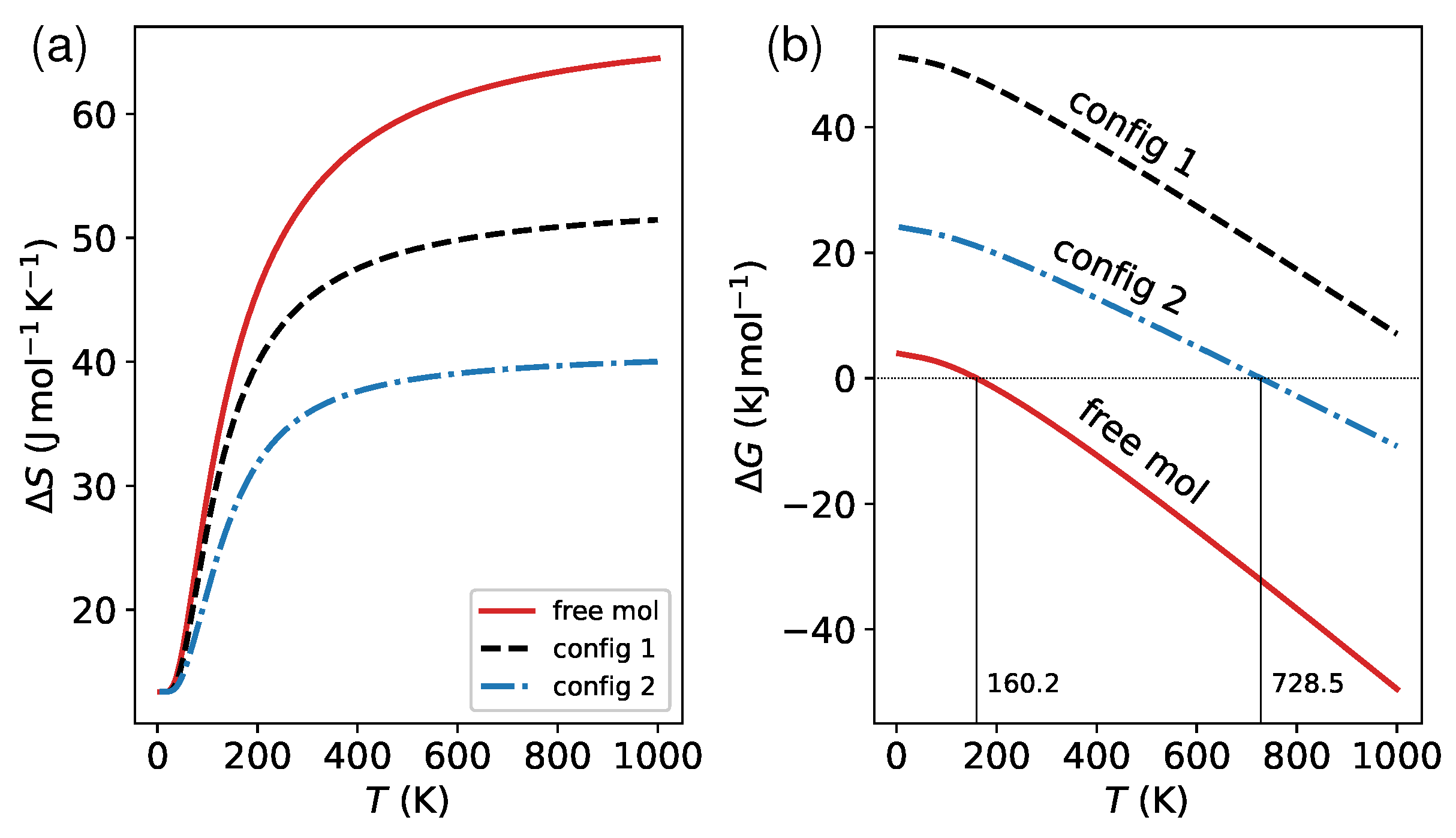
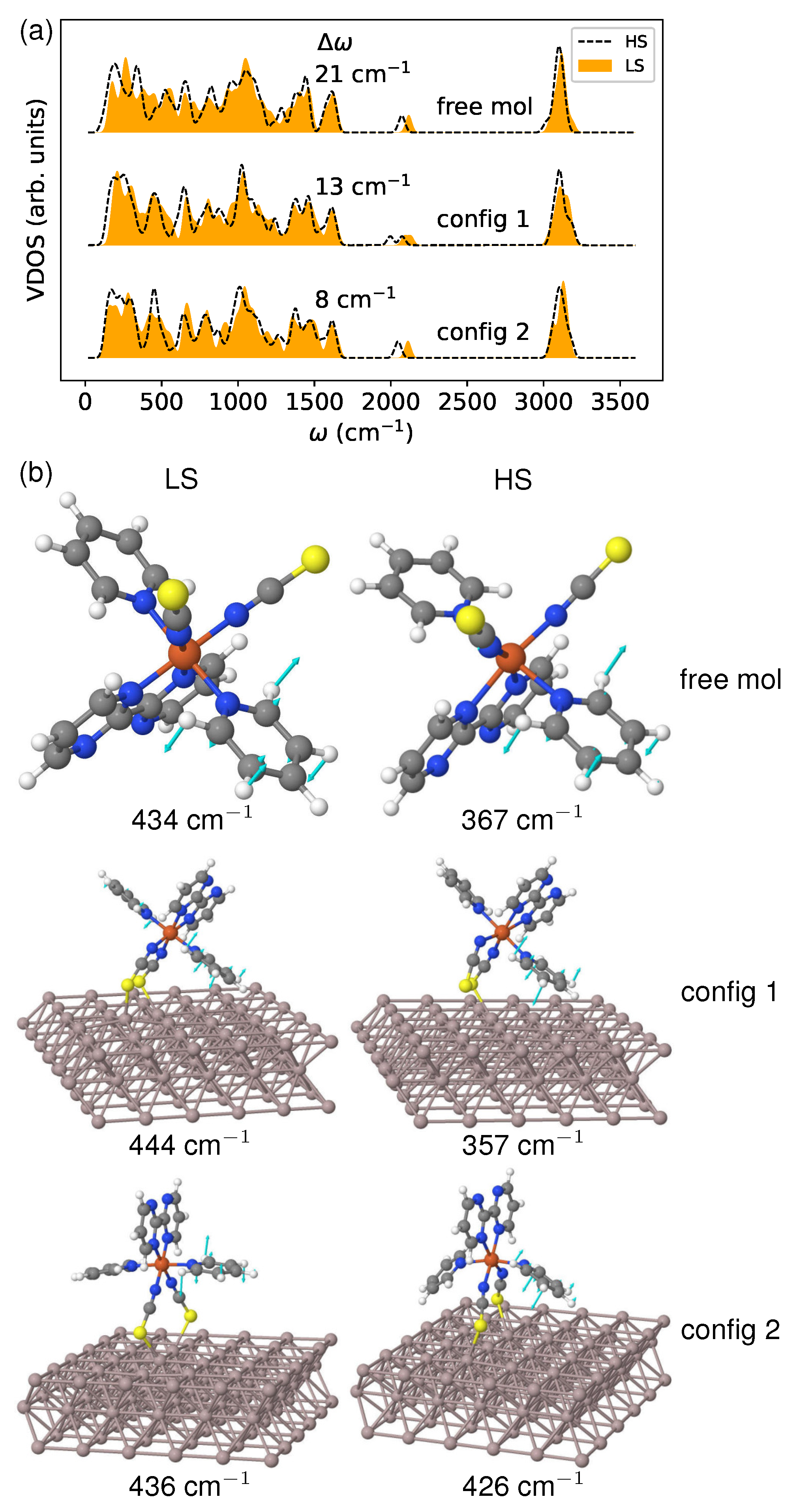
| Config 1 | Config 2 | |||
|---|---|---|---|---|
| w/ DC | w/o DC | w/ DC | w/o DC | |
| LDA + U | ||||
| (eV) 1 | ||||
| (eV) | ||||
| () | ||||
| PBE + D3 | ||||
| (eV) | ||||
| (eV) | ||||
| () | ||||
| Config 1 | Config 2 | Free mol | |
|---|---|---|---|
| 1 | |||
| m () | () 2 | () | () |
| () | () | () | () |
| Config 1 | Config 2 | |||
|---|---|---|---|---|
| HS | LS | HS | LS | |
| (eV) | ||||
| (eV) | ||||
| (eV) | ||||
| (e Å) | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y. Surface-Induced Electronic and Vibrational Level Shifting of [Fe(py)2bpym(NCS)2] on Al(100). Materials 2023, 16, 6150. https://doi.org/10.3390/ma16186150
Zhang Y. Surface-Induced Electronic and Vibrational Level Shifting of [Fe(py)2bpym(NCS)2] on Al(100). Materials. 2023; 16(18):6150. https://doi.org/10.3390/ma16186150
Chicago/Turabian StyleZhang, Yachao. 2023. "Surface-Induced Electronic and Vibrational Level Shifting of [Fe(py)2bpym(NCS)2] on Al(100)" Materials 16, no. 18: 6150. https://doi.org/10.3390/ma16186150






