Modeling and Analysis of a Conical Bridge-Type Displacement Amplification Mechanism Using the Non-Uniform Rational B-Spline Curve
Abstract
:1. Introduction
2. Analytical Modeling
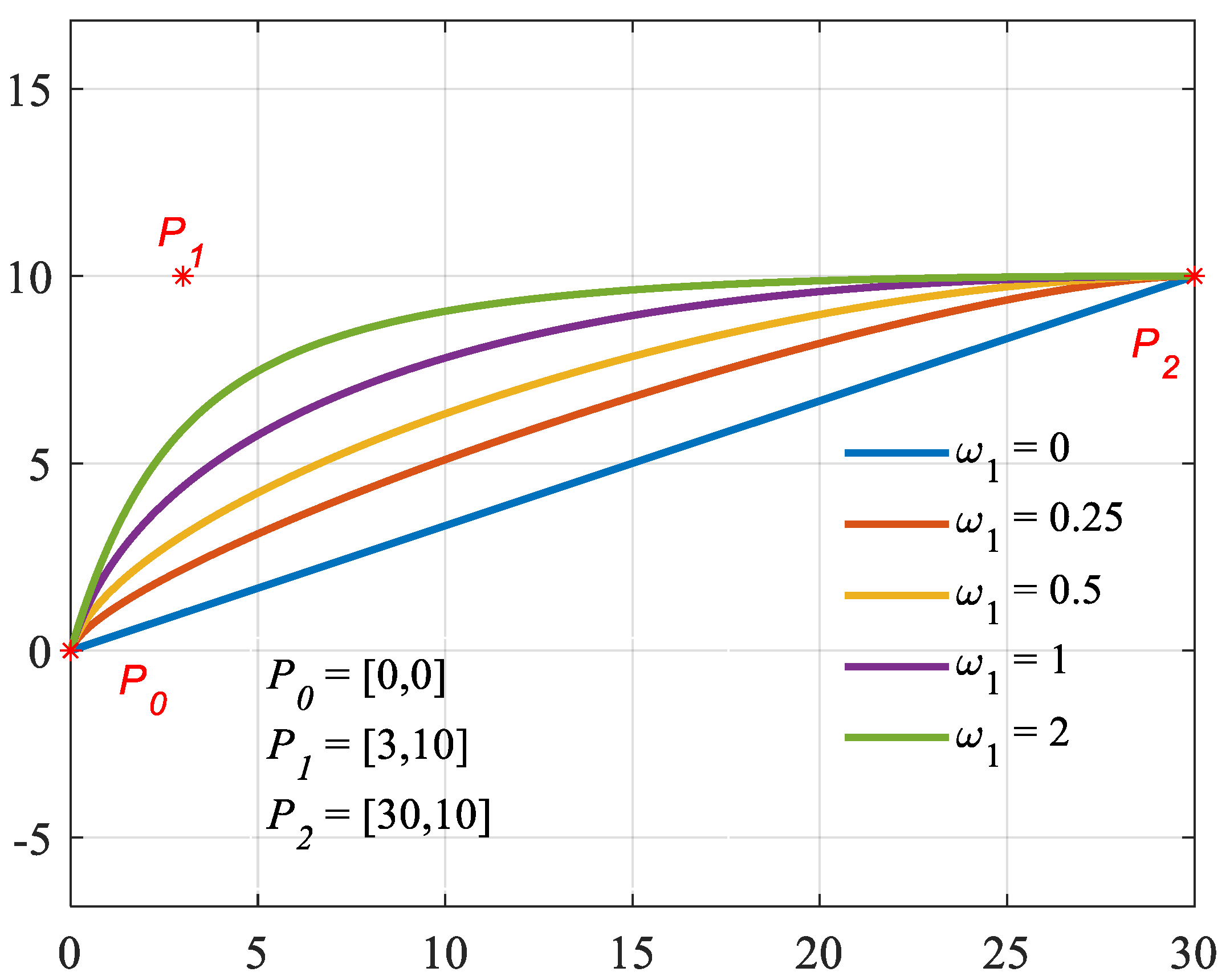
2.1. Expression of Conical Curves Using NURBS
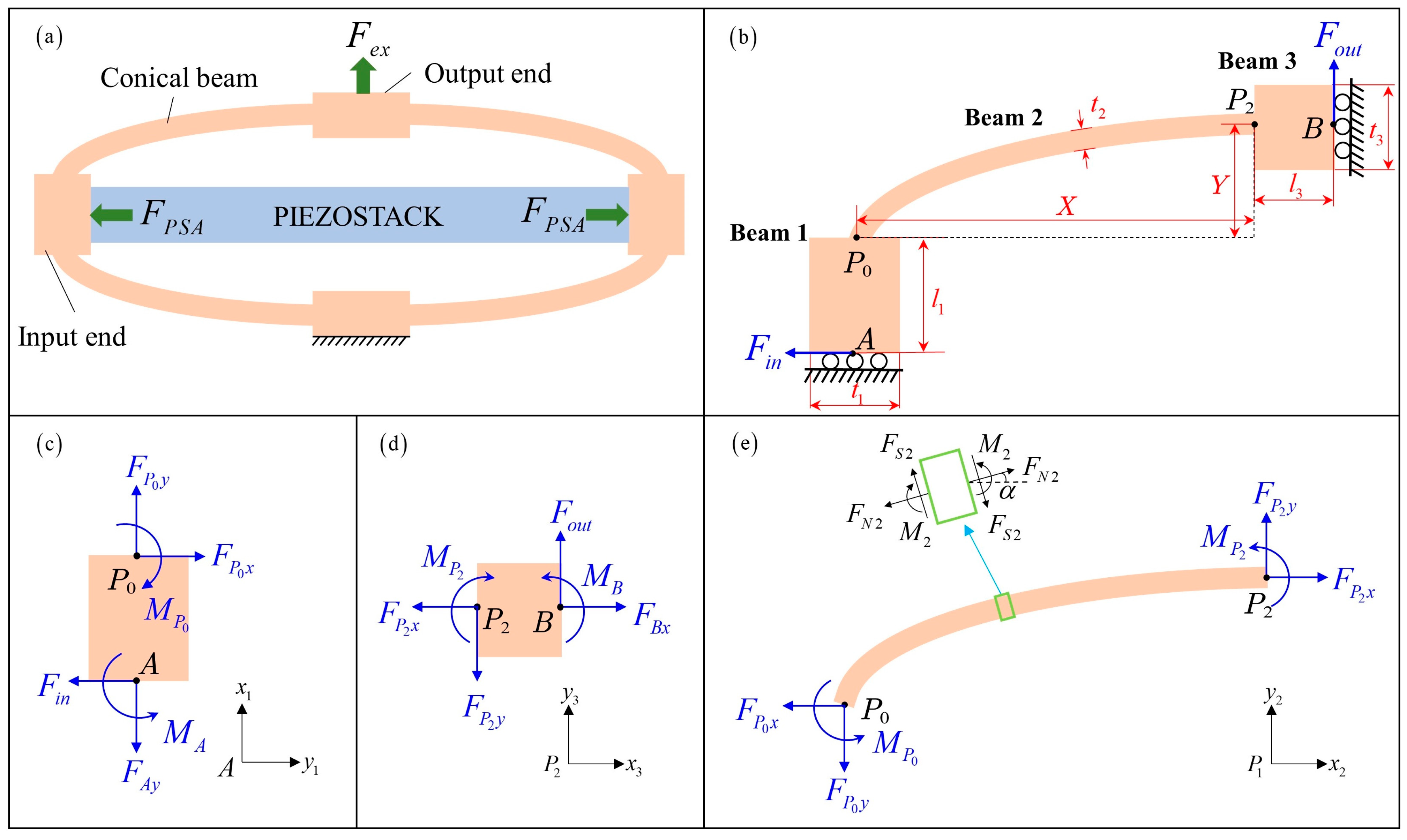
2.2. Static Analysis of the DAM
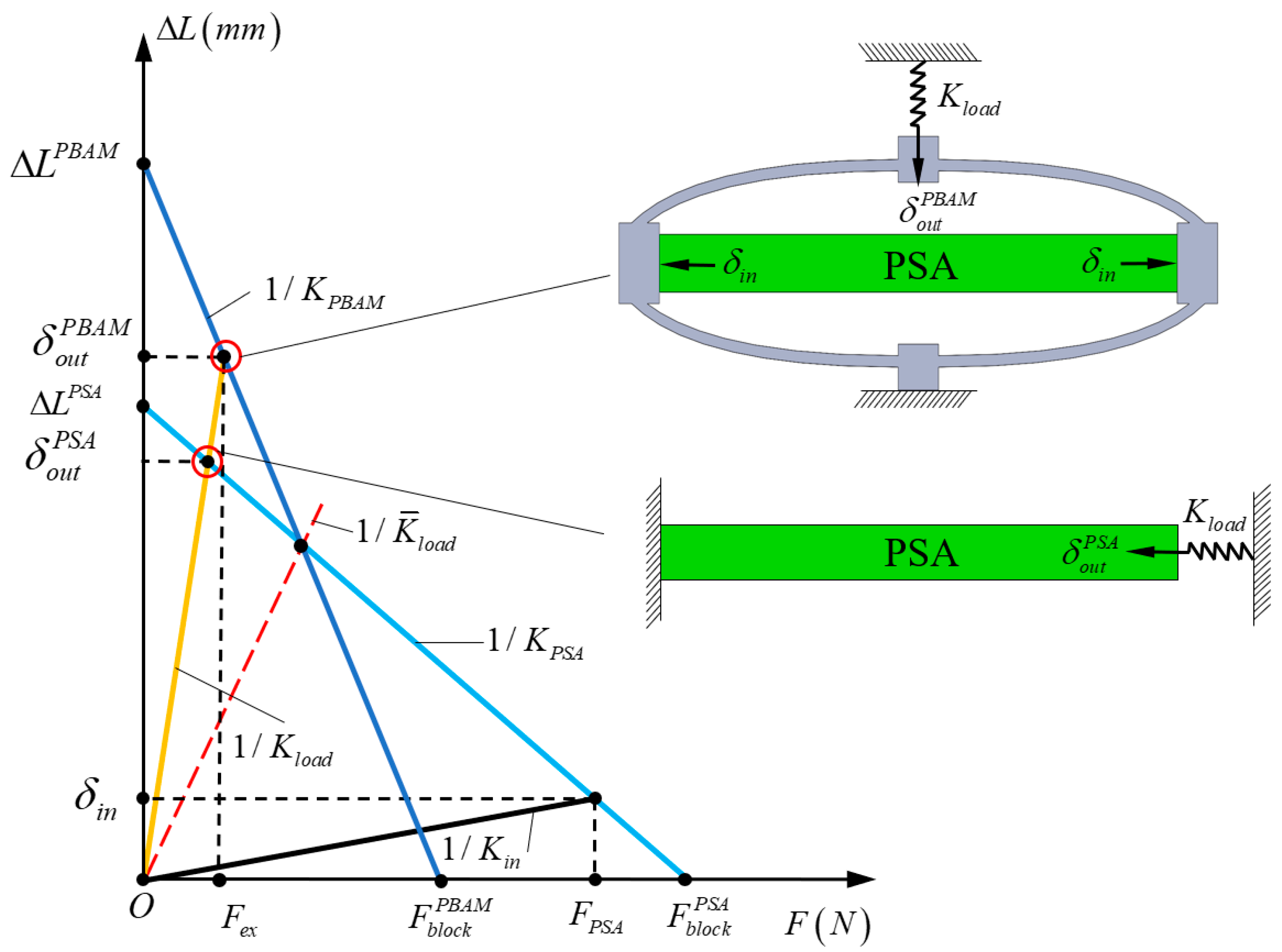
2.3. Analytical Model Considering the Effect of PSA and External Load
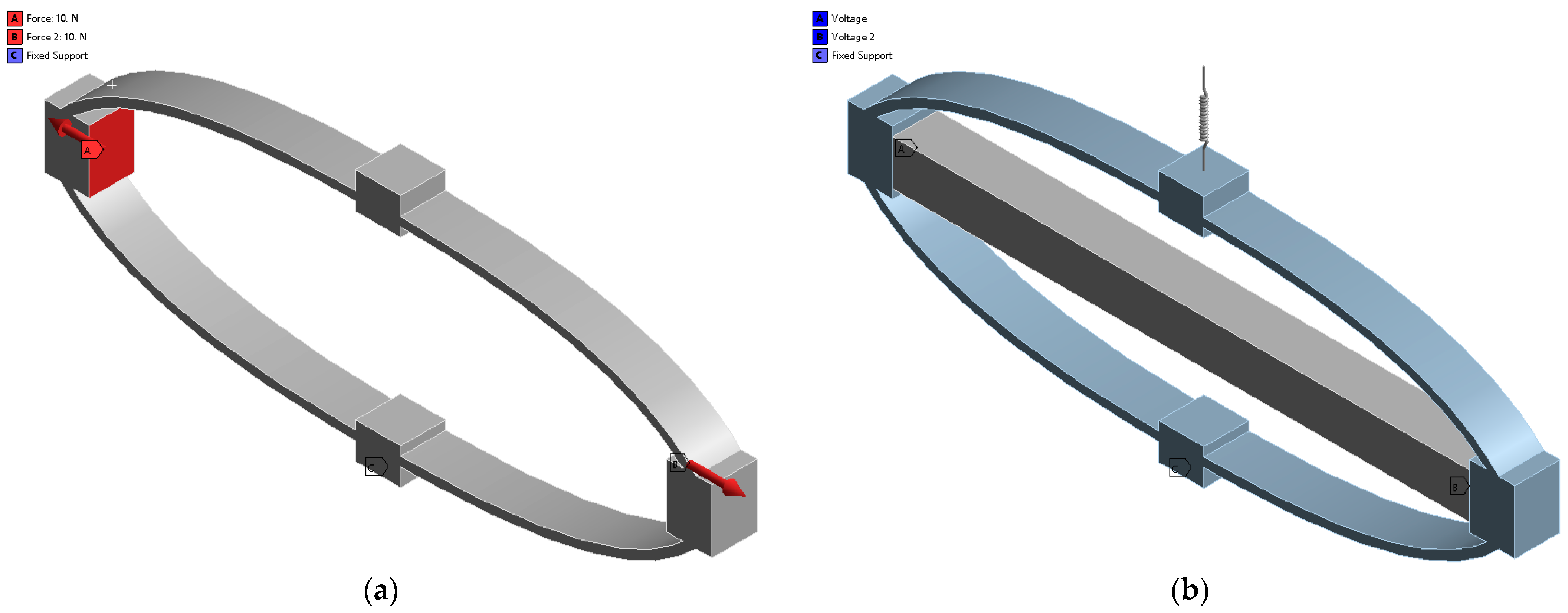
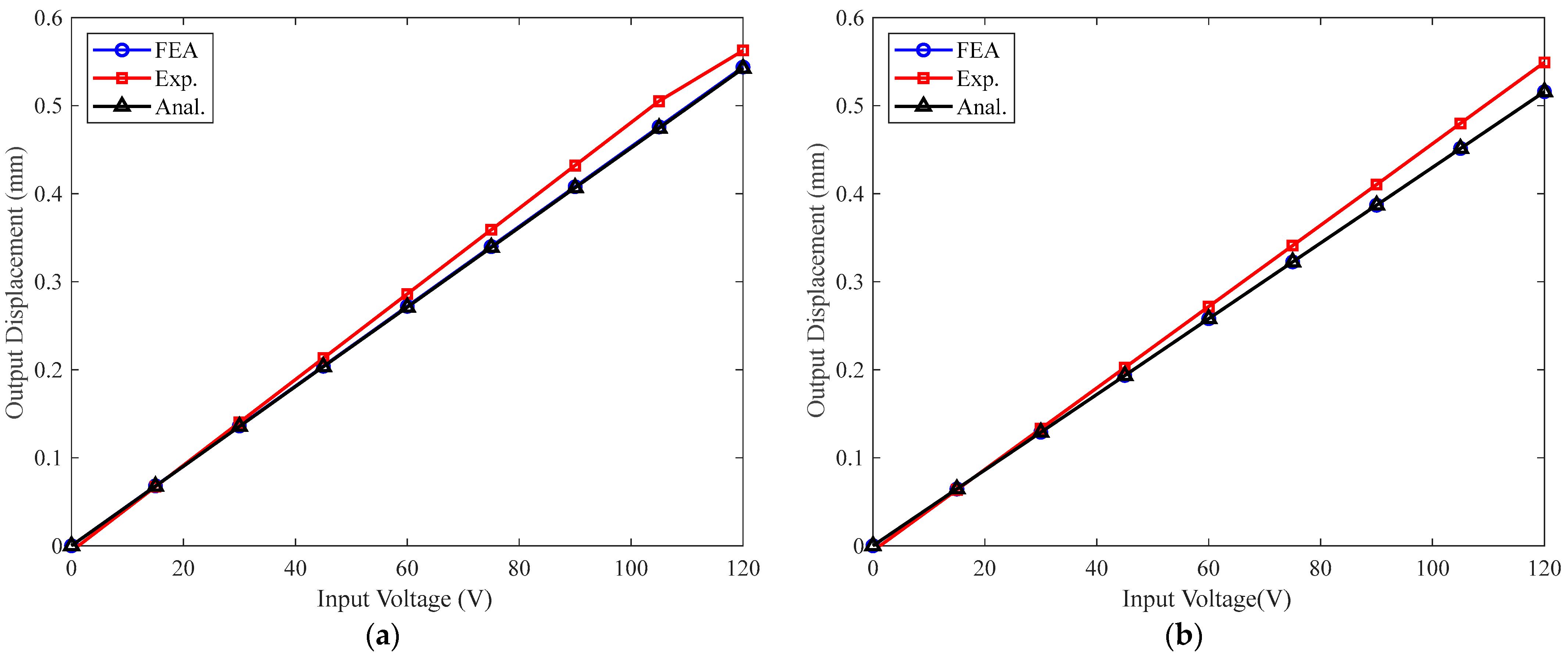
3. FEA Verification
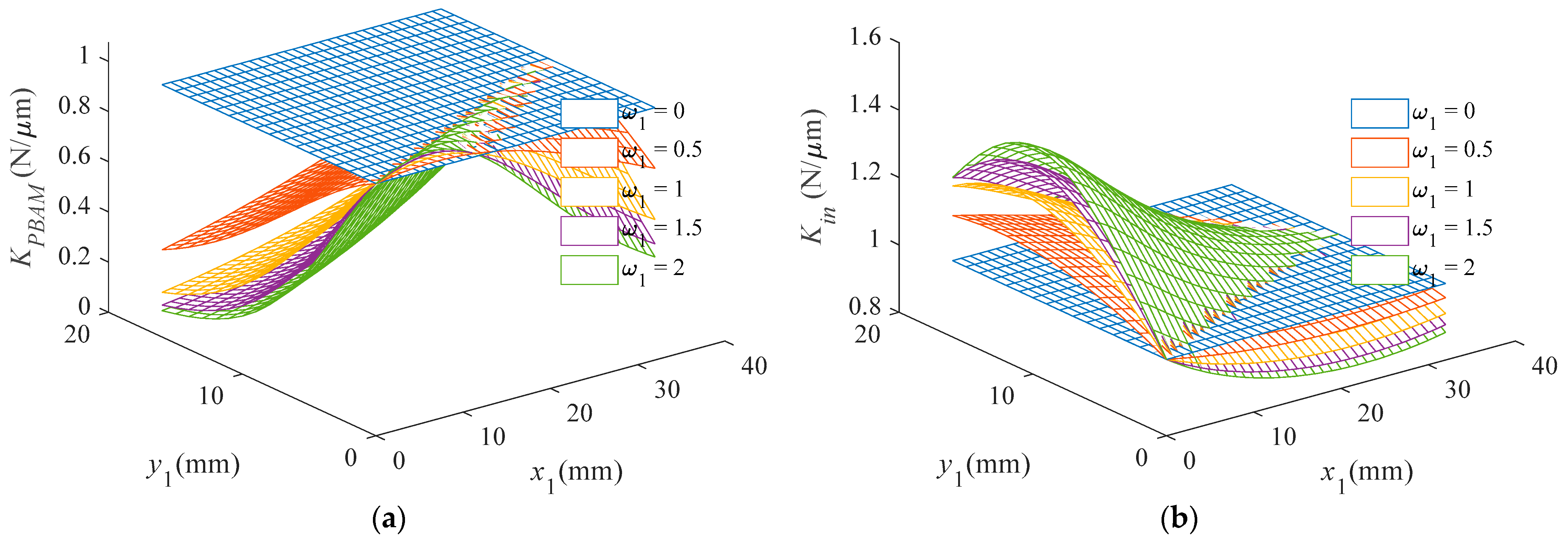
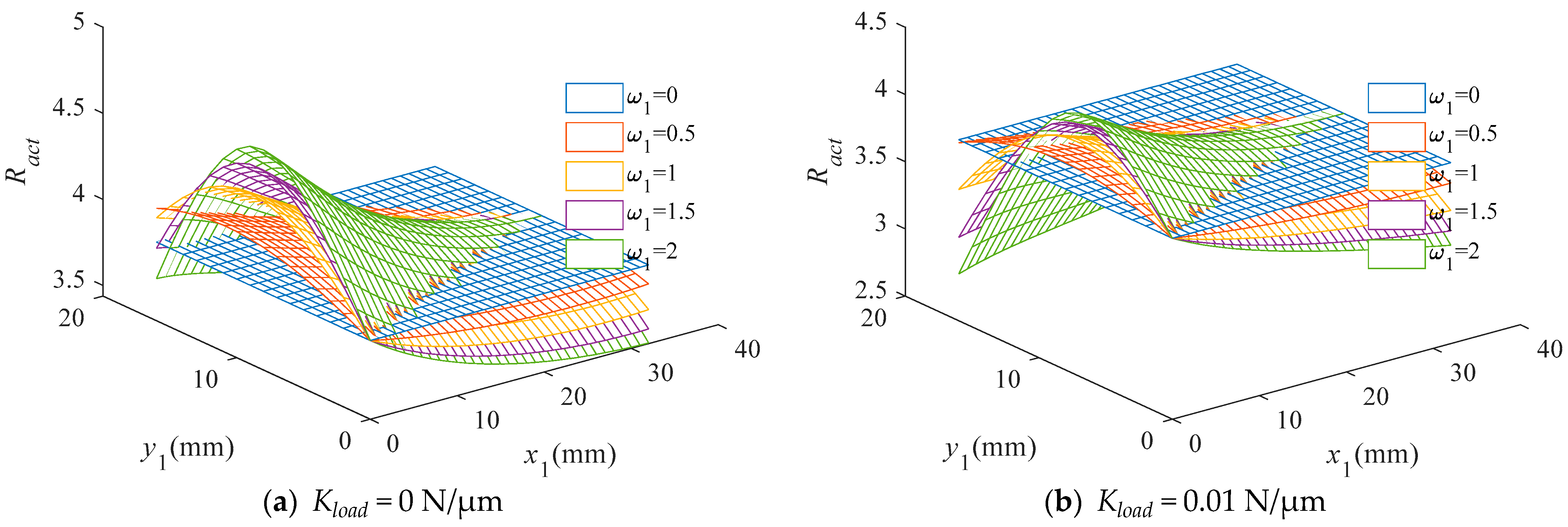
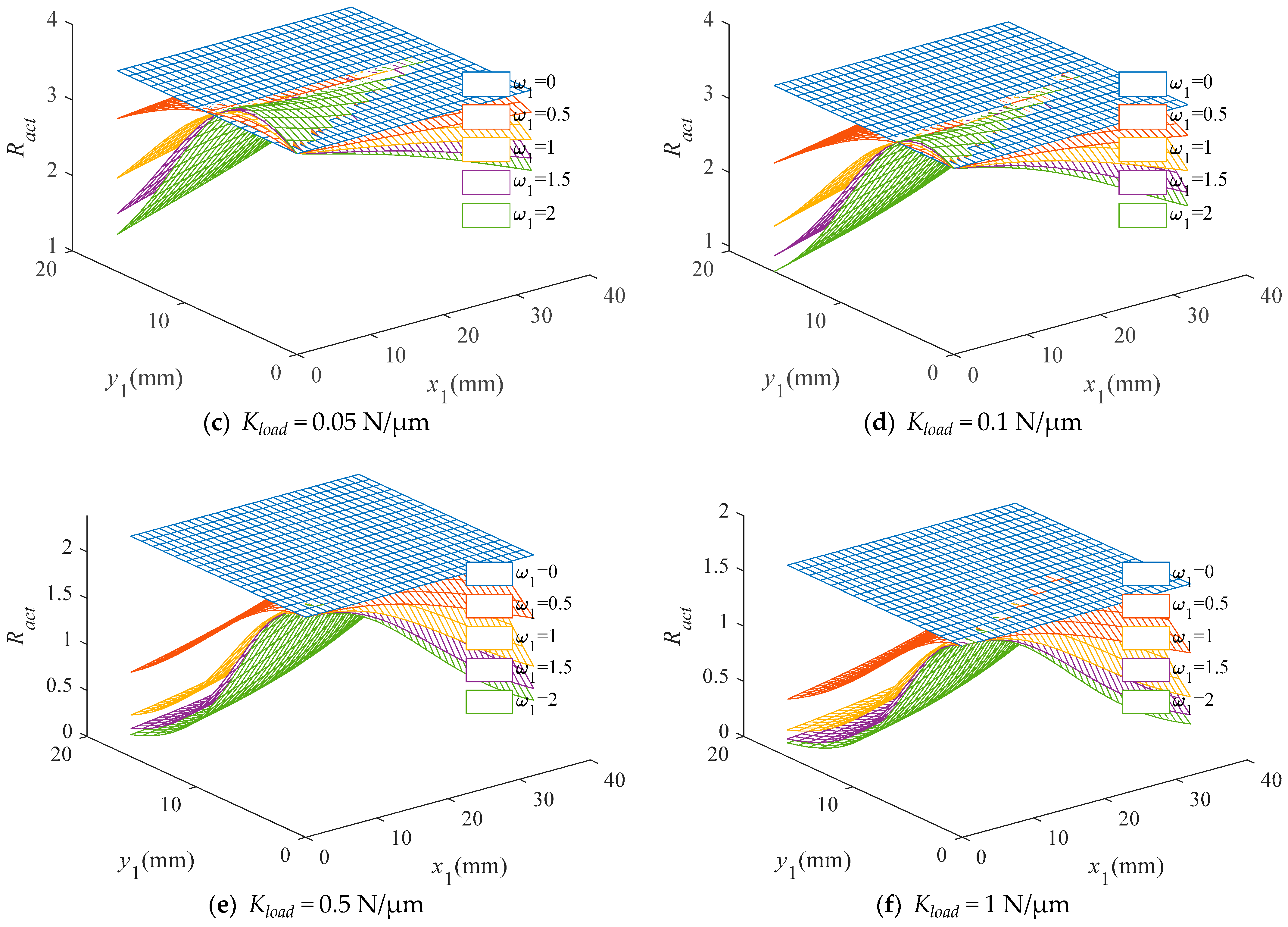
4. Parameter Analysis and Optimization
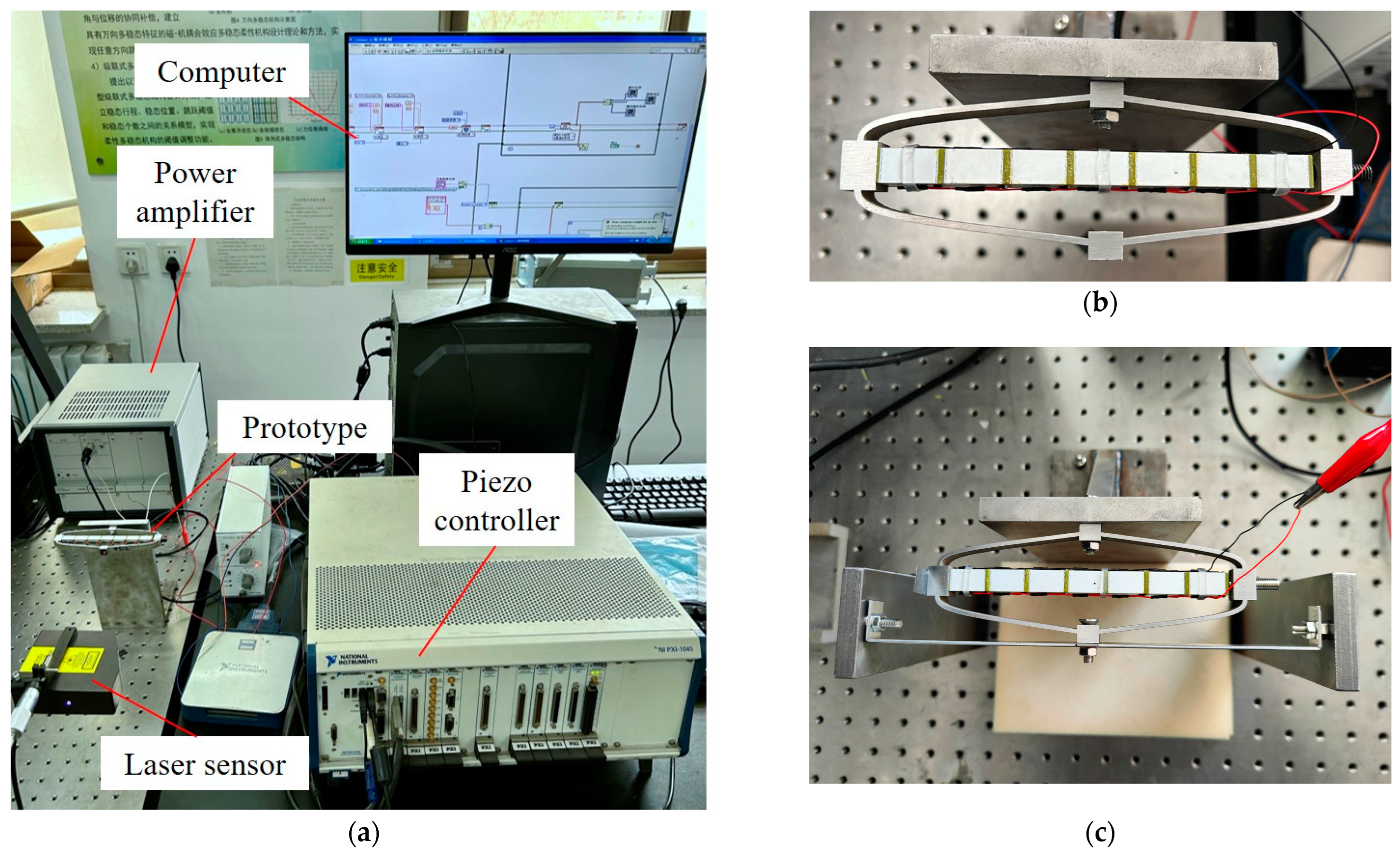
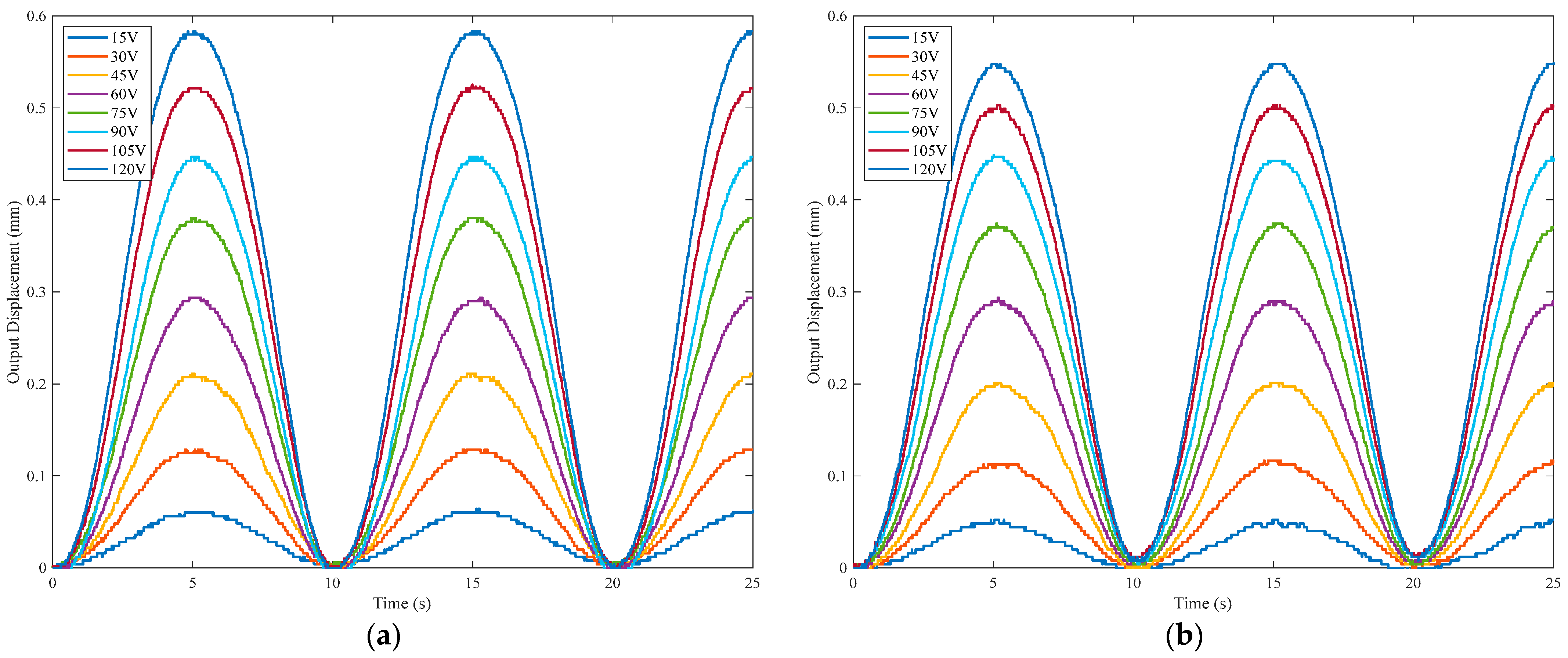
5. Experimental Testing
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lee, H.J.; Kim, H.C.; Kim, H.Y.; Gweon, D.G. Optimal Design and Experiment of a Three-Axis out-of-Plane Nano Positioning Stage Using a New Compact Bridge-Type Displacement Amplifier. Rev. Sci. Instrum. 2013, 84, 4827087. [Google Scholar] [CrossRef] [PubMed]
- Hwang, D.; Byun, J.; Jeong, J.; Lee, M.G. Robust Design and Performance Verification of an In-Plane XYθ Micropositioning Stage. IEEE Trans. Nanotechnol. 2011, 10, 1412–1423. [Google Scholar] [CrossRef]
- Mohith, S.; Upadhya, A.R.; Navin, K.P.; Kulkarni, S.M.; Rao, M. Recent Trends in Piezoelectric Actuators for Precision Motion and Their Applications: A Review. Smart Mater. Struct. 2021, 30, 013002. [Google Scholar] [CrossRef]
- Das, T.K.; Shirinzadeh, B.; Al-Jodah, A.; Ghafarian, M.; Pinskier, J. Computational Parametric Analysis and Experimental Investigations of a Compact Flexure-Based Microgripper. Precis. Eng. 2020, 66, 363–373. [Google Scholar] [CrossRef]
- Dao, T.P.; Huang, S.C. Design and Analysis of a Compliant Micro-Positioning Platform with Embedded Strain Gauges and Viscoelastic Damper. Microsyst. Technol. 2017, 23, 441–456. [Google Scholar] [CrossRef]
- Ghafarian, M.; Shirinzadeh, B.; Al-Jodah, A.; Das, T.K.; Wei, W.; Tian, Y.; Zhang, D. An XYZ Micromanipulator for Precise Positioning Applications. J. Micro-Bio Robot. 2020, 16, 53–63. [Google Scholar] [CrossRef]
- Wu, Z.; Xu, Q. Design and Testing of a Novel Bidirectional Energy Harvester with Single Piezoelectric Stack. Mech. Syst. Signal Process. 2019, 122, 139–151. [Google Scholar] [CrossRef]
- Jasim, A.; Yesner, G.; Wang, H.; Safari, A.; Maher, A.; Basily, B. Laboratory Testing and Numerical Simulation of Piezoelectric Energy Harvester for Roadway Applications. Appl. Energy 2018, 224, 438–447. [Google Scholar] [CrossRef]
- Sezer, N.; Koç, M. A Comprehensive Review on the State-of-the-Art of Piezoelectric Energy Harvesting. Nano Energy 2021, 80, 105567. [Google Scholar] [CrossRef]
- Straub, F.K.; Kennedy, D.K.; Stemple, A.D.; Anand, V.R.; Birchette, T.S. Development and Whirl Tower Test of the SMART Active Flap Rotor. In Proceedings of the Smart Structures and Materials 2004: Industrial and Commercial Applications of Smart Structures Technologies, San Diego, CA, USA, 14–18 March 2004; SPIE: Bellingham, WA, USA, 2004; Volume 5388, p. 202. [Google Scholar]
- Lee, J.H.; Natarajan, B.; Eun, W.J.; Viswamurthy, S.R.; Park, J.S.; Kim, T.; Shin, S.J. Structural and Mechanism Design of an Active Trailing-Edge Flap Blade. J. Mech. Sci. Technol. 2013, 27, 2605–2617. [Google Scholar] [CrossRef]
- Lee, T.; Chopra, I. Design Issues of a High-Stroke, on-Blade Piezostack Actuator for a Helicopter Rotor with Trailing-Edge Flaps. J. Intell. Mater. Syst. Struct. 2000, 11, 328–342. [Google Scholar] [CrossRef]
- Viswamurthy, S.R.; Ganguli, R. Using the Complete Authority of Multiple Active Trailing-Edge Flaps for Helicopter Vibration Control. J. Vib. Control 2008, 14, 1175–1199. [Google Scholar] [CrossRef]
- Patterson, K.; Pellegrino, S. Ultralightweight Deformable Mirrors. Appl. Opt. 2013, 52, 5327–5341. [Google Scholar] [CrossRef] [PubMed]
- Ahn, K.; Rhee, H.-G.; Yang, H.-S.; Kihm, H. CVD SiC Deformable Mirror with Monolithic Cooling Channels. Opt. Express 2018, 26, 9724. [Google Scholar] [CrossRef] [PubMed]
- Toporovsky, V.; Kudryashov, A.; Skvortsov, A.; Rukosuev, A.; Samarkin, V.; Galaktionov, I. State-of-the-Art Technologies in Piezoelectric Deformable Mirror Design. Photonics 2022, 9, 321. [Google Scholar] [CrossRef]
- Samarkin, V.; Alexandrov, A.; Galaktionov, I.; Kudryashov, A.; Nikitin, A.; Rukosuev, A.; Toporovsky, V.; Sheldakova, J. Wide-Aperture Bimorph Deformable Mirror for Beam Focusing in 4.2 PW Ti:Sa Laser. Appl. Sci. 2022, 12, 1144. [Google Scholar] [CrossRef]
- Schmerbauch, A.E.M.; Vasquez-Beltran, M.A.; Vakis, A.I.; Huisman, R.; Jayawardhana, B. Influence Functions for a Hysteretic Deformable Mirror with a High-Density 2D Array of Actuators. Appl. Opt. 2020, 59, 8077. [Google Scholar] [CrossRef]
- Wang, G.; Yan, Y.; Ma, J.; Cui, J. Design, Test and Control of a Compact Piezoelectric Scanner Based on a Compound Compliant Amplification Mechanism. Mech. Mach. Theory 2019, 139, 460–475. [Google Scholar] [CrossRef]
- Simic, M.; Herakovic, N. Characterization of Energy Consumption of New Piezo Actuator System Used for Hydraulic on/off Valves. J. Clean. Prod. 2021, 284, 124748. [Google Scholar] [CrossRef]
- Bazaei, A.; Ettefagh, M.H.; Chen, Z. Displacement Amplification and Differential Actuation in Piezo Driven Nanopositioners. Mech. Syst. Signal Process. 2021, 151. [Google Scholar] [CrossRef]
- Nguyen, V.K.; Pham, H.T.; Pham, H.H.; Dang, Q.K. Optimization Design of a Compliant Linear Guide for High-Precision Feed Drive Mechanisms. Mech. Mach. Theory 2021, 165, 104442. [Google Scholar] [CrossRef]
- Qi, K.Q.; Xiang, Y.; Fang, C.; Zhang, Y.; Yu, C.S. Analysis of the Displacement Amplification Ratio of Bridge-Type Mechanism. Mech. Mach. Theory 2015, 87, 45–56. [Google Scholar] [CrossRef]
- Huynh, N.T.; Huang, S.C.; Dao, T.P. Optimal Displacement Amplification Ratio of Bridge-Type Compliant Mechanism Flexure Hinge Using the Taguchi Method with Grey Relational Analysis. Microsyst. Technol. 2021, 27, 1251–1265. [Google Scholar] [CrossRef]
- Shiryayev, O.; Vahdati, N.; Yap, F.F.; Butt, H. Compliant Mechanism-Based Sensor for Large Strain Measurements Employing Fiber Optics. Sensors 2022, 22, 3987. [Google Scholar] [CrossRef] [PubMed]
- Koyuncu, A.; Karaağaçlı, T.; Şahin, M.; Özgüven, H.N. Experimental Modal Analysis of Nonlinear Amplified Piezoelectric Actuators by Using Response-Controlled Stepped-Sine Testing. Exp. Mech. 2022, 62, 1579–1594. [Google Scholar] [CrossRef]
- Chen, C.M.; Hsu, Y.C.; Fung, R.F. System Identification of a Scott-Russell Amplifying Mechanism with Offset Driven by a Piezoelectric Actuator. Appl. Math. Model. 2012, 36, 2788–2802. [Google Scholar] [CrossRef]
- Clark, L.; Shirinzadeh, B.; Bhagat, U.; Smith, J.; Zhong, Y. Development and Control of a Two DOF Linear-Angular Precision Positioning Stage. Mechatronics 2015, 32, 34–43. [Google Scholar] [CrossRef]
- Ueda, J.; Secord, T.W.; Asada, H.H. Large Effective-Strain Piezoelectric Actuators Using Nested Cellular Architecture with Exponential Strain Amplification Mechanisms. IEEE/ASME Trans. Mechatron. 2010, 15, 770–782. [Google Scholar] [CrossRef]
- Lobontiu, N.; Garcia, E. Analytical Model of Displacement Amplification and Stiffness Optimization for a Class of Flexure-Based Compliant Mechanisms. Comput. Struct. 2003, 81, 2797–2810. [Google Scholar] [CrossRef]
- Ma, H.W.; Yao, S.M.; Wang, L.Q.; Zhong, Z. Analysis of the Displacement Amplification Ratio of Bridge-Type Flexure Hinge. Sens. Actuators A Phys. 2006, 132, 730–736. [Google Scholar] [CrossRef]
- Wei, H.; Shirinzadeh, B.; Li, W.; Clark, L.; Pinskier, J.; Wang, Y. Development of Piezo-Driven Compliant Bridge Mechanisms: General Analytical Equations and Optimization of Displacement Amplification. Micromachines 2017, 8, 238. [Google Scholar] [CrossRef]
- Ling, M. A General Two-Port Dynamic Stiffness Model and Static/Dynamic Comparison for Three Bridge-Type Flexure Displacement Amplifiers. Mech. Syst. Signal Process. 2019, 119, 486–500. [Google Scholar] [CrossRef]
- Pan, B.; Zhao, H.; Zhao, C.; Zhang, P.; Hu, H. Nonlinear Characteristics of Compliant Bridge-Type Displacement Amplification Mechanisms. Precis. Eng. 2019, 60, 246–256. [Google Scholar] [CrossRef]
- Liu, P.; Yan, P. A New Model Analysis Approach for Bridge-Type Amplifiers Supporting Nano-Stage Design. Mech. Mach. Theory 2016, 99, 176–188. [Google Scholar] [CrossRef]
- Cao, J.; Ling, M.; Inman, D.J.; Lin, J. Generalized Constitutive Equations for Piezo-Actuated Compliant Mechanism. Smart Mater. Struct. 2016, 25, 095005. [Google Scholar] [CrossRef]
- Lin, C.; Jiang, M.; Zheng, S. Establishment and Verification of the Analytical Model for the Critical Parameters in the Kinematics Model of the Precision Positioning Stage. Sens. Actuators A Phys. 2021, 320, 112572. [Google Scholar] [CrossRef]
- Tian, F.; Li, S.; Hu, B.; Wang, P.; Hao, X.; Zhao, W. A Structure Load Performance Integrated Model Method for the Bridge-Type Displacement Amplification Mechanism. Machines 2022, 10, 792. [Google Scholar] [CrossRef]
- Wu, H.; Lai, L.; Zhu, L. Analytical Model and Experimental Verification of an Elliptical Bridge-Type Compliant Displacement Amplification Mechanism. Rev. Sci. Instrum. 2021, 92, 055109. [Google Scholar] [CrossRef] [PubMed]
- Lalande, F.; Chaudhry, Z.; Rogers, C.A. A Simplified Geometrically Nonlinear Approach to the Analysis of the Moonie Actuator. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1995, 42, 21–27. [Google Scholar] [CrossRef]
- Piegl, W.T.L. The NURBS Book; Springer: New York, NY, USA, 1996. [Google Scholar]
- Li, B.; Ding, S.; Guo, S.; Su, W.; Cheng, A.; Hong, J. A Novel Isogeometric Topology Optimization Framework for Planar Compliant Mechanisms. Appl. Math. Model. 2021, 92, 931–950. [Google Scholar] [CrossRef]
- Radaelli, G.; Herder, J.L. Isogeometric shape optimization for compliant mechanisms with prescribed load paths. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Buffalo, NY, USA, 17–20 August 2014. [Google Scholar]
| Samples | Materials | Control Points (mm) | Control Points (mm) | Load Stiffness ) | |
|---|---|---|---|---|---|
| 1 | Structural steel | 0.5 | (30,16) | (64,16) | 0.05 |
| 2 | Al-6061 | 0.5 | (16,16) | (64,16) | 0.01 |
| 3 | Structural steel | 1 | (16,16) | (64,16) | 0.01 |
| 4 | Al-6061 | 1 | (5,16) | (64,16) | 0.01 |
| 5 | Al-6061 | 1 | (16,10) | (64,10) | 0.05 |
| 6 | Structural steel | 1.5 | (16,16) | (64,16) | 0.05 |
| 7 | Structural steel | 2 | (16,16) | (64,16) | 0.01 |
| 8 | Al-6061 | 2 | (16,16) | (64,16) | 0.01 |
| Parameters | ||||||
|---|---|---|---|---|---|---|
| Values | 7 | 5 | 10 | 2 | 8 | 10 |
| Materials | Young’s Modulus E (GPa) | ||
|---|---|---|---|
| Al-6061 | 69 | 0.33 | 2713 |
| Structural steel | 200 | 0.3 | 7850 |
| Samples | (N/µm) | (N/µm) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| FEA | Anal. | Error (%) | FEA | Anal. | Error (%) | FEA | Anal. | Error (%) | FEA | Anal. | Error (%) | |
| 1 | 3.87 | 3.82 | 1.38 | 0.94 | 0.89 | 5.32 | 0.84 | 0.84 | 0.48 | 3.58 | 3.53 | 1.42 |
| 2 | 3.95 | 3.92 | 0.67 | 0.33 | 0.33 | 1.38 | 0.22 | 0.23 | 2.10 | 3.76 | 3.72 | 0.67 |
| 3 | 3.82 | 3.80 | 0.60 | 0.97 | 0.96 | 0.75 | 0.29 | 0.30 | 2.06 | 3.62 | 3.59 | 0.80 |
| 4 | 3.94 | 3.99 | 1.32 | 0.36 | 0.38 | 4.42 | 0.07 | 0.07 | 3.71 | 3.43 | 3.48 | 1.51 |
| 5 | 6.13 | 5.98 | 2.59 | 0.95 | 0.89 | 6.31 | 0.09 | 0.09 | 0.13 | 3.93 | 3.83 | 2.72 |
| 6 | 3.69 | 3.66 | 0.10 | 0.97 | 0.95 | 1.13 | 0.21 | 0.22 | 1.93 | 2.91 | 2.92 | 0.68 |
| 7 | 3.57 | 3.54 | 0.97 | 1.00 | 0.95 | 5.12 | 0.18 | 0.18 | 1.89 | 3.30 | 3.28 | 0.63 |
| 8 | 3.58 | 3.54 | 0.99 | 0.33 | 0.33 | 1.68 | 0.06 | 0.06 | 0.14 | 3.08 | 3.04 | 1.35 |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Dimensions (mm) | 10 × 10 × 128 | Stiffness (N/µm) | 38 |
| Maximum displacement (µm) | 143.1 | Electrical capacitance (µF) | 50.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Zhang, C.; Liu, S.; Wang, X. Modeling and Analysis of a Conical Bridge-Type Displacement Amplification Mechanism Using the Non-Uniform Rational B-Spline Curve. Materials 2023, 16, 6162. https://doi.org/10.3390/ma16186162
Wang M, Zhang C, Liu S, Wang X. Modeling and Analysis of a Conical Bridge-Type Displacement Amplification Mechanism Using the Non-Uniform Rational B-Spline Curve. Materials. 2023; 16(18):6162. https://doi.org/10.3390/ma16186162
Chicago/Turabian StyleWang, Mingze, Cheng Zhang, Shutian Liu, and Xiaoli Wang. 2023. "Modeling and Analysis of a Conical Bridge-Type Displacement Amplification Mechanism Using the Non-Uniform Rational B-Spline Curve" Materials 16, no. 18: 6162. https://doi.org/10.3390/ma16186162





