Damage Detection in a Polymer Matrix Composite from 4D Displacement Field Measurements
Abstract
:1. Introduction
2. Material and Methods
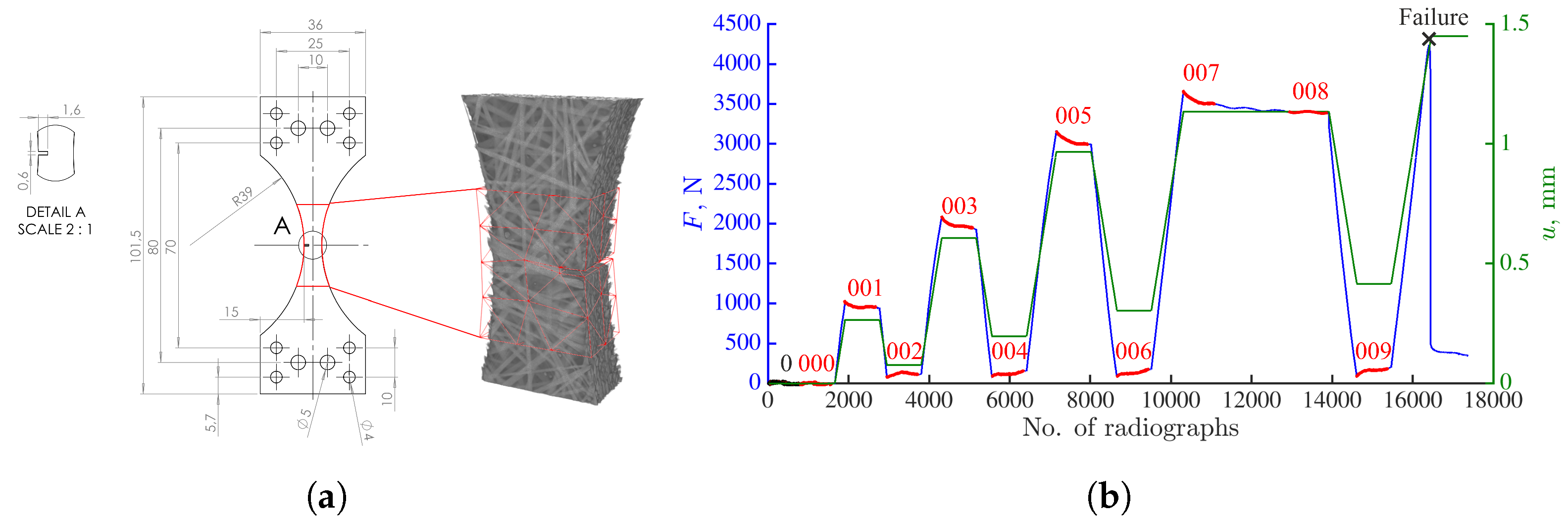
2.1. Material and Experimental Setup
2.2. Projection-Based Digital Volume Correlation
| Algorithm 1: P-DVC with DVC spatial modes |
Select spatial modes Choose an initial guess of whiledo Corrections Update and Solve Update temporal amplitudes Update displacement fields Update projection residuals end |
3. Results
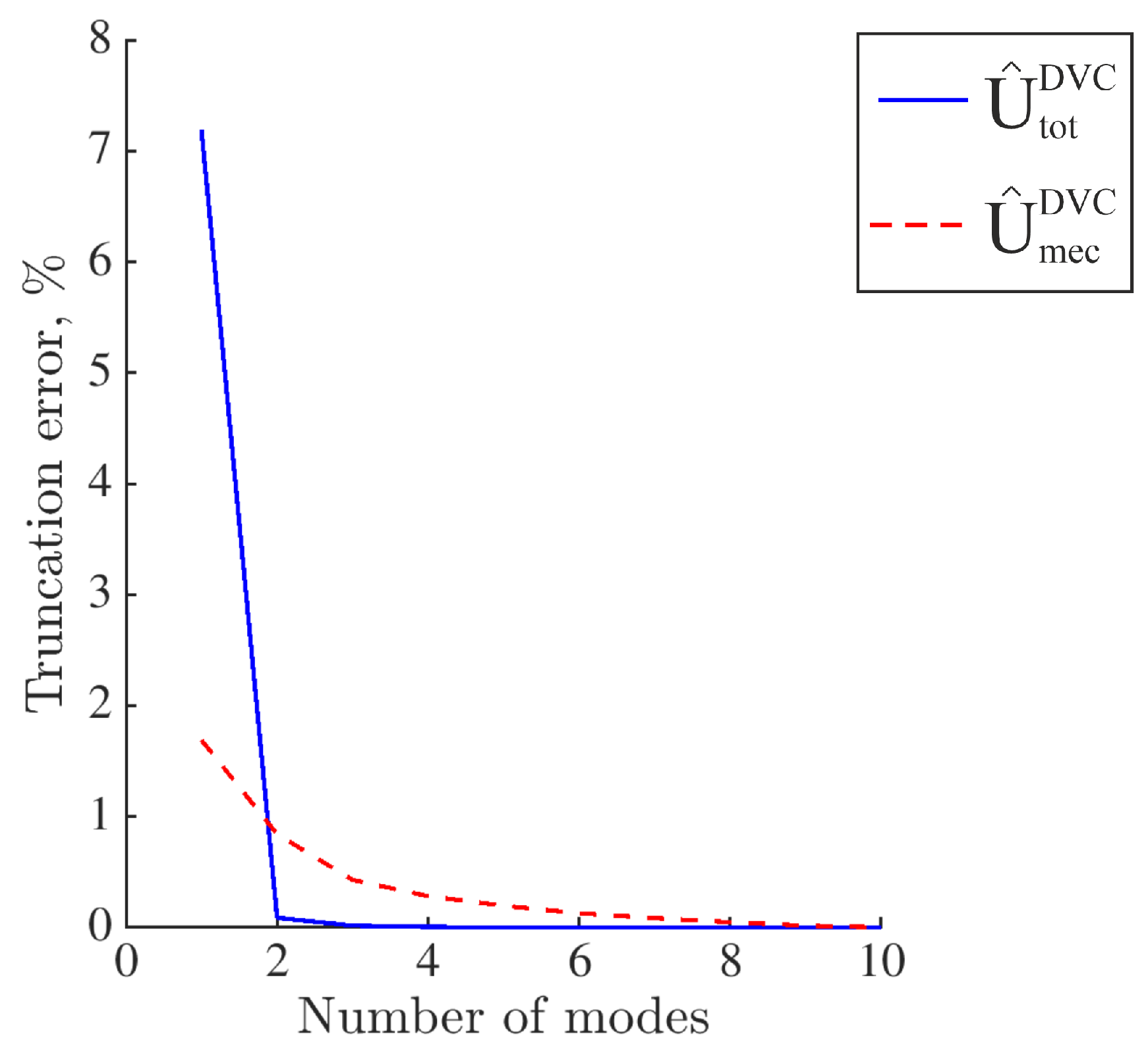
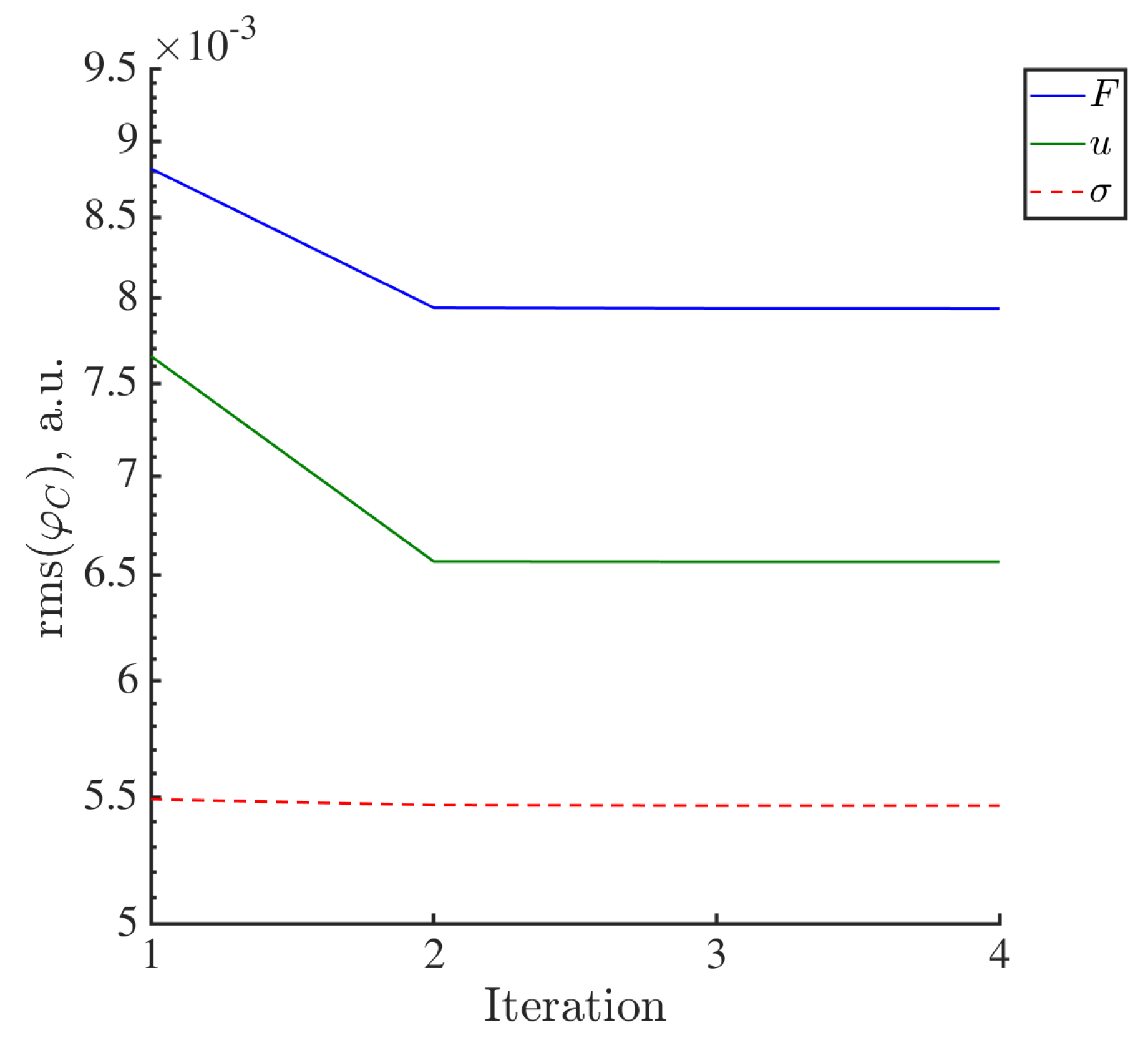
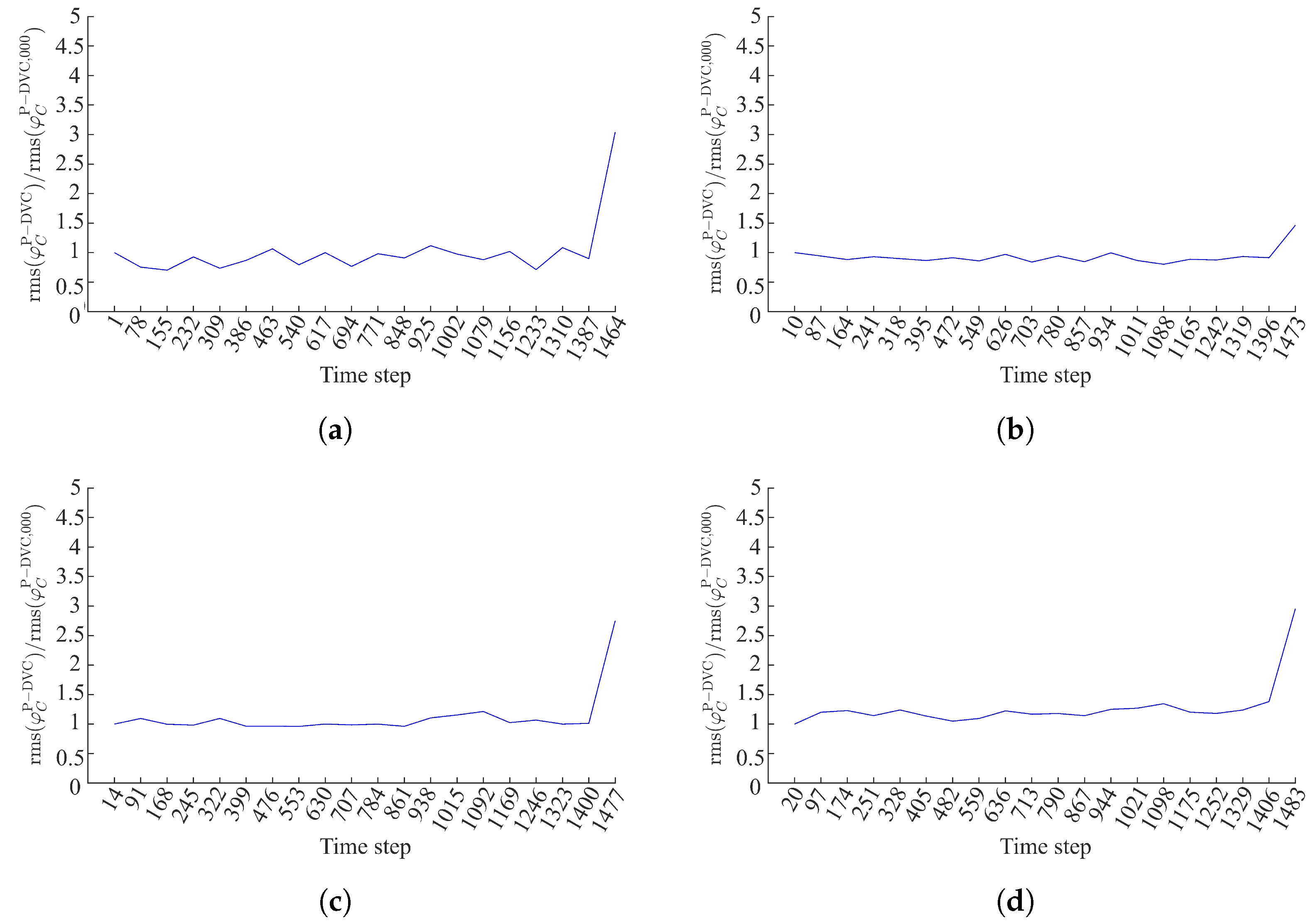
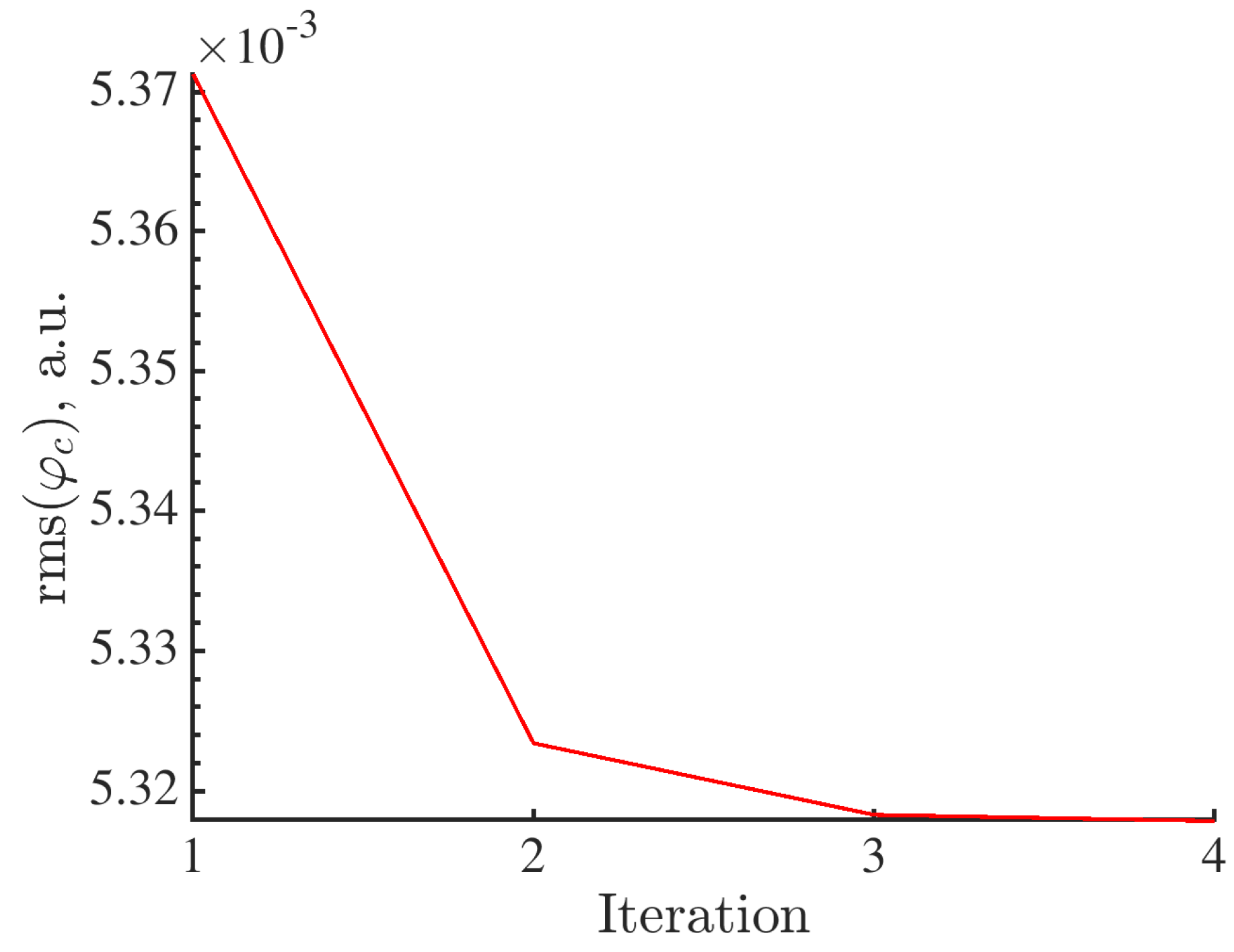
3.1. Evaluation of Reconstruction Error
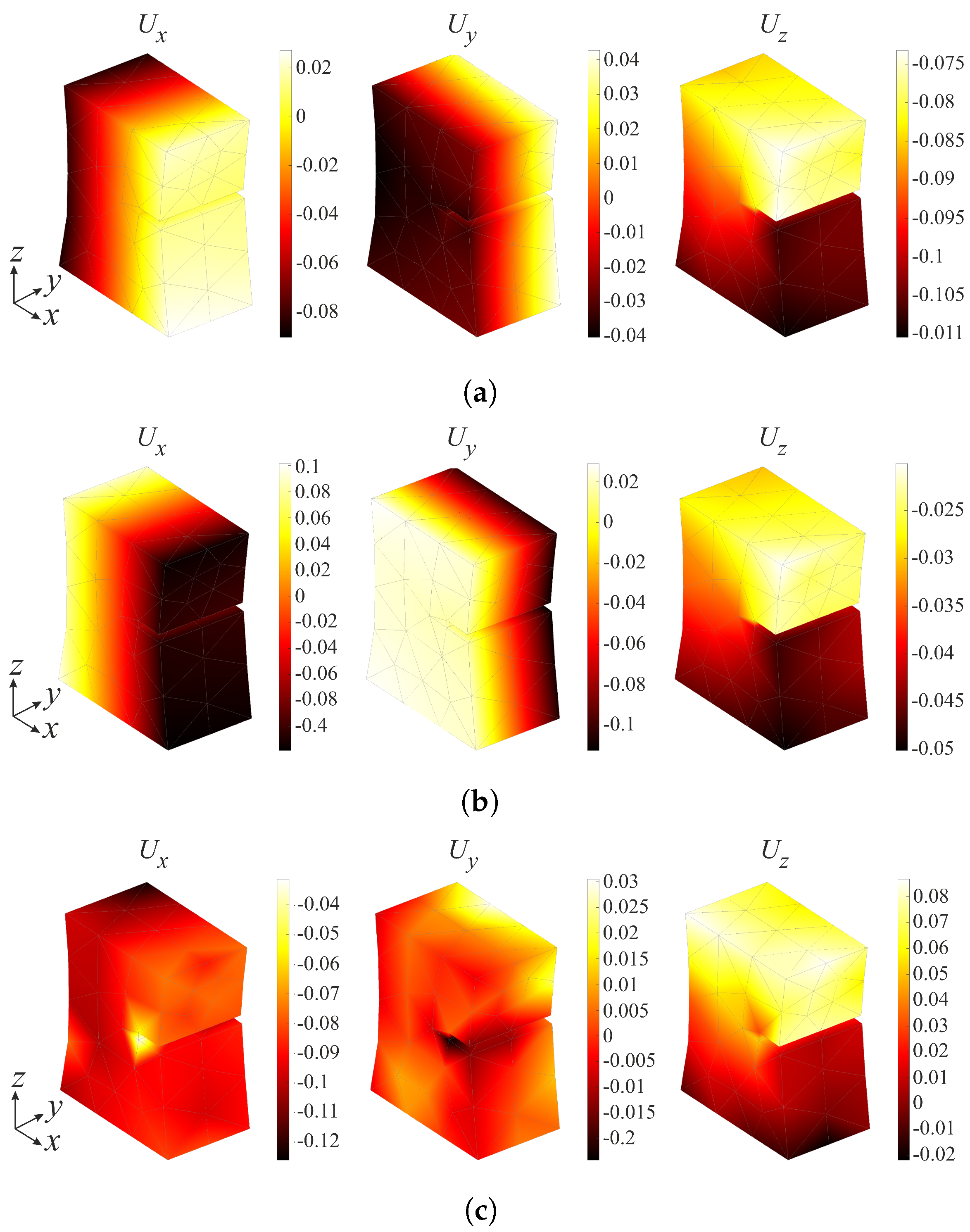
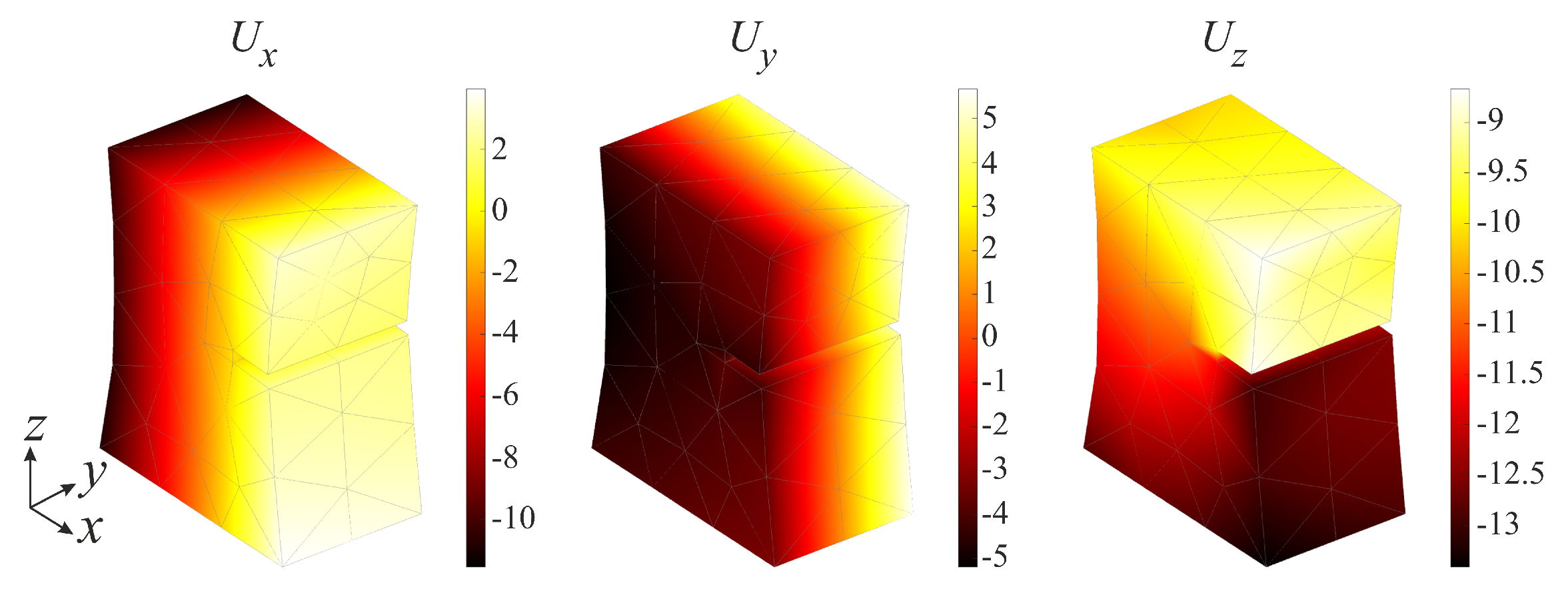
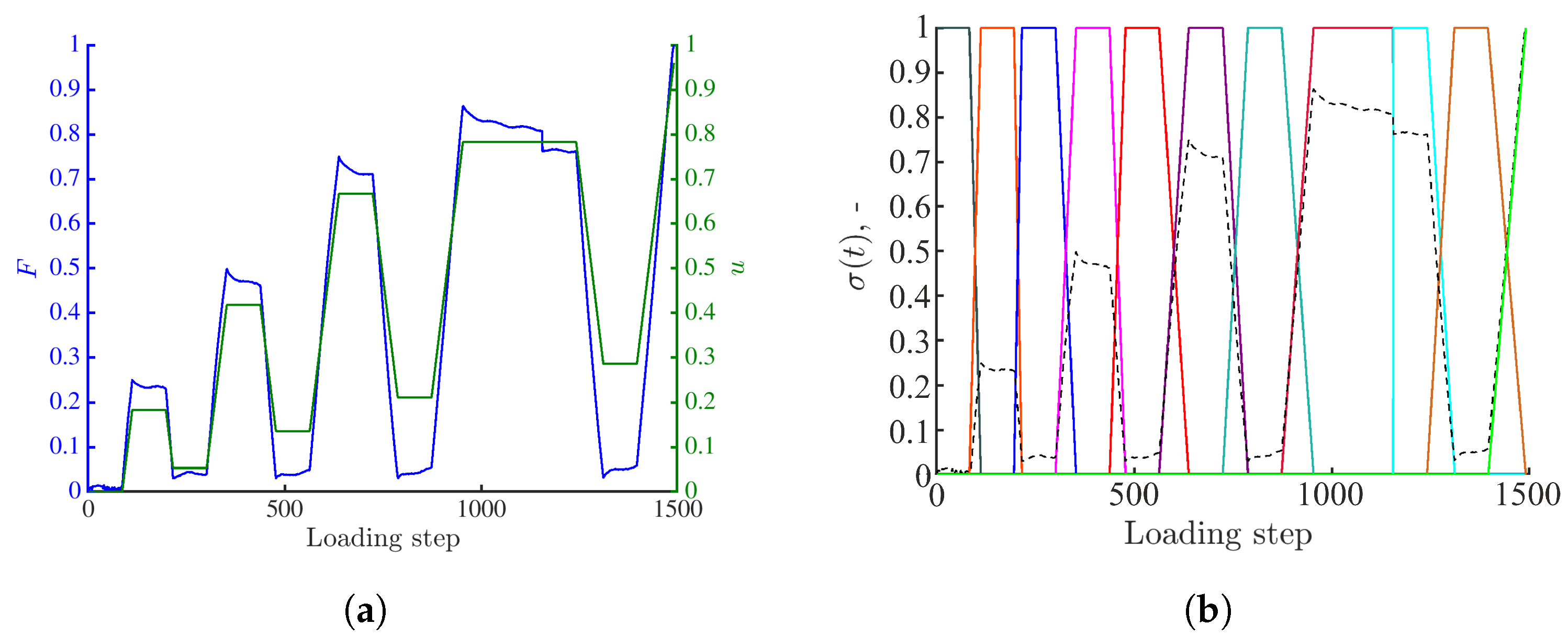
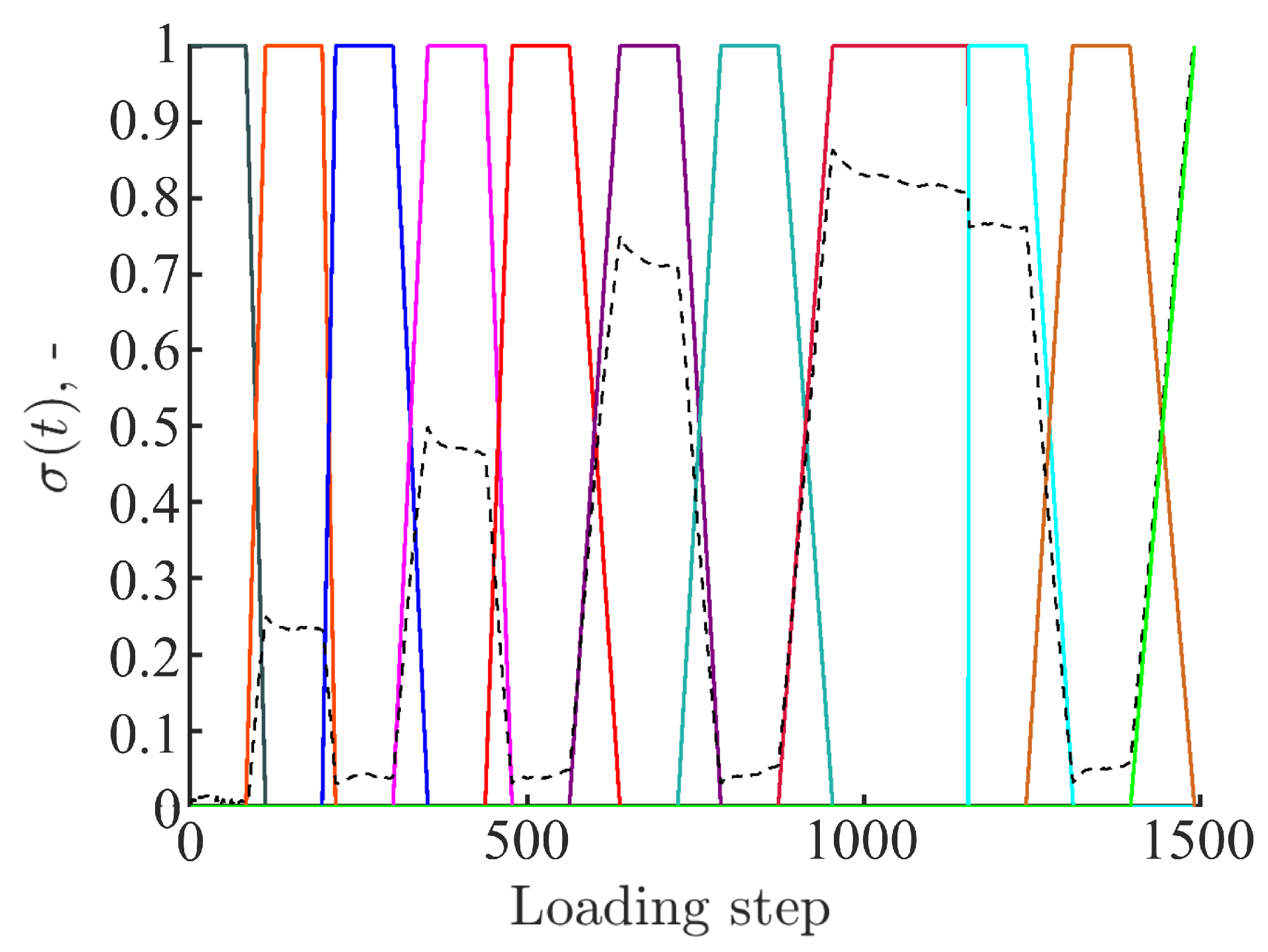
3.2. Full-Field Measurements over the Entire Loading History
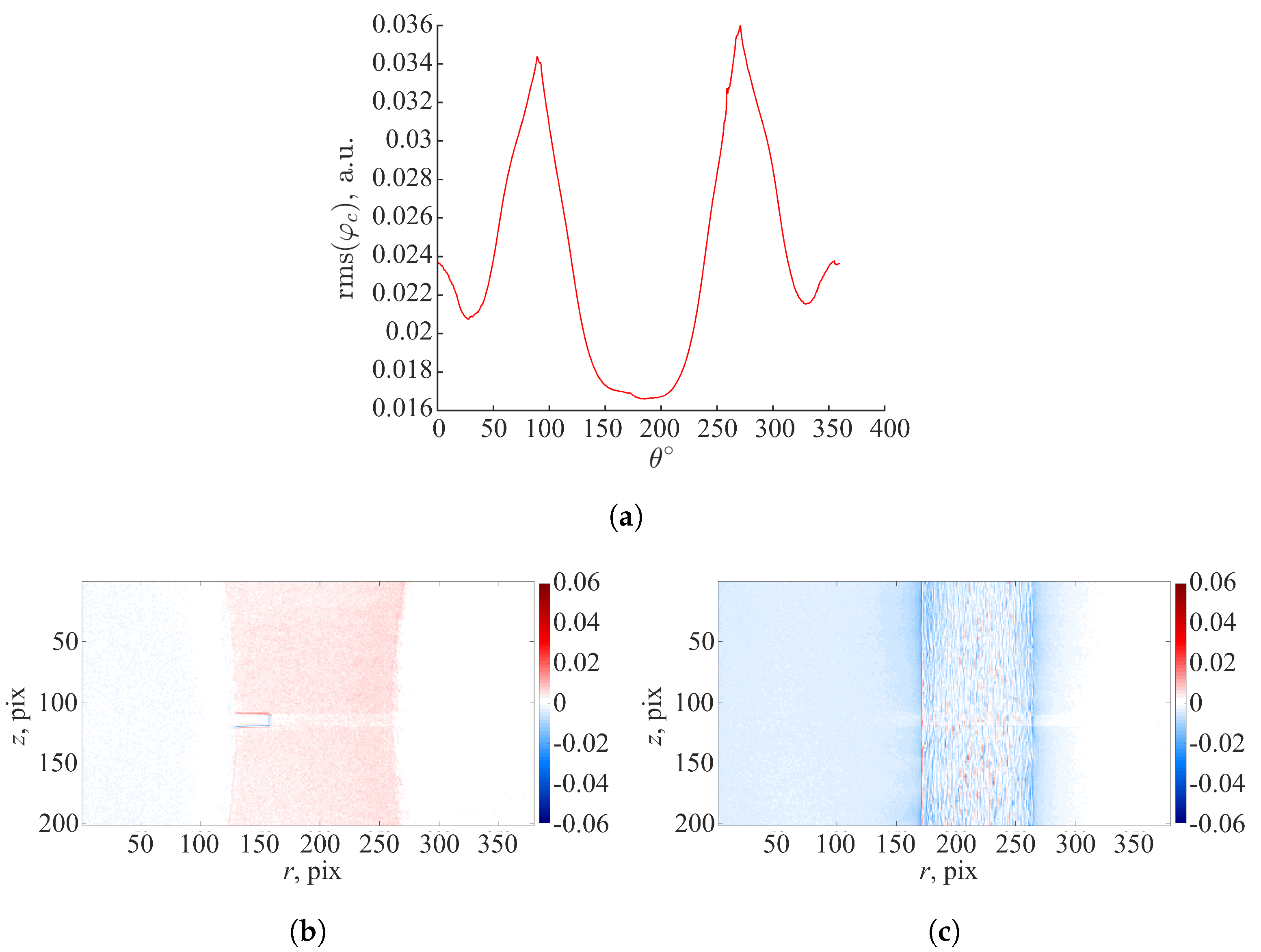
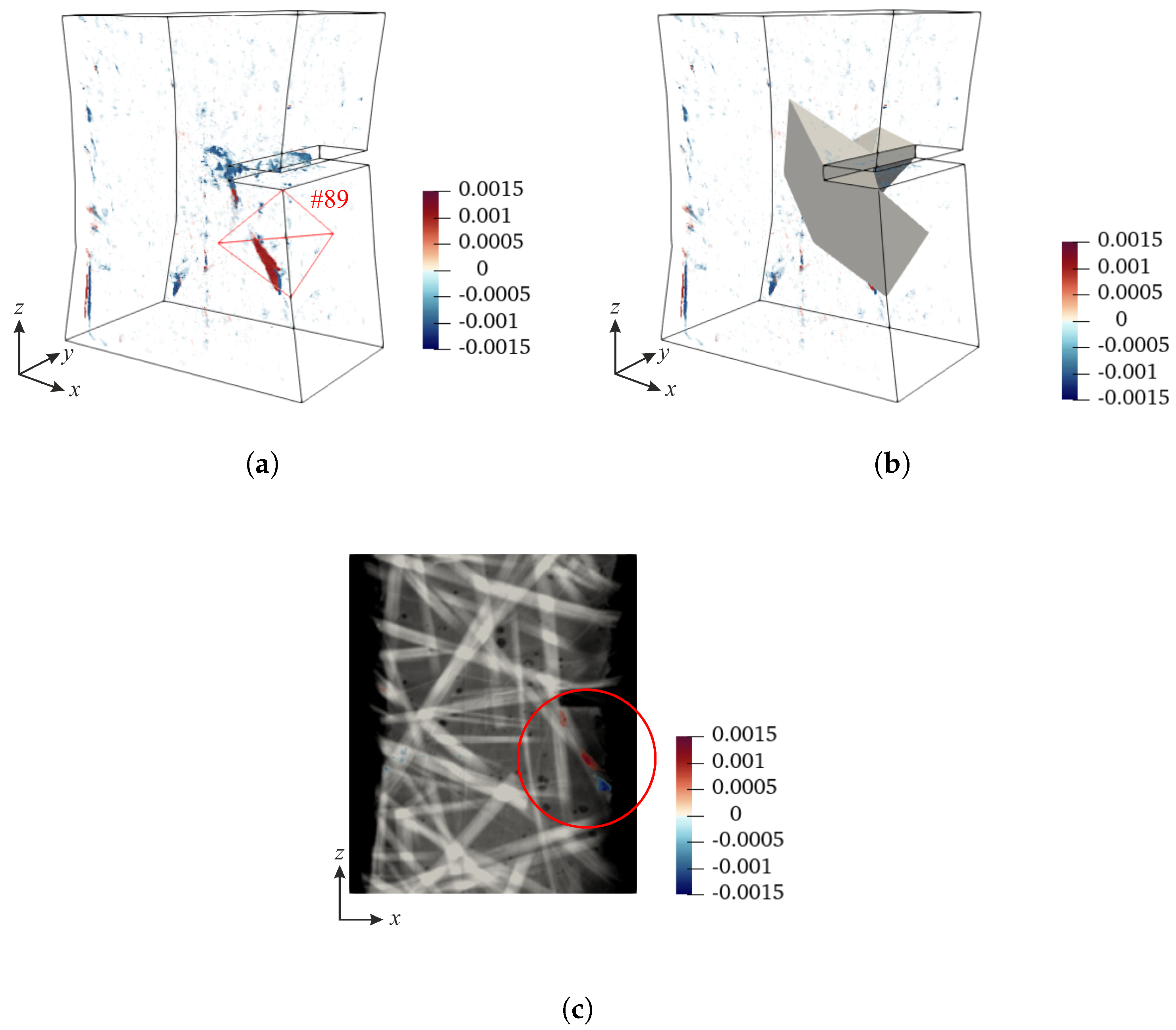
4. Discussion: Quantification of Damage Growth
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DVC | Digital Volume Correlation |
| FE | Finite Element |
| FDK | Feldkamp–Davis–Kress |
| FRP | Fiber Reinforced Polymer |
| HQ | High Quality |
| P-DVC | Projection-based Digital Volume Correlation |
| RBM | Rigid Body Motion |
| RBR | Rigid Body Rotation |
| rms | Root mean square |
| ROI | Region Of Interest |
| SIRT | Simultaneous Iterative Reconstruction |
| SVD | Singular Value Decomposition |
| TTC | Tension, Torsion and Compression |
| XCT | X-ray Computed Tomography |
| 4D | Four-dimensional (3D space and 1D time) |
Appendix A. Hardware Parameters
| Tomograph | North Star Imaging X50+ | |
|---|---|---|
| X-ray source | XRayWorX XWT-240-CT | |
| Target/Anode | W (reflection mode) | |
| Filter | None | |
| Voltage | 150 kV | |
| Current | 7.8 µA | |
| Focal spot size | 5 µm | |
| Tube to detector | 910 mm | |
| Tube to object | 53 mm | |
| Detector | Dexela 2923 | |
| Definition | 1944 × 1536 pixels (2 × 2 binning) | |
| Scanning settings | High quality | Continuous |
| Number of projections | 800 | 768 |
| Angular amplitude | 360° | 360° |
| Frame average | 20 per projection | Continuous (1 per step) |
| Frame rate | 3 fps | 3 fps |
| Acquisition duration | 1 h 46 min 26 s | 4 min 26 s |
| Reconstruction algorithm | SIRT | SIRT |
| Field of view | 7.3 × 10 × 20.5 mm3 | 7.3 × 10 × 20.5 mm3 |
| Image scale | 14.6 µm/voxel | 14.6 µm/voxel |
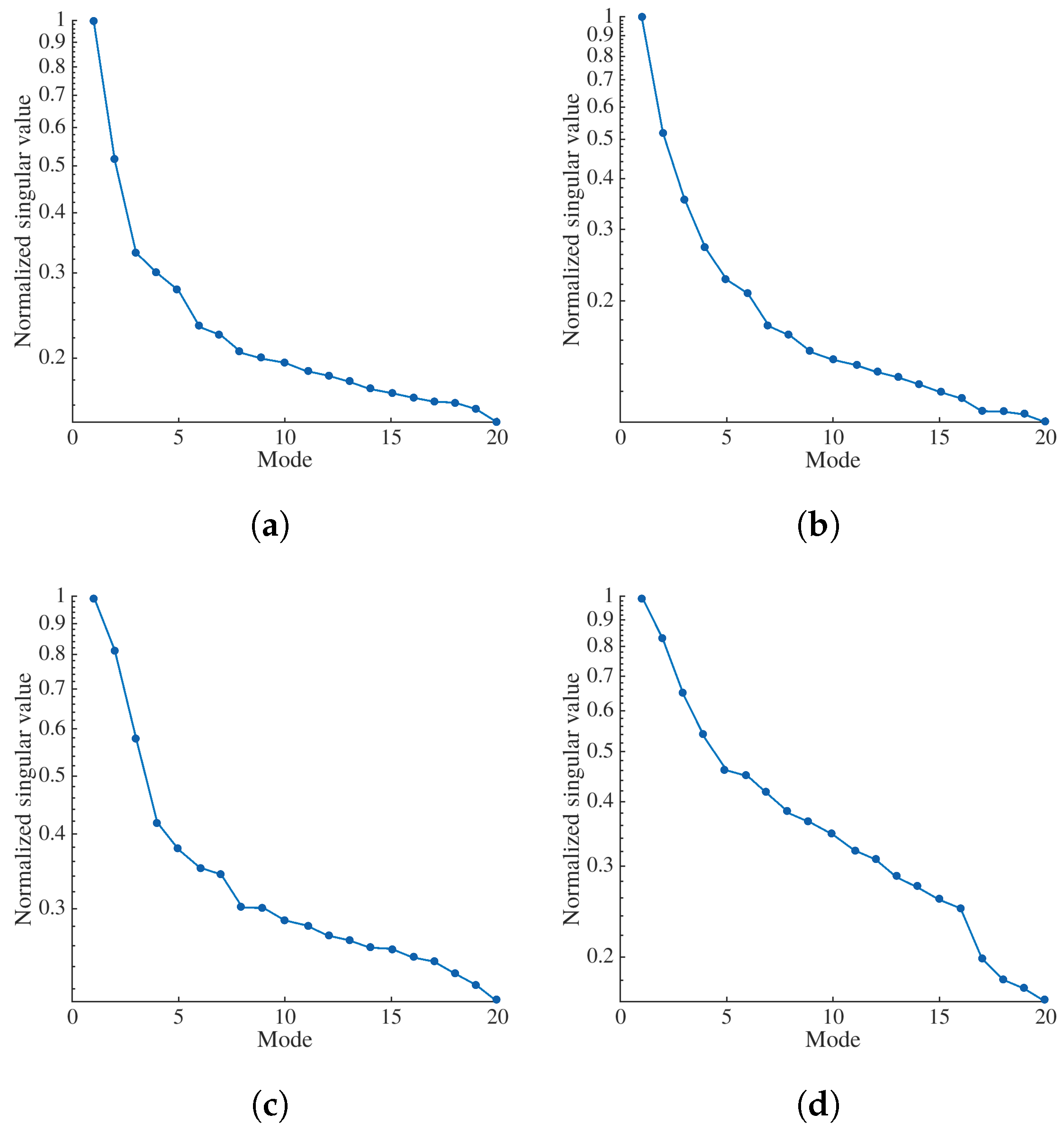
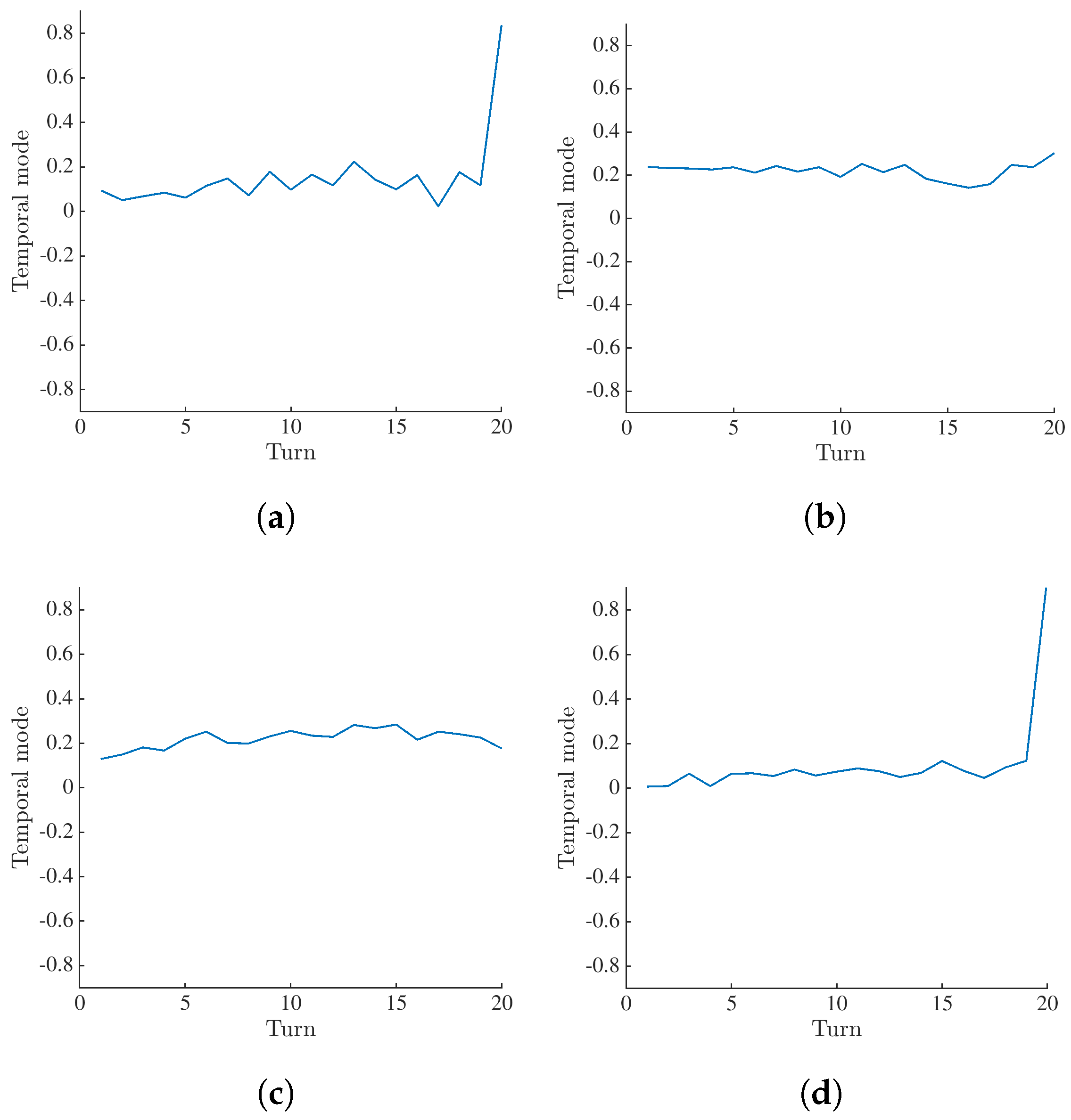
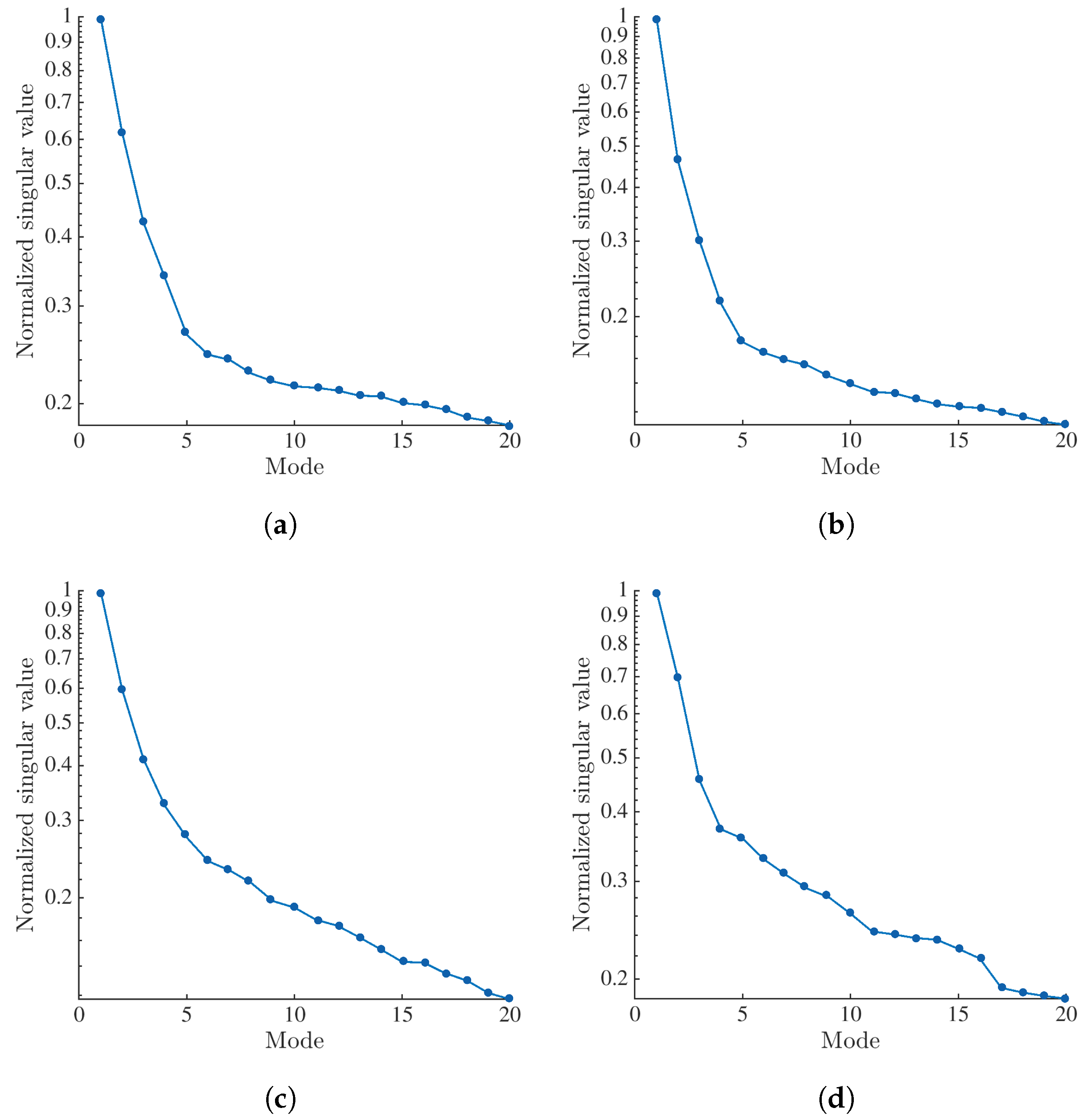
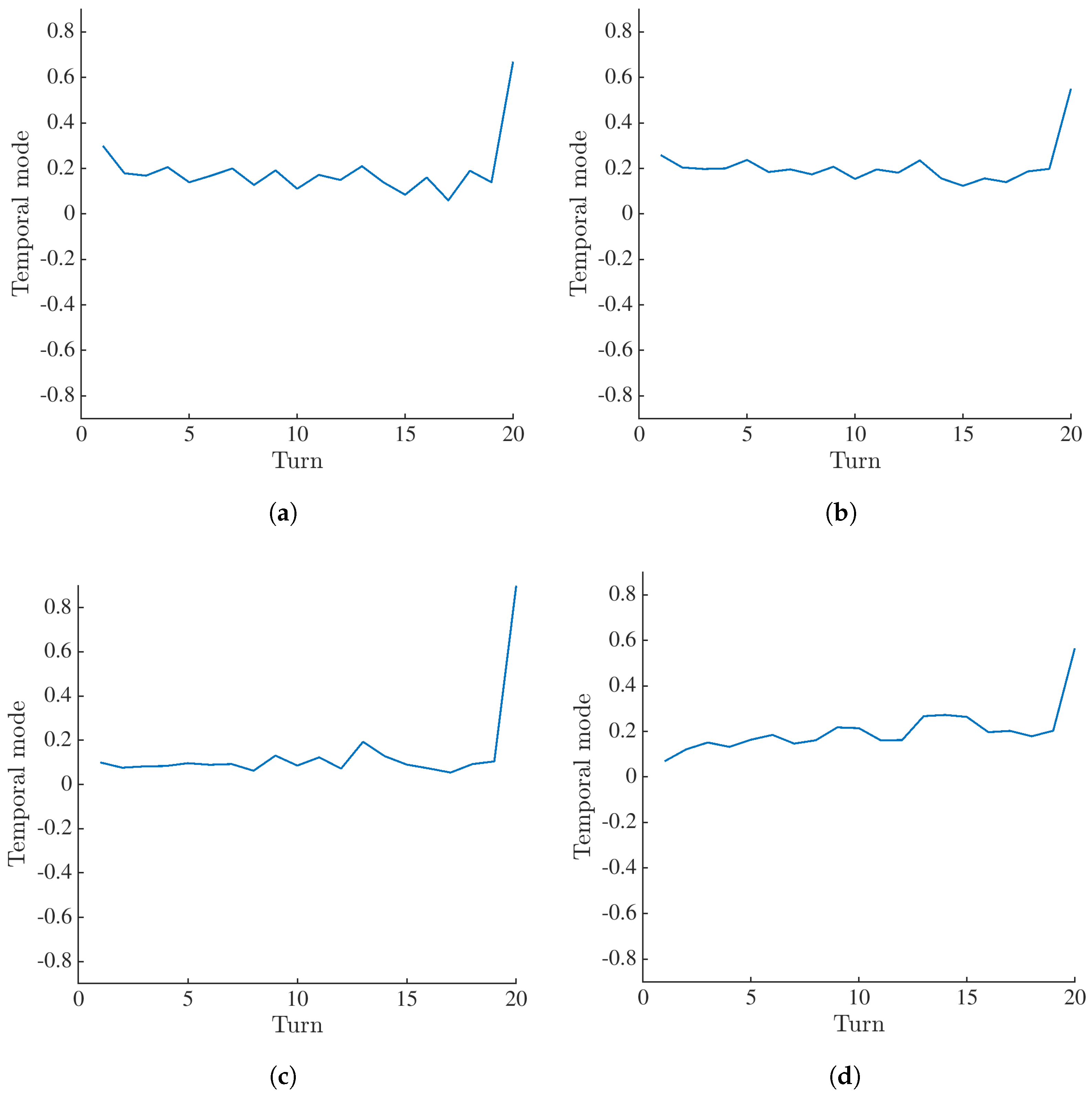
Appendix B. Selection of Temporal Bases
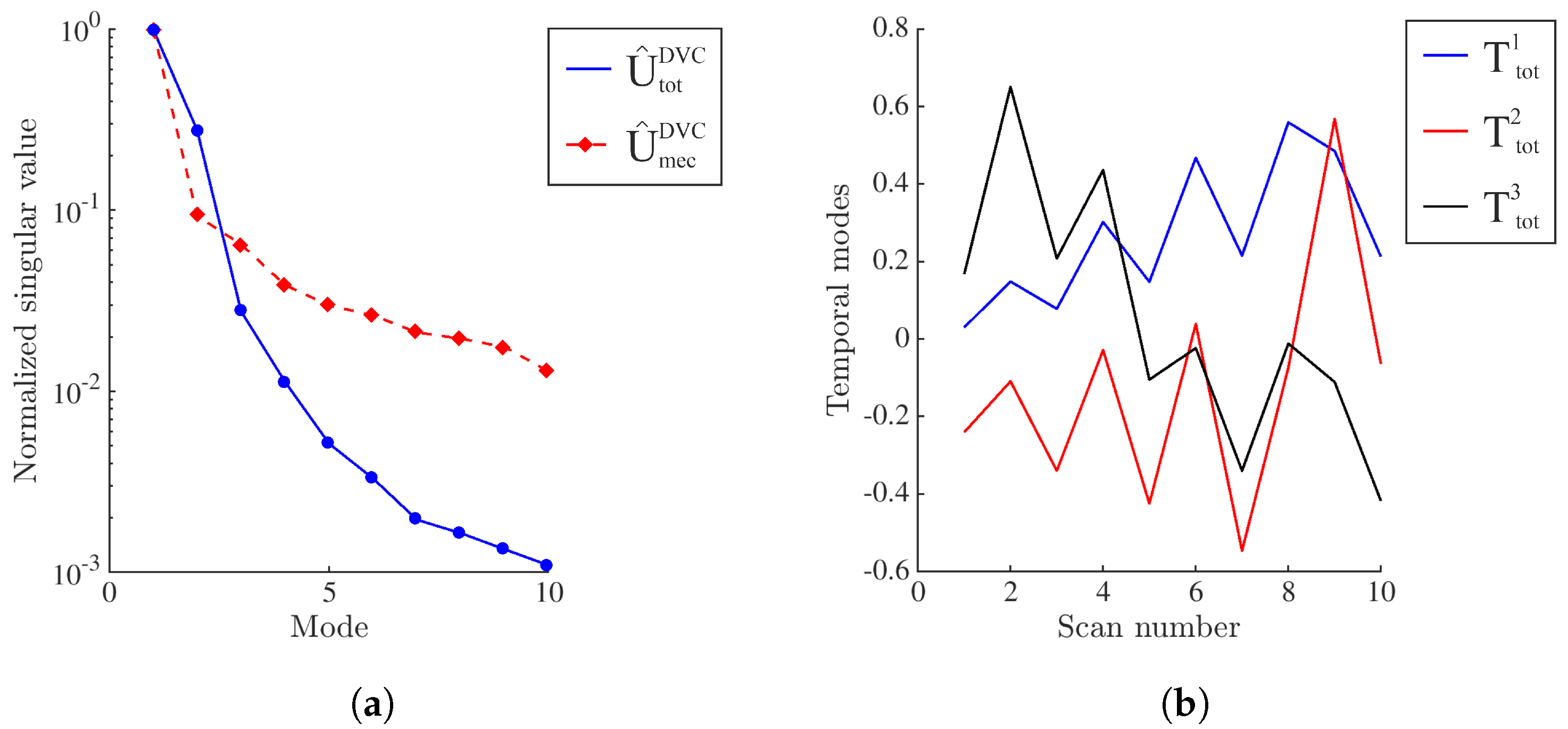
| x | y | z | |
|---|---|---|---|
| 1st mode | 0.34 | 0.08 | 0.09 |
| 2nd mode | 4.6 | 2.0 | 1.2 |
| 3rd mode | 4.4 | 2.7 | 7.8 |
| F | u | |||
|---|---|---|---|---|
| Scan | Mechanical State | |||
| 000 | Unloaded | 0.05 | 0.05 | 0.005 |
| 001 | Loaded | 0.81 | 0.05 | 0.007 |
| 002 | Unloaded | 0.35 | 0.06 | 0.01 |
| 003 | Loaded | 0.88 | 0.06 | 0.007 |
| 004 | Unloaded | 1.56 | 0.22 | 0.012 |
| 005 | Loaded | 0.73 | 0.08 | 0.002 |
| 006 | Unloaded | 2.77 | 0.3 | 0.011 |
| 007 | Loaded | 0.78 | 0.09 | 0.012 |
| 008 | Loaded | 0.76 | 0.08 | 0.011 |
| 009 | Unloaded | 3.76 | 0.25 | 0.011 |
| F | u | |||
|---|---|---|---|---|
| Scan | Mechanical State | |||
| 000 | Unloaded | 1.005 | ||
| 001 | Loaded | 1.007 | ||
| 002 | Unloaded | 0.983 | ||
| 003 | Loaded | 1.007 | ||
| 004 | Unloaded | 1.012 | ||
| 005 | Loaded | 1.002 | ||
| 006 | Unloaded | 0.998 | ||
| 007 | Loaded | 1.011 | ||
| 008 | Loaded | 1.006 | ||
| 009 | Unloaded | 0.996 | ||
| 007 * | Loaded | 1.206 | 1.197 | 1.128 |
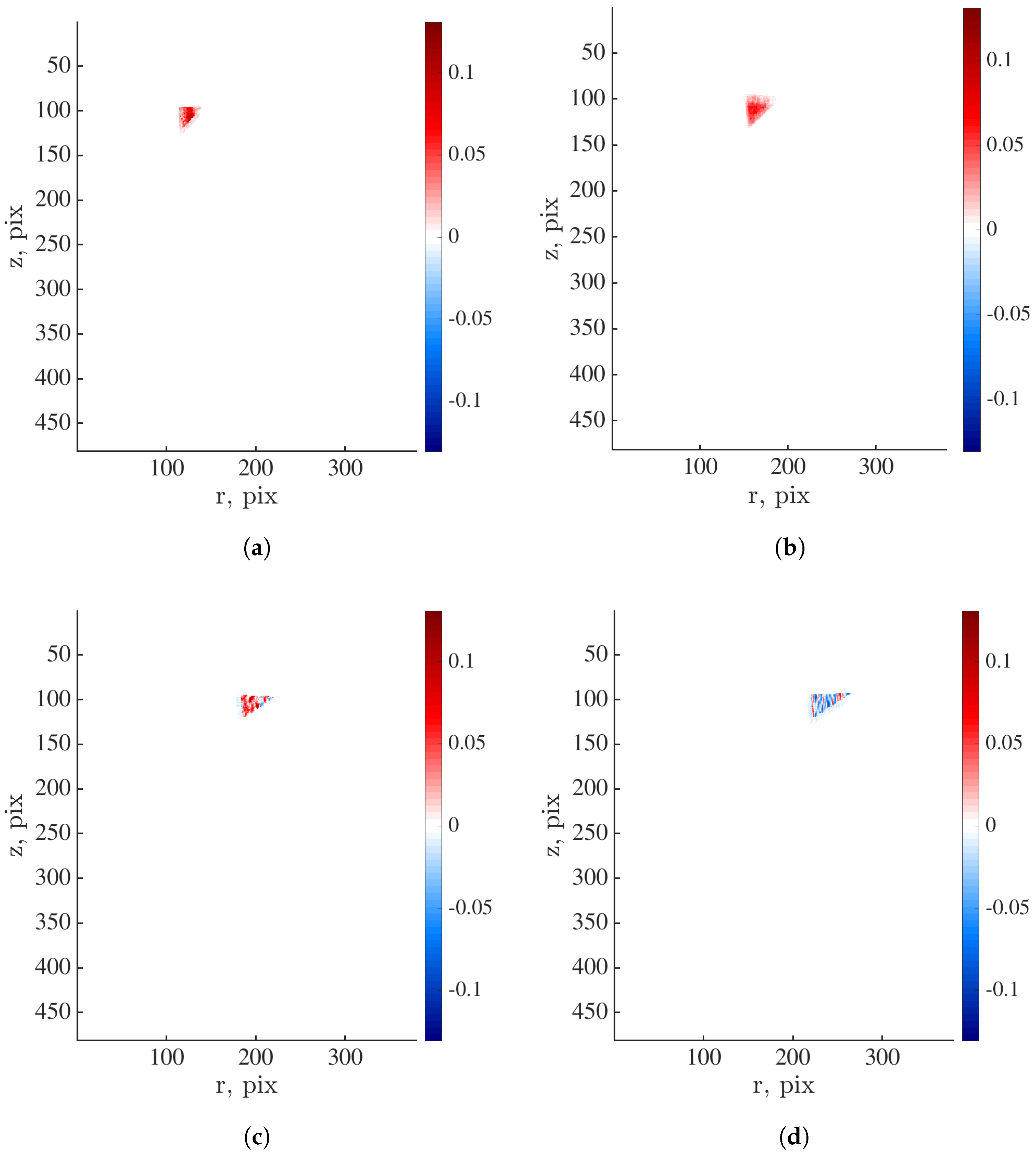
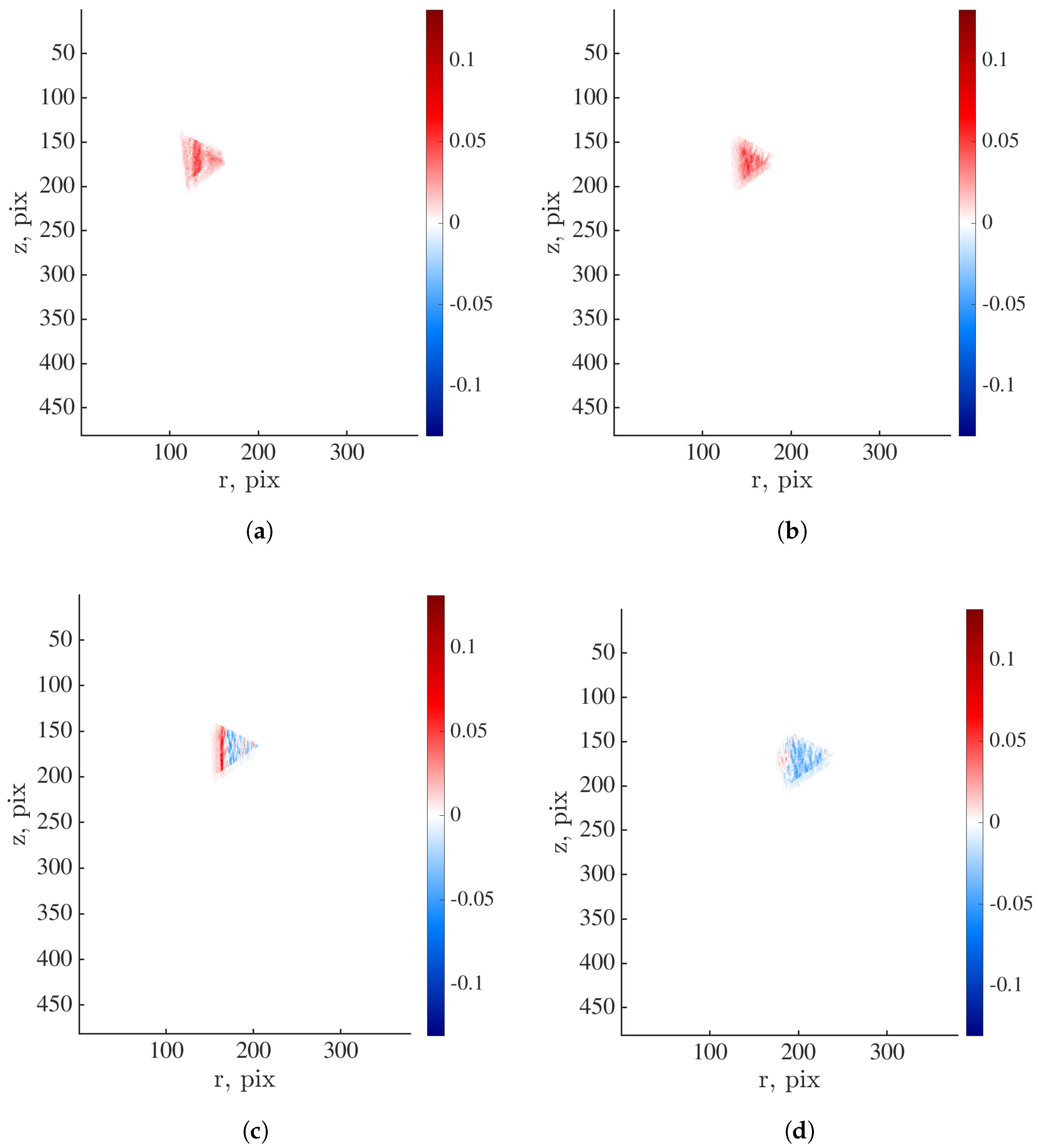
Appendix C. Validation of the Methodology for Quantification of Damage Growth


References
- Salvo, L.; Cloetens, P.; Maire, E.; Zabler, S.; Blandin, J.J.; Buffière, J.Y.; Ludwig, W.; Boller, E.; Bellet, D.; Josserond, C. X-ray micro-tomography an attractive characterisation technique in materials science. Nucl. Instrum. Methods Phys. Res. Sect.-Beam Interact. Mater. At. 2003, 200, 273–286. [Google Scholar] [CrossRef]
- Maire, E.; Buffière, J.Y.; Salvo, L.; Blandin, J.J.; Ludwig, W.; Létang, J.M. On the application of x-ray microtomography in the field of materials science. Adv. Eng. Mater. 2001, 3, 539–546. [Google Scholar] [CrossRef]
- Bay, B. Methods and applications of digital volume correlation. J. Strain Anal. 2008, 43, 745–760. [Google Scholar] [CrossRef]
- Buljac, A.; Jailin, C.; Mendoza, A.; Neggers, J.; Taillandier-Thomas, T.; Bouterf, A.; Smaniotto, B.; Hild, F.; Roux, S. Digital Volume Correlation: Review of Progress and Challenges. Exp. Mech. 2018, 58, 661–708. [Google Scholar] [CrossRef]
- Maire, E.; Bourlot, C.L.; Adrien, J.; Mortensen, A.; Mokso, R. 20 Hz X-ray tomography during an in situ tensile test. Int. J. Fract. 2016, 200, 3–12. [Google Scholar] [CrossRef]
- García-Moreno, F.; Kamm, P.H.; Neu, T.R.; Bülk, F.; Mokso, R.; Schlepütz, C.M.; Stampanoni, M.F.M.; Banhart, J. Using X-ray tomoscopy to explore the dynamics of foaming metal. Nat. Commun. 2019, 10, 3762. [Google Scholar] [CrossRef]
- Leclerc, H.; Roux, S.; Hild, F. Projection Savings in CT-based Digital Volume Correlation. Exp. Mech. 2015, 55, 275–287. [Google Scholar] [CrossRef]
- Jailin, C.; Bouterf, A.; Poncelet, M.; Roux, S. In situ μ CT-scan Mechanical Tests: Fast 4D Mechanical Identification. Exp. Mech. 2017, 57, 1327–1340. [Google Scholar] [CrossRef]
- Jailin, C.; Buljac, A.; Bouterf, A.; Hild, F.; Roux, S. Fast four-dimensional tensile test monitored via X-ray computed tomography: Single projection–based digital volume correlation dedicated to slender samples. J. Strain Anal. Eng. Des. 2018, 53, 473–484. [Google Scholar] [CrossRef]
- Prashanth, S.; Km, S.; Nithin, K.; Sachhidan, S. Fiber Reinforced Composites—A Review. J. Mater. Sci. Eng. 2017, 6, 1–6. [Google Scholar]
- Cosmi, F.; Ravalico, C. Threshold Identification for Micro-Tomographic Damage Characterisation in a Short-Fibre-Reinforced Polymer. Strain 2015, 51, 171–179. [Google Scholar] [CrossRef]
- Sket, F.; Enfedaque, A.; Lopez, C.D.; González, C.; Molina-Aldareguia, J.M.; Llorca, J. X-ray computed tomography analysis of damage evolution in open hole carbon fiber-reinforced laminates subjected to in-plane shear. Compos. Sci. Technol. 2016, 133, 40–50. [Google Scholar] [CrossRef]
- Rolland, H.; Saintier, N.; Wilson, P.; Merzeau, J.; Robert, G. In situ X-ray tomography investigation on damage mechanisms in short glass fibre reinforced thermoplastics: Effects of fibre orientation and relative humidity. Compos. Part B-Eng. 2017, 109, 170–186. [Google Scholar]
- Ortiz-Morales, A.M.; Hanhan, I.; Solano, J.J.; Sangid, M.D. Observing progressive damage in carbon fiber epoxy laminate composites via 3D in situ X-ray tomography. Eng. Fract. Mech. 2021, 246, 107626. [Google Scholar] [CrossRef]
- Buljac, A.; Navas, V.M.T.; Shakoor, M.; Bouterf, A.; Neggers, J.; Bernacki, M.; Bouchard, P.; Morgeneyer, T.; Hild, F. On the calibration of elastoplastic parameters at the microscale via X-ray microtomography and digital volume correlation for the simulation of ductile damage. Eur. J. Mech. A-Solids 2018, 72, 287–297. [Google Scholar] [CrossRef]
- Tomičević, Z.; Bouterf, A.; Surma, R.; Hild, F. Damage observation in glass fiber reinforced composites via μ-tomography. Mater. Today Proc. 2019, 12, 185–191. [Google Scholar] [CrossRef]
- Brault, R.; Germaneau, A.; Dupré, J.; Doumalin, P.; Mistou, S.; Fazzini, M. In-situ Analysis of Laminated Composite Materials by X-ray Micro-Computed Tomography and Digital Volume Correlation. Exp. Mech. 2013, 53, 1143–1151. [Google Scholar] [CrossRef]
- Croom, B.; Jin, H.; Mills, B.E.; Carroll, J.; Long, K.; Brown, J.A.; Li, X. Damage mechanisms in elastomeric foam composites: Multiscale X-ray computed tomography and finite element analyses. Compos. Sci. Technol. 2019, 169, 195–202. [Google Scholar] [CrossRef]
- Wang, K.; Pei, S.; Li, Y.; Li, J.; Zeng, D.; Su, X.; Xiao, X.; Chen, N. In-situ 3D fracture propagation of short carbon fiber reinforced polymer composites. Compos. Sci. Technol. 2019, 182, 107788. [Google Scholar]
- Roux, S.; Hild, F.; Viot, P.; Bernard, D. Three dimensional image correlation from X-ray computed tomography of solid foam. Compos. Part A-Appl. Sci. Manuf. 2008, 39, 1253–1265. [Google Scholar] [CrossRef]
- Réthoré, J.; Tinnes, J.; Roux, S.; Buffière, J.; Hild, F. Extended three-dimensional digital image correlation (X3D-DIC). Comptes Rendus Mécanique 2008, 336, 643–649. [Google Scholar] [CrossRef]
- Leclerc, H.; Périé, J.; Roux, S.; Hild, F. Voxel-scale digital volume correlation. Exp. Mech. 2011, 51, 479–490. [Google Scholar] [CrossRef]
- Réthoré, J.; Limodin, N.; Buffière, J.; Hild, F.; Ludwig, W.; Roux, S. Digital volume correlation analyses of synchrotron tomographic images. J. Strain Anal. Eng. Des. 2011, 46, 683–695. [Google Scholar] [CrossRef]
- Tomičević, Z.; Kodvanj, J.; Hild, F. Characterization of the nonlinear behavior of nodular graphite cast iron via inverse identification. Analysis of uniaxial tests. Eur. J. Mech.-A/Solids 2016, 59, 330–343. [Google Scholar] [CrossRef]
- Vrgoč, A.; Tomičević, Z.; Smaniotto, B.; Hild, F. Application of different imaging techniques for the characterization of damage in fiber reinforced polymer. Compos. Part A Appl. Sci. Manuf. 2021, 150, 106576. [Google Scholar] [CrossRef]
- Maurer, J.; Jerabek, M.; Salaberger, D.; Thor, M.; Kastner, J.; Major, Z. Stress relaxation behaviour of glass fibre reinforced thermoplastic composites and its application to the design of interrupted in situ tensile tests for investigations by X-ray computed tomography. Polym. Test. 2022, 109, 107551. [Google Scholar] [CrossRef]
- Vrgoč, A.; Tomičević, Z.; Smaniotto, B.; Hild, F. Characterization of glass fiber reinforced polymer via Digital Volume Correlation: Investigation of notch sensitivity. Mech. Mater. 2023, 177, 104552. [Google Scholar] [CrossRef]
- Kosin, V.; Fau, A.; Jailin, C.; Smaniotto, B.; Wick, T.; Hild, F. A projection-based approach to extend digital volume correlation for 4D spacetime measurements. Comptes Rendus Mécanique 2023, 351, 265–280. [Google Scholar] [CrossRef]
- Leclerc, H.; Neggers, J.; Mathieu, F.; Hild, F.; Roux, S. Correli 3.0; IDDN.FR.001.520008.000.S.P.2015.000.31500; Agence de Protection des Programmes: Paris, France, 2015. [Google Scholar]
- Van Aarle, W.; Palenstijn, W.J.; De Beenhouwer, J.; Altantzis, T.; Bals, S.; Batenburg, K.J.; Sijbers, J. The ASTRA Toolbox: A platform for advanced algorithm development in electron tomography. Ultramicroscopy 2015, 157, 35–47. [Google Scholar] [CrossRef]
- Kak, A.; Slaney, M. Principles of Computerized Tomographic Imaging; IEEE Press: New York, NY, USA, 1988. [Google Scholar]
- Jailin, C.; Buljac, A.; Bouterf, A.; Poncelet, M.; Hild, F.; Roux, S. Self-calibration for lab-μCT using space-time regularized projection-based DVC and model reduction. Meas. Sci. Technol. 2018, 29, 024003. [Google Scholar] [CrossRef]
- Hallo, G.; Lacombe, C.; Parreault, R.; Roquin, N.; Donval, T.; Lamaignère, L.; Néauport, J.; Hild, F. Sub-pixel detection of laser-induced damage and its growth on fused silica optics using registration residuals. Opt. Express 2021, 29 22, 35820–35836. [Google Scholar] [CrossRef]
- Vrgoč, A.; Tomičević, Z.; Smaniotto, B.; Hild, F. Characterization of glass fiber reinforced polymer via digital volume correlation: Quantification of strain activity and damage growth. Compos. Sci. Technol. 2023, 234, 109932. [Google Scholar] [CrossRef]



| Scan | Mechanical State | |
|---|---|---|
| 000 | Unloaded | 1.005 |
| 001 | Loaded | 1.007 |
| 002 | Unloaded | 0.983 |
| 003 | Loaded | 1.007 |
| 004 | Unloaded | 1.012 |
| 005 | Loaded | 1.002 |
| 006 | Unloaded | 0.998 |
| 007 | Loaded | 1.011 |
| 008 | Loaded | 1.006 |
| 009 | Unloaded | 0.996 |
| 007 * | Loaded | 1.128 |
| Scan | Mechanical State | z |
|---|---|---|
| 000 | Unloaded | 0.005 |
| 001 | Loaded | 0.007 |
| 002 | Unloaded | 0.01 |
| 003 | Loaded | 0.007 |
| 004 | Unloaded | 0.012 |
| 005 | Loaded | 0.002 |
| 006 | Unloaded | 0.011 |
| 007 | Loaded | 0.012 |
| 008 | Loaded | 0.011 |
| 009 | Unloaded | 0.011 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mandić, A.; Kosin, V.; Jailin, C.; Tomičević, Z.; Smaniotto, B.; Hild, F. Damage Detection in a Polymer Matrix Composite from 4D Displacement Field Measurements. Materials 2023, 16, 6300. https://doi.org/10.3390/ma16186300
Mandić A, Kosin V, Jailin C, Tomičević Z, Smaniotto B, Hild F. Damage Detection in a Polymer Matrix Composite from 4D Displacement Field Measurements. Materials. 2023; 16(18):6300. https://doi.org/10.3390/ma16186300
Chicago/Turabian StyleMandić, Ana, Viktor Kosin, Clément Jailin, Zvonimir Tomičević, Benjamin Smaniotto, and François Hild. 2023. "Damage Detection in a Polymer Matrix Composite from 4D Displacement Field Measurements" Materials 16, no. 18: 6300. https://doi.org/10.3390/ma16186300
APA StyleMandić, A., Kosin, V., Jailin, C., Tomičević, Z., Smaniotto, B., & Hild, F. (2023). Damage Detection in a Polymer Matrix Composite from 4D Displacement Field Measurements. Materials, 16(18), 6300. https://doi.org/10.3390/ma16186300







