An Analysis of the Vibration Transmission Properties of Assemblies Using Honeycomb Paperboard and Expanded Polyethylene
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
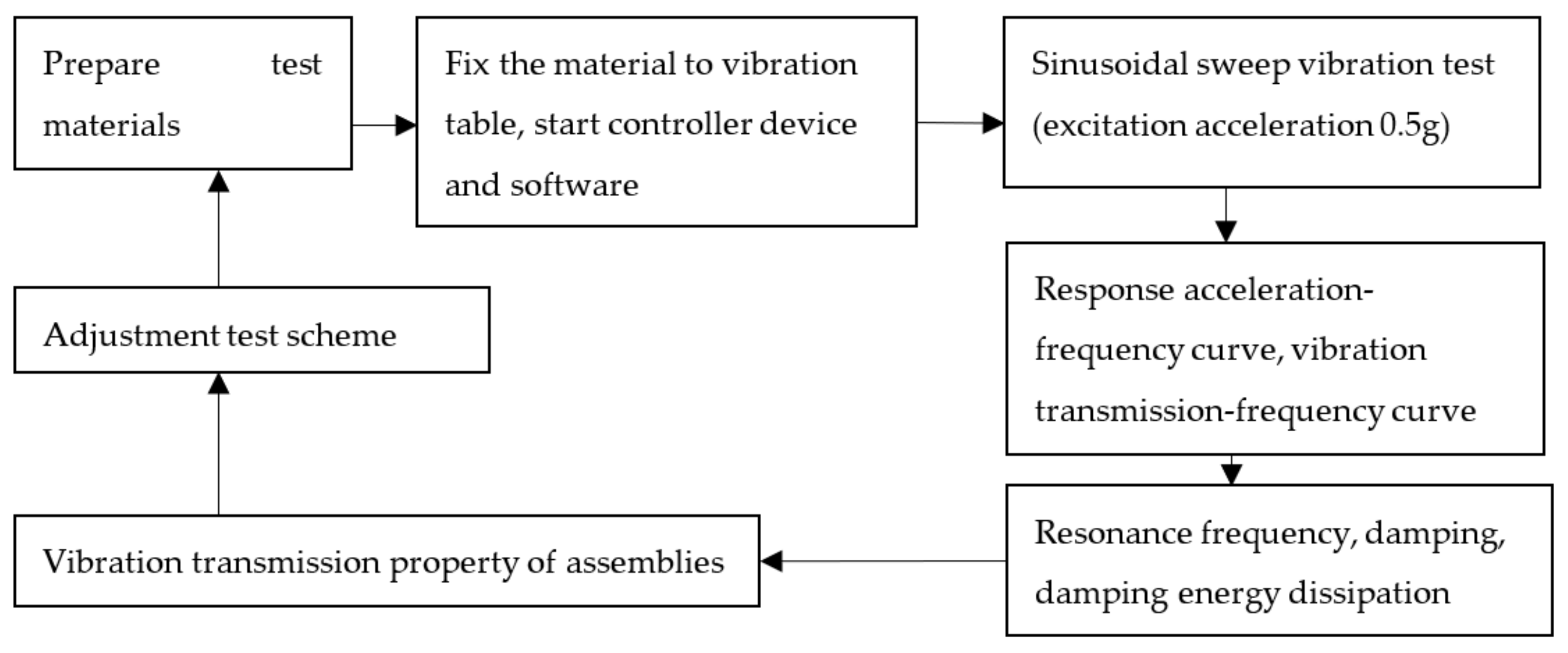
2.2. Vibration Test Equipment and Method
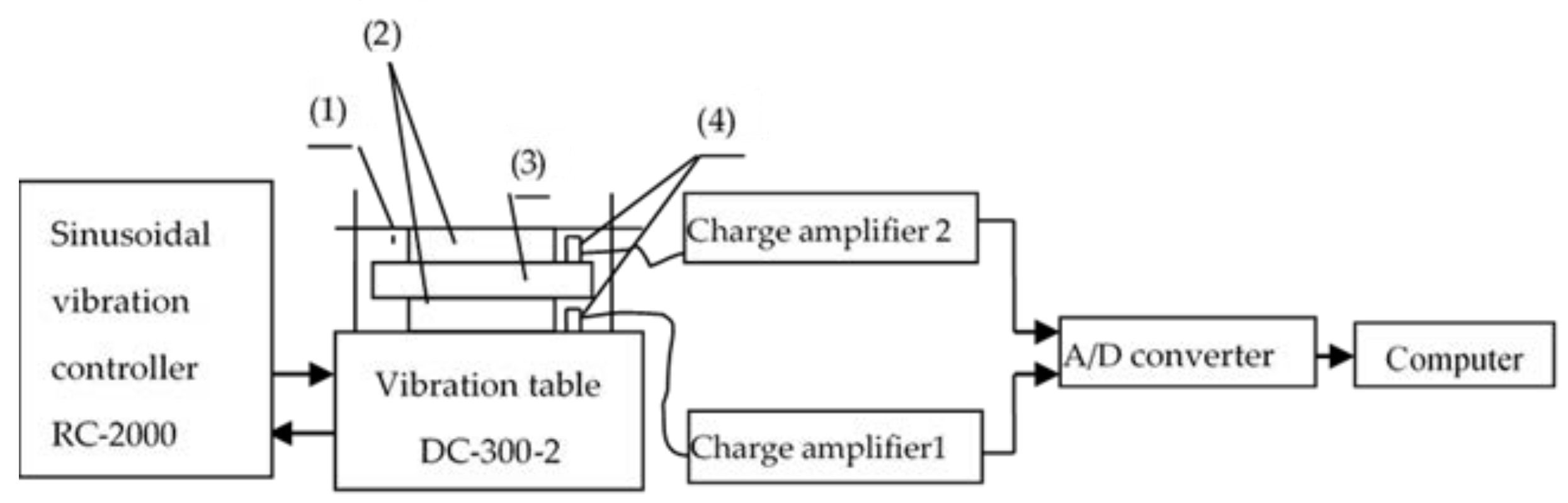
2.3. Vibration Test System
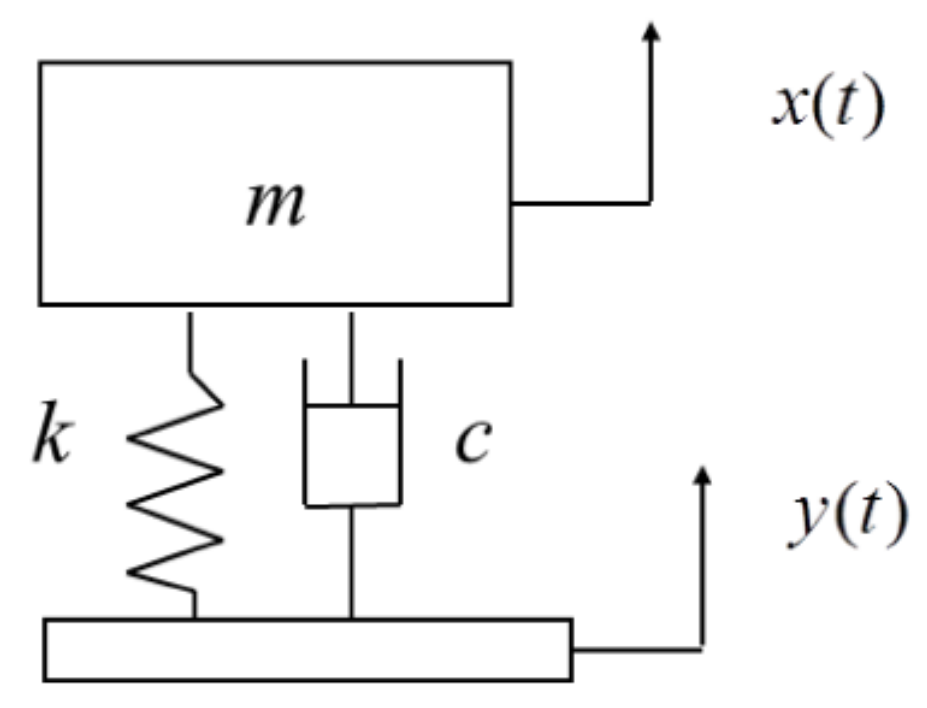
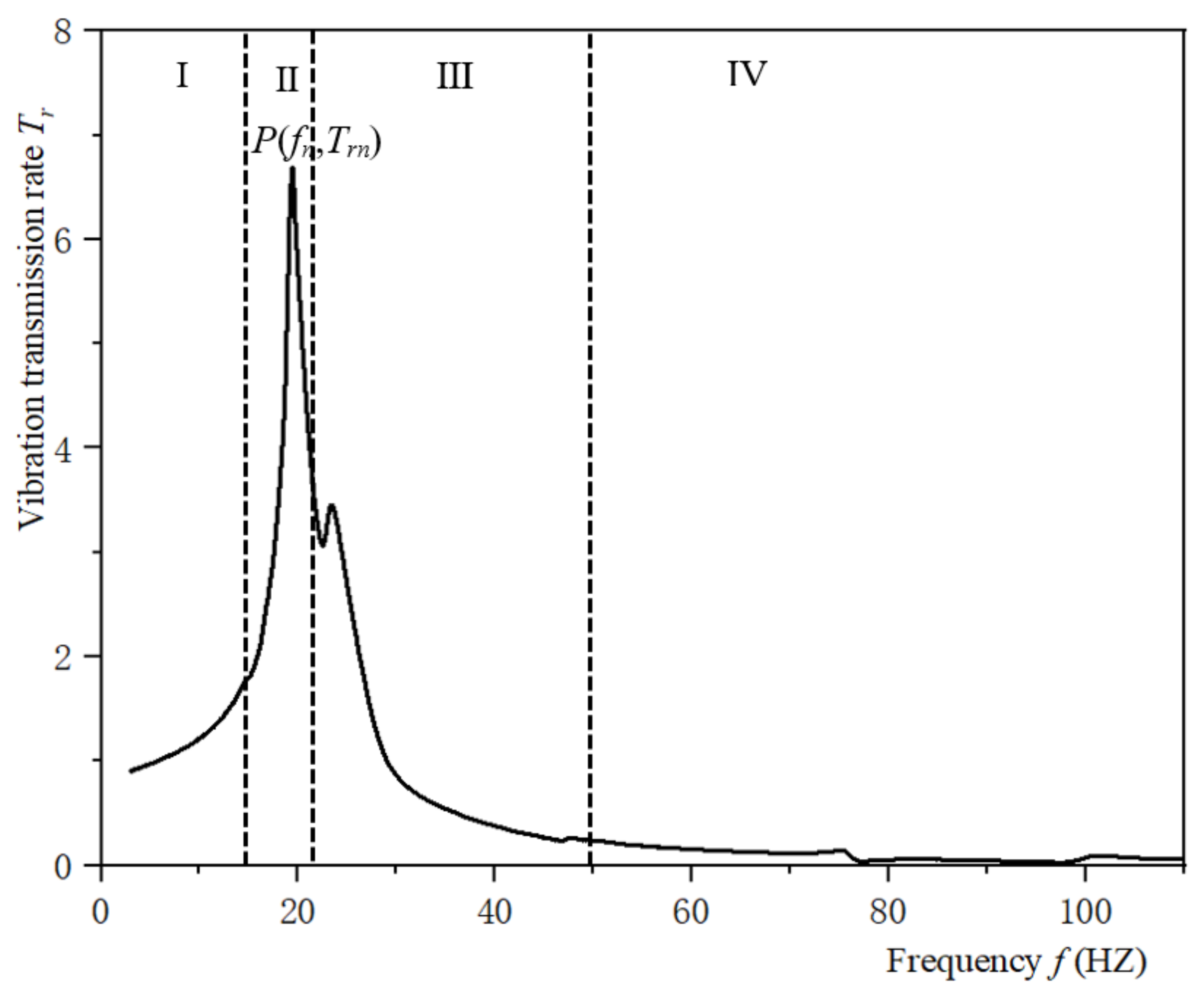
2.4. Vibration Property Criteria
3. Results
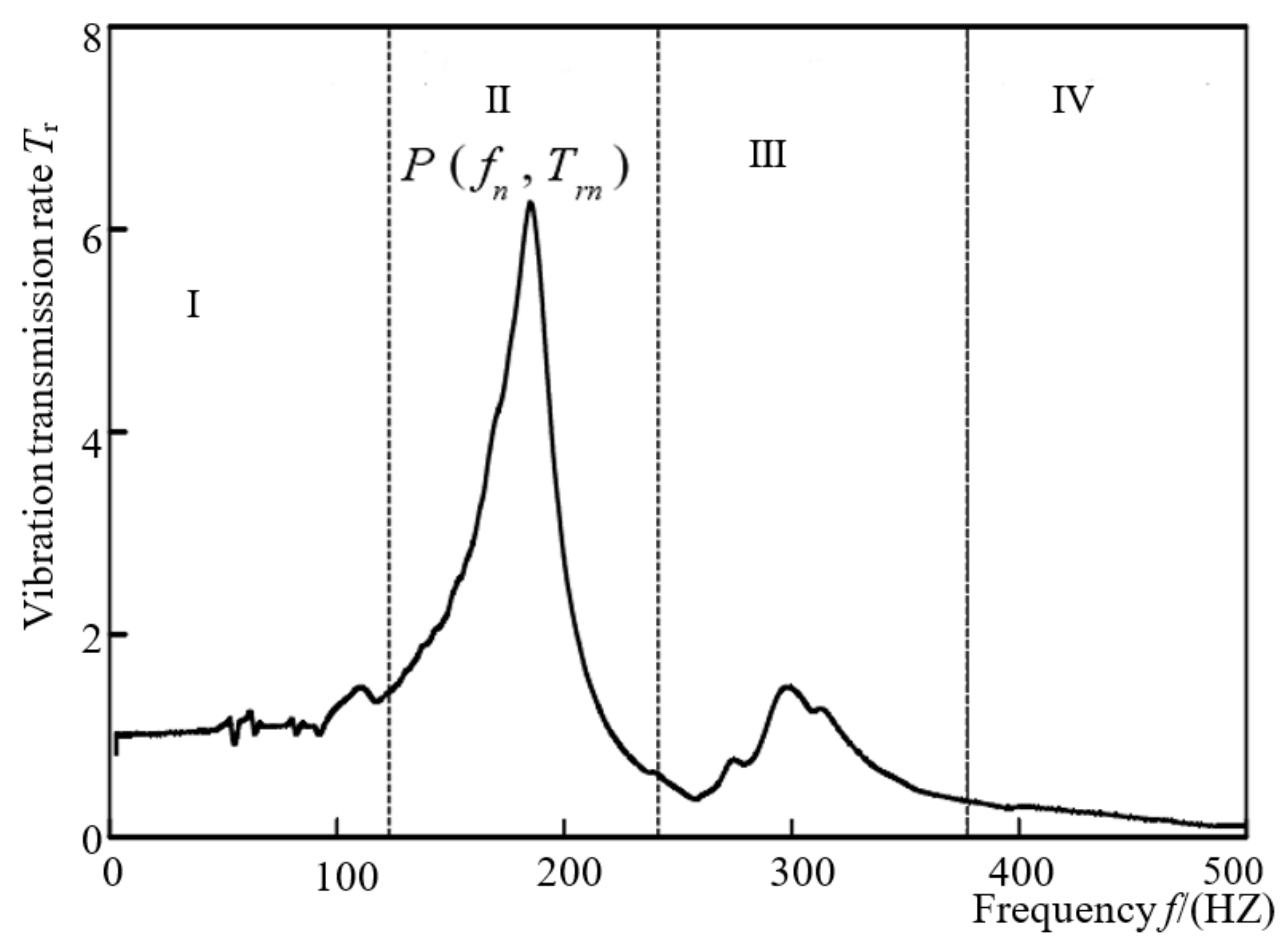
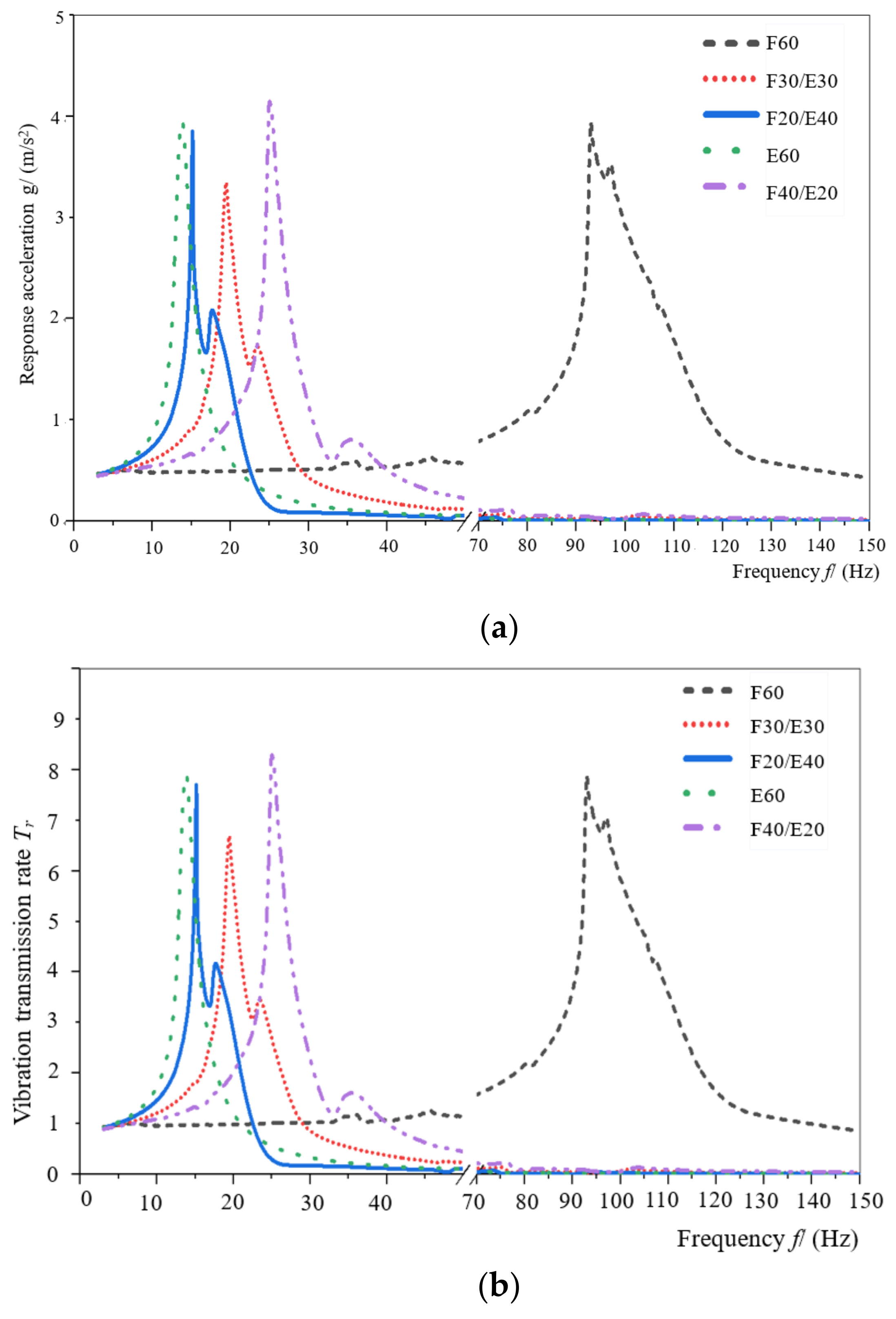
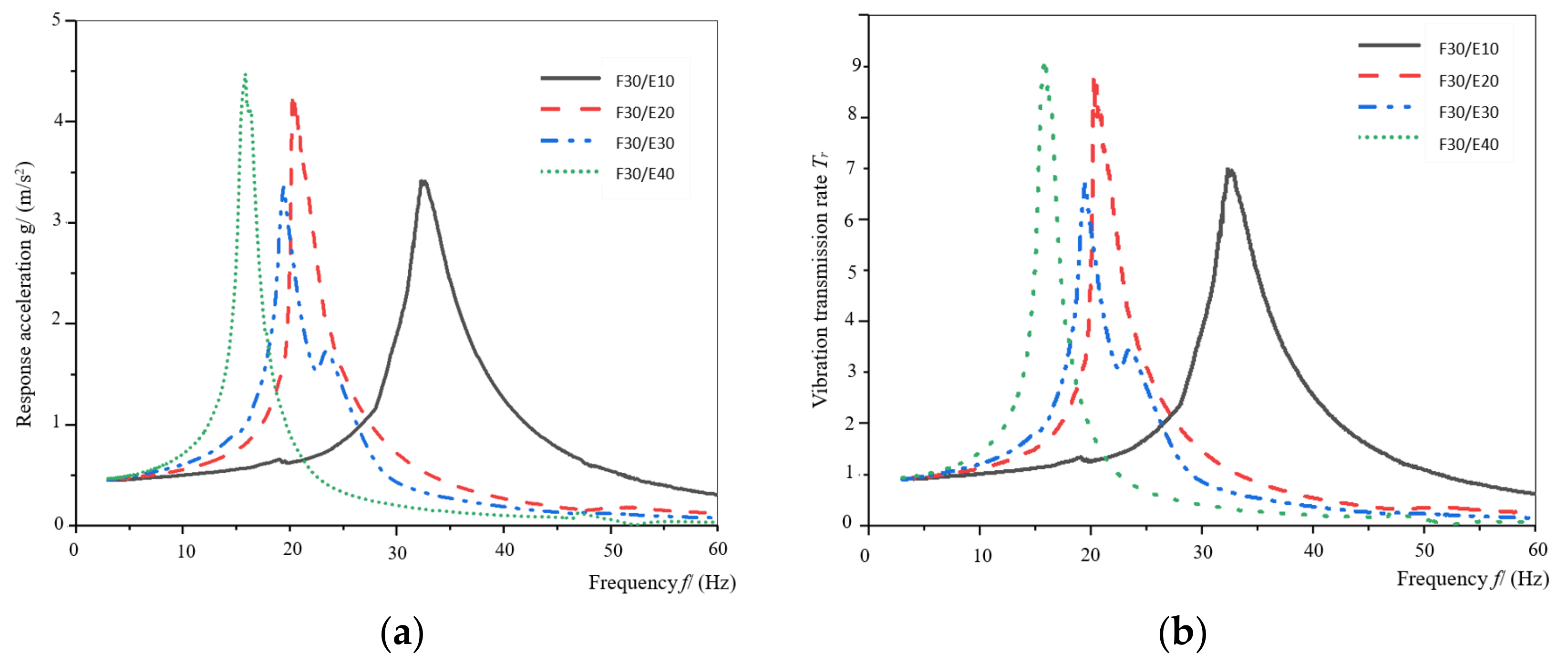
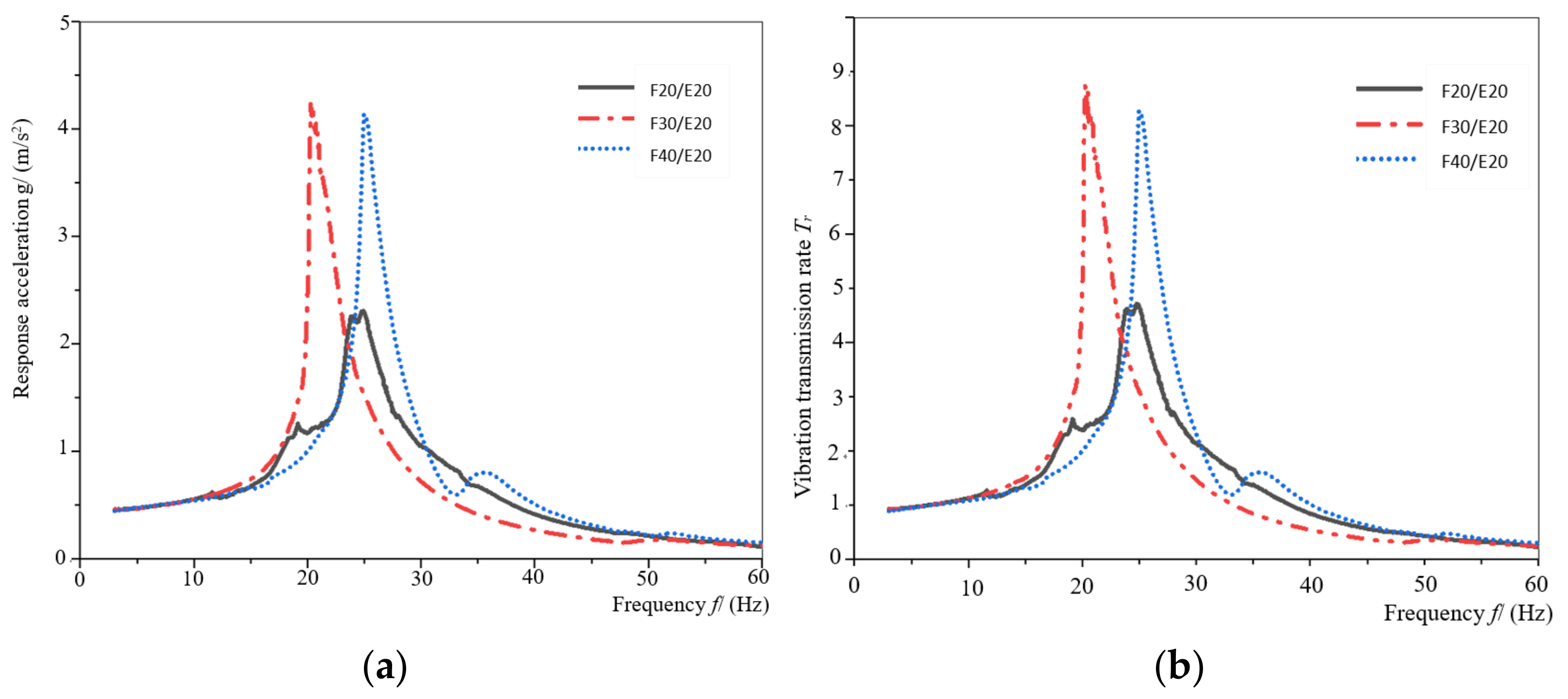
3.1. Response Acceleration and Vibration Transmission Property Curve
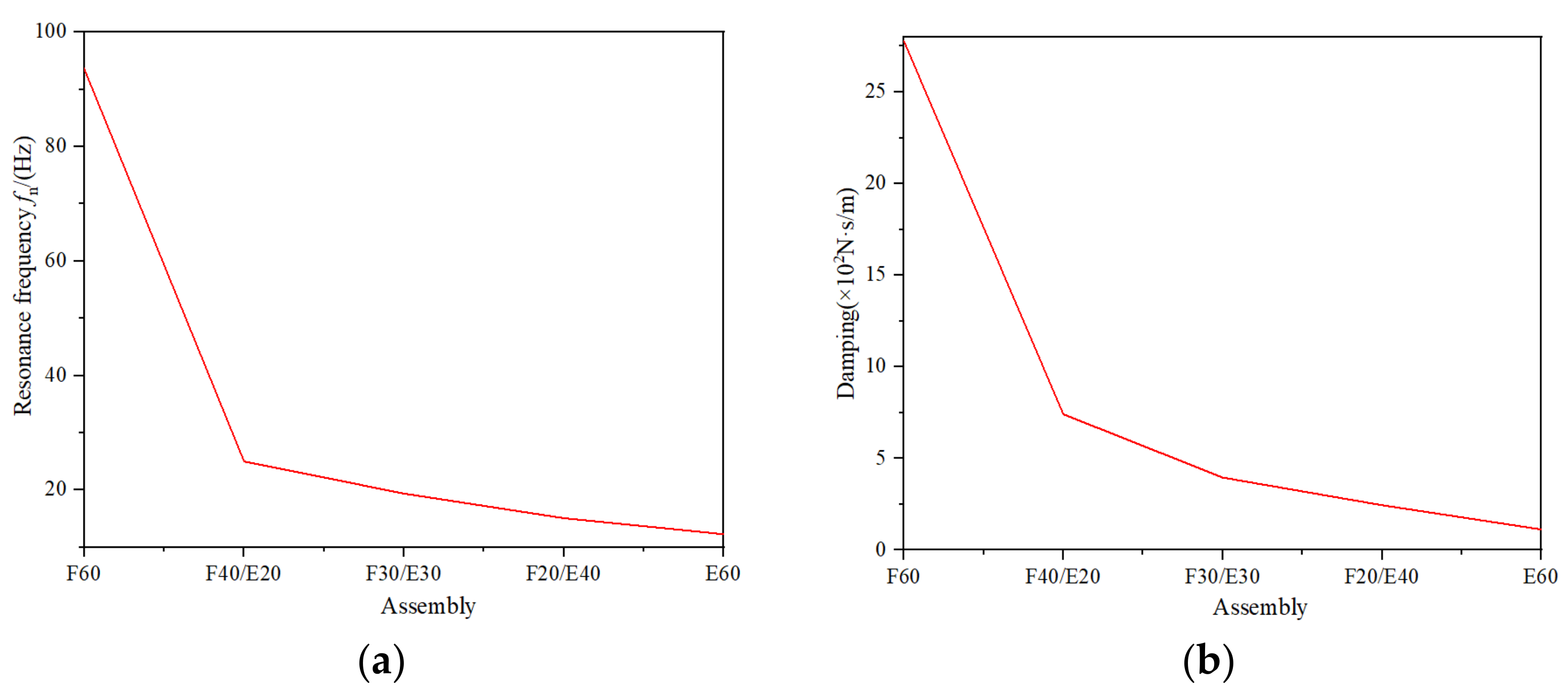
3.2. Analysis of Damping Performance of Assemblies
3.3. Damping Energy Dissipation
4. Discussion
5. Conclusions
- (1)
- The obtained vibration transmission rate curve shows that the assembly generally has four stages, according to the frequency range. In the amplification region, the acceleration transmitted to the product will be multiplied by several times, especially at the resonance frequency, and the product is likely to be damaged. In the attenuation region, the protective ability for the product is better, and the response acceleration to the product is small.
- (2)
- When the aperture of honeycomb paperboard and the density of EPE were constant, the vibration transmission rate and damping energy dissipation of different assemblies were studied. Among all the assemblies, the assembly of F30/E30 had better damping energy dissipation and a lower vibration transmission rate. In the cushioning packaging design, it can be assumed that a thickness of the honeycomb paperboard and EPE are equal; then, the assembly has a lower vibration transmission rate and greater damping energy dissipation, which can minimize the maximum acceleration value transmitted to the internal product and protect the product from being damaged.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Tr-f | the vibration transmission rate-frequency |
| EPP | expanded polypropylene |
| EVA | ethylene vinyl acetate |
| Wc | damping energy dissipation |
| F60 | honeycomb paperboard with a thickness of 60 mm |
| E60 | EPE with a thickness of 60 mm |
| F30/E30 | assembly with a thickness of 30 mm for honeycomb paperboard and a thickness of 30 mm for EPE |
| F20/E40 | assembly with a thickness of 20 mm for honeycomb paperboard and a thickness of 40 mm for EPE |
| F40/E20 | assembly with a thickness of 40 mm for honeycomb paperboard and a thickness of 20 mm for EPE |
| F20/E20 | assembly with a thickness of 20 mm for honeycomb paperboard and a thickness of 20 mm for EPE |
References
- Gao, D. Packaging of Applied Mechanics, 1st ed.; Chinese Light Industry Press: Beijing, China, 2013. [Google Scholar]
- Peng, G. Logistics Transportation Packaging Design, 2nd ed.; Printing Industry Press: Beijing, China, 2012. [Google Scholar]
- Nikbakt, S.; Kamarian, S.; Shakeri, M. A review on optimization of composite structures Part I: Laminated composites. Compos. Struct. 2018, 195, 158–185. [Google Scholar] [CrossRef]
- Birman, V.; Kardomateas, G.A. Review of current trends in research and applications of sandwich structures. Compos. Part B Eng. 2018, 142, 221–240. [Google Scholar] [CrossRef]
- Sun, Y.L.; Li, Q.M. Dynamic compressive behavior of cellular materials: A review of phenomenon, mechanism and modeling. Int. J. Impact Eng. 2018, 112, 74–115. [Google Scholar] [CrossRef]
- Jing, L.; Wang, Z.; Zhao, L. Research progress on mechanical properties of porous metal and its sandwich structures. Mech. Pract. 2015, 37, 1–24. [Google Scholar]
- Du, S.; Guo, Y.; Wang, D. Research on Applicability of equivalent model of Honeycomb paperboard considering Structural factors. J. Vib. Meas. Diagn. 2019, 43, 31–36. [Google Scholar]
- Yuping, E.; Wang, Z. Research progress on energy absorption characteristics of paper cushioning materials. J. Vib. Shock. 2010, 29, 40–45. [Google Scholar]
- Wang, Z.; Wang, L.; Xu, C. Effect of multiple low strength impact on buffering properties of honeycomb paperboard. Appl. Mech. J. Sci. 2015, 32, 441–445. [Google Scholar]
- Abd Kadir, N.; Aminanda, Y.; Ibrahim, M.S.; Mokhtar, H. Experimental study on energy absorption of foam filled Kraft paper honeycomb subjected to quasi-static uniform compression loading. IOP Conf. Ser. Mater. Sci. Eng. 2016, 152, 12048. [Google Scholar] [CrossRef]
- Guo, Y.F.; Becker, W.; Xu, W.C. Vertical static compression performance of honeycomb. Int. J. Mater. Res. 2013, 104, 598–602. [Google Scholar] [CrossRef]
- Song, J. Research on the Linearization Method of Dynamic Characteristics of Drop Shock of Nonlinear Buffer Packaging System. Ph.D. Thesis, Jiangnan University, Wuxi, China, 2021. [Google Scholar]
- Yang, F.-y.; Li, Z.-j.; Liu, Z.-l.; Zhuang, Z. Shock Loading Mitigation Performance and Mechanism of the PE/Wood/PU/Foam Structures. Int. J. Impact Eng. 2021, 155, 103904. [Google Scholar] [CrossRef]
- Feng, Y. Comparison and Analysis for Double Direction Performances of EPE Cushioning Materials. China Packag. Ind. 2007, 10, 47–48. [Google Scholar]
- Zhang, Y.; Rodrigue, D.; Ait-Kadi, A. High density polyethylene foams. II. Elastic modulus. JAPS 2003, 90, 2120–2129. [Google Scholar] [CrossRef]
- Ramírez-Arreola, D.E.; Sedano-de la Rosa, C.; Haro-Mares, N.B.; Ramírez-Morán, J.A.; Pérez-Fonseca, A.A.; Robledo-Ortíz, J.R. Compressive strength study of cement mortars lightened with foamed HDPE nanocomposites. Mater. Design 2015, 74, 119–124. [Google Scholar] [CrossRef]
- Guo, Y.; Zhu, D.; Chen, X.; Sun, D.; Zhang, J. Test and Analysis of Vibration Transmission Characteristics of Honeycomb paperboard. Packag. Eng. 2003, 24, 12–13. [Google Scholar]
- Guo, Y.F.; Zhang, J.H. Shock Absorbing Characteristics and Vibration Transmissibility of Honeycomb Paperboard. Shock Vib. 2004, 11, 521–531. [Google Scholar] [CrossRef]
- Zhang, J. Research and Application on anti-vibration buffering characteristics of Honeycomb paperboard. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China, 2004. [Google Scholar]
- Park, J.; Kim, G.; Kim, H.; Kwon, S.; Mitusoka, M.; Inoue, E.; Okayasu, T. Characteristics of Vibration Transmissibility for Corrugated Paperboard. J. Fac. Agric. Kyushu Univ. 2011, 56, 327–333. [Google Scholar] [CrossRef]
- Xing, Y.-Q.; Sun, D.-Q.; Fang, J. Data processing of Vibration transfer Characteristics Test System of Buffer Materials. Packag. Eng. 2015, 36, 77–82. [Google Scholar]
- Liang, N. Study on Vibration Transfer Characteristics and Energy Dissipation Model of Honeycomb Paperboard. Ph.D. Thesis, Xi ’an University of Technology, Xi′an, China, 2019. [Google Scholar]
- Gong, G.; Li, C. Experimental study on vibration transmission characteristics of cylindrical air gaskets. Packag. Eng. 2019, 40, 92–96. [Google Scholar]
- Xing, Y.; Sun, D.; Zhang, M.; Shu, G. Crushing responses of expanded polypropylene foam. Polymers 2023, 15, 2059. [Google Scholar] [CrossRef]
- Xing, Y.; Guo, X.; Shu, G.; He, X. Dynamic Crushing Behavior of Ethylene Vinyl Acetate Copolymer Foam Based on Energy Method. Polymers 2023, 15, 3016. [Google Scholar] [CrossRef]
- Wang, Z.W.; Wang, J. Inverse substructure method of three-substructure coupled system and its application in product-transport-system. J. Vib. Control 2011, 6, 943–952. [Google Scholar] [CrossRef]
- Wang, Z.W.; Zhang, Y.B. Dynamic characteristic analysis of refrigerator-truck transport system by using inverse substructure method. Packag. Technol. Sci. 2015, 27, 883–900. [Google Scholar] [CrossRef]
- Matter, M.; Gmür, T.; Cugnoni, J.; Schorderet, A. Identification of the elastic and damping properties in sandwich structures with a low core-to-skin stiffness ratio. Compos. Struct. 2011, 93, 331–341. [Google Scholar] [CrossRef]
- Tsai, J.L.; Chang, N.R. Investigating damping properties of nanocomposites and sandwich structures with nanocomposites as core materials. J. Compos. Mater. 2011, 45, 2157–2164. [Google Scholar] [CrossRef]
- Wei, C.Y.; Kukureka, S.N. Evaluation of damping and elastic properties of composites and composite structures by the resonance technique. J. Mater. Sci. 2000, 35, 3785–3792. [Google Scholar] [CrossRef]
- Shan, J. Packaging Test Technology, 2nd ed.; Printing Industry Press: Beijing, China, 2013. [Google Scholar]
- GB 8169-2008; Testing Method of Vibration Transmissibility for Packaging Cushioning Materials. Standards Press of China: Beijing, China, 2009; pp. 1–3.
- Fu, Y. Study on Vibration Transmission Characteristics of Double-Corrugated Cardboard. Ph.D. Thesis, Xi’an University of Technology, Xi′an, China, 2005. [Google Scholar]
- Yang, R. Study on the Influence of Relative Humidity on Vibration Transmissibility and Vibration Reduction Characteristics of Honeycomb Paperboard. Ph.D. Thesis, Xi’an University of Technology, Xi′an, China, 2019. [Google Scholar]
- Li, A. Study on External Load Bearing Performance of a New Type of Honeycomb Core Layer Paper Board. Ph.D. Thesis, Jiangnan University, Wuxi, China, 2022. [Google Scholar]
- Du, S. Research on Damping Characteristics and Energy Transfer Model of Honeycomb Paperboard. Ph.D. Thesis, Xi’an University of Technology, Xi′an, China, 2021. [Google Scholar]

| Specimen | Specimen Size (mm × mm) | Thickness of Honeycomb Paperboard (mm) | Thickness of EPE (mm) | Aperture of Honeycomb Paperboard (mm) | Density of EPE (kg/m3) |
|---|---|---|---|---|---|
| F60 | 100 × 100 | 60 | 6 | ||
| E60 | 100 × 100 | 60 | 15.3 | ||
| F30/E30 | 100 × 100 | 30 | 30 | 6 | 15.3 |
| F20/E20 | 100 × 100 | 20 | 20 | 6 | 15.3 |
| F20/E40 | 100 × 100 | 20 | 40 | 6 | 15.3 |
| F40/E20 | 100 × 100 | 40 | 20 | 6 | 15.3 |
| Sweep Frequency Speed (oct/min) | Sweep Frequency Range (HZ) | Target Spectral Acceleration Peak (m/s2) | Frequency Sweep Mode | Control Sensor Sensitivity (V/g) | Monitoring Sensor Sensitivity (V/g) |
|---|---|---|---|---|---|
| 0.5 oct/min | 3–150 Hz | 0.5 g | logarithm | 24.50 V/g | 24.40 V/g |
| Specimen | Resonance Frequency fn/(Hz) | Maximum Vibration Transmission Rate Tr | Damping Ratio ξ | Damping c/(N·s/m) | Wc/(J) |
|---|---|---|---|---|---|
| F60 | 93.6 | 7.89 | 0.06 | 2776.4 | 0.06 |
| F40/E20 | 25.0 | 8.29 | 0.07 | 741.8 | 0.99 |
| F30/E30 | 19.4 | 7.00 | 0.07 | 396.7 | 1.75 |
| F20/E40 | 15.1 | 7.84 | 0.06 | 245.9 | 1.82 |
| E60 | 12.3 | 6.34 | 0.08 | 113.4 | 0.75 |
| F20/E30 | 18.1 | 8.58 | 0.06 | 231.8 | 1.36 |
| F30/E20 | 20.2 | 8.74 | 0.06 | 302.1 | 1.14 |
| F30/E40 | 15.8 | 9.17 | 0.05 | 490.4 | 1.75 |
| F20/E20 | 24.7 | 4.72 | 0.09 | 217.7 | 0.88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, Y.; Sun, D.; Deng, Z. An Analysis of the Vibration Transmission Properties of Assemblies Using Honeycomb Paperboard and Expanded Polyethylene. Materials 2023, 16, 6554. https://doi.org/10.3390/ma16196554
Xing Y, Sun D, Deng Z. An Analysis of the Vibration Transmission Properties of Assemblies Using Honeycomb Paperboard and Expanded Polyethylene. Materials. 2023; 16(19):6554. https://doi.org/10.3390/ma16196554
Chicago/Turabian StyleXing, Yueqing, Deqiang Sun, and Zelong Deng. 2023. "An Analysis of the Vibration Transmission Properties of Assemblies Using Honeycomb Paperboard and Expanded Polyethylene" Materials 16, no. 19: 6554. https://doi.org/10.3390/ma16196554
APA StyleXing, Y., Sun, D., & Deng, Z. (2023). An Analysis of the Vibration Transmission Properties of Assemblies Using Honeycomb Paperboard and Expanded Polyethylene. Materials, 16(19), 6554. https://doi.org/10.3390/ma16196554






