A Microscale Analysis of Thermal Residual Stresses in Composites with Different Ply Orientations
Abstract
:1. Introduction
2. Simulation Configuration
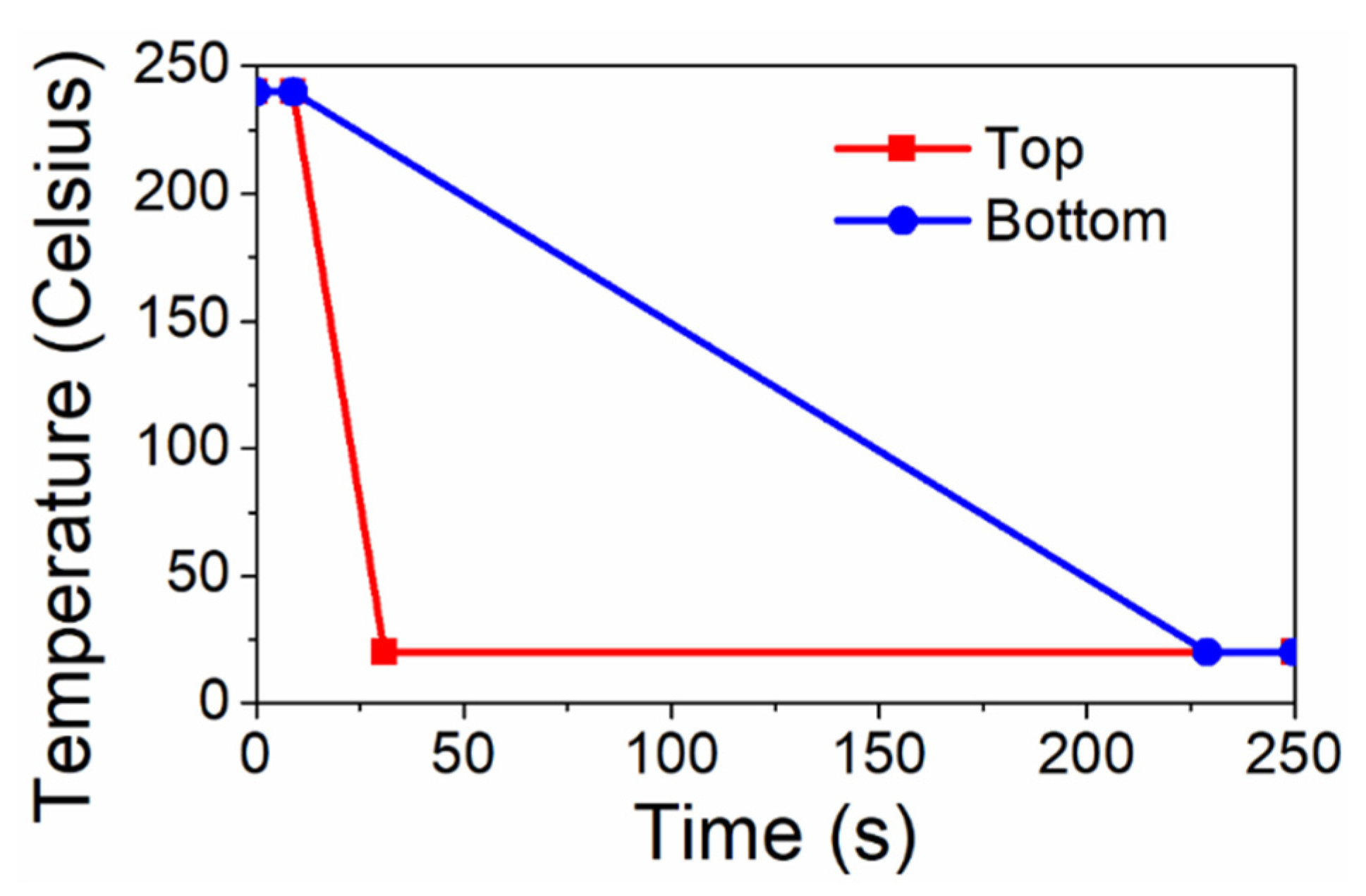
2.1. Forming of Thermoplastic Composite
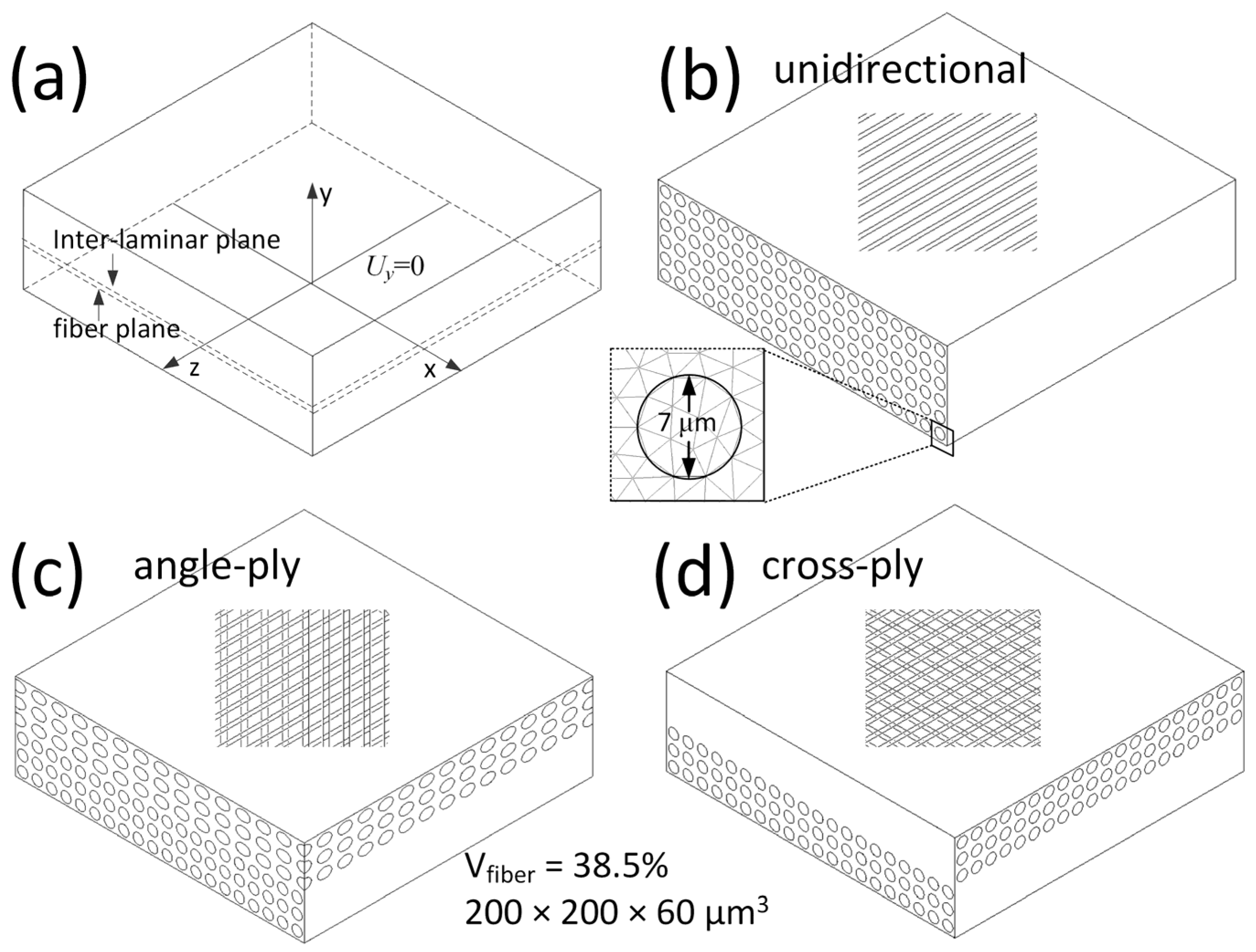
2.2. Simplified Geometric Model
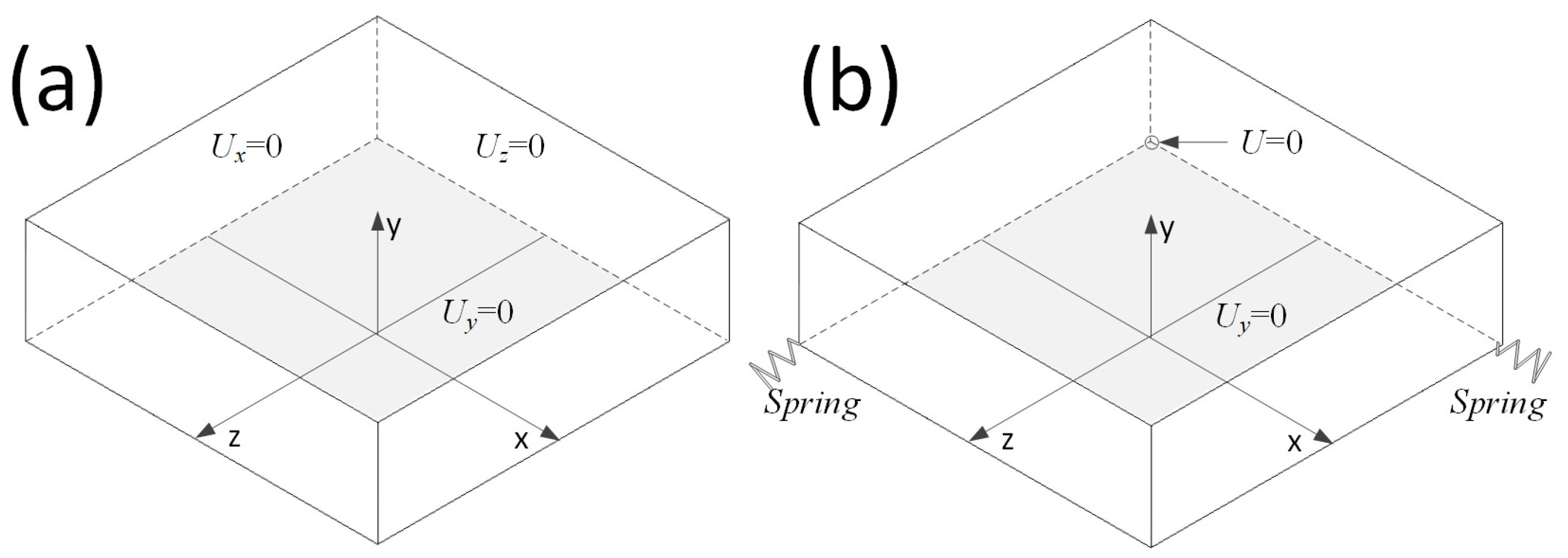
2.3. Boundary Condition
2.4. Finite Element Analysis
3. Results and Discussions
3.1. Deformation of Model
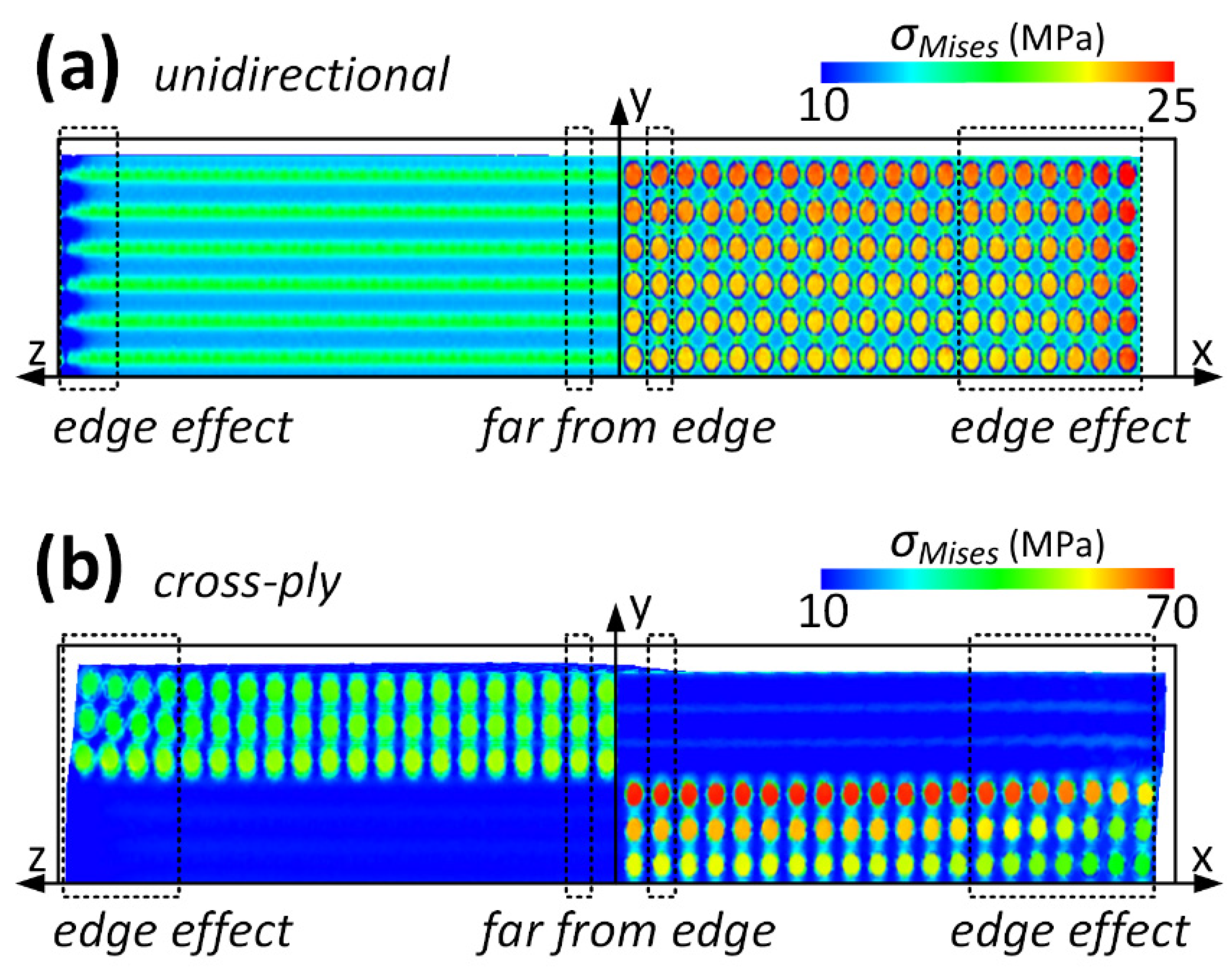
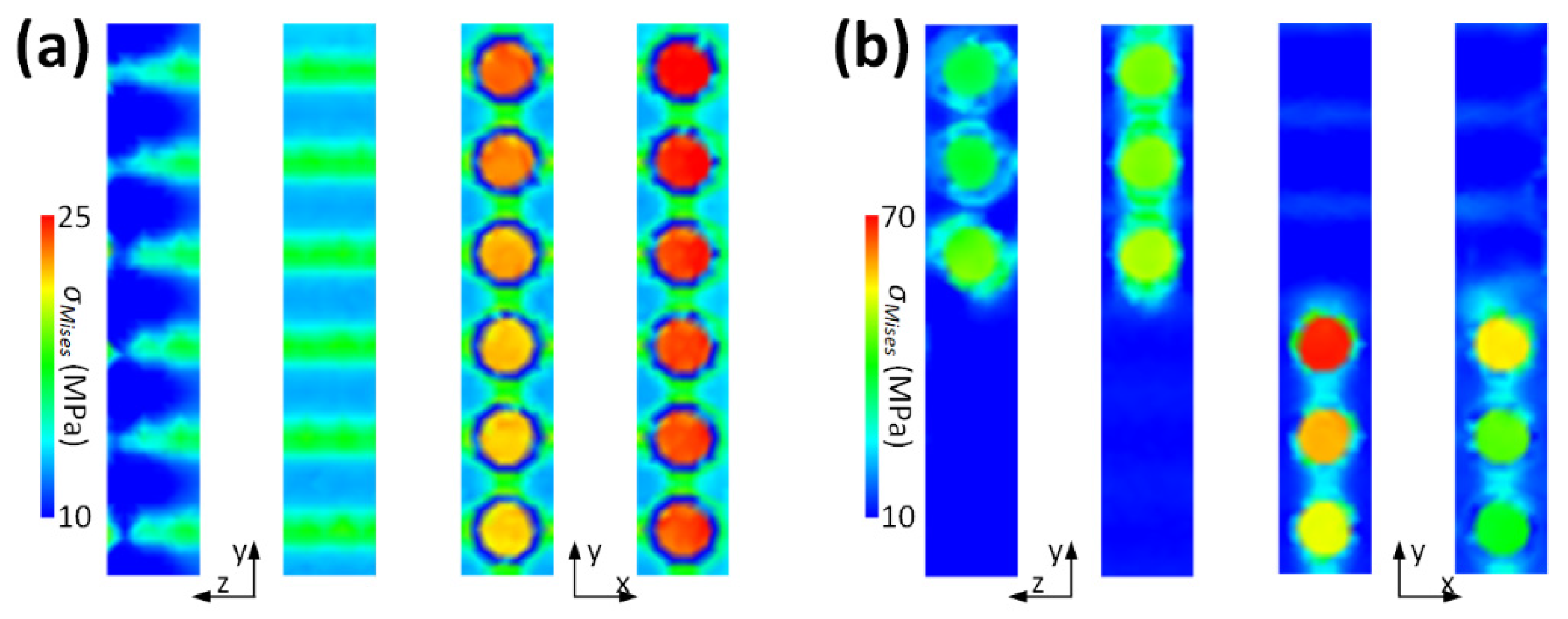
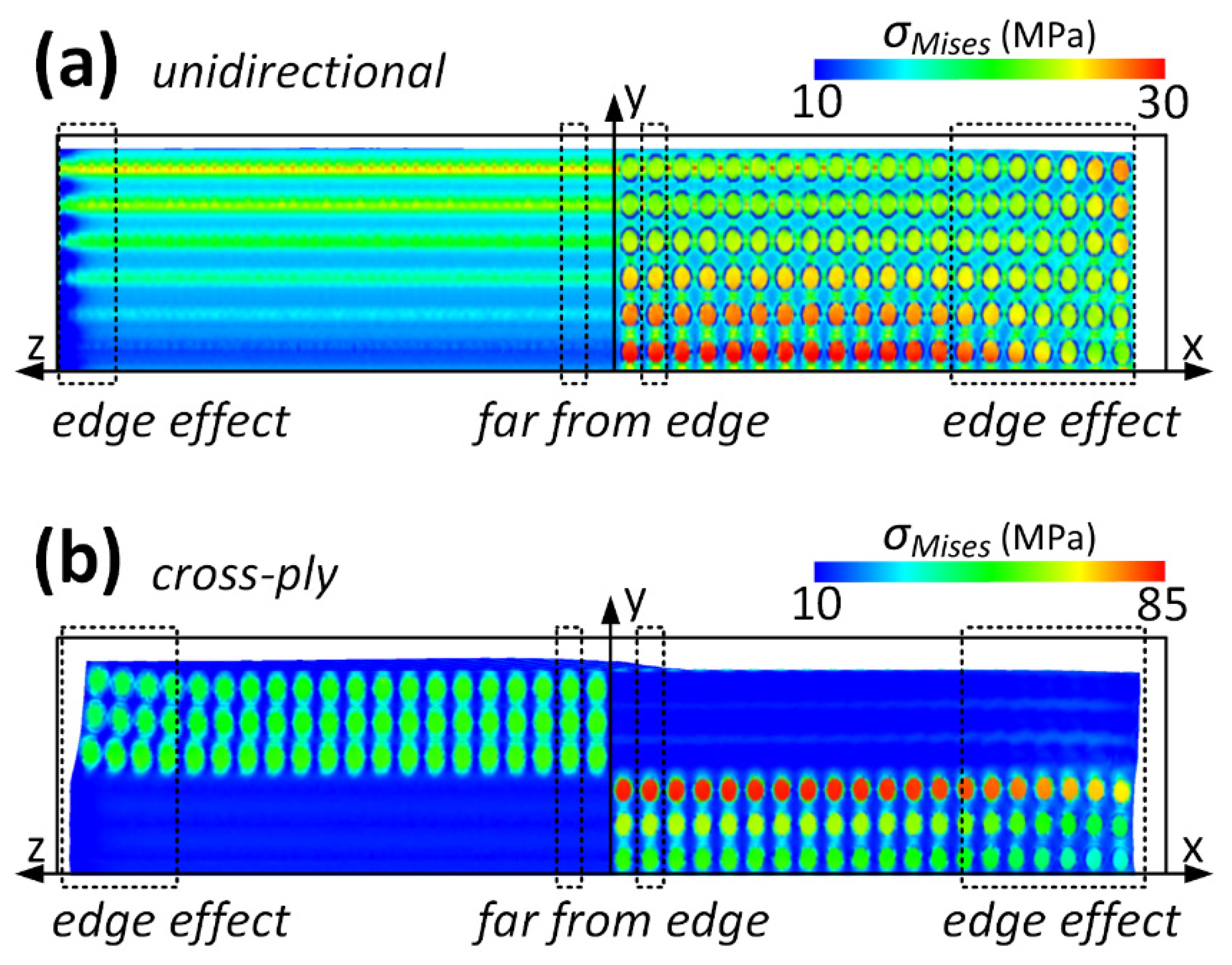
3.2. Edge Effect
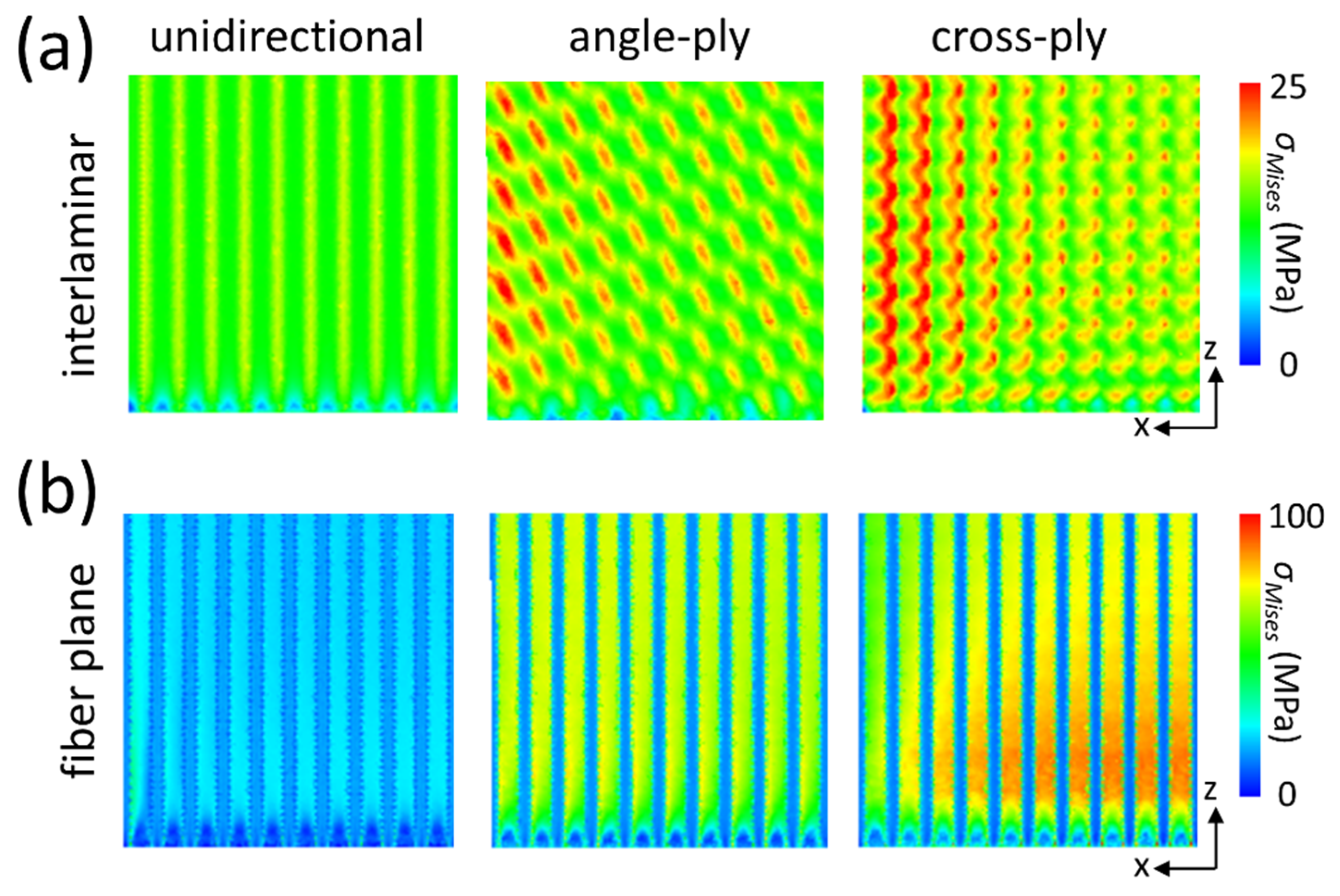
3.3. Interlaminar Stresses
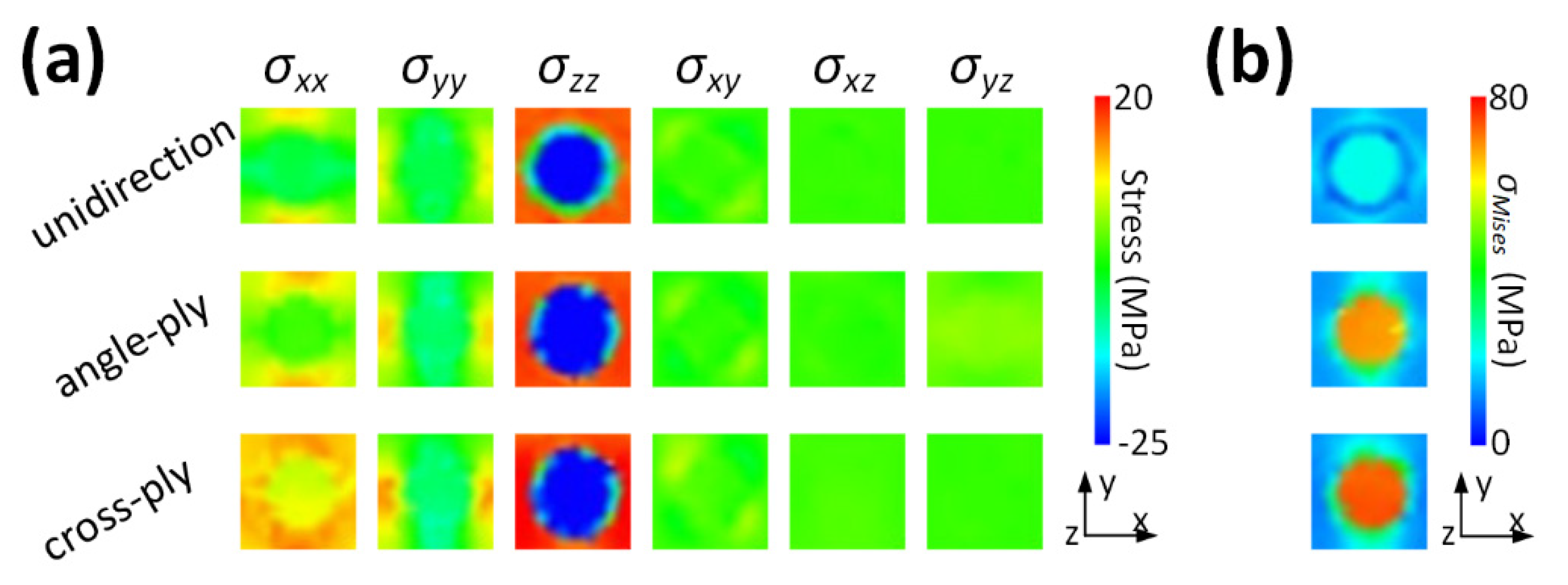
3.4. Influence of Ply Orientation
3.5. Influence of Cooling
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Fan, S.; Zhang, J.; Wang, B.; Chen, J.; Yang, W.; Liu, W.; Li, Y. A deep learning method for fast predicting curing process-induced deformation of aeronautical composite structures. Compos. Sci. Technol. 2023, 232, 109844. [Google Scholar] [CrossRef]
- Ji, M.; Zhang, H.; Wu, Q.; Zhang, H.; Huan, B.; Wang, G. Ply Angle Effects on Cavitating Flow Induced Structural Response Characteristics of the Composite Hydrofoils. Ocean Eng. 2023, 285, 115425. [Google Scholar]
- Takeda, N.; Kobayashi, S.; Ogihara, S.; Kobayashi, A. Experimental characterization of microscopic damage progress in quasi-isotropic CFRP laminates: Effect of interlaminar-toughened layers. Adv. Compos. Mater. 1998, 7, 183–199. [Google Scholar] [CrossRef]
- Andersons, J.; König, M. Dependence of fracture toughness of composite laminates on interface ply orientations and delamination growth direction. Compos. Sci. Technol. 2004, 64, 2139–2152. [Google Scholar] [CrossRef]
- Stango, R.J.; Wang, S.S. Process-induced residual thermal stresses in advanced fiber-reinforced composite laminates. J. Eng. Ind. 1984, 106, 48–54. [Google Scholar] [CrossRef]
- Wang, C.; Sun, C.T. Thermoelastic behavior of PEEK thermoplastic composite during cooling from forming temperatures. J. Compos. Mater. 1997, 31, 2230–2248. [Google Scholar] [CrossRef]
- Chapman, T.J.; Gillespie, J.W.; Pipes, R.B.; Manson, J.A.; Seferis, J.C. Prediction of process-induced residual stresses in thermoplastic composites. J. Compos. Mater. 1990, 24, 616–643. [Google Scholar] [CrossRef]
- Trende, A.; Astrom, B.T.; Nilsson, G. Modelling of residual stresses in compression moulded glass-mat reinforced thermoplastics. Compos. Part A Appl. Sci. Manufac. 2000, 31, 1241–1254. [Google Scholar] [CrossRef]
- Golanski, D.; Terada, K.; Kikuchi, N. Macro and micro scale modeling of thermal residual stresses in metal matrix composite surface layers by the homogenization method. Comput. Mech. 1997, 19, 188–202. [Google Scholar] [CrossRef]
- Zhao, L.G.; Warrior, N.A.; Long, A.C. A micromechanical study of residual stress and its effect on transverse failure in polymer–matrix composites. Int. J. Solids Struct. 2006, 43, 5449–5467. [Google Scholar] [CrossRef]
- Zhao, L.G.; Warrior, N.A.; Long, A.C. A thermo-viscoelastic analysis of process-induced residual stress in fibre-reinforced polymer-matrix composites. Mater. Sci. Eng. A 2007, 452, 483–498. [Google Scholar] [CrossRef]
- Lu, C.; Chen, P.; Yu, Q.; Gao, J.; Yu, B. Thermal residual stress distribution in carbon fiber/novel thermal plastic composite. Appl. Compos. Mater. 2008, 15, 157–169. [Google Scholar] [CrossRef]
- Chen, Q.; Chen, X.; Zhai, Z.; Zhu, X.; Yang, Z. Micromechanical modeling of viscoplastic behavior of laminated polymer composites with thermal residual stress effect. J. Eng. Mater. Technol. 2016, 138, 31005. [Google Scholar] [CrossRef]
- Ballard, M.K.; Whitcomb, J.D. Effect of heterogeneity at the fiber–matrix scale on predicted free-edge stresses for a [0°/90°]s laminated composite subjected to uniaxial tension. J. Compos. Mater. 2019, 53, 625–639. [Google Scholar] [CrossRef]
- Ballard, M.K.; Whitcomb, J.D. Multiscale analysis of interlaminar stresses near a free-edge in a [±45/0/90]s laminate. J. Compos. Mater. 2020, 54, 1627–1638. [Google Scholar] [CrossRef]
- Wu, Q.; Zhai, H.; Yoshikawa, N.; Ogasawara, T. Localization simulation of a representative volume element with prescribed displacement boundary for investigating the thermal residual stresses of composite forming. Compos. Struct. 2020, 235, 111723. [Google Scholar] [CrossRef]
- Japan Society for Composite Materials. Composite Material Utilization Dictionary; Dictionary Publishing Center of Industry Research Committee: Tokyo, Japan, 2001. [Google Scholar]
- Wu, Q.; Ogasawara, T.; Yoshikawa, N.; Zhai, H. Stress evolution of amorphous thermoplastic plate during forming process. Materials 2018, 11, 464. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q.; Yoshikawa, N.; Morita, N.; Ogasawara, T. Investigation of residual stresses induced by composite forming using macro-micro simulation. J. Reinf. Plast. Compos. 2020, 39, 654–664. [Google Scholar] [CrossRef]
- Zhai, H.; Wu, Q.; Bai, T.; Yoshikawa, N.; Xiong, K.; Chen, C. Multi-scale finite element simulation of the thermoforming of a woven fabric glass fiber/ polyetherimide thermoplastic composite. J. Compos. Mater. 2023, 57, 2933–2954. [Google Scholar] [CrossRef]

| Property | Axial | Transverse |
|---|---|---|
| Density (g/cm3) | 1810 | |
| Specific heat capacity (JK−1kg−1) | 710 | |
| Thermal conductivity (Wm−1K−1) | 8.9 | 0.89 |
| Coefficient of thermal expansion (−−1) | −4.1 × 10−7 | 7 × 10−6 |
| Young’s modulus (GPa) | 290 | 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Wu, Q. A Microscale Analysis of Thermal Residual Stresses in Composites with Different Ply Orientations. Materials 2023, 16, 6567. https://doi.org/10.3390/ma16196567
Wang Y, Wu Q. A Microscale Analysis of Thermal Residual Stresses in Composites with Different Ply Orientations. Materials. 2023; 16(19):6567. https://doi.org/10.3390/ma16196567
Chicago/Turabian StyleWang, Yanfeng, and Qi Wu. 2023. "A Microscale Analysis of Thermal Residual Stresses in Composites with Different Ply Orientations" Materials 16, no. 19: 6567. https://doi.org/10.3390/ma16196567
APA StyleWang, Y., & Wu, Q. (2023). A Microscale Analysis of Thermal Residual Stresses in Composites with Different Ply Orientations. Materials, 16(19), 6567. https://doi.org/10.3390/ma16196567






