Study on the Dynamic Mechanical Properties of Ultrahigh-Performance Concrete under Triaxial Constraints
Abstract
:1. Introduction
2. True Triaxial Test
2.1. Sample Materials
2.2. Triaxial Test
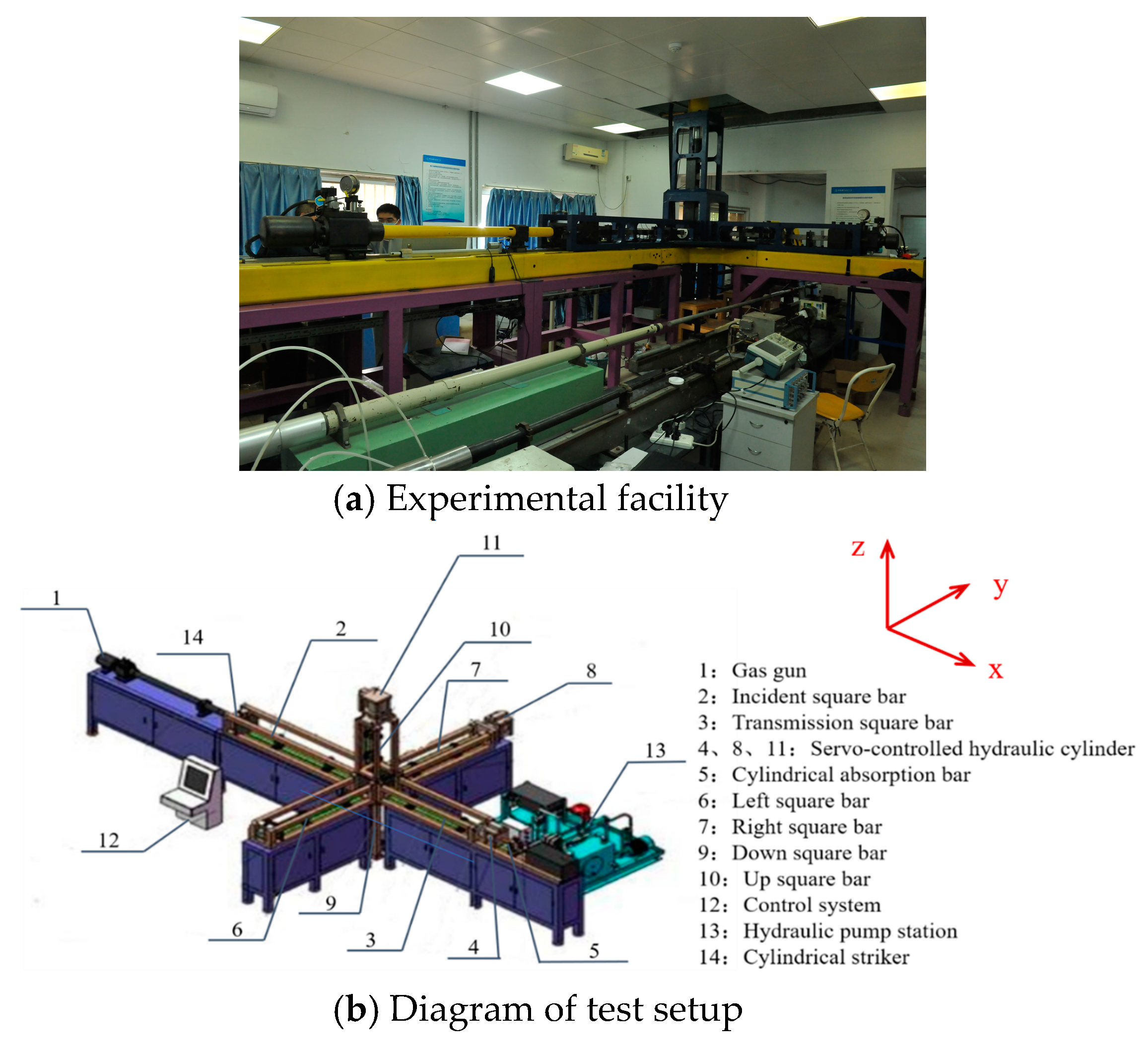
2.2.1. Test Equipment
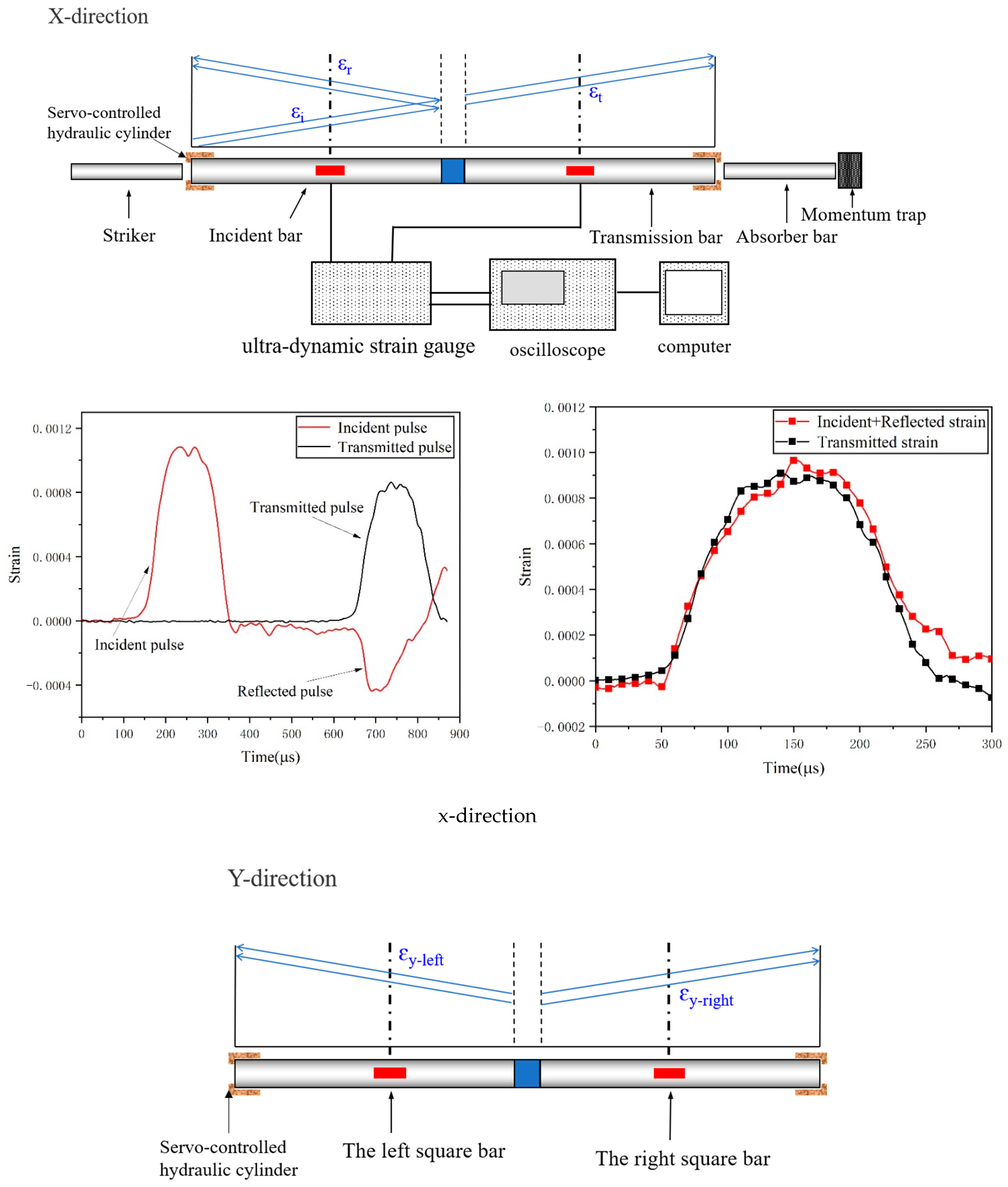
2.2.2. Testing Techniques
3. Test Results and Analysis
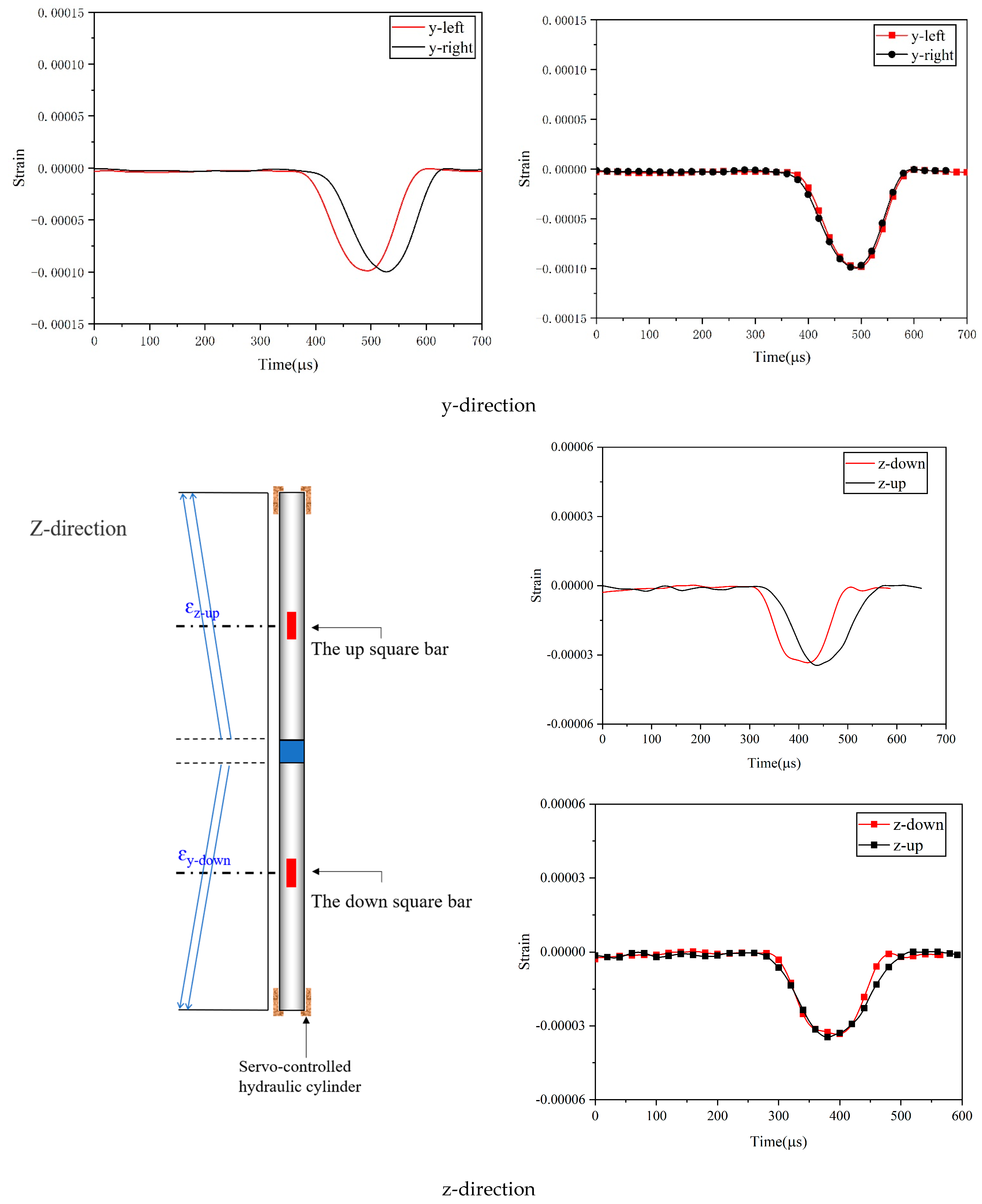
3.1. Test Waveform Analysis
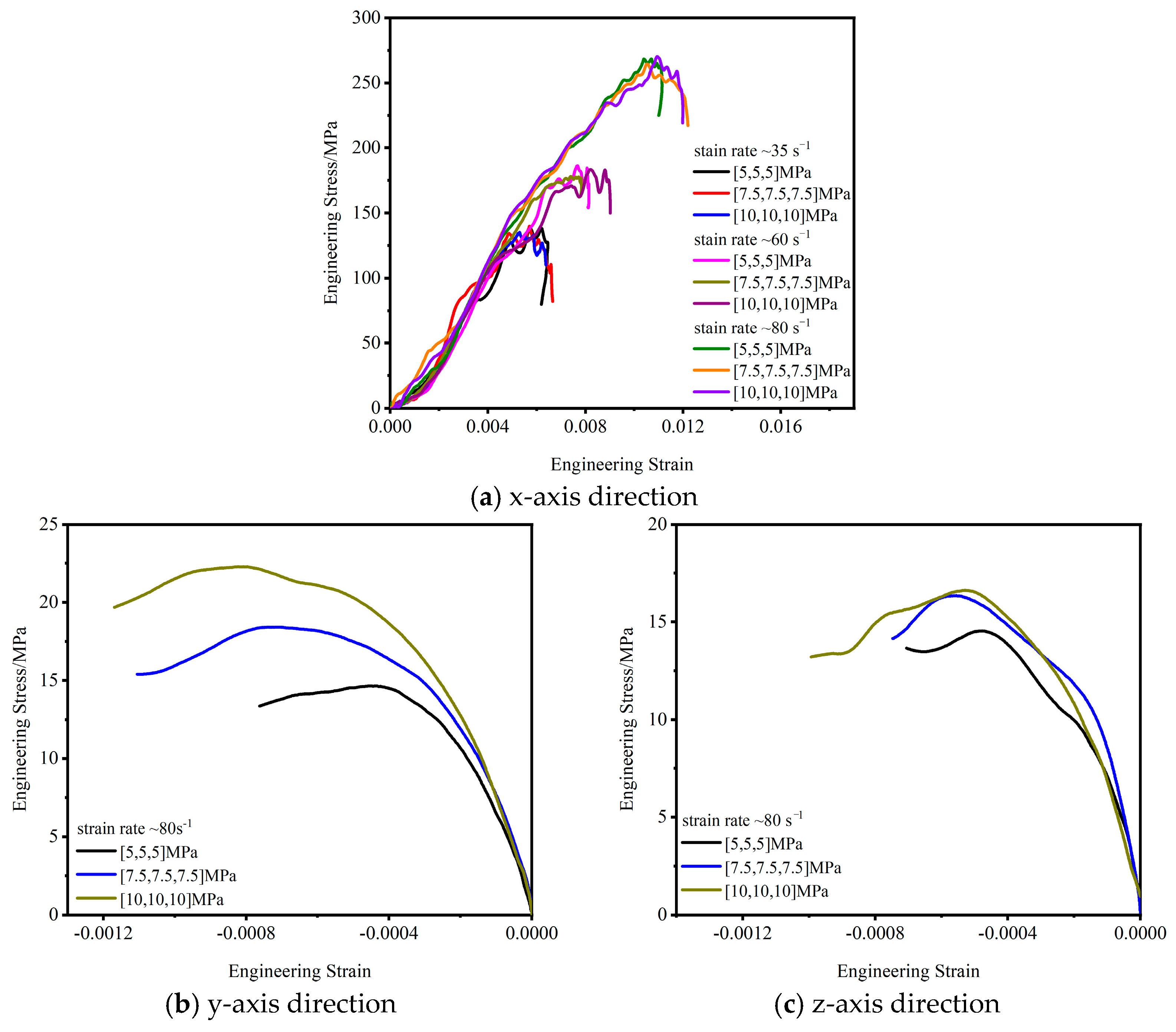
3.2. Dynamic Stress-Strain Relationship
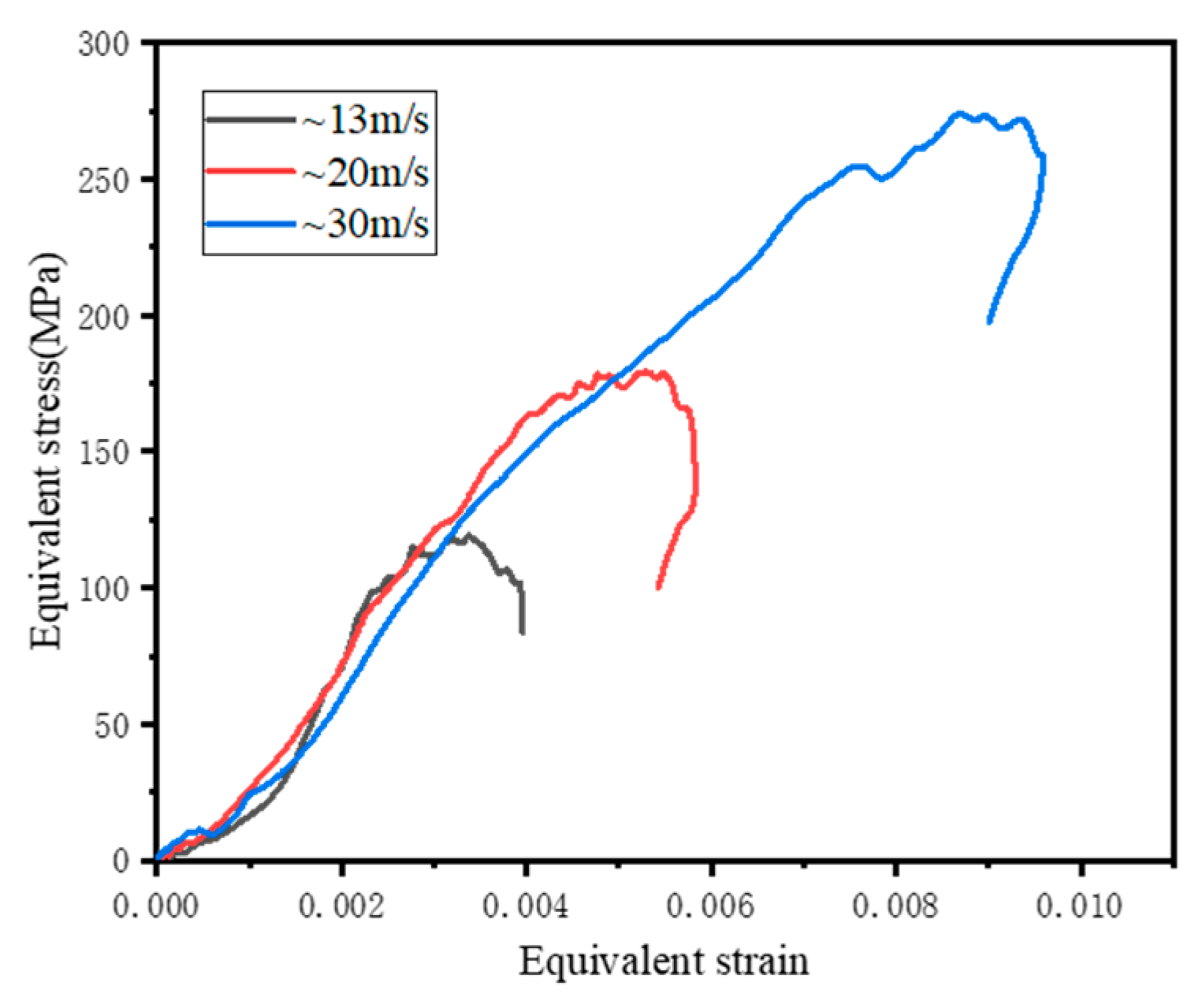
3.3. Relationship between Dynamic Equivalent Stress and Equivalent Strain
3.4. Dynamic Strength Enhancement Factor
4. Discussion
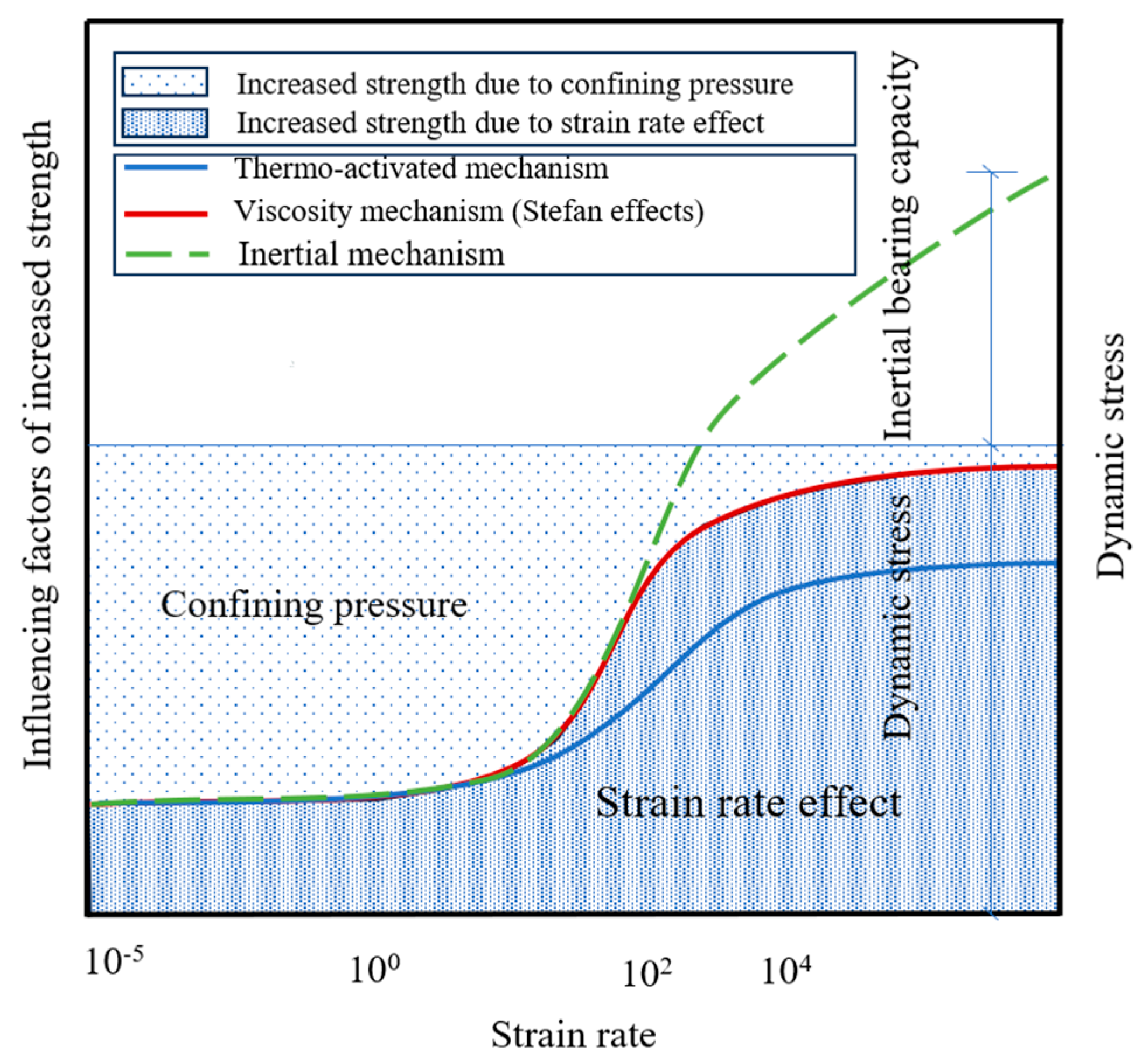
4.1. Analysis of the Dynamic Enhancement Mechanism under Confining Pressure
4.2. Failure Criterion
5. Conclusions
- The peak stress, peak strain, equivalent peak stress and equivalent peak strain of UHPC increase obviously with an increasing strain rate in the x-axis loading direction. The confining pressure has little influence on the dynamic response in the x-axis direction, but has a greater influence on the stress and strain in the y-axis and z-axis directions.
- The equivalent strength enhancement factor DIFc of UHPC under confining pressure is established and fitted. Under the same strain rate, the equivalent strength, DIFc, is larger than the DIF obtained from the 1D SHPB test. Based on this, the empirical formula of the DIFc of UHPC under confining pressure is fitted.
- There is a coupling effect between the enhancement caused by the confining pressure and the strain rate effect. When the strain rate is low, the extent of the dynamic strength increase caused by the strain rate effect is small, and the strength increase caused by the confining pressure is the main reason for the increase in concrete strength. As the strain rate increases, the weakening effect of the confining pressure gradually weakens, and the strength increase caused by the strain rate effect becomes the main reason for the increase in concrete strength.
- An improved three-parameter dynamic failure criterion is established and calibrated for this failure criterion.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Poinard, C.; Malecot, Y.; Daudeville, L. Damage of concrete in a very high stress state: Experimental investigation. Mater. Struct. 2010, 43, 15–29. [Google Scholar] [CrossRef]
- Yan, D.; Lin, G.; Chen, G. Dynamic Properties of Plain Concrete in Triaxial Stress State. ACI Mater. J. 2009, 106, 89–94. [Google Scholar]
- Wang, C.Z.; Guo, Z.H.; Zhang, X.Q. Experimental investigation of biaxial and triaxial compressive concrete strength. ACI Mater. J. 1987, 84, 92–100. [Google Scholar]
- Noori, A.; Shekarchi, M.; Moradian, M.; Moosavi, M. Behavior of steel fiber-reinforced cementitious mortar and high-performance concrete in triaxial loading. ACI Mater. J. 2015, 112, 95. [Google Scholar] [CrossRef]
- Ren, G.M.; Wu, H.; Fang, Q.; Liu, J.Z.; Gong, Z.M. Triaxial compressive behavior of UHPCC and applications in the projectile impact analyses. Constr. Build. Mater. 2016, 113, 1–14. [Google Scholar] [CrossRef]
- Lu, X.; Hsu, C.T.T. Behavior of high strength concrete with and without steel fiber reinforcement in triaxial compression. Cem. Concr. Res. 2006, 36, 1679–1685. [Google Scholar] [CrossRef]
- Chi, Y.; Xu, L.; Mei, G.; Hu, N.; Su, J. A unified failure envelope for hybrid fibre reinforced concrete subjected to true triaxial compression. Compos. Struct. 2014, 109, 31–40. [Google Scholar] [CrossRef]
- Sirijaroonchai, K.; EI-Tawil, S. Parra-Montesinos, Behavior of high performance fiber reinforced cement composites under multi-axial compressive loading, Cem. Concr. Compos. 2010, 32, 62–72. [Google Scholar] [CrossRef]
- Jiang, J.; Xiao, P.; Li, B. True-triaxial compressive behaviour of concrete under passive confinement. Constr. Build. Mater. 2017, 156, 584–598. [Google Scholar] [CrossRef]
- Imran, I.; Pantazopoulou, S.J. Experimental study of plain concrete under triaxial stress. ACI Mater. J. 1996, 93, 589–601. [Google Scholar]
- Vu, X.H.; Daudeville, L.; Malecot, Y. Effect of coarse aggregate size and cement paste volume on concrete behavior under high triaxial compression loading. Constr. Build. Mater. 2011, 25, 3941–3949. [Google Scholar] [CrossRef]
- Piotrowska, E.; Malecot, Y.; Ke, Y. Experimental investigation of the effect of coarse aggregate shape and composition on concrete triaxial behavior. Mech. Mater. 2014, 79, 45–57. [Google Scholar] [CrossRef]
- Frew, D.J.; Akers, S.A.; Chen, W.; Green, M.L. Development of a dynamic triaxial Kolsky bar. Meas. Sci. Technol. 2010, 21, 105704. [Google Scholar] [CrossRef]
- Gran, J.K.; Florence, A.L.; Colton, J.D. Dynamic triaxial tests of high-strength concrete. J. Eng. Mech. 1989, 115, 891–904. [Google Scholar] [CrossRef]
- Zeng, S.; Ren, X.; Li, J. Triaxial behavior of concrete subjected to dynamic compression. J. Struct. Eng. 2013, 139, 1582–1592. [Google Scholar] [CrossRef]
- Xue, Z.; Hu, S. Dynamic behavior of cement mortar under active confinement. Explos. Shock. Waves 2008, 6, 561–564. (In Chinese) [Google Scholar]
- Malvern, L.E.; Jenkins, D. Dynamic Testing of Laterally Confined Concrete; Deptartment of Information Sciences, California Insti-tute of Technology: Pasadena, CA, USA, 1990. [Google Scholar]
- Gary, G.; Bailly, P. Behaviour of quasi-brittle material at high strain rate. Experiment and modelling. Eur. J. Mech. A Solids 1998, 17, 403–420. [Google Scholar] [CrossRef]
- Fujikake, K.; Mori, K.; Uebayashi, K.; Ohno, T.; Mizuncr, J. Dynamic properties of concrete materials with high rates of triaxial compressive loads. WIT Trans. Built Environ. 2000, 48. [Google Scholar] [CrossRef]
- Fu, Q.; Xu, W.; Li, D.; Li, N.; Niu, D.; Zhang, L.; Guo, B.; Zhang, Y. Dynamic compressive behaviour of hybrid basalt-polypropylene fibre-reinforced concrete under confining pressure: Experimental characterisation and strength criterion. Cem. Concr. Compos. 2021, 118, 103954. [Google Scholar]
- Liu, P.; Zhou, X.; Qian, Q. Experimental investigation of rigid confinement effects of radial strain on dynamic mechanical properties and failure modes of concrete. Int. J. Min. Sci. Technol. 2021, 31, 939–951. [Google Scholar] [CrossRef]
- Li, Q.M.; Meng, H. About the dynamic strength enhancement of concrete-like materials in a split Hopkinson pressure bar test. Int. J. Solids Struct. 2003, 40, 343–360. [Google Scholar] [CrossRef]
- Zhang, Q.B.; Zhao, J. A review of dynamic experimental techniques and mechanical behaviour of rock materials. Rock Mech. Rock Eng. 2014, 47, 1411–1478. [Google Scholar]
- Cui, J.; Hao, H.; Shi, Y.; Zhang, X.; Huan, S. Volumetric properties of concrete under true triaxial dynamic compressive loadings. J. Mater. Civ. Eng. 2019, 31, 04019126. [Google Scholar] [CrossRef]
- Liu, P.; Liu, K.; Zhang, Q.B. Experimental characterisation of mechanical behaviour of concrete-like materials under multiaxial confinement and high strain rate. Constr. Build. Mater. 2020, 258, 119638. [Google Scholar]
- Xu, S.; Shan, J.; Zhang, L.; Zhou, L.; Gao, G.; Hu, S.; Wang, P. Dynamic compression behaviors of concrete under true triaxial confinement: An experimental technique. Mech. Mater. 2020, 140, 103220. [Google Scholar]
- Liu, P.; Liu, J.; Bi, J. Experimental and theoretical study of dynamic mechanical behavior of concrete subjected to triaxial confining and impact loads. J. Build. Eng. 2023, 64, 105715. [Google Scholar] [CrossRef]
- Lu, F.; Lin, Y.; Wang, X.; Lu, L.; Chen, R. A theoretical analysis about the influence of interfacial friction in SHPB tests. Int. J. Impact Eng. 2015, 79, 95–101. [Google Scholar] [CrossRef]
- Cadoni, E.; Albertini, C. Modified Hopkinson bar technologies applied to the high strain rate rock tests. In Advances in Rock Dynamics and Applications; CRC Press: Boca Raton, FL, USA, 2011; pp. 79–104. [Google Scholar]
- Lu, Y.B.; Li, Q.M. Appraisal of pulse-shaping technique in split Hopkinson pressure bar tests for brittle materials. Int. J. Prot. Struct. 2010, 1, 363–390. [Google Scholar] [CrossRef]
- Li, S.H.; Zhu, W.C.; Niu, L.L.; Yu, M.; Chen, C.F. Dynamic characteristics of green sandstone subjected to repetitive impact loading: Phenomena and mechanisms. Rock Mech. Rock Eng. 2018, 51, 1921–1936. [Google Scholar]
- Wang, R.; Zhu, H.X. Theory of Plasticity; Science China Press Ltd.: Beijing, China, 1998; pp. 93–101. [Google Scholar]
- Ren, G.M.; Wu, H.; Fang, Q.; Liu, J.Z. Effects of steel fiber content and type on dynamic compressive mechanical properties of UHPCC. Constr. Build. Mater. 2018, 164, 29–43. [Google Scholar] [CrossRef]
- Comite Euro-International du Beton. Fib Model Code for Concrete Structures 2010; Redwood Books: Trowbridge, UK, 2013. [Google Scholar]
- Tedesco, J.W.; Ross, C.A. Strain-rate-dependent constitutive equations for concrete. ASME J. Press. Vessel Technol. 1998, 120, 398–405. [Google Scholar] [CrossRef]
- Qi, C.Z.; Wang, M.Y.; Qian, Q.H. Strain-rate effects on the strength and fragmentation size of rocks. Int. J. Impact Eng. 2009, 36, 1355–1364. [Google Scholar] [CrossRef]
- Qi, C.Z.; Qian, Q.H. Physical mechanism of dependence of material strength on strain rate for rock-like material. Chin. J. Rock Mech. Eng. 2003, 22, 177–181. [Google Scholar]
- Rossi, P. A physical phenomenon which can explain the mechanical behaviour of concrete under high strain rates. Mater. Struct. 1991, 24, 422–424. [Google Scholar] [CrossRef]
- Bresler, B.; Pister, K.S. Strength of concrete under combined stresses. ACI Struct. J. 1958, 55, 321–345. [Google Scholar]






| Cement | Silica Fume | Fine Aggregate | Superplasticizer | Water | Steel Fibers | |
|---|---|---|---|---|---|---|
| U0.5 | 850 | 200 | 1000 | 40 | 150 | 39 |
| U1 | 850 | 200 | 1000 | 40 | 150 | 79 |
| U2 | 850 | 200 | 1000 | 40 | 150 | 158 |
| Measured Strength | Average Strength | |||
|---|---|---|---|---|
| U0.5 | 110.4 | 110.0 | 115.6 | 112.0 |
| U1 | 126.4 | 130.5 | 131.0 | 129.3 |
| U2 | 146.4 | 150.2 | 149.8 | 148.8 |
| Sample No. | Strain Rate (s−1) | Confining Pressure (MPa) | Dynamic Pressure (MPa) | ||||
|---|---|---|---|---|---|---|---|
| x | y | z | x | y | z | ||
| U0.5 | ~35 | 5.0 | 5.0 | 5.0 | 124.8 | 7.2 | 5.4 |
| 7.5 | 7.5 | 7.5 | 118.8 | 9.3 | 10.0 | ||
| 10.0 | 10.0 | 10.0 | 119.1 | 11.0 | 8.1 | ||
| ~60 | 5.0 | 5.0 | 5.0 | 183.6 | 8.9 | 8.3 | |
| 7.5 | 7.5 | 7.5 | 181.7 | 11.2 | 9.4 | ||
| 10.0 | 10.0 | 10.0 | 183.1 | 13.9 | 10.8 | ||
| ~80 | 5.0 | 5.0 | 5.0 | 257.2 | 14.7 | 15.9 | |
| 7.5 | 7.5 | 7.5 | 263.6 | 17.4 | 18.1 | ||
| 10.0 | 10.0 | 10.0 | 264.4 | 22.5 | 17.3 | ||
| U1 | ~35 | 5.0 | 5.0 | 5.0 | 138.0 | 7.8 | 7.8 |
| 7.5 | 7.5 | 7.5 | 143.2 | 7.8 | 9.86 | ||
| 10.0 | 10.0 | 10.0 | 144.9 | 8.5 | 11.8 | ||
| ~60 | 5.0 | 5.0 | 5.0 | 187.7 | 10.2 | 8.8 | |
| 7.5 | 7.5 | 7.5 | 188.4 | 10.9 | 10.8 | ||
| 10.0 | 10.0 | 10.0 | 190.7 | 11.7 | 14.0 | ||
| ~80 | 5.0 | 5.0 | 5.0 | 273.7 | 15.8 | 15.7 | |
| 7.5 | 7.5 | 7.5 | 272.3 | 14.9 | 17.2 | ||
| 10.0 | 10.0 | 10.0 | 283.1 | 16.2 | 16.1 | ||
| U2 | ~35 | 5.0 | 5.0 | 5.0 | 153.1 | 7.3 | 11.1 |
| 7.5 | 7.5 | 7.5 | 151.4 | 9.8 | 8.2 | ||
| 10.0 | 10.0 | 10.0 | 154.1 | 14.5 | 8.9 | ||
| ~60 | 5.0 | 5.0 | 5.0 | 188.5 | 11.4 | 10.6 | |
| 7.5 | 7.5 | 7.5 | 192.3 | 11.8 | 11.0 | ||
| 10.0 | 10.0 | 10.0 | 185.6 | 12.1 | 8.6 | ||
| ~80 | 5.0 | 5.0 | 5.0 | 288.1 | 16.8 | 18.5 | |
| 7.5 | 7.5 | 7.5 | 288.8 | 19.4 | 20.2 | ||
| 10.0 | 10.0 | 10.0 | 290.0 | 18.6 | 18.0 | ||
| Refs | DIF(DIFc) Relations |
|---|---|
| CEB mode [34] | |
| Tedesco & Ross [35] | |
| Li & Meng [22] | |
| Xu & Shan [26] | |
| Ren & Wu [33] | |
| Present study |
| Strain Rate/s−1 | a | b | c | R2 |
|---|---|---|---|---|
| 35 | −0.69 | −4.31 | −3.82 | 0.84 |
| 60 | −0.32 | −2.28 | −1.12 | 0.91 |
| 80 | −1.21 | −4.02 | −1.76 | 0.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Mao, J.; Yu, X.; Zhou, B.; Wang, L. Study on the Dynamic Mechanical Properties of Ultrahigh-Performance Concrete under Triaxial Constraints. Materials 2023, 16, 6591. https://doi.org/10.3390/ma16196591
Zhang W, Mao J, Yu X, Zhou B, Wang L. Study on the Dynamic Mechanical Properties of Ultrahigh-Performance Concrete under Triaxial Constraints. Materials. 2023; 16(19):6591. https://doi.org/10.3390/ma16196591
Chicago/Turabian StyleZhang, Wei, Jize Mao, Xiao Yu, Bukui Zhou, and Limei Wang. 2023. "Study on the Dynamic Mechanical Properties of Ultrahigh-Performance Concrete under Triaxial Constraints" Materials 16, no. 19: 6591. https://doi.org/10.3390/ma16196591
APA StyleZhang, W., Mao, J., Yu, X., Zhou, B., & Wang, L. (2023). Study on the Dynamic Mechanical Properties of Ultrahigh-Performance Concrete under Triaxial Constraints. Materials, 16(19), 6591. https://doi.org/10.3390/ma16196591






